2 Math expressions

Mathematical expressions are written using LaTeX code.

Equations must be written between $ $ or $$ $$. For inline equations you must use $<equation>$.

2.1 Inline equations

My first inline equation: x=−b±√b2−4ac2a.

My first inline equation: $x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}$.

2.2 Math environments

2.2.1 Equation

Equation (2.1)

θ∗|L∗,δ2,Y,σ2u∼N(B−1W′L∗,δ2B−1)

The equation reference is defined by \@ref(eq:name) which must defined in equation as (\#eq:name)

Equation \@ref(eq:ncrep)

\begin{equation}
    \theta^{*}|L^{*}, \delta^{2},Y,\sigma^{2}_{u} \sim N\left(B^{-1}W'L^{*},\delta^{2}B^{-1} \right)
    (\#eq:ncrep)
\end{equation}

2.2.2 Matrix

Matrix (2.2)

Xm,n=(x1,1x1,2⋯x1,nx2,1x2,2⋯x2,n⋮⋮⋱⋮xm,1xm,2⋯xm,n)


Matrix \@ref(eq:matex)


\begin{equation}
X_{m,n} = 
\begin{pmatrix}
  x_{1,1} & x_{1,2} & \cdots & x_{1,n} \\
  x_{2,1} & x_{2,2} & \cdots & x_{2,n} \\
  \vdots  & \vdots  & \ddots & \vdots  \\
  x_{m,1} & x_{m,2} & \cdots & x_{m,n} 
\end{pmatrix}
(\#eq:matex)
\end{equation}

An extensive list of examples and mathematical symbols can be viewed in the references.

2.3 LyX for mathematical expressions

We can use LyX to insert any equation or matrix in your report. Just copy and paste the LyX code (Figure 2.1 into your R Markdown file.

To view your LyX code, follow these steps after open the LyX: View > Source Pane.

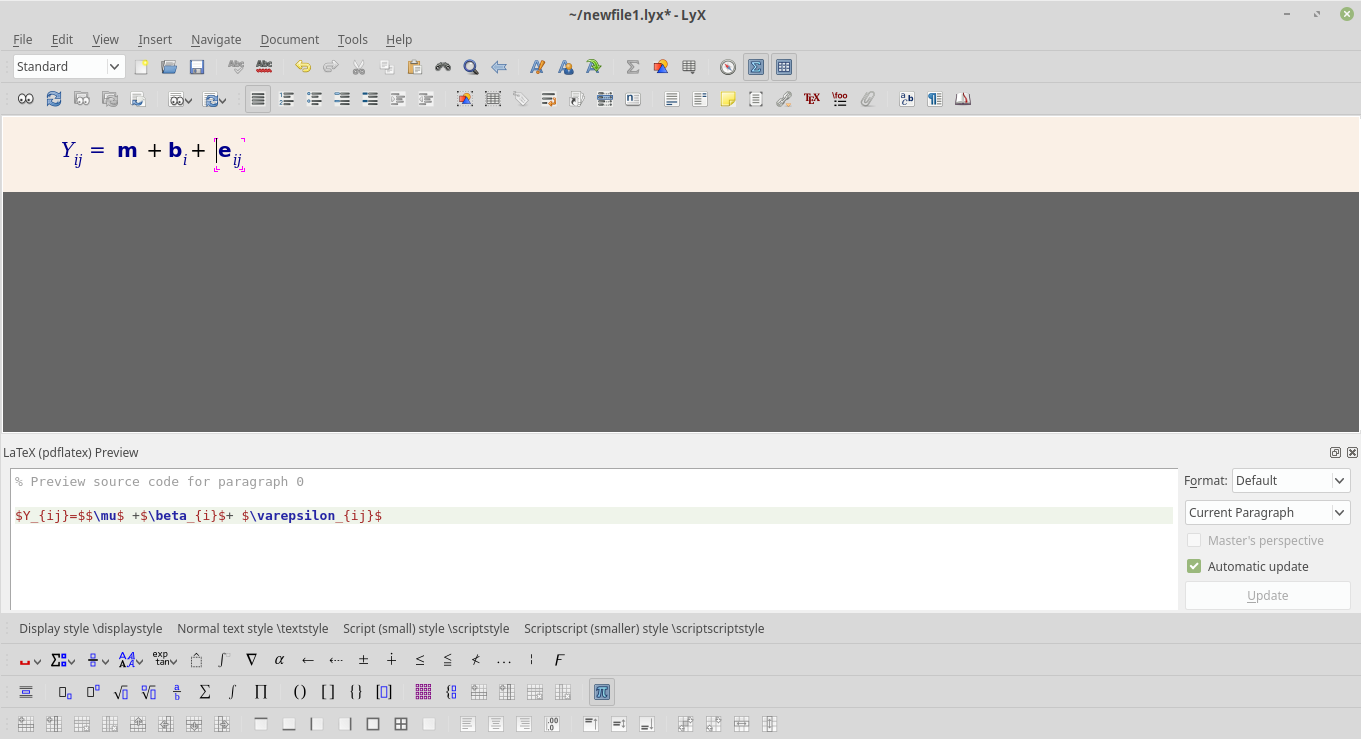
LyX code

Figure 2.1: LyX code

My LyX code is Yij=μ +βi+ εij

My LyX code is $Y_{ij}=$$\mu$ +$\beta_{i}$+ $\varepsilon_{ij}$

For matrices or equations with references, just add the equation environment.

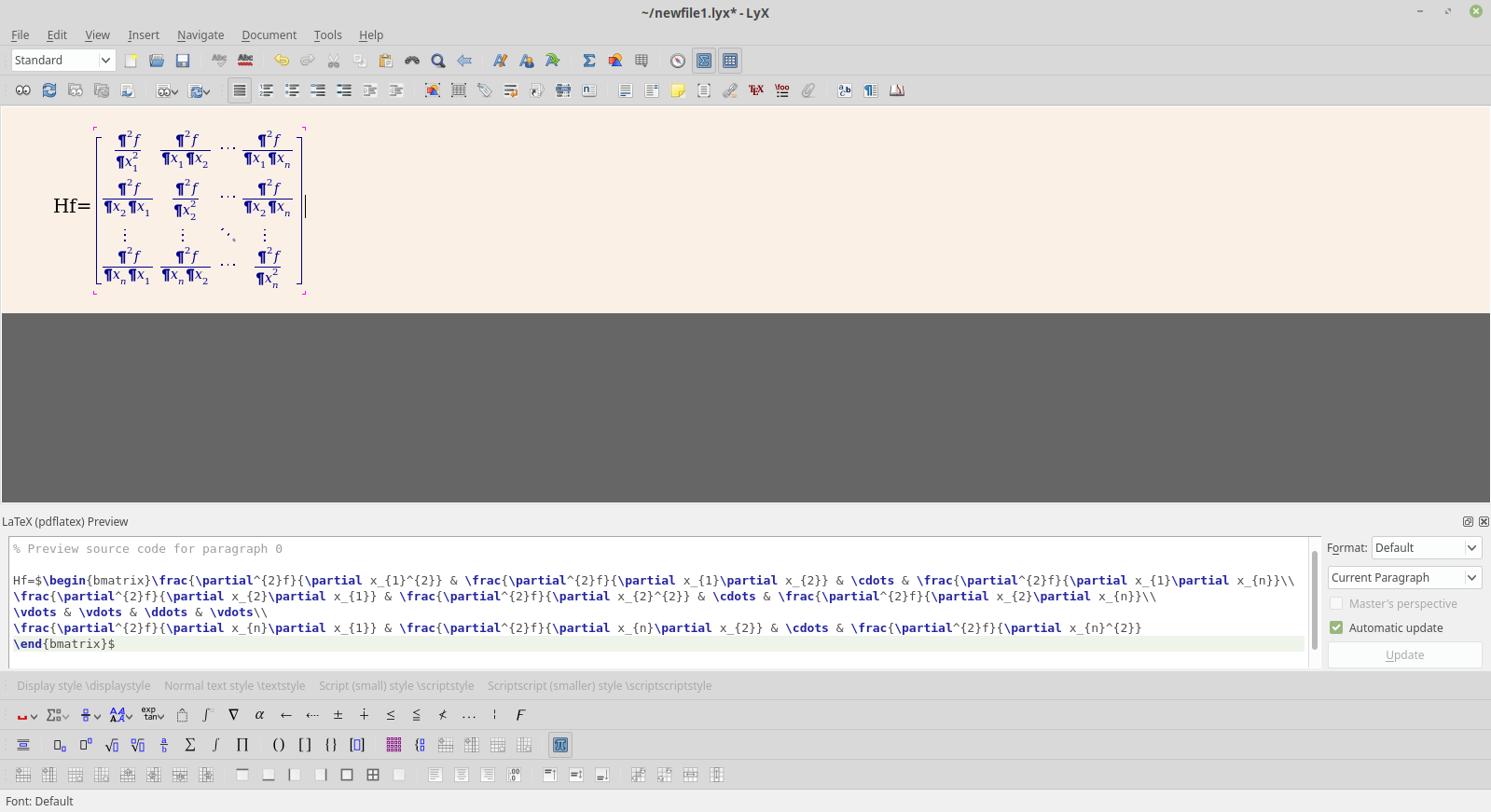
LyX code

Figure 2.2: LyX code

My Hessian matrix (Figure (2.3))

Hf=[∂2f∂x21∂2f∂x1∂x2⋯∂2f∂x1∂xn∂2f∂x2∂x1∂2f∂x22⋯∂2f∂x2∂xn⋮⋮⋱⋮∂2f∂xn∂x1∂2f∂xn∂x2⋯∂2f∂x2n]

My Hessian matrix (Figure \@ref(eq:lyxmat))

\begin{equation}
Hf=\begin{bmatrix}\frac{\partial^{2}f}{\partial x_{1}^{2}} & \frac{\partial^{2}f}{\partial x_{1}\partial x_{2}} & \cdots & \frac{\partial^{2}f}{\partial x_{1}\partial x_{n}}\\
\frac{\partial^{2}f}{\partial x_{2}\partial x_{1}} & \frac{\partial^{2}f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2}f}{\partial x_{2}\partial x_{n}}\\
\vdots & \vdots & \ddots & \vdots\\
\frac{\partial^{2}f}{\partial x_{n}\partial x_{1}} & \frac{\partial^{2}f}{\partial x_{n}\partial x_{2}} & \cdots & \frac{\partial^{2}f}{\partial x_{n}^{2}}
\end{bmatrix}
(\#eq:lyxmat)
\end{equation}