6  Weighing Terms

needs(hcandersenr, tidyverse, tidytext)

A common task in the quantitative analysis of text is to determine how documents differ from each other concerning word usage. This is usually achieved by identifying words that are particular for one document but not for another. These words are referred to by Monroe, Colaresi, and Quinn (2008) as fighting words or, by Grimmer, Roberts, and Stewart (2022), discriminating words. To use the techniques that will be presented today, an already existing organization of the documents is assumed.

The most simple approach to determine which words are more correlated to a certain group of documents is by merely counting them and determining their proportion in the document groups. For illustratory purposes, I use fairy tales from H.C. Andersen which are contained in the hcandersenr package.

fairytales <- hcandersen_en |> 
  filter(book %in% c("The princess and the pea",
                     "The little mermaid",
                     "The emperor's new suit"))

fairytales_tidy <- fairytales |> 
  unnest_tokens(token, text)

6.1 Counting words per document

For a first, naive analysis, I can merely count the times the terms appear in the texts. Since the text is in tidytext format, I can do so using means from traditional tidyverse packages. I will then visualize the results with a bar plot.

fairytales_top10 <- fairytales_tidy |> 
  group_by(book) |> 
  count(token) |> 
  slice_max(n, n = 10, with_ties = FALSE)

fairytales_top10 |> 
  ggplot()  +
  geom_col(aes(x = n, y = reorder_within(token, n, book))) +
  scale_y_reordered() +
  labs(y = "token") +
  facet_wrap(vars(book), scales = "free") +
  theme(strip.text.x = element_blank())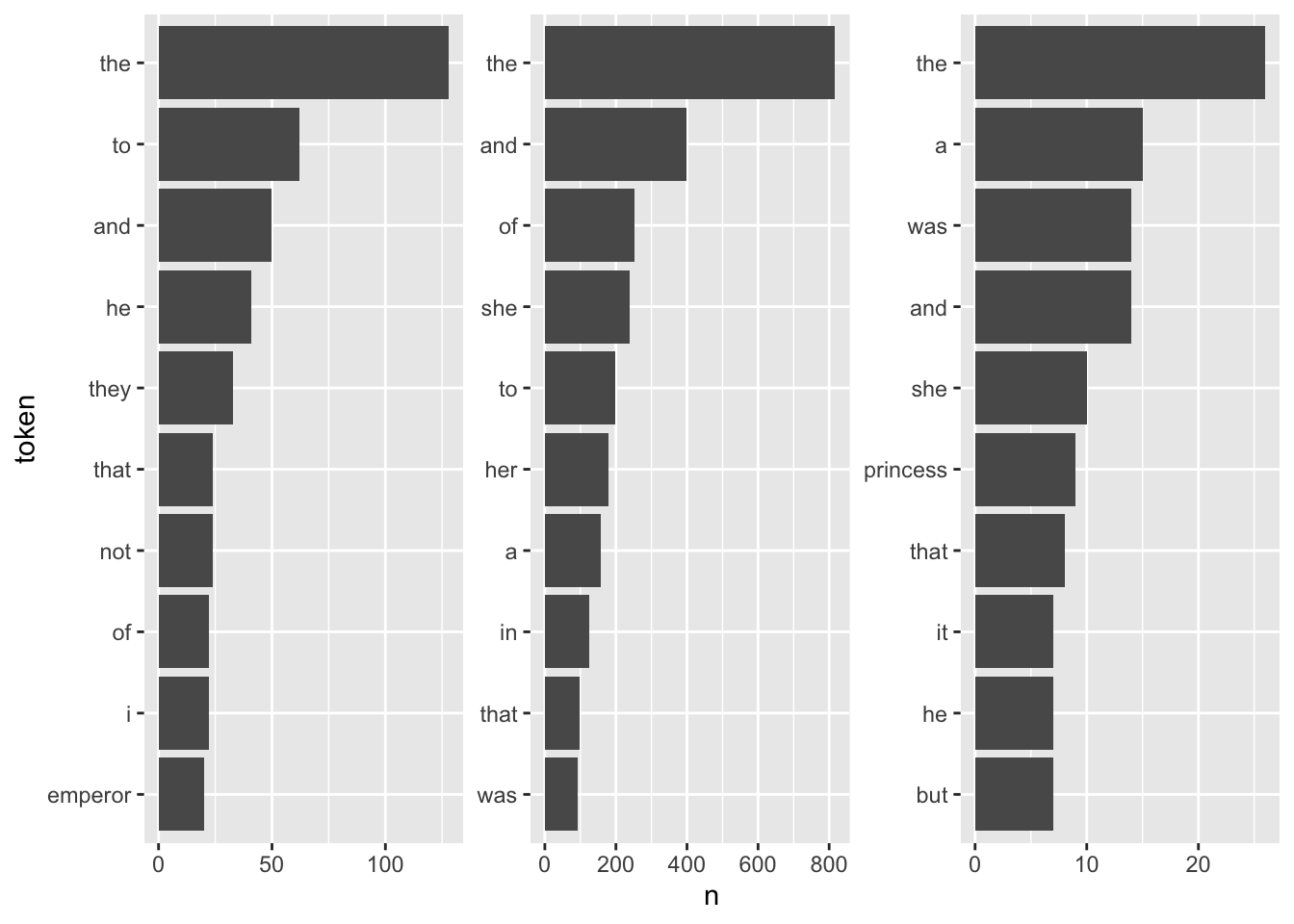

It is quite hard to draw inferences on which plot belongs to which book since the plots are crowded with stopwords. However, there are pre-made stopword lists I can harness to remove some of this “noise” and perhaps catch a bit more signal for determining the books.

# get_stopwords()
# stopwords_getsources()
# stopwords_getlanguages(source = "snowball")

fairytales_top10_nostop <- fairytales_tidy |> 
  anti_join(get_stopwords(), by = c("token" = "word")) |> 
  group_by(book) |> 
  count(token) |> 
  slice_max(n, n = 10, with_ties = FALSE)

fairytales_top10_nostop |> 
  ggplot()  +
  geom_col(aes(x = n, y = reorder_within(token, n, book))) +
  scale_y_reordered() +
  labs(y = "token") +
  facet_wrap(vars(book), scales = "free_y") +
  scale_x_continuous(breaks = scales::pretty_breaks()) +
  theme(strip.text.x = element_blank())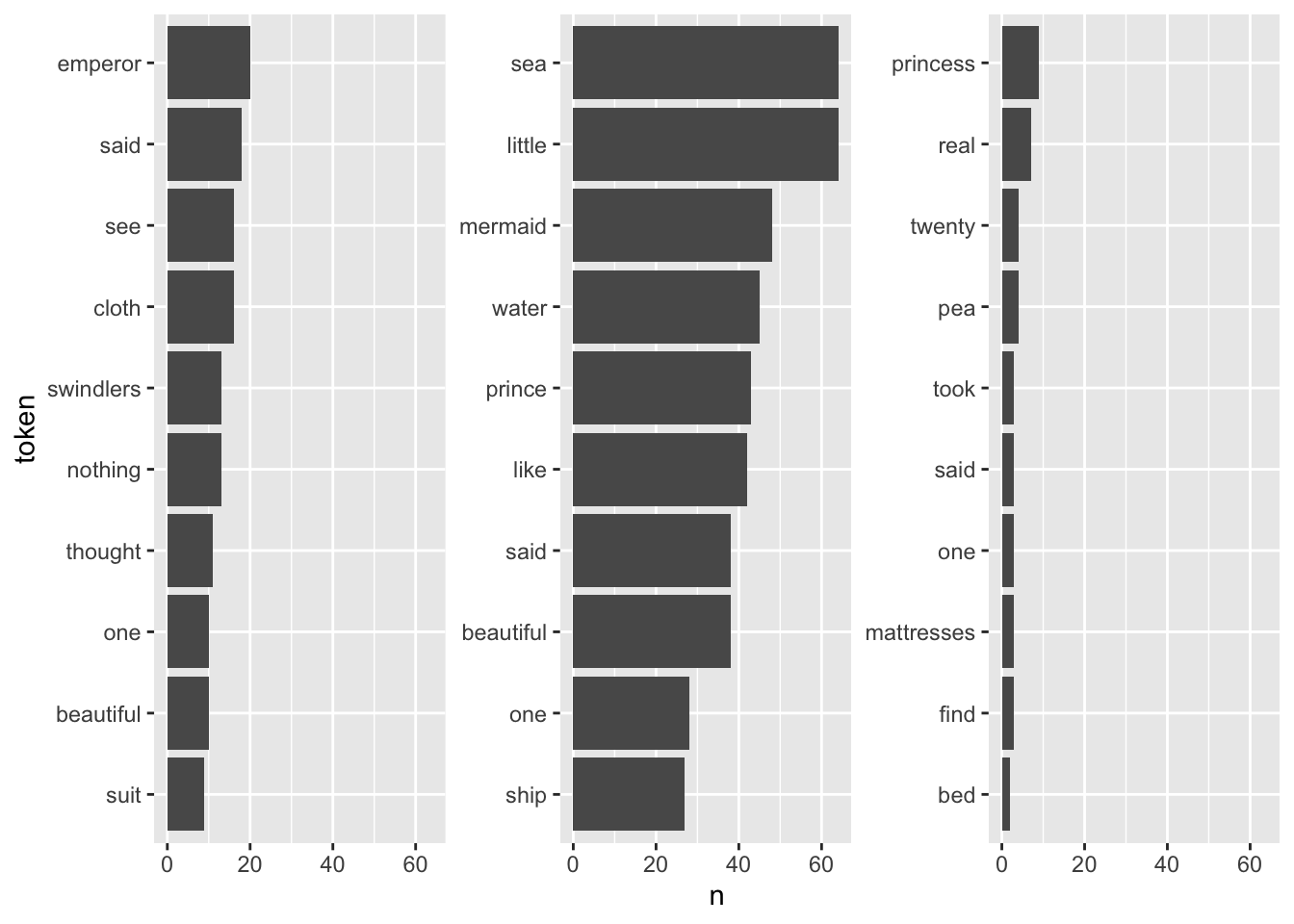

This already looks quite nice, it is quite easy to see which plot belongs to the respective book.

6.2 TF-IDF

A better definition of words that are particular to a group of documents is “the ones that appear often in one group but rarely in the other one(s)”. So far, the measure of term frequency only accounts for how often terms are used in the respective document. I can take into account how often it appears in other documents by including the inverse document frequency. The resulting measure is called tf-idf and describes “the frequency of a term adjusted for how rarely it is used.” (Silge and Robinson 2016: 31) If a term is rarely used overall but appears comparably often in a singular document, it might be safe to assume that it plays a bigger role in that document.

The tf-idf of a word in a document is commonly¹. One implementation is calculated as follows:

\[w_{i,j}=tf_{i,j}\times ln(\frac{N}{df_{i}})\]

–> \(tf_{i,j}\): number of occurrences of term \(i\) in document \(j\)

–> \(df_{i}\): number of documents containing \(i\)

–> \(N\): total number of documents

Note that the \(ln\) is included so that words that appear in all documents – and do therefore not have discriminatory power – will automatically get a value of 0. This is because \(ln(1) = 0\). On the other hand, if a term appears in, say, 4 out of 20 documents, its ln(idf) is \(ln(20/4) = ln(5) = 1.6\).

The tidytext package provides a neat implementation for calculating the tf-idf called bind_tfidf(). It takes as input the columns containing the term, the document, and the document-term counts n.

fairytales_top10_tfidf <- fairytales_tidy |> 
  group_by(book) |> 
  count(token) |> 
  bind_tf_idf(token, book, n) |> 
  slice_max(tf_idf, n = 10)

fairytales_top10_tfidf |> 
  ggplot()  +
  geom_col(aes(x = tf_idf, y = reorder_within(token, tf_idf, book))) +
  scale_y_reordered() +
  labs(y = "token") +
  facet_wrap(vars(book), scales = "free") +
  theme(strip.text.x = element_blank(),
        axis.title.x = element_blank(),
        axis.text.x = element_blank(),
        axis.ticks.x = element_blank())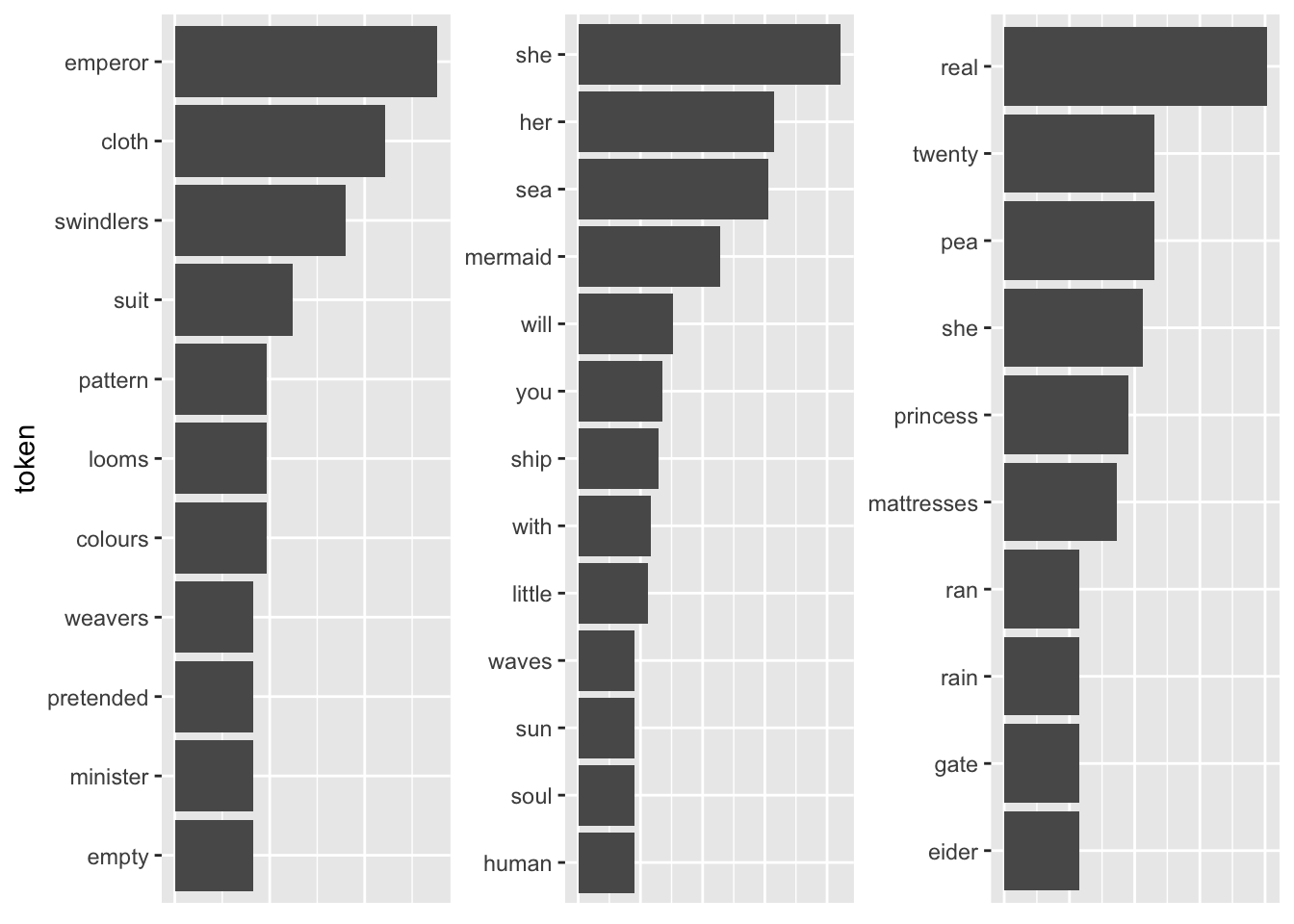

Pretty good already! All the fairytales can be clearly identified. A problem with this representation is that I cannot straightforwardly interpret the x-axis values (they can be removed by uncommenting the last four lines). A way to mitigate this is using odds.

Another shortcoming becomes visible when I take the terms with the highest TF-IDF as compared to all other fairytales.

tfidf_vs_full <- hcandersenr::hcandersen_en |> 
  unnest_tokens(output = token, input = text) |> 
  count(token, book) |> 
  bind_tf_idf(book, token, n) |> 
  filter(book %in% c("The princess and the pea",
                     "The little mermaid",
                     "The emperor's new suit")) 

plot_tf_idf <- function(df, group_var){
  df |> 
    group_by({{ group_var }}) |> 
    slice_max(tf_idf, n = 10, with_ties = FALSE) |> 
    ggplot()  +
    geom_col(aes(x = tf_idf, y = reorder_within(token, tf_idf, {{ group_var }}))) +
    scale_y_reordered() +
    labs(y = "token") +
    facet_wrap(vars({{ group_var }}), scales = "free") +
    #theme(strip.text.x = element_blank()) +
    theme(axis.title.x=element_blank(),
          axis.text.x=element_blank(),
          axis.ticks.x=element_blank())
} 
  
plot_tf_idf(tfidf_vs_full, book)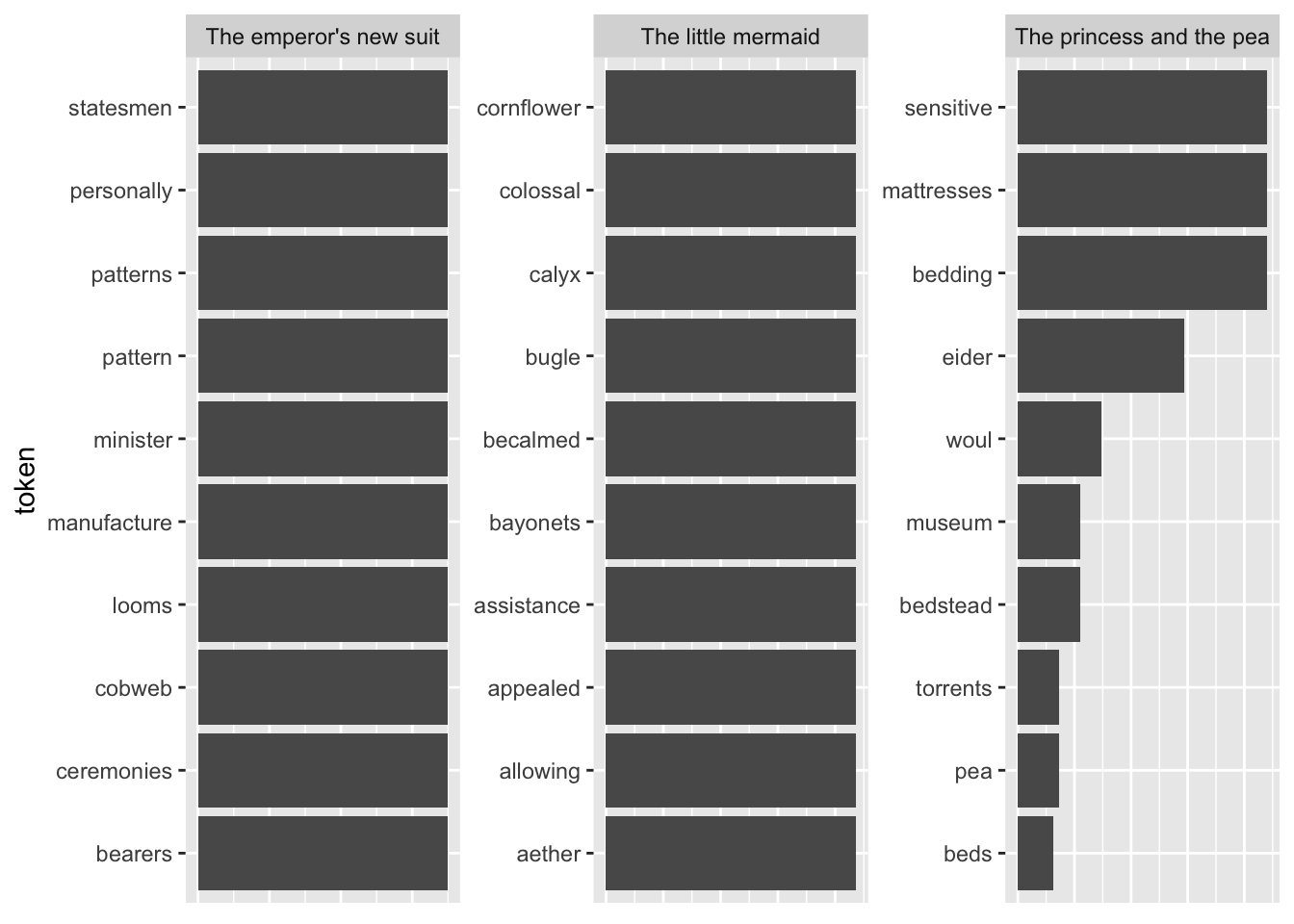

The tokens are far too specific to make any sense. Introducing a lower threshold (i.e., limiting the analysis to terms that appear at least x times in the document) might mitigate that. Yet, this threshold is of course arbitrary.

tfidf_vs_full |> 
  #group_by(token) |> 
  filter(n > 3) |> 
  ungroup() |> 
  plot_tf_idf(book)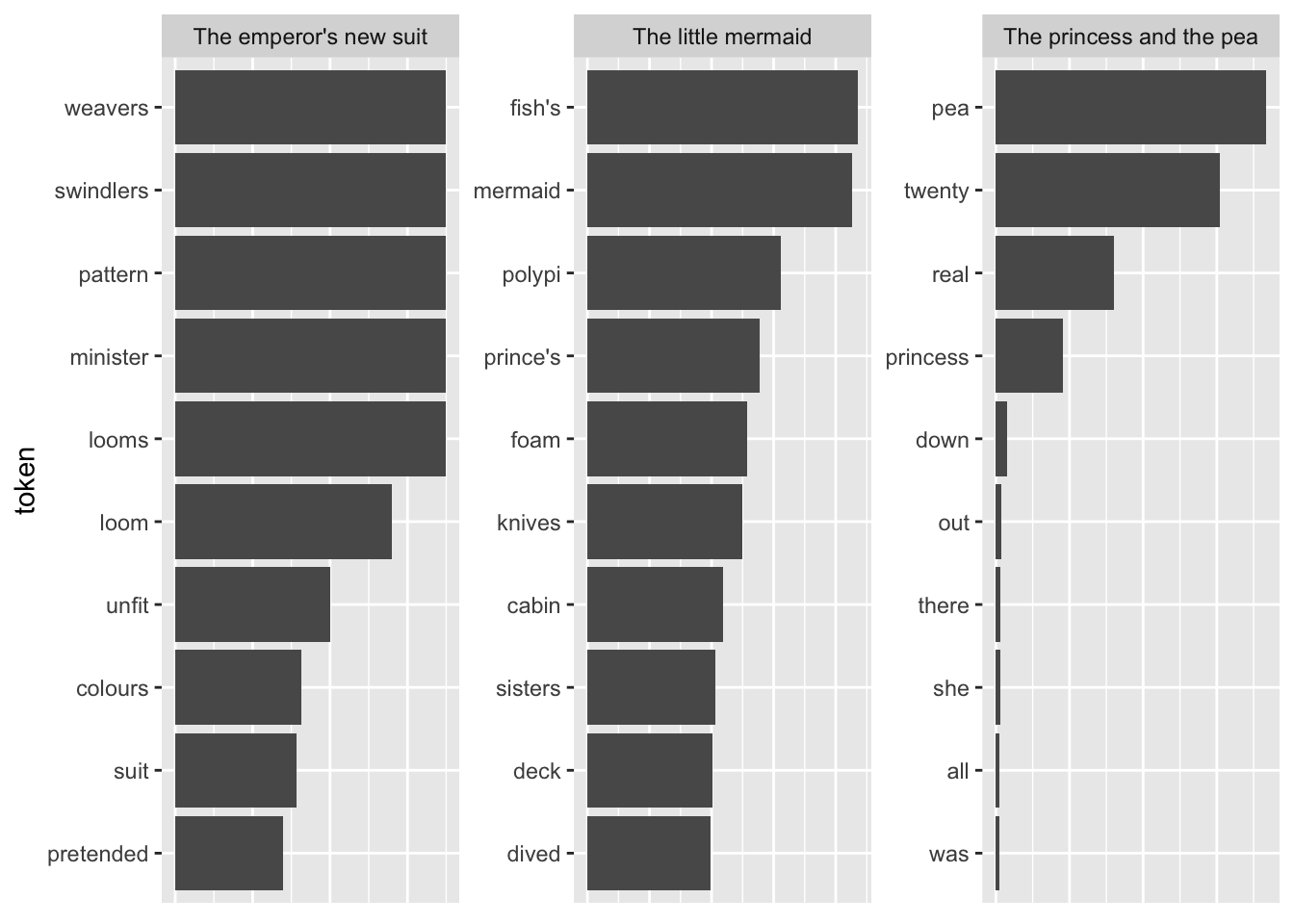

6.3 Exercises

1. Take the State of the Union addresses from the preprocessing script. Create a column that contains the decade.

1. Calculate the TF-IDF for each term per decade.

2. Plot the results in the way they’re plotted above (i.e., one facet per decade, 10 terms with highest TF-IDF.

3. Can you tell what happened during these decades? Would you remove some of the words?

Grimmer, Justin, Margaret Roberts, and Brandon Stewart. 2022. Text as Data: A New Framework for Machine Learning and the Social Sciences. Princeton: Princeton University Press.

Manning, Christopher D, Prabhakar Raghavan, and Hinrich Schütze. 2008. Introduction to Information Retrieval. New York: Cambridge University Press.

Monroe, Burt L., Michael P. Colaresi, and Kevin M. Quinn. 2008. “Fightin’ Words: Lexical Feature Selection and Evaluation for Identifying the Content of Political Conflict.” Political Analysis 16 (4): 372–403. https://doi.org/10.1093/pan/mpn018.

Silge, Julia, and David Robinson. 2016. “Tidytext: Text Mining and Analysis Using Tidy Data Principles in R.” The Journal of Open Source Software 1 (3): 37. https://doi.org/10.21105/joss.00037.

---

1. Note that multiple implementations exist, for an overview see, for instance, Manning, Raghavan, and Schütze (2008)