library(tidyverse)
library(tidymodels)
library(visdat)
library(gridExtra)
library(factoextra)Ejemplo de un modelo no supervisado
Descargue este documento aquí y ábralo en Rstudio
Relacionado a la base datos
La base de datos heart.csv de UCI Machine Learning Repository, contiene datos de pacientes con enfermedades cardíacas. Los datos incluyen información sobre la edad, el sexo, el colesterol, la presión arterial y otros factores de riesgo. El objetivo de este análisis es identificar patrones en los datos que puedan ayudar a predecir la presencia de enfermedades cardíacas en los pacientes.
Las variables son las siguientes:
age: Edad del paciente en años.
sex: Género del paciente
- 1 = Masculino
- 0 = Femenino
cp (Tipo de dolor en el pecho):
- 0: Angina típica.
- 1: Angina atípica.
- 2: Dolor no anginoso.
- 3: Asintomático.
trestbps (Presión arterial en reposo): Presión arterial en reposo del paciente, medida en mm Hg.
chol (Colesterol sérico): Nivel de colesterol en sangre en mg/dl.
fbs (Glucosa en sangre en ayunas): Nivel de glucosa en sangre al ayuno
- 1 = Verdadero (si el nivel es superior a 120 mg/dl)
- 0 = Falso
restecg (Resultados del electrocardiograma en reposo):
- 0: Normal.
- 1: Con anomalías en la onda ST-T (inversión de la onda T o elevación/depresión de la onda ST).
- 2: Hipertrofia ventricular izquierda probable o definitiva según los criterios de Estes.
thalach (Frecuencia cardíaca máxima alcanzada): Máxima frecuencia cardíaca alcanzada durante el ejercicio.
exang (Angina inducida por ejercicio): Indica si el paciente experimenta angina al hacer ejercicio
- 1 = Sí
- 0 = No
oldpeak (Depresión del ST): Depresión del segmento ST inducida por el ejercicio en relación con el reposo. Mide la diferencia entre la actividad de reposo y la respuesta al ejercicio, y puede indicar problemas cardíacos.
slope (Pendiente del segmento ST durante el ejercicio máximo):
- 0: Pendiente ascendente.
- 1: Pendiente plana.
- 2: Pendiente descendente.
ca (Número de vasos principales coloreados por fluoroscopia): Número de vasos sanguíneos (de 0 a 3) que muestran un estrechamiento significativo.
thal (Estado de la talasemia):
- 1: Normal.
- 2: Defecto fijo.
- 3: Defecto reversible.
target: Variable de resultado o etiqueta que indica la presencia de una enfermedad cardíaca.
- 1 = Presencia de enfermedad cardíaca
- 0 = Ausencia de enfermedad cardíaca
Cargar librerías
Comenzaremos con cargar las librerías necesarias
Importar y transformar la base de datos
df <- read.csv("https://raw.githubusercontent.com/michhottinger/CS-Data-Science-Build-Week-1/refs/heads/master/datasets_33180_43520_heart.csv")Trnasformar la base de datos
Vamos a transformar la base de datos para que sea más fácil de trabajar con ella. Vamos a convertir los valores de las variables a factores y a cambiar los nombres de las variables para que sean más descriptivos.
data2 <- df %>%
mutate(sex = if_else(sex == 1, "MALE", "FEMALE"),
fbs = if_else(fbs == 1, ">120", "<=120"),
exang = if_else(exang == 1, "YES" ,"NO"),
cp = if_else(cp == 1, "ATYPICAL ANGINA",
if_else(cp == 2, "NON-ANGINAL PAIN", "ASYMPTOMATIC")),
restecg = if_else(restecg == 0, "NORMAL",
if_else(restecg == 1, "ABNORMALITY", "PROBABLE OR DEFINITE")),
slope = as.factor(slope),
ca = as.factor(ca),
thal = as.factor(thal),
target = if_else(target == 1, "YES", "NO")
) %>%
mutate_if(is.character, as.factor) %>%
dplyr::select(target, sex, fbs, exang, cp, restecg, slope, ca, thal, everything())Podemos visualizar las variables y el contenido de la base de datos
vis_dat(data2)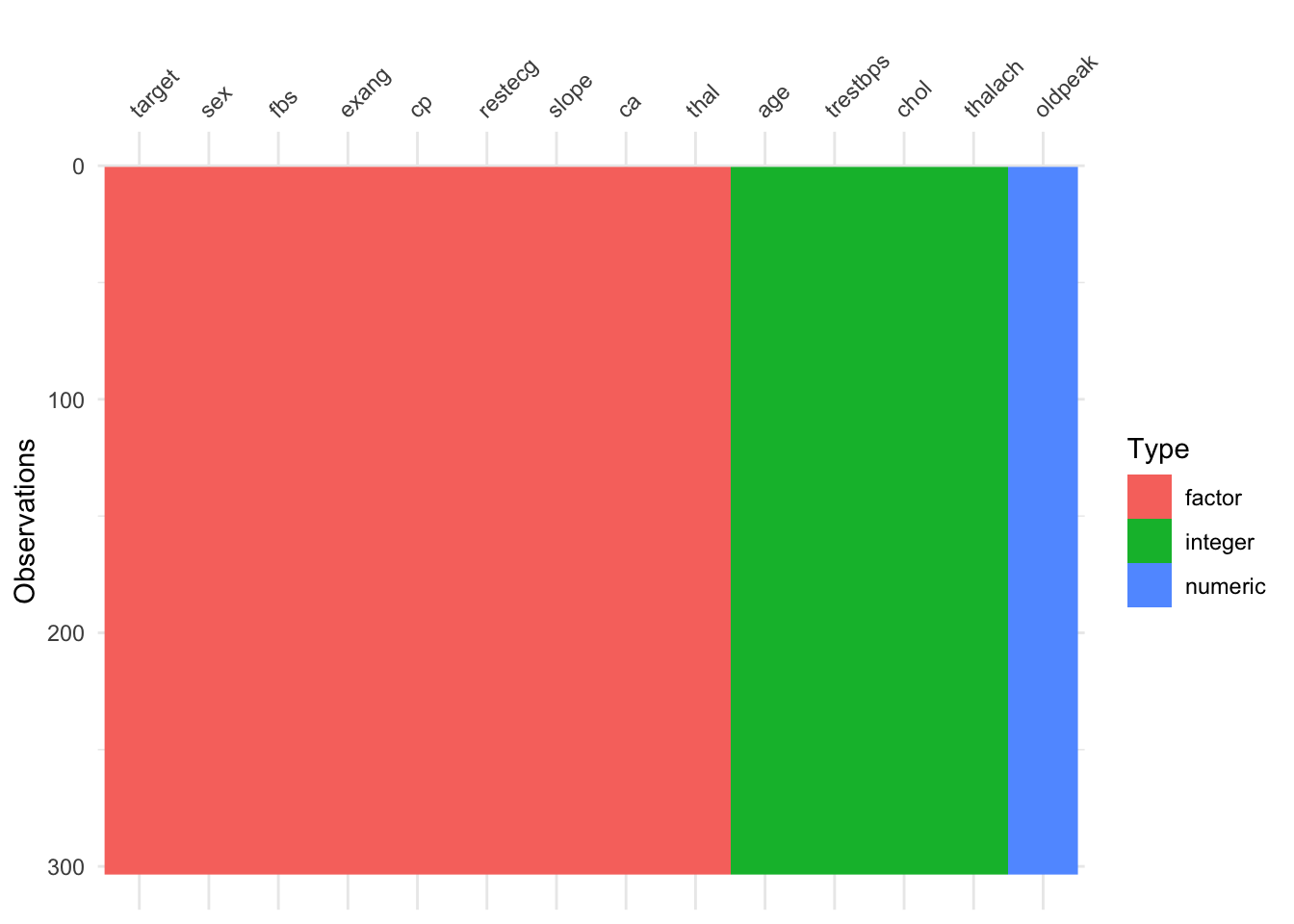
Objetivo del análisis
Los investigadores están interesados en identificar patrones en los datos que les permitan identificar a los pacientes que tienen una enfermedad cardíaca. Para ello, se propone realizar un análisis de clustering para identificar grupos de pacientes con características similares. Este tipo de análisis requiere trabajar con variables de tipo numérico, por lo que se propone únicamente seleccionares las variables: age, trestbps, chol, thalach, oldpeak. Posterioremente probaremos un modelo de ML para aprendizaje no supervisado.
K-means
k-means es un método de agrupamiento (clustering) no supervisado que se usa para clasificar datos en grupos o clústers . Es ampliamente utilizado en análisis de datos y machine learning para encontrar patrones o segmentos dentro de un conjunto de datos.
Se describen de forma muy general los pasos involucradros en el algoritmo de de clustering con k-means:
- Definición del Número de clústers (k): Primero, se elige un número k de grupos en los que se quiere dividir los datos. Este número lo selecciona el usuario con base en la estructura de los datos o en experimentación.
- Inicialización de los Centroides: El algoritmo elige k puntos al azar en el espacio de datos para que actúen como los “centroides” iniciales de cada clúster. Estos son puntos de referencia alrededor de los cuales se agruparán los datos.
- Asignación de Datos a los clústers : Cada punto de datos se asigna al clúster cuyo centroide esté más cercano. Esto se basa en una métrica de distancia, generalmente la distancia euclidiana.
- Recalcular los Centroides: Una vez que se han asignado todos los puntos, el algoritmo recalcula el centroide de cada clúster tomando el promedio de todos los puntos asignados a ese clúster.
- Repetición del Proceso: Los pasos de asignación de datos y recalculación de centroides se repiten hasta que ya no hay cambios significativos en los centroides o en las asignaciones de los puntos de datos. Esto indica que el algoritmo ha convergido y encontrado los clústers finales.
Selección de variables cuantitativas
Recuerde que solo nos interesa trabajar con las variables numéricas, por lo que vamos a seleccionar únicamente las variables: age, trestbps, chol, thalach, oldpeak.
df_num <- data2 %>%
select(age, trestbps, chol, thalach, oldpeak)head(df_num) age trestbps chol thalach oldpeak
1 63 145 233 150 2.3
2 37 130 250 187 3.5
3 41 130 204 172 1.4
4 56 120 236 178 0.8
5 57 120 354 163 0.6
6 57 140 192 148 0.4Además los datos deben ser escalados para que tengan la misma importancia en el análisis.
df_num_sacaled <- scale(df_num)Visualización de los Clústers
Se probaránn varios números de clúster y se graficarán:
# Creación de los clústers
k2 <- kmeans(df_num_sacaled, centers = 2, nstart = 25)
k3 <- kmeans(df_num_sacaled, centers = 3, nstart = 25)
k4 <- kmeans(df_num_sacaled, centers = 4, nstart = 25)
k5 <- kmeans(df_num_sacaled, centers = 5, nstart = 25)
# Crear objetos y gráficar los clústers
p1 <- fviz_cluster(k2, geom = "point", data = df_num_sacaled)+
ggtitle("k = 2")
p2 <- fviz_cluster(k3, geom = "point", data = df_num_sacaled)+
ggtitle("k = 3")
p3 <- fviz_cluster(k4, geom = "point", data = df_num_sacaled)+
ggtitle("k = 4")
p4 <- fviz_cluster(k5, geom = "point", data = df_num_sacaled)+
ggtitle("k = 5")
grid.arrange(p1,p2,p3,p2, nrow = 2)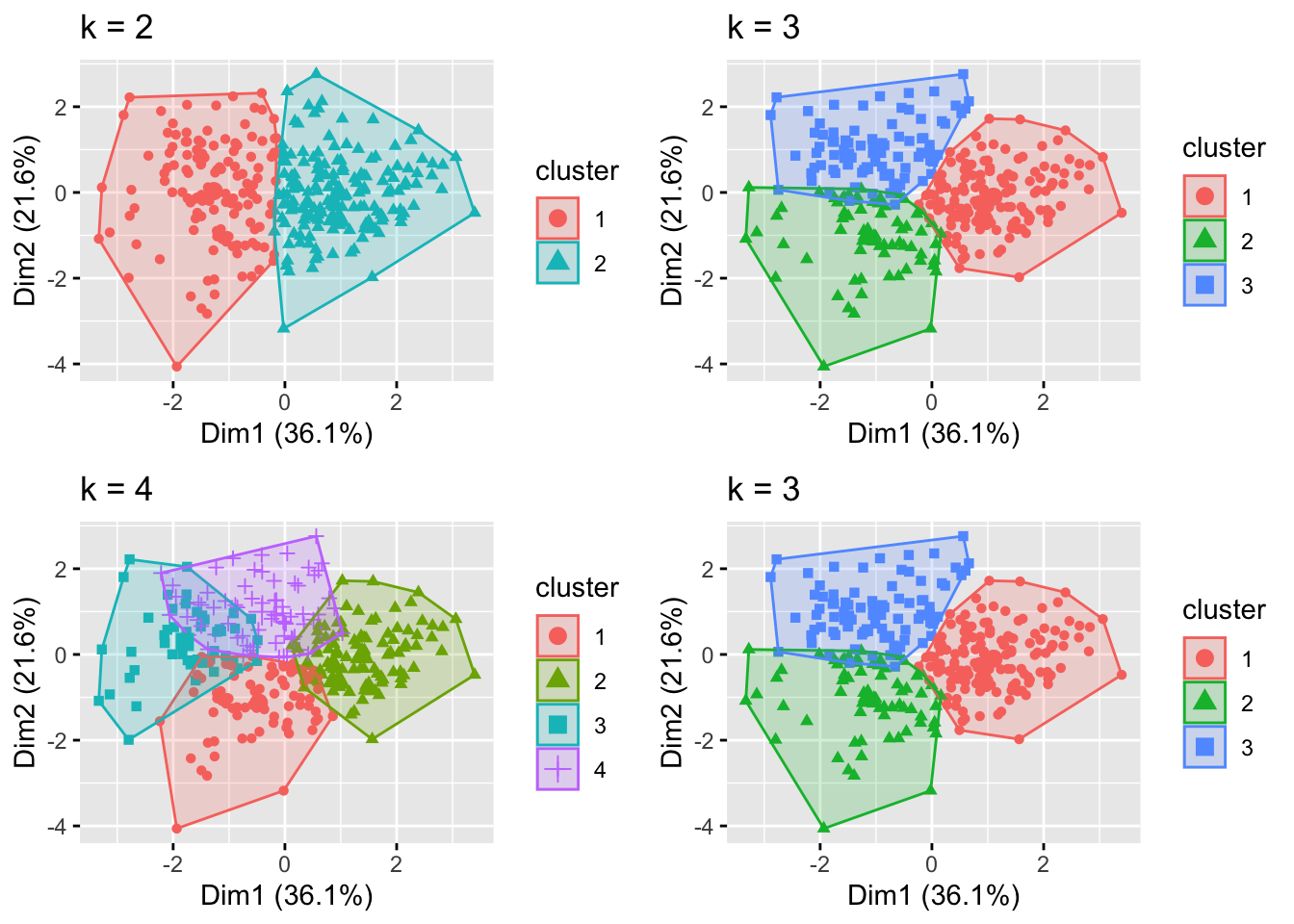
No es posible indentificar cual es el número correcto de clústers , por lo que se probará determinar el número de clústers óptimo utilizando el método del codo.
# Método del codo
wss <- sapply(1:10, function(k) {
kmeans(df_num_sacaled, centers = k, nstart = 10)$tot.withinss
})
# Graficar el método del codo
plot(1:10, wss, type = "b", pch = 19, frame = FALSE,
xlab = "Número de clústers K",
ylab = "Suma de errores cuadráticos totales")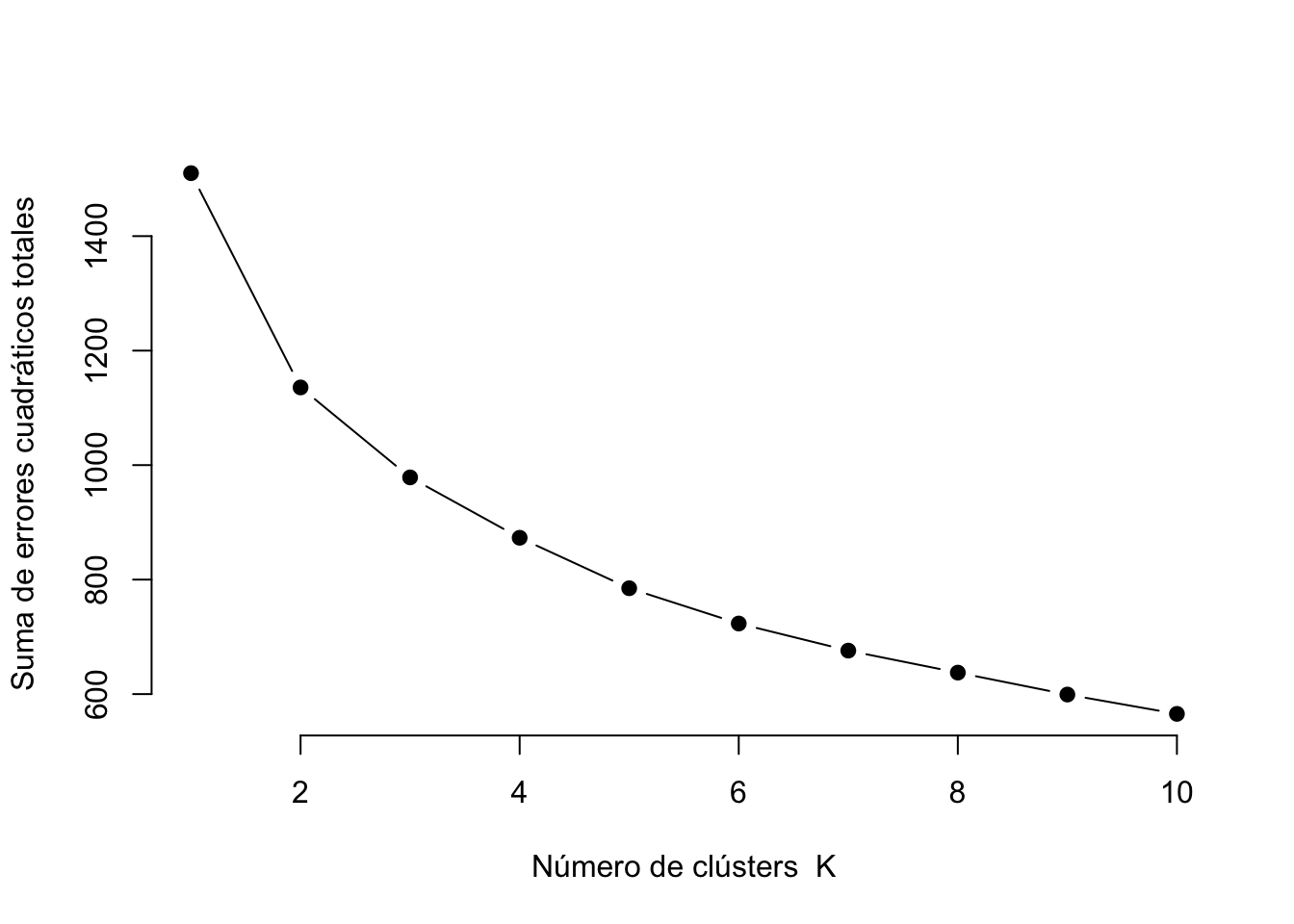
En la gráfica anterior, en el eje de las x se encuentran el número de clústers, y en el eje de las y la suma de los errores cuadráticos. Entre menor sea el valor de y más compactos están los puntos de los centroides (centro de cada clúster). Se selecciona el punto donde se observa un cambio en la pendiente de la gráfica, en este caso se seleccionará k=3, aunque también podría considerarse K=2.
Algoritmo de K-means
Supongamos que se selecciona k=3, se procede a realizar el algoritmo de k-means:
set.seed(123) # Sembrar semilla
kmeans_result <- kmeans(df_num_sacaled, centers = 3, nstart = 10)
# Agregar los clústers a los datos originales df
data2$Cluster <- as.factor(kmeans_result$cluster)Visualización de los Clústers
# Visualizar clústers
ggplot(data2, aes(x = age, y = chol, color = Cluster)) +
geom_point(size = 3, alpha=0.8) +
labs(title = "Clustering de Datos de Enfermedades Cardíacas", x = "Edad", y = "Colesterol") +
theme_dark()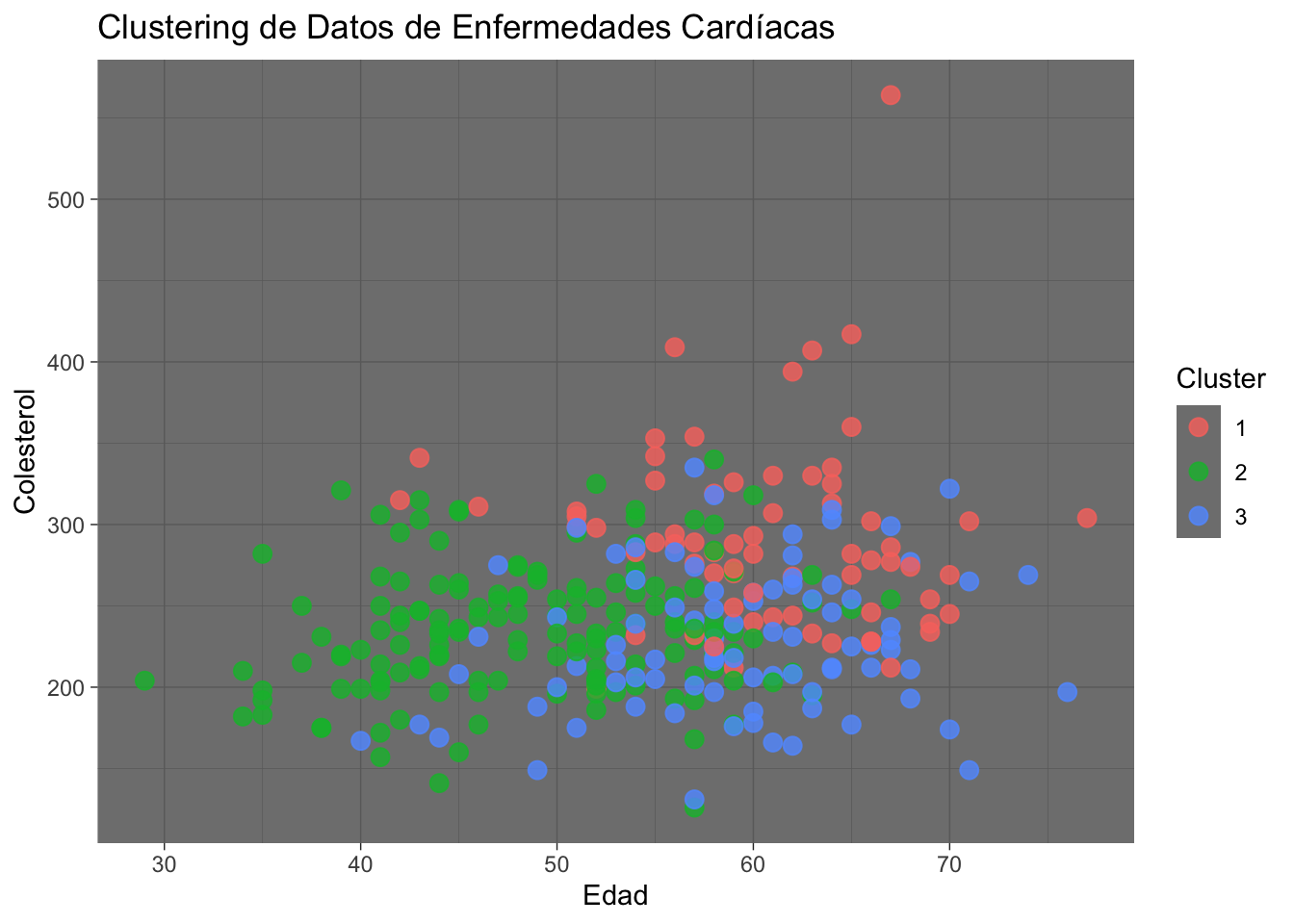
Una explicacipon de esta gráfica es:
- Rojo (Clúster 1): Representa un grupo de individuos que tienen niveles de colesterol más elevados y tienden a ser mayores. Este grupo podría representar personas en un rango de mayor riesgo debido a la combinación de colesterol alto y mayor edad.
- Verde (Clúster 2): Agrupa a individuos de varias edades, pero con niveles de colesterol más moderados. Este grupo parece ser el más diverso en cuanto a edad.
- Azul (Clúster 3): Incluye principalmente a individuos de edad más avanzada con niveles de colesterol variados, pero generalmente más bajos que el grupo en rojo.
# Visualizar clústers
ggplot(data2, aes(x = age, y = oldpeak, color = Cluster)) +
geom_point(size = 3, alpha=0.8) +
labs(title = "Clustering de Datos de Enfermedades Cardíacas", x = "Edad", y = "Oldpeak") +
theme_dark()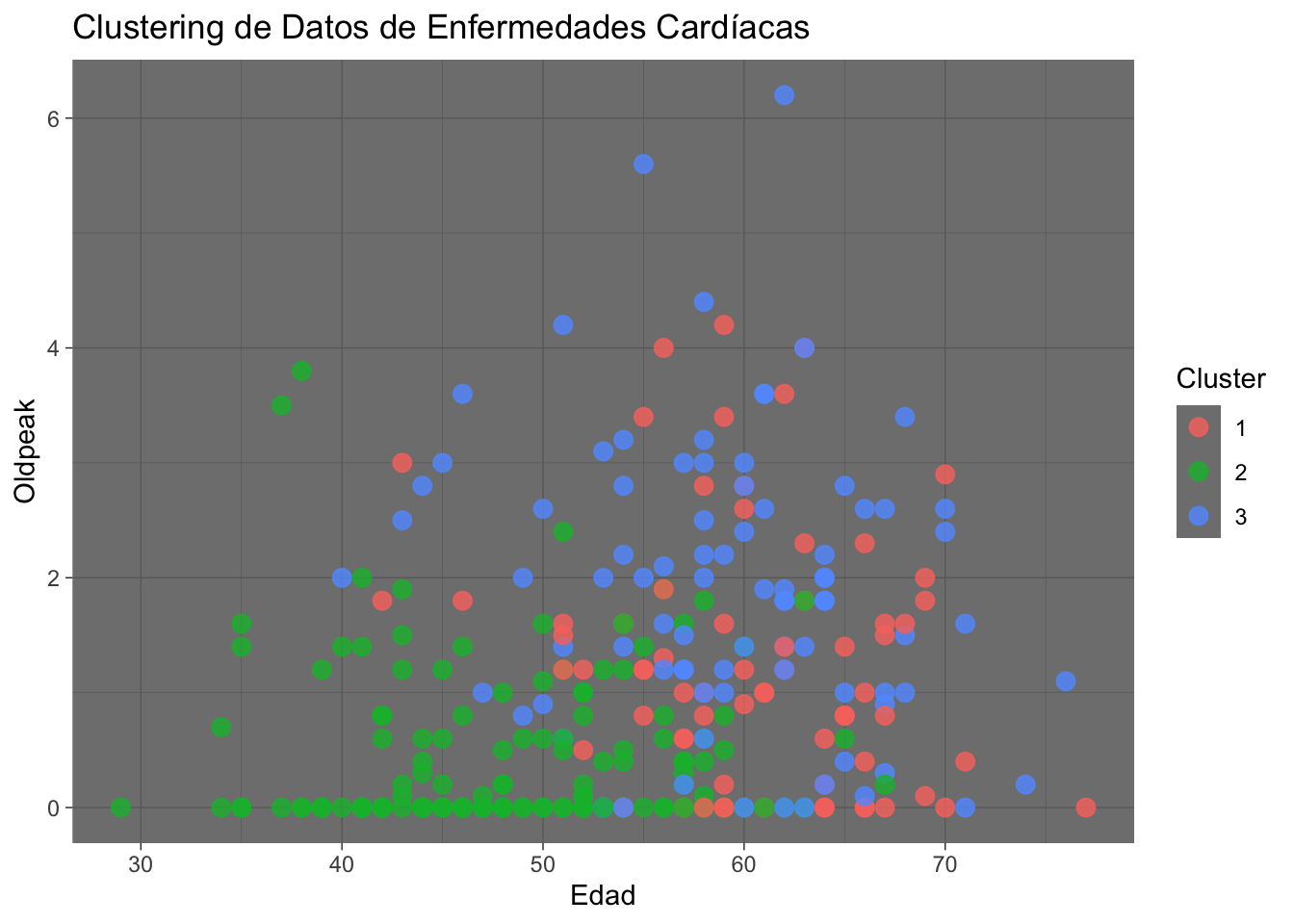
# Visualizar clústers
ggplot(data2, aes(x = age, y = trestbps, color = Cluster)) +
geom_point(size = 3, alpha=0.8) +
labs(title = "Clustering de Datos de Enfermedades Cardíacas", x = "Edad", y = "trestbps") +
theme_dark()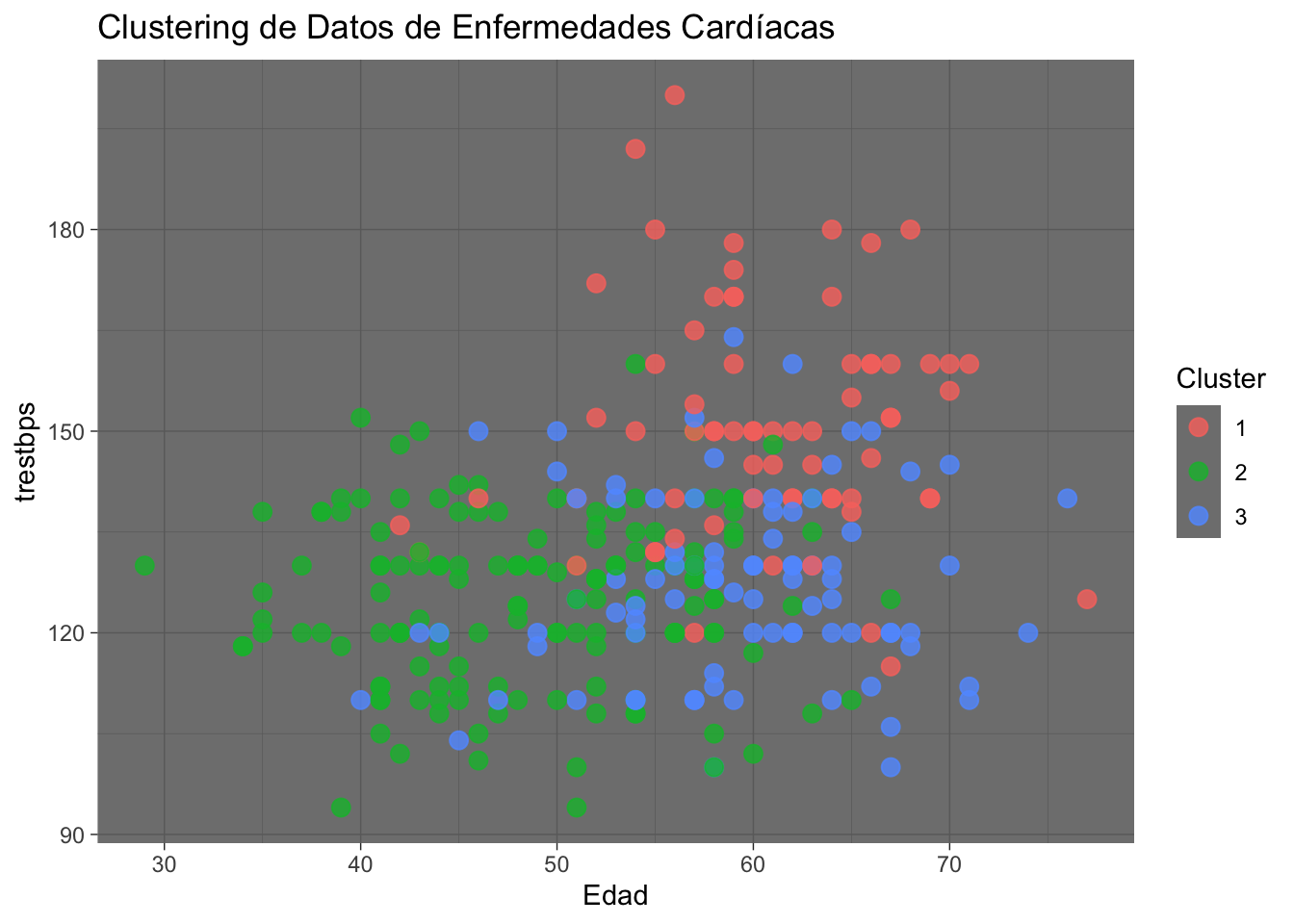
aggregate(data2[, sapply(data2, is.numeric)], by = list(Cluster = data2$Cluster), mean) Cluster age trestbps chol thalach oldpeak
1 1 60.47826 150.8841 292.1449 148.3913 1.2898551
2 2 48.75676 125.2500 235.2432 164.1149 0.4358108
3 3 59.11628 127.1395 228.4186 125.7558 1.8779070Ahora probaremos 2 clústers
set.seed(123) # Sembrar semilla
kmeans_result2 <- kmeans(df_num_sacaled, centers = 2, nstart = 10)
# Agregar los clústers a los datos originales df
data2$Cluster2 <- as.factor(kmeans_result2$cluster)Visualización de los Clústers
# Visualizar clústers
ggplot(data2, aes(x = age, y = chol, color = Cluster2)) +
geom_point(size = 3, alpha=0.8) +
labs(title = "Clustering de Datos de Enfermedades Cardíacas", x = "Edad", y = "Colesterol") +
theme_dark()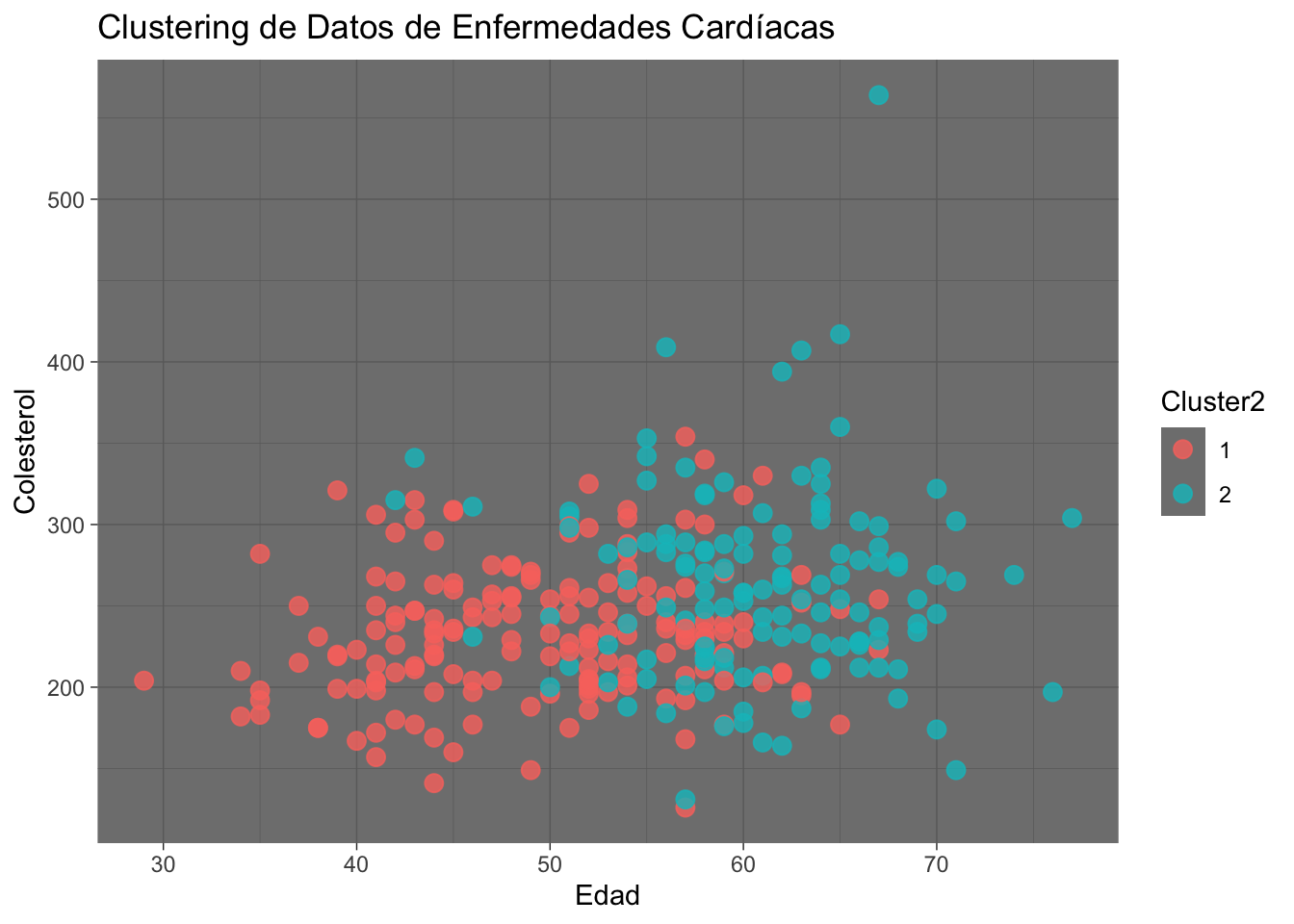
# Visualizar clústers
ggplot(data2, aes(x = age, y = oldpeak, color = Cluster2)) +
geom_point(size = 3, alpha=0.8) +
labs(title = "Clustering de Datos de Enfermedades Cardíacas", x = "Edad", y = "Oldpeak") +
theme_dark()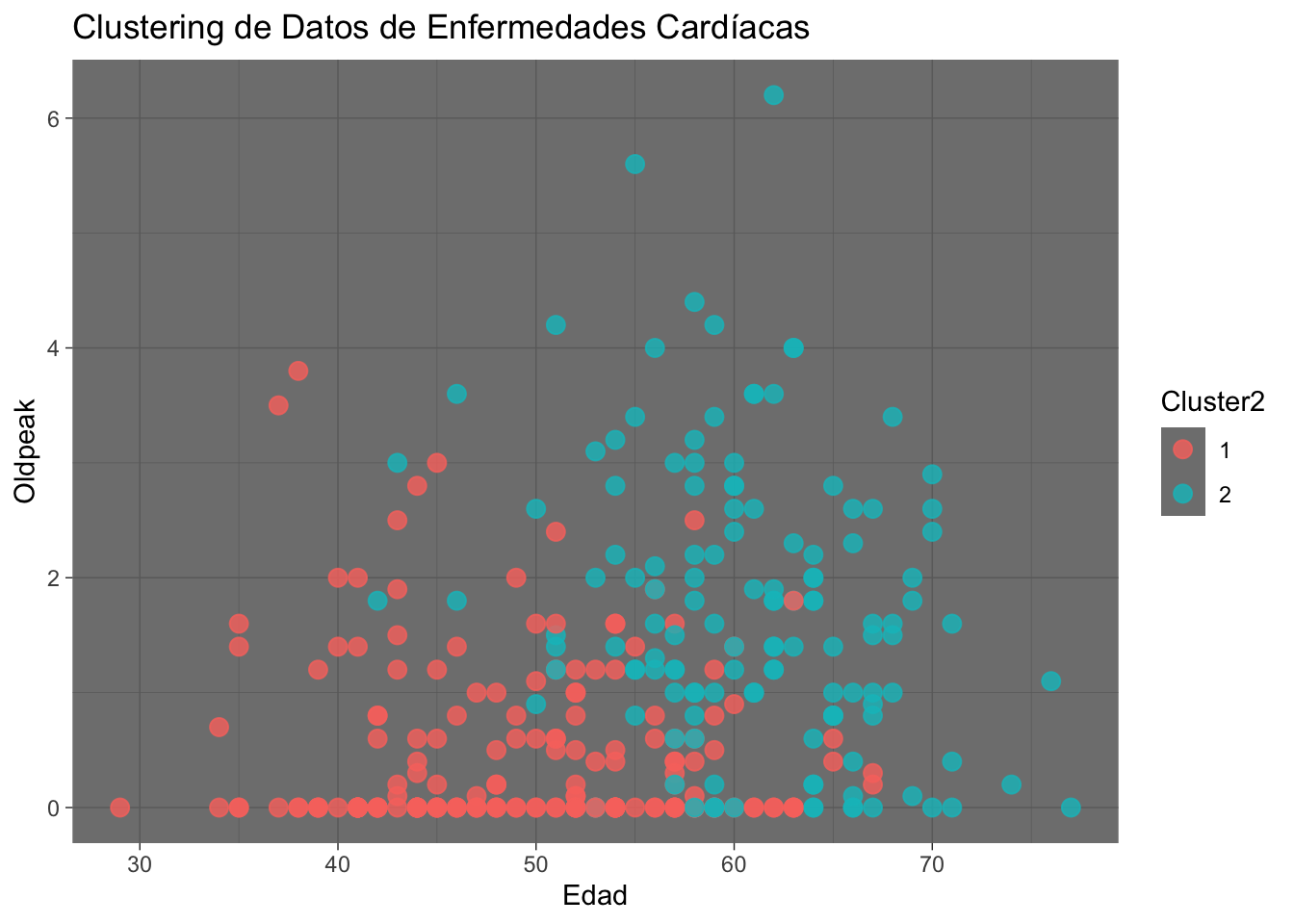
# Visualizar clústers
ggplot(data2, aes(x = age, y = trestbps, color = Cluster2)) +
geom_point(size = 3, alpha=0.8) +
labs(title = "Clustering de Datos de Enfermedades Cardíacas", x = "Edad", y = "trestbps") +
theme_dark()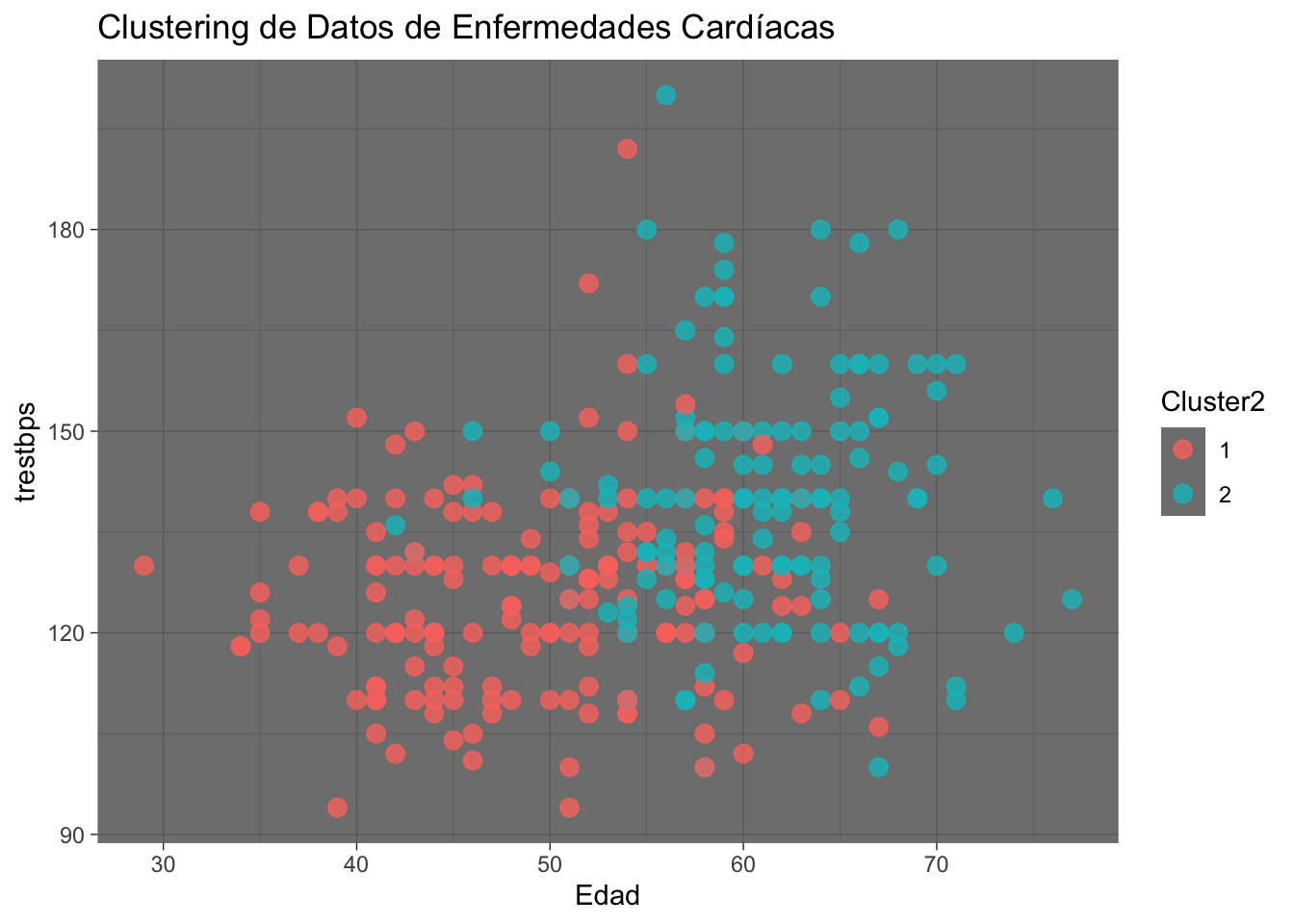
aggregate(data2[, sapply(data2, is.numeric)], by = list(Cluster = data2$Cluster2), mean) Cluster age trestbps chol thalach oldpeak
1 1 49.44767 125.7384 233.7384 161.564 0.5127907
2 2 60.82443 139.3511 262.7099 134.000 1.7312977Validación de los clústers
library(cluster)
silhouette_score <- silhouette(kmeans_result$cluster, dist(df_num_sacaled))
plot(silhouette_score, col = c("red", "green", "blue"))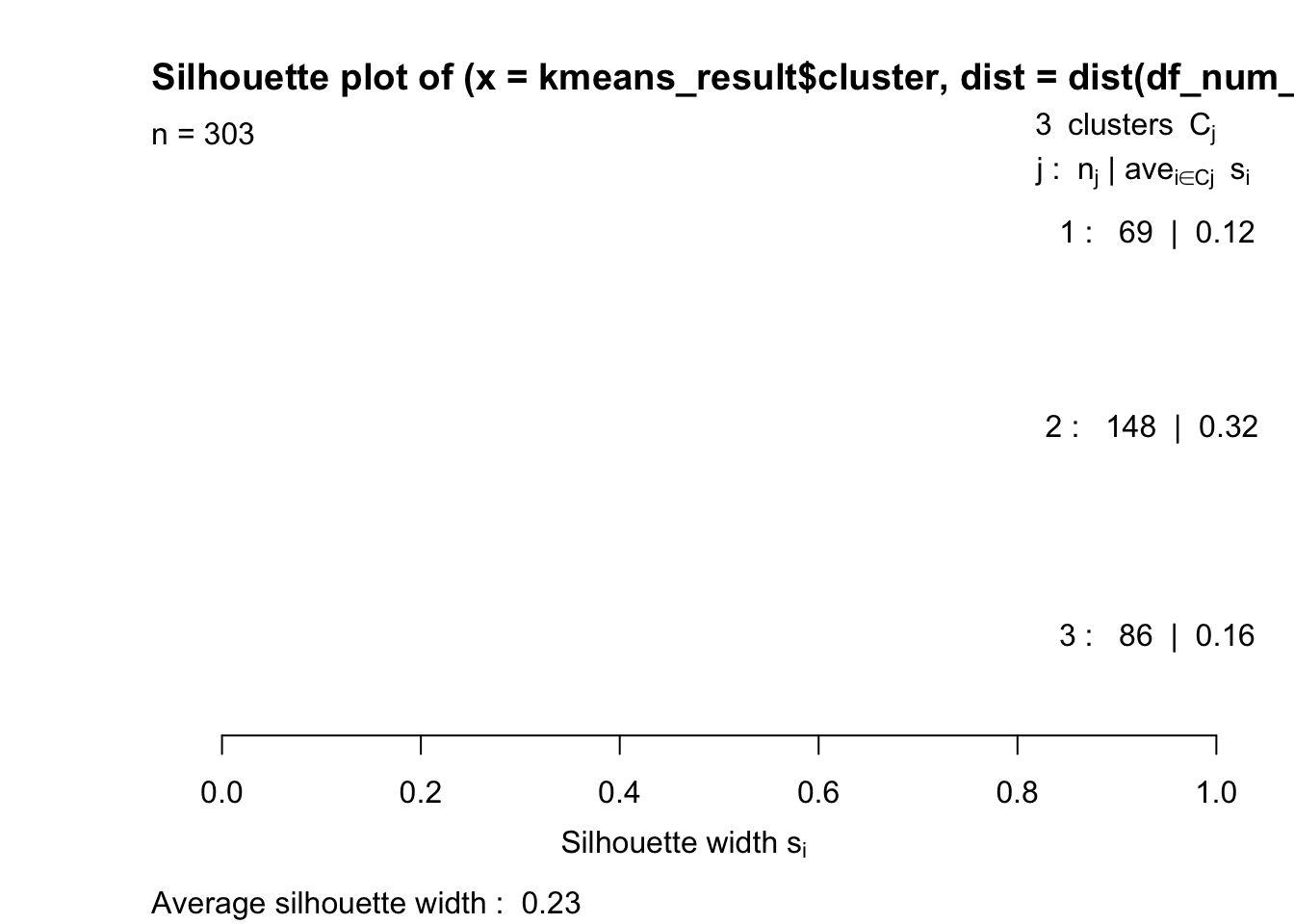
- Clúster 1 (Rojo): Tiene un promedio de ancho de Silhouette de 0.12 y 69 elementos. Este valor es bajo, lo que sugiere que muchos puntos en este clúster no están bien agrupados o están cerca de otros clústers .
- Clúster 2 (Verde): Tiene el mayor promedio de ancho de Silhouette, con 0.32 y 148 elementos. Esto indica que este es el clúster con mejor cohesión y separación de los demás, aunque el valor sigue siendo moderado.
- Clúster 3 (Azul): Presenta un promedio de 0.16 y contiene 86 elementos. Este clúster tiene una cohesión baja, aunque es ligeramente mejor que el Clúster 1.
silhouette_score <- silhouette(kmeans_result2$cluster, dist(df_num_sacaled))
plot(silhouette_score, col = c("red", "green", "blue"))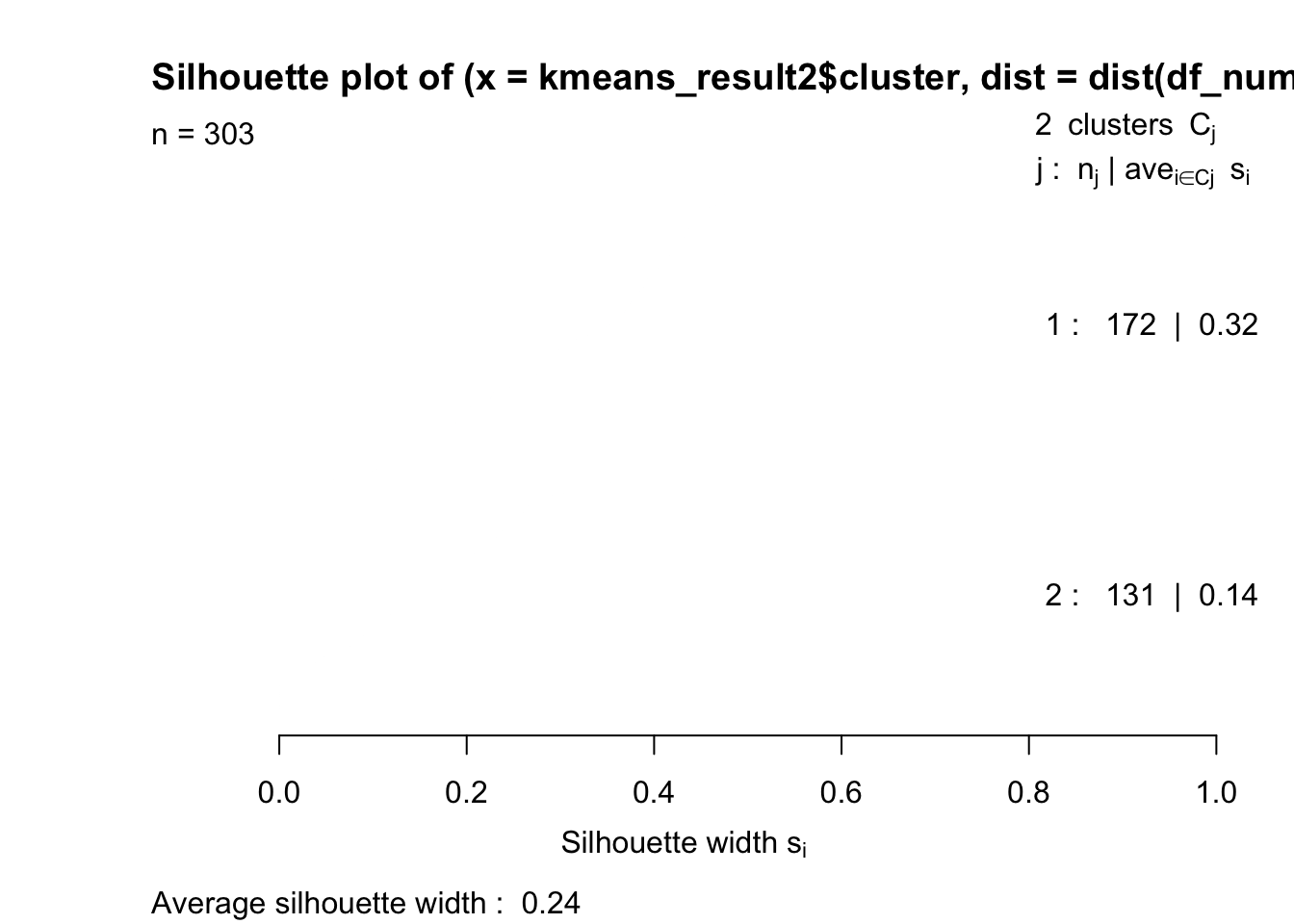
Pasos siguientes:
- Probar otros número de agrupamientos para aumentar el promerio de los anchos de Silhouette (idealmente hasta 0.5)
- Probar otros métodos de agrupación
- Probar si los clústers se relacionan con otras variables
- Realizar modelos predictivos
Relación de los clústers con otras variables
Por ejemplo:
data2 %>%
ggplot(aes(x = Cluster, fill = target)) +
geom_bar(position = "dodge", col="black", alpha=0.5) +
theme_classic()+
labs(title = "Comparación de Clústers y Enfermedad Cardíaca", x = "Clúster", y = "Conteo")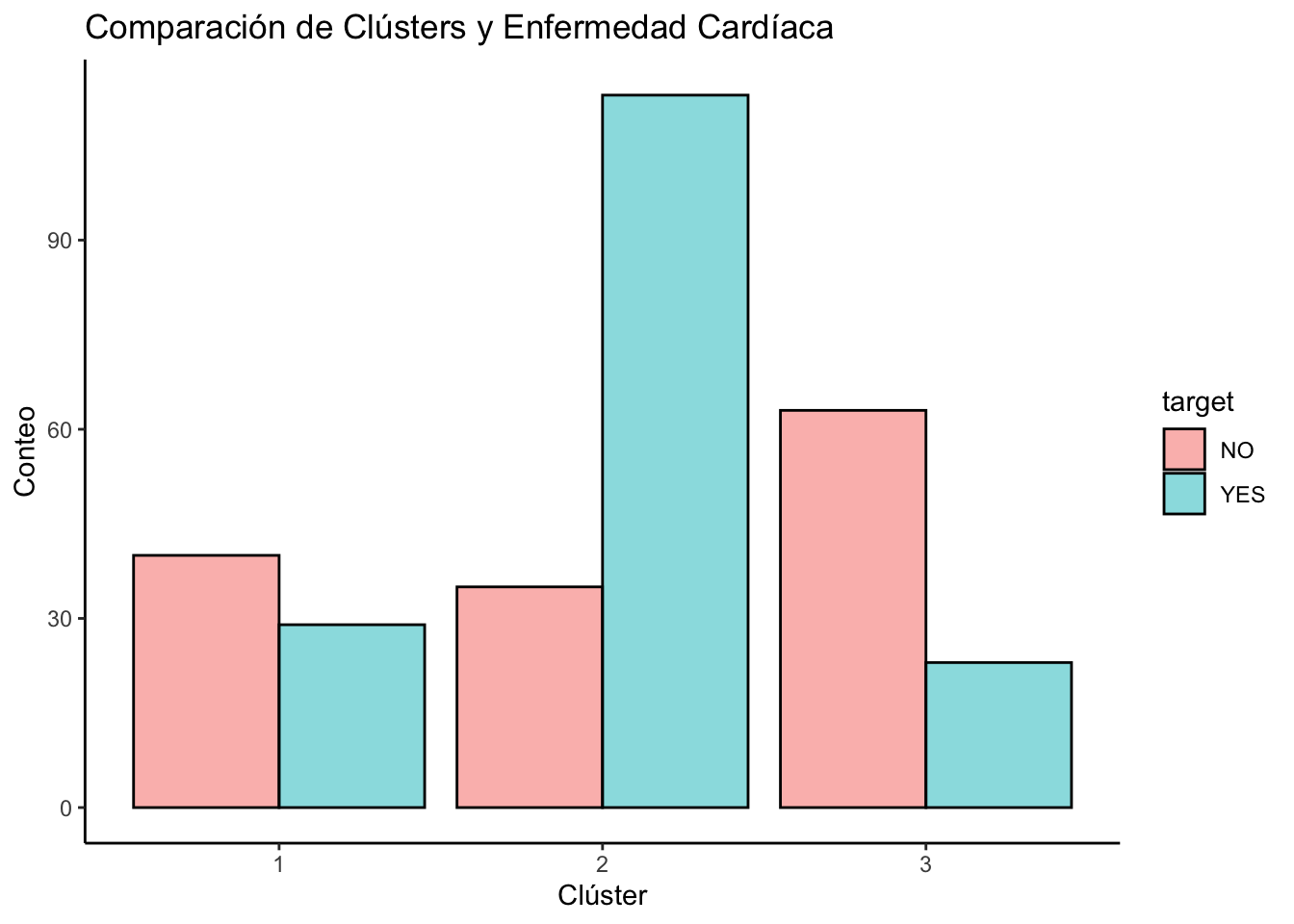
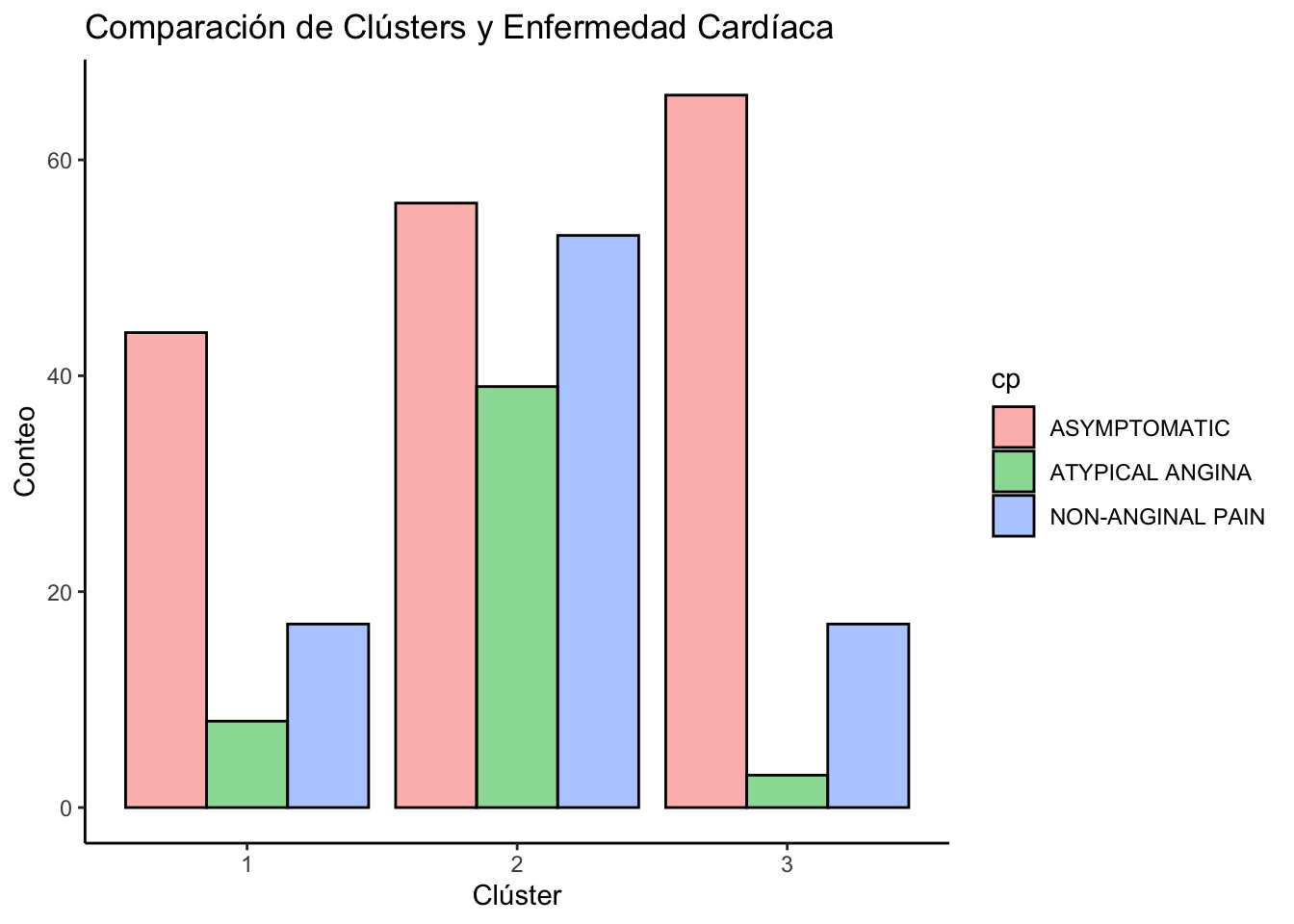
data2 %>%
ggplot(aes(x = Cluster, fill = cp)) +
geom_bar(position = "dodge", col="black", alpha=0.5) +
theme_classic()+
labs(title = "Comparación de Clústers y Enfermedad Cardíaca", x = "Clúster", y = "Conteo")