df <- read.csv("Bases/bodyfat.txt", sep="")Documento clase correlacion
Pruebas de hipótesis en correlación y coeficientes de correlación
Existen tres formas de estimar la correlación mediante los coeficientes de correlación de pearson, spearman y kendall. Se describen a continuación las principales características de los primeros dos.
Coeficiente de correlación pearson
La formula para estimar el coeficiente de correlación de pearson es:
\[\begin{equation} r_{xy} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i - \bar{y})^2}} \end{equation}\]
En esta fórmula, \(r_{xy}\) representa el coeficiente de correlación entre las variables \(x\) e \(y\). \(x_i\) e \(y_i\) son los valores de las variables \(x\) e \(y\) en la i-ésima observación, mientras que \(\bar{x}\) y \(\bar{y}\) son las medias de x e y, respectivamente.
Existe una relación muy importante entre el coeficiente de correlación de pearson y la covarianza. Para fines prácticos la covarianza mide cuanto variación hay entre una variable y una segunda, es decir, la covarianza se refiere a cuanto varía y si una segunda variable lo hace de la misma forma. Por ejemplo, si dos variables tienen la misma variación una con respecto de la otra, la covariación sería de uno. Un ejemplo de esto, aunque quizá cerece se sentido, imagine que mide el peso de un paciente en kg y en libras. Estas mediciones tendrían una covarición de 1.
Por lo tanto la formula para estimación del coeficiente de correlación de pearson se puede simplificar como:
\[\begin{equation} r_{xy} = \frac{cov(x, y)}{s_x s_y} \end{equation}\]
Donde: \(r_{xy}\) representa el coeficiente de correlación entre las variables \(x\) e \(y\). \(cov(x, y)\) es la covarianza entre \(x\) e \(y\), mientras que \(s_x\) y \(s_y\) son las desviaciones estándar de \(x\) e \(y\), respectivamente.
Prueba de hipótesis en el coeficiente de correlación pearson
Nuestra intención es tratar de demostrar que el coeficiente de correlación es distinto de cero. Por lo tanto:
- \(H_0: r = 0\)
- \(H_A: r \neq 0\)
Para poder concluir si rechazamos o aceptamos nuestra hipótesis, utilizamos la distribución \(t\) y la siguiente formula que :
\[\begin{equation} t = \frac{r_{xy} \sqrt{n-2}}{\sqrt{1-r_{xy}^2}} \end{equation}\]
Donde: \(t\) es el valor calculado para la prueba de significancia del coeficiente de correlación de Pearson. \(r_{xy}\) es el coeficiente de correlación de Pearson, y \(n\) es el tamaño de la muestra
Los supuestos que se deben cumplir para utilizar el coeficiente de correlación de Pearson son:
- Las variables se observan sobre una muestra aleatoria de individuos (cada individuo debe tener un par de valores).
- Existe una asociación lineal entre las dos variables.
- Para una prueba de hipótesis válida y cálculo de intervalos de confianza, ambas variables deben tener una distribución aproximadamente normal.
- Ausencia de valores atípicos en el conjunto de datos.
Coeficiete de correlación Spearman
Mientras que el coeficiente de correlación de Pearson asume linealidad, el coeficiente de correlación de Spearman asume una relación monotónica (las variables tienden a moverse en la misma dirección relativa, pero no necesariamente a un ritmo constante) entre dos variables. El coeficiente de correlación de Spearman se utiliza como una alternativa no paramétrica al coeficiente de correlación de Pearson. Se aplica en casos en los que los valores son ordinales o en aquellos casos en los que los valores son continuos, pero no cumplen con la condición de normalidad. La ventaja de utilizar el coeficiente de Spearman es que trabaja con rangos, lo que lo hace menos sensible a valores extremos que el coeficiente de Pearson.
La estimación del coeficiente de correlación de Spearman \(\rho\) o \(r_s\) se basa en la siguiente ecuación:
\[\begin{equation} \rho = 1 - \frac{6\sum d_i^2}{n(n^2 - 1)} \end{equation}\]
En esta fórmula, \(\rho\) es el coeficiente de correlación de Spearman, \(n\) es el tamaño de la muestra y \(d_i\) es la diferencia en los rangos de los valores i en cada variable.
La hipótesis nula para este coeficiente es: \(H_0: \rho = 0\) que se puede comprobar mediante el estadístico \(t\) con la siguiente formula:
\[\begin{equation} t = \frac{r_s}{\sqrt{\frac{1-r_s^2}{n-2}}} \end{equation}\]
Donde: \(t\) es el valor calculado para la prueba de significancia del coeficiente de correlación de Spearman. \(r_s\) es el coeficiente de correlación de Spearman, y \(n\) es el tamaño de la muestra.
Para utilizar el coeficiente de correlación de Spearman, es necesario que:
- las variables se observen en una muestra aleatoria de individuos y que haya una asociación monótona entre ellas.
- Que la varible utiliazada sea al menos de tipo ordinal.
No olvide que: La asociación monótona indica que las variables tienden a moverse en la misma dirección relativa, pero no necesariamente a un ritmo constante. Es importante destacar que todas las correlaciones lineales son monótonas, pero no todas las asociaciones monótonas son lineales, ya que también puede haber asociaciones monótonas no lineales. Simplemente un número de \(\rho\) positivo indica que ambas variables incrementan o disminuyen en el mismo sentido, mientras que un coeficiente negativo indica que una aumenta y la otra disminuye.
La siguiente taba muestra una comparación entre el coeficiente de correlación de Spearman y Pearson:
| Coeficiente de correlación de Pearson | Coeficiente de correlación de Spearman | |
|---|---|---|
| Tipo de variable | Variables continuas que tengan una relación lineal y una distribución normal | Variables continuas que no cumplen con e supuesto de normalidad o variables ordinales |
| Supuestos | 1. Las variables se observan sobre una muestra aleatoria de individuos (cada individuo debe tener un par de valores). 2. Existe una asociación lineal entre las dos variables. 3. Para una prueba de hipótesis válida y cálculo de intervalos de confianza, ambas variables deben tener una distribución aproximadamente normal. 4. Ausencia de valores atípicos en el conjunto de datos. |
No tiene supuestos específicos sobre la distribución o la forma funcional de las variables. Los datos son obtenidos de una muestra aleatoria |
| Fórmula | \(r_{xy} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i - \bar{y})^2}}\) o \(r_{xy} = \frac{cov(x, y)}{s_x s_y}\) | \(\rho = 1 - \frac{6\sum d_i^2}{n(n^2 - 1)}\) |
| Interpretación | El coeficiente de correlación de Pearson mide la fuerza y la dirección de la relación lineal entre dos variables continuas. Los valores oscilan entre -1 y 1. Una correlación cercana a 1 indica una fuerte correlación positiva, mientras que una correlación cercana a -1 indica una fuerte correlación negativa. Una correlación cercana a 0 indica que no hay correlación lineal. |
El coeficiente de correlación de Spearman mide la fuerza y la dirección de la relación monotónica entre dos variables. Los valores oscilan entre -1 y 1. Una correlación cercana a 1 indica una fuerte correlación positiva, mientras que una correlación cercana a -1 indica una fuerte correlación negativa. Una correlación cercana a 0 indica que no hay correlación monotónica. |
| Ventajas | Funciona bien cuando las variables tienen una relación lineal. Permite la prueba de hipótesis y el cálculo de intervalos de confianza. |
No requiere una distribución normal. Menos sensible a valores atípicos que el coeficiente de Pearson debido a que se basa en los rangos de los valores. |
| Desventajas | Requiere que las variables sean continuas y lineales. Sensible a valores atípicos. |
No proporciona información sobre la fuerza de la relación monotónica, solo su dirección. No se pueden calcular intervalos de confianza. |
Ejercicios práctica para purebas de correlación
Utilizando R base
En R base podemos utilizar la función plot(), cor y cor.testt() para estimar graficar y estimar los coeficientes de correlación. A continuación se presenta un ejemplo de cómo hacerlo:
Para realizar los siguientes ejemplos utilice la base de datos “bodyfat” la cual contiene mediciones antopométricas de un grupo de pacientes. Puede descargar la base aquí. Utilice el menú de RStudio para la importanción de la base de datos, tome en cuenta que es un archivo .txt.
Para obtener los coeficientes de correlación de dos variables específicas:
cor.test(df$Density, df$Fat)
Pearson's product-moment correlation
data: df$Density and df$Fat
t = -100.22, df = 250, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9904570 -0.9843641
sample estimates:
cor
-0.9877824 plot(df$Density, df$Fat)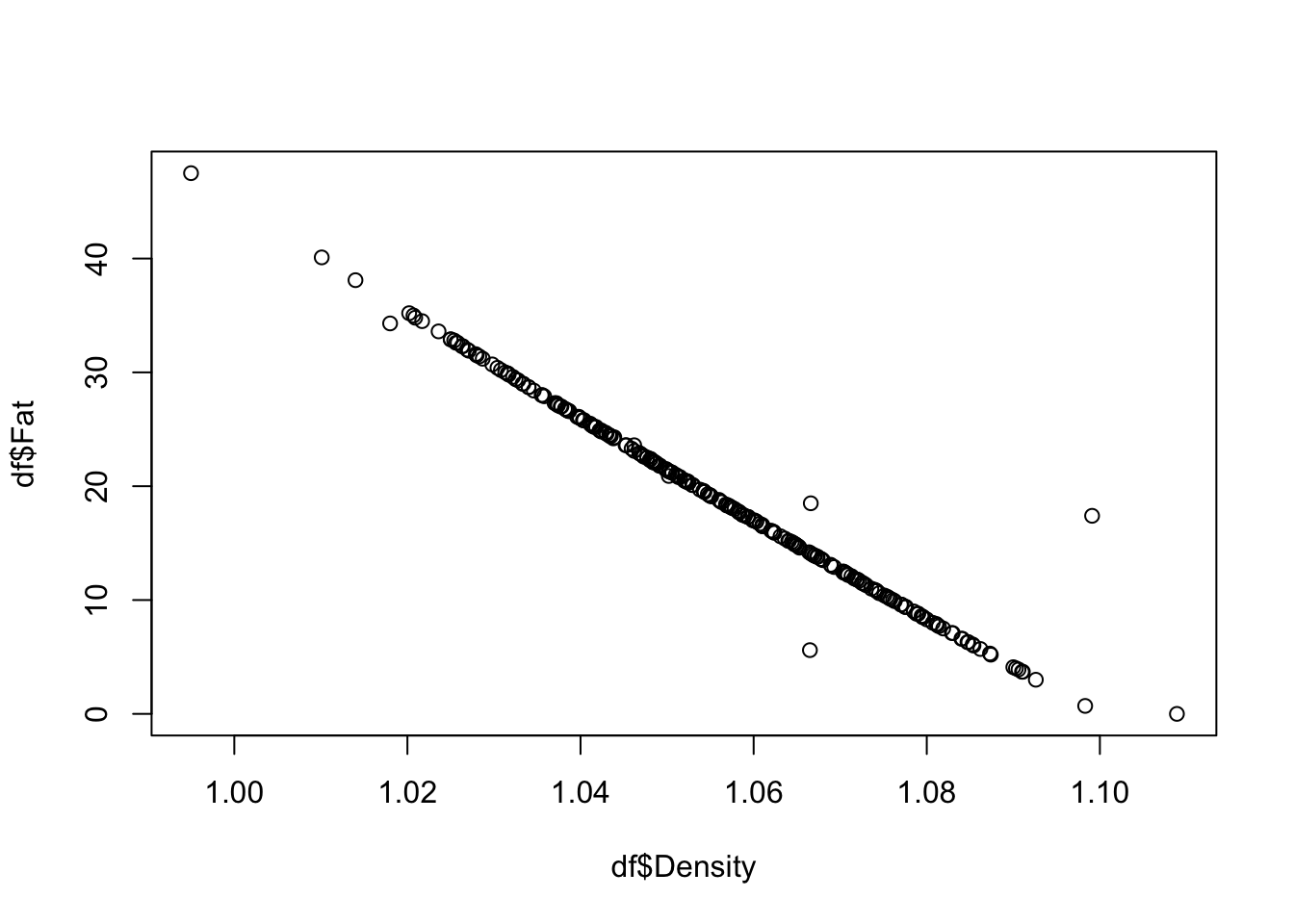
Utilizando ggplot la gráfica podría quedar:
library(ggplot2)
df|>
ggplot(aes(x = Density, y = Fat)) +
geom_point(col="#08a4a7", alpha=0.8) +
geom_smooth(method = "lm", se = FALSE, col="#e9ffff")+
theme_dark()`geom_smooth()` using formula = 'y ~ x'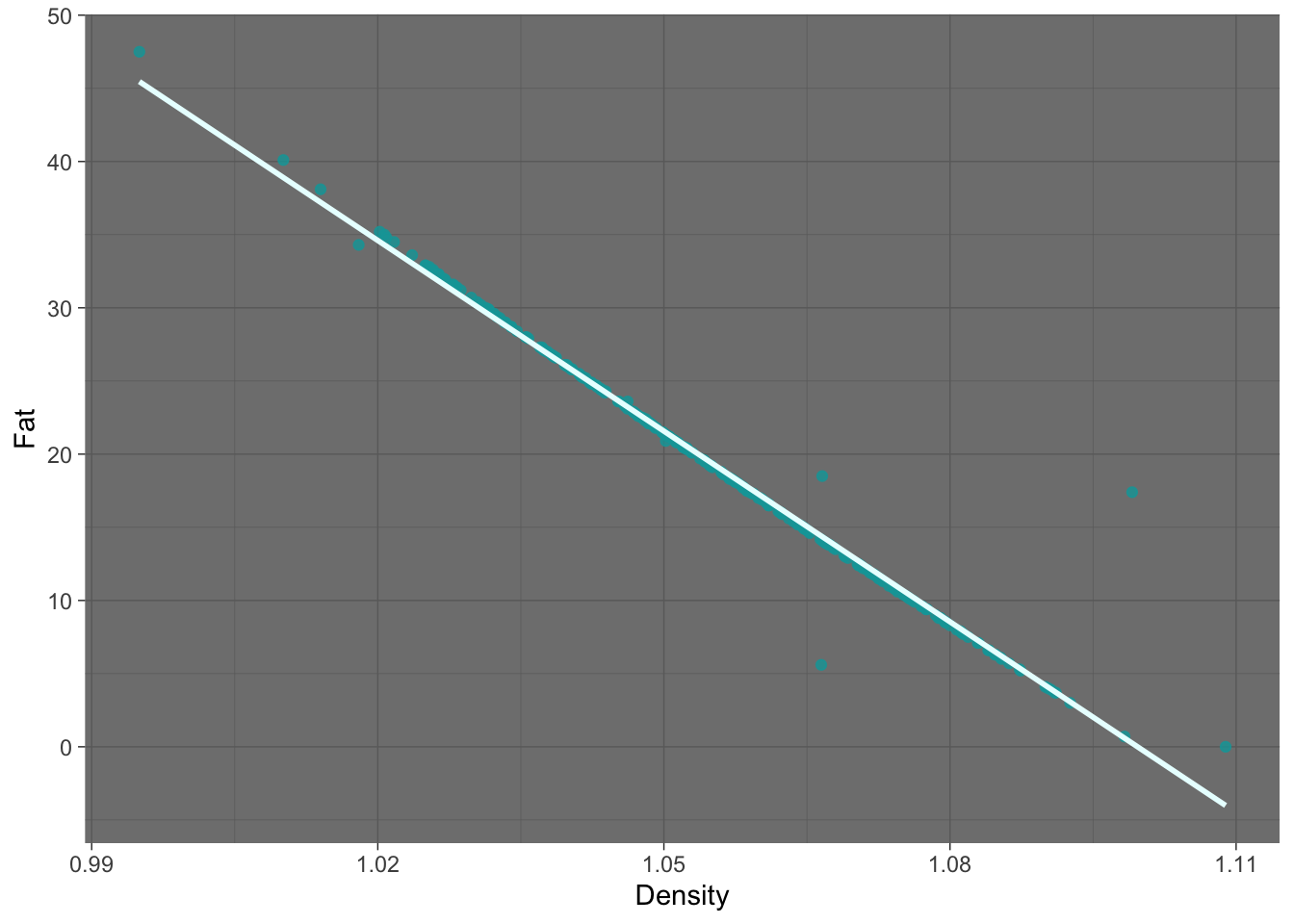
Para obtener los coeficientes de correlación de toda la base:
cor(df) Density Fat Age Weight Height Neck
Density 1.00000000 -0.98778240 -0.27763721 -0.59406188 0.09788114 -0.4729664
Fat -0.98778240 1.00000000 0.29145844 0.61241400 -0.08949538 0.4905919
Age -0.27763721 0.29145844 1.00000000 -0.01274609 -0.17164514 0.1135052
Weight -0.59406188 0.61241400 -0.01274609 1.00000000 0.30827854 0.8307162
Height 0.09788114 -0.08949538 -0.17164514 0.30827854 1.00000000 0.2537099
Neck -0.47296636 0.49059185 0.11350519 0.83071622 0.25370988 1.0000000
Chest -0.68259865 0.70262034 0.17644968 0.89419052 0.13489181 0.7848350
Abdomen -0.79895463 0.81343228 0.23040942 0.88799494 0.08781291 0.7540774
Hip -0.60933143 0.62520092 -0.05033212 0.94088412 0.17039426 0.7349579
Thigh -0.55309098 0.55960753 -0.20009576 0.86869354 0.14843561 0.6956973
Knee -0.49504035 0.50866524 0.01751569 0.85316739 0.28605321 0.6724050
Ankle -0.26489003 0.26596977 -0.10505810 0.61368542 0.26474369 0.4778924
Biceps -0.48710872 0.49327113 -0.04116212 0.80041593 0.20781557 0.7311459
Forearm -0.35164842 0.36138690 -0.08505555 0.63030143 0.22864922 0.6236603
Wrist -0.32571598 0.34657486 0.21353062 0.72977489 0.32206533 0.7448264
Chest Abdomen Hip Thigh Knee Ankle
Density -0.6825987 -0.79895463 -0.60933143 -0.5530910 -0.49504035 -0.2648900
Fat 0.7026203 0.81343228 0.62520092 0.5596075 0.50866524 0.2659698
Age 0.1764497 0.23040942 -0.05033212 -0.2000958 0.01751569 -0.1050581
Weight 0.8941905 0.88799494 0.94088412 0.8686935 0.85316739 0.6136854
Height 0.1348918 0.08781291 0.17039426 0.1484356 0.28605321 0.2647437
Neck 0.7848350 0.75407737 0.73495788 0.6956973 0.67240498 0.4778924
Chest 1.0000000 0.91582767 0.82941992 0.7298586 0.71949640 0.4829879
Abdomen 0.9158277 1.00000000 0.87406618 0.7666239 0.73717888 0.4532227
Hip 0.8294199 0.87406618 1.00000000 0.8964098 0.82347262 0.5583868
Thigh 0.7298586 0.76662393 0.89640979 1.0000000 0.79917030 0.5397971
Knee 0.7194964 0.73717888 0.82347262 0.7991703 1.00000000 0.6116082
Ankle 0.4829879 0.45322269 0.55838682 0.5397971 0.61160820 1.0000000
Biceps 0.7279075 0.68498272 0.73927252 0.7614774 0.67870883 0.4848545
Forearm 0.5801727 0.50331609 0.54501412 0.5668422 0.55589819 0.4190500
Wrist 0.6601623 0.61983243 0.63008954 0.5586848 0.66450729 0.5661946
Biceps Forearm Wrist
Density -0.48710872 -0.35164842 -0.3257160
Fat 0.49327113 0.36138690 0.3465749
Age -0.04116212 -0.08505555 0.2135306
Weight 0.80041593 0.63030143 0.7297749
Height 0.20781557 0.22864922 0.3220653
Neck 0.73114592 0.62366027 0.7448264
Chest 0.72790748 0.58017273 0.6601623
Abdomen 0.68498272 0.50331609 0.6198324
Hip 0.73927252 0.54501412 0.6300895
Thigh 0.76147745 0.56684218 0.5586848
Knee 0.67870883 0.55589819 0.6645073
Ankle 0.48485454 0.41904999 0.5661946
Biceps 1.00000000 0.67825513 0.6321264
Forearm 0.67825513 1.00000000 0.5855883
Wrist 0.63212642 0.58558825 1.0000000Predefinidamente en R obtenemos el coeficiente de correlación de pearson. Si quisieramos emplear el coeficiente de correlación de spearman, podemos hacerlo de la siguiente manera:
cor(df, method = "spearman") Density Fat Age Weight Height
Density 1.00000000 -0.993404323 -0.26269733 -0.60144106 0.014081872
Fat -0.99340432 1.000000000 0.27469064 0.61286851 -0.008456305
Age -0.26269733 0.274690642 1.00000000 -0.01300141 -0.230043110
Weight -0.60144106 0.612868513 -0.01300141 1.00000000 0.515336168
Height 0.01408187 -0.008456305 -0.23004311 0.51533617 1.000000000
Neck -0.47950949 0.491252281 0.12310818 0.80476777 0.321004209
Chest -0.66282362 0.673999018 0.16782571 0.89739613 0.257839693
Abdomen -0.80764992 0.816248250 0.22103581 0.87397187 0.219105351
Hip -0.60132153 0.612124869 -0.07203904 0.92942651 0.421303295
Thigh -0.53723555 0.544957052 -0.20302107 0.83706722 0.332800841
Knee -0.47953057 0.489284616 0.00551996 0.82962994 0.494740803
Ankle -0.29691723 0.299645674 -0.13084711 0.69560365 0.458250549
Biceps -0.48919274 0.493651842 -0.04404584 0.78220426 0.301624270
Forearm -0.38332269 0.392696388 -0.06691445 0.74995492 0.334254215
Wrist -0.30176899 0.313796524 0.21659214 0.69926978 0.398278857
Neck Chest Abdomen Hip Thigh Knee
Density -0.4795095 -0.6628236 -0.8076499 -0.60132153 -0.5372355 -0.47953057
Fat 0.4912523 0.6739990 0.8162483 0.61212487 0.5449571 0.48928462
Age 0.1231082 0.1678257 0.2210358 -0.07203904 -0.2030211 0.00551996
Weight 0.8047678 0.8973961 0.8739719 0.92942651 0.8370672 0.82962994
Height 0.3210042 0.2578397 0.2191054 0.42130329 0.3328008 0.49474080
Neck 1.0000000 0.7821002 0.7431570 0.70896007 0.6494913 0.64100422
Chest 0.7821002 1.0000000 0.8952563 0.81195787 0.7198653 0.71108092
Abdomen 0.7431570 0.8952563 1.0000000 0.84511166 0.7341936 0.71587266
Hip 0.7089601 0.8119579 0.8451117 1.00000000 0.8782066 0.80293643
Thigh 0.6494913 0.7198653 0.7341936 0.87820658 1.0000000 0.76994585
Knee 0.6410042 0.7110809 0.7158727 0.80293643 0.7699459 1.00000000
Ankle 0.5176869 0.5587411 0.5066666 0.62527112 0.6128329 0.72537138
Biceps 0.6947236 0.7400505 0.6729340 0.73595165 0.7362760 0.63189135
Forearm 0.7137403 0.6813946 0.5948076 0.67921972 0.6650186 0.62543231
Wrist 0.7216557 0.6506508 0.5939925 0.59280726 0.4963634 0.64768125
Ankle Biceps Forearm Wrist
Density -0.2969172 -0.48919274 -0.38332269 -0.3017690
Fat 0.2996457 0.49365184 0.39269639 0.3137965
Age -0.1308471 -0.04404584 -0.06691445 0.2165921
Weight 0.6956036 0.78220426 0.74995492 0.6992698
Height 0.4582505 0.30162427 0.33425421 0.3982789
Neck 0.5176869 0.69472359 0.71374034 0.7216557
Chest 0.5587411 0.74005051 0.68139462 0.6506508
Abdomen 0.5066666 0.67293396 0.59480757 0.5939925
Hip 0.6252711 0.73595165 0.67921972 0.5928073
Thigh 0.6128329 0.73627597 0.66501861 0.4963634
Knee 0.7253714 0.63189135 0.62543231 0.6476813
Ankle 1.0000000 0.52706875 0.56207850 0.6521559
Biceps 0.5270687 1.00000000 0.76298050 0.6017552
Forearm 0.5620785 0.76298050 1.00000000 0.6415378
Wrist 0.6521559 0.60175515 0.64153784 1.0000000Este argumento también puede ser utilizado para la función cor.test() y para el coeficiente de correlación de kendall
En R base también podemos utilizar la función pairs() para obtener una matriz de gráficos de dispersión y correlación.
pairs(df[,1:8])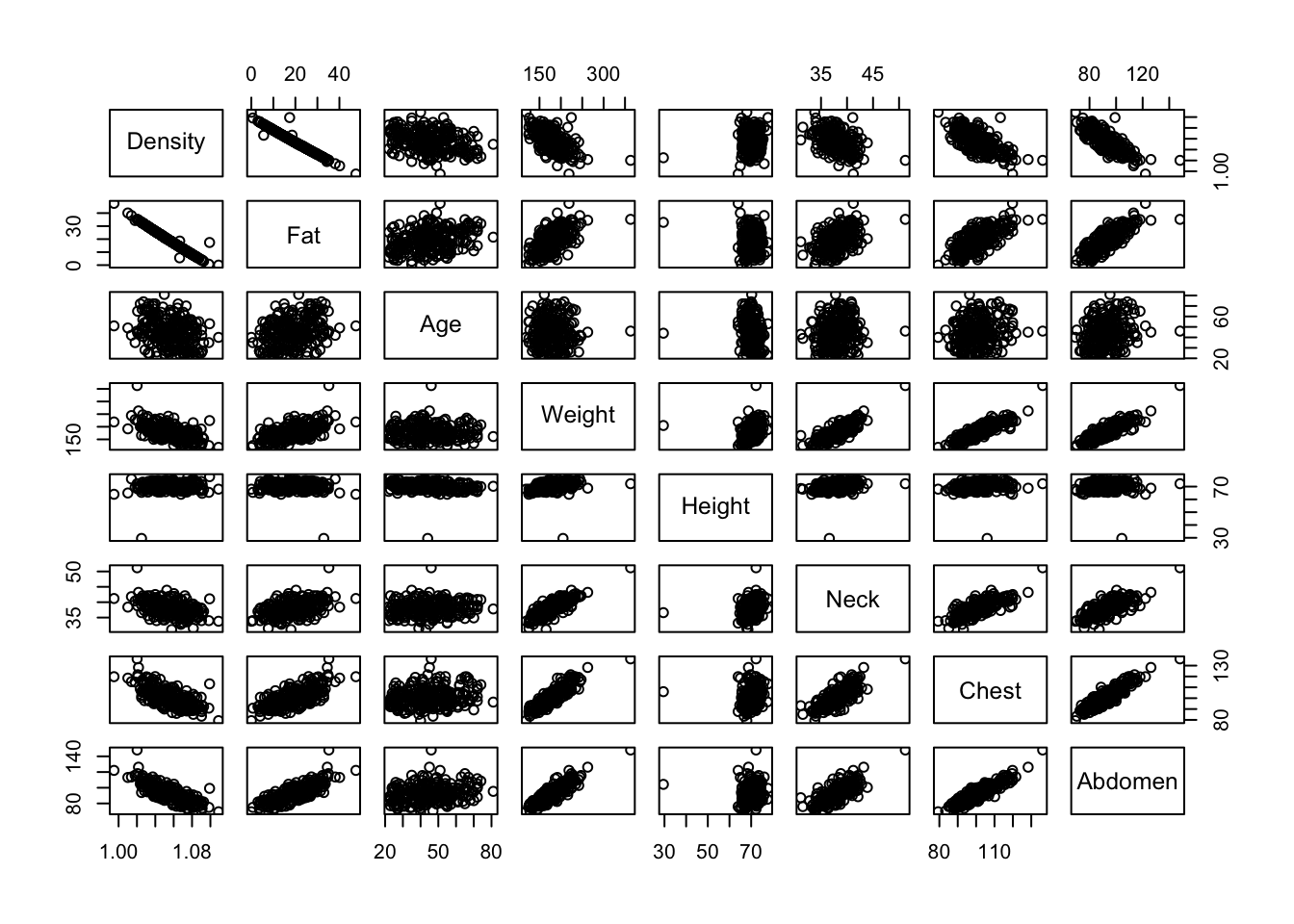
Utilizando al librería corrplot
# Instalar y cargar la librería
install.packages("corrplot")
library(corrplot)
# Cálculo de la matriz de correlación
cor_matrix <- cor(df, use = "complete.obs")
# Generar gráfico de correlación
corrplot(cor_matrix, method = "circle")corrplot 0.94 loaded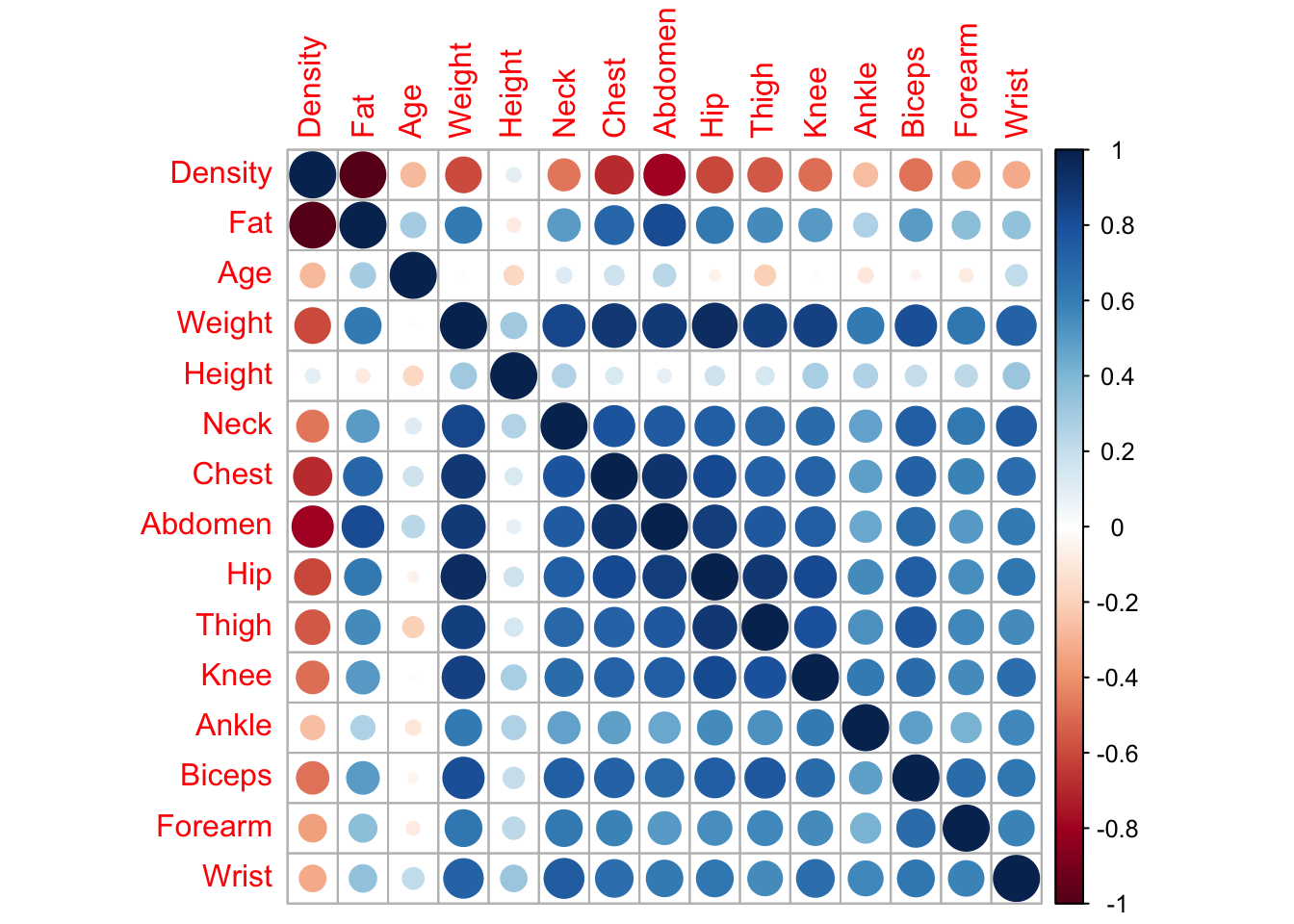
Podemos modificar algunos de los argumentos:
Utilizando ggcorrplot
# Instalar y cargar la librería
install.packages("ggcorrplot")
library(ggcorrplot)
# Cálculo de la matriz de correlación
cor_matrix <- cor(df, use = "complete.obs")
# Generar gráfico de correlación
ggcorrplot(cor_matrix, lab = TRUE)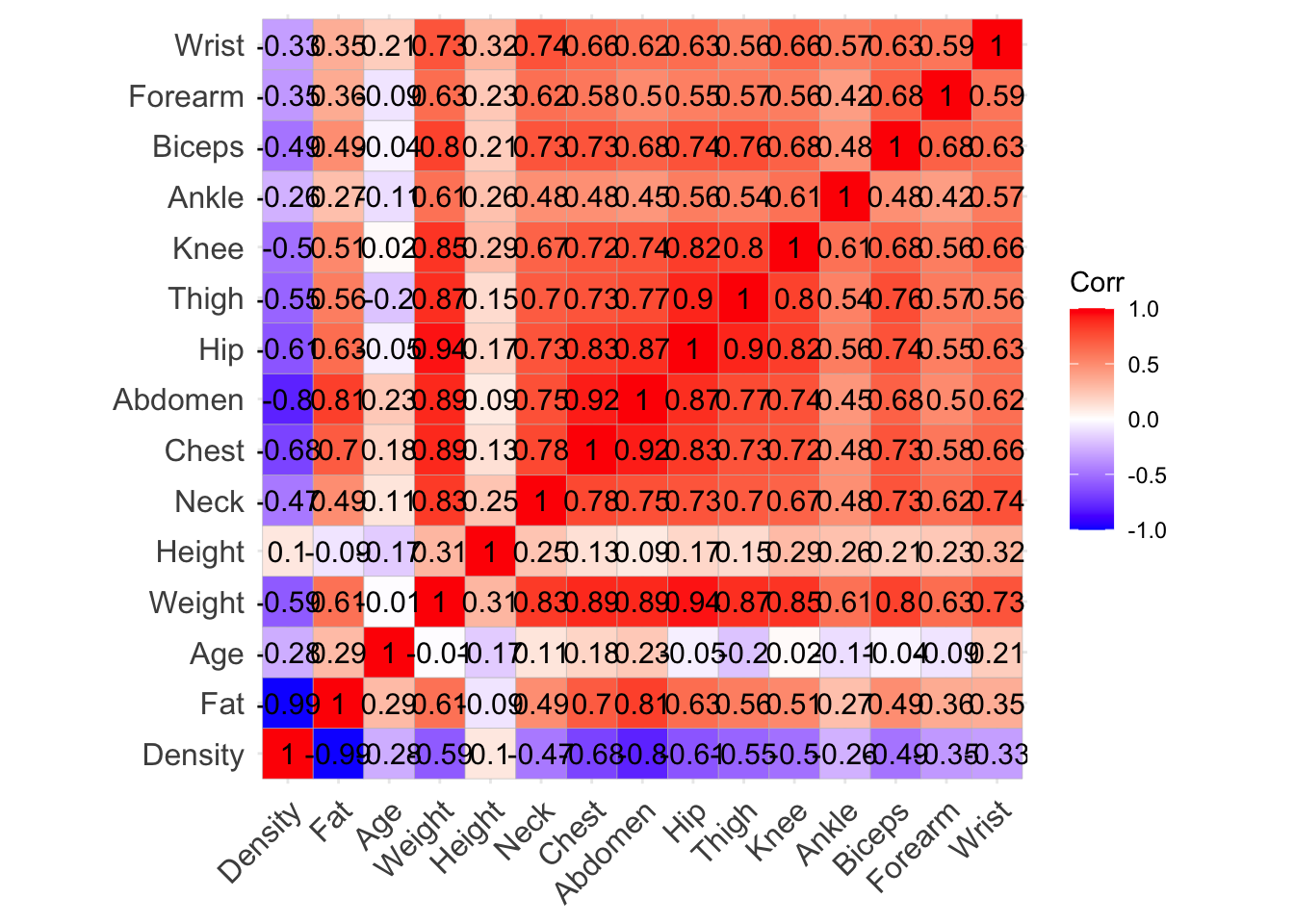
Podemos hacer algunas modificaciones:
# Generar gráfico de correlación
ggcorrplot(cor_matrix, lab = TRUE, type = "lower",
colors = c("#1e4356" , "#f3f8fa", "#a2cce3"),
method = "circle", insig = "blank") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))+
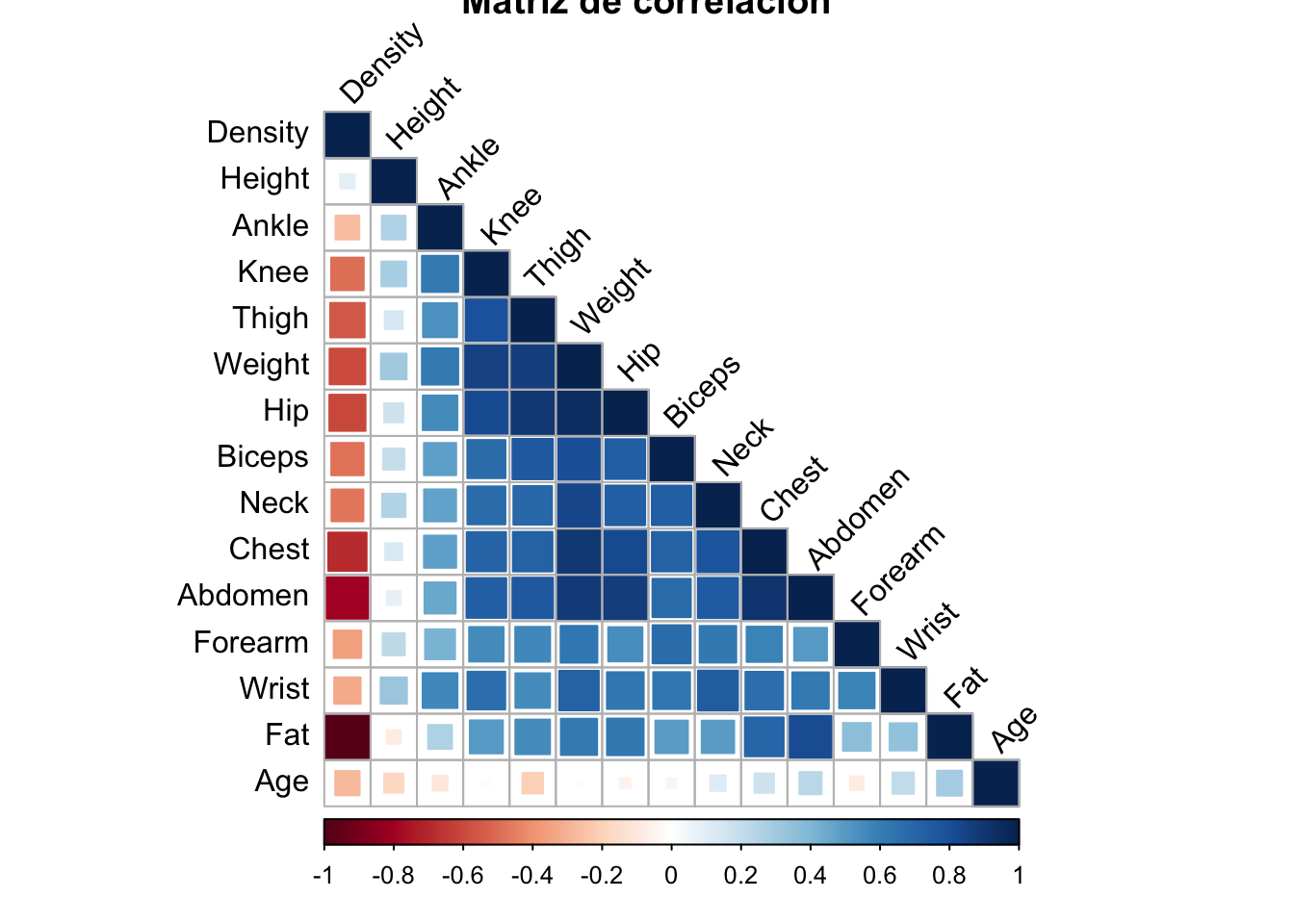
labs(title = "Matriz de correlación", x="", y="")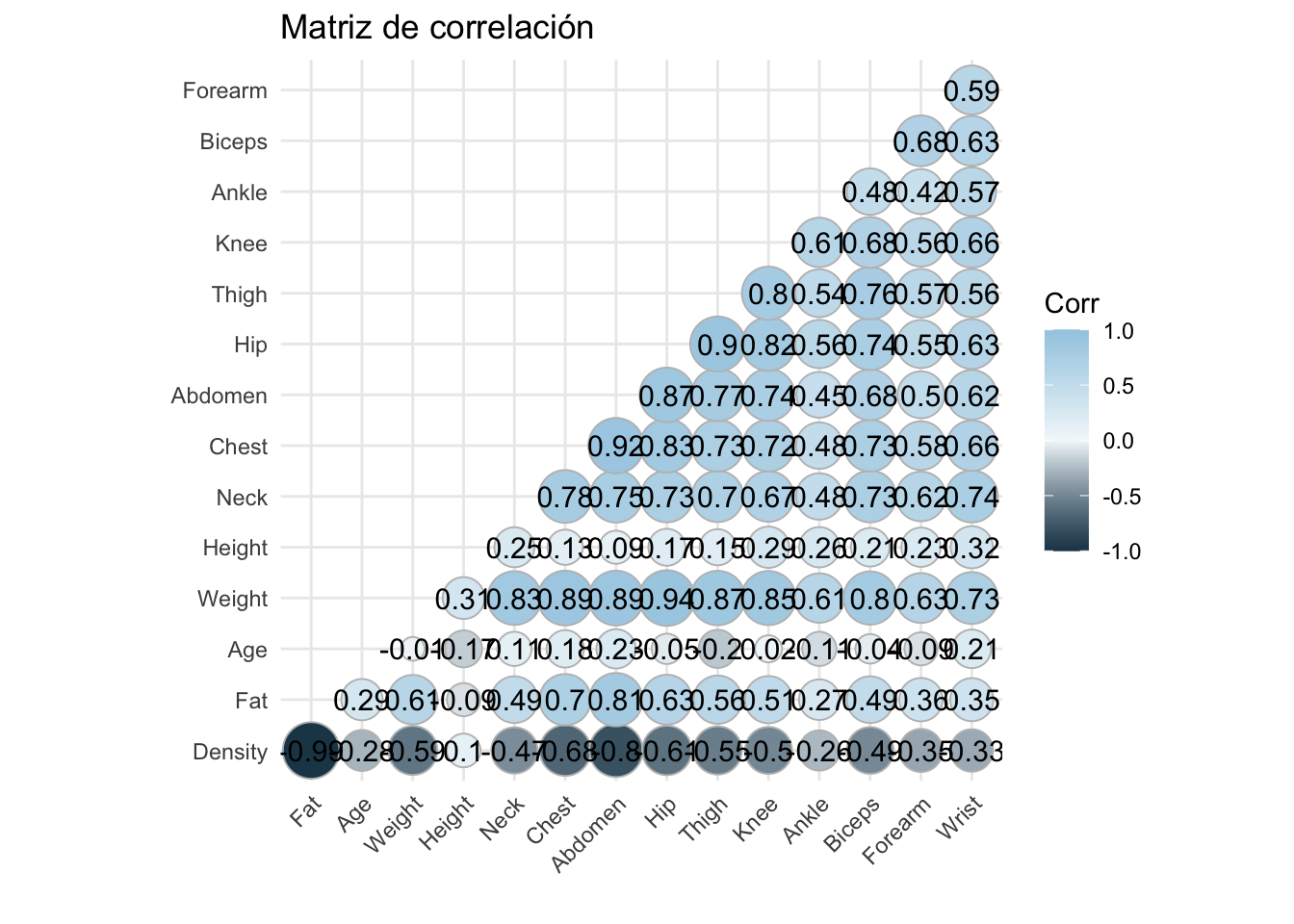
GGally
# Instalar y cargar la librería
install.packages("GGally")
library(GGally)
# Gráfico de pares con correlación
ggpairs(df[,1:8] )Registered S3 method overwritten by 'GGally':
method from
+.gg ggplot2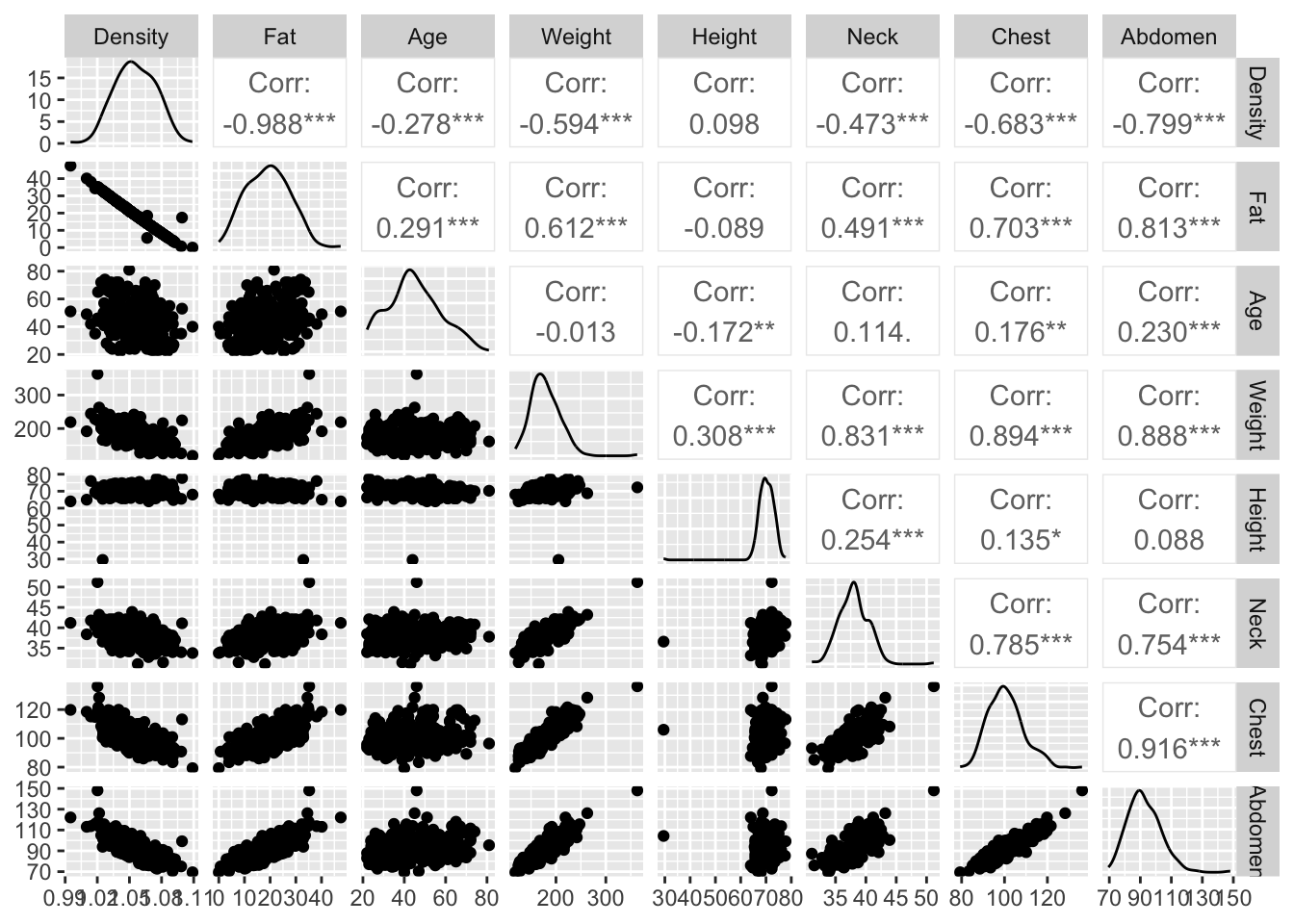
ggstatplot
library(ggstatsplot)You can cite this package as:
Patil, I. (2021). Visualizations with statistical details: The 'ggstatsplot' approach.
Journal of Open Source Software, 6(61), 3167, doi:10.21105/joss.03167df |>
ggcorrmat()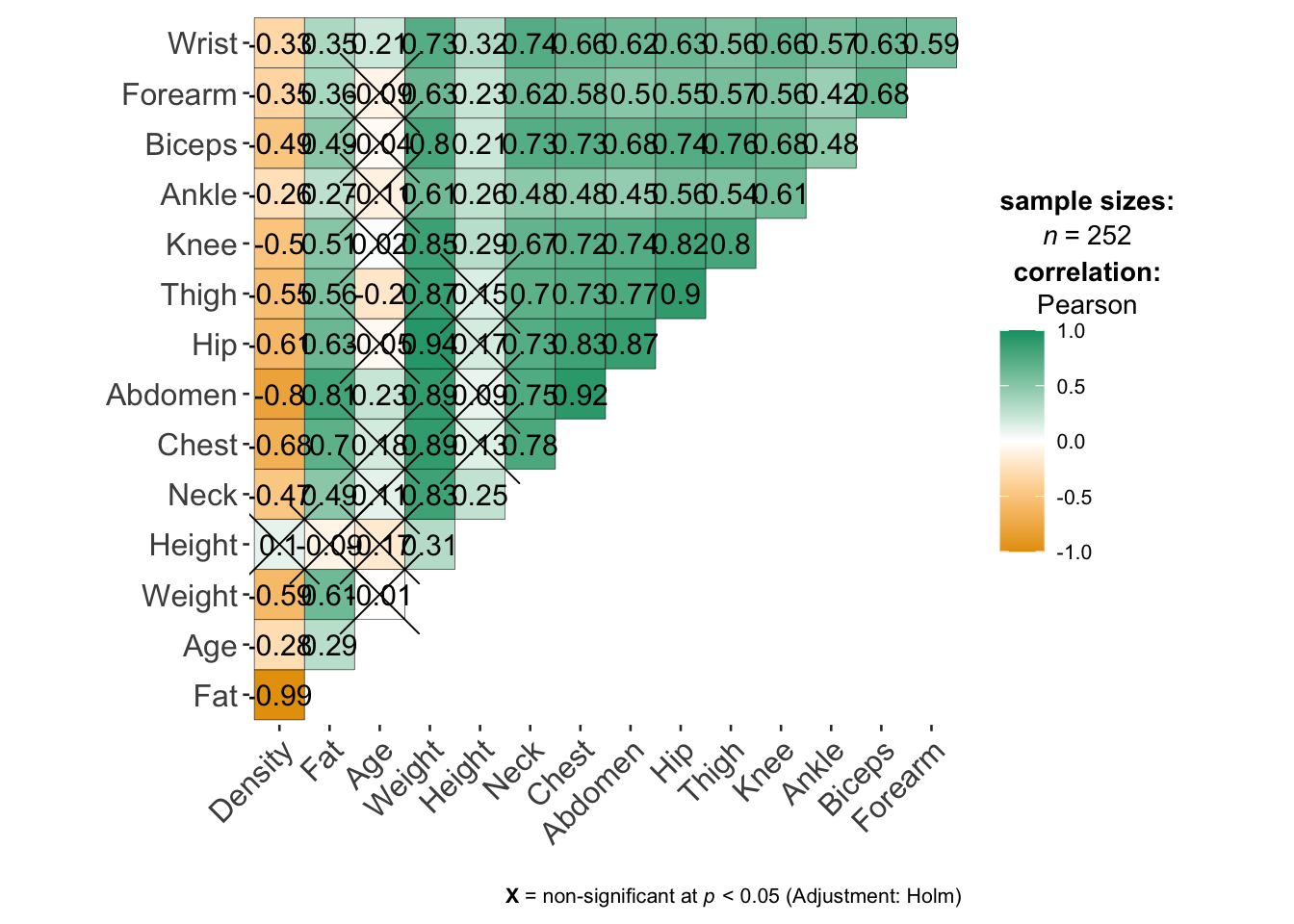
PerformanceAnalytics
# Instalar y cargar la librería
install.packages("PerformanceAnalytics")
library(PerformanceAnalytics)
# Gráfico de correlación avanzado
chart.Correlation(df[,1:8], histogram = TRUE, pch = 19)Loading required package: xtsLoading required package: zoo
Attaching package: 'zoo'The following objects are masked from 'package:base':
as.Date, as.Date.numeric
Attaching package: 'PerformanceAnalytics'The following object is masked from 'package:graphics':
legendWarning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter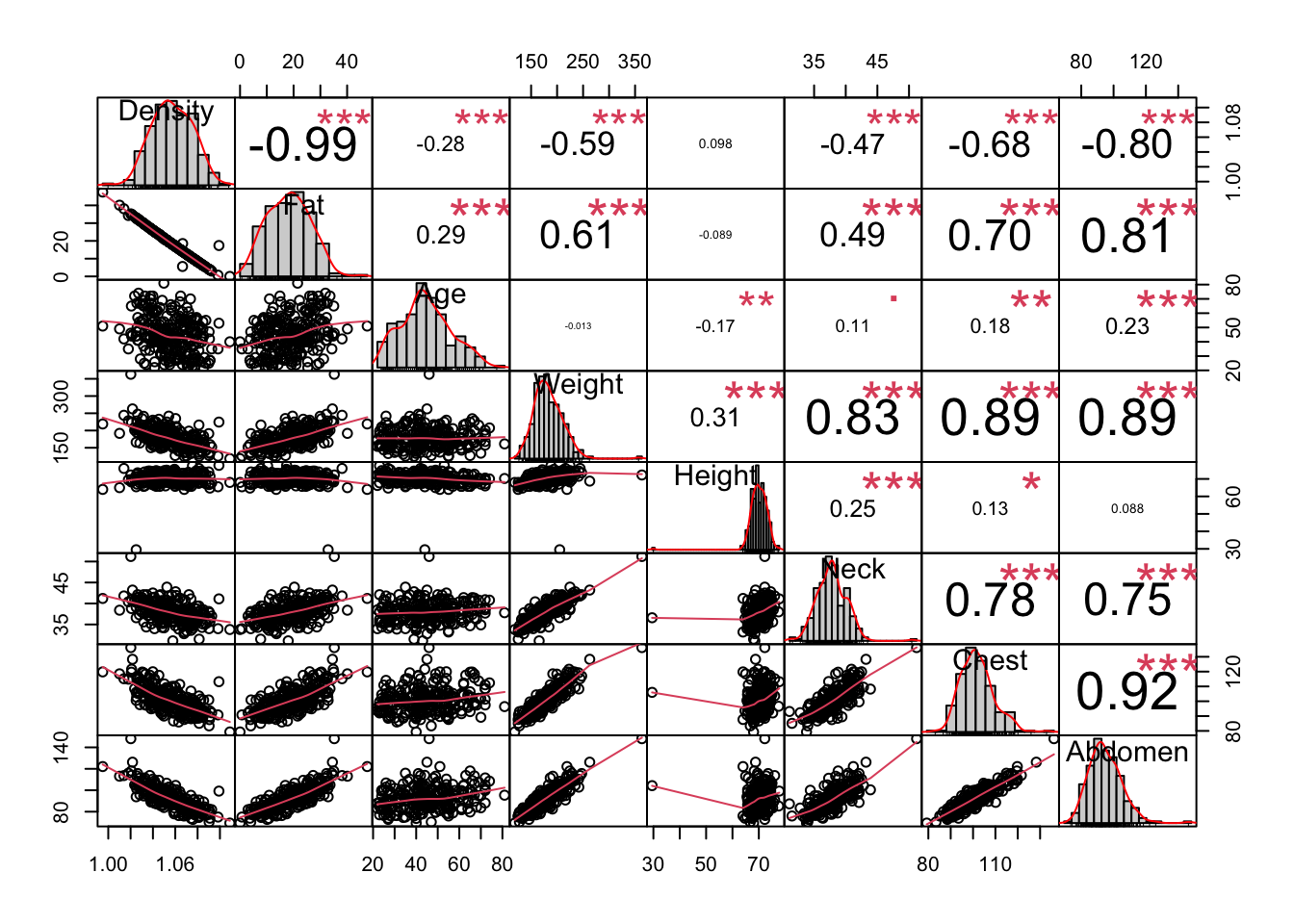
Librería corrr
# Instalar y cargar la librería
install.packages("corrr")
library(corrr)
# Calcular la matriz de correlación
correlation_matrix <- correlate(df)
# Visualizar la matriz de correlación en formato tidy
correlation_matrix
# Generar un gráfico con correlaciones significativas
rplot(correlation_matrix)Correlation computed with
• Method: 'pearson'
• Missing treated using: 'pairwise.complete.obs'# A tibble: 15 × 16
term Density Fat Age Weight Height Neck Chest Abdomen Hip
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Density NA -0.988 -0.278 -0.594 0.0979 -0.473 -0.683 -0.799 -0.609
2 Fat -0.988 NA 0.291 0.612 -0.0895 0.491 0.703 0.813 0.625
3 Age -0.278 0.291 NA -0.0127 -0.172 0.114 0.176 0.230 -0.0503
4 Weight -0.594 0.612 -0.0127 NA 0.308 0.831 0.894 0.888 0.941
5 Height 0.0979 -0.0895 -0.172 0.308 NA 0.254 0.135 0.0878 0.170
6 Neck -0.473 0.491 0.114 0.831 0.254 NA 0.785 0.754 0.735
7 Chest -0.683 0.703 0.176 0.894 0.135 0.785 NA 0.916 0.829
8 Abdomen -0.799 0.813 0.230 0.888 0.0878 0.754 0.916 NA 0.874
9 Hip -0.609 0.625 -0.0503 0.941 0.170 0.735 0.829 0.874 NA
10 Thigh -0.553 0.560 -0.200 0.869 0.148 0.696 0.730 0.767 0.896
11 Knee -0.495 0.509 0.0175 0.853 0.286 0.672 0.719 0.737 0.823
12 Ankle -0.265 0.266 -0.105 0.614 0.265 0.478 0.483 0.453 0.558
13 Biceps -0.487 0.493 -0.0412 0.800 0.208 0.731 0.728 0.685 0.739
14 Forearm -0.352 0.361 -0.0851 0.630 0.229 0.624 0.580 0.503 0.545
15 Wrist -0.326 0.347 0.214 0.730 0.322 0.745 0.660 0.620 0.630
# ℹ 6 more variables: Thigh <dbl>, Knee <dbl>, Ankle <dbl>, Biceps <dbl>,
# Forearm <dbl>, Wrist <dbl>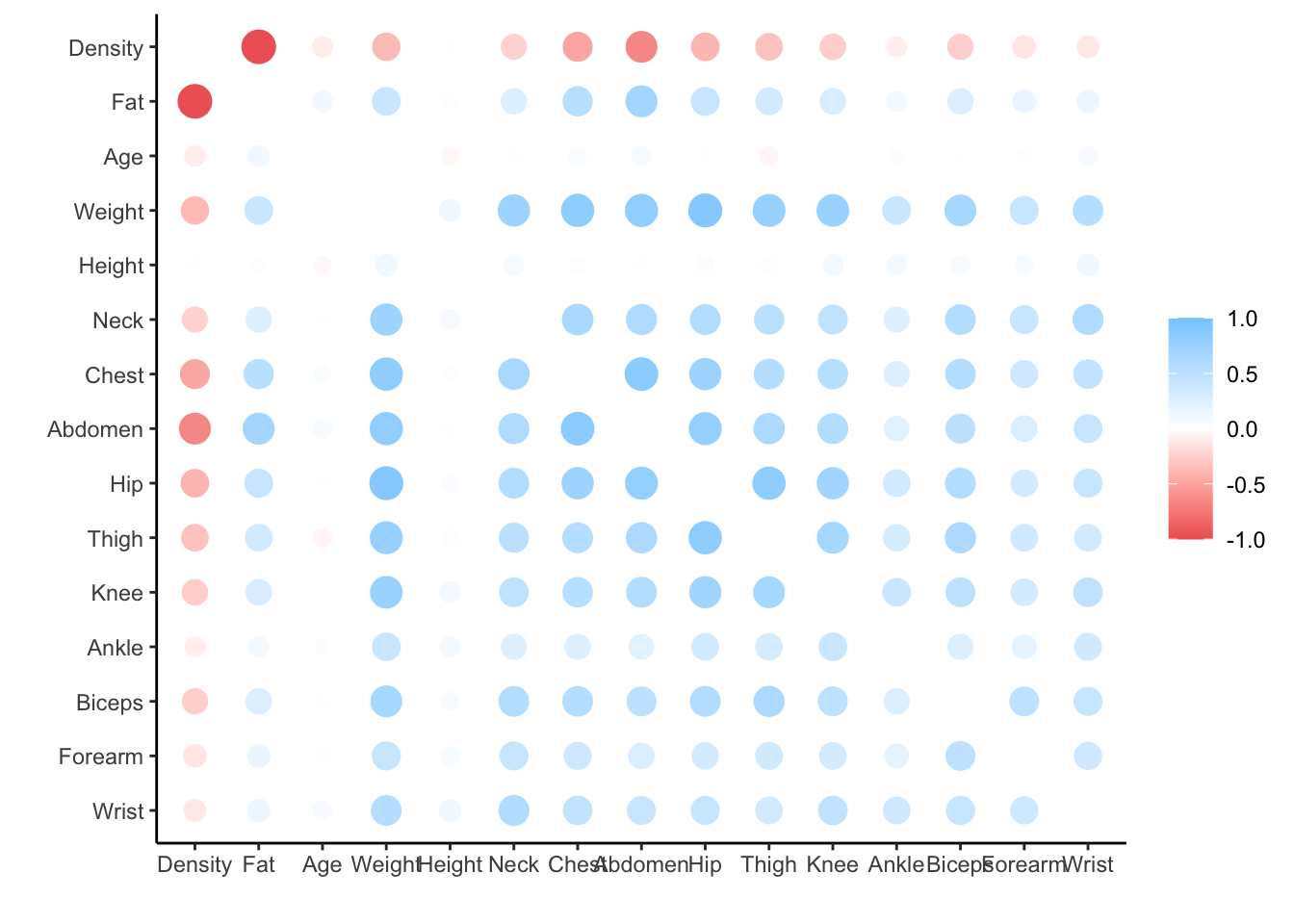
Hearmaply
# Instalar y cargar la librería
install.packages("heatmaply")
library(heatmaply)
# Cálculo de la matriz de correlación
cor_matrix <- cor(df, use = "complete.obs")
# Generar mapa de calor interactivo
heatmaply(cor_matrix, k_col = 2, k_row = 2)Loading required package: plotly
Attaching package: 'plotly'The following object is masked from 'package:ggplot2':
last_plotThe following object is masked from 'package:stats':
filterThe following object is masked from 'package:graphics':
layoutLoading required package: viridisLoading required package: viridisLite
======================
Welcome to heatmaply version 1.5.0
Type citation('heatmaply') for how to cite the package.
Type ?heatmaply for the main documentation.
The github page is: https://github.com/talgalili/heatmaply/
Please submit your suggestions and bug-reports at: https://github.com/talgalili/heatmaply/issues
You may ask questions at stackoverflow, use the r and heatmaply tags:
https://stackoverflow.com/questions/tagged/heatmaply
======================Warning in doTryCatch(return(expr), name, parentenv, handler): unable to load shared object '/Library/Frameworks/R.framework/Resources/modules//R_X11.so':
dlopen(/Library/Frameworks/R.framework/Resources/modules//R_X11.so, 0x0006): Library not loaded: /opt/X11/lib/libSM.6.dylib
Referenced from: <BDCE065B-0E14-3F82-A5E6-7C0A970A6C32> /Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/modules/R_X11.so
Reason: tried: '/opt/X11/lib/libSM.6.dylib' (no such file), '/System/Volumes/Preboot/Cryptexes/OS/opt/X11/lib/libSM.6.dylib' (no such file), '/opt/X11/lib/libSM.6.dylib' (no such file), '/Library/Frameworks/R.framework/Resources/lib/libSM.6.dylib' (no such file), '/Library/Java/JavaVirtualMachines/jdk-11.0.18+10/Contents/Home/lib/server/libSM.6.dylib' (no such file)install.packages("easystats")library(easystats)# Attaching packages: easystats 0.7.3 (red = needs update)
✔ bayestestR 0.14.0 ✔ correlation 0.8.5
✖ datawizard 0.12.3 ✔ effectsize 0.8.9
✖ insight 0.20.4 ✔ modelbased 0.8.8
✔ performance 0.12.3 ✔ parameters 0.22.2
✔ report 0.5.9 ✔ see 0.9.0
Restart the R-Session and update packages with `easystats::easystats_update()`.correlaciones <- correlation::correlation(df[,1:5])
print(correlaciones)# Correlation Matrix (pearson-method)
Parameter1 | Parameter2 | r | 95% CI | t(250) | p
----------------------------------------------------------------------
Density | Fat | -0.99 | [-0.99, -0.98] | -100.22 | < .001***
Density | Age | -0.28 | [-0.39, -0.16] | -4.57 | < .001***
Density | Weight | -0.59 | [-0.67, -0.51] | -11.68 | < .001***
Density | Height | 0.10 | [-0.03, 0.22] | 1.56 | 0.364
Fat | Age | 0.29 | [ 0.17, 0.40] | 4.82 | < .001***
Fat | Weight | 0.61 | [ 0.53, 0.68] | 12.25 | < .001***
Fat | Height | -0.09 | [-0.21, 0.03] | -1.42 | 0.364
Age | Weight | -0.01 | [-0.14, 0.11] | -0.20 | 0.840
Age | Height | -0.17 | [-0.29, -0.05] | -2.75 | 0.025*
Weight | Height | 0.31 | [ 0.19, 0.42] | 5.12 | < .001***
p-value adjustment method: Holm (1979)
Observations: 252correlaciones|>
summary(redundant = T)|>
plot()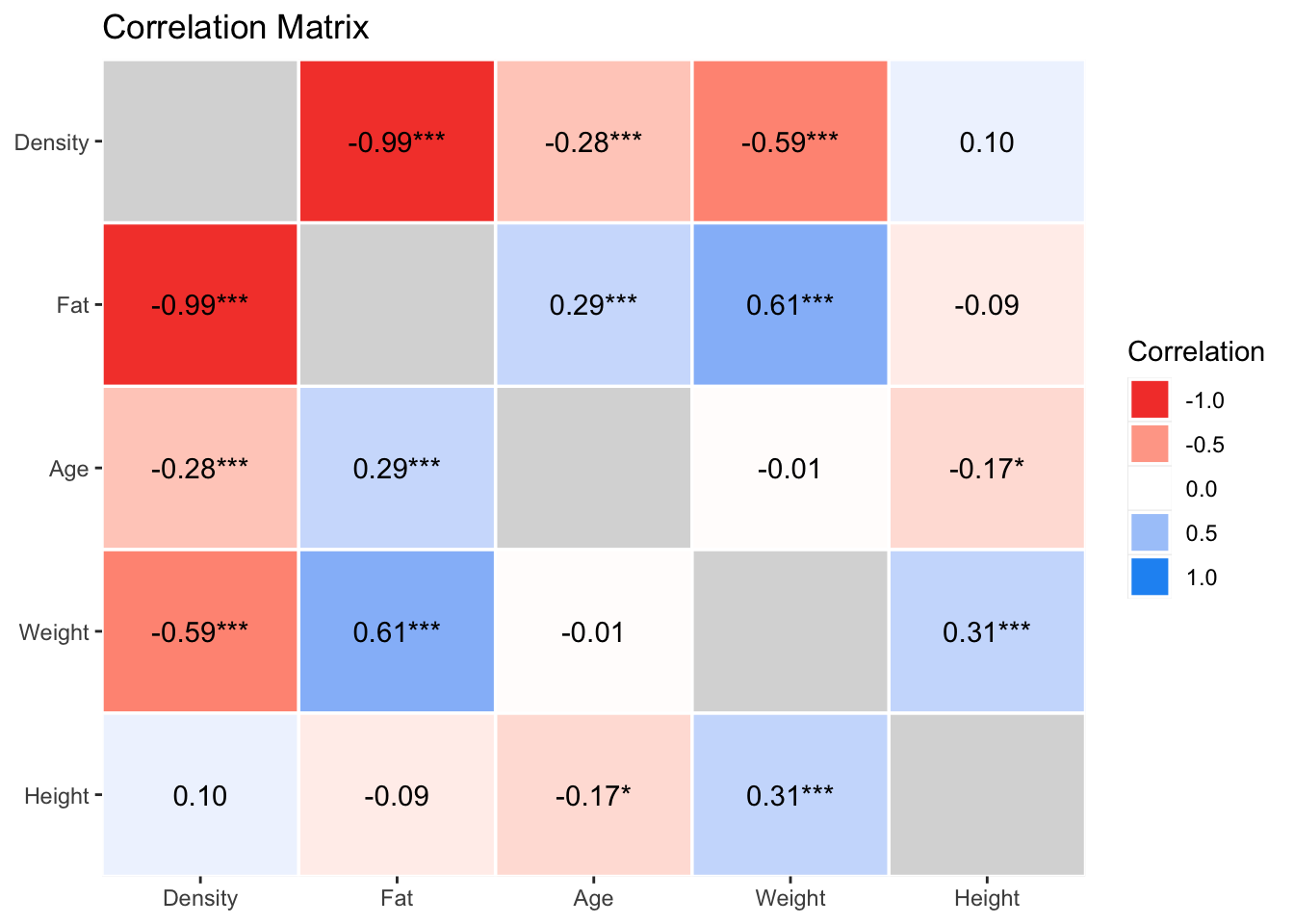
Para correlaciones parciales.
Las correlaciones parciales miden la relación entre dos variables mientras se controlan o eliminan los efectos de una o más variables adicionales. Es decir, muestran el grado de asociación entre dos variables después de ajustar por el impacto de otras variables que podrían estar influyendo en esa relación.
Una comparación entre las correlaciones parciales y simple se muestra a continuación:
Correlación simple: Indica la relación entre dos variables sin considerar ninguna otra.
Correlación parcial: Controla el efecto de una o más variables adicionales, eliminando su influencia para medir la relación entre dos variables de manera más precisa.
La librería easystats tiene herramientas para la realización de gráficos de correlaciones parciales:
correlation::correlation(df[,1:5], partial = TRUE)|>
plot()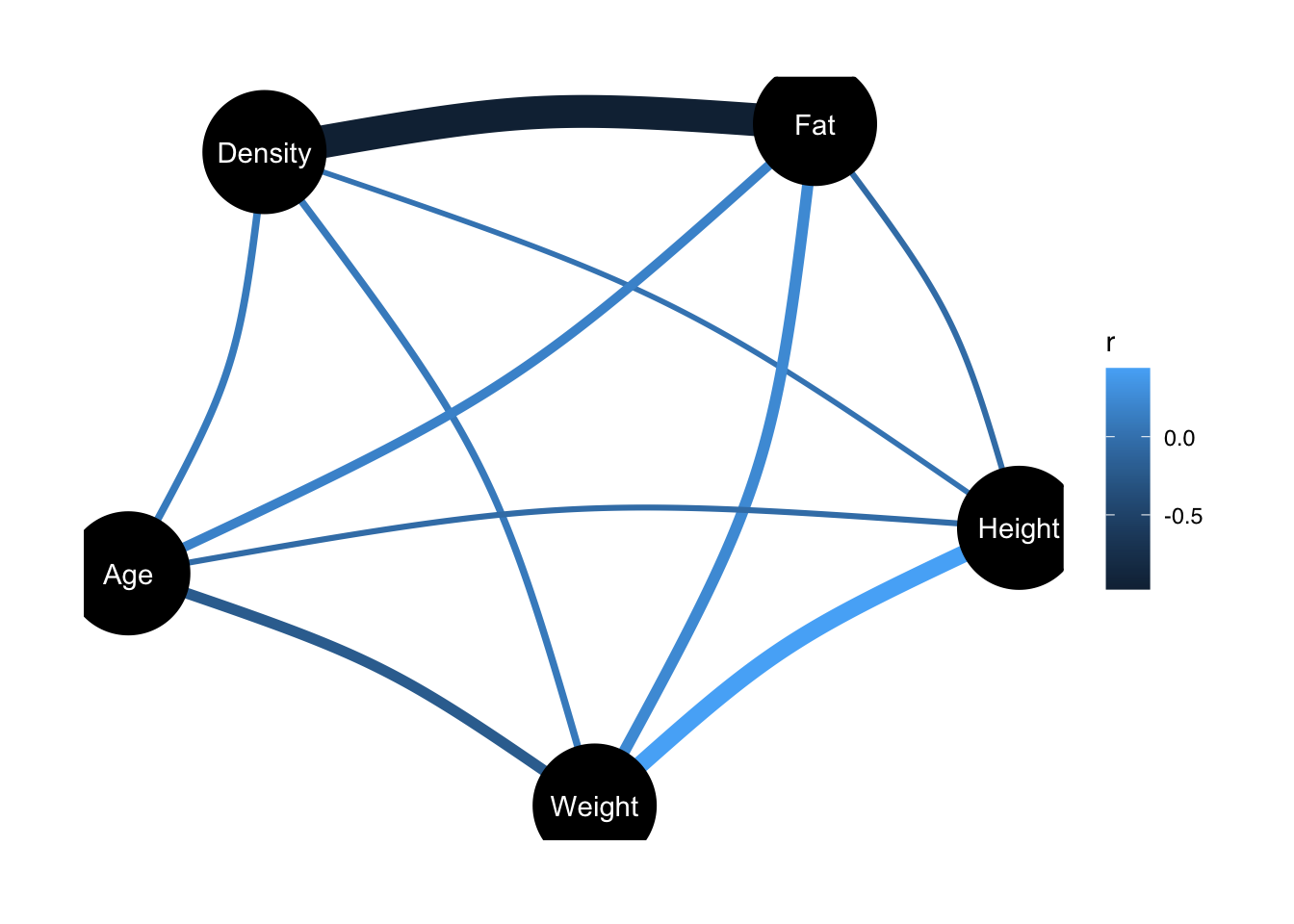
Una interpretación sencilla de la gráfica anterior es:
- Los nodos (círculos) representan las diferentes variables en tu análisis (Density, Fat, Height, Weight, Age).
- Las líneas entre los nodos representan las correlaciones parciales entre esas variables.
- El grosor y el color de las líneas indican la fuerza y dirección de la correlación:
- Colores oscuros más cercanos al negro o azul oscuro indican correlaciones negativas fuertes.
- Colores más claros indican correlaciones más débiles.
- El grosor refleja la magnitud de la correlación.
- La barra de color a la derecha es una leyenda que muestra cómo interpretar el color de las líneas según el valor de la correlación parcial.