| Density | Fat |
|---|---|
| 1.0708 | 12.3 |
| 1.0853 | 6.1 |
| 1.0414 | 25.3 |
| 1.0751 | 10.4 |
| 1.0340 | 28.7 |
| 1.0502 | 20.9 |
Correlación. Aspectos teóricos
Bioestadística Avanzada/Posgrados CUCS
Relación de dos variables numéricas
¿Qué hacer cuando se busca evaluar la relación entre dos variables numéricas?
Relación de dos variables numéricas
Relación de dos varaibles numéricas
Transformar una de las variables cuantitativas a un factor y poder hacer la comparación de la segunda variable cuantitativa entre este factor. Sin embargo, este proceso muchas de las ocasiones, fomenta la pérdida de información.
La segunda opción es emplear técnicas de regresión o de
correlación
Diferencias entre correlación y regresión
Por definición la la correlación mide la asociación de dos variables numéricas y en cierta medida mide que tanto cambia una variable con respecto al cambio de la otra. Aunque este relación nunca será causal.
Mientras que la La regresión se usa para explicar o modelar la relación entre una variable continua Y, llamada variable respuesta o variable dependiente.
Diferencias entre correlación y regresión
- La correlación se usa para medir el grado de asociación entre dos variables sin implicar causalidad, mientras que la regresión lineal se utiliza para generar un modelo matemático que permita predecir el valor de una variable a partir de la otra.
Diferencias entre correlación y regresión
- A diferencia de la regresión lineal, la correlación no tiene en cuenta la asignación de las variables a X e Y, únicamente mide la relación entre dos variables y no es necesario que una de ellas sea dependiente o independiente. De hecho en la correlación no hay una variable dependiente ni independiente (Y y X, respectivamente). En cambio, la regresión lineal si hay una variable dependiente (Y) que dependerá de los cambios que suceden en un variable independiente (X).
Diferencias entre correlación y regresión
- A nivel experimental, la correlación se suele emplear cuando ninguna de las variables se ha controlado, simplemente se han medido ambas y se desea saber si están relacionadas. En el caso de estudios de regresión lineal, es más común que una de las variables se controle (tiempo, concentración de reactivo, temperatura…) y se mida la otra.
Diferencias entre correlación y regresión
- Es común que los estudios de correlación precedan a los de regresión lineal para analizar la relación entre las variables y, si se comprueba que están correlacionadas, se procede a generar el modelo de regresión lineal. Es importante tener en cuenta que la regresión lineal no implica causalidad, sino que proporciona una manera de predecir la relación entre las variables.
Diferencias entre correlación y regresión
La correlación es una medida estadística que indica el grado de asociación entre dos variables, pero no implica causalidad. En cambio, la regresión lineal es un modelo matemático que puede utilizarse para predecir la relación entre dos variables y puede proporcionar información sobre la causalidad. En resumen, la correlación se utiliza para medir la fuerza de la relación entre dos variables, mientras que la regresión lineal se utiliza para modelar y predecir la relación entre ellas.
Pruebas de correlación
- Su finalidad es examinar la dirección y la magnitud de la asociación entre dos variables cuantitativas.
- La correlación es una medida que va de -1 a 1, donde -1 indica una correlación negativa perfecta, 0 indica que no hay correlación y 1 indica una correlación positiva perfecta.
- La correlación no implica causalidad. Aunque dos variables puedan estar correlacionadas, no significa que una variable cause la otra.
- La correlación se puede calcular utilizando diferentes métodos, siendo el coeficiente de correlación de Pearson el más común, sobre todo cuando los datos tienen una relación lineal.
Preubas de correlación
- La correlación es simétrica, es decir, que la correlación entre A y B es igual a la correlación entre B y A.
- Permite conocer si al aumentar una variable, aumenta la otra o disminuye.
- Si la relación entre dos variables es perfecta e inversa, r=–1, mientras que si es lineal y directa, r=1.
- Cuando las dos variables no están correlacionadas, r=0
Pruebas de correlación

Pruebas de correlación
- 0.1: Efecto pequeño (relación pequeña)
- 0.3: Efecto moderado (Relación moderada)
- 0.5: Efecto fuerte (Relación fuerte)
Fuente: https://psychology.emory.edu/clinical/bliwise/Tutorials/SCATTER/scatterplots/effect.htm
Purebas de correlación y tamaño del efecto

Coeficiente de correlación pearson
La formula para estimar el coeficiente de correlación de pearson es:
\[\begin{equation} r_{xy} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i - \bar{y})^2}} \end{equation}\]
En esta fórmula, \(r_{xy}\) representa el coeficiente de correlación entre las variables \(x\) e \(y\). \(x_i\) e \(y_i\) son los valores de las variables \(x\) e \(y\) en la i-ésima observación, mientras que \(\bar{x}\) y \(\bar{y}\) son las medias de x e y, respectivamente.
Coeficiente de correlación pearson
\[\begin{equation} r_{xy} = \frac{cov(x, y)}{s_x s_y} \end{equation}\]
Donde: \(r_{xy}\) representa el coeficiente de correlación entre las variables \(x\) e \(y\). \(cov(x, y)\) es la covarianza entre \(x\) e \(y\), mientras que \(s_x\) y \(s_y\) son las desviaciones estándar de \(x\) e \(y\), respectivamente.
Coeficiente de correlación pearson
Nuestra intención es tratar de demostrar que el coeficiente de correlación es distinto de cero. Por lo tanto:
- \(H_0: r = 0\)
- \(H_A: r \neq 0\)
Para poder concluir si rechazamos o aceptamos nuestra hipótesis, utilizamos la distribución \(t\) y la siguiente formula que :
\[\begin{equation} t = \frac{r_{xy} \sqrt{n-2}}{\sqrt{1-r_{xy}^2}} \end{equation}\]
Coeficiente de correlación pearson
Los supuestos que se deben cumplir para utilizar el coeficiente de correlación de Pearson:
- Las variables se observan sobre una muestra aleatoria de individuos (cada individuo debe tener un par de valores).
- Existe una asociación lineal entre las dos variables.
- Para una prueba de hipótesis válida y cálculo de intervalos de confianza, ambas variables deben tener una distribución aproximadamente normal.
- Ausencia de valores atípicos en el conjunto de datos.
Coeficiete de correlación Spearman
- Asume una relación monotónica (las variables tienden a moverse en la misma dirección relativa, pero no necesariamente a un ritmo constante) entre dos variables.
- El coeficiente de correlación de Spearman se utiliza como una alternativa no paramétrica al coeficiente de correlación de Pearson.
- Se puede utilizar con variables ordinales y se trabaja con rangos.
Coeficiete de correlación Spearman
La estimación del coeficiente de correlación de Spearman \(\rho\) o \(r_s\) se basa en la siguiente ecuación:
\[\begin{equation} \rho = 1 - \frac{6\sum d_i^2}{n(n^2 - 1)} \end{equation}\]
En esta fórmula, \(\rho\) es el coeficiente de correlación de Spearman, \(n\) es el tamaño de la muestra y \(d_i\) es la diferencia en los rangos de los valores i en cada variable.
Coeficiete de correlación Spearman
La hipótesis nula para este coeficiente es: \(H_0: \rho = 0\) que se puede comprobar mediante el estadístico \(t\) con la siguiente formula:
\[\begin{equation} t = \frac{r_s}{\sqrt{\frac{1-r_s^2}{n-2}}} \end{equation}\]
Donde: \(t\) es el valor calculado para la prueba de significancia del coeficiente de correlación de Spearman. \(r_s\) es el coeficiente de correlación de Spearman, y \(n\) es el tamaño de la muestra.
Coeficiete de correlación Spearman
Para utilizar el coeficiente de correlación de Spearman, es necesario que:
- las variables se observen en una muestra aleatoria de individuos y que haya una asociación monótona entre ellas.
- Que la varible utiliazada sea al menos de tipo ordinal.
Coeficiete de correlación Spearman
No olvide que: La asociación monótona indica que las variables tienden a moverse en la misma dirección relativa, pero no necesariamente a un ritmo constante. Es importante destacar que todas las correlaciones lineales son monótonas, pero no todas las asociaciones monótonas son lineales, ya que también puede haber asociaciones monótonas no lineales. Simplemente un número de \(\rho\) positivo indica que ambas variables incrementan o disminuyen en el mismo sentido, mientras que un coeficiente negativo indica que una aumenta y la otra disminuye.
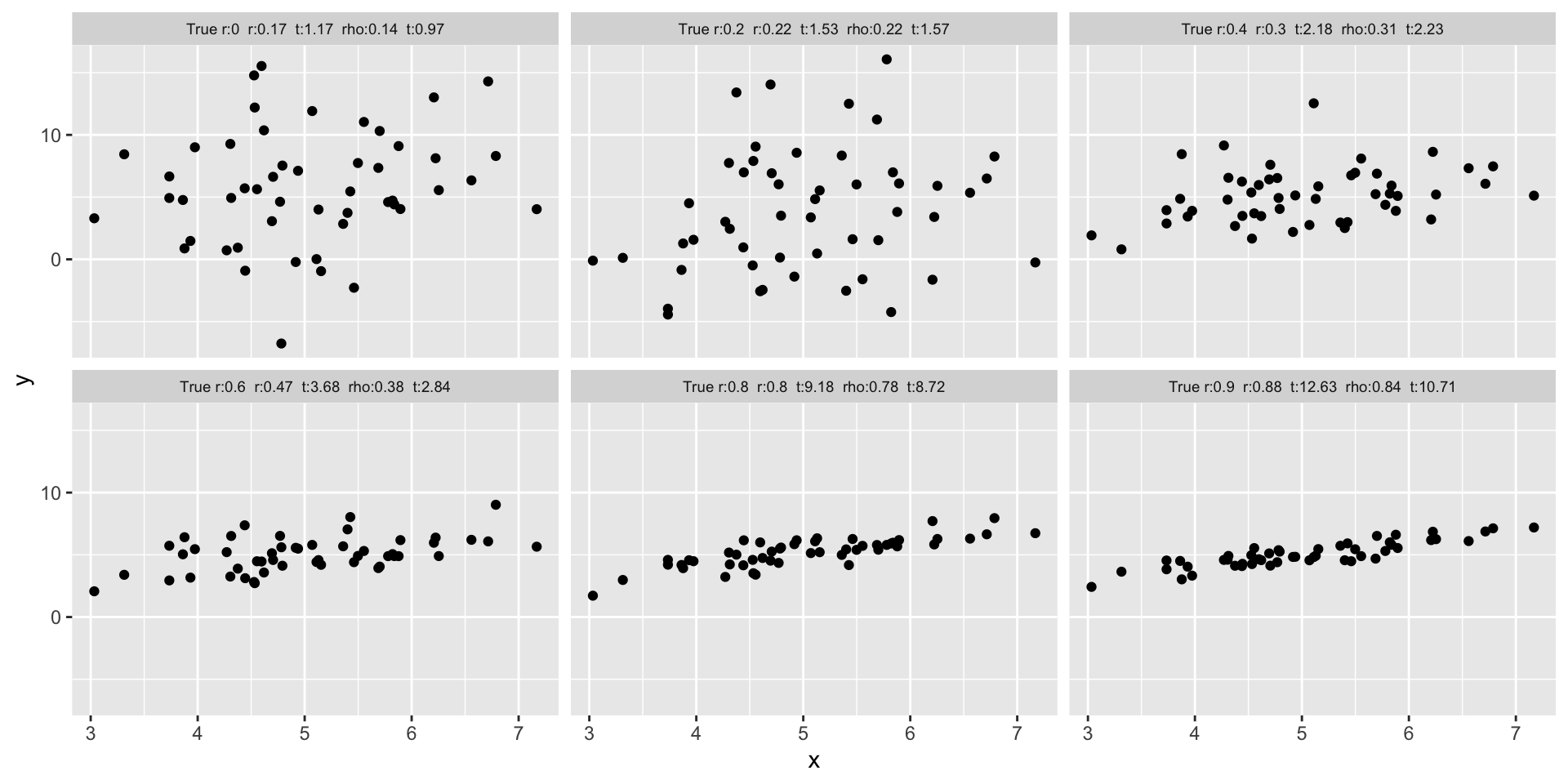
La correlación y el problema visual
Establecer la fuerza de correlación es muy difícil de visualizar mediante gráficas.