Capítulo 2 Manipulación de data frames

Hemos venido manipulando vectores, pero aun es insuficiente para resolver nuestro caso/problemática. Necesitamos ver más datos y no solo vector por vector.

Para ello vamos a utilizar el paquete tidyverse, el cual nos incluye librerías como dplyr la cual provee intuitivas funcionalidades para trabajar con tablas.

# Primero instalamos el paquete tidyverse
install.packages("tidyverse")

# Para empezar a usarlo cargamos la librería dplyr
library(dplyr)

# No olvides haber cargado dslabs para usar "murders"
library(dslabs)

2.1 El mágico operador pipeline

Si bien hay más de una forma de acceder a las funciones de la librería dplyr para visualizar o manipular data frames, el operador pipeline %>% es el más intuitivo por su facilidad de uso.

Por ejemplo, si queremos visualizar solo los datos estado, poblacion y total lo podemos hacer primero digitando el data frame murders y aplicándole un pipeline de esta forma:

murders %>% select(state, population, total)

Esta es una vista, no estamos aun editando el data frame murders.

En capítulos anteriores habíamos utilizado la función head(x) para mostrar las 6 primeras líneas de un vector o un data frame x. Así, podríamos reportar las primeras filas:

head(murders %>% select(state, population, total))
#>        state population total
#> 1    Alabama    4779736   135
#> 2     Alaska     710231    19
#> 3    Arizona    6392017   232
#> 4   Arkansas    2915918    93
#> 5 California   37253956  1257
#> 6   Colorado    5029196    65

Sin embargo, también podemos reportar las primeras filas usando el operador pipeline. Solo tenemos que agregar el operador %>% y agregar el código que queremos aplicar:

murders %>% select(state, population, total) %>% head()
#>        state population total
#> 1    Alabama    4779736   135
#> 2     Alaska     710231    19
#> 3    Arizona    6392017   232
#> 4   Arkansas    2915918    93
#> 5 California   37253956  1257
#> 6   Colorado    5029196    65

Obtenemos el mismo resultado que usando funciones con argumentos.

Así mismo, vamos a utilizar una sola función por línea para hacer más estética la programación y poder comentar más fácilmente. Quedando de esta forma:

murders %>%
  select(state, population, total) %>% #Con esta función selecciono
  head() #Con esta función muestro las 6 primeras filas

2.2 Transformar una tabla

En nuestro caso/problemática sería útil tener una columna más con el ratio de homicios por cada 100 mil habitantes. Esto lo podemos hacer fácilmente con la función mutate()

murders %>%
  mutate(ratio = total / population * 100000) %>%
  head()

Vemos lo fácil que es crear una vista con una columna adicional ratio que, mediante operaciones vectoriales, divide el total de homicidios entre la población y multiplica por 100 mil para calcular por cada uno de los estados el ratio de homicios por cada 100 mil habitantes.

Cuando usamos pipeline no es necesario utilizar el símbolo $ (p.ej. murders$total). Esto es porque hemos empezado el pipeline con el nombre del data frame. Todo lo que viene a continuación hace referencia a lo existente antes de ese pipeline.

Si quisiéramos transformar el data frame con esta mutación usaríamos el símbolo de asignar <-

murders <- murders %>%
  mutate(ratio = total / population * 100000)

En este caso no coloco head() para no perder datos. Con head solo tengo las 6 primeras filas.

2.3 Filtrando datos

Podemos filtrar fácilmente utilizando la función filter. Por ejemplo, si queremos quedarnos con todos los estados en donde se han cometido menos de 1 asesinato por cada 100 mil habitantes tendríamos que agregar un pipeline al código:

# Primero vuelvo a extraer los datos de la fuente
data(murders)

# Y ahora creo mi vista
murders %>%
  mutate(ratio = total / population * 100000) %>%
  filter(ratio < 1)
#>            state abb        region population total     ratio
#> 1         Hawaii  HI          West    1360301     7 0.5145920
#> 2          Idaho  ID          West    1567582    12 0.7655102
#> 3           Iowa  IA North Central    3046355    21 0.6893484
#> 4          Maine  ME     Northeast    1328361    11 0.8280881
#> 5      Minnesota  MN North Central    5303925    53 0.9992600
#> 6  New Hampshire  NH     Northeast    1316470     5 0.3798036
#> 7   North Dakota  ND North Central     672591     4 0.5947151
#> 8         Oregon  OR          West    3831074    36 0.9396843
#> 9   South Dakota  SD North Central     814180     8 0.9825837
#> 10          Utah  UT          West    2763885    22 0.7959810
#> 11       Vermont  VT     Northeast     625741     2 0.3196211
#> 12       Wyoming  WY          West     563626     5 0.8871131

Si tuviésemos la preferencia de que sea un ratio menor a 1 y en la región Oeste (West en inglés) sería de esta forma:

murders %>%
  mutate(ratio = total / population * 100000) %>%
  filter(ratio < 1 & region == "West")
#>     state abb region population total     ratio
#> 1  Hawaii  HI   West    1360301     7 0.5145920
#> 2   Idaho  ID   West    1567582    12 0.7655102
#> 3  Oregon  OR   West    3831074    36 0.9396843
#> 4    Utah  UT   West    2763885    22 0.7959810
#> 5 Wyoming  WY   West     563626     5 0.8871131

En R, el operador AND es representado por el símbolo “&”. Para comparar si es igual utilizamos el símbolo “==”

2.4 Ejercicios

Reporta las columnas abreviación del estado abb y la población population del data frame murders

Solución

murders %>%
  select(abb, population)

Reporta todos los datos de data frame que no sean de la región sur (“South” en inglés).

Solución

murders %>%
  filter(region != "South")

Si queremos filtrar todos los registros que sean de la región South y West usaremos %in% en vez de == para comparar versus un vector

Crea el vector sur_y_oeste que contenga los valores “South” y “West”. Luego filtra los registros que sean de esas dos regiones.

Solución

sur_y_oeste <- c("South", "West")
  
murders %>%
  filter(region %in% sur_y_oeste)

Agrega la columna ratio al data frame murders con el ratio de asesinatos por 100 mil habitantes. Luego, filtra los que tengan un ratio menor a 0.5 y sean de las regiones “South” y “West”. Reporta las columnas state, abb y ratio.

Solución

data(murders)

sur_y_oeste <- c("South", "West")
  
murders <- murders %>%
  mutate(ratio = total/population*100000) %>%
  filter(ratio < 0.9 & region %in% sur_y_oeste) %>%
  select(state, abb, ratio)

murders

Para ordenar usando pipeline utilizamos la función arrange(x), donde xes el nombre de la columna que queremos tomar tomo referencia la cual ordenará de forma ascendente o arrange(desc(x)) para ordenar en forma descendente.

Modifica el código generado en el ejercicio anterior para ordenar el resultado por el campo ratio.

Solución

data(murders)

sur_y_oeste <- c("South", "West")
  
murders <- murders %>%
  mutate(ratio = total/population*100000) %>%
  filter(ratio < 0.9 & region %in% sur_y_oeste) %>%
  select(state, abb, ratio) %>%
  arrange(ratio)

murders

Así, finalmente podemos saber qué opciones de estados tenemos para poder mudarnos y resolver el caso presentado.

2.5 Data frames en gráficos

Ahora que resolvimos el problema y tenemos opciones de estado dónde mudarnos, veremos algunas funciones que nos permiten visualizar nuestra data. Poco a poco iremos construyendo gráficos más complejos y visualmente más estéticos para presentar. Primero veamos las funciones más básicas que R nos presenta. En el siguiente capítulo veremos más a detalle los tipos de gráficos y en qué situaciones es recomendable usar uno u otro gráfico.

2.5.1 Gráficos de dispersión

Uno de los gráficos más utilizados en R es el gráfico o diagrama de dispersión, el cual es un tipo de diagrama matemático que utiliza las coordenadas cartesianas para mostrar los valores de dos variables para un conjunto de datos (Jarrell 1994, 492). Por defecto asumimos que las variables a analizar son independientes. Así, el diagrama de dispersión mostrará el grado de correlación (no causalidad) entre las dos variables.

La manera más sencilla de graficar un gráfico de dispersión es con la función plot(x,y), donde x y y son vectores que indican las coordenas del eje-x y las coordenadas del eje-y de cada punto que queremos graficar. Por ejemplo, veamos la relación entre el tamaño de la población y el total de asesinatos.

# Almacenemos en el objeto eje_x los datos de población
eje_x <- murders$population

# Almacenemos en el objeto eje_x los datos de población
eje_y <- murders$total

# Con este código creamos el gráfico de dispersión
plot(eje_x, eje_y)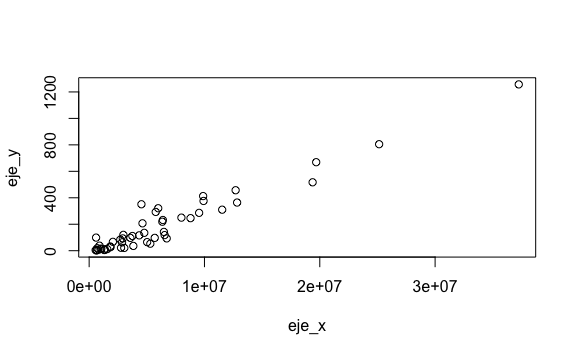

Podemos ver una correlación entre la población y el número de casos. Transformemos el eje_x dividiendo por un millón (${10}^6$). Así tendremos el eje x expresado en millones.

eje_x <- murders$population/10^6
eje_y <- murders$total

plot(eje_x, eje_y)

2.5.2 Histogramas

También podemos crear histogramas a partir de un vector con la función hist.

data(murders)

murders <- murders %>%
  mutate(ratio = total/population*100000)

hist(murders$ratio)

La facilidad que nos da R para crear gráficos nos ahorrará tiempo para el análisis. De aquí podemos ver rápidamente que la mayoría de estados tiene un ratio < 5.

2.5.3 Diagrama de cajas

Finalmente, R nos permite crear diagramas de cajas de forma sencilla con la función boxplot. Asi, si quisiéramos analizar la distribución del ratio usaríamos el siguiente código:

boxplot(murders$ratio)

2.6 Interpretación de datos

Hemos visto gráficos que se pueden generar con una línea de código, pero necesitamos interpretarlos. Para ello, necesitamos aprender o recordar algunos estadísticos. Vamos a aprender a lo largo de este libro concepto estadísticos no entrando a profundidad en la parte matemática, sino desde la parte práctica y aprovechando que ya existen las funciones en R.

Recordemos nuestro caso/problemática. Tenemos un listado de asesinatos en cada uno de los 51 estados. Si los ordenemos por la columna total tendríamos:

murders %>% 
  arrange(total) %>%
  head()
#>           state abb        region population total     ratio
#> 1       Vermont  VT     Northeast     625741     2 0.3196211
#> 2  North Dakota  ND North Central     672591     4 0.5947151
#> 3 New Hampshire  NH     Northeast    1316470     5 0.3798036
#> 4       Wyoming  WY          West     563626     5 0.8871131
#> 5        Hawaii  HI          West    1360301     7 0.5145920
#> 6  South Dakota  SD North Central     814180     8 0.9825837

R nos provee con la función summary(), la cual nos da un resumen de los datos de un vector.

summary(murders$total)
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>     2.0    24.5    97.0   184.4   268.0  1257.0

Min.: Mínimo valor del vector
1st Qu.: Primer cuartil
Median: Mediana o segundo cuartil
Mean: Promedio
3rd Qu.: Tercer cuartil
Max.: Máximo valor del vector

2.6.1 Cuartiles

Para comprender los cuartiles visualicemos el total de los datos de forma ordenada. Para solo obtener una sola columna en pipeline usaremos .$ antes del nombre de la variable:

murders %>% 
  arrange(total) %>%
  .$total
#>  [1]    2    4    5    5    7    8   11   12   12   16   19   21   22   27   32
#> [16]   36   38   53   63   65   67   84   93   93   97   97   99  111  116  118
#> [31]  120  135  142  207  219  232  246  250  286  293  310  321  351  364  376
#> [46]  413  457  517  669  805 1257

Los cuartiles dividen nuestro vector en 4 partes con la misma cantidad de datos. Dado que tenemos 51 valores, tendríamos grupos de 51/4 = 12.75. Tendríamos grupos de 13 valores (3 grupos de 13 elementos y uno de 12 elementos).

Por ejemplo, el primer grupo estaría compuesto por estos números:

#>  [1]  2  4  5  5  7  8 11 12 12 16 19 21 22

El segundo grupo estaría compuesto por estos números:

#>  [1] 27 32 36 38 53 63 65 67 84 93 93 97 97

Y así sucesivamente. En total 4 grupos conformado por el 25% de los datos c/u.

2.6.1.1 Primer cuartil

Por lo tanto, cuando veamos el 1er cuartil, 1st Qu., pensemos que ese es el corte que nos indica hasta dónde puedo encontrar al 25% de los datos.

summary(murders$total)
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>     2.0    24.5    97.0   184.4   268.0  1257.0

En nuestro ejemplo 24.5 indica que todo número menor o igual que es número estará dentro del 25% de los primeros datos (25% de 51 datos = 12.75, redondeado a 13 datos).

Si listamos los números menores o iguales a 24.5 tendremos este listado:

murders %>%
  arrange(total) %>%
  filter(total <= 24.5) %>%
  .$total
#>  [1]  2  4  5  5  7  8 11 12 12 16 19 21 22

Que es exactamente el mismo listado que obtuvimos anteriormente para el primer grupo.

2.6.1.2 Segundo cuartil o mediana

El segundo cuartil, también llamado la mediana (Median), nos indica el corte del segundo grupo. El primer grupo contiene los primeros 25% datos, el segundo grupo tiene 25% adicionales. Así que este corte nos daría exactamente el valor que se encuentra al medio.

summary(murders$total)
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>     2.0    24.5    97.0   184.4   268.0  1257.0

En nuestro ejemplo 97 indica que debajo de es número encontraremos 50% del total de datos (50% de 51 datos = 25.5, redondeado a 26 datos).

murders %>%
  arrange(total) %>%
  filter(total <= 97) %>%
  .$total
#>  [1]  2  4  5  5  7  8 11 12 12 16 19 21 22 27 32 36 38 53 63 65 67 84 93 93 97
#> [26] 97

2.6.1.3 Tercer cuartil

El tercer cuartil es el corte del tercer grupo. Hasta la mediana ya teníamos 50%, si agregamos otro 25% de datos tendríamos 75%.

summary(murders$total)
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>     2.0    24.5    97.0   184.4   268.0  1257.0

En nuestro ejemplo 268 indica que debajo de es número encontraremos 75% del total de datos (75% de 51 datos = 26.01, redondeado a 26 datos).

2.6.2 Interpretación del gráfico de cajas

Ya estamos listos para crear un gráfico de cajas con el total de asesinatos e interpretar los resultados.

boxplot(murders$total)

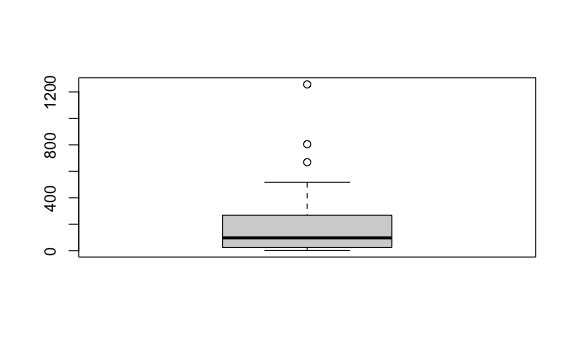
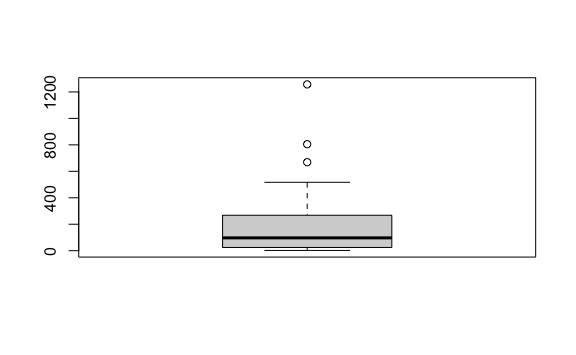
La caja empieza en el valor 24.5 (primer cuartil) y termina en el valor de 268 (tercer cuartil). La línea ancha representa la mediana (segundo cuartil), 97 en nuestro ejemplo.

Entre el primer cuartil y el tercer cuartil (entre 24.5 y 97 para nuestro ejemplo) encontraremos 50% de la data, también llamado rango intercuartil or IQRpor sus siglas en inglés.

Fuera de la caja vemos una línea vertical hacia arriba y otra hacia abajo, mostrando el rango de nuestros datos. Fuera de esas líneas vemos unos puntos que son datos atípicos muy alejados de la media, conocidos como outliers.

Podemos encontrar rápidamente a qué estados pertenecen estos datos extremos si ordenamos la tabla descendentemente usando la función desc:

murders %>%
  arrange(desc(total)) %>%
  head()
#>          state abb        region population total    ratio
#> 1   California  CA          West   37253956  1257 3.374138
#> 2        Texas  TX         South   25145561   805 3.201360
#> 3      Florida  FL         South   19687653   669 3.398069
#> 4     New York  NY     Northeast   19378102   517 2.667960
#> 5 Pennsylvania  PA     Northeast   12702379   457 3.597751
#> 6     Michigan  MI North Central    9883640   413 4.178622

Vemos que en California se reportaron 1257 casos. Ese es uno de los datos extremo que vemos en el gráfico de cajas.

2.7 Ejercicios

Crea la variable pob_log10 y almacena los datos del logaritmo 10 de la población (función log10()). Realiza la misma transformación a logaritmo 10 para el total de asesinatos y almacénalo en la variable tot_log10. Genera un gráfico de dispersión de estas dos variables.

Solución

pob_log10 <- log10(murders$population)
tot_log10 <- log10(murders$total)

plot(pob_log10, tot_log10)

Crea un histograma de la población en millones (dividido por ${10}^6$).

Solución

hist(murders$population/10^6)

Crea un diagrama de cajas de la población.

Solución

boxplot(murders$population)

2.8 Ejercicios integrados

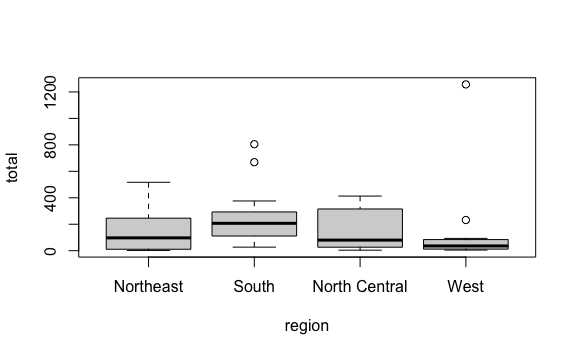
Analiza visualmente el siguiente gráfico que describe la distribución del total de asesionatos por regiones. Solo visualizándolo podrías señalar ¿qué región tiene el menor rango de datos, obviando outliers? ¿qué región tiene la mediana más alta?

Solución

El oeste (West) tiene el menor rango de datos y tiene dos outliers. El sur (South) tiene la mediana más alta entre todas las regiones.

Analizar únicamente viendo un gráfico nos permite colocarnos en los zapatos del observador final y comprender si solo con la información presentada se puede tomar decisiones.

Crea el vector sur donde almacenes los datos filtrados del total de asesinatos que ocurrieron en la región sur. Luego, crea un histograma del vector sur.

Solución

sur <- murders %>%
  filter(region == "South") %>%
  .$total

hist(sur)

Referencias

Jarrell, Stephen B. 1994. Basic Statistics. 1st ed. US: Brown (William C.) Co.