2 Introduction
Modeling = development of mathematical expressions that describe the behavior of a random variable of interest.
This variable is called the response (or dependent) variable and denoted with \(Y\).
Other variables which are thought to provide information on the behavior of \(Y\) are incorporated into the model as predictor or explanatory variables (also called the independent variables). We denote them with \(X\).
Data consist of information taken from \(n\) units. Subscripts \(i = 1,..., n\) identify the particular unit from which the observations were taken.
Additional subscripts can be used to identify different predictors.
All models involve unknown constants, called parameters, which control the behavior of the model. These parameters are denoted by Greek letters (e.g. \(\beta\)) and are to be estimated from the data.
We denote estimates using hat notation, e.g. \(\hat{\beta}\).
In this module we will study linear models. Here the parameters enter the model as simple coefficients on the \(X\)s or functions of \(X\)s.
2.1 Introductory Examples
A first look at how \(Y\) changes as \(X\) is varied is seen in a scatterplot.
2.1.1 Mother and daughter heights
Data from Pearson and Lee (1903).
- \(\bar{y}=\) 63.75, sd(\(y\)) = 2.6
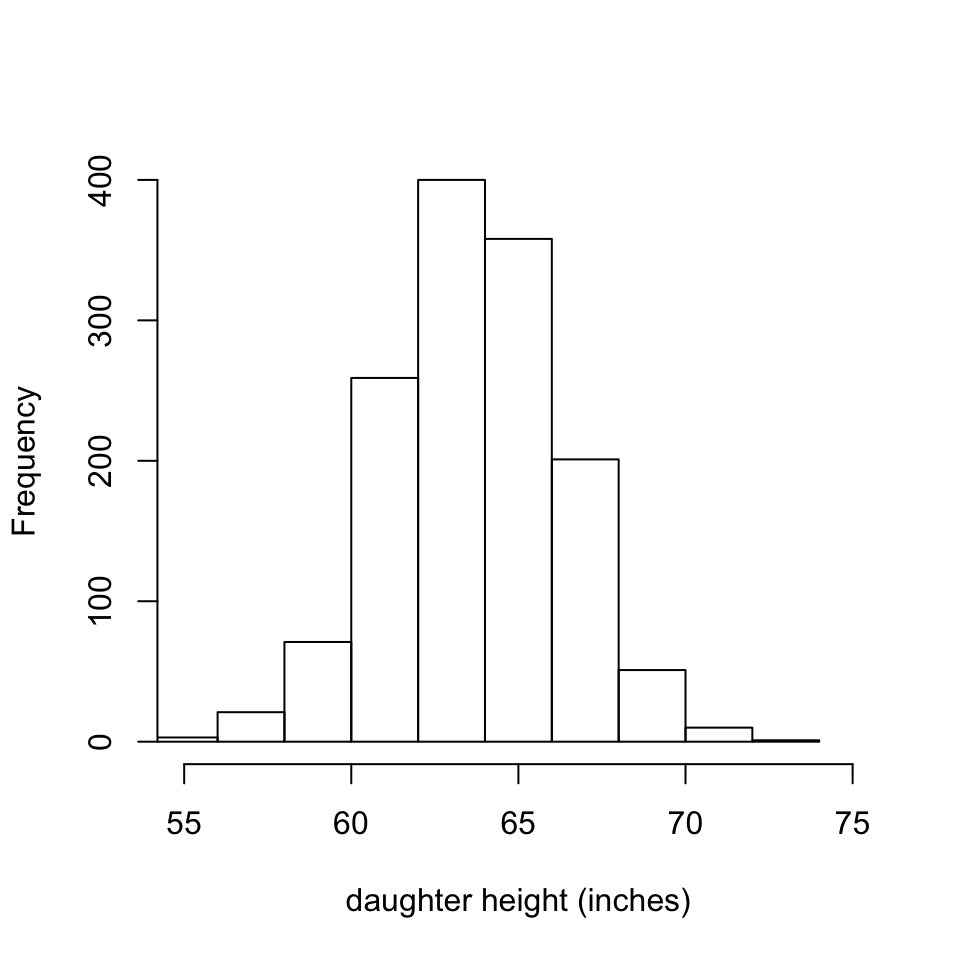
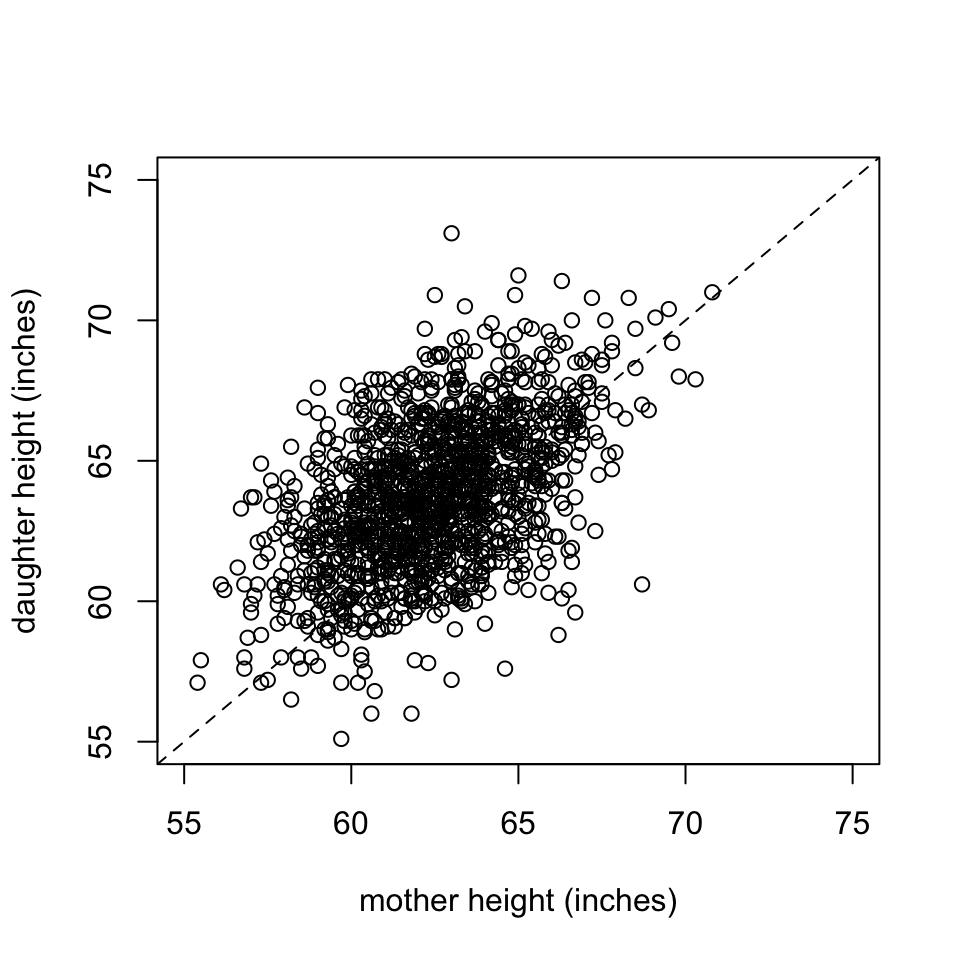
- Taller mothers have taller daughters.
- Since most points fall above line \(y=x\) most daughters are taller.
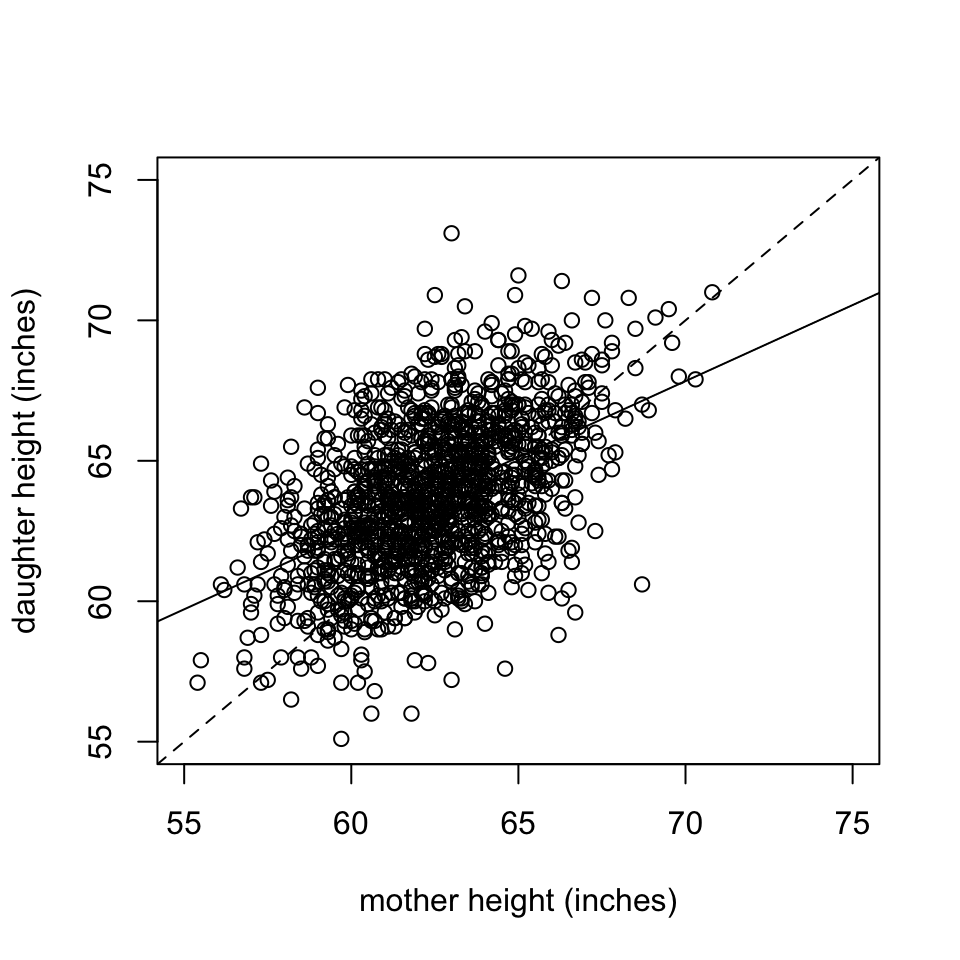
- Does the data follow a linear pattern? If so we can use the linear regression line to summarise the data.
- We can use the regression line to predict a daughters height based on her mother’s height.
- \(\hat{y}=\) 29.92 +0.54 \(x\)
2.1.2 Bacterial count and storage temperature
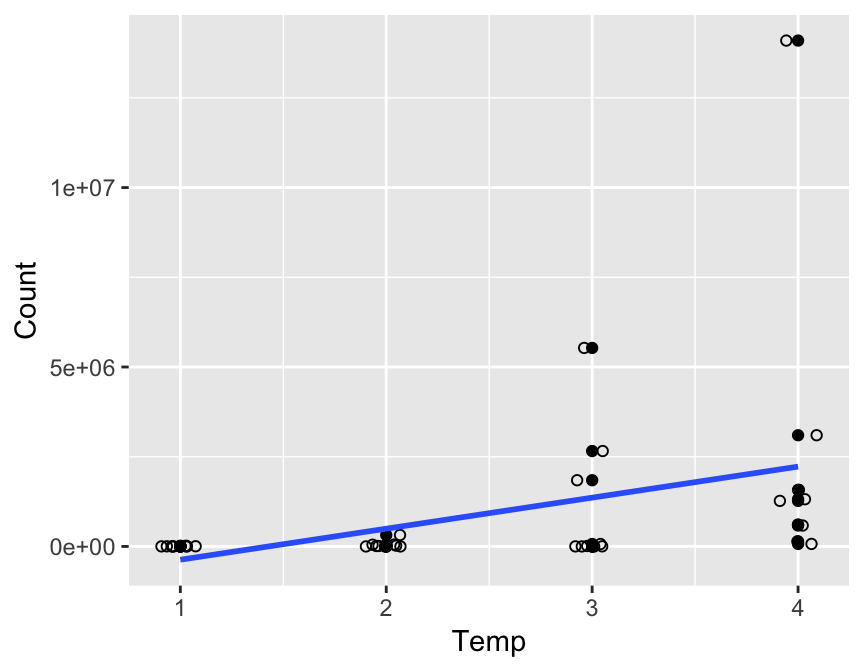
- Points are jittered to avoid overprinting.
- It does not appear to be a linear relationship.
- Consider a transformation?
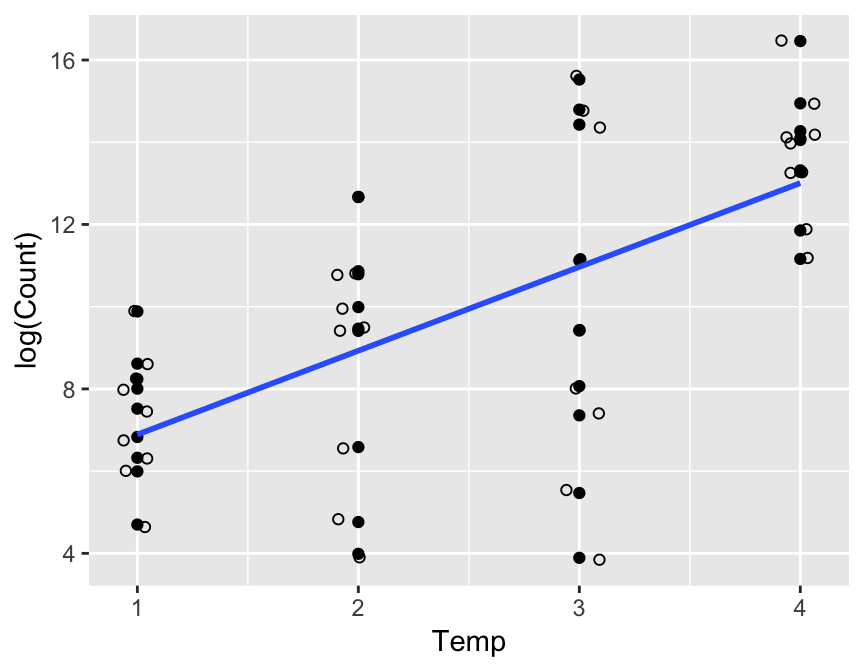
- Log transformed bacteria counts appear to have a linear relationship with temperature.
2.1.3 Yield and Rainfall
The dataset is from Ramsey and Schafer (2002). The data on corn yields and rainfall are in `ex0915’ in library(Sleuth3). Variables:
- Yield: corn yield (bushels/acre)
- Rainfall: rainfall (inches/year)
- Year: year.
## The following objects are masked from ex0915 (pos = 9):
##
## Rainfall, Year, Yield## The following objects are masked from ex0915 (pos = 16):
##
## Rainfall, Year, Yield## The following objects are masked from ex0915 (pos = 23):
##
## Rainfall, Year, Yield## The following objects are masked from ex0915 (pos = 30):
##
## Rainfall, Year, Yield## The following objects are masked from ex0915 (pos = 37):
##
## Rainfall, Year, Yield## The following objects are masked from ex0915 (pos = 44):
##
## Rainfall, Year, Yield## The following objects are masked from ex0915 (pos = 51):
##
## Rainfall, Year, Yield## The following objects are masked from ex0915 (pos = 59):
##
## Rainfall, Year, Yield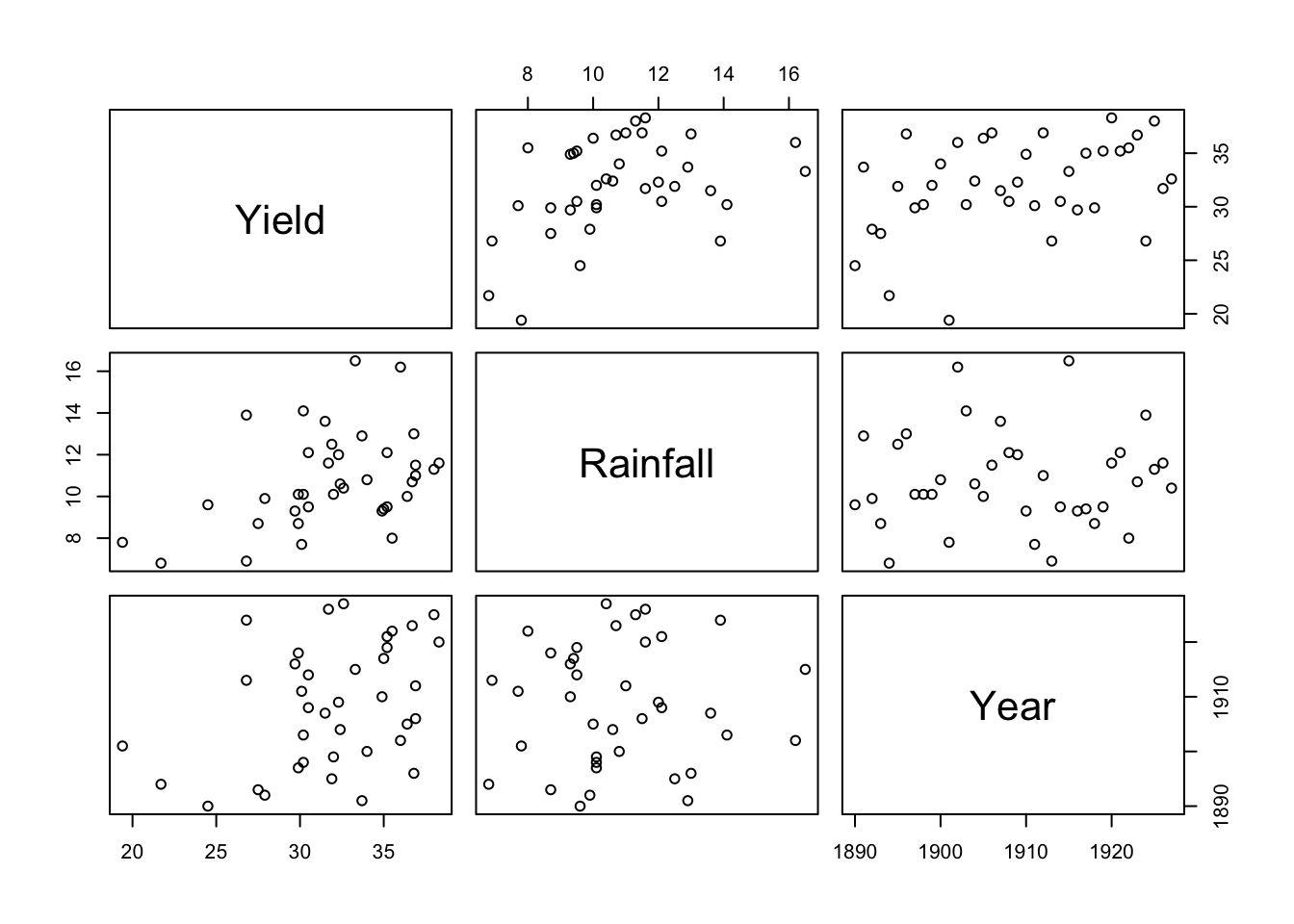
You must enable Javascript to view this page properly.
2.1.4 Driving
Example from: Weisberg (2005). Study how fuel consumption varies over 50 US states and the District of Columbia and the effect of state gasoline tax on the consuption.
Variable:
- FuelC: Gasoline sold for road use, thousands of gallons
- Drivers: Number of licensed drivers in the state
- Income: Per person personal income for the year 2000, in thousands of dollars
- Miles: Miles of Federal-aid highway miles in the state
- Pop: 2001 population age 16 and over
- Tax: Gasoline state tax rate, cents per gallon
- State: State name
We will use a scatterplot matrix.
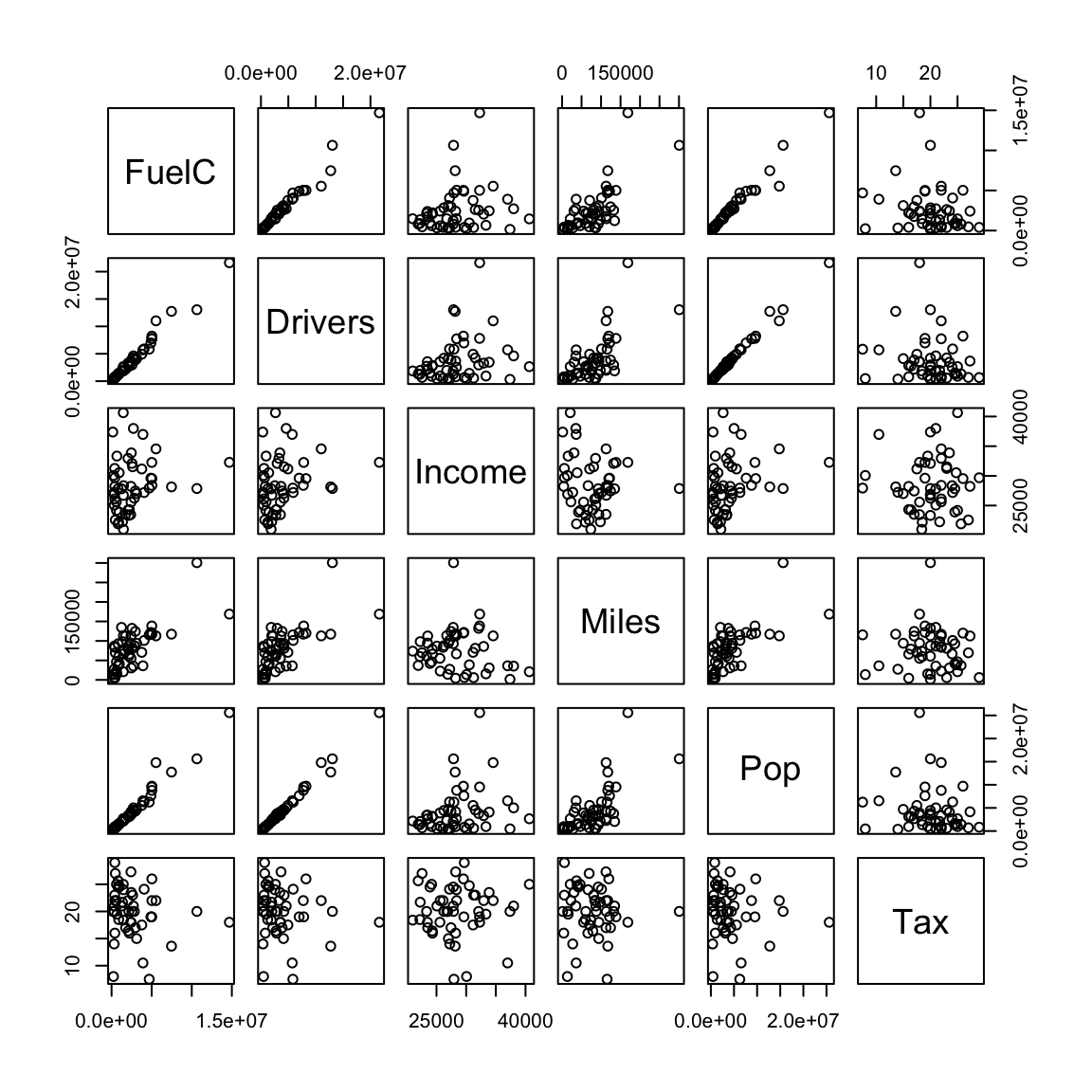
- Both Drivers and FuelC are state totals so will be larger in more populous states.
- Income is per person, we want to make variables comparable.
Transform variables:
- FuelC2:FuelC/Pop
- Drivers2: Drivers/Pop
- Miles2:log\(_2\)(Miles)
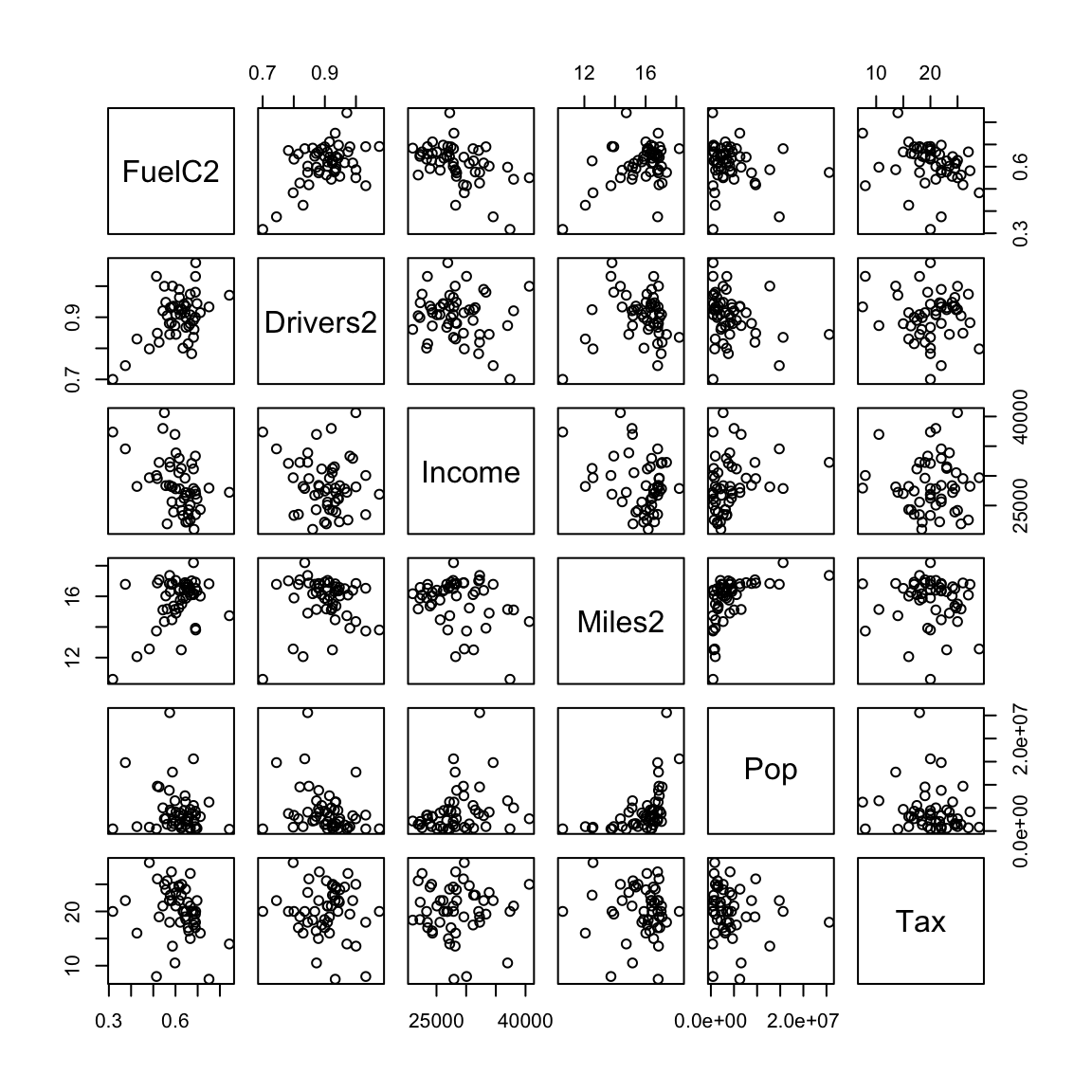
- FuelC decreases as tax increases but there is a lot of variation.
- Fuel is weakly related to a number of other variables.
Other graphical representations of the dataset:
library(MASS)
parcoord(driving2[, c(2,6, 1,3,4,5)])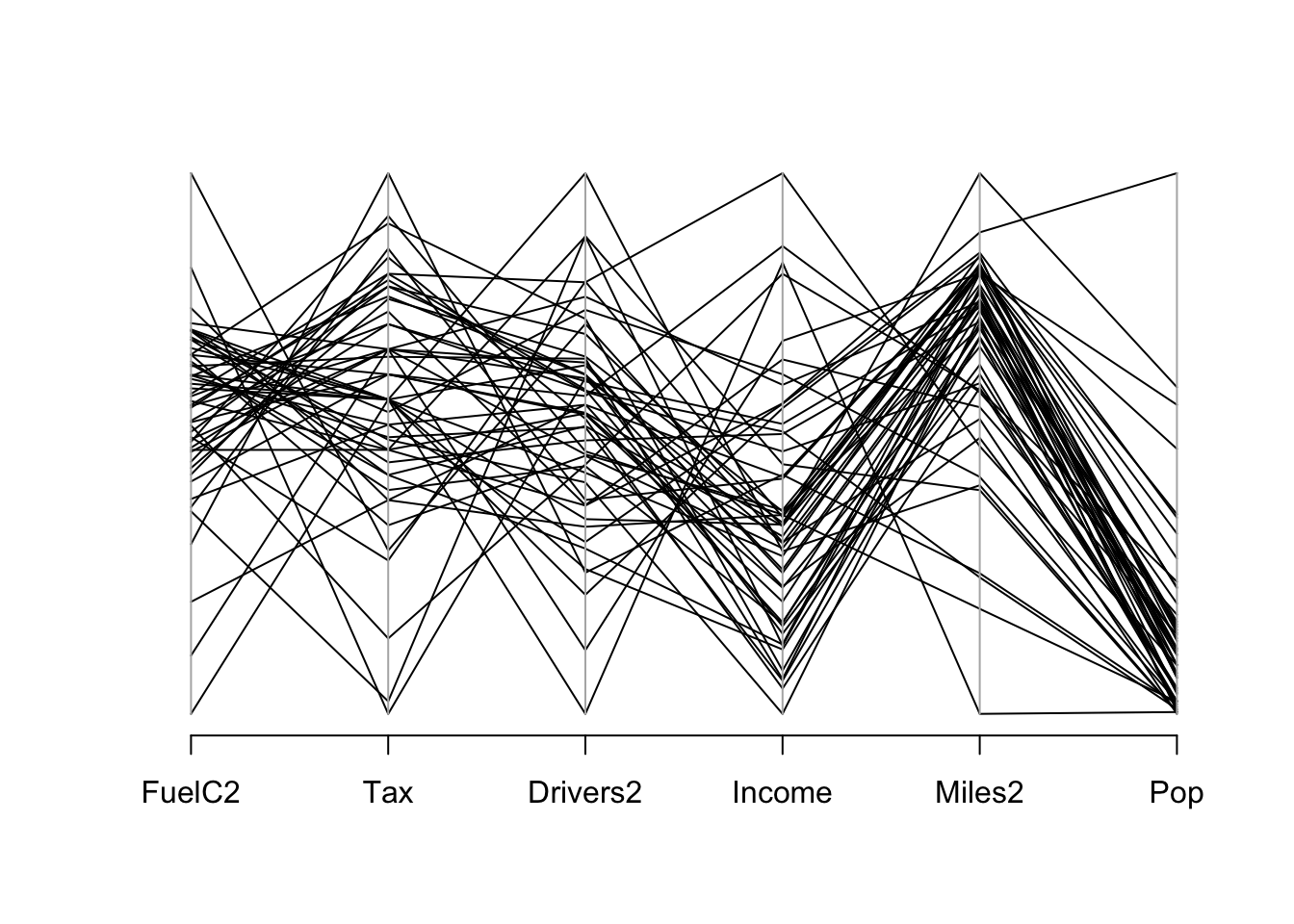
2.1.5 Fuel Consumption
Information was recorded on fuel usage and average temperature (\(^oF\)) over the course of one week for eight office complexes of similar size. Data from Bowerman and Schafer (1990).
We expect fuel use to be driven by weather conditions.
Fuel use: response or dependent variable. Denoted by \(Y\).
Temperature: Explanatory or predictor variable. Denoted by \(X\).
We observe n=8 pairs: \((x_{i}, y_{i}), i =1,...,8\).
| Temp | Fuel |
|---|---|
| 28.0 | 12.4 |
| 28.0 | 11.7 |
| 32.5 | 12.4 |
| 39.0 | 10.8 |
| 45.9 | 9.4 |
| 57.8 | 9.5 |
| 58.1 | 8.0 |
| 62.5 | 7.5 |
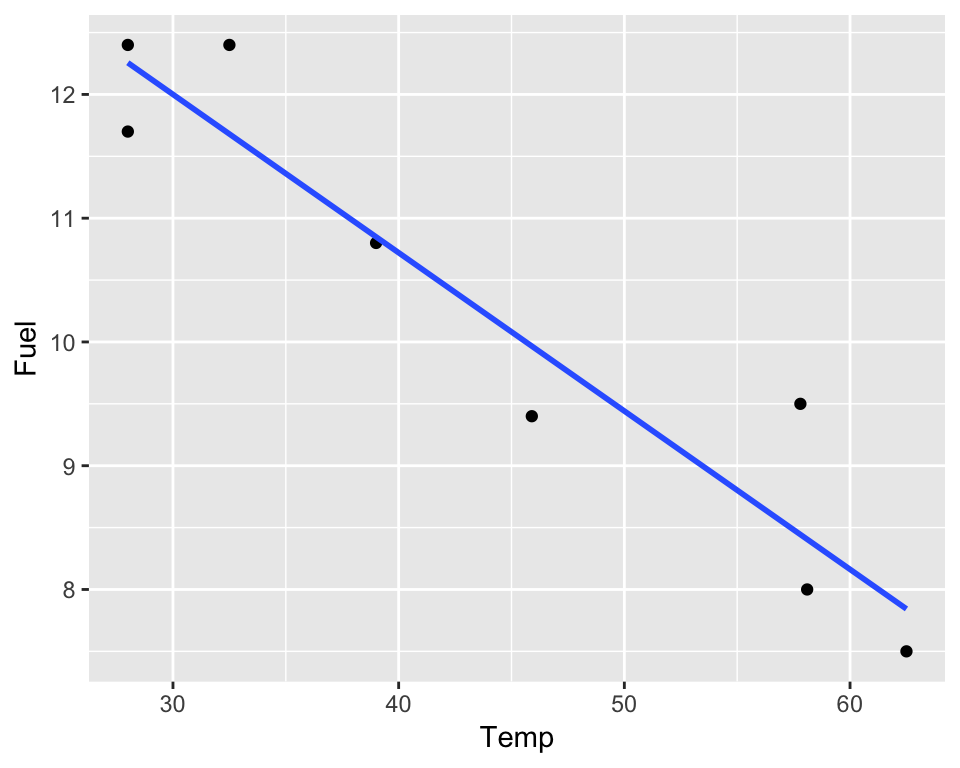
The scatterplot shows that fuel use decreases roughly linearly as temperature increases.
We assume there’s an underlying true line: \[\mbox{Fuel} =\beta_{0} + \beta_{1}\mbox{Temp} + \epsilon\]
or, more generally: \(y =\beta_{0} + \beta_{1}x + \epsilon.\)
The intercept (\(\beta_0\)) and slope (\(\beta_1\)), are unknown parameters and \(\epsilon\) is the random error component.
For each observation we have: \(y_i =\beta_{0} + \beta_{1}x_i + \epsilon_i\).
We can estimate \(\beta_0\) and \(\beta_1\) from the available data.
One method that can be used to do this is the method of ordinary least squares.
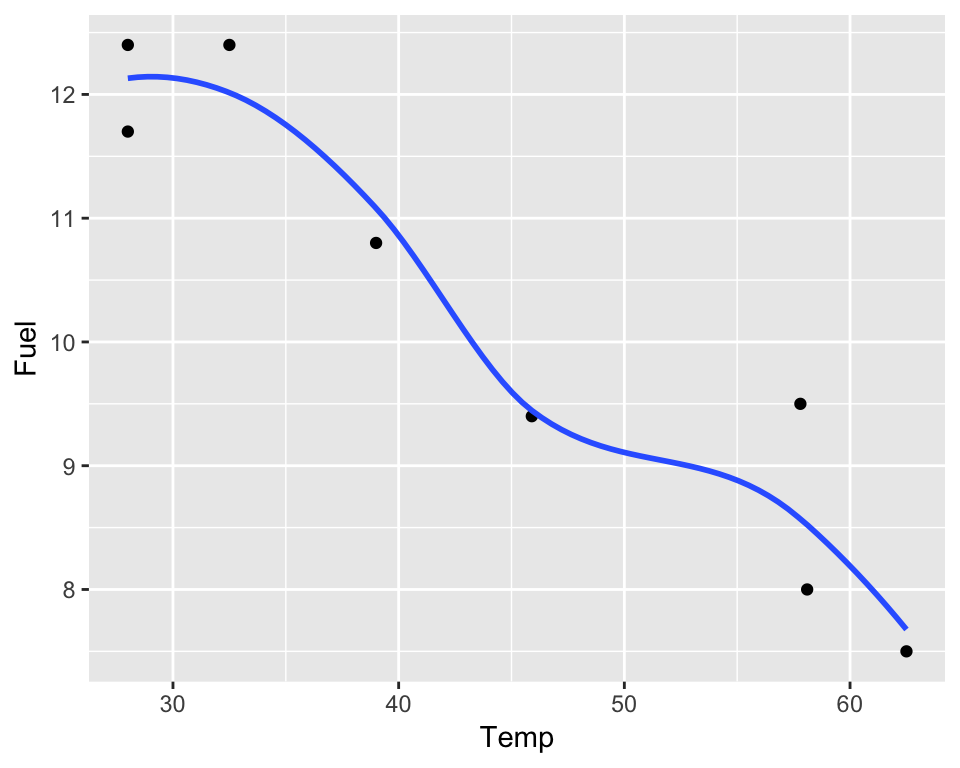
NOTE: other models are possible:
References
Pearson, K, and A Lee. 1903. “On the Laws of Inheritance in Man: I. Inheritance of Physical Characters.” Biometrika 2: 357–462.
Ramsey, Fred, and Daniel Schafer. 2002. The Statistical Sleuth: A Course in Methods of Data Analysis. 2nd ed. Duxbury Press.
Weisberg, Sanford. 2005. Applied linear regression. Wiley-Blackwell.
Bowerman, Bruce L., and Daniel Schafer. 1990. Linear Statistical Models. 2nd ed. Thomson Wadsworth.