data1 <- data.frame(var1 = c(NA, 5, 12, 1, 31), # NA como número
var2 = as.factor(c(2, 1, NA, NA, 3)), # NA como factor)
var3 = c(10, 6, 0/0, 9, Inf), # NaN e Inf
var4 = c("Hola Mundo", "Texto NA", NA, "NA", NA)) # NA como texto3 Manejo de Datos
3.1 Identificación y manejo de datos missing
3.2 Datos missing en R
El término Missing data o Missing value hace referencia al concepto de no tener el valor de un registro guardado, es decir, que se encuentre vacío.
Dependiendo del Software que se utilice y del tipo de variable al que pertenezca para el dato faltante pueden usarse diferentes términos.
En SQL por ejemplo cuando no se tiene información se utiliza NULL. En python por el contrario, se tiene una gestión de los valores faltantes más compleja. Se utiliza el objeto None según la documentación oficial para denotar la falta de valor. Pero al utilizar librerías más enfocadas a la ciencia de datos o análisis estadístico como pandas, para optimizar el uso de la memoria se tienen diferentes términos según el tipo de datos. np.nan es el término por defecto aunque internamente se comporta como un número de tipo doble, para fechas (datatime64) se utiliza NaT. Sin embargo, es posible aplicar las mismas funciones de detección de datos faltantes a ambos.
En R los valores faltantes se representan con el símbolo NA (Not Available). Los valores imposibles (por ejemplo, dividir por cero) se representan con el símbolo NaN (Not a Number). Esto no incluye los valores infinitos, que disponen de sus propios términos (-inf, inf).
Para un entendimiento mas adecuado se presentara el siguiente ejemplo.
3.3 Identificación de datos missing
Para explicar este tema se usará el ejemplo anterior y aunque en este ejemplo es fácil de identificar donde se encuentran los NA, en la mayoría de los casos prácticos el volumen de datos no permitirá que se identifique con facilidad la presencia de algún valor perdido. Sin embargo, en R la función is.na() permite obtener un vector lógico con TRUE en los casos de valores perdidos. Al anidar la función any() con la función is.na() se verifica si hay algún valor perdido, además la función which() permite identificar la posición de estos valores, mean() el porcentaje de NA y sum() la cantidad de NA.
Primero usaremos la funcion is.na() para obtener un vector lógico con TRUE en los casos de valores perdidos (datos missing).
is.na(data1) var1 var2 var3 var4
[1,] TRUE FALSE FALSE FALSE
[2,] FALSE FALSE FALSE FALSE
[3,] FALSE TRUE TRUE TRUE
[4,] FALSE TRUE FALSE FALSE
[5,] FALSE FALSE FALSE TRUEAhora anidaremos la función any() con la función is.na() para verificar si hay algún valor perdido en el ejemplo.
any(is.na(data1))[1] TRUEUna alternativa para este codigo es el siguiente:
anyNA(data1)[1] TRUECon respecto a la función which() esta permite identificar la posición de los datos missing.
which(is.na(data1))[1] 1 8 9 13 18 20Tambien podemos usar la funcion mean() para hallar el porcentaje de datos missing.
mean(is.na(data1))[1] 0.3Finalmente podemos usar la funcion sum() para identificar la cantidad de datos missing en el ejemplo.
sum(is.na(data1))[1] 63.4 Manejo de datos missing
Estos son algunos manejos que se puede hacer con los datos missing.
3.4.1 Omitir datos missing
Se puede omitir valores NA mediante indexación lógica, por ejemplo:
data1[!is.na(data1)] [1] " 5" "12" " 1" "31" "2"
[6] "1" "3" " 10" " 6" " 9"
[11] "Inf" "Hola Mundo" "Texto NA" "NA" 3.4.2 Imprimir un error de no encontrar datos missing
La función na.fail() imprime un error en caso de encontrar valores perdidos, esta es usada como mensaje de advertencia en caso de condicionales o estructuras como las funciones:
na.fail(data) -> Error in na.fail.default(data) : missing values in object
3.4.3 Contabilizar datos missing
Una forma de contabilizar datos missing es mediante la función table(), esta nos permite obtener una tabla de frecuencia de nuestros datos:
t <-c(1, 0, 1, 1, 1, 0, NA, 0)
table(t)t
0 1
3 4 table(t, useNA = "always")t
0 1 <NA>
3 4 1 y<-c(24, 14, 17, 25, 12, NA, 11, NA)En el caso de bases datos, que son más frecuente que los vectores, podemos también identificar datos missing. Las siguientes líneas de códigos insertan una base de datos llamada data2, con los vectores creados anteriormente.
data2 <- data.frame(mujer=t, edad=y)
data2 mujer edad
1 1 24
2 0 14
3 1 17
4 1 25
5 1 12
6 0 NA
7 NA 11
8 0 NAMediante la función vectorizada apply(), podemos obtener, por columna o variable, la cantidad, el porcentaje o la ubicación de los valores lógicos de nuestra base de datos. Esto se logra anidando esta función apply() con la función is.na() vista anteriormente. Verifique que si cambiamos el 2 por el 1, repite el ejercicio anterior para cada una de las observaciones.
apply(is.na(data2), 2, mean) # Porcentaje de NA por columnamujer edad
0.125 0.250 apply(is.na(data2), 2, sum) # Cantidad de NA por columnamujer edad
1 2 apply(is.na(data2), 2, which) # Posición de NA por columna$mujer
[1] 7
$edad
[1] 6 8Esta posición se puede verificar de forma directa para cada variable (columna):
which(is.na(data2[ , 2]))[1] 6 8Ahora bien, si queremos ambos operadores, lo que hacemos para que la función apply() aplique dos funciones, es crear una nueva función que haga las dos tareas a la vez:
f1 <-function(y) {
a<-mean(y);
b<-sum(y)
return(c(a,b))
}apply(is.na(data2), 2, f1) mujer edad
[1,] 0.125 0.25
[2,] 1.000 2.003.4.4 Verificar variables con datos missing
Primero para este manejo agregaremos una variable llamada peso a nuestra base de datos (data2), la cual, de manera intencional no contiene datos missing:
data2$peso <- c(70, 63, 68, 82, 74, 58, 63, 71)La función apply(), usando como argumento la función sum(), nos permite verificar cuales variables tienen al menos un dato missing. Como ejemplo, creamos un vector lógico llamado f2 = TRUE en los casos donde la columna tenga al menos un dato missing. Posteriormente usamos la indexación lógica para acceder a los nombres de las columnas identificadas:
f2 <- apply(is.na(data2), 2, sum)>=1
f2mujer edad peso
TRUE TRUE FALSE f2[f2==TRUE]mujer edad
TRUE TRUE 3.4.5 Obtener la cantidad de observaciones de la data, donde ninguna observación contiene datos missing
La función complete.case() permite obtener la cantidad de observaciones en cualquier data, donde ninguna observación contiene datos missing. En este caso usaremos la data2, en tal caso, se utiliza el vector lógico complete.cases(data2) para poder indexar la data2, para poder acceder a estas observaciones, donde ninguna de las variables cumplen con ser NA.
complete.cases(data2)[1] TRUE TRUE TRUE TRUE TRUE FALSE FALSE FALSEdata2[complete.cases(data2), ] mujer edad peso
1 1 24 70
2 0 14 63
3 1 17 68
4 1 25 82
5 1 12 74De forma más directa, na.omit() permite realizar esta tarea directamente:
na.omit(data2) mujer edad peso
1 1 24 70
2 0 14 63
3 1 17 68
4 1 25 82
5 1 12 743.4.6 Acceder a las variables que tengan un dato missing
Adicionalmente a lo anteior, mediante el operador de negación (!) podemos acceder a las observaciones donde alguna de las variables tiene un dato missing.
data2[!complete.cases(data2), ] mujer edad peso
6 0 NA 58
7 NA 11 63
8 0 NA 713.5 Identificación y manejo de datos outlier e inconsistentes
3.6 Datos outlier
Se denominan casos outliers u atípicos a aquellas observaciones con características diferentes de las demás. Este tipo de casos no pueden ser caracterizados categoricamente como benéficos o problemáticos sino que deben ser contemplados en el contexto del análisis y debe evaluarse el tipo de información que pueden proporcionar. Su principal problema radica en que son elementos que pueden no ser representativos de la población pudiendo distorsionar seriamente el comportamiento de los contrastes estadísticos. Por otra parte, aunque diferentes a la mayor parte de la muestra, pueden ser indicativos de las características de un segmento válido de la población y, por consiguiente, una señal de la falta de representatividad de la muestra.
3.7 Identificación de datos outlier
Para la identificación de datos outlier se mostrara 5 formas de identificar, pero antes se generará una variable aleatoria x con valores aleatorios de 100 edades de niños en un determinado centro escolar (x< sample(5:16,100,replace=T)) y se introducen tres valores atípicos intencionalmente en las observaciones [10,21,33] correspondiente a las edades de 21,31 y 40 años, respectivamente.
x<-sample(5:16,100,replace=T)
x[c(10,21,33)]<- c(21,31,40)
plot(x, type="b", pch=16)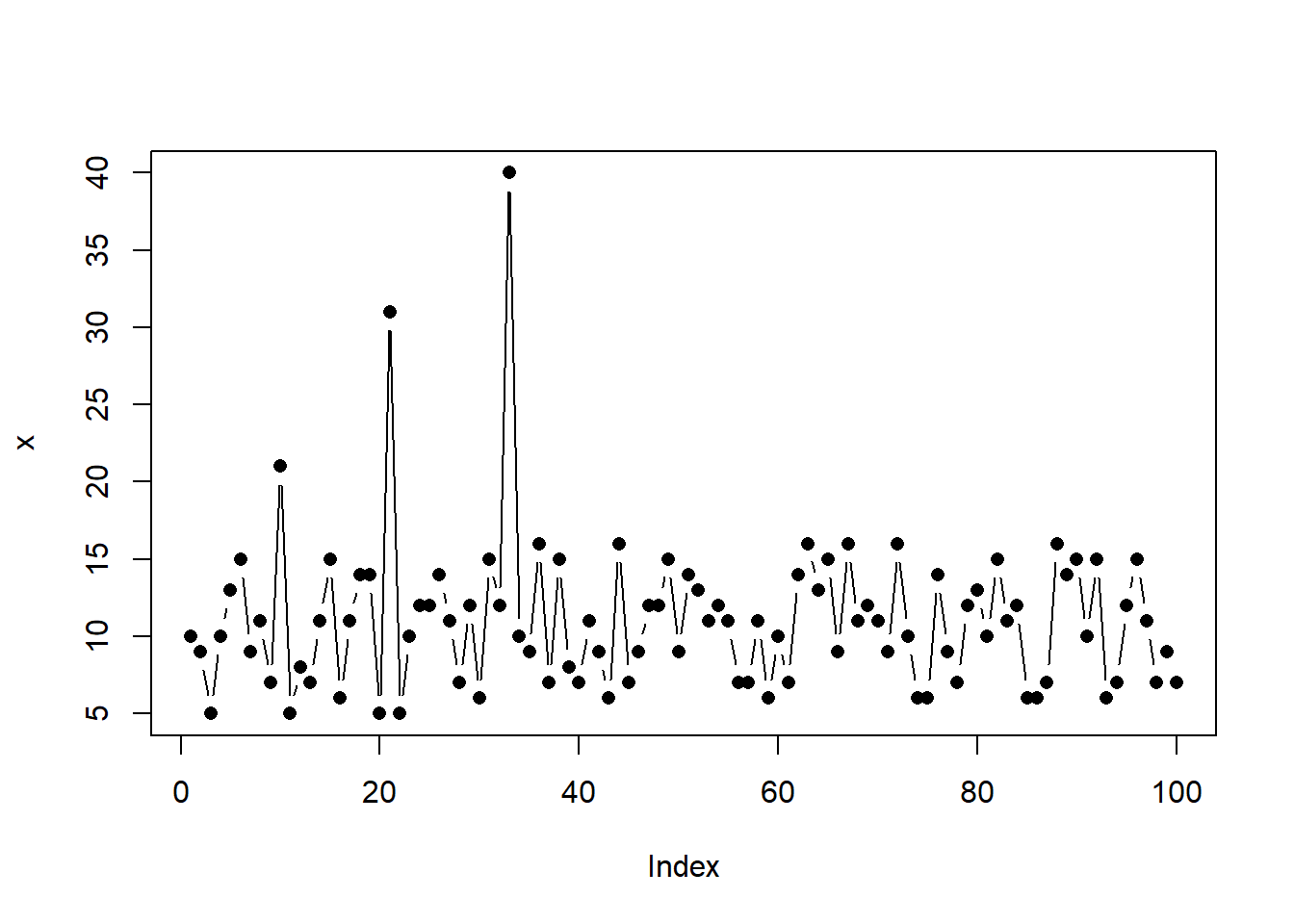
3.7.1 Identificación a partir de gráficos
El gráfico de caja (boxplot) constituye una primera opción al momento de analizar e identificar datos atípicos, el mismo presenta la mediana, el primer y tercer cuartil, además del 1.5*iqr o rango intercuartílico. En el caso de R, se puede verificar que la opción boxplot.stats(x)$out permite identificar los valores considerados como outliers y los valores utilizados para representar el boxplot.
boxplot(x)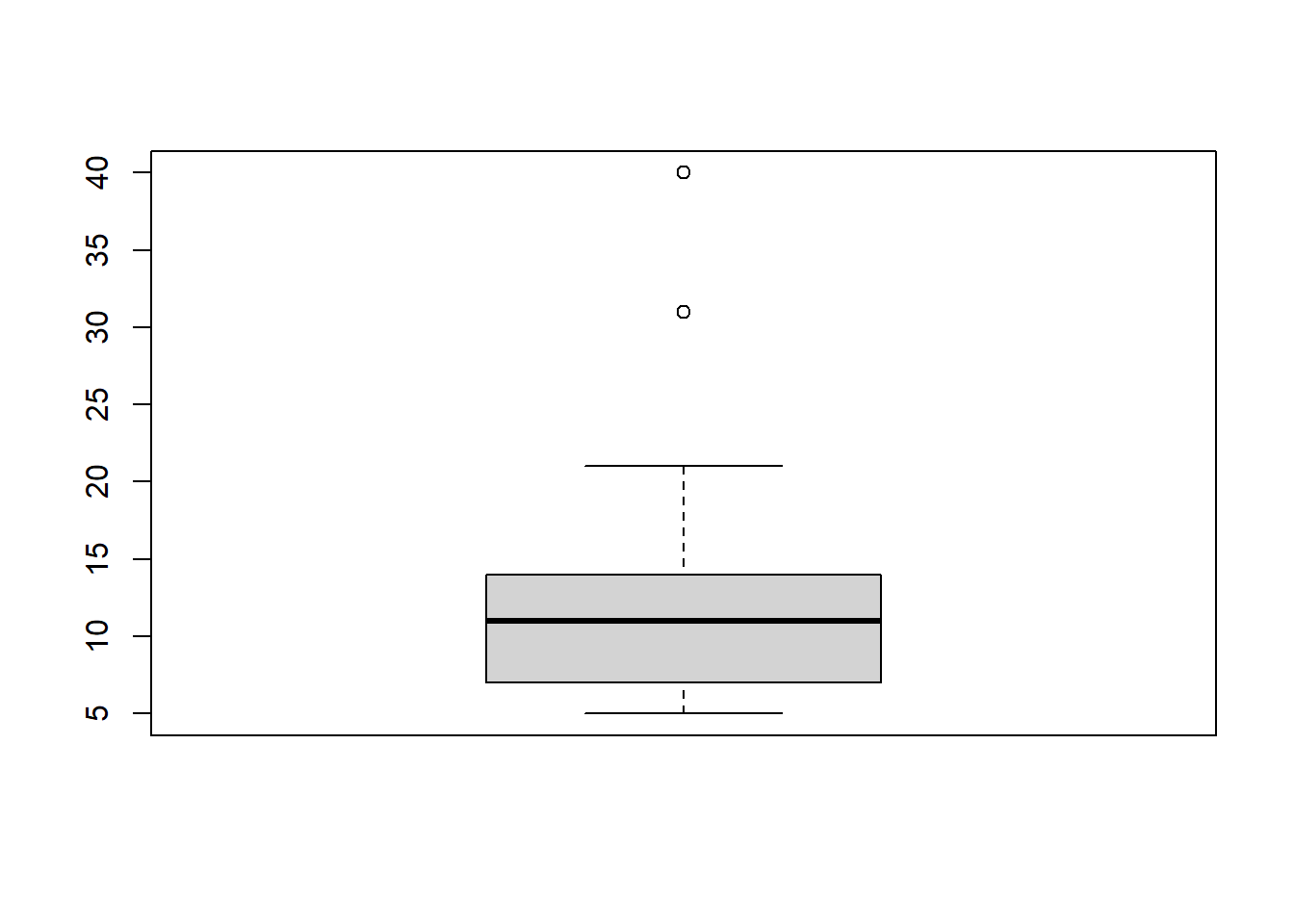
boxplot.stats(x)$stats
[1] 5 7 11 14 21
$n
[1] 100
$conf
[1] 9.894 12.106
$out
[1] 31 403.7.2 Normalización de variables: identificación a partir de la distancia de la media
Otra estrategia para la identificación de valores outliers, consiste en normalizar la variable de interés de la forma tradicional, lo que permite obtener una nueva variable zx, que se interpreta como el número de unidades (positivas o negativas, dependiendo del signo) en que se una observación se encuentre alejada de la media de la serie.
zx<- (x-mean(x))/sd(x) Una vez tenemos la variable normalizada, se consideran como valores outliers las observaciones que se encuentren a más de 3 desviaciones estándar del promedio (abs(zx)>3). En tal sentido, verifique que las próximas líneas de instrucciones muestran:
i) La creación de la variable edad normalizada;
ii) El uso de la función which() para identificar la posición de aquellas observaciones que cumplen la regla establecida (abs(zx)>3), en palabras, edades que se encuentren a más de 3 desviaciones desde su media;
iii) Por último, se utiliza el concepto de indexación, para acceder mediante las coordenadas de posición, a las edades que superan este margen [x[which(zx>3)]]. Este valor se deriva del hecho que Zx~N(0,1), por tanto, una observación que diste de 3 desviaciones de la media se considera como un valor atípico.
which(abs(zx)>3)[1] 21 33x[which(zx>3)][1] 31 40pch_site<-as.numeric(abs(zx)>3)
plot(x, pch = pch_site, col = gray((1:4)/6)[abs(zx)])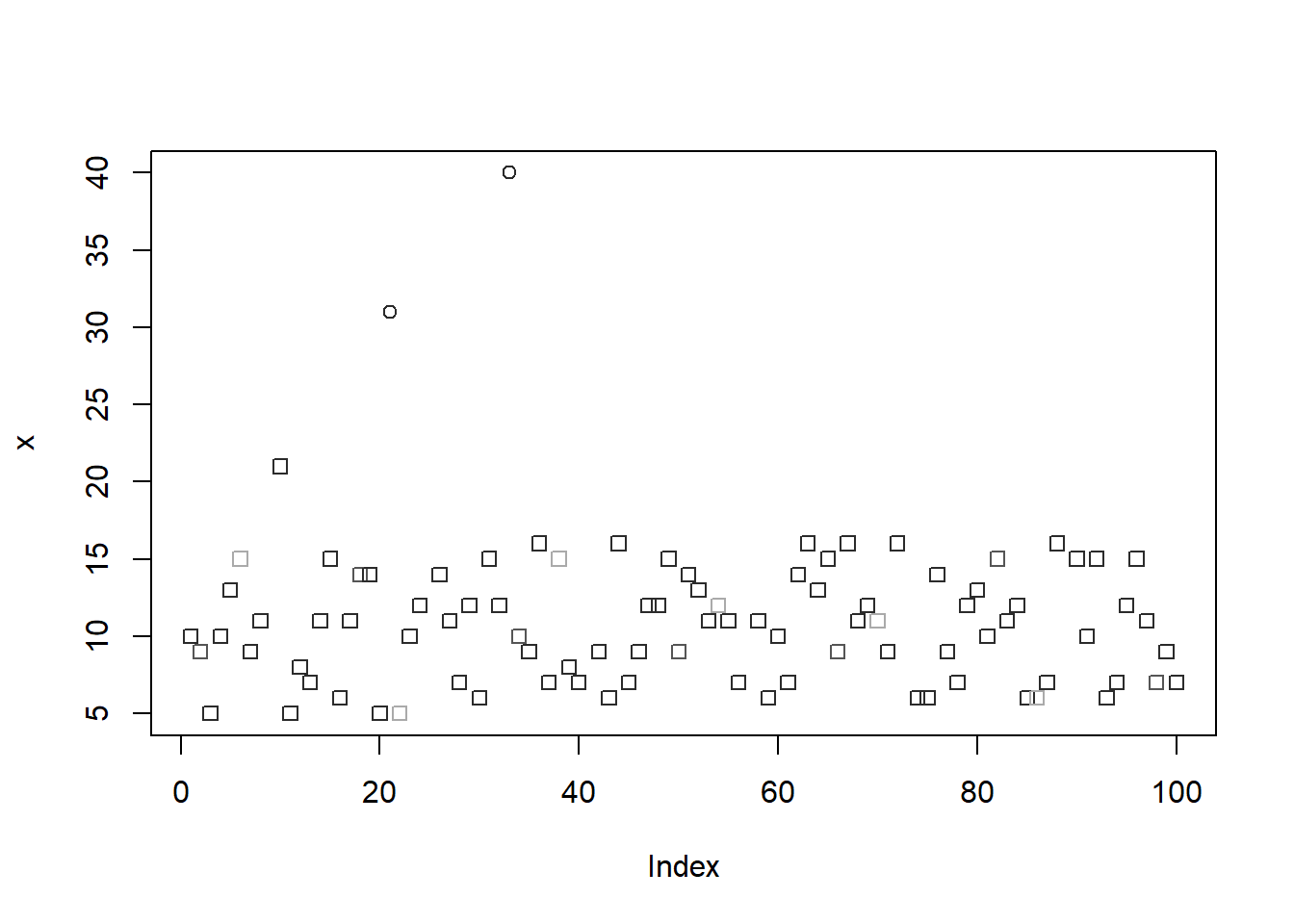
valcol <- (x + abs(min(x)))/max(x + abs(min(x)))
plot(x, pch = 16, col = rgb(0, 0, valcol))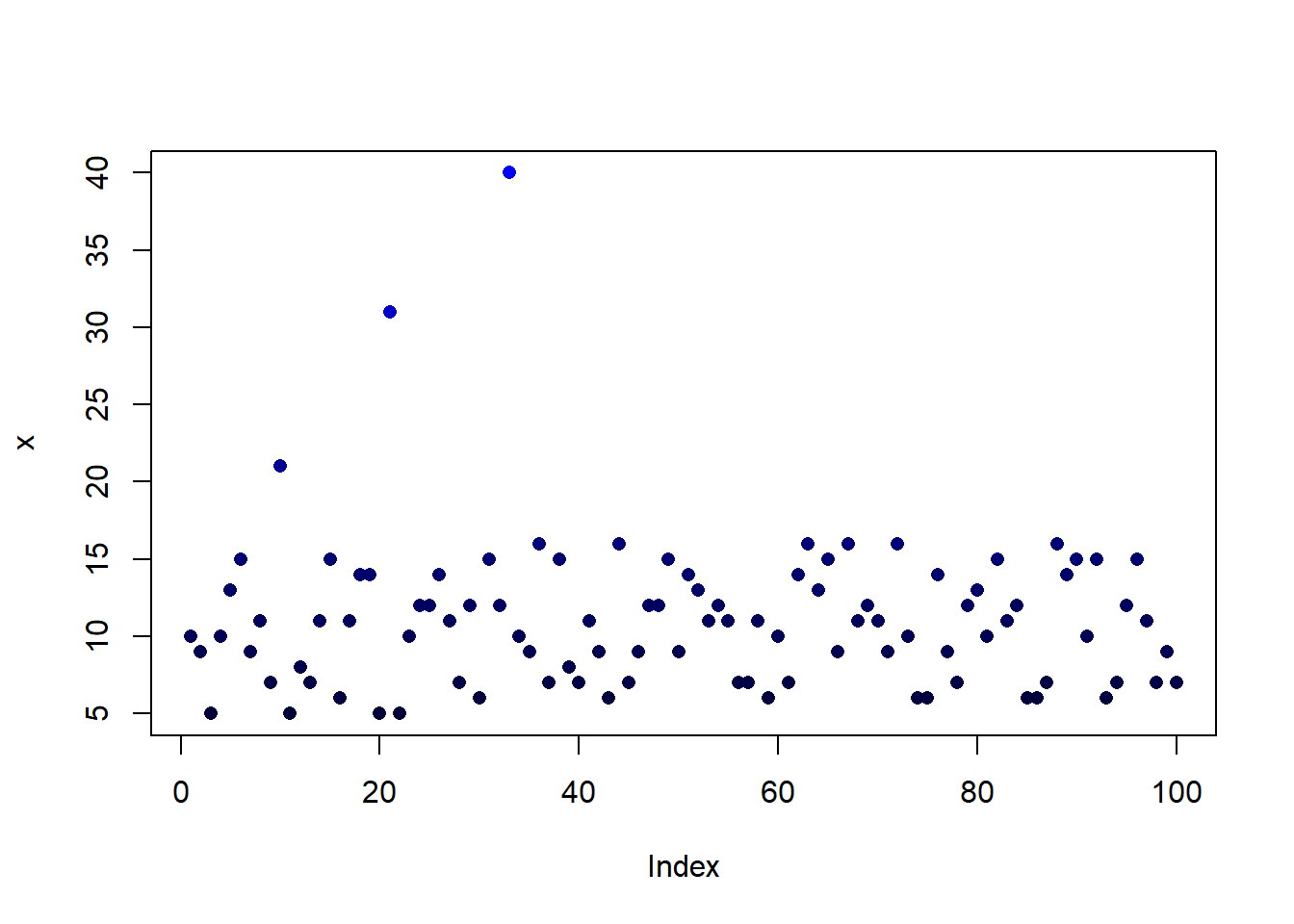
3.7.3 Identificación a partir de la prueba de Tukey
El problema de la identificación anterior es que los mementos a partir del cual se estandariza la variable, dependen del valor medio estimado, y por tanto, están incidido por los valores robustos. Una alternativa es utilizar una medida de dispersión robusta a valores atípicos o outliers, y posteriormente establecer los rangos que permitan la identificación de estos datos.
La prueba Tukey propone establecer un rango a partir del rango intercuartílico (IQR=q3-q1), que no depende de los valores extremos. Este no es una regla del universo, más bien es una convención o acuerdo entre los estadísticos. Posteriormente, se establece un rango para determinar datos atípicos a partir de los datos que excedan el intervalo:
q1 <- quantile(x, 0.25)
q125%
7 q3 <- quantile(x, 0.75)
q375%
14 iqr<-q3-q1 # Rango = IQR(x)
iqr75%
7 tukey <- x<(q1-1.5*iqr) | x>(q3+1.5*iqr)
which(tukey)[1] 21 33x[tukey][1] 31 403.7.4 Identificación a partir de la prueba de Tukey ajustada
Como observan en el ejemplo anterior, las observaciones identificadas como outliers siguen siendo 21 y 33, donde se registran individuos con edades de 31 y de 40 años, por lo que, continua sin reconocer el valor de 21 años (insertado intencionalmente) como un outlier. Una alternativa práctica para aumentar la sensibilidad de la prueba, es obtener los quintiles a partir del vector de variables originales recortado a partir de los valores extremos. Es decir, desprendernos de un porcentaje determinado de los valores extremos (por ejemplo el 5% de los datos colocados en el extremo en ambas colas de la distribución de la variable) y a partir de este vector recortado [xrecortada<-x[x>w5_95[1]& x<x5_95[2]]], obtener los quantiles y el rango intercuartílico (quantile(xrecortada, 0.25)), por tanto, obteniendo un rango más estrecho. Ahora, se obtienen los valores anormales, utilizando el rango creado a partir del vector recortado (tukeyR <- x<(q1a-1.5*iqra)| x>(q3a+1.5*iqra)).
(x5_95 <- quantile(x, c(0.1, 0.90)))10% 90%
6 15 xrecortada<-x[x>x5_95[1] & x<x5_95[2]](q1a <- quantile(xrecortada, 0.25))25%
9 (q3a <- quantile(xrecortada, 0.75))75%
12 iqra<-q3a-q1a # Rango = IQR(x)
tukeyR <- x<(q1a-1.5*iqra) | x>(q3a+1.5*iqra)
which(tukeyR)[1] 10 21 33x[tukeyR][1] 21 31 40plot(x, pch = 16, col = rgb(0, 0, valcol), ylim=c(-0,50))
abline(h=c(q1-1.5*iqr,q3+1.5*iqr), col="#FF4040")
abline(h=c(q1a-1.5*iqra,q3a+1.5*iqra), col="#1874CD", lwd=3, lty=2)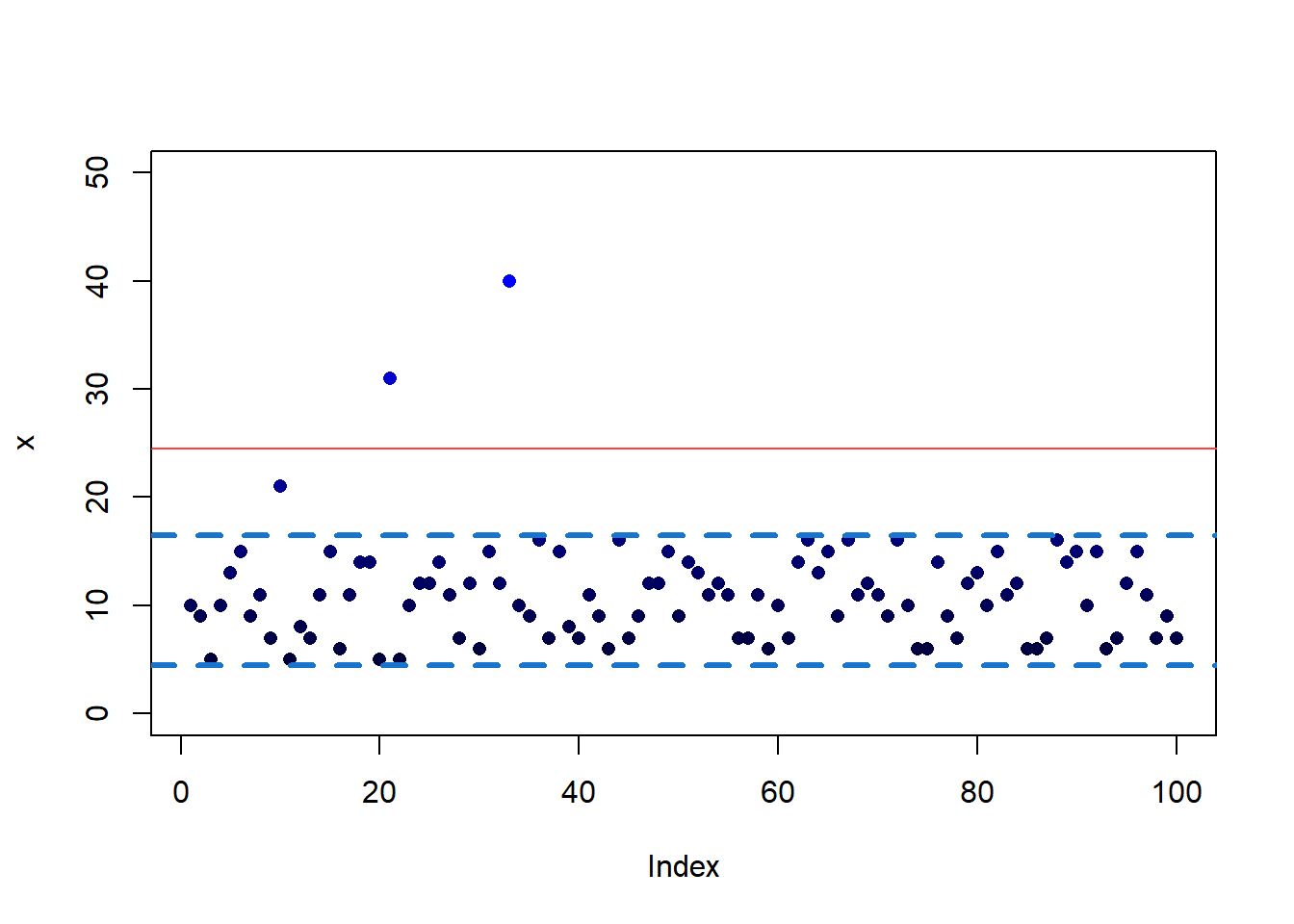
Las líneas discontinuas representan el rango creado a partir del vector recortado.
3.7.5 Identificación a partir de la distancia de Cooks
A partir del enfoque de regresión se puede utilizar el concepto de distancia de Cooks. Esta realiza la estimación del cambio de cada valor ajustado, con yhat sin la i-ésima observación. Por lo que, mide la influencia de cada observación. yhat(j) es el valor de la respuesta ajustada j, cuando se incluyen todas las observaciones; yhat(ji) es el valor de la observación j cuando no se incluye la observación i, P es el número de coeficientes en el modelo de regresión; por último, MSE es el error cuadrático medio del modelo con todas las observaciones.
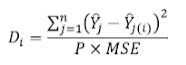
Considere el siguiente ejemplo, donde solo se regresa la variable de interés en función de una constante (ln(x ~ 1)), por lo que, el ajuste condicionado del modelo corresponde al promedio.
#Distancia de cooks
mod <- lm(x ~ 1)
cooksd <- cooks.distance(mod)
plot(cooksd, pch="*", cex=2)
abline(h = 4*mean(cooksd, na.rm=T), col="#008B8B")
text(x=1:length(cooksd)+1, y=cooksd,
labels=ifelse(cooksd > 4 * mean(cooksd, na.rm = TRUE),
names(cooksd),""),
col="#008B8B")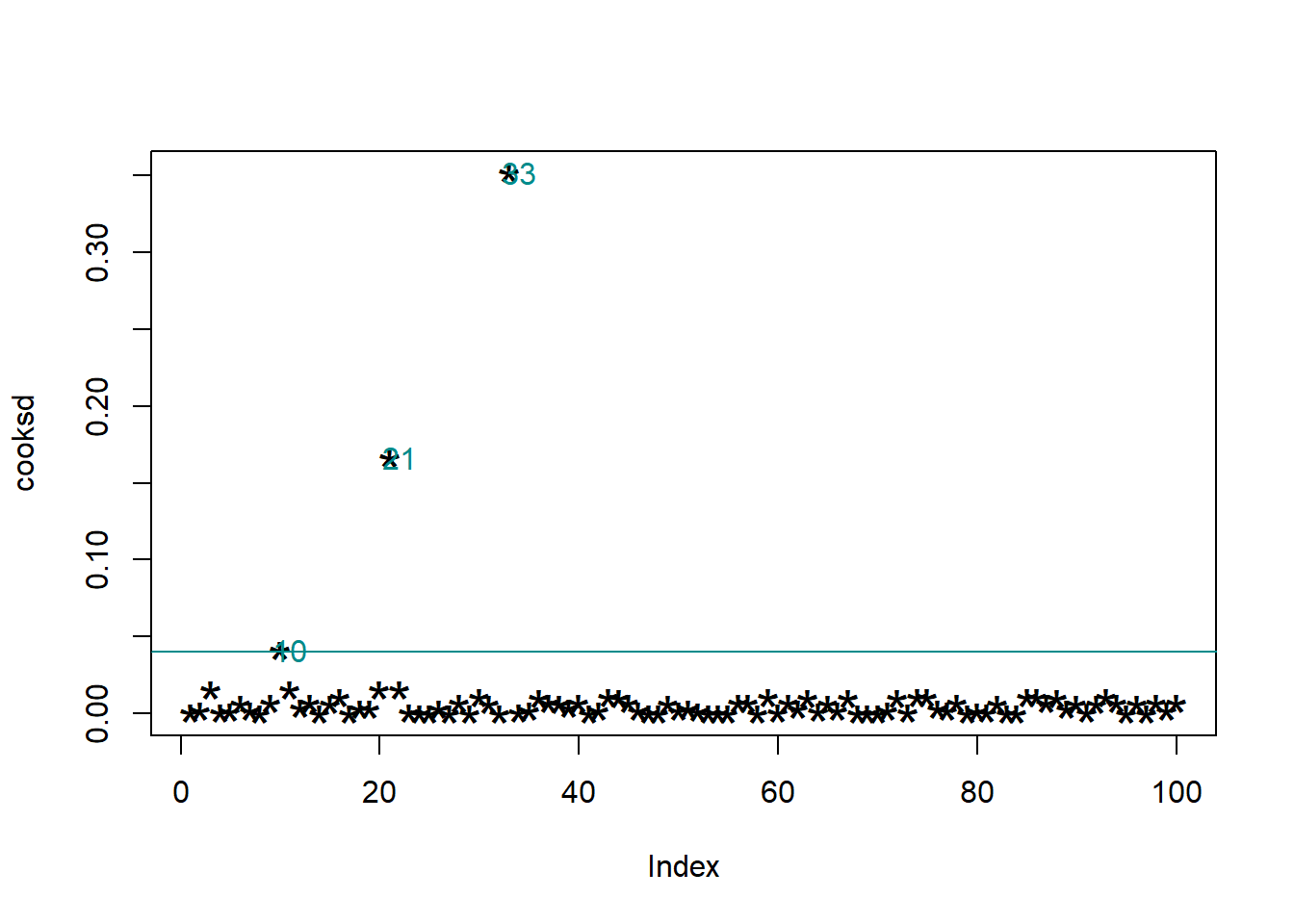
3.8 Manejo de datos outlier
3.8.1 Datos outliers univariados
En el caso univariado, cuando se tiene un conjunto de datos, se dice que un dato es un outlier, si es un punto que no esta de acuerdo con el conjunto de datos, o es un valor atípico o raro, o es una observación extrema. Datos reales que proporcionan gran información.
CyCC.data<-read.csv("C:/Users/Sebastian H/Documents/Trabajo Final PLE/duke-forest.csv",
stringsAsFactors = F)
names(CyCC.data) [1] "address" "price" "bed" "bath" "area"
[6] "type" "year_built" "heating" "cooling" "parking"
[11] "lot" "hoa" "url" boxplot(CyCC.data$area,
main = "Area",
boxwex = 0.5,col="#CAFF70")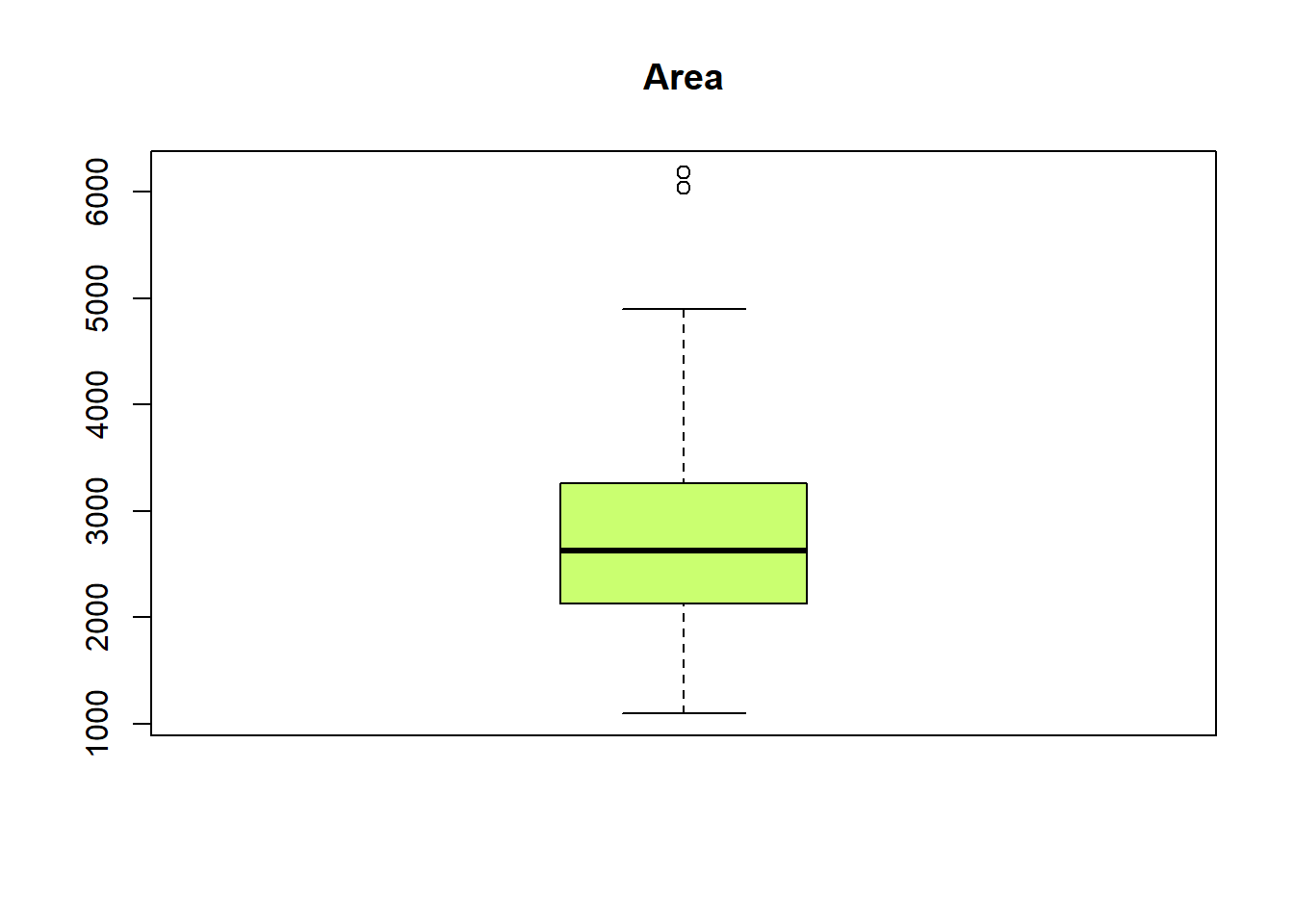
3.8.1.1 Remplazar los valores outliers
replace_outliers <- function(x, removeNA = TRUE){
qrts <- quantile(x, probs = c(0.25, 0.75), na.rm = removeNA)
caps <- quantile(x, probs = c(.05, .95), na.rm = removeNA)
iqr <- qrts[2]-qrts[1]
h <- 1.5 * iqr
x[x<qrts[1]-h] <- caps[1]
x[x>qrts[2]+h] <- caps[2]
x
}
capped_area <- replace_outliers(CyCC.data$area)par(mfrow = c(1,2))
boxplot(CyCC.data$area, main = "Presión con outliers"
,col=22)
boxplot(capped_area, main = "Presión sin outliers",col=2)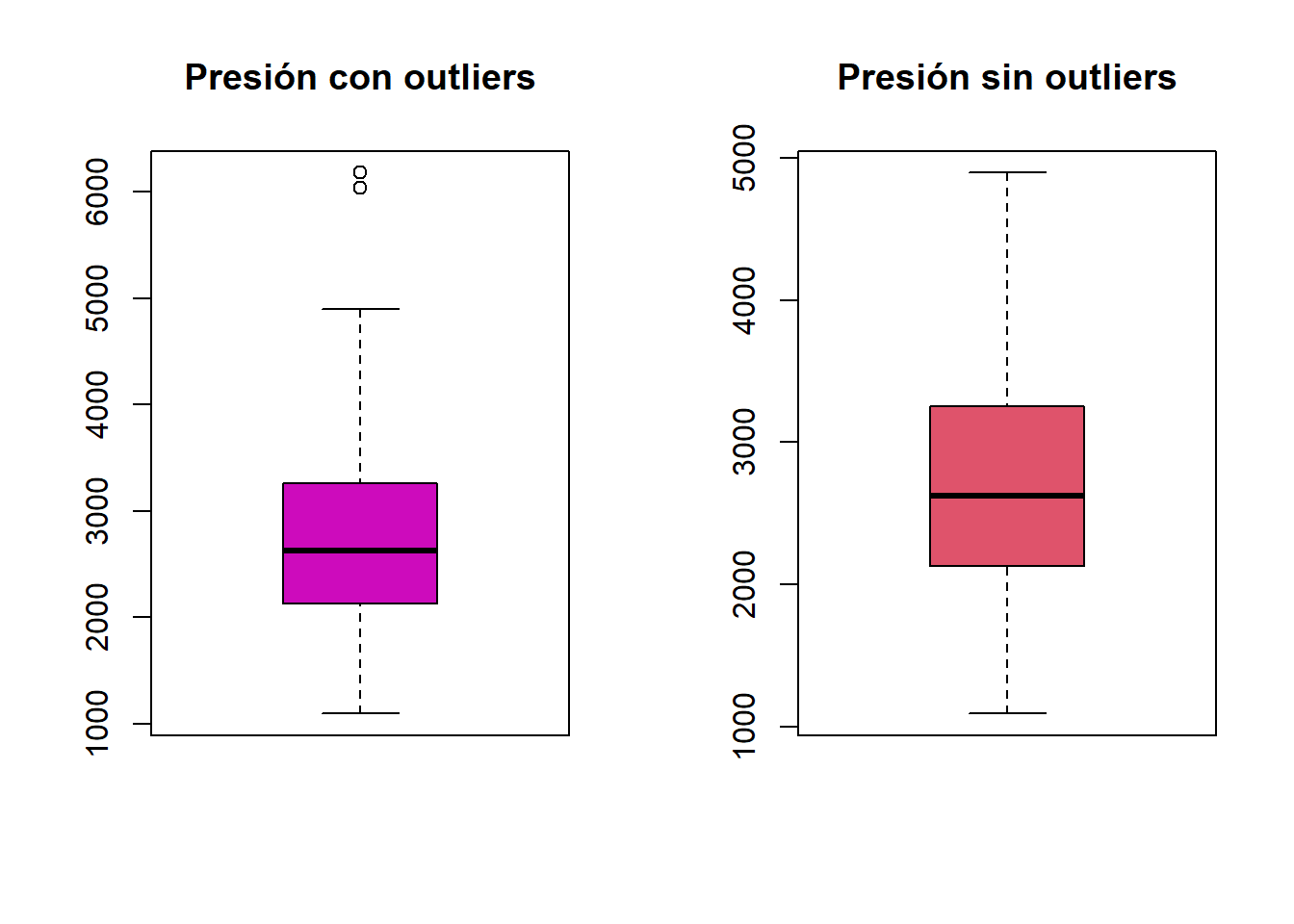
3.8.2 Datos outliers multivariados
Según Gnanadesikan y Kettenring, los outliers multivariantes son observaciones que se consideran extrañas no por el valor que toman en una determinada variable, sino en el conjunto de aquellas.
with(cars, plot(x=speed, y=dist))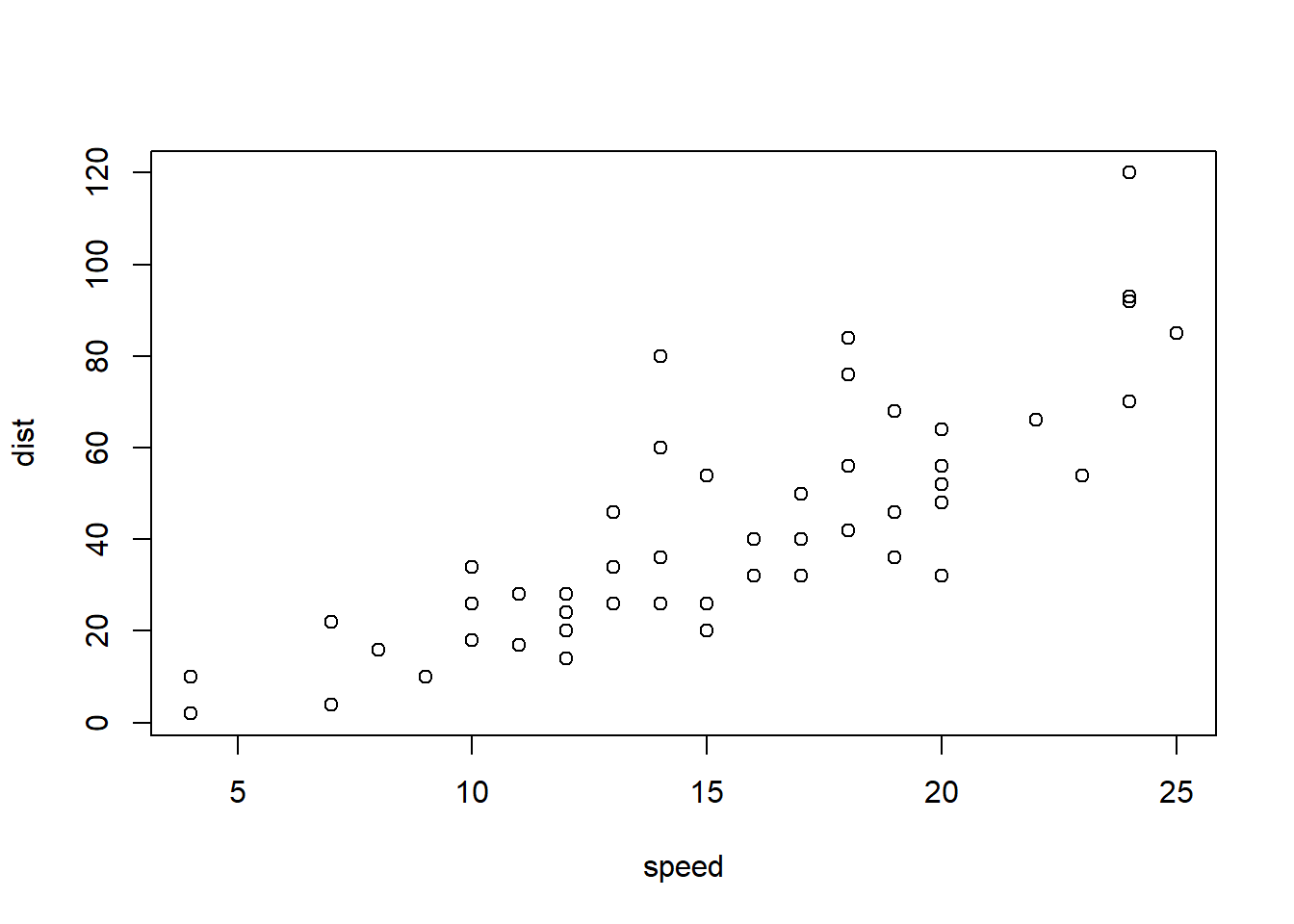
#Punto de balanceo
n <- dim(cars)[1]
mycars <- rbind(cars, c(60, 218.3649))
with(mycars, plot(x=speed, y=dist))
points(mycars[n + 1, ], pch=20, col='yellow')
mod1 <- lm(dist ~ speed, data=cars);abline(mod1)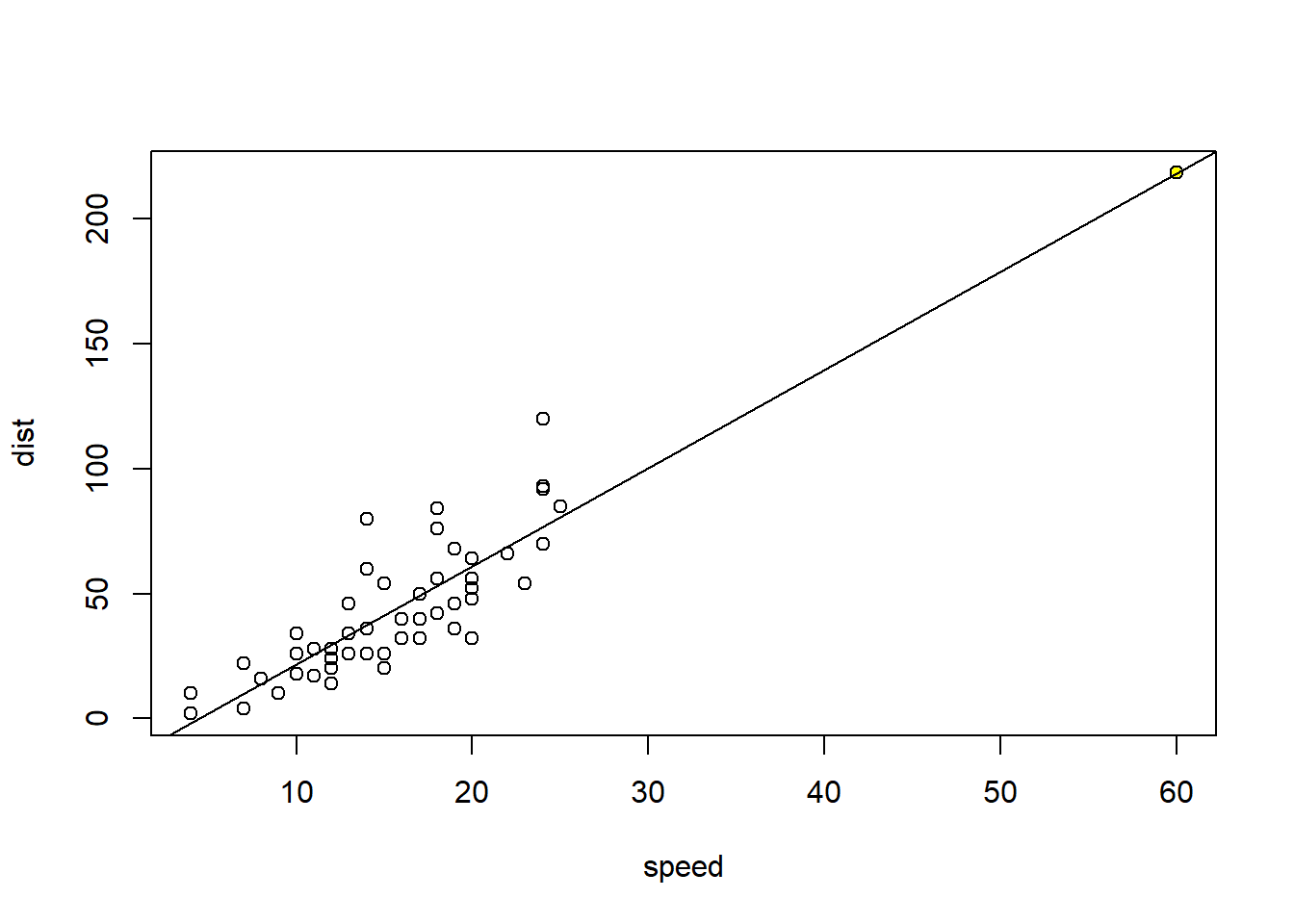
3.8.2.1 Punto de influencia
Es un punto que tiene impacto en las estimativas del modelo.
mycars1 <- rbind(cars, c(25, 10))
with(mycars1, plot(x=speed, y=dist,ylim = c(0,200),xlim = c(0,50),
points(25,10,col=2,pch=20)))
mod3 <- lm(dist ~ speed, data=mycars1);abline(mod1);abline(mod3,col=4)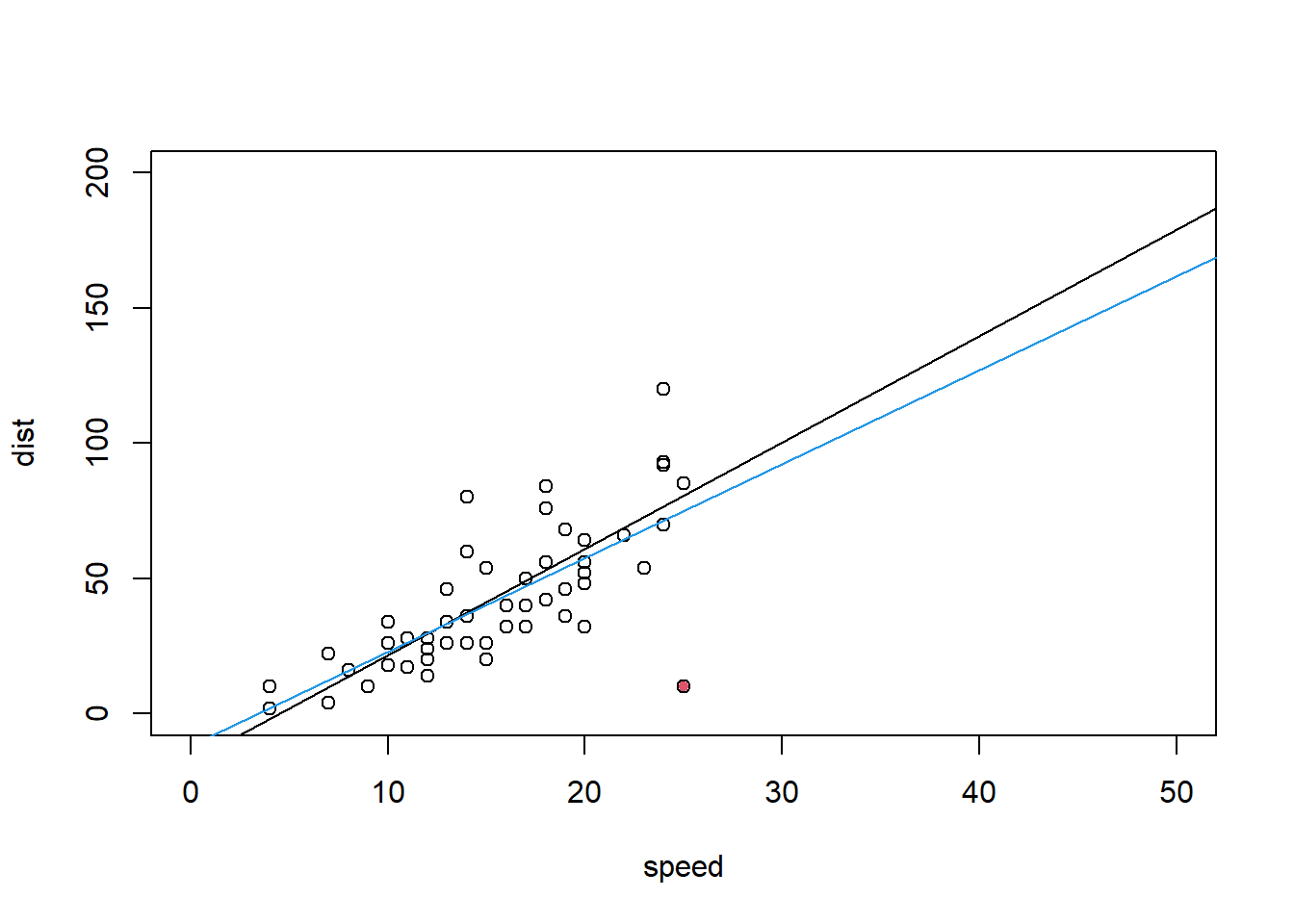
3.8.2.2 Eliminación de datos outliers
Para esto primero cargaremos una base de datos la cual es la siguiente:
df<-read.csv("C:/Users/Sebastian H/Documents/Trabajo Final PLE/wage.csv")
names(df) [1] "X" "year" "age" "maritl" "race"
[6] "education" "region" "jobclass" "health" "health_ins"
[11] "logwage" "wage" Realizamos un gráfico de caja de la variable age
caja_c<-boxplot(df$age, col="#2F4F4F", frame.plot=F)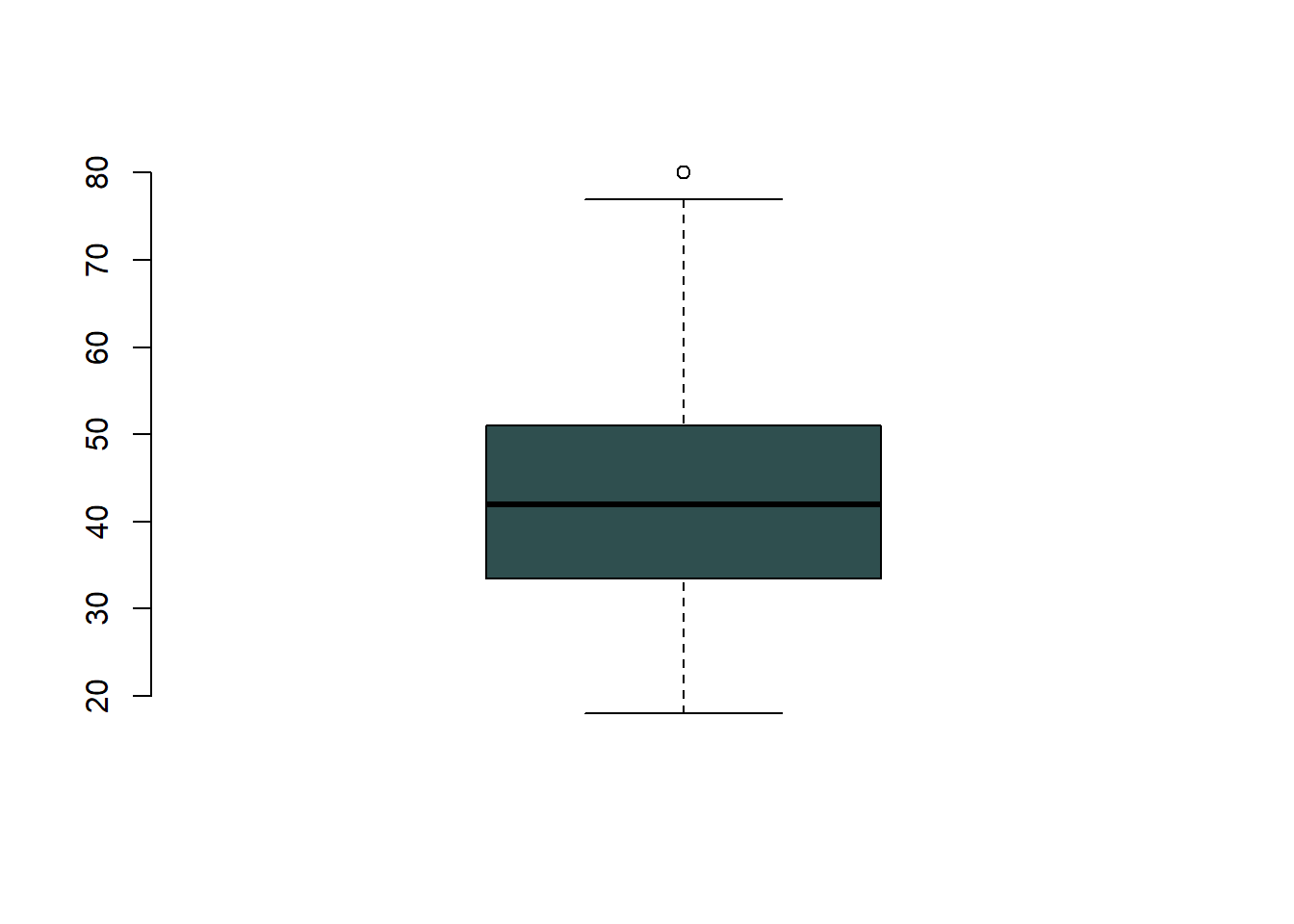
Se puede ver que hay algunos outliers. Entonces si queremos conocer los outliers. sólo llamamos a los outliers con el comando $out
caja_c$out[1] 80 80 80 80Nos muestra cuatro outliers. Entonces un método de correción sería el de eliminar los outliers (en realidad, es el método que no debería de usarse. Es mejor considerar la discretización, que se verá posteriormente).
Entonces para eliminar los outliers usamos el operador pertenece %in% que funciona igual que el símbolo matemático ∈ que se usa en la teoría de conjuntos.
df<-df[!(df$age %in% caja_c$out),]Para comprobar que los outliers han sido eliminados volvamos a ver el gráfico de caja.
boxplot(df$age, col="#2F4F4F", frame.plot=F)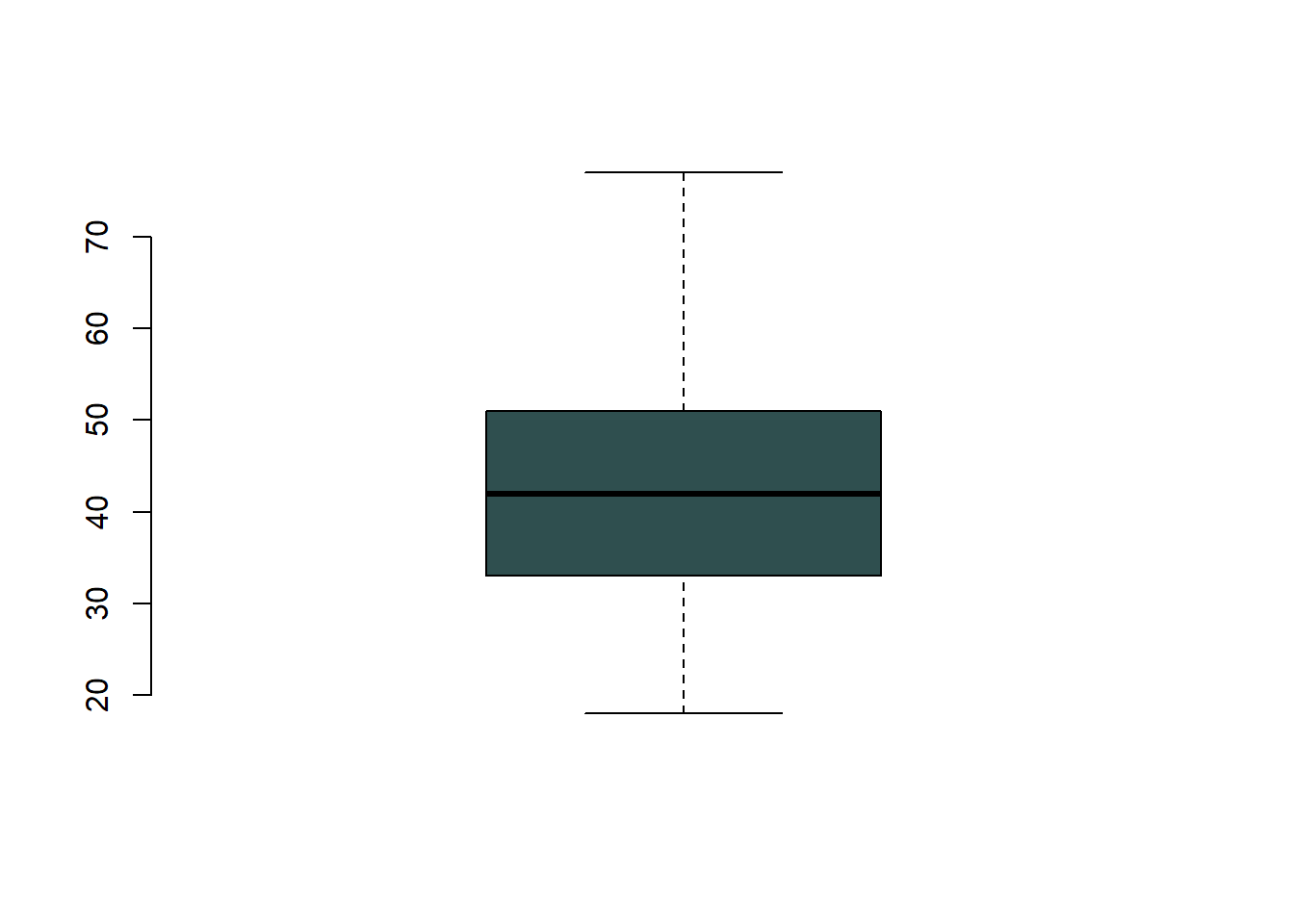
En efecto, los outliers han sido eliminados.
3.9 Limpieza de datos y preparación de datos
3.9.1 Limpieza de datos
La limpieza de datos es la parte dentro del proceso de la Ciencia de Datos que consume más tiempo. De acuerdo al paper de Dasu and Johnson (2003), el 80% del tiempo se consume en limpieza de datos.
¿Cómo aprender a limpiar data? Así como se aprende un nuevo lenguaje (alemán, francés, chino,etc), es necesario una cantidad importante de práctica y conocer los principios de la limpieza de datos.
3.9.1.1 Principios de Limpieza de datos
Los principios de limpieza de datos proveen un estándar para limpiar la data para no reinventar la rueda cada vez que tratamos de limpiar base de datos. La idea de la bases de datos limpias es hacer el análisis de datos más fácil, permitiendo enfocarnos en entender el problema y no la logística de la data.
Una base de datos limpia tiene las siguientes características:
Cada variable forma una columna.
Cada observación forma una fila.
Cada tipo de unidad observacional forma una tabla.
3.9.2 Paquetes para la limpieza de datos
Los paquetes mas usados para la limpieza de datos en R son los siguientes:
library(dplyr)Warning: package 'dplyr' was built under R version 4.3.2
Attaching package: 'dplyr'The following objects are masked from 'package:stats':
filter, lagThe following objects are masked from 'package:base':
intersect, setdiff, setequal, unionlibrary(tidyr) Warning: package 'tidyr' was built under R version 4.3.2library(readxl)Warning: package 'readxl' was built under R version 4.3.23.9.3 Importación de datos
Importa tus datos desde archivos o fuentes externas utilizando funciones como read.csv(), read.table(), read_excel(), o paquetes específicos según el formato de tus datos.
Para esta sección se usara un archivo.csv extraído de kaggle.com el cual es “titanic_dataset”
datos <- read.csv("C:\\Users\\Sebastian H\\Documents\\Trabajo Final PLE\\titanic.csv")3.9.4 Exploración inicial
Realiza una exploración inicial de tus datos para entender su estructura y contenido. Se utiliza funciones como head(), summary(), str(), y colnames().
head(datos) PassengerId Survived Pclass
1 1 0 3
2 2 1 1
3 3 1 3
4 4 1 1
5 5 0 3
6 6 0 3
Name Sex Age SibSp Parch
1 Braund, Mr. Owen Harris male 22 1 0
2 Cumings, Mrs. John Bradley (Florence Briggs Thayer) female 38 1 0
3 Heikkinen, Miss. Laina female 26 0 0
4 Futrelle, Mrs. Jacques Heath (Lily May Peel) female 35 1 0
5 Allen, Mr. William Henry male 35 0 0
6 Moran, Mr. James male NA 0 0
Ticket Fare Cabin Embarked
1 A/5 21171 7.2500 S
2 PC 17599 71.2833 C85 C
3 STON/O2. 3101282 7.9250 S
4 113803 53.1000 C123 S
5 373450 8.0500 S
6 330877 8.4583 Qsummary(datos) PassengerId Survived Pclass Name
Min. : 1.0 Min. :0.0000 Min. :1.000 Length:891
1st Qu.:223.5 1st Qu.:0.0000 1st Qu.:2.000 Class :character
Median :446.0 Median :0.0000 Median :3.000 Mode :character
Mean :446.0 Mean :0.3838 Mean :2.309
3rd Qu.:668.5 3rd Qu.:1.0000 3rd Qu.:3.000
Max. :891.0 Max. :1.0000 Max. :3.000
Sex Age SibSp Parch
Length:891 Min. : 0.42 Min. :0.000 Min. :0.0000
Class :character 1st Qu.:20.12 1st Qu.:0.000 1st Qu.:0.0000
Mode :character Median :28.00 Median :0.000 Median :0.0000
Mean :29.70 Mean :0.523 Mean :0.3816
3rd Qu.:38.00 3rd Qu.:1.000 3rd Qu.:0.0000
Max. :80.00 Max. :8.000 Max. :6.0000
NA's :177
Ticket Fare Cabin Embarked
Length:891 Min. : 0.00 Length:891 Length:891
Class :character 1st Qu.: 7.91 Class :character Class :character
Mode :character Median : 14.45 Mode :character Mode :character
Mean : 32.20
3rd Qu.: 31.00
Max. :512.33
str(datos)'data.frame': 891 obs. of 12 variables:
$ PassengerId: int 1 2 3 4 5 6 7 8 9 10 ...
$ Survived : int 0 1 1 1 0 0 0 0 1 1 ...
$ Pclass : int 3 1 3 1 3 3 1 3 3 2 ...
$ Name : chr "Braund, Mr. Owen Harris" "Cumings, Mrs. John Bradley (Florence Briggs Thayer)" "Heikkinen, Miss. Laina" "Futrelle, Mrs. Jacques Heath (Lily May Peel)" ...
$ Sex : chr "male" "female" "female" "female" ...
$ Age : num 22 38 26 35 35 NA 54 2 27 14 ...
$ SibSp : int 1 1 0 1 0 0 0 3 0 1 ...
$ Parch : int 0 0 0 0 0 0 0 1 2 0 ...
$ Ticket : chr "A/5 21171" "PC 17599" "STON/O2. 3101282" "113803" ...
$ Fare : num 7.25 71.28 7.92 53.1 8.05 ...
$ Cabin : chr "" "C85" "" "C123" ...
$ Embarked : chr "S" "C" "S" "S" ...colnames(datos) [1] "PassengerId" "Survived" "Pclass" "Name" "Sex"
[6] "Age" "SibSp" "Parch" "Ticket" "Fare"
[11] "Cabin" "Embarked" 3.9.5 Agrupación y resumen
Si estás trabajando con conjuntos de datos grandes, puedes agrupar y resumir datos utilizando funciones como group_by() y summarize() del paquete dplyr.
Para la agrupación y resumen se escogieron las siguientes variables las cuales son: “Ticket”, “PassengerId” y “Survived” respectivamente.
library(dplyr)
datos_resumidos <- datos %>%
group_by(Ticket) %>%
summarize(media = mean(PassengerId), total = sum(Survived))
datos_resumidos # A tibble: 681 × 3
Ticket media total
<chr> <dbl> <int>
1 110152 508. 3
2 110413 469. 2
3 110465 294. 0
4 110564 431 1
5 110813 367 1
6 111240 171 0
7 111320 463 0
8 111361 427 2
9 111369 890 1
10 111426 605 1
# ℹ 671 more rows3.9.6 Normalización o estandarización
En algunos casos, es útil normalizar o estandarizar variables numéricas para compararlas más fácilmente.
Para la estandarización se necesita una variable numérica y en este caso se escogió la variable “Survived” y sale lo siguiente:
datos$columna_estandarizada <- scale(datos$Survived)
datos$columna_estandarizada [,1]
[1,] -0.7888293
[2,] 1.2662786
[3,] 1.2662786
[4,] 1.2662786
[5,] -0.7888293
[6,] -0.7888293
[7,] -0.7888293
[8,] -0.7888293
[9,] 1.2662786
[10,] 1.2662786
[11,] 1.2662786
[12,] 1.2662786
[13,] -0.7888293
[14,] -0.7888293
[15,] -0.7888293
[16,] 1.2662786
[17,] -0.7888293
[18,] 1.2662786
[19,] -0.7888293
[20,] 1.2662786
[21,] -0.7888293
[22,] 1.2662786
[23,] 1.2662786
[24,] 1.2662786
[25,] -0.7888293
[26,] 1.2662786
[27,] -0.7888293
[28,] -0.7888293
[29,] 1.2662786
[30,] -0.7888293
[31,] -0.7888293
[32,] 1.2662786
[33,] 1.2662786
[34,] -0.7888293
[35,] -0.7888293
[36,] -0.7888293
[37,] 1.2662786
[38,] -0.7888293
[39,] -0.7888293
[40,] 1.2662786
[41,] -0.7888293
[42,] -0.7888293
[43,] -0.7888293
[44,] 1.2662786
[45,] 1.2662786
[46,] -0.7888293
[47,] -0.7888293
[48,] 1.2662786
[49,] -0.7888293
[50,] -0.7888293
[51,] -0.7888293
[52,] -0.7888293
[53,] 1.2662786
[54,] 1.2662786
[55,] -0.7888293
[56,] 1.2662786
[57,] 1.2662786
[58,] -0.7888293
[59,] 1.2662786
[60,] -0.7888293
[61,] -0.7888293
[62,] 1.2662786
[63,] -0.7888293
[64,] -0.7888293
[65,] -0.7888293
[66,] 1.2662786
[67,] 1.2662786
[68,] -0.7888293
[69,] 1.2662786
[70,] -0.7888293
[71,] -0.7888293
[72,] -0.7888293
[73,] -0.7888293
[74,] -0.7888293
[75,] 1.2662786
[76,] -0.7888293
[77,] -0.7888293
[78,] -0.7888293
[79,] 1.2662786
[80,] 1.2662786
[81,] -0.7888293
[82,] 1.2662786
[83,] 1.2662786
[84,] -0.7888293
[85,] 1.2662786
[86,] 1.2662786
[87,] -0.7888293
[88,] -0.7888293
[89,] 1.2662786
[90,] -0.7888293
[91,] -0.7888293
[92,] -0.7888293
[93,] -0.7888293
[94,] -0.7888293
[95,] -0.7888293
[96,] -0.7888293
[97,] -0.7888293
[98,] 1.2662786
[99,] 1.2662786
[100,] -0.7888293
[101,] -0.7888293
[102,] -0.7888293
[103,] -0.7888293
[104,] -0.7888293
[105,] -0.7888293
[106,] -0.7888293
[107,] 1.2662786
[108,] 1.2662786
[109,] -0.7888293
[110,] 1.2662786
[111,] -0.7888293
[112,] -0.7888293
[113,] -0.7888293
[114,] -0.7888293
[115,] -0.7888293
[116,] -0.7888293
[117,] -0.7888293
[118,] -0.7888293
[119,] -0.7888293
[120,] -0.7888293
[121,] -0.7888293
[122,] -0.7888293
[123,] -0.7888293
[124,] 1.2662786
[125,] -0.7888293
[126,] 1.2662786
[127,] -0.7888293
[128,] 1.2662786
[129,] 1.2662786
[130,] -0.7888293
[131,] -0.7888293
[132,] -0.7888293
[133,] -0.7888293
[134,] 1.2662786
[135,] -0.7888293
[136,] -0.7888293
[137,] 1.2662786
[138,] -0.7888293
[139,] -0.7888293
[140,] -0.7888293
[141,] -0.7888293
[142,] 1.2662786
[143,] 1.2662786
[144,] -0.7888293
[145,] -0.7888293
[146,] -0.7888293
[147,] 1.2662786
[148,] -0.7888293
[149,] -0.7888293
[150,] -0.7888293
[151,] -0.7888293
[152,] 1.2662786
[153,] -0.7888293
[154,] -0.7888293
[155,] -0.7888293
[156,] -0.7888293
[157,] 1.2662786
[158,] -0.7888293
[159,] -0.7888293
[160,] -0.7888293
[161,] -0.7888293
[162,] 1.2662786
[163,] -0.7888293
[164,] -0.7888293
[165,] -0.7888293
[166,] 1.2662786
[167,] 1.2662786
[168,] -0.7888293
[169,] -0.7888293
[170,] -0.7888293
[171,] -0.7888293
[172,] -0.7888293
[173,] 1.2662786
[174,] -0.7888293
[175,] -0.7888293
[176,] -0.7888293
[177,] -0.7888293
[178,] -0.7888293
[179,] -0.7888293
[180,] -0.7888293
[181,] -0.7888293
[182,] -0.7888293
[183,] -0.7888293
[184,] 1.2662786
[185,] 1.2662786
[186,] -0.7888293
[187,] 1.2662786
[188,] 1.2662786
[189,] -0.7888293
[190,] -0.7888293
[191,] 1.2662786
[192,] -0.7888293
[193,] 1.2662786
[194,] 1.2662786
[195,] 1.2662786
[196,] 1.2662786
[197,] -0.7888293
[198,] -0.7888293
[199,] 1.2662786
[200,] -0.7888293
[201,] -0.7888293
[202,] -0.7888293
[203,] -0.7888293
[204,] -0.7888293
[205,] 1.2662786
[206,] -0.7888293
[207,] -0.7888293
[208,] 1.2662786
[209,] 1.2662786
[210,] 1.2662786
[211,] -0.7888293
[212,] 1.2662786
[213,] -0.7888293
[214,] -0.7888293
[215,] -0.7888293
[216,] 1.2662786
[217,] 1.2662786
[218,] -0.7888293
[219,] 1.2662786
[220,] -0.7888293
[221,] 1.2662786
[222,] -0.7888293
[223,] -0.7888293
[224,] -0.7888293
[225,] 1.2662786
[226,] -0.7888293
[227,] 1.2662786
[228,] -0.7888293
[229,] -0.7888293
[230,] -0.7888293
[231,] 1.2662786
[232,] -0.7888293
[233,] -0.7888293
[234,] 1.2662786
[235,] -0.7888293
[236,] -0.7888293
[237,] -0.7888293
[238,] 1.2662786
[239,] -0.7888293
[240,] -0.7888293
[241,] -0.7888293
[242,] 1.2662786
[243,] -0.7888293
[244,] -0.7888293
[245,] -0.7888293
[246,] -0.7888293
[247,] -0.7888293
[248,] 1.2662786
[249,] 1.2662786
[250,] -0.7888293
[251,] -0.7888293
[252,] -0.7888293
[253,] -0.7888293
[254,] -0.7888293
[255,] -0.7888293
[256,] 1.2662786
[257,] 1.2662786
[258,] 1.2662786
[259,] 1.2662786
[260,] 1.2662786
[261,] -0.7888293
[262,] 1.2662786
[263,] -0.7888293
[264,] -0.7888293
[265,] -0.7888293
[266,] -0.7888293
[267,] -0.7888293
[268,] 1.2662786
[269,] 1.2662786
[270,] 1.2662786
[271,] -0.7888293
[272,] 1.2662786
[273,] 1.2662786
[274,] -0.7888293
[275,] 1.2662786
[276,] 1.2662786
[277,] -0.7888293
[278,] -0.7888293
[279,] -0.7888293
[280,] 1.2662786
[281,] -0.7888293
[282,] -0.7888293
[283,] -0.7888293
[284,] 1.2662786
[285,] -0.7888293
[286,] -0.7888293
[287,] 1.2662786
[288,] -0.7888293
[289,] 1.2662786
[290,] 1.2662786
[291,] 1.2662786
[292,] 1.2662786
[293,] -0.7888293
[294,] -0.7888293
[295,] -0.7888293
[296,] -0.7888293
[297,] -0.7888293
[298,] -0.7888293
[299,] 1.2662786
[300,] 1.2662786
[301,] 1.2662786
[302,] 1.2662786
[303,] -0.7888293
[304,] 1.2662786
[305,] -0.7888293
[306,] 1.2662786
[307,] 1.2662786
[308,] 1.2662786
[309,] -0.7888293
[310,] 1.2662786
[311,] 1.2662786
[312,] 1.2662786
[313,] -0.7888293
[314,] -0.7888293
[315,] -0.7888293
[316,] 1.2662786
[317,] 1.2662786
[318,] -0.7888293
[319,] 1.2662786
[320,] 1.2662786
[321,] -0.7888293
[322,] -0.7888293
[323,] 1.2662786
[324,] 1.2662786
[325,] -0.7888293
[326,] 1.2662786
[327,] -0.7888293
[328,] 1.2662786
[329,] 1.2662786
[330,] 1.2662786
[331,] 1.2662786
[332,] -0.7888293
[333,] -0.7888293
[334,] -0.7888293
[335,] 1.2662786
[336,] -0.7888293
[337,] -0.7888293
[338,] 1.2662786
[339,] 1.2662786
[340,] -0.7888293
[341,] 1.2662786
[342,] 1.2662786
[343,] -0.7888293
[344,] -0.7888293
[345,] -0.7888293
[346,] 1.2662786
[347,] 1.2662786
[348,] 1.2662786
[349,] 1.2662786
[350,] -0.7888293
[351,] -0.7888293
[352,] -0.7888293
[353,] -0.7888293
[354,] -0.7888293
[355,] -0.7888293
[356,] -0.7888293
[357,] 1.2662786
[358,] -0.7888293
[359,] 1.2662786
[360,] 1.2662786
[361,] -0.7888293
[362,] -0.7888293
[363,] -0.7888293
[364,] -0.7888293
[365,] -0.7888293
[366,] -0.7888293
[367,] 1.2662786
[368,] 1.2662786
[369,] 1.2662786
[370,] 1.2662786
[371,] 1.2662786
[372,] -0.7888293
[373,] -0.7888293
[374,] -0.7888293
[375,] -0.7888293
[376,] 1.2662786
[377,] 1.2662786
[378,] -0.7888293
[379,] -0.7888293
[380,] -0.7888293
[381,] 1.2662786
[382,] 1.2662786
[383,] -0.7888293
[384,] 1.2662786
[385,] -0.7888293
[386,] -0.7888293
[387,] -0.7888293
[388,] 1.2662786
[389,] -0.7888293
[390,] 1.2662786
[391,] 1.2662786
[392,] 1.2662786
[393,] -0.7888293
[394,] 1.2662786
[395,] 1.2662786
[396,] -0.7888293
[397,] -0.7888293
[398,] -0.7888293
[399,] -0.7888293
[400,] 1.2662786
[401,] 1.2662786
[402,] -0.7888293
[403,] -0.7888293
[404,] -0.7888293
[405,] -0.7888293
[406,] -0.7888293
[407,] -0.7888293
[408,] 1.2662786
[409,] -0.7888293
[410,] -0.7888293
[411,] -0.7888293
[412,] -0.7888293
[413,] 1.2662786
[414,] -0.7888293
[415,] 1.2662786
[416,] -0.7888293
[417,] 1.2662786
[418,] 1.2662786
[419,] -0.7888293
[420,] -0.7888293
[421,] -0.7888293
[422,] -0.7888293
[423,] -0.7888293
[424,] -0.7888293
[425,] -0.7888293
[426,] -0.7888293
[427,] 1.2662786
[428,] 1.2662786
[429,] -0.7888293
[430,] 1.2662786
[431,] 1.2662786
[432,] 1.2662786
[433,] 1.2662786
[434,] -0.7888293
[435,] -0.7888293
[436,] 1.2662786
[437,] -0.7888293
[438,] 1.2662786
[439,] -0.7888293
[440,] -0.7888293
[441,] 1.2662786
[442,] -0.7888293
[443,] -0.7888293
[444,] 1.2662786
[445,] 1.2662786
[446,] 1.2662786
[447,] 1.2662786
[448,] 1.2662786
[449,] 1.2662786
[450,] 1.2662786
[451,] -0.7888293
[452,] -0.7888293
[453,] -0.7888293
[454,] 1.2662786
[455,] -0.7888293
[456,] 1.2662786
[457,] -0.7888293
[458,] 1.2662786
[459,] 1.2662786
[460,] -0.7888293
[461,] 1.2662786
[462,] -0.7888293
[463,] -0.7888293
[464,] -0.7888293
[465,] -0.7888293
[466,] -0.7888293
[467,] -0.7888293
[468,] -0.7888293
[469,] -0.7888293
[470,] 1.2662786
[471,] -0.7888293
[472,] -0.7888293
[473,] 1.2662786
[474,] 1.2662786
[475,] -0.7888293
[476,] -0.7888293
[477,] -0.7888293
[478,] -0.7888293
[479,] -0.7888293
[480,] 1.2662786
[481,] -0.7888293
[482,] -0.7888293
[483,] -0.7888293
[484,] 1.2662786
[485,] 1.2662786
[486,] -0.7888293
[487,] 1.2662786
[488,] -0.7888293
[489,] -0.7888293
[490,] 1.2662786
[491,] -0.7888293
[492,] -0.7888293
[493,] -0.7888293
[494,] -0.7888293
[495,] -0.7888293
[496,] -0.7888293
[497,] 1.2662786
[498,] -0.7888293
[499,] -0.7888293
[500,] -0.7888293
[501,] -0.7888293
[502,] -0.7888293
[503,] -0.7888293
[504,] -0.7888293
[505,] 1.2662786
[506,] -0.7888293
[507,] 1.2662786
[508,] 1.2662786
[509,] -0.7888293
[510,] 1.2662786
[511,] 1.2662786
[512,] -0.7888293
[513,] 1.2662786
[514,] 1.2662786
[515,] -0.7888293
[516,] -0.7888293
[517,] 1.2662786
[518,] -0.7888293
[519,] 1.2662786
[520,] -0.7888293
[521,] 1.2662786
[522,] -0.7888293
[523,] -0.7888293
[524,] 1.2662786
[525,] -0.7888293
[526,] -0.7888293
[527,] 1.2662786
[528,] -0.7888293
[529,] -0.7888293
[530,] -0.7888293
[531,] 1.2662786
[532,] -0.7888293
[533,] -0.7888293
[534,] 1.2662786
[535,] -0.7888293
[536,] 1.2662786
[537,] -0.7888293
[538,] 1.2662786
[539,] -0.7888293
[540,] 1.2662786
[541,] 1.2662786
[542,] -0.7888293
[543,] -0.7888293
[544,] 1.2662786
[545,] -0.7888293
[546,] -0.7888293
[547,] 1.2662786
[548,] 1.2662786
[549,] -0.7888293
[550,] 1.2662786
[551,] 1.2662786
[552,] -0.7888293
[553,] -0.7888293
[554,] 1.2662786
[555,] 1.2662786
[556,] -0.7888293
[557,] 1.2662786
[558,] -0.7888293
[559,] 1.2662786
[560,] 1.2662786
[561,] -0.7888293
[562,] -0.7888293
[563,] -0.7888293
[564,] -0.7888293
[565,] -0.7888293
[566,] -0.7888293
[567,] -0.7888293
[568,] -0.7888293
[569,] -0.7888293
[570,] 1.2662786
[571,] 1.2662786
[572,] 1.2662786
[573,] 1.2662786
[574,] 1.2662786
[575,] -0.7888293
[576,] -0.7888293
[577,] 1.2662786
[578,] 1.2662786
[579,] -0.7888293
[580,] 1.2662786
[581,] 1.2662786
[582,] 1.2662786
[583,] -0.7888293
[584,] -0.7888293
[585,] -0.7888293
[586,] 1.2662786
[587,] -0.7888293
[588,] 1.2662786
[589,] -0.7888293
[590,] -0.7888293
[591,] -0.7888293
[592,] 1.2662786
[593,] -0.7888293
[594,] -0.7888293
[595,] -0.7888293
[596,] -0.7888293
[597,] 1.2662786
[598,] -0.7888293
[599,] -0.7888293
[600,] 1.2662786
[601,] 1.2662786
[602,] -0.7888293
[603,] -0.7888293
[604,] -0.7888293
[605,] 1.2662786
[606,] -0.7888293
[607,] -0.7888293
[608,] 1.2662786
[609,] 1.2662786
[610,] 1.2662786
[611,] -0.7888293
[612,] -0.7888293
[613,] 1.2662786
[614,] -0.7888293
[615,] -0.7888293
[616,] 1.2662786
[617,] -0.7888293
[618,] -0.7888293
[619,] 1.2662786
[620,] -0.7888293
[621,] -0.7888293
[622,] 1.2662786
[623,] 1.2662786
[624,] -0.7888293
[625,] -0.7888293
[626,] -0.7888293
[627,] -0.7888293
[628,] 1.2662786
[629,] -0.7888293
[630,] -0.7888293
[631,] 1.2662786
[632,] -0.7888293
[633,] 1.2662786
[634,] -0.7888293
[635,] -0.7888293
[636,] 1.2662786
[637,] -0.7888293
[638,] -0.7888293
[639,] -0.7888293
[640,] -0.7888293
[641,] -0.7888293
[642,] 1.2662786
[643,] -0.7888293
[644,] 1.2662786
[645,] 1.2662786
[646,] 1.2662786
[647,] -0.7888293
[648,] 1.2662786
[649,] -0.7888293
[650,] 1.2662786
[651,] -0.7888293
[652,] 1.2662786
[653,] -0.7888293
[654,] 1.2662786
[655,] -0.7888293
[656,] -0.7888293
[657,] -0.7888293
[658,] -0.7888293
[659,] -0.7888293
[660,] -0.7888293
[661,] 1.2662786
[662,] -0.7888293
[663,] -0.7888293
[664,] -0.7888293
[665,] 1.2662786
[666,] -0.7888293
[667,] -0.7888293
[668,] -0.7888293
[669,] -0.7888293
[670,] 1.2662786
[671,] 1.2662786
[672,] -0.7888293
[673,] -0.7888293
[674,] 1.2662786
[675,] -0.7888293
[676,] -0.7888293
[677,] -0.7888293
[678,] 1.2662786
[679,] -0.7888293
[680,] 1.2662786
[681,] -0.7888293
[682,] 1.2662786
[683,] -0.7888293
[684,] -0.7888293
[685,] -0.7888293
[686,] -0.7888293
[687,] -0.7888293
[688,] -0.7888293
[689,] -0.7888293
[690,] 1.2662786
[691,] 1.2662786
[692,] 1.2662786
[693,] 1.2662786
[694,] -0.7888293
[695,] -0.7888293
[696,] -0.7888293
[697,] -0.7888293
[698,] 1.2662786
[699,] -0.7888293
[700,] -0.7888293
[701,] 1.2662786
[702,] 1.2662786
[703,] -0.7888293
[704,] -0.7888293
[705,] -0.7888293
[706,] -0.7888293
[707,] 1.2662786
[708,] 1.2662786
[709,] 1.2662786
[710,] 1.2662786
[711,] 1.2662786
[712,] -0.7888293
[713,] 1.2662786
[714,] -0.7888293
[715,] -0.7888293
[716,] -0.7888293
[717,] 1.2662786
[718,] 1.2662786
[719,] -0.7888293
[720,] -0.7888293
[721,] 1.2662786
[722,] -0.7888293
[723,] -0.7888293
[724,] -0.7888293
[725,] 1.2662786
[726,] -0.7888293
[727,] 1.2662786
[728,] 1.2662786
[729,] -0.7888293
[730,] -0.7888293
[731,] 1.2662786
[732,] -0.7888293
[733,] -0.7888293
[734,] -0.7888293
[735,] -0.7888293
[736,] -0.7888293
[737,] -0.7888293
[738,] 1.2662786
[739,] -0.7888293
[740,] -0.7888293
[741,] 1.2662786
[742,] -0.7888293
[743,] 1.2662786
[744,] -0.7888293
[745,] 1.2662786
[746,] -0.7888293
[747,] -0.7888293
[748,] 1.2662786
[749,] -0.7888293
[750,] -0.7888293
[751,] 1.2662786
[752,] 1.2662786
[753,] -0.7888293
[754,] -0.7888293
[755,] 1.2662786
[756,] 1.2662786
[757,] -0.7888293
[758,] -0.7888293
[759,] -0.7888293
[760,] 1.2662786
[761,] -0.7888293
[762,] -0.7888293
[763,] 1.2662786
[764,] 1.2662786
[765,] -0.7888293
[766,] 1.2662786
[767,] -0.7888293
[768,] -0.7888293
[769,] -0.7888293
[770,] -0.7888293
[771,] -0.7888293
[772,] -0.7888293
[773,] -0.7888293
[774,] -0.7888293
[775,] 1.2662786
[776,] -0.7888293
[777,] -0.7888293
[778,] 1.2662786
[779,] -0.7888293
[780,] 1.2662786
[781,] 1.2662786
[782,] 1.2662786
[783,] -0.7888293
[784,] -0.7888293
[785,] -0.7888293
[786,] -0.7888293
[787,] 1.2662786
[788,] -0.7888293
[789,] 1.2662786
[790,] -0.7888293
[791,] -0.7888293
[792,] -0.7888293
[793,] -0.7888293
[794,] -0.7888293
[795,] -0.7888293
[796,] -0.7888293
[797,] 1.2662786
[798,] 1.2662786
[799,] -0.7888293
[800,] -0.7888293
[801,] -0.7888293
[802,] 1.2662786
[803,] 1.2662786
[804,] 1.2662786
[805,] 1.2662786
[806,] -0.7888293
[807,] -0.7888293
[808,] -0.7888293
[809,] -0.7888293
[810,] 1.2662786
[811,] -0.7888293
[812,] -0.7888293
[813,] -0.7888293
[814,] -0.7888293
[815,] -0.7888293
[816,] -0.7888293
[817,] -0.7888293
[818,] -0.7888293
[819,] -0.7888293
[820,] -0.7888293
[821,] 1.2662786
[822,] 1.2662786
[823,] -0.7888293
[824,] 1.2662786
[825,] -0.7888293
[826,] -0.7888293
[827,] -0.7888293
[828,] 1.2662786
[829,] 1.2662786
[830,] 1.2662786
[831,] 1.2662786
[832,] 1.2662786
[833,] -0.7888293
[834,] -0.7888293
[835,] -0.7888293
[836,] 1.2662786
[837,] -0.7888293
[838,] -0.7888293
[839,] 1.2662786
[840,] 1.2662786
[841,] -0.7888293
[842,] -0.7888293
[843,] 1.2662786
[844,] -0.7888293
[845,] -0.7888293
[846,] -0.7888293
[847,] -0.7888293
[848,] -0.7888293
[849,] -0.7888293
[850,] 1.2662786
[851,] -0.7888293
[852,] -0.7888293
[853,] -0.7888293
[854,] 1.2662786
[855,] -0.7888293
[856,] 1.2662786
[857,] 1.2662786
[858,] 1.2662786
[859,] 1.2662786
[860,] -0.7888293
[861,] -0.7888293
[862,] -0.7888293
[863,] 1.2662786
[864,] -0.7888293
[865,] -0.7888293
[866,] 1.2662786
[867,] 1.2662786
[868,] -0.7888293
[869,] -0.7888293
[870,] 1.2662786
[871,] -0.7888293
[872,] 1.2662786
[873,] -0.7888293
[874,] -0.7888293
[875,] 1.2662786
[876,] 1.2662786
[877,] -0.7888293
[878,] -0.7888293
[879,] -0.7888293
[880,] 1.2662786
[881,] 1.2662786
[882,] -0.7888293
[883,] -0.7888293
[884,] -0.7888293
[885,] -0.7888293
[886,] -0.7888293
[887,] -0.7888293
[888,] 1.2662786
[889,] -0.7888293
[890,] 1.2662786
[891,] -0.7888293
attr(,"scaled:center")
[1] 0.3838384
attr(,"scaled:scale")
[1] 0.4865925