Chapter 3 Data generation processes

The contemporary world is full of data and, especially, it is becoming easier and easier to transform it into data. Data analysis is about making good use of data for certain purposes, such as to predict or to make inferences about the world. For these tasks, a first step is to have a sound understanding on how the data was generated, i.e., which processes lead to its creation. The analytical strategy for data analysis will be highly dependent on which processes have generated the data under scrutiny.

3.1 Survey data

This course focuses on data analysis of survey data, which is a particular – yet broad – type of data. Survey data can come from a simple Google forms used to arrange a meeting as well as from a panel study following for decades a representative sample of a country’s population – e.g., SOEP in Germany, LISS in the Netherlands or Understanding Society in the UK –. The notion of representativeness here means that it is possible to say something about the population just by using a sample of it. Formally, this is justified by sampling theory and applied in practice in many fields.

One central claim in sampling theory is that for a sample to be representative of a population, the data generation mechanism has to be (partially) known. Data generation can be described as the upper part of Fig. 3.1, where multiple processes could have produced the sample data from the population.

Figure 3.1: Producing data and making statistical inferences. Source: Lumen learning

Overall, we will consider two general type of data generation processes: (1) probability based, and (2) non-probability based. In the former, data is generated by a probabilistic process, i.e., each element of the population is selected with a (known) probability to form part of the sample data. One possible way to achieve this is by using a random mechanism when generating the data. In the latter, data is generated in such a way that the selection process does not follow probabilistic procedures. Imagine that two hungry friends (a population) decide to order food and neither of them want to actually do it, so they decide to toss a coin to decide. Assuming a fair coin, we know that the looser had a probability of 0.5 of having to order. So the sample of size one (the friend who has to order) was generated by a random mechanism, i.e., the toss of a coin.

Just by looking to Fig. 3.1 it is not possible to determine if the sample data was generated by a probability based process – e.g., a coin was tossed for every point of the population – or by a non-probability based process – e.g., someone just grabbed those points because they were together and easy to reach with the hand –. In fact, this last process might be probabilistically described, the issue is that in principle we do not know a way to determine the probability of grabbing with the hand this particular area of the large circle (the population).

Sampling theory proposes that when data generation mechanisms are probability based and known, it is possible to infer features of the population. Of course, this comes with a cost in terms of uncertainty, which will be discussed in Chapter 4. These probability based data generation mechanisms are what we will call sampling designs. It is important to note that it is by design that we choose random mechanisms to create samples from a population, thus it is possible to determine the probabilities behind the selection or generation procedures.

In survey research the data generation process goes beyond the selection of the sample data, as each feature of the population or combinations of them have particularities that produce them. Also, the designed samples are seldom the actual samples achieved after fieldwork. In general, statistical models are used to approach these data generation processes by having a sound theoretical knowledge of such particularities and substantive phenomena underlying populations.

So now let’s create an example for generating data with a known probability. We have five individuals whose names are: Hannah, Noah, Emma, Ben and Mia.

population <- c("Hannah", "Noah", "Emma", "Ben", "Mia")

Let’s say we want to select a sample of four of them, which implies that five different combinations exist:

combinations <- combn(population, 4)
combinations
#>      [,1]     [,2]     [,3]     [,4]     [,5]  
#> [1,] "Hannah" "Hannah" "Hannah" "Hannah" "Noah"
#> [2,] "Noah"   "Noah"   "Noah"   "Emma"   "Emma"
#> [3,] "Emma"   "Emma"   "Ben"    "Ben"    "Ben" 
#> [4,] "Ben"    "Mia"    "Mia"    "Mia"    "Mia"

Each column in the above matrix represents a different possible sample of size four. For choosing one of the five samples we will randomly draw a number from 1 to 5

sample_number <- sample(x = 1:5, size = 1) # draw a random integer from 1 to 5
sample_number
#> [1] 2

Sample 2 was chosen, so the sample data would be formed by Hannah, Noah, Emma, Mia. Additionally, we know that the data was generated in such a way that each of the five possible samples had a known probability of 0.2 (\(\frac{1}{5}\)) of being selected. In this case, our data generating mechanism was a random number generator, i.e., the R function sample(). You can try it by executing multiple times the command sample(x = 1:5, size = 1) and seeing how the output changes (pseudo) randomly (see this link for learning more about the generation of random numbers in computers).

3.2 Population and surveys

“A”survey" is a systematic method for gathering information from (a sample of) entities for the purposes of constructing quantitative descriptors of the attributes of the larger population of which the entities are members

(Groves et al. 2009, 2)

So what is a complex survey? Although a survey can be complex in many senses – questionnaire design, survey mode, target population, etc. –, commonly this concept is used to describe a survey that comes from a complex sampling design. For now, let’s focus on the general idea of surveys, either complex or not.

In general, surveys are intended to represent a target population, i.e., the complete set of observations we want to study. For optimizing resources and making the process viable, instead of trying to collect data from all of the population units, a sample of them is selected. It is also necessary to have an available list or specification for the units that are going to be sampled, which is the sampling frame. For example, if you are going to conduct a survey about the health status of the employees in a big firm, you should have a list of those employees that allows you to contact them in some way, e.g., by email, telephone, office number, etc.

The match between the target population and the sampling frame is never not always perfect, as it is depicted in Fig. 3.2. Imagine that in the firm the human resources department only has an outdated list of the employees, so the most recent workers will not be able to be sampled as they are not included in the sampling frame. Moreover, as the list is outdated some former employees might be included, but they are not eligible for the survey as the target population refers to actual employees. Finally, a part of the employees might not be reachable – e.g., those on vacations –, some of them might refuse to respond – e.g., due to privacy concerns –, or might not be able to respond – e.g., because of a serious ill –.

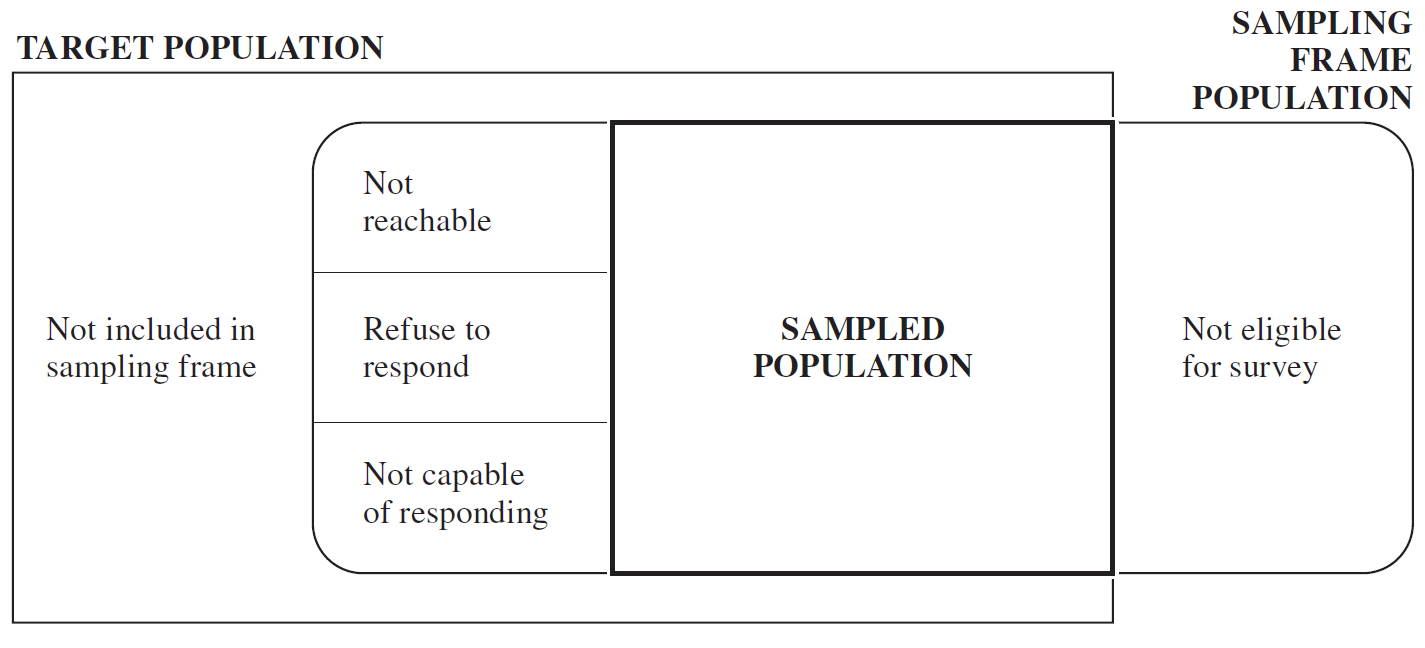
Figure 3.2: The relation of target population and sampling frame. Source: Lohr, 2009, p. 4