2 Ejemplo 1

Se sabe que el dióxido de carbono tiene un efecto crítico en el crecimiento microbiológico. Cantidades pequeñas de \(CO_2\) estimulan el crecimiento de muchos microorganismos, mientras que altas concentraciones inhiben el crecimiento de la mayor parte de ellos. Este último efecto se utiliza comercialmente cuando se almacenan productos alimenticios perecederos. Se realizó un estudio para investigar el efecto de \(CO_2\) sobre la tasa de crecimiento de Pseudomonas fragi, un corruptor de alimentos. Se administró \(CO_2\) a cinco presiones atmosféricas diferentes (0.0, 0.083, 0.29, 0.50, 0.86). La respuesta anotada fue el cambio porcentual en la masa celular después de un tiempo de crecimiento de una hora. Se obtuvieron los siguientes datos:

0.0	0.083	0.29	0.5	0.86
62.6	50.9	45.5	29.5	24.9
59.6	44.3	41.1	22.8	17.2
64.5	47.5	29.8	19.2	7.8
59.3	49.5	38.3	20.6	10.5
58.6	48.5	40.2	29.2	17.8
64.6	50.4	38.5	24.1	22.1
50.9	35.2	30.2	22.6	22.6
56.2	49.9	27.0	32.7	16.8
52.3	42.6	40.0	24.4	15.9
62.8	41.6	33.9	29.6	8.8

2.1 Data.frame

CO2<-factor(rep(c("0.0","0.083","0.29","0.50","0.86"),
                 each = 10))
respuesta<- c(62.6,59.6,64.5,59.3,58.6,64.6,50.9,56.2,52.3,62.8,50.9,44.3,47.5,49.5,48.5,50.4,35.2,49.9,42.6,41.6,45.5,41.1,29.8,38.3,40.2,38.5,30.2,27.0,40.0,33.9,29.5,22.8,19.2,20.6,29.2,24.1,22.6,32.7,24.4,29.6,24.9,17.2,7.8,10.5,17.8,22.1,22.6,16.8,15.9,8.8)
data<- data.frame(CO2, respuesta)    
head(data)

##   CO2 respuesta
## 1 0.0      62.6
## 2 0.0      59.6
## 3 0.0      64.5
## 4 0.0      59.3
## 5 0.0      58.6
## 6 0.0      64.6

str(data)

## 'data.frame':    50 obs. of  2 variables:
##  $ CO2      : Factor w/ 5 levels "0.0","0.083",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ respuesta: num  62.6 59.6 64.5 59.3 58.6 64.6 50.9 56.2 52.3 62.8 ...

2.2 ANOVA

ANOVA<-aov(data = data, respuesta~CO2)
summary(ANOVA)

##             Df Sum Sq Mean Sq F value Pr(>F)    
## CO2          4  11274  2818.6   101.6 <2e-16 ***
## Residuals   45   1248    27.7                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

2.3 TUKEY

2.3.1 TukeyHSD

TUKEY<-TukeyHSD(ANOVA,trt= "trat", conf.level=0.95)
TUKEY

##   Tukey multiple comparisons of means
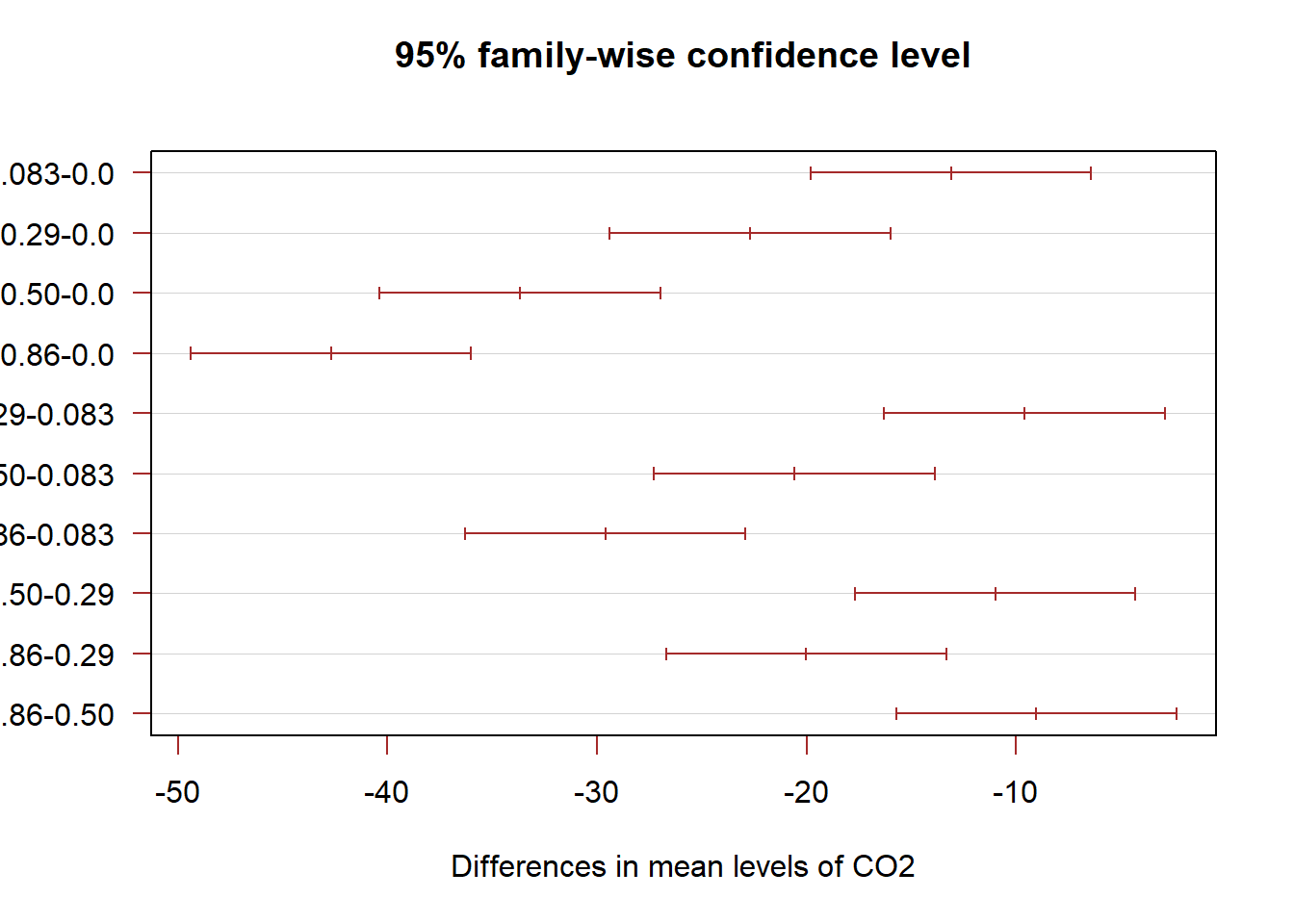
##     95% family-wise confidence level
## 
## Fit: aov(formula = respuesta ~ CO2, data = data)
## 
## $CO2
##              diff      lwr        upr     p adj
## 0.083-0.0  -13.10 -19.7921  -6.407896 0.0000133
## 0.29-0.0   -22.69 -29.3821 -15.997896 0.0000000
## 0.50-0.0   -33.67 -40.3621 -26.977896 0.0000000
## 0.86-0.0   -42.70 -49.3921 -36.007896 0.0000000
## 0.29-0.083  -9.59 -16.2821  -2.897896 0.0016698
## 0.50-0.083 -20.57 -27.2621 -13.877896 0.0000000
## 0.86-0.083 -29.60 -36.2921 -22.907896 0.0000000
## 0.50-0.29  -10.98 -17.6721  -4.287896 0.0002615
## 0.86-0.29  -20.01 -26.7021 -13.317896 0.0000000
## 0.86-0.50   -9.03 -15.7221  -2.337896 0.0034105

2.3.2 Interpretaciones

El p-valor nos está indicando que hay diferencias estadísticas significativas entre todas las comparaciones de los tratamientos evaluados. La mayor diferencia de medias se observa entre los tratamientos 0.86-0.0. Y la menor diferencia de medias se observa entre los tratamientos 0.86-0.50.

2.3.3 Plot

plot(TUKEY,las=1,col="brown")

2.3.4 Interpretaciones

Este gráfico nos está indicando que hay menor diferencia de medias entre los tratamientos 0.86-0.50. También existen diferencias estadísticas significativas entre todas las comparaciones de los tratamientos evaluados. Por otro lado, la mayor diferencia de medias se observa entre los tratamientos 0.86-0.0.

2.3.5 Recomendación

¿Cuál tratamiento elijo?

Se busca un tratamiento que inhiba la tasa de crecimiento de Pseudomonas fragi. Según analíticamente y gráficamente se observa que con el tratamiento 0.86 se obtiene menor promedio de tasa de crecimiento. Por lo que se recomienda usar este tratamiento.

2.3.6 Tukey con ggplot

Para realizar gráficos de comparaciones de medias se necesita instalar los siguientes paquetes: multcompViewy tidyverse. Para ello, utilizar los siguientes comandos para su instalación: install.packages("multcompView") y install.packages("tidyverse").

CO2<-factor(rep(c("0.0","0.083","0.29","0.50","0.86"),
                 each = 10))
respuesta<- c(62.6,59.6,64.5,59.3,58.6,64.6,50.9,56.2,52.3,62.8,50.9,44.3,47.5,49.5,48.5,50.4,35.2,49.9,42.6,41.6,45.5,41.1,29.8,38.3,40.2,38.5,30.2,27.0,40.0,33.9,29.5,22.8,19.2,20.6,29.2,24.1,22.6,32.7,24.4,29.6,24.9,17.2,7.8,10.5,17.8,22.1,22.6,16.8,15.9,8.8)
data<- data.frame(CO2, respuesta)    
head(data)

##   CO2 respuesta
## 1 0.0      62.6
## 2 0.0      59.6
## 3 0.0      64.5
## 4 0.0      59.3
## 5 0.0      58.6
## 6 0.0      64.6

str(data)

## 'data.frame':    50 obs. of  2 variables:
##  $ CO2      : Factor w/ 5 levels "0.0","0.083",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ respuesta: num  62.6 59.6 64.5 59.3 58.6 64.6 50.9 56.2 52.3 62.8 ...

# Continuamos con el ejercicio 1

library(multcompView)

## Warning: package 'multcompView' was built under R version 4.2.3

letras<- multcompLetters4(ANOVA,TUKEY)
letras

## $CO2
##   0.0 0.083  0.29  0.50  0.86 
##   "a"   "b"   "c"   "d"   "e"

library(tidyverse)

## ── Attaching packages ─────── tidyverse 1.3.2 ──
## ✔ ggplot2 3.4.0      ✔ purrr   0.3.5 
## ✔ tibble  3.1.8      ✔ dplyr   1.0.10
## ✔ tidyr   1.2.1      ✔ stringr 1.5.0 
## ✔ readr   2.1.3      ✔ forcats 0.5.2 
## ── Conflicts ────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()

tabla_tukey<-data %>% 
  group_by(CO2) %>% 
  summarise(media=mean(respuesta),
            sd=sd(respuesta)) %>% 
  arrange(media)
tabla_tukey

## # A tibble: 5 × 3
##   CO2   media    sd
##   <fct> <dbl> <dbl>
## 1 0.86   16.4  5.89
## 2 0.50   25.5  4.48
## 3 0.29   36.4  5.93
## 4 0.083  46.0  5.05
## 5 0.0    59.1  4.80

letras<-as.data.frame.list(letras$CO2)
tabla_tukey$letras<-letras$Letters
tabla_tukey

## # A tibble: 5 × 4
##   CO2   media    sd letras
##   <fct> <dbl> <dbl> <chr> 
## 1 0.86   16.4  5.89 a     
## 2 0.50   25.5  4.48 b     
## 3 0.29   36.4  5.93 c     
## 4 0.083  46.0  5.05 d     
## 5 0.0    59.1  4.80 e

print(tabla_tukey)

## # A tibble: 5 × 4
##   CO2   media    sd letras
##   <fct> <dbl> <dbl> <chr> 
## 1 0.86   16.4  5.89 a     
## 2 0.50   25.5  4.48 b     
## 3 0.29   36.4  5.93 c     
## 4 0.083  46.0  5.05 d     
## 5 0.0    59.1  4.80 e

tabla_tukey %>% 
  ggplot(aes(CO2,media))+
  geom_bar(stat = "identity", aes(fill = letras), show.legend = F)+
  geom_errorbar(aes(ymin= media-sd, ymax= media+sd), width=0.1)+
  geom_text(aes(label=letras, y= media+sd), vjust=-0.5)+
  ylim(0,80)+
  theme_minimal()+
  labs(x="Tratamiento",
       y="Variable respuesta")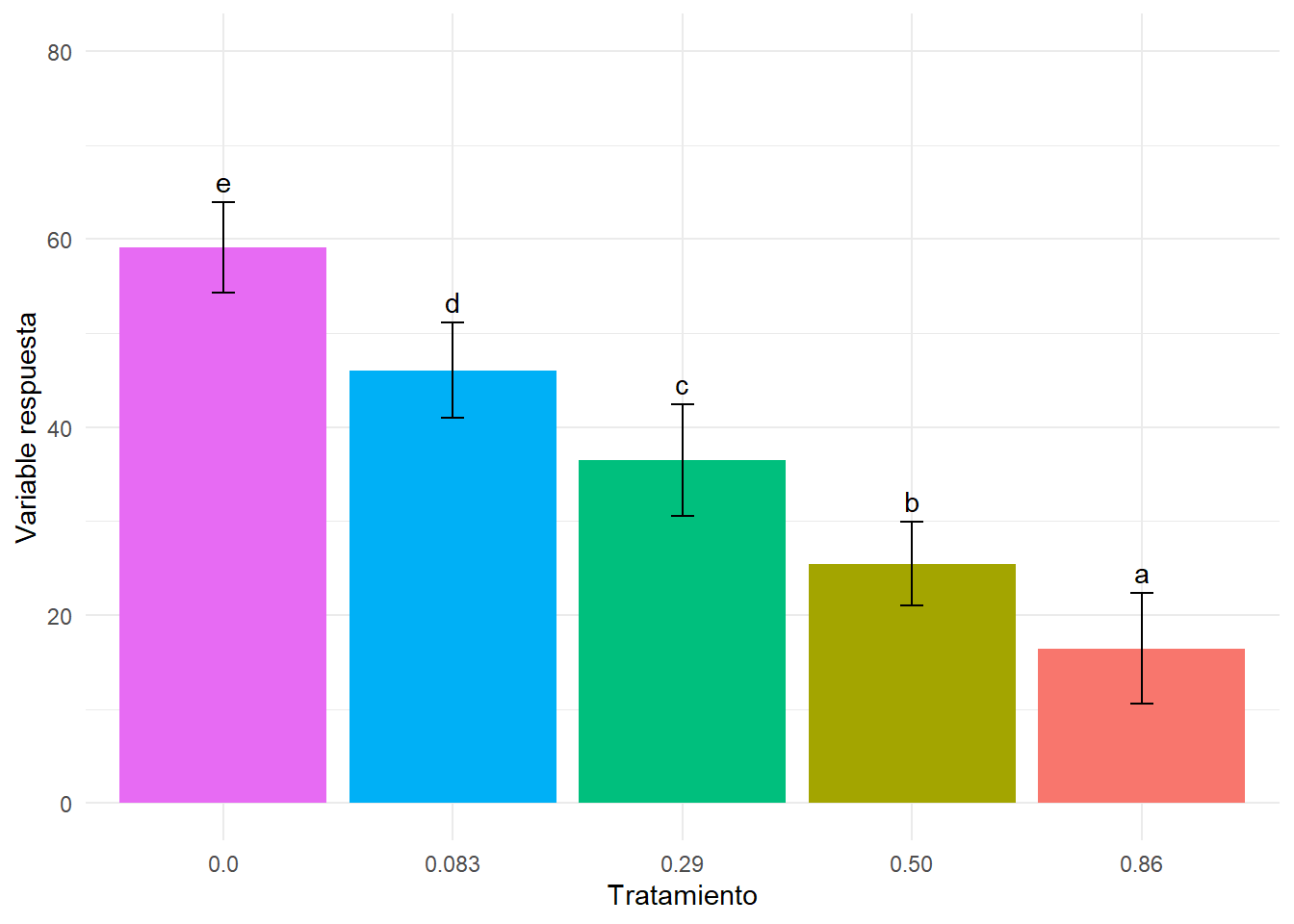

Diferentes letras indica que existen diferencias estadísticas significativas. Como hemos mencionado anteriormente, el tratamiento que se recomienda utilizar es el 0.86 ya que obtiene una menor tasa de crecimiento del corruptor de alimentos.

2.4 DUNNET

library(multcomp)

## Warning: package 'multcomp' was built under R version 4.2.3

## Loading required package: mvtnorm

## Loading required package: survival

## Loading required package: TH.data

## Warning: package 'TH.data' was built under R version 4.2.3

## Loading required package: MASS

## 
## Attaching package: 'MASS'

## The following object is masked from 'package:dplyr':
## 
##     select

## 
## Attaching package: 'TH.data'

## The following object is masked from 'package:MASS':
## 
##     geyser

Dunnet<-glht(model = ANOVA, linfct = mcp(CO2="Dunnett"))
summary(Dunnet)

## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Dunnett Contrasts
## 
## 
## Fit: aov(formula = respuesta ~ CO2, data = data)
## 
## Linear Hypotheses:
##                  Estimate Std. Error t value Pr(>|t|)    
## 0.083 - 0.0 == 0  -13.100      2.355  -5.562 3.95e-06 ***
## 0.29 - 0.0 == 0   -22.690      2.355  -9.634  < 1e-06 ***
## 0.50 - 0.0 == 0   -33.670      2.355 -14.296  < 1e-06 ***
## 0.86 - 0.0 == 0   -42.700      2.355 -18.130  < 1e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

plot(Dunnet,cex.axis=0.8,sub="Mean difference between two groups",col ="red")
mtext(text = "Prueba de Dunnet",side = 3,line = 0)