Hoofdstuk 4 Datavoorbereiding
4.1 Beginnen bij het begin
- Alvorens we aan een exploratieve data analyse kunnen beginnen, moeten we eerst onze data voorbereiden.
- Deze voorbereiding kan in twee belangrijke stappen opgedeeld worden:
- Opkuisen van de data (data cleaning).
- Transformeren van de data (data transformation).
- Het opkuisen van de data moet er voor zorgen dat de data geen ‘fouten’ meer bevat.
- Er zijn verschillende soorten fouten die in de data kunnen sluipen. Enkele mogelijke fouten zijn:
- Variabelen worden als verkeerd variabele-type herkend (vb. character ipv numeric).
- Sommige waarden ontbreken (geen waarde voor bepaalde variabele bij bepaalde observaties).
- Sommige waarden zijn fout. Bijvoorbeeld: voor een deel observaties is de afstand in km opgeslagen ipv mijl of is er een typfout in de waarde van een categorische variabele.
- Sommige observaties staan meerdere keren in de dataset.
- Het opkuisen van data gebeurt in principe in 2 stappen:
- Eerst moeten we de data bestuderen en fouten identificeren.
- Vervolgens moeten we de fouten in de data ‘corrigeren’ (indien mogelijk).
- Er zijn verschillende soorten fouten die in de data kunnen sluipen. Enkele mogelijke fouten zijn:
- Het transformeren van de data heeft als doel de data bruikbaarder te maken voor exploratieve data analyse. Er zijn verschillende manieren om dit te bereiken:
- Bestaande variabelen transformeren naar nieuwe variabelen die geschikter zijn om patronen in de data bloot te leggen. Bijvoorbeeld het transformeren van een continue variabele naar een categorische variabele of het creëren van een nieuwe variabele ‘gemiddelde snelheid’ op basis van de variabelen ‘reistijd’ en ‘totaal afgelegde afstand’.
- Het opsplitsen van de dataset in meerdere datasets die apart bestudeerd worden. Dit is vooral zinvol indien de dataset verschillende soorten observaties bevat of een deel observaties met uitzonderlijke waarden.
Case: Vluchtdata NYC
- We zullen de datavoorbereidingsfase illustreren aan de hand van de vluchtgegevens van de drie luchthavens in New York City.
- Voor we kunnen beginnen is het altijd verstandig een snel overzicht te maken van de dataset, zodat we weten welke variabelen we voor handen hebben.
- Met de glimpse functie krijg je snel een overzicht van de verschillende variabelen en van welk type ze zijn.
glimpse(df)## Observations: 329,174
## Variables: 7
## $ luchthaven <fctr> EWR, LGA, JFK, LGA, EWR, EWR, LGA, JFK, L...
## $ maatschappij <fctr> United Air Lines Inc., United Air Lines I...
## $ vertrek_vertraging <dbl> 2, 4, 2, -6, -4, -5, -3, -3, -2, -2, -2, -...
## $ aankomst_vertraging <dbl> 11, 20, 33, -25, 12, 19, -14, -8, 8, -2, -...
## $ afstand <chr> "1400", "1416", "1089", "762", "719", "106...
## $ vliegtijd <dbl> 227, 227, 160, 116, 150, 158, 53, 140, 138...
## $ vluchttype <ord> normaal, normaal, kort, kort, kort, kort, ...Deze output bevat al een opmerkelijk resultaat. Zo zien we dat de variabele ‘afstand’ als tekst is opgeslagen in plaats van als een continue (numerieke) variabele.
Met de summary functie krijg je snel een zicht op de data zelf.
summary(df)## luchthaven maatschappij vertrek_vertraging
## EWR:119282 United Air Lines Inc. :57491 Min. : -43.00
## JFK:105230 ExpressJet Airlines Inc.:54172 1st Qu.: -5.00
## LGA:104662 JetBlue Airways :50940 Median : -2.00
## Delta Air Lines Inc. :46779 Mean : 12.71
## American Airlines Inc. :31327 3rd Qu.: 11.00
## Envoy Air :26378 Max. :1301.00
## (Other) :62087 NA's :8214
## aankomst_vertraging afstand vliegtijd
## Min. : -86.000 Length:329174 Min. : 0.583
## 1st Qu.: -17.000 Class :character 1st Qu.: 81.000
## Median : -5.000 Mode :character Median :127.000
## Mean : 6.987 Mean :149.561
## 3rd Qu.: 14.000 3rd Qu.:184.000
## Max. :1272.000 Max. :695.000
## NA's :9365 NA's :9365
## vluchttype
## lang : 50980
## kort :245666
## normaal : 31813
## intercontinentaal: 715
##
##
## - Ook hier kan je al opmerkelijke dingen waarnemen. Zo blijken er vuchten te zijn die tot 43 minuten te vroeg vertrekken, alsook vluchten die meer dan 21 uur te laat vertrekken.
- Verder lijken er vluchten te zijn die opmerkelijk kort duren (minder dan 1 minuut).
4.2 Fase 1: Opkuisen van de data
4.2.1 Foutieve variabeletypes
- Soms gebeurt het dat R niet het juiste variabeletype herkent. Zo kan het zijn dat een categorische variabele als numerieke variabele wordt beschouwd omdat de categorieën gehele getallen zijn (vb. aantal cylinders: 4, 6 of 8).
- In onze dataset hebben we opgemerkt dat de variabele ‘afstand’ niet als numerieke variabele wordt geïnterpreteerd, maar als een ‘tekst’-variabele. Dit kan verschillende oorzaken hebben.
- Zo kan het zijn dat er voor 1 van de observaties een waarde geregistreerd is met een niet-numeriek teken (vb. 1OO ipv 100). In dat geval zal je eerst deze waarden moeten corrigeren naar de juiste waarde.
- Een andere vaak voorkomende oorzaak is dat R een punt als decimaalteken verwacht, terwijl dat een komma is in de dataset. Dit valt vaak op te lossen door de data met andere opties in te lezen in R.
- Indien de fouten zijn gecorrigeerd, dan moeten we nog altijd de data omzetten van een ‘tekst’-variabele naar een numerieke variabele (in ons geval). Dit doen we door middel van de ‘mutate’-functie en de ‘as.numeric’-functie.
df <- df %>%
mutate(afstand = as.numeric(afstand))- Merk op dat als er toch nog een waarde aanwezig is die niet kan omgezet worden naar het nieuwe variabeletype, R een waarschuwing zal geven en de waarde zal vervangen door ‘NA’. In dat geval ga je eerst moeten zoeken naar de oorzaak van de waarschuwing, deze aanpakken en dan de variabele transformeren naar het nieuwe type.
test <- c('1', '2', '3A')
test## [1] "1" "2" "3A"as.numeric(test)## [1] 1 2 NA4.2.2 Coderingsfouten
4.2.2.1 Categorische variabele
- Coderingsfouten bij categorische variabelen uiten zich typisch in redundante categorielabels. Dit zijn labels met een typfout die door R als een aparte categorie worden beschouwd, maar dit niet zijn.
- Om dit soort coderingsfouten te detecteren, moet je de verschillende labels van een categorische variabele bestuderen.
- Omdat deze foute categorielabels meestal uitzonderlijk zijn, kan je best de verschillende categorielabels bekijken volgens stijgende frequentie.
- Een andere aanpak is de categorielabels alfabetisch te ordenen.
- Eenmaal men deze coderingsfouten gedetecteerd heeft, kan men ze manueel corrigeren door gebruik te maken van de functies mutate (dplyr) en fct_recode (forcats).
Case: Vluchtdata NYC
- Als we de categorische variabele maatschappij analyseren op foutieve labels dan zien we dat 1 vlucht foutief het label ‘XpressJet Airlines Inc.’ heeft gekregen in plaats van ‘ExpressJet Airlines Inc.’.
df %>%
group_by(maatschappij) %>%
tally() %>%
arrange(n)| maatschappij | n |
|---|---|
| XpressJet Airlines Inc. | 1 |
| Envoi Air | 19 |
| SkyWest Airlines Inc. | 32 |
| Hawaiian Airlines Inc. | 342 |
| Mesa Airlines Inc. | 601 |
| Frontier Airlines Inc. | 685 |
| Alaska Airlines Inc. | 714 |
| AirTran Airways Corporation | 3260 |
| Virgin America | 5162 |
| Southwest Airlines Co. | 12275 |
| Endeavor Air Inc. | 18460 |
| US Airways Inc. | 20536 |
| Envoy Air | 26378 |
| American Airlines Inc. | 31327 |
| Delta Air Lines Inc. | 46779 |
| JetBlue Airways | 50940 |
| ExpressJet Airlines Inc. | 54172 |
| United Air Lines Inc. | 57491 |
- Indien we de labels van de categorische variabele maatschappij alfabetisch ordenen dan zien we ook dat er een aantal vluchten foutief gecodeerd zijn als ‘Envoi Air’ in plaats van ‘Envoy Air’.
df %>%
group_by(maatschappij) %>%
tally() %>%
arrange(maatschappij)| maatschappij | n |
|---|---|
| AirTran Airways Corporation | 3260 |
| Alaska Airlines Inc. | 714 |
| American Airlines Inc. | 31327 |
| Delta Air Lines Inc. | 46779 |
| Endeavor Air Inc. | 18460 |
| Envoi Air | 19 |
| Envoy Air | 26378 |
| ExpressJet Airlines Inc. | 54172 |
| Frontier Airlines Inc. | 685 |
| Hawaiian Airlines Inc. | 342 |
| JetBlue Airways | 50940 |
| Mesa Airlines Inc. | 601 |
| SkyWest Airlines Inc. | 32 |
| Southwest Airlines Co. | 12275 |
| United Air Lines Inc. | 57491 |
| US Airways Inc. | 20536 |
| Virgin America | 5162 |
| XpressJet Airlines Inc. | 1 |
- Vervolgens zullen we deze foutieve labels corrigeren.
df %>%
mutate(maatschappij = fct_recode(maatschappij,
"ExpressJet Airlines Inc." = "XpressJet Airlines Inc.",
"Envoy Air" = "Envoi Air")) -> dfdf %>%
group_by(maatschappij) %>%
tally() %>%
arrange(maatschappij)| maatschappij | n |
|---|---|
| AirTran Airways Corporation | 3260 |
| Alaska Airlines Inc. | 714 |
| American Airlines Inc. | 31327 |
| Delta Air Lines Inc. | 46779 |
| Endeavor Air Inc. | 18460 |
| Envoy Air | 26397 |
| ExpressJet Airlines Inc. | 54173 |
| Frontier Airlines Inc. | 685 |
| Hawaiian Airlines Inc. | 342 |
| JetBlue Airways | 50940 |
| Mesa Airlines Inc. | 601 |
| SkyWest Airlines Inc. | 32 |
| Southwest Airlines Co. | 12275 |
| United Air Lines Inc. | 57491 |
| US Airways Inc. | 20536 |
| Virgin America | 5162 |
4.2.2.2 Ordinale variabelen
- Bij ordinale variabelen kunnen dezelfde coderingsfouten voorkomen als bij categorische variabelen. Deze worden op dezelfde manier gedetecteerd en gecorrigeerd.
- Er is echter nog een bijkomende coderingsfout voor ordinale variabelen, namelijk wanneer de voorgedefinieerde volgorde tussen de labels fout is.
- Om dit te detecteren, moet je de verschillende labels (‘levels’) opvragen met behulp van de unique-functie.
- We kunnen de volgorde tussen de labels van een ordinale variabele corrigeren met behulp van de functies mutate (dplyr) en fct_relevel (forcats).
Case: Vluchtdata NYC
- Indien we de ordinale variabele vluchttype analyseren dan zien we dat de voorgedefinieerde volgorde van de labels foutief is.
unique(df$vluchttype)## [1] normaal kort lang intercontinentaal
## Levels: lang < kort < normaal < intercontinentaal- Vervolgens corrigeren we dit met behulp van de functies mutate (dplyr) en fct_relevel (forcats).
df %>%
mutate(vluchttype = fct_relevel(df$vluchttype, "lang", after = 2)) -> df
unique(df$vluchttype)## [1] normaal kort lang intercontinentaal
## Levels: kort < normaal < lang < intercontinentaal4.2.2.3 Continue variabelen
- Foutieve waarden bij een continue variabelen detecteren is een stuk moeilijker omdat een foutieve waarde nog steeds een geldige waarde kan zijn (nog steeds een getal).
- Ook de aanpak om naar weinig voorkomende waarden te kijken, zoals bij categorische variabelen, werkt niet goed omdat bij een continue variabele vaak veel waarden zijn zeer weinig voorkomen.
- De meest voor de hand liggende aanpak is de waarden te bestuderen die opmerkelijk hoog of laag zijn in vergelijking met de andere waarden van de variabele.
- Het is belangrijk te beseffen dat niet iedere extreme waarde per definitie een foutieve waarde is. Uitzonderlijk hoge of lage waardes zijn natuurlijk altijd mogelijk.
- Daarom moet men altijd voorzichtig te werk gaan bij het bepalen of iets een foutieve waarde is (meetfout, ingavefout) of een uitzonderlijke doch correcte waarde. Domeinkennis kan hierbij helpen.
- Indien je door te kijken naar de uiterste waarden mogelijke problemen hebt gedetecteerd, moet je deze observaties van nabij bestuderen om te achterhalen of het meetfouten kunnen zijn of niet. Ga hiervoor steeds naar de volledige observatie kijken en niet enkel naar de waarde voor de continue variabele.
- Bij foutieve waarden van een continue variabele is het vaak niet mogelijk om de correcte waarde af te leiden (zoals bij een categorische variabele). Daarom is de enige juiste correctie deze foutieve waarden te vervangen met “missing values”.
Case: Vluchtdata NYC
- We zullen de variabele vliegtijd analyseren op foutieve waarden.
- We zullen eerst de kleinste waarden bestuderen. Hiervoor selecteren we de 10 vluchten met de kortste vliegtijd en rangschikken deze volgens stijgende vliegtijd. We kijken hierbij niet alleen naar de vliegtijd, maar ook naar de luchthaven, de maatschappij en de afgelegde afstand.
df %>%
arrange(vliegtijd) %>%
select(luchthaven, maatschappij, afstand, vliegtijd) %>%
filter(row_number()<11)| luchthaven | maatschappij | afstand | vliegtijd |
|---|---|---|---|
| JFK | Endeavor Air Inc. | 94 | 0.5833333 |
| EWR | JetBlue Airways | 1065 | 2.7666667 |
| JFK | Delta Air Lines Inc. | 2248 | 5.1500000 |
| EWR | ExpressJet Airlines Inc. | 116 | 20.0000000 |
| EWR | ExpressJet Airlines Inc. | 116 | 20.0000000 |
| EWR | ExpressJet Airlines Inc. | 116 | 21.0000000 |
| EWR | ExpressJet Airlines Inc. | 80 | 21.0000000 |
| EWR | ExpressJet Airlines Inc. | 116 | 21.0000000 |
| EWR | ExpressJet Airlines Inc. | 80 | 21.0000000 |
| LGA | US Airways Inc. | 184 | 21.0000000 |
- Deze analyse doet vermoeden dat de eerste drie vluchten waarschijnlijk meetfouten zijn. Het betreffen hier drie vluchten van minder dan 6 minuten wat zeer onwaarschijnlijk is, zeker wanneer we we zien dat de tweede en derde vlucht lange vluchten zijn. * De overige vluchten zijn vluchten van 20 minuten of meer, maar aangezien het hier om korte vluchten gaan is dit mogelijk correct. We zullen enkel de eerste drie observaties (met een vliegtijd kleiner dan 6) als foutief beschouwen.
- We bestuderen vervolgens de vluchten met de grootste vliegtijd.
df %>%
arrange(-vliegtijd) %>%
select(luchthaven, maatschappij, afstand, vliegtijd) %>%
filter(row_number()<11)| luchthaven | maatschappij | afstand | vliegtijd |
|---|---|---|---|
| EWR | United Air Lines Inc. | 4963 | 695 |
| JFK | Hawaiian Airlines Inc. | 4983 | 691 |
| JFK | Hawaiian Airlines Inc. | 4983 | 686 |
| JFK | Hawaiian Airlines Inc. | 4983 | 686 |
| JFK | Hawaiian Airlines Inc. | 4983 | 683 |
| JFK | Hawaiian Airlines Inc. | 4983 | 679 |
| EWR | United Air Lines Inc. | 4963 | 676 |
| JFK | Hawaiian Airlines Inc. | 4983 | 676 |
| JFK | Hawaiian Airlines Inc. | 4983 | 675 |
| EWR | United Air Lines Inc. | 4963 | 671 |
Deze resultaten doen vermoeden dat het hier NIET om meetfouten gaat. Het gaat hier immers om zeer verre vluchten en de maatschappijnaam doet vermoeden dat het hoofdzakelijk vluchten naar Hawaï zijn. We hebben daarom via Google opgezocht hoe lang een vlucht van New York naar Hawaï duurt en dit komt overeen met de vliegtijden van 11 tot 12u in deze dataset. Daarom besluiten we dat deze waarden geen foutieve waarden zijn.
Vervolgens zullen we voor de drie vluchten met een vliegtijd van minder dan 6 minuten de waarde van de vliegtijd vervangen door een ontbrekende waarde. In R wordt dit aangegeven door de waarde NA dat voor ‘not available’ staat.
df <- df %>%
mutate(vliegtijd = ifelse(vliegtijd<6,NA,vliegtijd))
df %>%
arrange(vliegtijd) %>%
select(luchthaven, maatschappij, afstand, vliegtijd) %>%
filter(row_number()<11)| luchthaven | maatschappij | afstand | vliegtijd |
|---|---|---|---|
| EWR | ExpressJet Airlines Inc. | 116 | 20 |
| EWR | ExpressJet Airlines Inc. | 116 | 20 |
| EWR | ExpressJet Airlines Inc. | 116 | 21 |
| EWR | ExpressJet Airlines Inc. | 80 | 21 |
| EWR | ExpressJet Airlines Inc. | 116 | 21 |
| EWR | ExpressJet Airlines Inc. | 80 | 21 |
| LGA | US Airways Inc. | 184 | 21 |
| JFK | Endeavor Air Inc. | 94 | 21 |
| EWR | ExpressJet Airlines Inc. | 116 | 21 |
| EWR | ExpressJet Airlines Inc. | 116 | 21 |
4.2.3 Missing Values
- Soms gebeurt het dat voor bepaalde cases waarden ontbreken voor een specifieke variabele. In zulke gevallen spreken we van ontbrekende waarden of missing values.
- Het detecteren van ontbrekende waarden is relatief eenvoudig, omdat deze normaal als NA gecodeerd zijn in een dataset (NA = ‘not available’).
- In descriptieve en exploratieve analyses zijn er 3 manieren om met ontbrekende waarden om te gaan:
- We verwijderen de variabele waarvoor we missing values hebben.
- We verwijderen de observaties met missing values.
- We beschouwen de missing values als een aparte waarde.
- Het verwijderen van de variabele zelf is een drastische maatregel. Dit betekent immers dat we de variabele volledig buiten beschouwing laten in onze analyse. Dit is vaak het laatste redmiddel en een vuistregel is dan ook deze tactiek enkel toe te passen bij variabelen met meer dan 20% ontbrekende waardes.
- Bij het verwijderen van observaties moet men met de nodige aandacht te werk gaan. Het is immers nuttig om te weten of de dataset zonder deze observaties nog steeds representatief is voor de onderzochte populatie.
- Een voldoende, doch niet noodzakelijke, vereiste voor representativiteit is dat de steekproef (geobserveerde data) willekeurig is verzameld.
- Indien het ontbreken van waarden niet willekeurig is, dan zal het verwijderen van deze observaties mogelijk leiden tot een dataset die niet meer representatief is voor de oorspronkelijke populatie.
- Daarom is het nuttig om na te gaan of het ontbreken van waarden voor variabele \(X_1\) gecorreleerd is met de waarden van variabele \(X_2\).
- In statistiek maakt men hierbij het onderscheid tussen 3 vormen van ontbrekende waarden:
- Missing completely at random (MCAR): Indien het ontbreken van waarden voor een specifieke variabele volledig willekeurig is, dan spreekt men over MCAR.
- Missing at random (MAR): Indien het ontbreken van waarden voor variabele \(X_1\) niet willekeurig is, maar afhankelijk van de waarden van andere variabelen \(X_2\), \(X_3\), …, dan spreekt men over MAR.
- Not missing at random (NMAR): Indien het ontbreken van waarden voor variabele \(X_1\) niet willekeurig is, maar afhankelijk is van de waarde van \(X_1\) of van de waarden van ongeobserveerde variabelen, dan spreekt men over NMAR.
- Om te bepalen of data al dan niet MCAR is, moet men achterhalen of het ontbreken van waarden voor variabele \(X_1\) gecorreleerd is met de waarden van een andere variabele \(X_2\). Een mogelijkheid is om de dataset in twee te splitsen, i.e. alle observaties met een waarde voor \(X_1\) en alle observaties met een missing value voor \(X_1\). Vervolgens kijken we naar de verdeling van variabele \(X_2\). Indien deze hetzelfde is voor beide datasets, dan suggereert dit dat er geen relatie bestaat tussen de waarde van \(X_2\) en het al dan niet ontbreken van de waarde voor \(X_1\). Indien deze verdeling van \(X_2\) sterkt verschilt tussen beide datasets, dan is er mogelijk wel een relatie en dan is de data niet MCAR.
- Indien de data suggereert dat de ontbrekende waarden MCAR zijn, dan kan men overwegen deze observaties te verwijderen. Indien dit niet het geval is, dan is het beter deze NA-waarden als een aparte categorie te beschouwen.
- Omdat R de waarde ‘NA’ anders behandelt dan reguliere waarden, is het vaak aangeraden om deze waarde te transformeren (indien je de ontbrekende waarden als een aparte categorie wenst te beschouwen).
- In geval van een categorische variabele, kan je de ‘NA’ waarde transformeren naar een aparte categorie (vb ‘waarde ontbreekt’).
- In geval van een continue variabele, is het aangeraden een nieuwe categorische variabele aan te maken die aangeeft of er wel of niet een waarde aanwezig was voor de continue variabele.
Case: Vluchtdata NYC
- De eerste stap is na te gaan welke variabelen ontbrekende waarden hebben en hoe vaak deze variabelen ontbrekende waarden hebben.
summary(df)## luchthaven maatschappij vertrek_vertraging
## EWR:119282 United Air Lines Inc. :57491 Min. : -43.00
## JFK:105230 ExpressJet Airlines Inc.:54173 1st Qu.: -5.00
## LGA:104662 JetBlue Airways :50940 Median : -2.00
## Delta Air Lines Inc. :46779 Mean : 12.71
## American Airlines Inc. :31327 3rd Qu.: 11.00
## Envoy Air :26397 Max. :1301.00
## (Other) :62067 NA's :8214
## aankomst_vertraging afstand vliegtijd
## Min. : -86.000 Min. : 17 Min. : 20.0
## 1st Qu.: -17.000 1st Qu.: 502 1st Qu.: 81.0
## Median : -5.000 Median : 820 Median :127.0
## Mean : 6.987 Mean :1027 Mean :149.6
## 3rd Qu.: 14.000 3rd Qu.:1372 3rd Qu.:184.0
## Max. :1272.000 Max. :4983 Max. :695.0
## NA's :9365 NA's :9368
## vluchttype
## kort :245666
## normaal : 31813
## lang : 50980
## intercontinentaal: 715
##
##
## - Uit deze analyse blijkt dat de variabelen vertrek_vertraging, aankomst_vertraging en vliegtijd last hebben van ontbrekende waarden.
- We kunnen vervolgens met de functie md.pattern (uit de package ‘mice’) de verschillende patronen van ontbrekende waarden identificeren.
library(mice)
md.pattern(df)## luchthaven maatschappij afstand vluchttype vertrek_vertraging
## 319806 1 1 1 1 1
## 3 1 1 1 1 1
## 1151 1 1 1 1 1
## 8214 1 1 1 1 0
## 0 0 0 0 8214
## aankomst_vertraging vliegtijd
## 319806 1 1 0
## 3 1 0 1
## 1151 0 0 2
## 8214 0 0 3
## 9365 9368 26947- Hieruit blijkt dan weer dat er slechts 3 observaties zijn waarvan enkel de vliegtijd ontbreekt (dit zijn de 3 observaties met foutieve waarden!), 1151 observaties waarvan de aankomstvertraging en de vliegtijd ontbreken en 8214 observaties waarbij de vertrekvertraging, aankomstvertraging en de vliegtijd ontbreken.
- Ook zien we opnieuw dat de variabele vliegtijd de meeste ontbrekende waarden heeft (9368), wat neerkomt op ongeveer 3%. Er is dus geen reden om deze variabelen te schrappen.
- Om vervolgens te analyseren of deze ontbrekende waarden MCAR zijn of niet, zullen we voor ieder van de drie continue variabelen een nieuwe categorische variabele maken die aangeeft of de waarde ontbreekt of niet.
df <- df %>%
mutate(vertrek_vertraging_na = is.na(vertrek_vertraging),
aankomst_vertraging_na = is.na(aankomst_vertraging),
vliegtijd_na = is.na(vliegtijd))- Nu kunnen we met ggplot achterhalen of de andere variabelen zich ‘anders’ gedragen als er voor één van deze drie variabelen een waarde ontbreekt.
- We illustreren voor ‘afstand’ (continu) en voor ‘maatschappij’ (categorisch).
- Indien we dit bestuderen voor ‘maatschappij’ gaan we voor iedere maatschappij laten zien welk percentage cases een ontbrekende waarde voor vliegtijd heeft. Indien er geen verband is, dan zouden we geen grote verschillen mogen zien tussen de maatschappijen.
df %>%
group_by(maatschappij, vliegtijd_na) %>%
summarise(aantal = n())%>%
ungroup() %>%
group_by(maatschappij) %>%
mutate(totaal = sum(aantal), percentage = aantal/totaal) %>%
ggplot(aes(x=maatschappij, y=percentage)) +
coord_flip() +
geom_col(aes(fill=vliegtijd_na), position = "stack")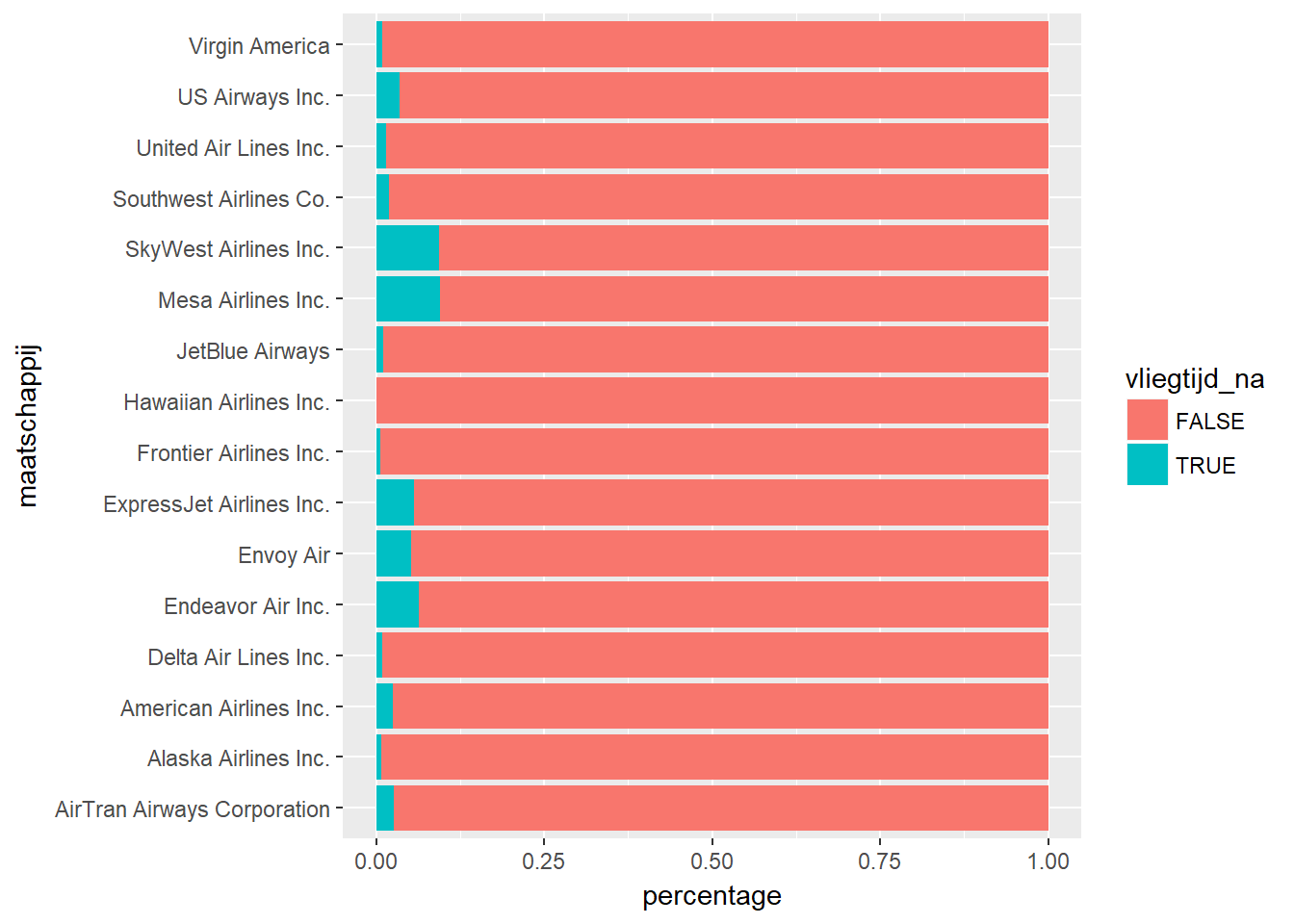
- Uit deze resultaten blijkt dat voor sommige maatschappijen een aanzienlijk hoger percentage ontbrekende waarden bij vliegtijd voorkomt (SkyWest, Mesa en ook ExpressJet, Envoy en Endeavor).
- We kunnen een soortgelijke analyse ook uitvoeren voor de variabele afstand. Hiervoor zullen we eerst de variabele afstand omvormen tot een categorische variabele. We doen dit door de gehele deling uit te voeren (hiervoor gebruik je de %/% operator).
binwidth <- 200
df %>%
mutate(afstand_cat = afstand %/% binwidth) %>%
group_by(afstand_cat, vliegtijd_na) %>%
summarise(aantal = n()) %>%
ungroup() %>%
group_by(afstand_cat) %>%
mutate(totaal = sum(aantal), rel_aantal = aantal/totaal) %>%
ggplot(aes(x=afstand_cat*binwidth, y=rel_aantal)) +
geom_col(aes(fill=vliegtijd_na), position = "stack") +
xlab("afstand")+
ylab("percentage")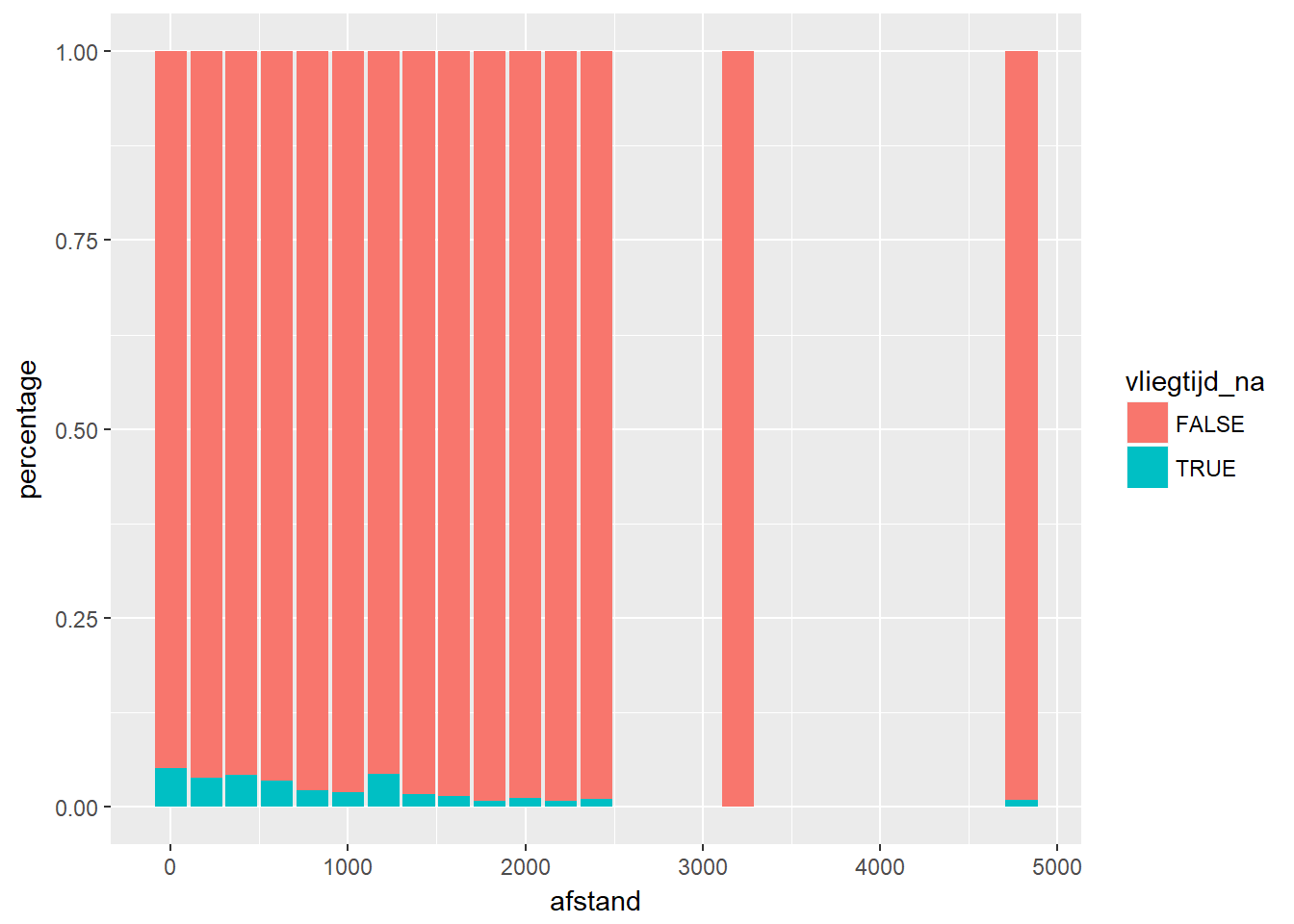
- Deze resultaten lijken te suggereren dat naarmate de vlucht langer wordt, het percentage ontbrekende waarden bij vliegtijd afneemt (met een uitzonderlijke piek bij vluchten rond 1200 mijl).
- Omdat het percentage ontbrekende waarden eerder klein is, is het moeilijk om het patroon duidelijk te zien. We kunnen ook dezelfde plot maken, maar de y-as laten stoppen bij een waarde van 0.25. Op deze manier wordt het patroon duidelijker.
binwidth <- 200
df %>%
mutate(afstand_cat = afstand %/% binwidth) %>%
group_by(afstand_cat, vliegtijd_na) %>%
summarise(aantal = n()) %>%
ungroup() %>%
group_by(afstand_cat) %>%
mutate(totaal = sum(aantal), rel_aantal = aantal/totaal) %>%
ggplot(aes(x=afstand_cat*binwidth, y=rel_aantal)) +
geom_col(aes(fill=vliegtijd_na), position = "stack") +
xlab("afstand")+
ylab("percentage")+
coord_cartesian(ylim = c(0, 0.25))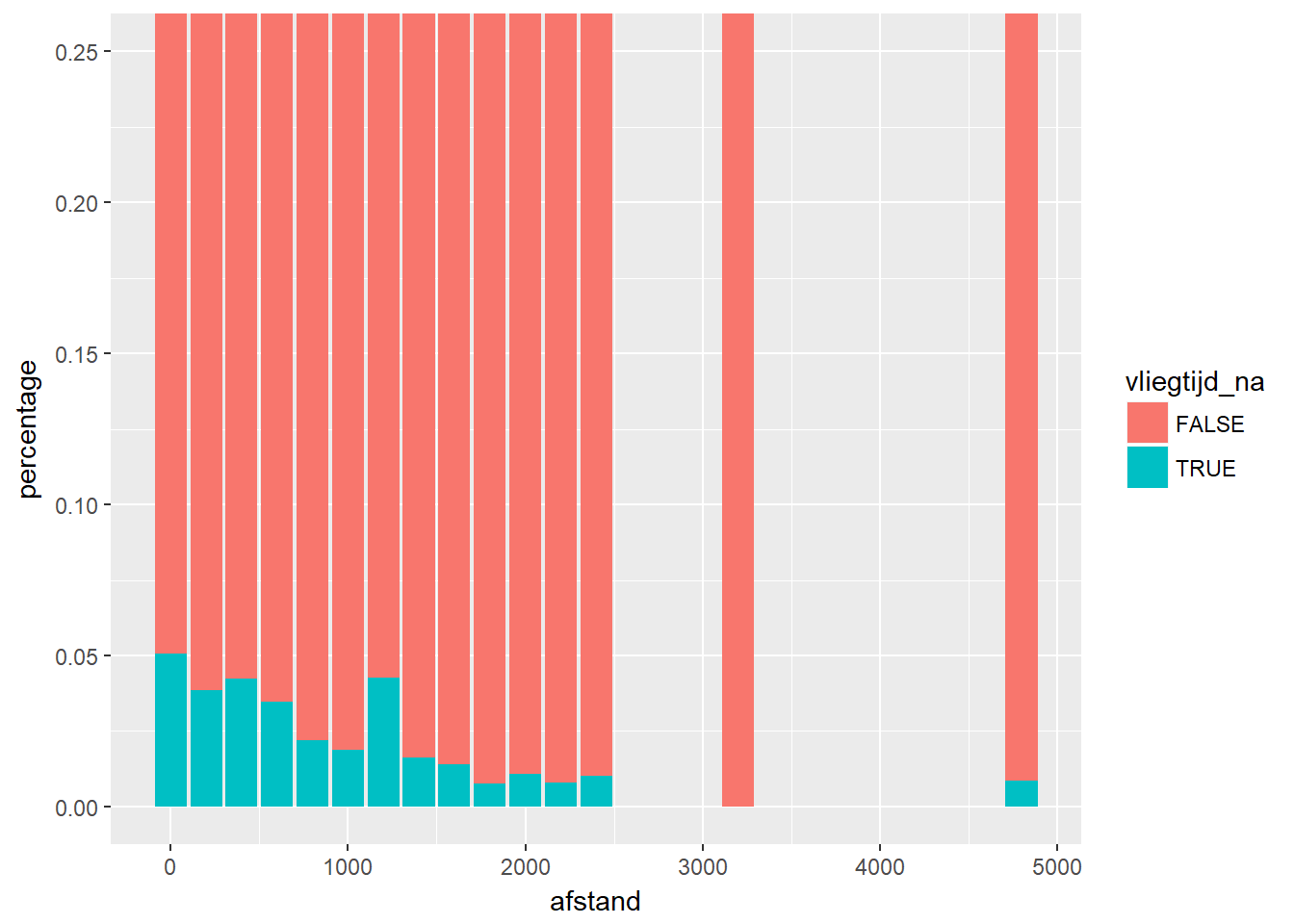
- Tenslotte kunnen we ook nog op een andere manier het verband tussen de afstand en het voorkomen van ontbrekende waarden bij vliegtijd bestuderen, nl. via 2 boxplots.
df %>%
ggplot(aes(x=vliegtijd_na, y=afstand)) +
geom_boxplot()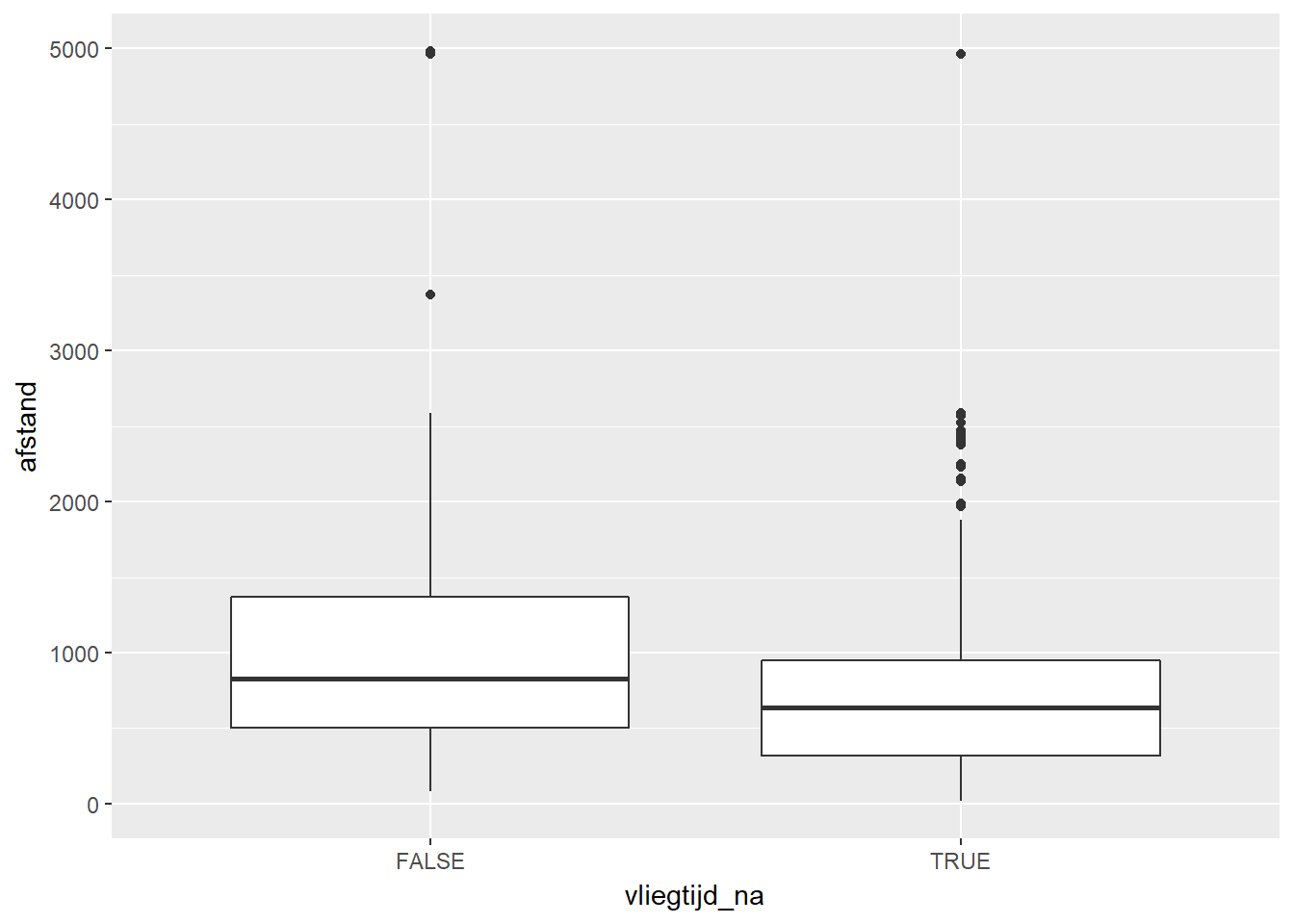
- Hier zien we dat vluchten waarvoor de vliegtijd ontbreekt vaak kortere vluchten zijn dan waarvoor we de vliegtijd wel hebben. Dit komt overeen met de vorige bevinding.
- Op basis van deze resultaten kunnen we dus stellen dat het ontbreken van de vliegtijd niet willekeurig is, maar vaker voorkomt bij bepaalde maatschappijen en eerder bij kortere dan bij langere vluchten.
- We zouden nog verder kunnen onderzoeken of deze maatschappijen eerder langere of kortere vluchten organiseren.
- Soortgelijke analyses kunnen we ook uitvoeren voor de variabelen vertrek_vertraging en aankomst_vertraging.
4.3 Fase 2: Data bruikbaarder maken
- Van zodra de data geen foutieve en/of ontbrekende waarde meer bevat, kunnen we een aantal technieken toepassen om de data bruikbaarder te maken voor exploratieve analyses. We onderscheiden hierbij 2 technieken:
- Transformatie van bestaande variabelen.
- Selectie van observaties.
4.3.1 Transformatie van bestaande variabelen
4.3.1.1 Categorische variabelen
- Soms is het beter om de categorieën van een categorische variabelen te wijzigen door sommige categorieën samen te nemen. Er zijn verschillende situaties waarbij dit het overwegen waard is, zoals:
- De labels van een categorische variabele is op een te gedetailleerd niveau gedefinieerd, met als gevolg dat de exploratieve analyse al snel complex wordt door de vele categorieën. In zulke gevallen kan het zinvol zijn om het aantal categorieën te verminderen door categorieën die inhoudelijk bij elkaar horen samen te nemen.
- Een categorische variabele bestaat uit een beperkt aantal categorieën met veel observaties en een groot aantal categorieën met zeer weinig observaties. In zulke gevallen kan het zinvol zijn om de categorieën met weinig observaties samen te nemen in 1 categorie “Overige”.
- Om te bepalen welke categorieën men kan samenvoegen, kan een frequentietabel of barplot gemaakt worden.
- Het herdefiniëren van de labels gebeurt vervolgens met de functie fct_recode (forcats). Hierbij heeft men steeds de keuze om de oorspronkelijke variabele te vervangen of een nieuwe variabele aan te maken.
Case: Vluchtdata NYC
- Laten we eens aan de hand van een barplot naar de variabele ‘luchtvaartmaatschappij’ kijken. We zien hierbij dat er relatief veel luchtvaartmaatschappijen (categorieën) in onze data zijn en dat er een aantal verwaarloosbaar weinig vluchten bevatten.
df %>%
ggplot(aes(x=fct_infreq(maatschappij))) +
geom_bar() +
coord_flip() +
xlab("Luchtvaartmaatschappij")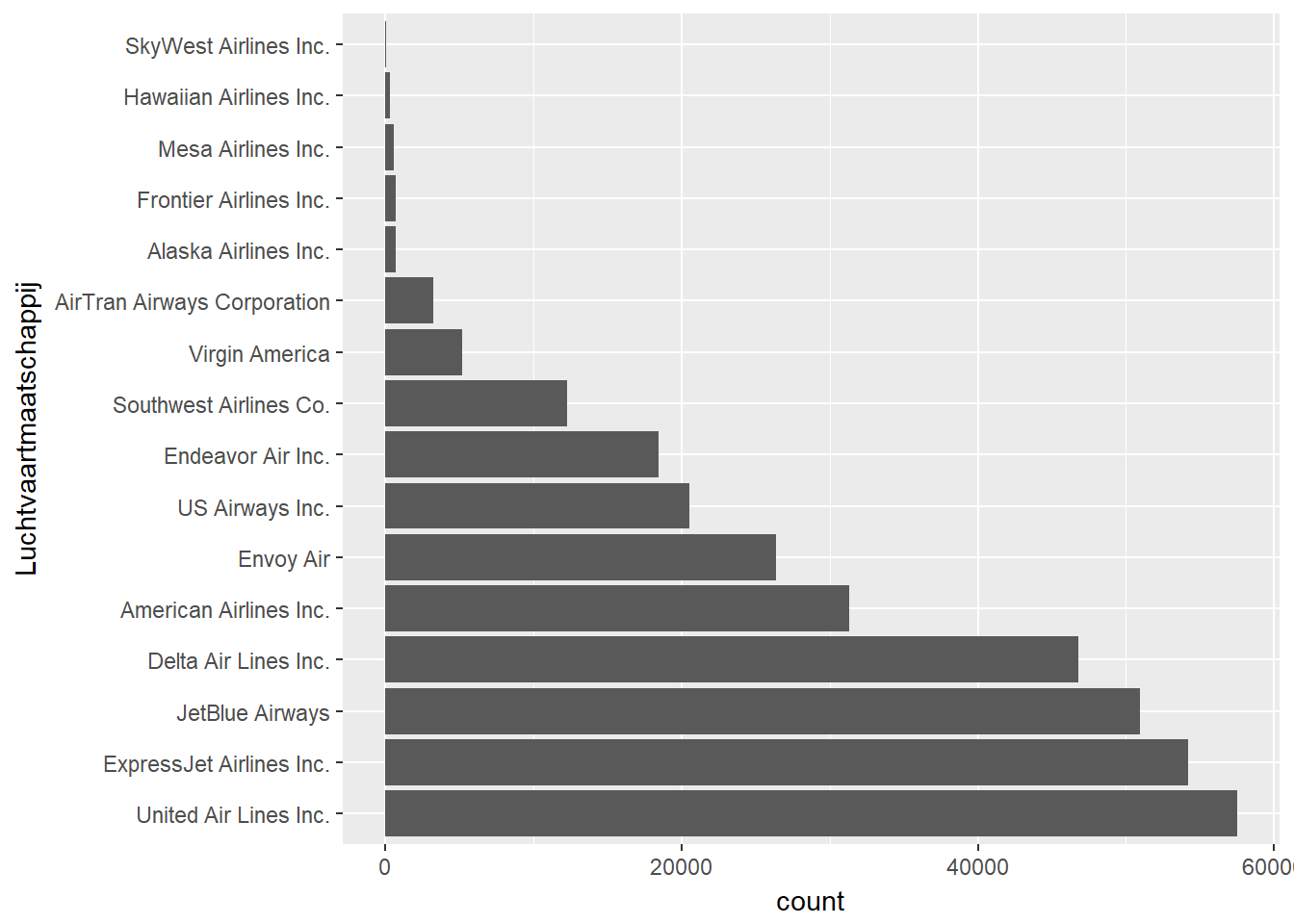
- We kunnen de exacte aantallen achterhalen met behulp van een frequentietabel.
df %>%
group_by(maatschappij) %>%
summarise(n = n()) %>%
arrange(n)| maatschappij | n |
|---|---|
| SkyWest Airlines Inc. | 32 |
| Hawaiian Airlines Inc. | 342 |
| Mesa Airlines Inc. | 601 |
| Frontier Airlines Inc. | 685 |
| Alaska Airlines Inc. | 714 |
| AirTran Airways Corporation | 3260 |
| Virgin America | 5162 |
| Southwest Airlines Co. | 12275 |
| Endeavor Air Inc. | 18460 |
| US Airways Inc. | 20536 |
| Envoy Air | 26397 |
| American Airlines Inc. | 31327 |
| Delta Air Lines Inc. | 46779 |
| JetBlue Airways | 50940 |
| ExpressJet Airlines Inc. | 54173 |
| United Air Lines Inc. | 57491 |
- Op basis van deze analyse beslissen we om de luchtvaartmaatschappijen met minder dan 10000 vluchten samen te voegen in een nieuwe categorie met het label “Overige”. We opteren ervoor de oorspronkelijke variabelen te vervangen.
df %>%
mutate(maatschappij = fct_lump(maatschappij,
n = 9,
other_level = "Overige")) -> df- De nieuwe frequentietabel toont het resultaat.
df.complete %>%
group_by(maatschappij) %>%
summarise(n = n()) %>%
arrange(n)| maatschappij | n |
|---|---|
| Overige | 10796 |
| Southwest Airlines Co. | 12275 |
| Endeavor Air Inc. | 18460 |
| US Airways Inc. | 20536 |
| Envoy Air | 26397 |
| American Airlines Inc. | 31327 |
| Delta Air Lines Inc. | 46779 |
| JetBlue Airways | 50940 |
| ExpressJet Airlines Inc. | 54173 |
| United Air Lines Inc. | 57491 |
4.3.1.2 Continue variabelen
- Bij continue variabelen zijn er verschillende transformaties die regelmatig uitgevoerd worden:
- De transformatie van een continue variabele naar een categorische variabele.
- Het herschalen van de continue variabele.
- De creatie van een nieuwe variabele op basis van bestaande continue variabelen.
- Ook hier hebben we weer steeds de mogelijkheid om de bestaande variabele te vervangen of een nieuwe variabele aan te maken.
Case: Vluchtdata NYC
- Laten we de variabele vliegtijd eens onder de loep nemen. We beginnen met een visuele analyse aan de hand van een violinplot.
df %>%
ggplot(aes(x="", y=vliegtijd)) +
geom_violin() +
xlab("Vliegtijd") +
scale_y_continuous(breaks=seq(0,800,50))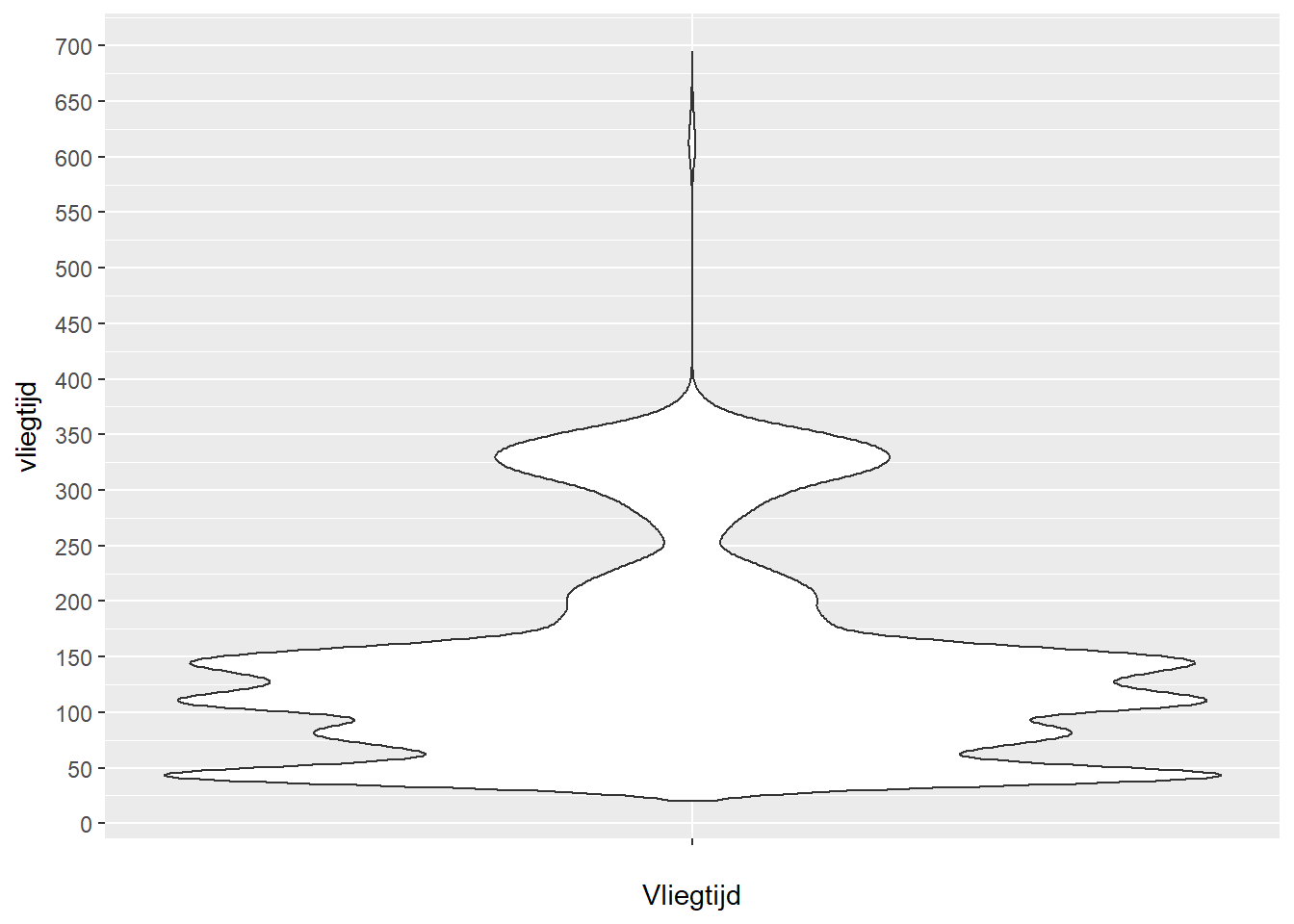
- Op basis van deze plot beslissen we een nieuwe categorische variabele “vliegtijd_fct” aan te maken, waarbij ‘kort’ overeenkomt met een vlucht die minder dan een uur duurt, ‘normaal’ overeenkomt met een vlucht tussen 1 en 4 uur (60-240) en ‘lang’ overeenkomt met een vlucht van meer dan 4 uur. Hiervoor maken we gebruik van de functie cut.
df %>%
mutate(vliegtijd_fct = cut(vliegtijd, c(-Inf,60,240,Inf),
labels=c('kort','normaal','lang'))) -> df- Aan de hand van een frequentietabel kunnen we nu het resultaat bekijken.
df.complete %>%
group_by(vliegtijd_fct) %>%
tally()| vliegtijd_fct | n |
|---|---|
| kort | 53220 |
| normaal | 210758 |
| lang | 55828 |
| NA | 9368 |
- Vervolgens beslissen we een nieuwe variabele te maken die de vliegtijd uitdrukt in uren in plaats van minuten.
df %>%
mutate(vliegtijd_uren = vliegtijd/60) -> df- We kunnen het resultaat bekijken met een violinplot.
df %>%
ggplot(aes(x="", y=vliegtijd_uren)) +
geom_violin() +
xlab("Vliegtijd (in uren)") +
scale_y_continuous(breaks=seq(0,12,2))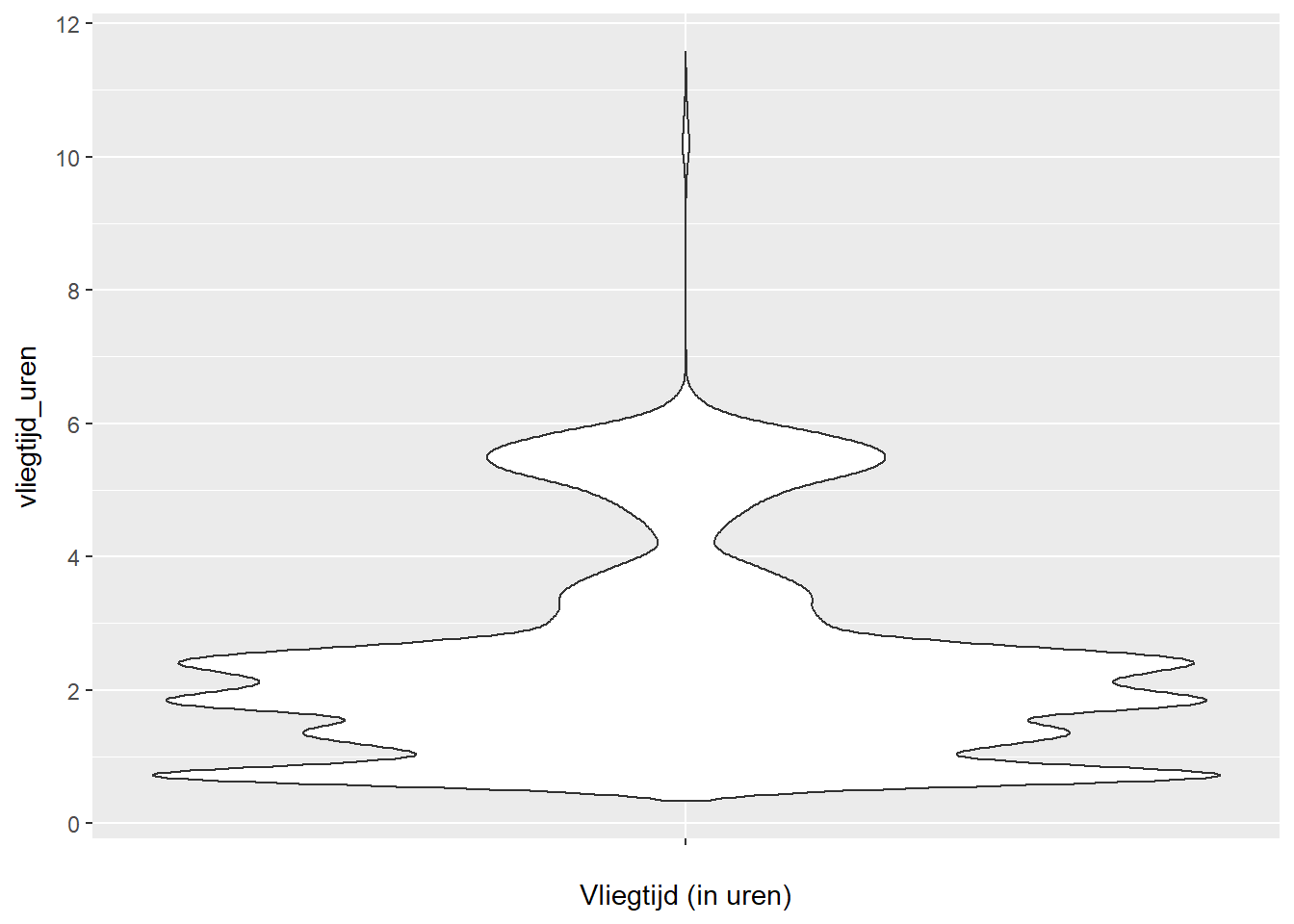
- Tenslotte maken we een nieuwe variabele die de gemiddelde snelheid van het vliegtuig uitdrukt door de afstand te delen door de vliegtijd.
df %>%
mutate(snelheid = afstand / vliegtijd_uren) -> df- Laten we het resultaat aan de hand van een histogram bekijken.
df %>%
ggplot(aes(x=snelheid)) +
geom_histogram(binwidth = 50) +
scale_x_continuous(breaks = seq(0,3000, 200))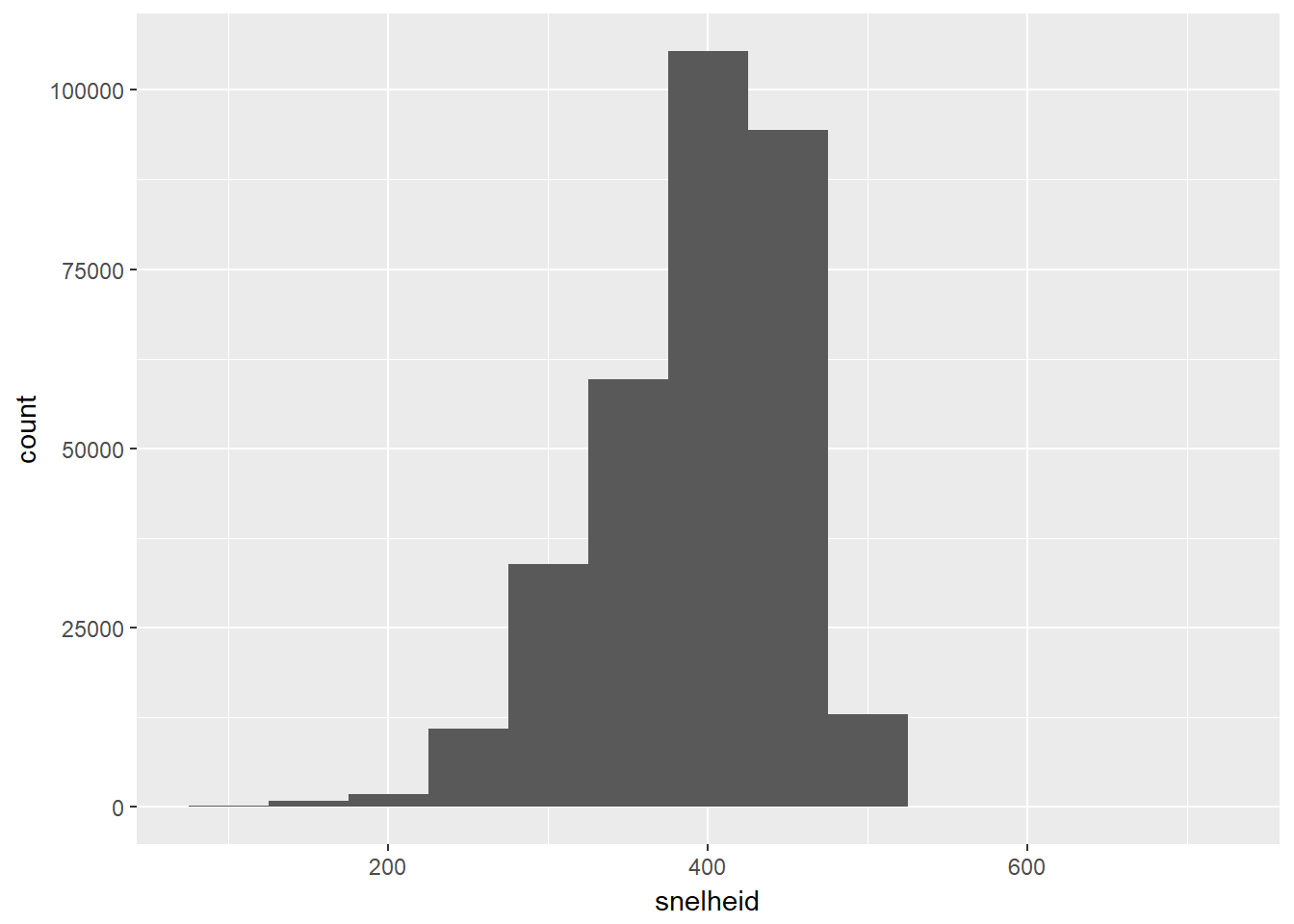
4.3.2 Sampling
- Soms is een dataset zo groot, dat analyses veel tijd in beslag nemen. In zulke gevallen kan het nuttig zijn om een random sample te nemen van de oorspronkelijke data om een eerste exploratieve analyse op uit te voeren.
- Zolang de sample willekeurig getrokken wordt en de nieuwe dataset niet te klein wordt, is de kans dat je patronen ontdekt in de sample die niet voorkomen in de volledige dataset eerder klein.
- Na een eerste exploratieve data analyse op de beperkte sample, kan men vervolgens gerichter de volledige dataset analyseren.
Case: Vluchtdata NYC
- Laten we een sample van 10000 vluchten nemen uit de oorspronkelijke dataset.
df.10000 <- df %>% sample_n(10000)- We kunnen nu een eerste blik op deze sample werpen met behulp van de summary functie.
summary(df.10000)## luchthaven maatschappij vertrek_vertraging
## EWR:3585 United Air Lines Inc. :1777 Min. :-20.00
## JFK:3205 ExpressJet Airlines Inc.:1619 1st Qu.: -5.00
## LGA:3210 JetBlue Airways :1544 Median : -2.00
## Delta Air Lines Inc. :1427 Mean : 12.78
## American Airlines Inc. : 880 3rd Qu.: 11.00
## Envoy Air : 834 Max. :592.00
## (Other) :1919 NA's :266
## aankomst_vertraging afstand vliegtijd
## Min. :-75.000 Min. : 80 Min. : 21.0
## 1st Qu.:-17.000 1st Qu.: 500 1st Qu.: 80.0
## Median : -5.000 Median : 820 Median :127.0
## Mean : 7.243 Mean :1030 Mean :149.9
## 3rd Qu.: 14.000 3rd Qu.:1372 3rd Qu.:185.0
## Max. :595.000 Max. :4983 Max. :671.0
## NA's :304 NA's :304
## vluchttype vertrek_vertraging_na aankomst_vertraging_na
## kort :7435 Mode :logical Mode :logical
## normaal : 997 FALSE:9734 FALSE:9696
## lang :1535 TRUE :266 TRUE :304
## intercontinentaal: 33
##
##
##
## vliegtijd_na vliegtijd_fct vliegtijd_uren snelheid
## Mode :logical kort :1625 Min. : 0.350 Min. :104.7
## FALSE:9696 normaal:6353 1st Qu.: 1.333 1st Qu.:354.8
## TRUE :304 lang :1718 Median : 2.117 Median :401.9
## NA's : 304 Mean : 2.499 Mean :391.3
## 3rd Qu.: 3.083 3rd Qu.:435.7
## Max. :11.183 Max. :703.4
## NA's :304 NA's :304- Als we dit vergelijken met de volledige dataset, dan zien we relatief weinig verschillen wat betreft de centrummaten en de robuste spreidingsmaten.
- Merk op dat minima’s en maxima’s wel sterk kunnen verschillen. Dit is omdat dit geen robuste maatstaven zijn.
summary(df)## luchthaven maatschappij vertrek_vertraging
## EWR:119282 United Air Lines Inc. :57491 Min. : -43.00
## JFK:105230 ExpressJet Airlines Inc.:54173 1st Qu.: -5.00
## LGA:104662 JetBlue Airways :50940 Median : -2.00
## Delta Air Lines Inc. :46779 Mean : 12.71
## American Airlines Inc. :31327 3rd Qu.: 11.00
## Envoy Air :26397 Max. :1301.00
## (Other) :62067 NA's :8214
## aankomst_vertraging afstand vliegtijd
## Min. : -86.000 Min. : 17 Min. : 20.0
## 1st Qu.: -17.000 1st Qu.: 502 1st Qu.: 81.0
## Median : -5.000 Median : 820 Median :127.0
## Mean : 6.987 Mean :1027 Mean :149.6
## 3rd Qu.: 14.000 3rd Qu.:1372 3rd Qu.:184.0
## Max. :1272.000 Max. :4983 Max. :695.0
## NA's :9365 NA's :9368
## vluchttype vertrek_vertraging_na aankomst_vertraging_na
## kort :245666 Mode :logical Mode :logical
## normaal : 31813 FALSE:320960 FALSE:319809
## lang : 50980 TRUE :8214 TRUE :9365
## intercontinentaal: 715
##
##
##
## vliegtijd_na vliegtijd_fct vliegtijd_uren snelheid
## Mode :logical kort : 53220 Min. : 0.333 Min. : 76.8
## FALSE:319806 normaal:210758 1st Qu.: 1.350 1st Qu.:356.3
## TRUE :9368 lang : 55828 Median : 2.117 Median :402.6
## NA's : 9368 Mean : 2.493 Mean :392.1
## 3rd Qu.: 3.067 3rd Qu.:436.2
## Max. :11.583 Max. :703.4
## NA's :9368 NA's :9368Referenties
- Unique-functie: https://chemicalstatistician.wordpress.com/2018/03/10/use-unique-instead-of-levels-to-find-the-possible-values-of-a-character-variable-in-r/
- Factors: http://r4ds.had.co.nz/factors.html
- Fct_relevel: http://forcats.tidyverse.org/reference/fct_relevel.html
- From continuous to categorical: http://rforpublichealth.blogspot.be/2012/09/from-continuous-to-categorical.html