2 Código Eficiente de R

Existen mecanismos más eficientes de ejecutar ciertas funciones sobre fragmentos de una estructura (vector, matriz, data frame, etc), que a través de los bucles. De cierta manera estas funciones mismas incorporan una lógica de bucle de repetición. Es conveniente empezar respondiendo estas preguntas para identificar si la solución que se desea implementar se aplica a estos casos.

1. ¿De qué clase son mis datos de entrada, los datos sobre los cuales quiero aplicar un proceso? - vector, matriz, data frame…).
2. ¿Sobre qué subconjunto (subset) de datos se desea aplicar la función ? – filas, columnas, todos los valores…
3. ¿Qué clase retornará la función? ¿Cómo se ha transformado la estructura original?

Existe una familia de comandos que permite aplicar funciones a varios elementos (subconjuntos de datos) de una estructura o clase simulando un proceso repetitivo más eficiente. Estos comandos son: apply, lapply , sapply, vapply, mapply, rapply, and tapply. En esta sesión ilustratemos algunos ejemplos de ellos y los que no se abordan aquí, se sugieren como revisión al lector.

2.1 Familia *apply

Para quienes han escuchado de esta familia de funciones, quizás la pregunta frecuente es, ¿en qué difieren estas funciones de las estructuras clásicas de bucles?.

En esta sesión exploraremos:

• apply() as well as
• lapply() and sapply().

Estas estructuras son muy particulares de R. Esto se debe a que R es un lenguaje de programación funcional, es decir que cada operación en R se efectúa por una función apropiada. Por ejemplo, el símbolo más básico de asignación <- se define como cualquier otra función.

a <- 10
a

## [1] 10

"<-"(b, 20)
b

## [1] 20

"+"(a, b)

## [1] 30

Todas las funciones *apply se caracterizan por tener funciones como un argumento, por esto son llamados funcionales.

Estos funcionales, toman un objeto y una función como entrada (argumentos) y aplican dicha función a cada entrada (fila, columna, elemento) del objeto. La diferencia entre las distintas funciones *apply es básicamente el tipo de objeto que manipulan.

2.1.1 apply()

Tiene tres argumentos principales:

Argumento	Descripción
X	Una matriz (o array) o un data.frame que puede reducirse a matriz.
MARGIN	Un entero especificando si aplicar la función indicada sobre filas (1) o columnas (2).
FUN	La función a ser aplicada.

Otros argumentos como na.rm pueden también ser indicados. Probemos ejemplos sencillos:

2.1.1.0.1 Ejemplo 1: Retornar el producto de cada fila

m<-matrix(c(seq(from=-98,to=100,by=2)),nrow=10,ncol=10)
apply(m,1,prod)

##  [1] -2.849130e+15 -5.344148e+15 -7.282577e+15 -8.510121e+15 -8.930250e+15
##  [6] -8.510121e+15 -7.282577e+15 -5.344148e+15 -2.849130e+15  0.000000e+00

2.1.1.0.2 Ejemplo 2: Retornar la suma de cada columna

apply(m,2,sum)

##  [1] -890 -690 -490 -290  -90  110  310  510  710  910

2.1.1.0.3 Ejemplo 3: Retornar una nueva matriz cuyos valores son ‘m’ modulo 10

apply(m,c(1,2),function(x) x%%10) 

##       [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
##  [1,]    2    2    2    2    2    2    2    2    2     2
##  [2,]    4    4    4    4    4    4    4    4    4     4
##  [3,]    6    6    6    6    6    6    6    6    6     6
##  [4,]    8    8    8    8    8    8    8    8    8     8
##  [5,]    0    0    0    0    0    0    0    0    0     0
##  [6,]    2    2    2    2    2    2    2    2    2     2
##  [7,]    4    4    4    4    4    4    4    4    4     4
##  [8,]    6    6    6    6    6    6    6    6    6     6
##  [9,]    8    8    8    8    8    8    8    8    8     8
## [10,]    0    0    0    0    0    0    0    0    0     0

Ahora probemos con una aplicación sobre un dataset conocido de R.

library(ggplot2)
class(diamonds)

## [1] "tbl_df"     "tbl"        "data.frame"

## subset diamonds to only numerical columns
diamonds_num <- diamonds[, -c(2:4)]

## apply function mean to all columns of diamonds
col_means <- apply(diamonds_num, 2, mean, na.rm = TRUE)
col_means

##        carat        depth        table        price            x 
##    0.7979397   61.7494049   57.4571839 3932.7997219    5.7311572 
##            y            z 
##    5.7345260    3.5387338

En R, cuando los datos a trabajar tienen una estructura tipo matriz, apply() es la opción más adecuada. Esta es más rápida que generar iteración en bucles a través de estructuras for() los cuales son estándar en otros lenguajes como Python o C++.

2.1.2 lapply() and sapply()

lapply() retorna una lista de la misma longitud de X, donde cada elemento corresponde al resultado de aplicar FUN a su respectivo elemento de X.

La ‘l’ significa lista, lo cual indica que lo que fuera que retorne de un proceso iterativo se guardará como una lista. Sabemos que en R, las listas son el modo más flexible de almacenar información (e.g, combinación de objetos en listas).

Aquí un ejemplo de una lista muy variada:

lst <- list(1:10, 
            "Ambato", 
            mean,
            mean(1:100),
            function(x) x + 1, 
            data.frame(col1 = rnorm(10), col2 = runif(10)),
            matrix(1:9, 3, 3))
lst

## [[1]]
##  [1]  1  2  3  4  5  6  7  8  9 10
## 
## [[2]]
## [1] "Ambato"
## 
## [[3]]
## function (x, ...) 
## UseMethod("mean")
## <bytecode: 0x7fcb61617bf8>
## <environment: namespace:base>
## 
## [[4]]
## [1] 50.5
## 
## [[5]]
## function (x) 
## x + 1
## 
## [[6]]
##           col1      col2
## 1  -0.99459269 0.6231016
## 2   1.11604877 0.2198673
## 3   0.05690111 0.2874198
## 4   1.06488278 0.5948170
## 5  -1.08273102 0.1894580
## 6   2.35058749 0.4094459
## 7  -0.40643017 0.0389849
## 8   1.35712530 0.9889320
## 9  -0.11880813 0.6518442
## 10 -1.31195018 0.4983812
## 
## [[7]]
##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9

Recuerda que para acceder a los elementos de una lista se requiere el uso de corchetes [[x]] donde x hace referencia a la posición en la lista. Es importante tener presente esta noción sobre listas para interpretar el proceso de iteración.

En sapply() la ‘s’ significa simplificada, esta es una versión amigable de lapply que por defecto retorna un vector o matriz según el caso.

Un ejemplo sencillo para ilustrar lapply() y sapply():

A<-matrix(1:9, 3,3)
B<-matrix(4:15, 4,3)
C<-matrix(8:10, 3,2)
myList<-list(A,B,C) 
myList

## [[1]]
##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9
## 
## [[2]]
##      [,1] [,2] [,3]
## [1,]    4    8   12
## [2,]    5    9   13
## [3,]    6   10   14
## [4,]    7   11   15
## 
## [[3]]
##      [,1] [,2]
## [1,]    8    8
## [2,]    9    9
## [3,]   10   10

lapply(myList,"[", 2,1 )

## [[1]]
## [1] 2
## 
## [[2]]
## [1] 5
## 
## [[3]]
## [1] 9

sapply(myList,"[", 2,1 )

## [1] 2 5 9

En tanto que lapply() y sapply() son sumamente similares, abordaremos a detalle implementaciones con lapply().

lapply() puede básicamente ser usado como un bucle for(), no obstante la semántica es un poco diferente, principalmente en estos dos aspectos:

1. El resultado final de una llamada lapply()se almacena en un objeto (una list), y
2. se requiere escribir el proceso interno del bucle como una función.

result <- lapply(1:5, function(i) i)
result

## [[1]]
## [1] 1
## 
## [[2]]
## [1] 2
## 
## [[3]]
## [1] 3
## 
## [[4]]
## [1] 4
## 
## [[5]]
## [1] 5

En un ejemplo práctico que considera análisis estadístico y visualización de resultados, generamos modelos lineales entre dos variables ‘carat’ y ‘price’ y sus correspondients gráficos de dispersión para todos los niveles de ‘cut’, pero únicamente para aquellos diamantes de ‘color = D’.

library(ggplot2)
## split diamonds by cut
cut_lst <- split(diamonds, f = diamonds$cut)

my_result_list <- lapply(seq(cut_lst), function(i) {
  
  ## subset to color = D
  dat <- cut_lst[[i]]
  dat_d <- subset(dat, dat$color == "D")
  
  ## calculate linear model
  lm1 <- lm(price ~ carat, data = dat_d)
  
  ## create scatterplot
  scatter_ggplot <- ggplot(aes(x = carat, y = price), data = dat_d)
  g_sc <- scatter_ggplot + 
    geom_point(colour = "grey60") +
    theme_bw() +
    stat_smooth(method = "lm", se = TRUE, 
                fill = "black", colour = "black") +
     geom_text(data = NULL, 
               x = min(dat_d$carat, na.rm = TRUE) + 0.2,  
               y = max(dat_d$price, na.rm = TRUE) * 0.98, 
               label = unique(dat_d$cut))
  
  ## return both the linear model and the plot as a list
  return(list(linmod = lm1,
              plt = g_sc))
})

## set names of list for clarity
names(cut_lst)

## [1] "Fair"      "Good"      "Very Good" "Premium"   "Ideal"

names(my_result_list) <- names(cut_lst)

str(my_result_list, 2)

## List of 5
##  $ Fair     :List of 2
##   ..$ linmod:List of 12
##   .. ..- attr(*, "class")= chr "lm"
##   ..$ plt   :List of 9
##   .. ..- attr(*, "class")= chr [1:2] "gg" "ggplot"
##  $ Good     :List of 2
##   ..$ linmod:List of 12
##   .. ..- attr(*, "class")= chr "lm"
##   ..$ plt   :List of 9
##   .. ..- attr(*, "class")= chr [1:2] "gg" "ggplot"
##  $ Very Good:List of 2
##   ..$ linmod:List of 12
##   .. ..- attr(*, "class")= chr "lm"
##   ..$ plt   :List of 9
##   .. ..- attr(*, "class")= chr [1:2] "gg" "ggplot"
##  $ Premium  :List of 2
##   ..$ linmod:List of 12
##   .. ..- attr(*, "class")= chr "lm"
##   ..$ plt   :List of 9
##   .. ..- attr(*, "class")= chr [1:2] "gg" "ggplot"
##  $ Ideal    :List of 2
##   ..$ linmod:List of 12
##   .. ..- attr(*, "class")= chr "lm"
##   ..$ plt   :List of 9
##   .. ..- attr(*, "class")= chr [1:2] "gg" "ggplot"

Ahora accedamos rápidamente a los resultados de cada análsis individual. Para visualizar el gráfico de dispersión de los diamantes de ‘cut = Premium’. Simplemente navegaremos a la entrada correspondiente:

my_result_list$Premium$plt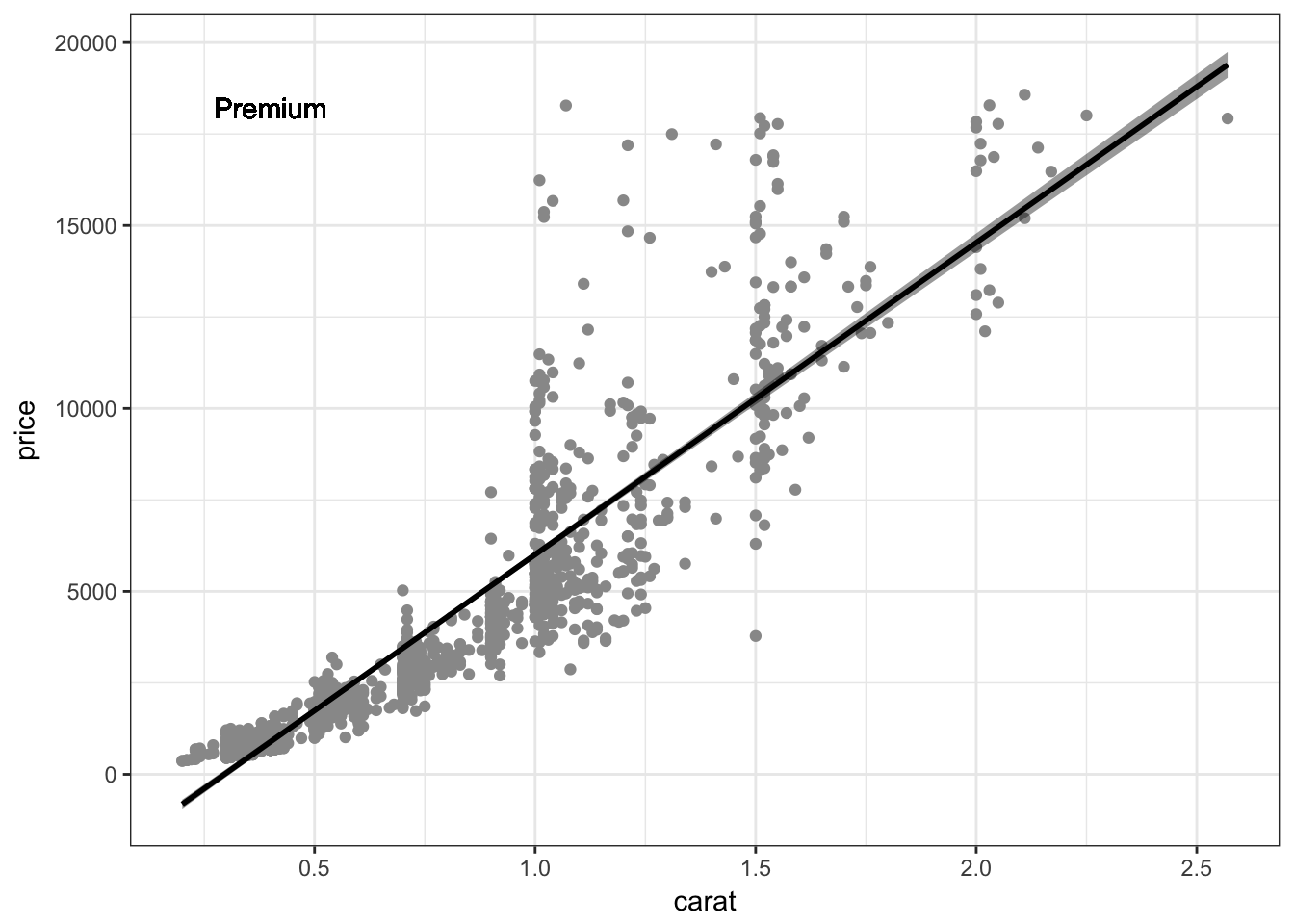

Nótese que ahora podemos utilizar la notación $ para acceder dado que hemos seteado los nombres de las listas resultantes. No obstante es posible navegar usando los corchetes dobles ([[]]). Para obtener el ‘summary’ del modelo lineal de ‘cut = Ideal’:

summary(my_result_list[[5]][[1]])

## 
## Call:
## lm(formula = price ~ carat, data = dat_d)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -9239.6  -611.1   -38.9   419.5 10759.7 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -2490.89      51.89  -48.01   <2e-16 ***
## carat        9049.65      81.06  111.64   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1292 on 2832 degrees of freedom
## Multiple R-squared:  0.8148, Adjusted R-squared:  0.8148 
## F-statistic: 1.246e+04 on 1 and 2832 DF,  p-value: < 2.2e-16

2.2 Programación Funcional

Ya se ha mencionado anteriormente que R es en su núcleo un lenguaje de programación funcional, es decir, en general

• todo lo que existe es un objeto y
• todo lo que sucede es una llamada a función.

2.2.1 Funciones Personalizadas

Si bien R posee una amplia variedad de funciones muy útiles para análisis de datos, en varias ocasiones es necesario crear nuestras propias funciones que sean capaces de efectuar sistemáticamente los cálculos de interés. De hecho las librerías de R que se construyen continuamente son el resultado de estas mismas necesidades.

Un ejemplo sencillo para recordar como se define una función:

pythagoreanTheorem <- function(a, b) {
  c <- sqrt(a*a + b*b)
  return(c)
}

pythagoreanTheorem(3, 4)

## [1] 5

2.2.2 Funcionales

Ya hemos abordado los llamados functionales, funciones que toman otras funciones como argumentos. A pesar de que lo más común es usar como argumento funciones básicas de R (sum, mean, etc), también es posible utilizar funciones personalizadas:

dat <- data.frame(a = c(3, 7, 11, 1, 24, 2),
                  b = c(4, 3, 2, 3, 12, 5))

sapply(seq(nrow(dat)), function(i) pythagoreanTheorem(dat[i, 1], dat[i, 2]))

## [1]  5.000000  7.615773 11.180340  3.162278 26.832816  5.385165

2.2.3 Closures

La contraparte de los funcionales son los llamados closures. Estas son funciones que retornan (o construyen) una función en base a algún argumento proporcionado. Consideremos la siguiente situación:

Se tiene un conjunto de posibles variables predictoras (pred), un conjunto de variables de respuesta (resp) y el objetivo es identificar la mejor combinación que explica las varianzas.

### generate some random data
set.seed(123)
pred <- data.frame(pred1 = rnorm(100, 2, 1),
                   pred2 = 1:100,
                   pred3 = rpois(100, 2),
                   pred4 = 200:101)

set.seed(234)
resp <- data.frame(resp1 = 1:100,
                   resp2 = rnorm(100, 2, 1),
                   resp3 = 200:101,
                   resp4 = rpois(100, 2))

Podríamos simplemente copiar y pegar sentencias para calcular cada combinación.

summary(lm(resp$resp1 ~ pred$pred1))$r.squared
summary(lm(resp$resp2 ~ pred$pred1))$r.squared
summary(lm(resp$resp2 ~ pred$pred1))$r.squared
summary(lm(resp$resp4 ~ pred$pred1))$r.squared

summary(lm(resp$resp1 ~ pred$pred2))$r.squared
summary(lm(resp$resp2 ~ pred$pred2))$r.squared
summary(lm(resp$resp3 ~ pred$pred2))$r.squared
summary(lm(resp$resp4 ~ pred$pred3))$r.squared

# ... and so forth

No obstante, esto está muy lejos de ser óptimo. Además de que se han generado varias líneas de código, es muy posible que se hayan indroducido errores (¿ya los ha identificado?) que son particularmente difíciles de rastrear. En este caso usar closures puede ser de gran ayuda.

### define closure
calcRsq <- function(pred) {
  function(y) {
    summary(lm(y ~ pred))$r.squared
  }
}

Ahora, tenemos una forma general de definir funciones para calcular valores de R-cuadrado:

## create function using pred$v1 as predictor
calcRsq_pred1 <- calcRsq(pred$pred1)
calcRsq_pred1(resp$resp1)

## [1] 0.006369369

Usar una llamada explícita como la que acabamos de definir realmente no es de mucha ayuda, aunque hemos reducido la posibilidad de errores de escritura pues el predictor se encuentra fijo en la función calcRsq_pred1(). Ahora, dado que tenemos una función que calcula el valor R-cuadrado entre un predictor fijo y cualquier variable respuesta que se proporcione, podemos usar un funcional como apply() para calcular la relación entre el predictor y el conjunto de variables respuesta.

apply(resp, 2, calcRsq_pred1)

##       resp1       resp2       resp3       resp4 
## 0.006369369 0.012977823 0.006369369 0.038727184

Podríamos complementar aún más nuestro beneficio utilizando sapply(), ahora calculemos cada posible combinación (preditor-respuesta) en un solo paso:

sapply(seq(ncol(pred)), function(i) {
  f <- calcRsq(pred[, i])
  apply(resp, 2, f)
})

##              [,1]        [,2]        [,3]        [,4]
## resp1 0.006369369 1.000000000 0.006326898 1.000000000
## resp2 0.012977823 0.012414970 0.006192994 0.012414970
## resp3 0.006369369 1.000000000 0.006326898 1.000000000
## resp4 0.038727184 0.002312083 0.007719519 0.002312083

Sintetizando:

1. iterar sobre las columnas de pred - seq(ncol(pred)),
2. definir una función f que setea el closure para usar la columna de la iteración actual; f <- calcRsq(pred[, i]), y
3. aplicar esta función f a todas las columnas de variables respuesta - apply(resp, 2, f).

Se ha evidenciado que la combinación de funcionales y closures es una forma poderosa, flexible y elegante de generalizar cálculos computacionales. Abajo un ejemplo adaptado usando data frames:

df1 <- data.frame(diamonds[, c(1, 5, 6)])
df2 <- data.frame(diamonds[, 7:10])

sapply(seq(ncol(df1)), function(i) {
  f <- calcRsq(df1[, i])
  apply(df2, 2, f)
})

##            [,1]         [,2]       [,3]
## price 0.8493305 0.0001133672 0.01616303
## x     0.9508088 0.0006395460 0.03815939
## y     0.9057751 0.0008608750 0.03376779
## z     0.9089475 0.0090105434 0.02277947

2.3 Librería dplyr

El paquete dplyr de R es parte del framework tidyverse de R. Este contiene un conjunto de herramientas (funciones) sumamente intuitivas y poderosas para una rápida y fácil manipulación y procesamiento de los datos. Las posibilidades de dplyr son muy extensas, pero abordaremos las más importantes aquí.

The diamonds dataset

En esta sección usaremos el dataset diamonds, el cual es parte del paquete ggplot2. Si no ha trabajado con estos datos anteriormente, se puede revisar su estructura usando ?diamonds.

Nota: diamonds no es un data.frame estándar de R (solía serlo), pero es actualmente un objeto de la clase tbl_df.

library(ggplot2)
class(diamonds)

## [1] "tbl_df"     "tbl"        "data.frame"

La ventaja de este tipo de objeto en R es que su función print() sintentiza varias funciones como head(), tail(), o str().

diamonds

## # A tibble: 53,940 x 10
##    carat       cut color clarity depth table price     x     y     z
##    <dbl>     <ord> <ord>   <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
##  1  0.23     Ideal     E     SI2  61.5    55   326  3.95  3.98  2.43
##  2  0.21   Premium     E     SI1  59.8    61   326  3.89  3.84  2.31
##  3  0.23      Good     E     VS1  56.9    65   327  4.05  4.07  2.31
##  4  0.29   Premium     I     VS2  62.4    58   334  4.20  4.23  2.63
##  5  0.31      Good     J     SI2  63.3    58   335  4.34  4.35  2.75
##  6  0.24 Very Good     J    VVS2  62.8    57   336  3.94  3.96  2.48
##  7  0.24 Very Good     I    VVS1  62.3    57   336  3.95  3.98  2.47
##  8  0.26 Very Good     H     SI1  61.9    55   337  4.07  4.11  2.53
##  9  0.22      Fair     E     VS2  65.1    61   337  3.87  3.78  2.49
## 10  0.23 Very Good     H     VS1  59.4    61   338  4.00  4.05  2.39
## # ... with 53,930 more rows

2.3.1 Summarizing data

Las funciones que cubriremos son:

• filter(),
• select(),
• arrange(),
• mutate(),
• summarise(), y
• group_by(),

estas serán comparadas con las versiones equivalentes en R estándar.

Obteniendo subconjunto de datos usando filter()

Así como las opciones básicas de R para obtener subconjuntos de datos a través de expresiones condicionales como el uso de corchetees doblesdf[,], filter() crear un subconjunto de datos basado en algún criterio definido por el usuario.

Supongamos que se desea crear un subconjunto de diamantes diamonds manteniendo todos aquellos de color D,E o F con un corte de calidad (cut quality) Premium’ or ‘Ideal’ y un peso de más de 3 carat.

Una forma estándar muy básica sería:

diamonds[diamonds$carat > 3 & 
           diamonds$cut %in% c("Premium", "Ideal") &
           diamonds$color %in% c("D", "E", "F"), ]

Usando filter() notemos que no se requiere repetir el nombre del data frame:

library(dplyr)

## 
## Attaching package: 'dplyr'

## The following objects are masked from 'package:stats':
## 
##     filter, lag

## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union

filter(diamonds, carat > 3 &
         cut %in% c("Premium", "Ideal") &
         color %in% c("D", "E", "F"))

## # A tibble: 2 x 10
##   carat     cut color clarity depth table price     x     y     z
##   <dbl>   <ord> <ord>   <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
## 1  3.01 Premium     F      I1  62.2    56  9925  9.24  9.13  5.73
## 2  3.05 Premium     E      I1  60.9    58 10453  9.26  9.25  5.66

Seleccinando columnas usando select()

dplyr::select(diamonds, carat, cut, color, clarity)

## # A tibble: 53,940 x 4
##    carat       cut color clarity
##    <dbl>     <ord> <ord>   <ord>
##  1  0.23     Ideal     E     SI2
##  2  0.21   Premium     E     SI1
##  3  0.23      Good     E     VS1
##  4  0.29   Premium     I     VS2
##  5  0.31      Good     J     SI2
##  6  0.24 Very Good     J    VVS2
##  7  0.24 Very Good     I    VVS1
##  8  0.26 Very Good     H     SI1
##  9  0.22      Fair     E     VS2
## 10  0.23 Very Good     H     VS1
## # ... with 53,930 more rows

Nótese que tanto el uso de c() para combinar los nombres de varias columnas como el uso de corchetes dobles se vuelve obsoleto. Además es posible omitir el criterio de conteo de columnas (2:5) y expresar la selección de columnas contiguas a través de los nombres.

dplyr::select(diamonds, carat:clarity, price)

## # A tibble: 53,940 x 5
##    carat       cut color clarity price
##    <dbl>     <ord> <ord>   <ord> <int>
##  1  0.23     Ideal     E     SI2   326
##  2  0.21   Premium     E     SI1   326
##  3  0.23      Good     E     VS1   327
##  4  0.29   Premium     I     VS2   334
##  5  0.31      Good     J     SI2   335
##  6  0.24 Very Good     J    VVS2   336
##  7  0.24 Very Good     I    VVS1   336
##  8  0.26 Very Good     H     SI1   337
##  9  0.22      Fair     E     VS2   337
## 10  0.23 Very Good     H     VS1   338
## # ... with 53,930 more rows

Note: otras funciones útiles para definir el criterio de selección: starts_with(), ends_with(), matches() and contains().

Pipelining

Ahora, supongamos que se desea seleccionar algunas columnas a partir de un subconjunto de datos creado anteriormente. Normalmente usaríamos dos pasos con resultados intermedios innecesarios:

## first, create subset
diamonds_sub <- filter(diamonds, carat > 3 &
                         cut %in% c("Premium", "Ideal") &
                         color %in% c("D", "E", "F"))

## second, select columns
select(diamonds_sub, carat:clarity, price)

o quizas funciones anidadas que usualmente son difíciles de interpretar:

## all-in-one nested solution
select(
  filter(diamonds, carat > 3 &
           cut %in% c("Premium", "Ideal") &
           color %in% c("D", "E", "F")), 
  carat:clarity, price
)

dplyr introduce el operador %>% el cual fue creado para interconectar los pasos de procesamiento en los datos, eliminando así el uso de variables intermedias o funciones anidadas como se ilustró anteriormente. Podemos pensar en %>% como una traducción de “entonces” o “luego” que conecta dos partes de una oración:

diamonds %>%
  filter(carat > 3 &
           cut %in% c("Premium", "Ideal") &
           color %in% c("D", "E", "F")) %>%
  dplyr::select(carat:clarity, price)

## # A tibble: 2 x 5
##   carat     cut color clarity price
##   <dbl>   <ord> <ord>   <ord> <int>
## 1  3.01 Premium     F      I1  9925
## 2  3.05 Premium     E      I1 10453

Este encadenamiento se vuelve aún más útil caundo se efectúan múltiples operaciones a la vez, reduciendo el código y haciéndolo fácil de leer e interpretar. La analogía es la lectura de la página de un libro, que se efectúa de arriba-abajo e izquierda-derecha.

Reordenar filas usando arrange()

arrange() facilita la rapidez en el reordenamiento de filas basada en criterios multi-columna.

Asumamos un ejemplo con nuestro data set diamonds. Se quiere obtener un listado de datos referentes a los atributos de color, precio y carat (color, price, carat) ordenados en base a los siguientes criterios.

1. De acuerdo al color, con el mejor al inicio de la lista (color D)
2. A partir de lo anterior, es decir sobre diamantes de igual color, ordenarlos desde el menor precio y
3. Finalmente de cada conjunto de color y precio iguales, se desea ordenar sus pesos de manera descendente.

La forma trivial:

diamonds_sub <- diamonds[, c("color", "price", "carat")]
diamonds_carat <- diamonds_sub[order(diamonds_sub$carat, decreasing = TRUE), ]
diamonds_carat[order(diamonds_carat$color, diamonds_carat$price), ]

Usando la librería dplyr:

diamonds %>%
  dplyr::select(color, price, carat) %>%
  arrange(color, price, desc(carat))

## # A tibble: 53,940 x 3
##    color price carat
##    <ord> <int> <dbl>
##  1     D   357  0.23
##  2     D   357  0.23
##  3     D   361  0.32
##  4     D   362  0.23
##  5     D   367  0.24
##  6     D   367  0.20
##  7     D   367  0.20
##  8     D   367  0.20
##  9     D   373  0.24
## 10     D   373  0.23
## # ... with 53,930 more rows

Añadir nuevas columnas usando mutate()

mutate() permite añadir nuevas variables a un data frame existente. Además tiene la ventaja de poder utilizar las columnas (variables) recién creadas, así:

diamonds %>%
  dplyr::select(color, carat, price) %>%
  mutate(ppc = price / carat, 
         ppc_rnd = round(ppc, 2))

## # A tibble: 53,940 x 5
##    color carat price      ppc ppc_rnd
##    <ord> <dbl> <int>    <dbl>   <dbl>
##  1     E  0.23   326 1417.391 1417.39
##  2     E  0.21   326 1552.381 1552.38
##  3     E  0.23   327 1421.739 1421.74
##  4     I  0.29   334 1151.724 1151.72
##  5     J  0.31   335 1080.645 1080.65
##  6     J  0.24   336 1400.000 1400.00
##  7     I  0.24   336 1400.000 1400.00
##  8     H  0.26   337 1296.154 1296.15
##  9     E  0.22   337 1531.818 1531.82
## 10     H  0.23   338 1469.565 1469.57
## # ... with 53,930 more rows

Resumir valores usando group_by() y summarise()

Asumamos que se desea calcular el mínimo, media y máximo precio por cada color de diamante. Usando la versión muy conocida de R estándar:

aggregate(diamonds$price, by = list(diamonds$color), FUN = function(x) {
  c(MIN = min(x), MEAN = mean(x), MAX = max(x))
})

Ahora, usando la solución de la función group_by, la cual es sumamente útil para trabajar sobre subconjuntos de datos:

diamonds %>% 
  group_by(color) %>%
  summarise(MIN = min(price), MEAN = mean(price), MAX = max(price))

## # A tibble: 7 x 4
##   color   MIN     MEAN   MAX
##   <ord> <dbl>    <dbl> <dbl>
## 1     D   357 3169.954 18693
## 2     E   326 3076.752 18731
## 3     F   342 3724.886 18791
## 4     G   354 3999.136 18818
## 5     H   337 4486.669 18803
## 6     I   334 5091.875 18823
## 7     J   335 5323.818 18710

2.4 Profiling y Benchmarking

El objetivo de esta sección es aplicar profiling y timing tools (herramientas de monitoreo del tiempo) para optimizar código R.

Cuando nuestras funciones personalizadas serán usadas repetidamente, a menudo vale la pena identificar secciones de código que tardan mucho tiempo en completarse y por lo tanto ralentizan la respuesta. Así, al identificar las secciones de código problemáticas se podrá mejorarlas y ejecutar el procesamiento más rápidamente.

En esta sección introduciremos las bases de profiling de código R usando funciones de dos paquetes: microbenchmark y profvis.

El paquete profvis es relativamente nuevo y requiere versiones actualizadas de R y RStudio.

2.4.1 microbenchmark

El paquete microbenchmark es útil para ejecutar secciones pequeñas de código y evaluar su rendimiento, así como comparar la velocidad de varias funciones que tienen el mismo objetivo.

La función del mismo nombre de este paquete ejecuta el código múltiples veces (100 por defecto) y provee un resumen de estadísticas del tiempo utilizado para ejecutar el código.

La ventaja de este paquete es que toma en cuenta el tiempo invertido en el procesamiento de la función de microbenchmark por sí misma y de esta manera utiliza iteraciones de “warm-up” antes de ejecutar las iteraciones para el procesamiento estadístico.

Se puede incluir múltiples líneas de código dentro de una única llamada de microbenchmark. Sin embargo, para obtener benchmarks independientes de cada línea de código se debe separarlas con una coma:

library(microbenchmark)
microbenchmark(a <- rnorm(1000), 
               b <- mean(rnorm(1000)))

Ahora trabajemos en un ejemplo donde vamos a comparar dos funciones que pretenden obtener los mismo resultados. Supongamos que se necesita una función que puede identificar los días que cumplen con dos condiciones: (a) la temperatura iguala o excede un umbral de temperatura (e.g., 25 grados centígrados) y (b) la temperatura iguala o excede la temperatura más alta registrada antes de ese día.

Los datos de entrada lucen como el data frame abajo que incluye una columna denominada “temp” que indica la temperatura media diaria registrada:

date	temp
2015-07-01	26.5
2015-07-02	27.2
2015-07-03	28.0
2015-07-04	26.9
2015-07-05	27.5
2015-07-06	25.9
2015-07-07	28.0
2015-07-08	28.2

y el data frame de salida se espera tenga una columna adicional de datos binarios denominda “record_temp” indicando si las dos condiciones se han cumplido:

date	temp	record_temp
2015-07-01	26.5	TRUE
2015-07-02	27.2	TRUE
2015-07-03	28.0	TRUE
2015-07-04	26.9	FALSE
2015-07-05	27.5	FALSE
2015-07-06	25.9	FALSE
2015-07-07	28.0	TRUE
2015-07-08	28.2	TRUE

Abajo se plantean dos ejemplos de funciones para este problema.

# Function that uses a loop 
find_records_1 <- function(datafr, threshold){
  highest_temp <- c()
  record_temp <- c()
  for(i in 1:nrow(datafr)){
    highest_temp <- max(highest_temp, datafr$temp[i])
    record_temp[i] <- datafr$temp[i] >= threshold & 
      datafr$temp[i] >= highest_temp
  }
  datafr <- cbind(datafr, record_temp)
  return(datafr)
}

# Function that uses tidyverse functions
find_records_2 <- function(datafr, threshold){
  datafr <- datafr %>%
    mutate_(over_threshold = ~ temp >= threshold,
            cummax_temp = ~ temp == cummax(temp),
            record_temp = ~ over_threshold & cummax_temp) %>%
    select_(.dots = c("-over_threshold", "-cummax_temp"))
  return(as.data.frame(datafr))
}

Si se aplican ambas funciones al los datos de ejemplo, los resultados son iguales:

example_data <- data_frame(date = c("2015-07-01", "2015-07-02",
                                    "2015-07-03", "2015-07-04",
                                    "2015-07-05", "2015-07-06",
                                    "2015-07-07", "2015-07-08"),
                           temp = c(26.5, 27.2, 28.0, 26.9, 
                                    27.5, 25.9, 28.0, 28.2))

(test_1 <- find_records_1(example_data, 25))

##         date temp record_temp
## 1 2015-07-01 26.5        TRUE
## 2 2015-07-02 27.2        TRUE
## 3 2015-07-03 28.0        TRUE
## 4 2015-07-04 26.9       FALSE
## 5 2015-07-05 27.5       FALSE
## 6 2015-07-06 25.9       FALSE
## 7 2015-07-07 28.0        TRUE
## 8 2015-07-08 28.2        TRUE

(test_2 <- find_records_2(example_data, 25))

##         date temp record_temp
## 1 2015-07-01 26.5        TRUE
## 2 2015-07-02 27.2        TRUE
## 3 2015-07-03 28.0        TRUE
## 4 2015-07-04 26.9       FALSE
## 5 2015-07-05 27.5       FALSE
## 6 2015-07-06 25.9       FALSE
## 7 2015-07-07 28.0        TRUE
## 8 2015-07-08 28.2        TRUE

all.equal(test_1, test_2)

## [1] TRUE

El rendimiento de las dos funciones se puede comparar usando microbenchmark:

library(microbenchmark)
record_temp_perf <- microbenchmark(find_records_1(example_data, 25), 
                                   find_records_2(example_data, 25))
record_temp_perf

## Unit: milliseconds
##                              expr       min        lq      mean    median
##  find_records_1(example_data, 25)  1.672851  1.873401  2.296974  2.051274
##  find_records_2(example_data, 25) 11.510512 13.977765 15.479439 14.792289
##         uq       max neval
##   2.618441  4.614763   100
##  16.541562 27.514042   100

Y ahora si comparamos el rendimiento en un conjunto de datos más extenso como chicagoNMMAPS de la librería dlnm que incluye temperatura de 15 años en Chicago.

library(dlnm)

## This is dlnm 2.3.4. For details: help(dlnm) and vignette('dlnmOverview').

data("chicagoNMMAPS")

record_temp_perf_2 <- microbenchmark(find_records_1(chicagoNMMAPS, 25), 
                                     find_records_2(chicagoNMMAPS, 25))
record_temp_perf_2

## Unit: milliseconds
##                               expr       min        lq      mean    median
##  find_records_1(chicagoNMMAPS, 25) 189.35671 196.96203 206.67910 202.44834
##  find_records_2(chicagoNMMAPS, 25)  12.97695  13.56571  14.53147  14.00789
##         uq       max neval
##  208.66957 341.78832   100
##   14.73603  20.82147   100

Incluso podemos graficar los resultados:

library(ggplot2)
# For small example data
autoplot(record_temp_perf)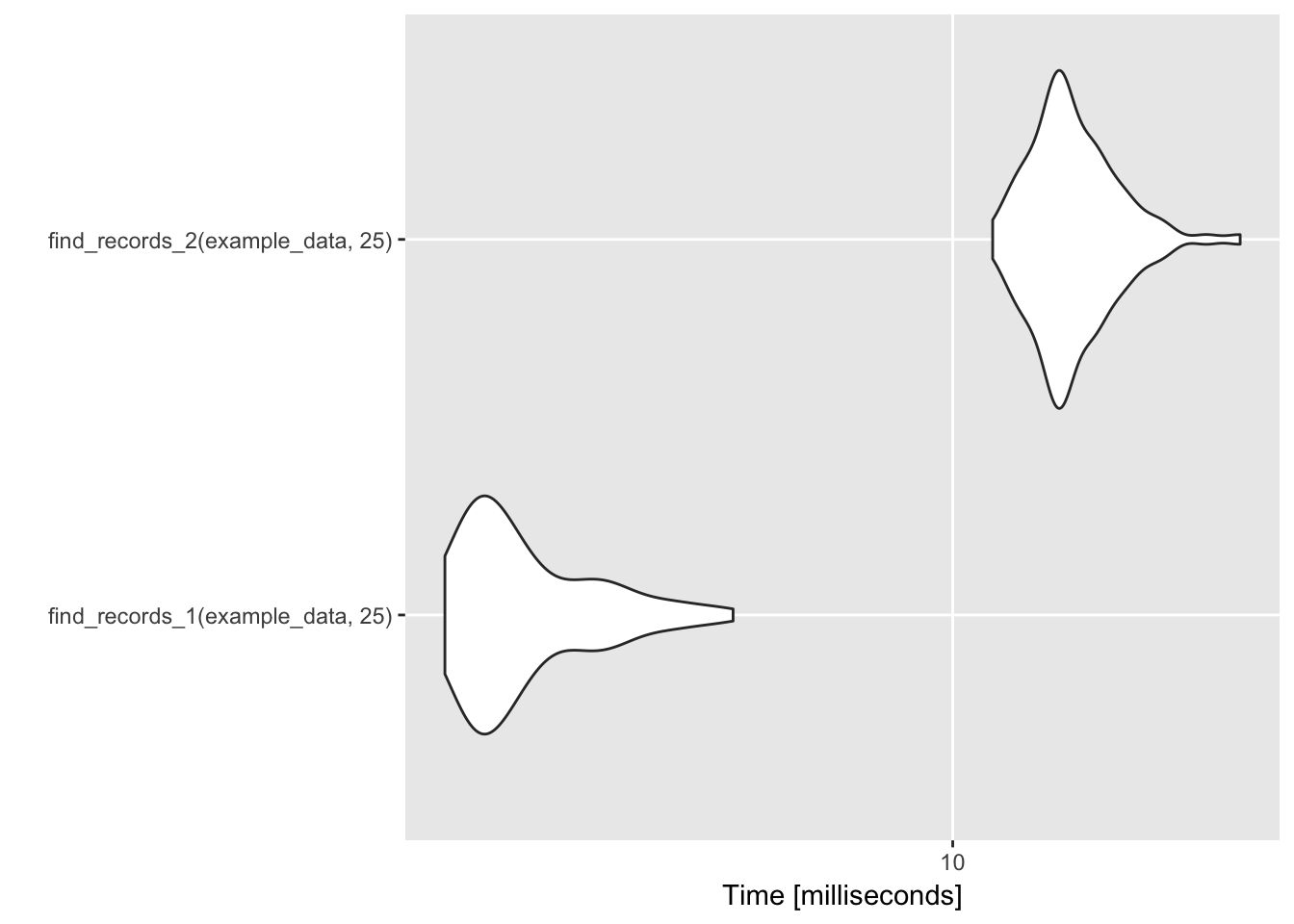

# For larger data set
autoplot(record_temp_perf_2)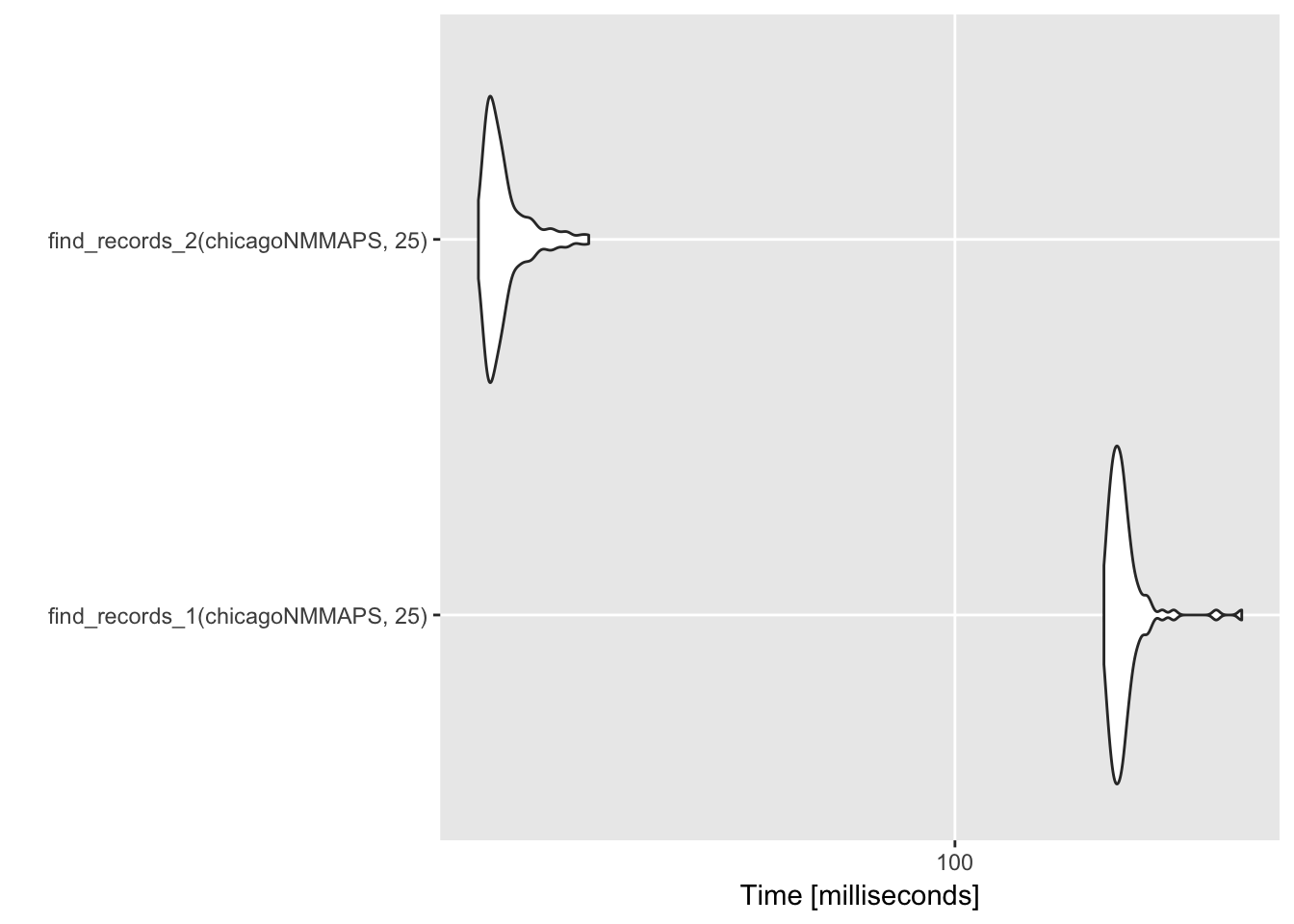

2.4.2 profvis

Una vez que se ha identificado el código cuya ejecución es más lenta, el siguiente paso es comprender que partes del código están causando los cuellos de botella.

La función profvis del paquete del mismo nombre es la herramienta adecuada para esto la cual usa la función RProf base de R y visualiza un entorno interactivo de navegación.

El profiling se efectúa escribiendo los resultados de la pila de llamadas (sentencias) cada 10 milisegundos.

Para usar esta herramienta, únicamente incluya el código en llaves en el caso de tener varias sentencias. Probemos a identificar cual fue el problema con la función find_records_1, para ejecutar el profiling:

library(profvis)
library(dlnm)
datafr <- chicagoNMMAPS
threshold <- 25

profvis({
  highest_temp <- c()
  record_temp <- c()
  for(i in 1:nrow(datafr)){
    highest_temp <- max(highest_temp, datafr$temp[i])
    record_temp[i] <- datafr$temp[i] >= threshold & 
      datafr$temp[i] >= highest_temp
  }
  datafr <- cbind(datafr, record_temp)
})

La salida de profvis proporciona dos opciones de visualización, “Flame Graph” o “Data”.

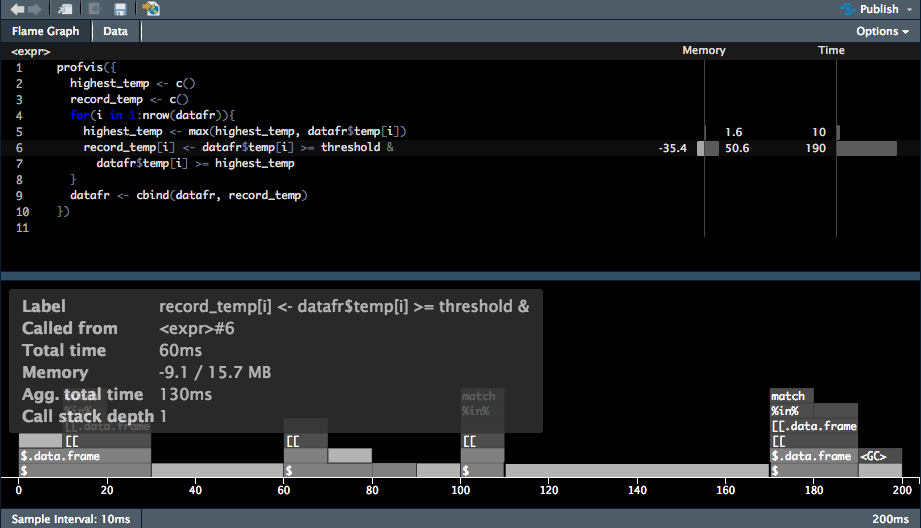
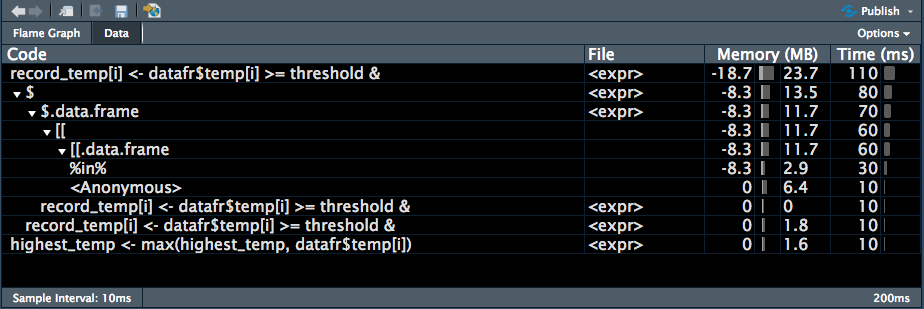
Es posible usar el agumento interval para personalizar el intervalo de muestreo (interval = 0.01 -> 10 milisegundos). Se sugiere evitar el uso de periodos de intervalo muy cortos (e.g., menores a 5 milisegundos). Esto puede provocar resultados no precisos. Incluso si el profiling corresponde a un código muy rápido es mejor utilizar microbenchmark el cual produce resultados más precisos a intervalos más cortos.