Chapter 9 Advanced Regression and Nonparametric Approaches

9.1 Ridge and Lasso Regression

The lm.ridge() and command, in the MASS package, can be used to fit a ridge regression model.

We first need to standardize each quantitative variable. This is done using the scale() command in R.

Train_sc <- Train %>% mutate_if(is.numeric, scale)

9.1.1 Fitting a Ridge Regression Model

We can perform ridge regression using the lm.ridge() command in the MASS package.

library(MASS)

M_Ridge1 <- lm.ridge(data=Train_sc, price~., lambda = 1)
head(M_Ridge1$coef)

##                       id property_typeCondominium       property_typeHouse 
##              0.036320094             -0.013032610             -0.006899487 
##   property_typeTownhouse       property_typeOther    room_typePrivate room 
##             -0.018020782              0.058907892             -0.288091484

9.1.2 Cross Validation with Ridge

We perform cross-validation to determine the optimal value of \(\lambda\). The command 10^seq(-3, 3, length = 100) defines values between 0 and 1000 for \(\lambda\), which will be tested in cross-validation.

This requires the glmnet package.

library(glmnet)

control = trainControl("repeatedcv", number = 5, repeats=5)
l_vals = 10^seq(-3, 3, length = 100)

set.seed(11162020)
AirBnB_ridge <- train(price ~., data = Train_sc, method = "glmnet", trControl=control , 
                      tuneGrid=expand.grid(alpha=0, lambda=l_vals))

Identify the optimal \(\lambda\).

AirBnB_ridge$bestTune$lambda

## [1] 0.4641589

Plot of RMSPE for each value of \(\lambda\).

lambda <- AirBnB_ridge$results$lambda
RMSPE <- AirBnB_ridge$results$RMSE
ggplot(data=data.frame(lambda, RMSPE), aes(x=lambda, y=RMSPE))+
  geom_line() + xlim(c(0,2)) + ylim(c(0.75, 0.82)) + 
  ggtitle("Ridge Regression Cross Validation Results")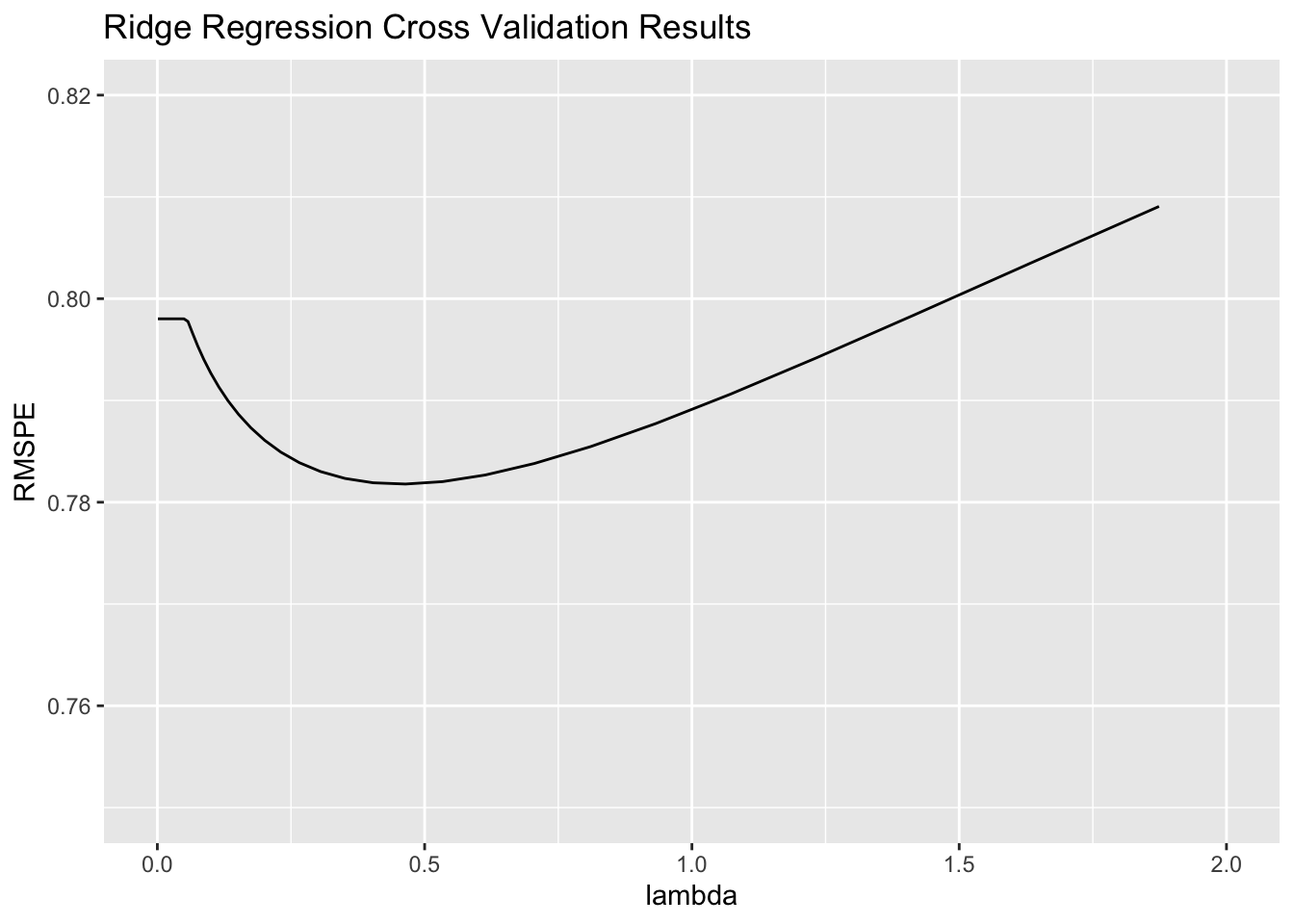

9.1.3 Cross-validation with Lasso Regression

For lasso regression, set alpha=1.

control = trainControl("repeatedcv", number = 5, repeats=5)
l_vals = 10^seq(-3, 3, length = 100)

set.seed(11162020)
AirBnB_lasso <- train(price ~., data = Train_sc, method = "glmnet", trControl=control , 
                      tuneGrid=expand.grid(alpha=1, lambda=l_vals))

Identify the optimal \(\lambda\).

AirBnB_lasso$bestTune$lambda

## [1] 0.04977024

Plot of RMSPE for each value of \(\lambda\).

lambda <- AirBnB_lasso$results$lambda
RMSPE <- AirBnB_lasso$results$RMSE
ggplot(data=data.frame(lambda, RMSPE), aes(x=lambda, y=RMSPE))+geom_line() + 
  xlim(c(0,0.2)) + ylim(c(0.75, 0.82)) + 
  ggtitle("Lasso Regression Cross Validation Results")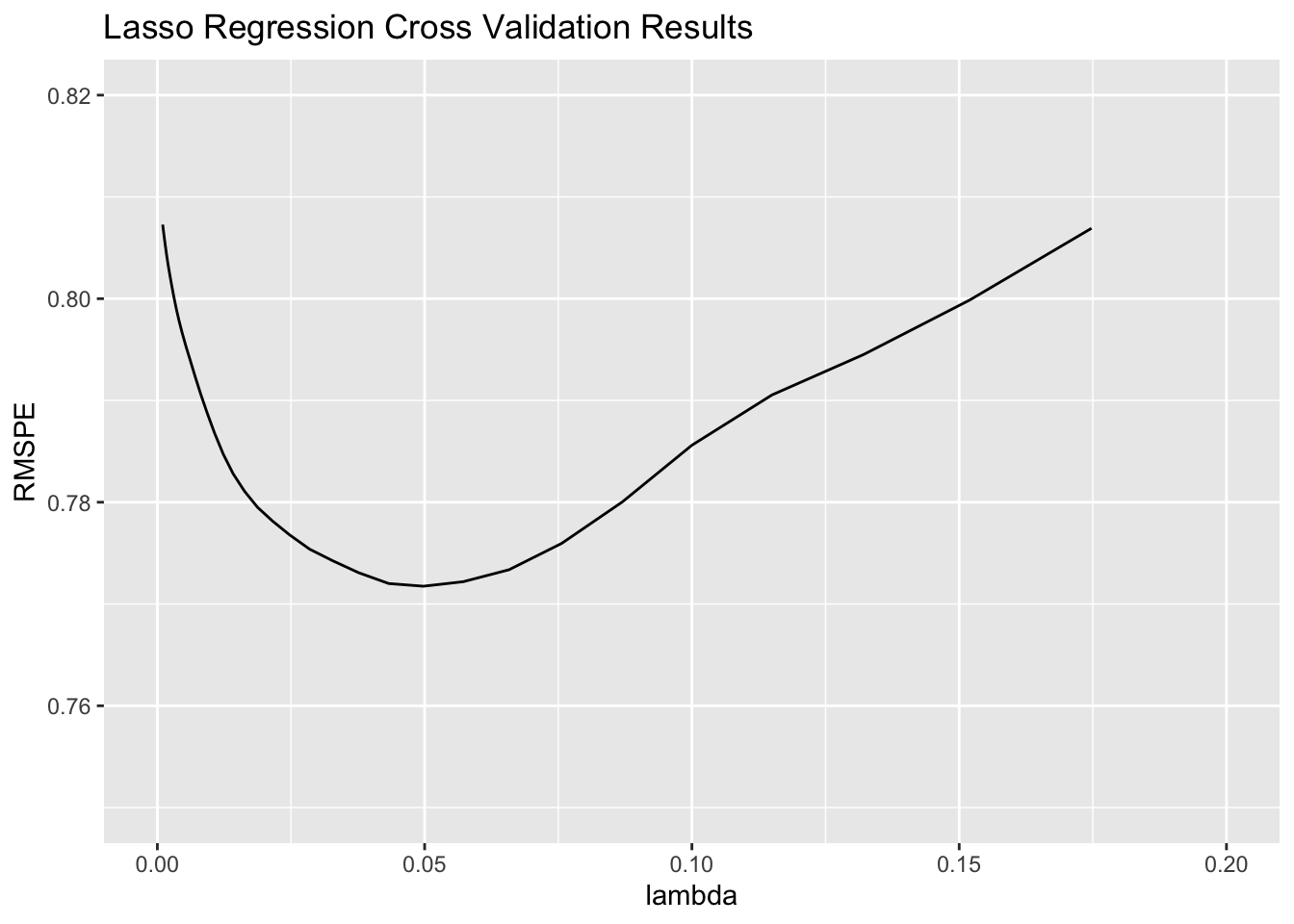

9.2 Decision Trees

We use the rpart package to grow trees, and the rpart.plot package to visualize them.

library(rpart)
library(rpart.plot)

The cp parameter is a complexity parameter that determines the depth of the tree. The smaller the value of cp, the deeper the tree.

9.2.1 Decision Tree Example

tree <- rpart(price~., data=Train, cp=0.02)
rpart.plot(tree, box.palette="RdBu", shadow.col="gray", nn=TRUE, cex=1, extra=1)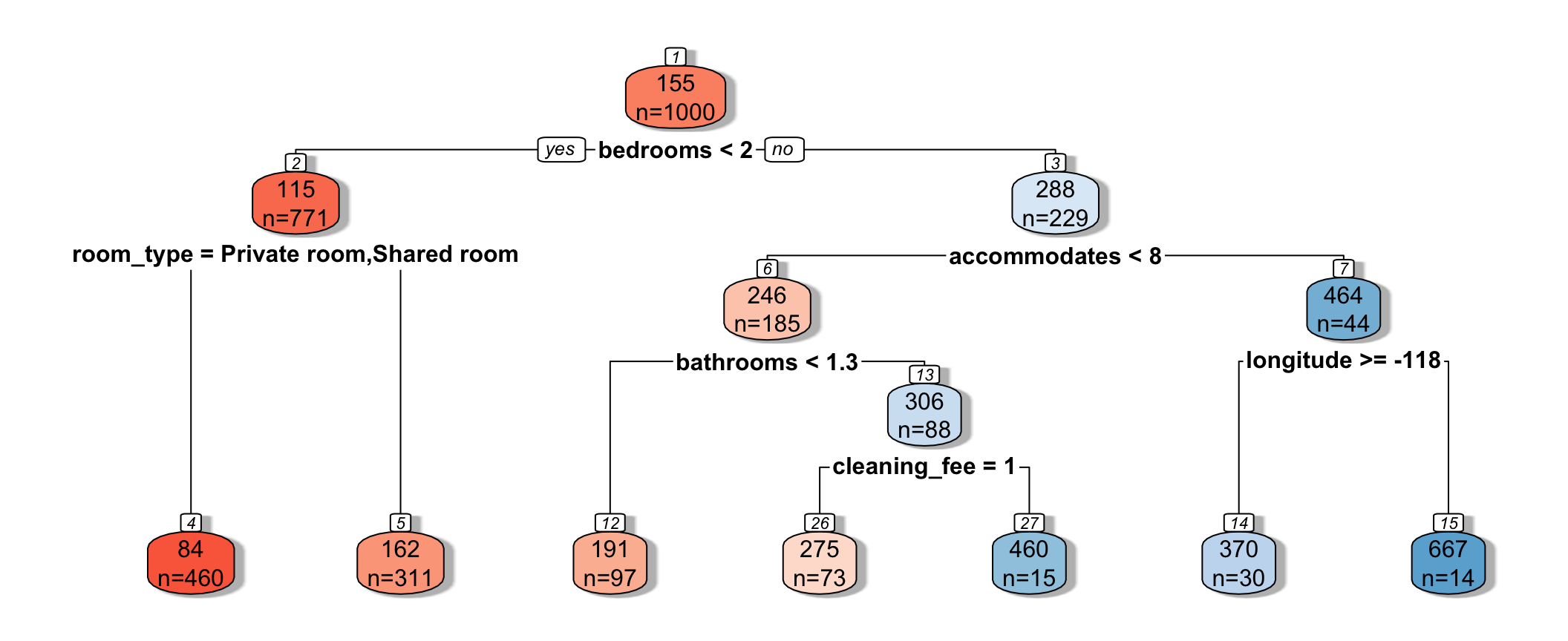

We can use cross-validation to determine the optimal value of cp.

cp_vals = 10^seq(-3, 3, length = 100)
set.seed(11162020)
AirBnB_Tree <- train(data=Train_sc, price ~ .,  method="rpart", trControl=control, 
                     tuneGrid=expand.grid(cp=cp_vals))
AirBnB_Tree$bestTune

##             cp
## 13 0.005336699