Chapter 9 Logic
9.1 To-do list (Week 13, finish before 4/13)
Assignment rubrics: Essay 3.
Watching: lecture by the instructor.
Finish the Inference exercises posted on Blackboard. Note there are two exercises, one for categorical syllogism and the other for hypothetical.
9.2 To-do list (Week 14, finish before 4/20)
- Assignment due: Speech 3 submitted the link of you video clip on Blackboard (you can delete the video after the end of the semester).
9.3 To-do list (Week 15, finish before 4/27)
- Assignment due: Essay 2.
- Assignment due: Essay 3.
9.4 Examples of inference
9.4.1 Categorical Syllogism
- “The chief foundations of all states, new as well as old or composite, are good laws and good arms; and as there cannot be good laws where the state is not well armed, it follows that where they are well armed they have good laws.” [Niccolo Machiavelli, The Prince]
9.4.2 Hypothetical Syllogism
The interview by Lesko.
- If Mueller is fired, then Trump obstructed justice.
- Mueller is not fired.
- Trump did not obstruct justice.
- If Mueller is fired, then Trump obstructed justice.
9.4.3 More examples
Next, a somewhat more difficult example in which the intermediate conclusions are not stated:
Since values are nothing more than our own evaluations of the facts, they are not objective. Knowledge of the facts is based on empirical evidence, and anything based on such evidence is objective. But evaluating facts is different from knowing them.
As unpleasant as the current shortage is, it means we are consuming less. And so in the long run our standard of living will rise. For in order to improve our standard of living, we must save, and in order to save, we must forgo current consumption.
9.5 Immediate Inference
In logic, two propositions are equivalent if the truth of each necessarily implies the truth of the other, and the falsity of each necessarily implies the falsity of the other. Logically equivalent propositions, in other words, must be either both true or both false.
Immediate inference means “the relationship between two propositions that are logically equivalent.” Read more from Philosophy Pages.
9.5.1 Immediate Inference Table
- Watch: The instructor’s explanations 1
- Watch: The instructor’s explanations 2
- Watch: The instructor’s explanations 3
- Watch: The instructor’s explanations 4
First, fill out the following table.
| Standard_form | Converse | Obverse | Contrapositive |
|---|---|---|---|
| All S are P | |||
| No S is P | |||
| Some S are P | |||
| Some S are not P |
- Catergorical proposition: an assertion about the relations among classes
- Content: subject (S) and predicate (P)
- Form: quantity and quality
- Converse: switch S and P
- Obverse: Change quality and replace predicate with complement (add non)
Contrapositive: Complement S and P, then swith
Read more from Philosophy Pages.
9.5.2 Immediate Inference
Cross out cells that are not logically equivalent
| Standard_form | Converse | Obverse | Contrapositive |
|---|---|---|---|
| All S are P | All P are S | No S is non-P | All non-P are non-S |
| No S is P | No P is S | All S are non-P | No non-P is non-S |
| Some S are P | Some P are S | Some S are not non-P | Some non-P are non-S |
| Some S are not P | Some P are not S | Some S are non-P | Some non-P are not non-S |
9.5.3 Venn Diagrams Explanation 1
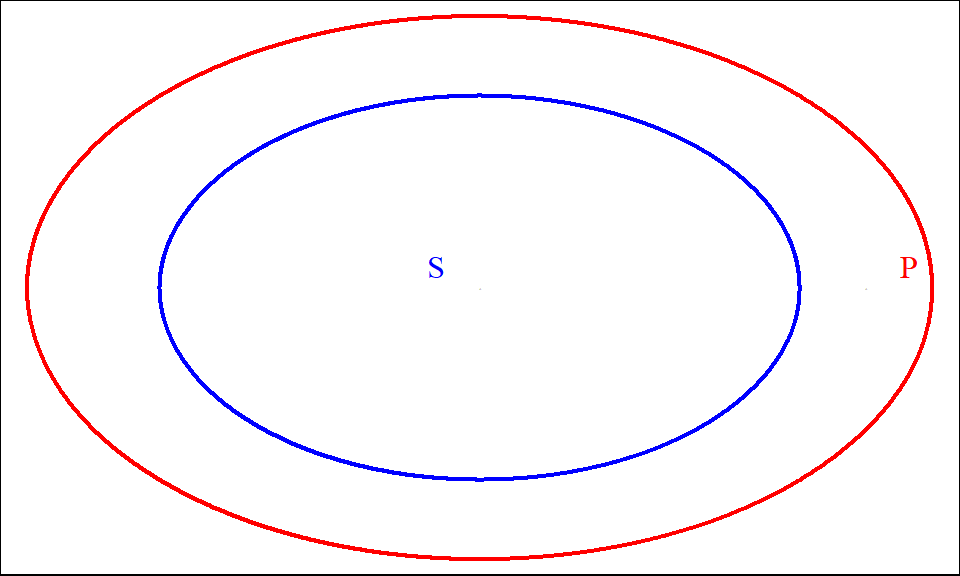
Figure 9.1: All S are P
9.5.4 Venn Diagrams Explanation 2
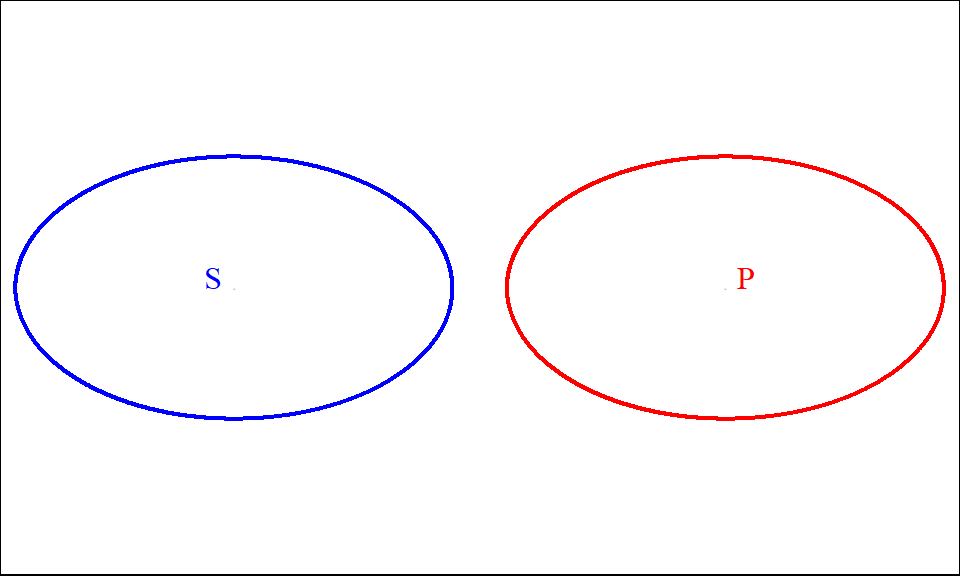
Figure 9.2: No S is P
9.5.5 Venn Diagrams Explanation 3
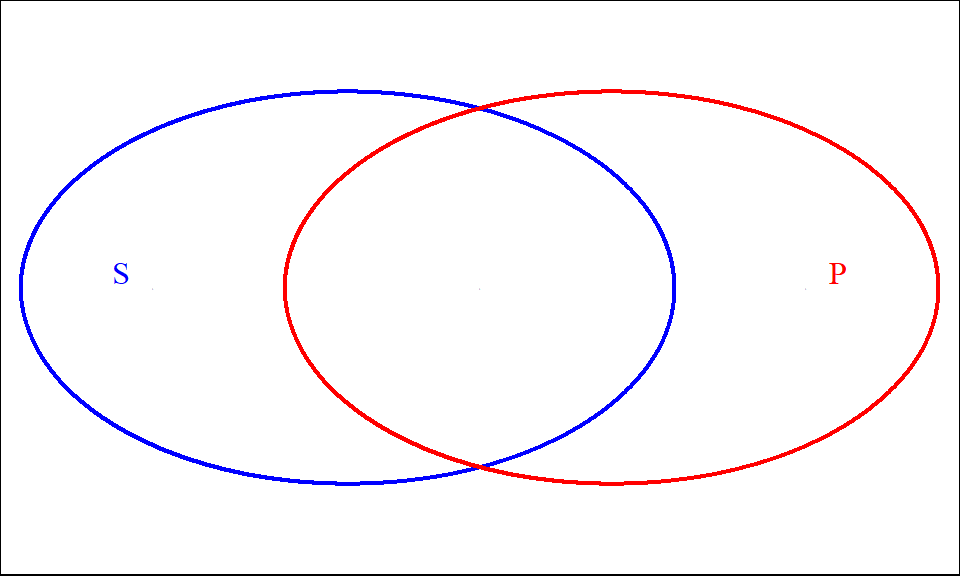
Figure 9.3: Some S are P
9.5.6 Venn Diagrams Explanation 4
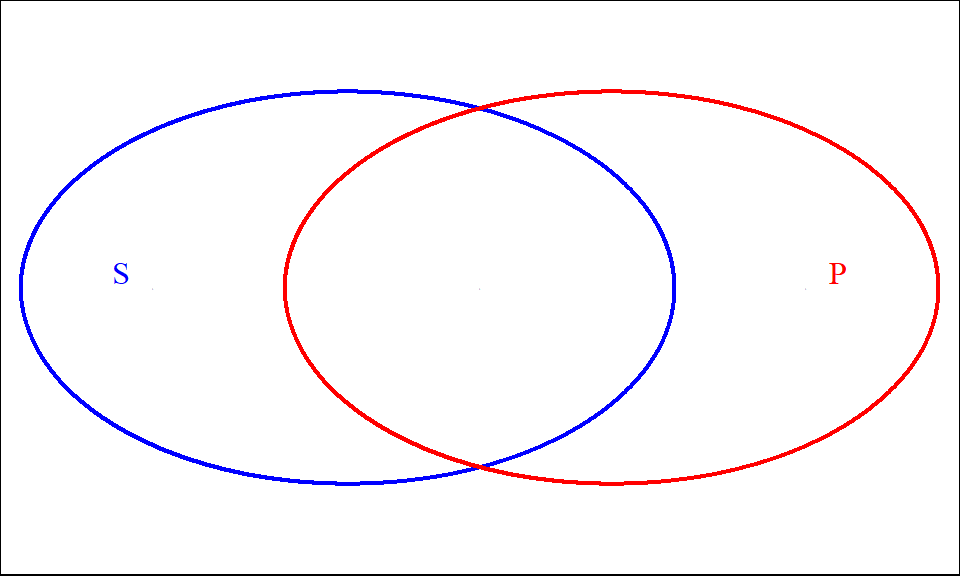
Figure 9.4: Some S are not P
9.5.7 Difficult Cases
Note that we only need to identify cases where one is true and the other is false. Two cells in the above table could be challenging for students, labelled as A and B in the following table.
| Standard_form | Converse | Obverse | Contrapositive |
|---|---|---|---|
| All S are P | |||
| No S is P | |||
| Some S are P | B | ||
| Some S are not P | A |
9.5.8 Some explanation
For cell A, note that when the venn diagram is this:
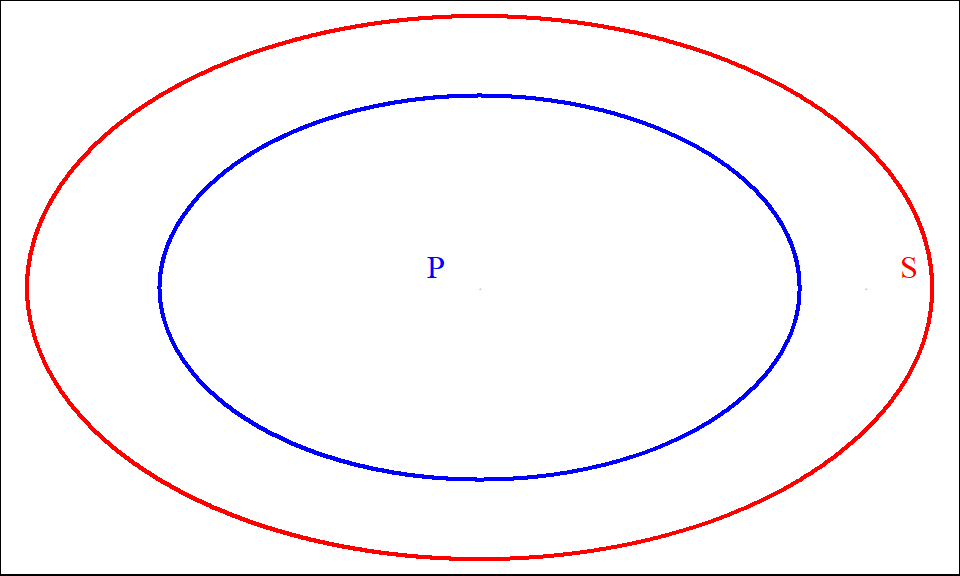
Figure 9.5: All S are P
The standard form is true, while the converse is false.
For cell B, when the venn diagram is this:
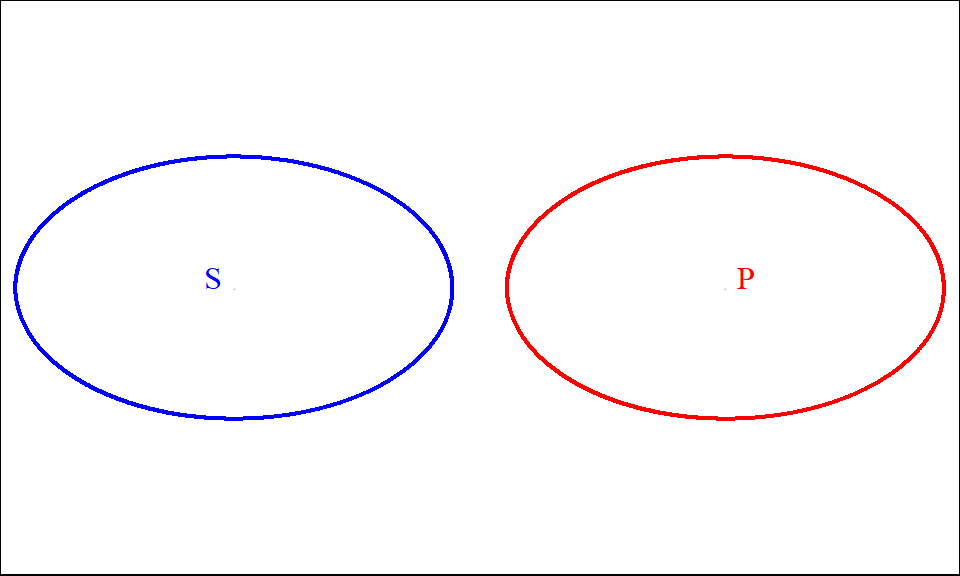
Figure 9.6: No S is P
The standard form is false, while the contrapositive is true.
9.6 Categorical Syllogism
Syllogism: deductive argument with two premises and a conclusion.
Categorical syllogism, both of the premises and the conclusion are categorical propositions.
9.6.1 Some examples
No horned animal is a carnivore.
All moose are horned animals.
No moose is a carnivore.
No privately held company is listed on stock exchanges.
Some privately held companies are large corporations.
Some large corporations are not listed in stock exchanges.
All athletes are people in good physical condition.
All fitness instructors are people in good physical condition.
All fitness instructors are athletes.
No member of the Green Party was elected to Congress.
Some candidates who favor strong environmental regulation are not members of the Green Party.
Some candidates who favor strong environmental regulation were elected to Congress.
9.6.2 Some examples 2
No horned animal is a carnivore. No M is P
All moose are horned animals. All S are M
No moose is a carnivore. No S is P
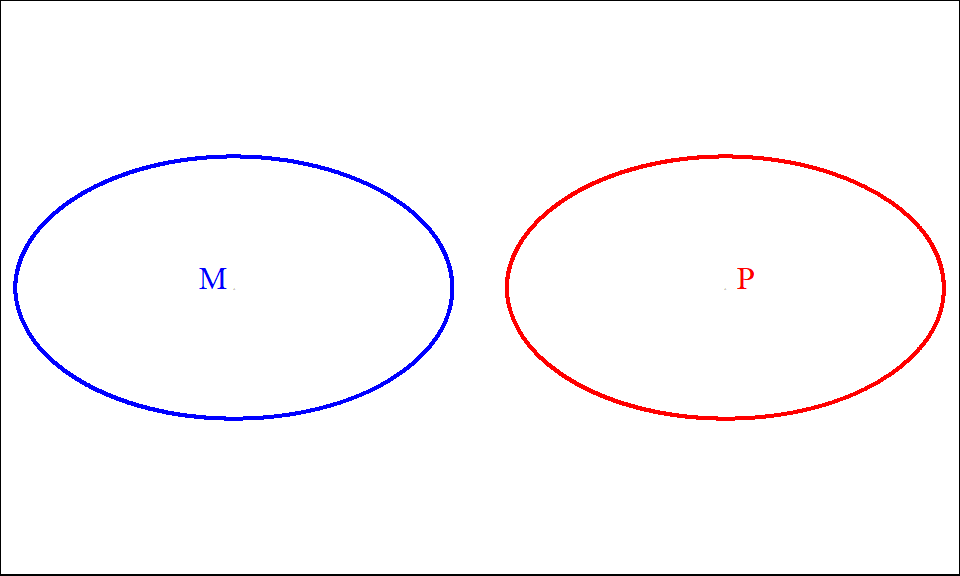
Figure 9.7: No M is P
9.6.3 Additional examples for you to check
No privately held company is listed on stock exchanges. No M is P
Some privately held companies are large corporations. Some M are S
Some large corporations are not listed in stock exchanges. Some S are not P
All athletes are people in good physical condition. All P are M
All fitness instructors are people in good physical condition. All S are M
All fitness instructors are athletes. All S are P
No member of the Green Party was elected to Congress. No M is P
Some candidates who favor strong environmental regulation are not members of the Green Party. Some S are not M
Some candidates who favor strong environmental regulation were elected to Congress. Some S are P
9.7 Hypothetical Syllogisms
First, some definition.
- The “if” component is called the antecedent and the “then” component is the consequent.
9.7.1 if, only if, if and only if
- (consequent) if (antecedent)
(antecedent) only if (consequent)
- A is sufficient for B = If A then B
A is necessary for B = If B then A
Finally,
- p unless q = If not-q, then p
- Without X, q = If X does not exist (occur), then q
9.7.2 Rules of Hypothetical Syllogism
| Valid | Invalid |
|---|---|
| Affirming the antecedent | Affirming the consequent |
| Denying the consequent | Denying the antecedent |
9.7.3 Example 1
- If Mueller is fired, then Trump obstructed justice.
- Mueller is not fired.
- Trump did not obstruct justice.
9.7.4 Example 2
- If Ukraine got the military aid after announcing an investigation into the Bidens, then there is quid pro quo.
- But Ukraine got the aid without announcing an investigation.
- Therefore, there is no quid pro quo.
9.7.5 Example 3
- Without some mechanism of natural selection, there would be no way for new species of organisms to arise—as they have. So clearly there is a mechanism of natural selection.
9.8 Acknowledgement
This section is taken from the Art of Reasoning by David Kelly.
I found this online tutor.