Chapter 3 W4 Class
3.1 Options
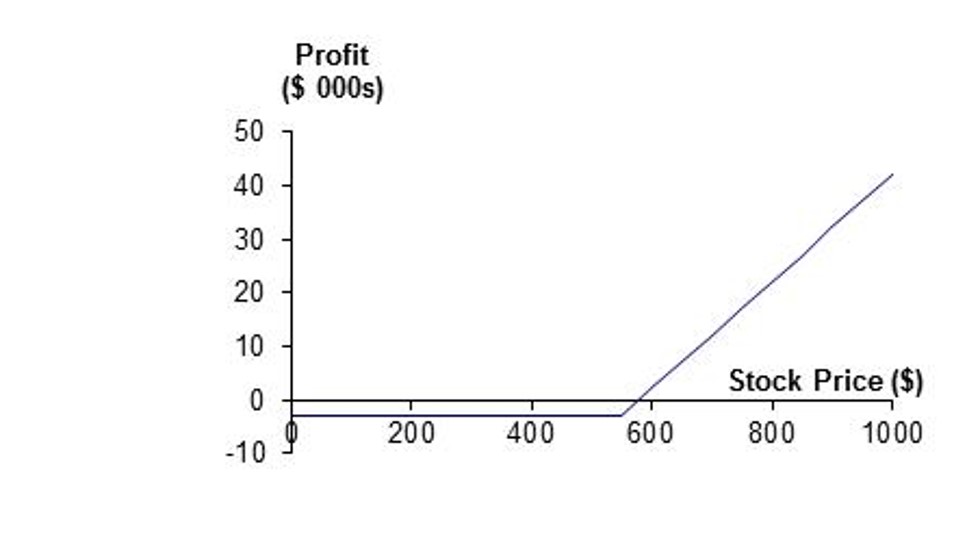
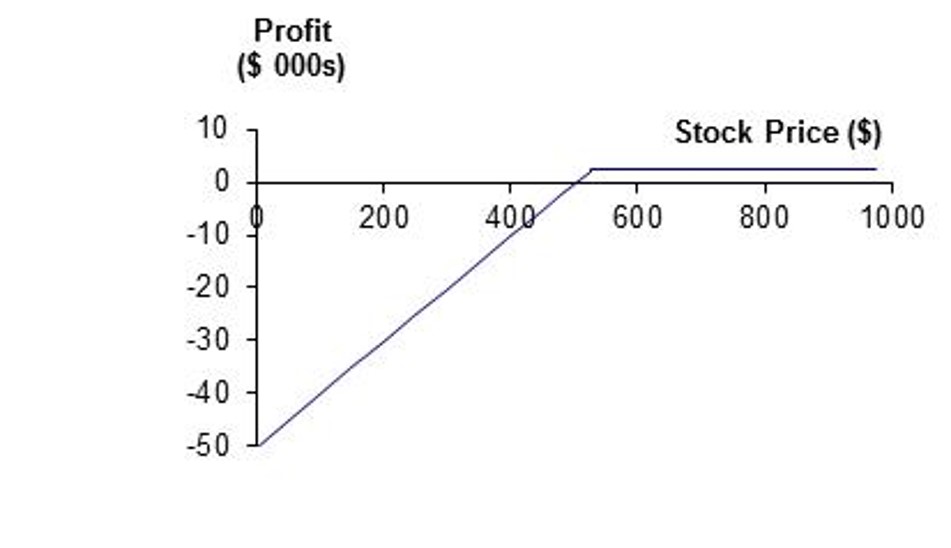
Do you know what kind of option they are?
Answer
First: Long Call; Second: Short Put
Definition
- A call is an option to buy
- A put is an option to sell
- European option: Exercisable only at expiration
- American option: Exercisable at any time
3.1.1 Option positions
- Long Call
- Long Put
- Short Call
- Short Put
3.1.2 Specification of Options
- Expiration Date
- Strike Price X
- E or A
- C or P
3.1.3 Moneyness:
- At-the-money
- In-the-money
- Out-of-the money option
| \(c\): European call option price | \(C\) American call option price |
| \(p\): European put option price | \(P\) American put option price |
| \(S_0\): Stock Price today | \(S_T\) Stock price at option maturity |
| \(K\): Strike price | \(D\) PV of dividends during option’s life |
| \(T\): Life of option | \(r\) risk-free rate for maturity T with cts compounding |
| \(\sigma\): Volatility of stock |
3.1.4 Stock Split
Suppose you own options with a strike price of K to buy (or sell) N shares: - No adjustments are made to the option terms for cash dividends - When there is an n-for-m stock split, - the strike price is reduced to mK/n - the no. of shares that can be bought (or sold) is increased to nN/m - Stock dividends are handled in a manner similar to stock splits
3.1.5 Market Makers
- Most exchanges use market makers to facilitate options trading
- A market maker quotes both bid and ask prices when requested
- The market maker does not know whether the individual requesting the quotes wants to buy or sell ### Margin
- Margin is required when options are sold (Example:A total of 100% of the proceeds of the sale plus 10% of the underlying share price (call) or exercise price (put))
3.1.6 Other information
- Warrants: options that are issued by a corporation or a financial institution
- Employee stock options: Employee stock options are a form of remuneration issued by a company to its executives
3.1.7 Effect of Variables on Option Pricing
| Var | c | p | C | P |
|---|---|---|---|---|
| \[ S_0 \] | + | - | + | - |
| \[ K \] | - | + | - | + |
| \[ T \] | ?? | ?? | + | + |
| \[ \sigma \] | + | + | + | + |
| \[ r \] | + | - | + | - |
| \[ D \] | - | + | - | + |
Explanation:
Keep other things unchanged, a higher S0 will be more likely to pass K, thus it’ll be price higher. Other logics follow
T for European options are murky. Since it’s exercisable only at a certain date, you never know what happens closer or on that date. The story is totally different in American options.
3.1.8 Option Bounds
- An American option is worth at least as much as the corresponding
European option
C>=c; P>=p
| Case | Eur opean call | Eur opean put | Ame rican | Put-call Parity |
|---|---|---|---|---|
| Basic | c>=m ax(So - Xe ^(-r T),0) | p> =max( Xe^( -rT)- So,0) | S0 - X < C - P < S0 - Xe^ (-rT) | c + Xe^(-rT) = p + S0 |
| Discrete Dividend | c ≥ m ax(S0 -D-Xe ^(-r T),0) | p ≥ m ax(D+ Xe^( -rT)- S0,0) | S0 - D - X < C - P < S0 - Xe^( –rT) | c + D + Xe^(-rT) = p + S0 |
| Dividend Yield | c ≥ max( S0e^ (-qT) - Xe^( -rT), 0) | p ≥ max (Xe^ (-rT) – S 0e^( -qT), 0) | - | c+ X e^(-rT)=p + S0e^(-qT) |
| Futures Options | c ≥ m ax((F 0-X)e ^(-r T),0) | p ≥ m ax((X -F0)e ^(-r T),0) | F0e C ≥F0-X and P ≥X-F0 |
c+ X e^(-rT)=p + F0e^(-rT) |