Chapter 2 W3 Class

In this week, we will first have a brief introduction to the course and review some basic derivatives concepts from 1000-level class

2.1 Introduction

2.1.1 Forwards & Futures

Definition

1. A spot contract is an agreement to buy or sell an asset immediately (or within a very short period of time) for a certain price.

2. A forward/futures contract is an agreement to buy or sell an asset at a certain time in the future for a certain price

Terms

long = buy short = sell

Payoff

As you are not buying immediately, there will be a payoff.

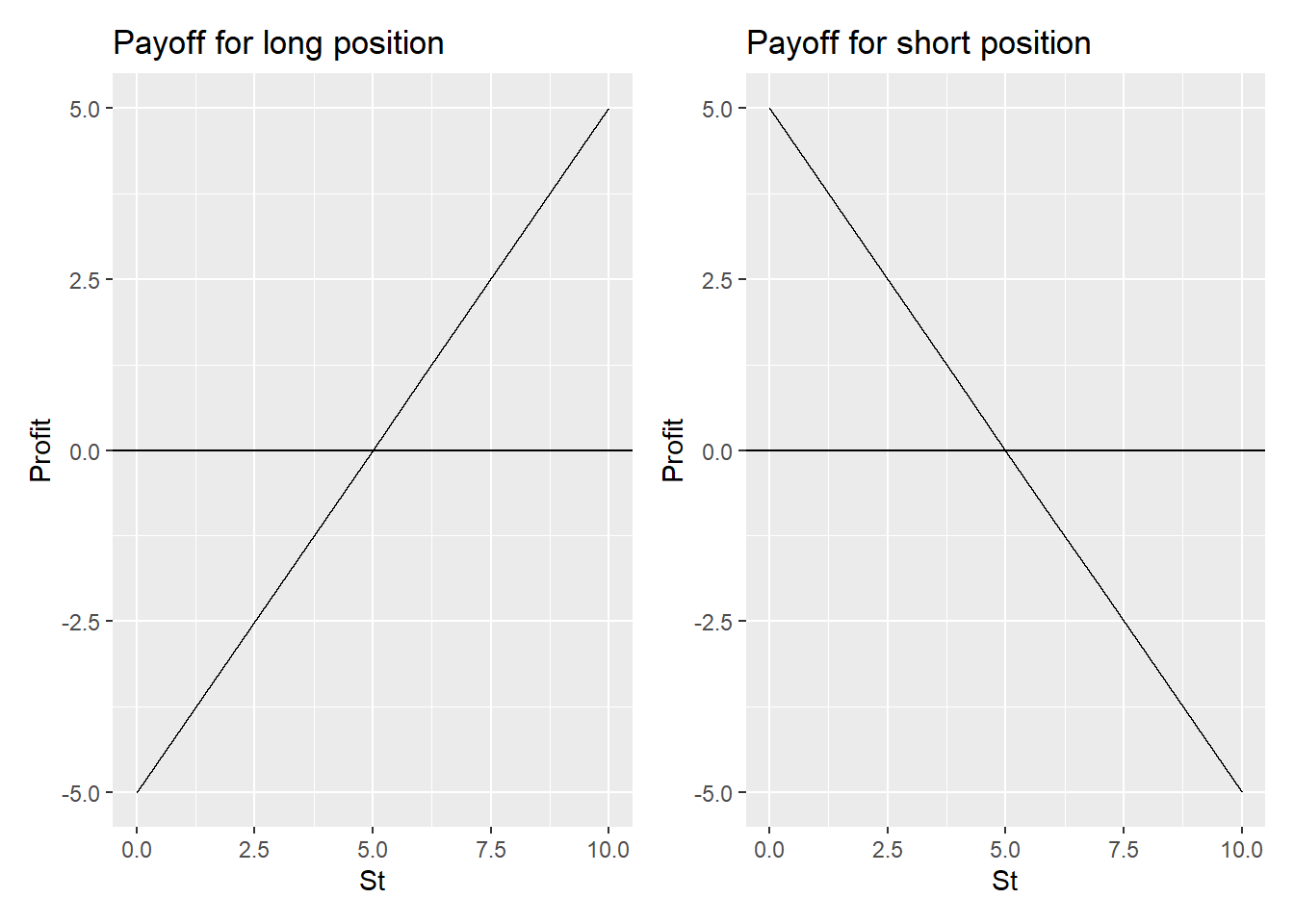
It is January and an investor enters into a futures contract to buy 100 oz of gold @ $1,200 in April. If in April the spot price of gold ends up being $1,215/oz, what is the investor’s profit?

• The investor has a long position, so the payoff is computed by St-F - ($1215 - $1200) x 100 = $1,500

2.1.1.1 Trading Mechanics

• No money changes hands when forward and futures contracts are first negotiated
• The contract is settled at maturity.
• Forward contracts trade in the over-the-counter market. Futures contracts, on the other hand, are exchange-traded instruments.

2.1.1.2 Forwards vs Futures

Forwards	Futures
Private contract between 2 parties	Exchange traded
Non-standard contract	standard contract
1 specified delivery date	Range of delivery dates
settled at maturity	settled daliy
delivery of final cash settlement usually occurs	contract usually closed out prior to maturity

2.1.1.3 Why the difference?

When interest rates are uncertain, they are, in theory, slightly different:

• A strong positive correlation between interest rates and the asset price

• Long position is ‘better off’ with futures

• Futures price is slightly higher than the forward price;

• A strong negative correlation implies the reverse.

Long position case

Interest rate	Asset Price	Reinvest/Finance	Futures Price	Total Gain
increase	increase	+	+	+
decrease	decrease	-	-	-

Detailed explanation

We can get a sense of the nature of the relationship by considering the situation where the price S of the underlying asset is strongly positively correlated with interest rates. When S increases, an investor who holds a long futures position makes an immediate gain because of the daily settlement procedure. The positive correlation indicates that it is likely that interest rates have also increased. The gain will therefore tend to be invested at a higher than average rate of interest. Similarly, when S decreases, the investor will incur an immediate loss. This loss will tend to be financed at a lower than average rate of interest. An investor holding a forward contract rather than a futures contract is not affected in this way by interest rate movements. It follows that a long futures contract will be slightly more attractive than a similar long forward contract. Hence, when S is strongly positively correlated with interest rates, futures prices will tend to be slightly higher than forward prices. When S is strongly negatively correlated with interest rates, a similar argument shows that forward prices will tend to be slightly higher than futures prices

2.1.2 Interest rate coversion

Basic idea: use a simpler way to represent interest rate

$ Amount in t years (Using Annual Nominal Rate, \(r_n\) ) = $ Amount in t years (Using Continuously Compounded Rate, \(r_c\) )

\(P(1+r_n/n)^{nt} = Pe^{r_ct}\) \(r_c = n*ln(1+r_n/n)\)

2.1.3 Hedging Strategies

2.1.3.1 Definition

• A short hedge is a hedge which involves a short position in futures contracts.

  • It is appropriate when the hedger already owns an asset (or will own it at some definite date) and expects to sell it at some time in the future. This allows them to lock in the rice they will receive.

• A long hedge involves taking a long position in futures contracts.

  • It is appropriate when a company knows it will have to purchase a certain asset in the future and wants to lock in the price now.

2.1.3.2 A perfect hedge example

For example, suppose that Company X knows that in six months it has to purchase 20,000 ounces of silver in order to fulfill an order. Assume the current market price for silver is $12 per ounce and the price of a six-month futures contract is $11 per ounce. By purchasing the futures contract, Company X can guarantee a price of $11 per ounce. This reduces the company’s risk because it will be able to close its futures position and buy 20,000 ounces of silver for $11 per ounce in six months at the contract’s expiration date.

But we usually do not have a perfect hedge!

2.1.3.3 Imperfect hedge is common

Main reasons for imperfect hedge

• Assets not matching

• Date not certain

• Contract closed out early

Detailed explanation

• The asset whose price is to be hedged may not be exactly the same as the asset underlying the futures contract;
• The hedger may not be certain of the exact date the asset will be bought or sold; and,
• The hedge may require the futures contract to be closed out before its delivery month.

2.1.3.4 Basis Risk

Definition of Basis

The difference between the spot price of asset to be hedged and the futures price of contract used to hedge. 基差 in Chinese

Basis = Spot price of asset to be hedged - futures price of contract used

Definition of Basis Risk

Arising from the hedger’s uncertainty as to the difference between the spot price and futures price at the expiration of the hedge

Basis Risk with a long hedge

If you hedge the future purchase of an asset by entering into a long futures contract, then cost of asset is \(S_2-(F_2-F_1) = F_1+(S_2-F_2) = F_1+b_2\)

Spot Price at T2 - Gain from Hedging = Futures Price at T1 + Basis at T2

Basis Risk with a short hedge

If you hedge the future sale of an asset by entering into a short futures contract, then the price realised is \(S_2+(F_1-F_2) = F_1+(S_2-F_2) = F_1+b_2\)

Question on Basis Risk

On March 1 a commodity’s spot price is $60 and its August futures price is $59. On July 1 the spot price is $64 and the August futures price is $63.50. A company entered into futures contracts on March 1 to hedge its purchase of the commodity on July 1. It closed out its position on July 1. What is the effective price (after taking account of hedging) paid by the company?

Answer

Answer: $59.50

The user of the commodity takes a long futures position. The gain on the futures is 63.50−59 or $4.50. The effective paid realized is therefore 64−4.50 or $59.50. This can also be calculated as the March 1 futures price (=59) plus the basis on July 1 (=0.50).

2.1.4 Cash Settlement

Let’s say you own an SPX 1360 Strike Call, SPX settles at 1364.59, then owners (with 100 units/contract) receive $459/contract. Basically you don’t receive shares (underlying assets), cash makes is easier.

Let’s think about the delivery of heavy commodity if you don’t want cash settlement.

2.2 Interest rate contracts and swaps

2.2.1 Type of rates

• Treasury rate: Rates on instruments issued by a government in its own currency

• LIBOR (now changed to SOFR*): LIBOR is the rate of interest at which a AA bank can borrow money on an unsecured basis from another bank

• Fed Funds rate: Unsecured interbank overnight rate of interest Allows banks to adjust the cash (i.e., reserves) on deposit with the Federal Reserve at the end of each day The effective fed funds rate is the average rate on brokered transactions The central bank may intervene with its own transactions to raise or lower the rate Similar arrangements in other countries

• Repo rate: Repurchase agreement is an agreement where a financial institution that owns securities agrees to sell them today for X and buy them bank in the future for a slightly higher price, Y The financial institution obtains a loan. The rate of interest is calculated from the difference between X and Y and is known as the repo rate

For more info on Secured Overnight Financing Rate SOFR, please visit https://www.forbes.com/advisor/investing/what-is-libor/#:~:text=Effective%20December%2031%2C%202021%2C%20Libor%20will%20no%20longer,a%20more%20accurate%20and%20more%20secure%20pricing%20benchmark.

2.2.2 Rates related to Bond Pricing

• Zero rate: the The n-year zero-coupon interest rate is the rate of interest earned on an investment that starts today and lasts for n years. (There are no coupon payments)

• (par) yield: The par yield for a certain bond is the coupon rate that causes the bond price to equal its par value (or face value).

• Forward rate: A forward rate is an interest rate which is fixed for a future transaction.(we’ll come back to this later)

• Forward Rate Agreement (FRA): an agreement that a certain rate will apply to a certain principal during a certain future time period.

• Interest rate swaps: Interest rate swaps are an agreement where a floating rate is exchanged for a fixed rate or vice versa. For Example: you have borrowed some money at LIBOR and now want to swap to a fixed rate exposure.

2.2.2.1 Forward Rate

Question on forward rate setting

A company knows it will need to borrow $104,000 for a term of one year in exactly twelve month’s time and wishes to fix the interest rate in advance.

The forward rate can be secured by (based on the yield-curve) 1. Borrowing for 2 years at 5%, and 2. Investing the proceeds for 1 year at 4%

well, how to calculate the fixed forward rate (ie from year 1 to year 2)?

Rate is calculated as CF EOY_2 / CF EOY_1 (CashFlow EndOfYear)

• CF EOY_1 = \(104,000\)
• CF EOY_2 = \(( 104,000/1.04 ) * 1.05^2\)

Therefore the rate is 110,250/104000 = 1.0601

>Look! \(1.0601 = 1.05^2/1.04\)

2.2.2.1.1 Generalizing from the example (Discrete case)

The discrete forward interest rate \(r_{x,y}\) on a security that commences in year x and matures in year y can be found by combining spot rates:

\(r_{x,y} = [(1+r_{0,y})^y /(1+r_{0,x})^x]-1\)

3-year spot is 6% and 2-year spot is 5% then \((1+r_{2,3})^1 = (1.06)^3 / (1.05)^2 = 1.0803 – 1 = 0.0803\).

2.2.2.1.2 Continuous Case

(Only need to remember formula) \(\frac{R_xT_x - R_yT_y}{T_x-T_y}\)

Reference: Old lecture slides

2.2.3 Interest Rate Swap

2.2.3.1 Rule

Remember: A->G->A->S->R

1. Determine the comparative advantage
2. Determine the gains from trade
3. Decide on how to allocate gains
4. Write out strategy and draw diagram
5. Calculate the net result

Example:

This is a typical diagram that two parties want to have

	Fixed	Floating	Wants
A	7%	L+1%	Floating
B	10%	L+2%	Fixed
Difference	3%	1%

1. A: A has comparative advantage in the fixed rate market since 3% >1%, B has this advantage in the floating rate market.

2. G: : we use 3%-1% to get total gains 2%.

3. A: **Assume equal split of gains**Equal split means 1% each. Therefore, A will pay L+1%-1% = LIBOR, B will pay 10%-1%=9%

4. S:

   1. From the external market, Company A borrows at 7%, and Company B borrows at LIBOR+2%;

   2. Company A pays Company B LIBOR+2%;

   3. Company B pays Company A 9% (Floating rate paid all the way across)

   

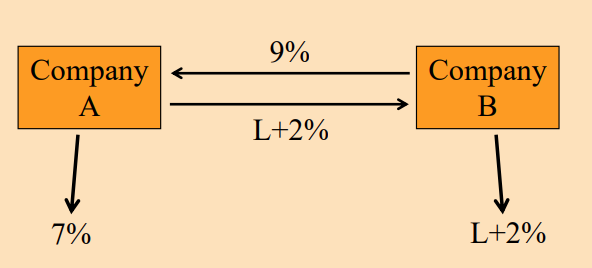
5. R:

   1. Company A: -7% - (LIBOR+2%) + 9% = - LIBOR -> 1% Better Off

   2. Company B: -(LIBOR+2%) + (LIBOR+2%) - 9% = -9% -> 1% Better Off

2.2.3.2 Valuation of IRS

When a swap is first entered into, it has a value of 0. As time proceeds, this swap may obtain a positive or negative value.

Receive fixed cash flow

\[ V_{swap} = B_{fixed} - B_{float} \]

Receive floating cash flow

\[ V_{swap} = B_{float} - B_{fixed} \]

2.2.3.3 Question on valuation of IRS

\[ Coupons: \frac{0.08}{2} *100 m =4m \\ B_{fixed} = 4m*e^{-0.1*0.25}+4m*e^{-0.1*0.75}+104m*e^{-0.1*1.25} = 98.238m \] \[ Coupons: \frac{0.102}{2} *100 m =5.1m \\ B_{floating} = 105.1m *e^{-0.1*0.25} = 102.505\\ V = B_{fixed} - B_{floating} = 98.238 - 102.505 = -4.267m \] Reference: Old lecture slides

2.3 Quiz on interest rate

1. (4-2) An interest rate is 6% per annum with annual compounding. What is the equivalent rate with continuous compounding?

   Answer

   Answer:  5.83%

2. (4-4) An interest rate is 12% per annum with semiannual compounding. What is the equivalent rate with quarterly compounding?

   Answer

   Answer:  11.83%

3. (4-6) The six-month zero rate is 8% per annum with semiannual compounding. The price of a one-year bond that provides a coupon of 6% per annum semiannually is 97. What is the one-year continuously compounded zero rate?

   Answer

   Answer:  9.03%

4. (4-9) The zero curve is upward sloping. Define X as the 1-year par yield, Y as the 1-year zero rate and Z as the forward rate for the period between 1 and 1.5 year. Which of the following is true?

   A) X is less than Y which is less than Z

   B) Y is less than X which is less than Z

   C) X is less than Z which is less than Y

   D) Z is less than Y which is less than X

   Answer

   Answer:  A

2.4 Quiz on Forwards

1. A one-year call option on a stock with a strike price of $30 costs $3; a one-year put option on the stock with a strike price of $30 costs $4. Suppose that a trader buys two call options and one put option. The breakeven stock price below which the trader makes a profit is

   A) $25

   B) $28

   C) $26

   D) $20

Answer

Answer:  D

2. Which of the following describes European options?

   A) Sold in Europe

   B) Priced in Euros

   C) Exercisable only at maturity

   D) Exercisable anytime until matruity

Answer

Answer:  C

3. A company knows it will have to pay a certain amount of a foreign currency to one of its suppliers in the future. Which of the following is true?

   A) A forward contract can be used to lock in the exchange rate

   B) A forward contract will always give a better outcome than an option

   C) An option will always give a better outcome than a forward contract

   D) An option can be used to lock in the exchange rate

Answer

Answer:  A

4. A short forward contract on an asset plus a long position in a European call option on the asset with a strike price equal to the forward price is equivalent to

   A) A short position in a call option

   B) A short position in a put option

   C) A long position in a put option

   D) None of the above

Answer

Answer:  C

5. A company knows it will have to pay a certain amount of a foreign currency to one of its suppliers in the future. Which of the following is true?

   A) A forward contract can be used to lock in the exchange rate

   B) A forward contract will always give a better outcome than an option

   C) An option will always give a better outcome than a forward contract

   D) An option can be used to lock in the exchange rate

Answer

Answer:  A

6. The price of a stock on February 1 is $48. A trader sells 200 put options on the stock with a strike price of $40 when the option price is $2. The options are exercised when the stock price is $39. The trader’s net profit or loss is

   A) Loss of $800

   B) Loss of $200

   C) Gain of $200

   D) Loss of $900

Answer

Answer:  A

7. (3-1) The basis is defined as spot minus futures. A trader is hedging the sale of an asset with a short futures position. The basis increases unexpectedly. Which of the following is true?

   A) The hedger’s position improves

   B) The hedger’s position worsens

   C) The hedger’s position sometimes worsens and sometimes improves

   D) The hedger’s position stays the same

Answer

Answer:  A

8. (3-2) Futures contracts trade with every month as a delivery month. A company is hedging the purchase of the underlying asset on June 15. Which futures contract should it use?

   A) The June contract

   B) The July contract

   C) The May contract

   D) The August contract

Answer

Answer:  B

As a general rule the futures maturity month should be as close as possible to but after the month when the asset will be purchased. In this case the asset will be purchased in June and so the best contract is the July contract.

9. (3-4) On March 1 the price of a commodity is $1,000 and the December futures price is $1,015. On November 1 the price is $980 and the December futures price is $981. A producer of the commodity entered into a December futures contracts on March 1 to hedge the sale of the commodity on November 1. It closed out its position on November 1. What is the effective price (after taking account of hedging) received by the company for the commodity?

Answer

Answer:  1014, notice it’s to hedge the sales

10. (3-13) Which of the following increases basis risk?

    A) A large difference between the futures prices when the hedge is put in place and when it is closed out

    B) Dissimilarity between the underlying asset of the futures contract and the hedger’s exposure

    C) A reduction in the time between the date when the futures contract is closed and its delivery month

    D) None of the above

Answer

Answer:  B

2.5 Summary

We introduced forwards, futures and interest rate swaps in this week. This class should be able to cover material from W1 to W3 in ANU. They are the basics of derivatives, indeed. Derivatives may be hard or unfamiliar to some, mainly because their values are derived from underlying assets. This creates another layer of complexity and adds the posibility of adding much more layers. Hard work will eventually pay off.

Please let me know if you have any question:)