Chapter 2 Allen Gale Model
Allen and Gale (2000) (AG) proposed a financial contagion model, where the network completeness plays the pivot role. The model shows that (1) when there is no aggregate liquidity shock, first-best allocation can be achieved in either complete or incomplete interbank market. (2) The first-best allocation is fragile. Even a small unexpected liquidity uncertainty will spread throughout the bank system. Especially, in a ring interbank network, AG described in detail how all banks in the economy go bankrupt successively if the shock is beyond the first two bank’s buffer. (3) Complete network is more robust than incomplete network. However, there is a nonmonotonic relationship between completeness of interbank markets and the extent of the financial crisis. The network separating the banks into isolated clusters will limit contagion.
2.1 Model Setup
There are three dates, \(t = 0, 1, 2\), and one kind of consumption good serving as the numeraire. The consumption good can be invested into short or long asset at date 0. One unit of short asset can produce only one unit of consumption good at date 1. The long asset mature at date 2 and provides \(R > 1\) units of consumption good. The long asset is not completely illiquid and can be liquidate at date 1 to return \(0<r<1\) units of consumption good.
The economy is divided into four identical regions, labeled as \(A\), \(B\), \(C\) and \(D\). A continuum of residents , which serve as consumers and depositors, live in each region. Each resident holds one unit of consumption good at date 0 but have nothing at date 1 and 2. The utility function of a resident takes the following form
\[ u(c_1, c_2) = \begin{cases} u(c_1) & \mbox{with probability } w \\ u(c_2) & \mbox{with probability } 1-w, \end{cases} \]
where \(u(\cdot)\) is twice continuously differentiable. \(u(c_1, c_2) = u(c_1)\) mean that the resident only care about his consumption at date 1, which is called early consumer, while \(u(c_1, c_2) = u(c_2)\) means the resident is more patient, which is called late consumer. At date 0, residents in all regions are ex ante identical, i.e. their liquidity preference is unknown to even themselves. The liquidity preference will revealed at date 1. There are two possible value of \(w\), \(w_H\) and \(w_L\) where \(w_H > w_L\), and two equally likely states \(S_1\) and \(S_2\) at which the realization of \(w\) for each region is described in Table 2.1 .
| A | B | C | D | |
|---|---|---|---|---|
| \(S_1\) | \(w_H\) | \(w_L\) | \(w_H\) | \(w_L\) |
| \(S_2\) | \(w_L\) | \(w_H\) | \(w_L\) | \(w_H\) |
2.2 First-best Risk Sharing
First we consider the social planner’s problem. As shown in Table 2.1, in aggregate, there is no uncertainty in liquidity preference: one half of the regions have high liquidity demand at date 1 and the other half have lower demand. On average, the fraction of early consumers is \(\gamma = (w_H + w_L) / 2\). The social planner allocate the consumption good between short and long asset at date 0, and meets the liquidity demand of early and late consumers using short and long asset respectively.
\[ \begin{aligned} \max\limits_{x, y, c_1, c_2} & \quad \gamma u(c_1) + (1-\gamma)u(c_2) \\ \mathrm{s.t.} & \quad x + y \leq 1 \\ & \quad \gamma c_1 \leq y \\ & \quad (1-\gamma)c_2 \leq Rx \end{aligned} \]
The FOCs are given by \[ \begin{aligned} & u'(c_1) = Ru'(c_2), \\ & x + y = 1, \\ & y = \gamma c_1, \\ & x = \frac{1-\gamma}{R} c_2. \end{aligned} \]
Note that \(u'(c_1) = Ru'(c_2)\) means that \(c_1 < c_2\) and thus any late consumer will not pretend to be a early consumer. The first-best allocation can be achieved at both state \(S_1\) and \(S_2\) since the social planner can shift the excess liquidity supply of one region to meet the excess demand of another region.
2.3 Decentralization and Interbank Market
Can the first-best allocation be achieved by a decentralized bank system? The answer is generally no if there is no interbank market. To see this, Suppose there is a continuum of banks in each region. At date 0, all residents will save their endowment into local banks. A bank in each region \(i\) invests the deposits of its’ consumers in a portfolio \((x, y)\), and provides a standard deposits contract \((c_1, c_2)\) to its depositors, including consumers or the bank in another region, where \((x, y)\) and \((c_1, c_2)\) is the first-best investment portfolio and consumption flow respectively. The contract allows depositor to save 1 unit of consumption good at date 0 and withdraw either \(c_1\) units of consumption good at date 1 or \(c_2\) units at date 2.
If \(S_1\) occurs, then region \(A\) and \(C\) are subject to high liquidity shocks at date 1, the short asset at disposal is \(\gamma c_1\), which can not meet the liquidity demand \(w_H c_1\). In state \(S_2\), it is turn of region \(B\) and \(D\) to face the same dilemma.
Things are different if there is a interbank market. First let us consider the complete interbank bank as depict in Figure 2.1, that is each bank holds deposit \(z = (w_H - \gamma)/2\) in other three region at date 0. We assume that if the demand for liquidity is \(w_H\) at date 1, then a bank will withdraw all its’ interbank deposit and withdraw all its’ remaining deposit at date 2. The book value of the left side of the balance sheet of any bank at date 0 is \(x+y+3z\), and the that of right side is \(1 + 3z\). The mutual interbank deposits cancel out so we still have \(x + y = 1\), which is the exact constraint of social planner’s problem at date 0. At date 1, suppose \(S_1\) occurs, then the bank in region \(A\) and \(D\) face total \((w_H + z) c_1\) liquidity demand and can supply \(y + 3 z c_1\) liquidity. For the bank in region \(B\) and \(C\), the demand they face and the liquidity the can supply is \((w_L + 2z)c_1\) and \(y\). According to the condition that supply equals demand, following equations hold and can be simplified into the constraint of social planner’s problem at date 1. \[ \begin{aligned} (w_H + z) c_1 = y + 3z c_1 \Longrightarrow \gamma c_1 = y, \\ (w_H + 2z) c_1 = y \Longrightarrow \gamma c_1 = y. \end{aligned} \] At date 2, all regions will liquidate the remaining asset on hand. For region \(A\) and \(C\), the liquidity demand and supply is \((1-w_H + 2z)c_2\) and \(Rx\). For \(B\) and \(D\), they are \((1-w_L + z)c_2\) and \(Rx + 3z c_2\). Similarly, we have \[ \begin{aligned} (1-w_H + 2z) c_2 = Rx \Longrightarrow (1-\gamma) c_2 = Rx, \\ (1-w_L + z) c_2 = Rx + 3z c_2 \Longrightarrow (1-\gamma) c_2 = Rx. \end{aligned} \] Once again the constraint of the social planner’s problem is satisfied!
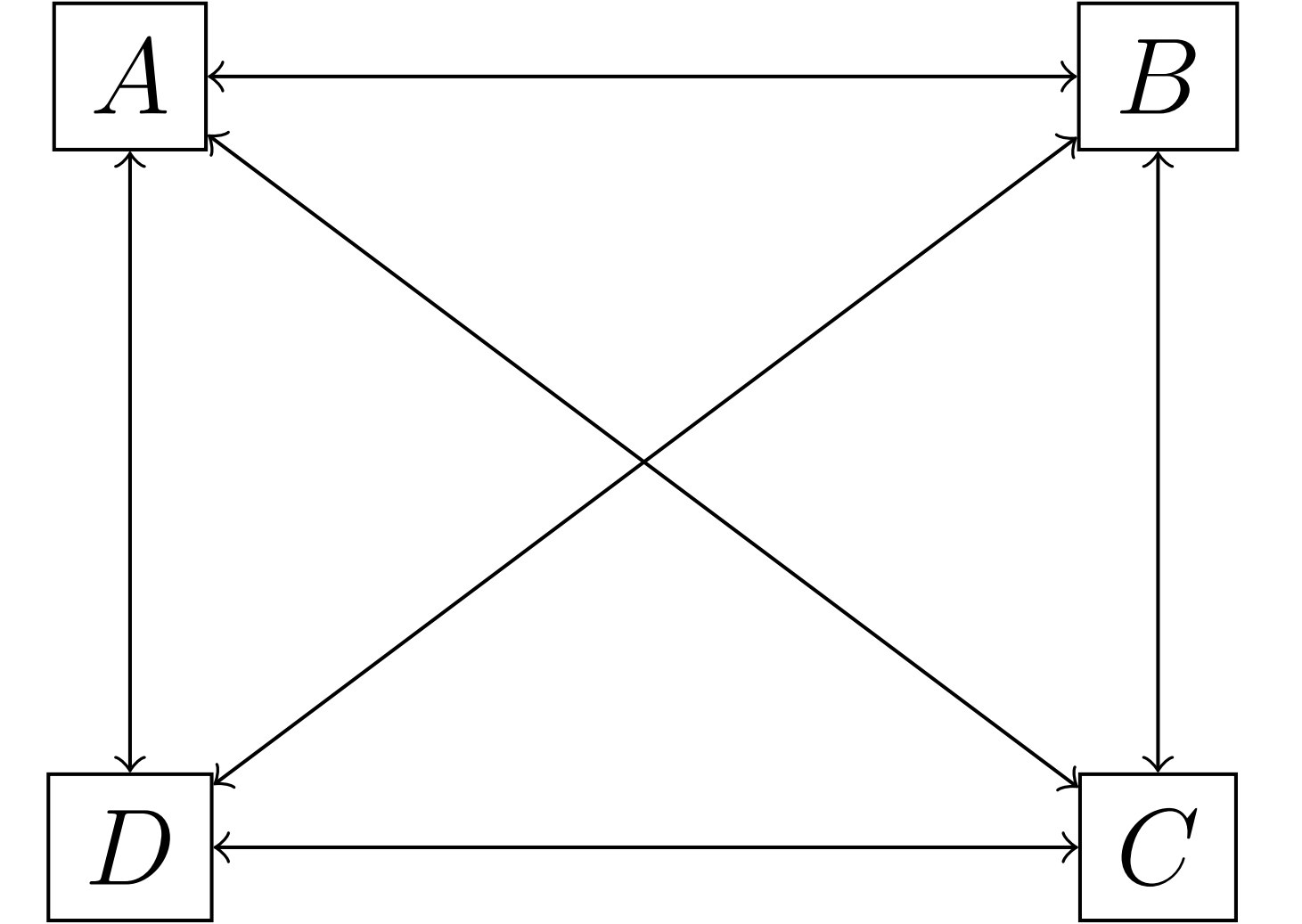
Figure 2.1: Complete Network
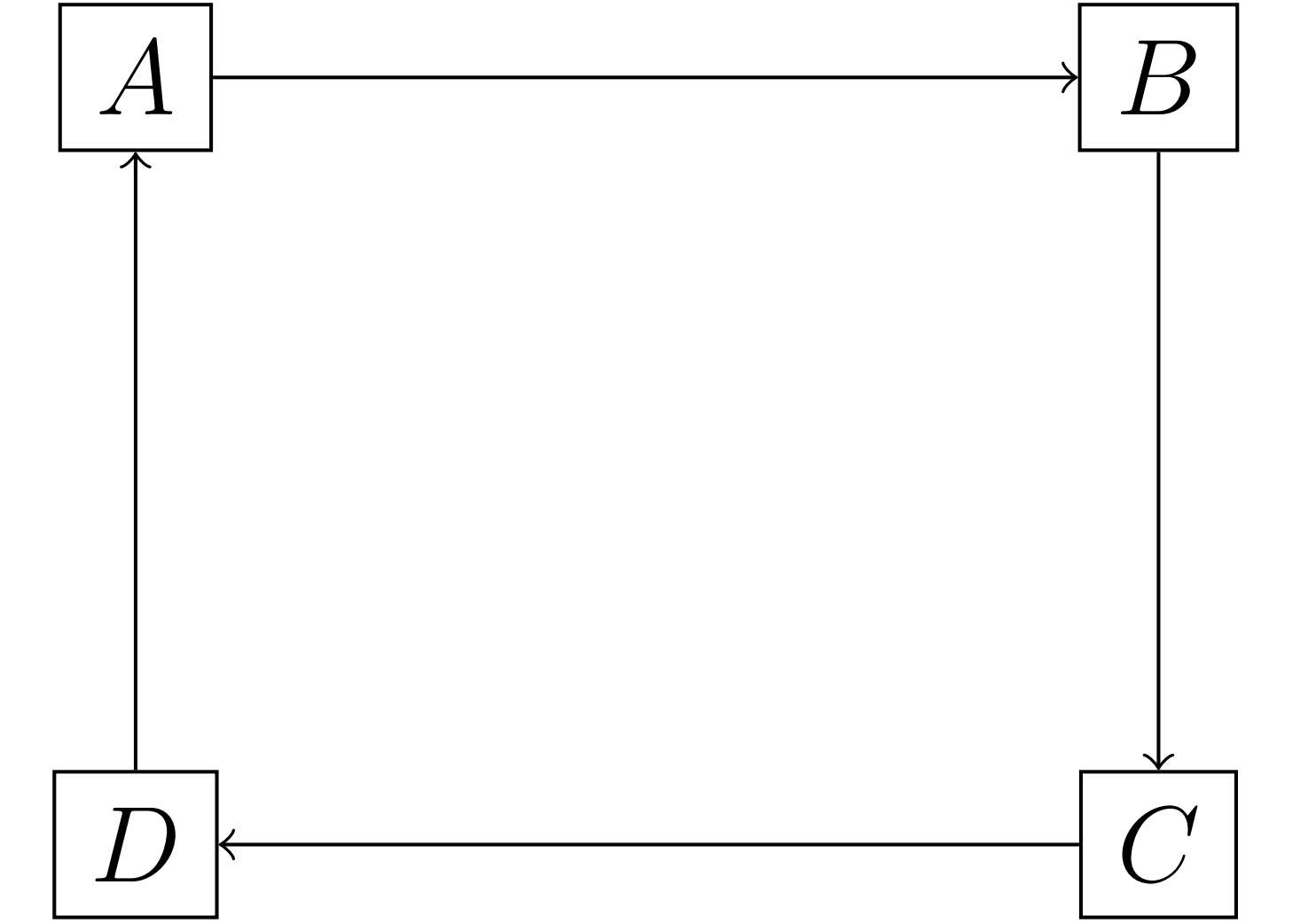
Figure 2.2: Incomplete Network

Figure 2.3: Disconnected Network
In fact, even an incomplete network, as depicted in Figure 2.2 and 2.3 can achieve the first-best allocation. For the case of Figure 2.2, the bank in \(A\) holds \(w_H - \gamma\) deposits in \(B\), \(B\) holds \(w_H - \gamma\) deposits in \(C\) and so on. For the case of Figure 2.3, the bank in region \(A\) and \(B\) mutually hold the deposits \(w_H - \gamma\). At any date, it can be verified that the FOCs of the social planner’s problem are also satisfied.
2.4 Fragility of Decentralization
In last section, we find that the incompleteness of interbank network does not prevent the achievement of the first-best allocation, when there is no aggregate uncertainty in liquidity preference. However, the incomplete bank system may be fragile when there is uncertainty. We take the network structure in Figure 2.2 as example.
2.4.1 Perturbation
Consider a new state \(\bar{S}\) where the fraction of early consumers in region A is slightly higher, that is \(\gamma + \epsilon\), at date 1 and other regions have the average liquidity demand \(\gamma\), as shown in Table 2.2.
| A | B | C | D | |
|---|---|---|---|---|
| \(S_1\) | \(w_H\) | \(w_L\) | \(w_H\) | \(w_L\) |
| \(S_2\) | \(w_L\) | \(w_H\) | \(w_L\) | \(w_H\) |
| \(\bar{S}\) | \(\gamma + \epsilon\) | \(\gamma\) | \(\gamma\) | \(\gamma\) |
The state \(\bar{S}\) is unexpected at date 0, so the introduction of \(\bar{S}\) does not change the initial allocation at date 0.
2.4.2 Pecking Order
There are three possible situations of banks at date 1: solvent, insolvent and bankrupt. A Solvent bank can meet the liquidity demand of depositors at date 1 by using only its’ short asset and the deposit in other regions. A insolvent bank can meet the liquidity demand of depositors at date 1 only by liquidating some of the long asset. A bankrupt bank can not meet the liquidity demand even it liquidating all its’ asset.
The definition of solvency, insolvency and bankruptcy implies that a bank will follow the order of short asset, deposits in other regions, long asset to liquidating its’ asset if necessary, so the cost of liquidating should make the liquidating order reasonable. The cost of liquidating the short asset is 1, since liquidating one unit of short asset at date 1 means giving up one unit of consumption good at date 2. Analogically, the cost of liquidating deposits and long asset is \(c_2/c_1\) and \(R/r\) respectively. Therefore, following relationship should holds: \[ \frac{R}{r} > \frac{c_2}{c_1} > 1 \]
2.4.3 Liquidation Values
Denote \(q^i\) as the real value of the one unit (book value) of deposit in region \(i\). If a bank in region \(i\) is solvent or insolvent, the real value equals the book value, that is \(q^i = c_1\) and all of its’ depositor can withdraw \(c_1\) unit of consumption good according to the contract. If the bank is bankrupt, then all depositor are treated equally and thus can withdraw only \(q^i < c_1\) for one unit deposit. How are the equilibrium of \(q^i, i = A,B,C,D\) determined? Take region A as example, the value of asset of a bankrupt bank is \(y + rx + zq^B\), the book value of its’ liability at date 0 is \(1+z\), so the liquidation value of the deposits in region \(A\) is \[ q^A = \frac{y + rx + z q^B}{1+z} \]
2.4.4 Long Asset Buffers
It seems that an insolvent bank can liquidating all of its’ long asset to avoid bankruptcy, but it is not so. Late consumers will compare the consumption good they can withdraw at date 1 and date 2, if \(c_1 > c_2\), then a late consumer will imitate early consumer to withdraw his deposit, so a bank must maintain \((1-w)c_1/R\) units of long asset given the fraction of early consumer \(w\). In other words, the maximal amount of consumption good can obtained to without causing bankruptcy is \[ b(w) = r\left[x - \frac{(1 - w)c_1}{R}\right], \] which is called the buffer of a bank.
2.4.5 Contagion Process in Incomplete Market
Suppose the initial liquidity shock to region \(A\) is small enough, then the bank in this region will find itself is self-sufficient at date 1. It can withdraw all its’ deposits in region \(B\) to satisfy the liquidity demand of early consumers. The action spreads the shock to region \(B\), the bank in \(B\) will response by withdrawing its’ deposits in region \(C\) rather than liquidating long asset (remember that \(R/r > c_2 / c_1\)), which also applies for region \(C\) and \(D\). Since the book value of interbank deposits are the same, so the effect of mutual withdraw will cancel out. The final effect of the liquidity shock is that the late consumers in region \(A\) will be worse off at date 2, but it is still optimal for them to be patient. What is the maximal liquidity shock the later consumers can tolerate? Obviously it is the buffer of the bank in region \(A\). \[ \epsilon c_1 \leq b(\gamma + \epsilon) \] If the above inequality is violated, then the bank can not keep the least amount of long asset to prevent the local late consumers to withdraw deposits in advance. The bank in region \(A\) will go bankrupt, then all depositors, including consumers and banks in other regions, will carve up the liquidation value of all asset of the bank in A.
The aftermath of the bankruptcy of the bank in region \(A\) should be further discussed. Of course, the bank in region \(D\) is the first one to be affected, the spillover effect it receives is \(z(c_1 - q^A)\) since it only receives \(q^A<c_1\) for each unit of the interbank deposits in \(A\) but redeem the book value \(c_1\) to the bank in \(C\). Whether the bank in region \(D\) will be bankrupt depends on the liquidation value \(q^A\). To simplify the problem, we just provide a sufficient condition for the bank in region \(D\) being bankrupt. Denote \(\bar{q}^A\) as the maximal liquidation value of the bank in \(A\), it can be achieved only when the bank in region \(B\) can fulfill the book value \(c_1\) to \(A\), so we have \[ q^A \leq \bar{q}^A = \frac{y+rx+zc_1}{1+z}, \] and the minimal liquidity shock spillover is \(z\left(c_1 - \bar{q}^A\right)\). The bank in region \(D\) must go bankrupt if \[ z\left(c_1 - \bar{q}^A\right) > b(\gamma). \]
The story continues. The bankruptcy of the bank in \(B\) generates spillover effect to region \(C\) and further to region \(B\). Note that the liquidation value \(q^C\) and \(q^B\) are less than \(\bar{q}^A\), the gap between the amount they pays and receives widens, we have \[ z\left(c_1 - q^B\right) > z\left(c_1 - q^C\right) > z\left(c_1 - \bar{q}^A\right) > b(\gamma). \] There is no doubt that the bank in region \(C\) and \(D\) must go bankrupt. Allen and Gale (2000) summarized as following:
Proposition 2.1 Consider the model with market structure described in Figure 2 and perturb it by the addition of zero probability \(\bar{S}\) described in Table 2.2. Suppose that each bank chooses an investment portfolio \((x, y, z)\) and offers a deposit contract \((c_1, c_2)\), where \((x, y)\) is the first-best investment portfolio, \((c_1, c_2)\) is the first-best consumption allocation, and \(z = w_H - \gamma\). If \(\epsilon c_1 > b(\gamma + \epsilon)\) and \(z\left(c_1 - \bar{q}^A\right) > b(\gamma)\), then, in any continuation equilibrium, the banks in all regions must go bankrupt at date 1 in state \(\bar{S}\).
2.5 Robustness of Complete Interbank Market
Compared to incomplete network, complete network is more robust in that it can tolerate higher aggregate liquidity shock. In other words, under the condition of proposition 2.1, some banks in the complete network will survive.
Suppose each bank holds \(z/2=(w_H - \gamma)/2\) deposits in the subsequent region. When \(\bar{S}\) occurs and the shock is large enough such that \(\epsilon c_1 > b(\gamma+\epsilon)\), the bank in region \(A\) will withdraw all deposits as response to the shock, but the withdraw action will loop back to itself. Finally, it will go bankrupt as we described in last section.
The problem is whether the bank in other regions will go bankrupt too. We need to recalculate the liquidation value of the bank in A. The maximal value of \(q^A\) is \[ \bar{q}^{A*} = \frac{y + rx + 1.5zc_1}{1+1.5z}. \] The loss of the bank in other regions due to the bankruptcy of the banks in \(A\) is \(0.5z\left(c_1 - \bar{q}^{A*}\right)\), other banks will just be insolvent rather than bankrupt if and only if \[ \frac{1}{2}z \left(c_1 - \bar{q}^{A*}\right) \leq b(\gamma), \] which can hold even if \(z(c_1 - \bar{q}^A) > b(\gamma)\).