Chapter 2 Estimation of BQVAR

2.1 Model Specification of QVAR

The \(P\)-order QVAR at probability vector \(\alpha=[\alpha_1\ \alpha_2\ \cdots\ \alpha_N]^{\top} \in (0, 1)^{N}\) without exogenous variable, denoted as \(\mathrm{QVAR}(P)\) takes the form of \[\begin{equation} \tag{2.1} \begin{gathered} \boldsymbol{Y}_t = \boldsymbol{q}(\boldsymbol{\alpha}) + \sum_{p=1}^P \mathbf{A}(\boldsymbol{\alpha})_p Y_{t-p} + \boldsymbol{u}(\boldsymbol{\alpha})_t, Q_{\boldsymbol{\alpha}}(\boldsymbol{u}(\boldsymbol{\alpha})_t|I_t) = \boldsymbol{0}, \\ \boldsymbol{Y}_t = \begin{bmatrix} Y_{1t} \\ Y_{2t} \\ \vdots \\ Y_{Nt} \end{bmatrix}, \boldsymbol{u}(\boldsymbol{\alpha})_t = \begin{bmatrix} u(\alpha_1)_{1t} \\ u(\alpha_2)_{2t} \\ \vdots \\ u(\alpha_N)_{Nt} \end{bmatrix}, \mathbf{A}(\boldsymbol{\alpha})_p=\begin{bmatrix} a(\alpha_1)_{11,p} & a(\alpha_1)_{12,p} & \cdots & a(\alpha_1)_{1N,p} \\ a(\alpha_2)_{21,p} & a(\alpha_2)_{22,p} & \cdots & a(\alpha_2)_{2N,p} \\ \vdots & \vdots & \ddots & \vdots \\ a(\alpha_N)_{N1,p} & a(\alpha_N)_{N2,p} & \cdots & a(\alpha_N)_{NN,p} \end{bmatrix}, \end{gathered} \end{equation}\]

where \(Q_{\boldsymbol{\alpha}}(\cdot)\) is quantile operator, which means that it calculates element-wise quantile of the random vector in the parenthesis according to the probability vector \(\boldsymbol{\alpha}\), that is \(Q_{\boldsymbol{\alpha}}(\boldsymbol{X}) = \begin{bmatrix}Q_{\alpha_1}(X_1) & Q_{\alpha_2}(X_2) & \cdots & Q_{\alpha_N}(X_N)\end{bmatrix}^{\top}\) . \(Q_{\boldsymbol{\alpha}}\left(\boldsymbol{u}(\boldsymbol{\alpha})_t|I_t\right)=\boldsymbol{0}\) implies that the conditional \(\boldsymbol{\alpha}\)-quantile of \(\boldsymbol{Y}_t\) is \(Q_{\boldsymbol{\alpha}}\left(\boldsymbol{Y}_t|I_t\right) = \boldsymbol{q}(\boldsymbol{\alpha}) + \sum_{p=1}^P \mathbf{A}(\boldsymbol{\alpha})_p \boldsymbol{Y}_{t-p}\). In other words, \(\boldsymbol{u}(\boldsymbol{\alpha})_t\) is the forecast error that drive the observation of \(\boldsymbol{y}_t\) to deviate from conditional \(\boldsymbol{\alpha}\)-quantile of \(\boldsymbol{Y}_t\). In this sense, \(\boldsymbol{u}(\boldsymbol{\alpha})_t\) can be named as quantile shock.

To consider the effect of common factors on \(\boldsymbol{Y}_t\), we can extend the model by introducing lagged exogenous variables.

2.2 Likelihood

2.2.1 Asymmetric Laplace Distribution

The first popular likelihood specification is to assume each element of quantile shocks obeies asymmetric Laplace distribution (ALD), i.e. \(u(\alpha_i)_{it}\sim \mathcal{AL}(0, \alpha_i, \delta_i)\), where \(\alpha_i\) is probability parameter and \(\delta_i>0\) is scale parameter. According to the property of ALD, the conditional distribution of \(Y_{it}\) is \(\mathcal{AL}\left(q(\alpha_i)_i + \sum_{p=1}^P\sum_{j=1}^N a(\alpha_i)_{ij,p} Y_{j,t-p}, \alpha_i, \delta_i\right)\). The density function of \(Y_{it}\) is \[ f_{Y_{it}}(y_{it}) = \frac{\alpha_i(1 - \alpha_i)}{\delta_i} \begin{cases} \exp\left(-\dfrac{\alpha_i}{\delta_i} e(\alpha_i)_{it} \right) & \text{if } e(\alpha_i) \geq 0, \\ \exp\left(\dfrac{1-\alpha_i}{\delta_i} e(\alpha_i)_{it} \right) & \text{if } e(\alpha_i) < 0. \end{cases} \] where \(e(\alpha_i)_{it} = y_{it} - q(\alpha_i)_i - \sum_{p=1}^P\sum_{j=1}^N a(\alpha_i)_{ij,p} Y_{j,t-p}\). For the facility of implementation of Bayesian estimation, we use the mixture representation property to write the distribtuion of \(Y_{it}\) as the mixture of standard normal distribution and exponential distribution, that is \[ Y_{it} = q(\alpha_i)_i + \sum_{p=1}^P\sum_{j=1}^N a(\alpha_i)_{ij,p} Y_{j,t-p} + \delta_i \tilde{\xi}_i W_{it} + \delta_i \tilde{\sigma}_i \sqrt{W_{it}} Z_{it}, \]

where \(W_{it}\sim \mathcal{EXP}(1)\), \(Z_{it} \sim \mathcal{N}(0,1)\) and they are independent. \(W_{it}\) is called the latent variable. The parameters \(\tilde{\xi}_i\) and \(\tilde{\sigma}_i\) should satisfy \[ \tilde{\xi}_i = \frac{1 - 2 \alpha_i}{ \alpha_i (1 - \alpha_i)}, \tilde{\sigma}_i^2 = \frac{2}{\alpha_i(1 - \alpha_i)}. \]

The restriction is to ensure that \(Q_{\alpha_i}(Y_{it}) = q(\alpha_i)_i + \sum_{p=1}^P\sum_{j=1}^N a(\alpha_i)_{ij,p} Y_{j,t-p}\), or equivalently, \(Q_{\alpha_i}(u(\alpha_i)_{it})=0\).

2.2.2 Multivariate Asymmetric Laplace Distribution

Another feasible likelihood function setting is to assume that \(\boldsymbol{Y}_t\) jointly obey multivariate asymmetric Laplace distribution (MALD), denoted as \(\boldsymbol{Y}_t \sim \mathcal{MAL}\left(\boldsymbol{q}(\boldsymbol{\alpha}) + \sum_{p=1}^P \mathbf{A}(\boldsymbol{\alpha})_p \boldsymbol{y}_{t-p}, \mathbf{D}\tilde{\boldsymbol{\xi}}, \mathbf{D}\tilde{\boldsymbol{\Sigma}} \mathbf{D} \right)\), where \(\mathbf{D}=\mathrm{diag}(\delta_1, \delta_2, \cdots, \delta_N)\) is the diagonal matrix of scale parameter, \(\tilde{\boldsymbol{\xi}}=\left[\tilde{\xi}_1\ \tilde{\xi}_2\ \cdots\ \tilde{\xi}_N\right]^{\top}\) and \(\tilde{\boldsymbol{\Sigma}}\) is a \(N\times N\) positive definite matrix . The density function of \(\boldsymbol{Y}_t\) is \[ f_{\boldsymbol{Y}_t}(\boldsymbol{y}_t) = \frac{2 \exp\left( \boldsymbol{e}(\boldsymbol{\alpha})_t^{\top} \mathbf{D}^{-1} \tilde{\boldsymbol{\Sigma}}^{-1} \tilde{\boldsymbol{\xi}} \right) }{(2\pi)^{N/2} \left|\mathbf{D} \tilde{\boldsymbol{\Sigma}} \mathbf{D}\right|^{1/2} } \left(\frac{m_t}{2+d}\right)^{\nu/2} K_{\nu}\left[\sqrt{(2+d)m_t}\right], \] where \(\boldsymbol{e}(\boldsymbol{\alpha})_t = \boldsymbol{y}_{it} - \boldsymbol{q}(\boldsymbol{\alpha}) - \sum_{p=1}^P \mathbf{A}(\boldsymbol{\alpha})_p \boldsymbol{y}_{t-p}\), \(m_t = \boldsymbol{e}(\boldsymbol{\alpha})^{\top} \mathbf{D}^{-1} \tilde{\boldsymbol{\Sigma}}^{-1} \mathbf{D}^{-1} \boldsymbol{e}(\boldsymbol{\alpha})\), \(d=\tilde{\xi}^{\top} \tilde{\boldsymbol{\Sigma}}^{-1} \tilde{\boldsymbol{\xi}}.\) \(K_{\nu}(\cdot)\) is the modified Bessel function of the third kind where \(\nu = (2-N)/2\). To fix that the \(\boldsymbol{\alpha}\)-quantile of \(\boldsymbol{u}(\boldsymbol{\alpha})_{t}\), \(\tilde{\boldsymbol{\xi}}\) and the diagonals of \(\tilde{\boldsymbol{\Sigma}}\) should satisfy \[ \tilde{\xi}_i = \frac{1 - 2 \alpha_i}{ \alpha_i (1 - \alpha_i)}, \tilde{\sigma}_i^2 = \frac{2}{\alpha_i(1 - \alpha_i)}, i=1,2,\cdots,N. \] Similarly, MALD also has a mixture representation, which takes the form of \[ \boldsymbol{Y}_t = \boldsymbol{q}(\boldsymbol{\alpha}) + \sum_{p=1}^P \mathbf{A}(\boldsymbol{\alpha})_p \boldsymbol{Y}_{t-p} + \mathbf{D}\tilde{\xi}W_t + \sqrt{W_t} \mathbf{D} \tilde{\boldsymbol{\Sigma}}^{1 }\boldsymbol{Z}_t, \] where \(W_t \sim \mathcal{EXP}(1)\), \(\mathbf{Z}_t \sim \mathcal{N}(\boldsymbol{0}, \mathbf{I}_N)\). Compared to the case of ALD likelihood, the latent variable \(W_t\) here is common for all cross-sectional units, which will reduce sampling burden of MCMC algorithm.

2.3 Prior Distribution

2.3.1 AL-likelihood Case

Define \(\boldsymbol{X}_t=[\boldsymbol{1}_N\ \boldsymbol{Y}_{t-1}\ \boldsymbol{Y}_{t-2}\ \cdots\ \boldsymbol{Y}_{t-P}]\), \(\mathbf{B}(\boldsymbol{\alpha})=[\boldsymbol{q}(\boldsymbol{\alpha})\ \mathbf{A}(\boldsymbol{\alpha})_1\ \mathbf{A}(\boldsymbol{\alpha})_2\ \cdots\ \mathbf{A}(\boldsymbol{\alpha})_P]\) and \(\boldsymbol{b}(\alpha_i)_{i\cdot}\) is the \(i\)-th row of the \(\mathbf{B}(\boldsymbol{\alpha})\). The prior distributions of parameter in the case of ALD are \[\begin{align} & \text{Prior:} \begin{cases} W_{it} \sim \mathcal{EXP}(1), \\ \boldsymbol{b}(\alpha_i)_{i\cdot} \sim \mathcal{N}\left(\boldsymbol{0}, \boldsymbol{\Lambda}_i \underline{\mathbf{V}}_i\right), \\ \delta_i \sim \mathcal{IG}\left(\underline{n}_{\delta,i}/2, \underline{s}_{\delta,i}/2 \right), \\ \lambda_{ij} \sim \mathcal{IG}\left(\underline{n}_{\lambda,ij}/2, \underline{s}_{\lambda,ij}/2 \right), \end{cases} \tag{2.2} \\ & \text{AL-Likelihood: } Y_{it} | \boldsymbol{b}(\alpha_i)_{i\cdot}, \delta_i, \tilde{\xi}_i, \tilde{\sigma}_i, \boldsymbol{x}_t, w_{it} \sim \mathcal{N}\left(\boldsymbol{x}_t^{\top} \boldsymbol{b}(\alpha_i)_{i\cdot} + \tilde{\xi}_i \delta_i w_{it},\ \delta_i^2 w_{it} \tilde{\sigma}_i^2 \right), \\ & i= 1,2,\cdots,N, j=1,2,\cdots,N, t=1,2,\cdots, T, \end{align}\] where \(\mathbf{\Lambda}_i = \mathrm{diag}(\lambda_{i1}, \lambda_{i2}, \cdots, \lambda_{i,NP+1})\) is the diagonal matrix of penalty parameters for \(\boldsymbol{b}(\alpha_i)_{i\cdot}\) The smaller is \(\lambda_{ij}\), the more concentrated is \(b(\alpha_i)_{ij}\) aounrd 0. \(\mathcal{IG}(\alpha, \beta)\) represents Inverse Gamma distribution with shape parameter \(\alpha > 0\) and scale parameter \(\beta > 0\).

2.3.2 MAL-likelihood Case

In MALD case, the prior are specified as \[\begin{align} & \text{Prior: } \begin{cases} W_t \sim \mathcal{EXP}(1), \\ \boldsymbol{b}(\alpha_i)_{i\cdot} \sim \mathcal{N}(\boldsymbol{0}, \mathbf{\Lambda}_i \underline{\mathbf{V}}_i), \\ \delta_i \sim \mathcal{IG}\left(\underline{n}_{\delta,i}/2, \underline{s}_{\delta,i}/2\right),\\ \tilde{\boldsymbol{\Sigma}} \sim \mathcal{IW}\left(\underline{\nu}, \underline{\boldsymbol{\Sigma}}\right), \\ \lambda_{ij} \sim \mathcal{IG}\left(\underline{n}_{\lambda,ij}/2, \underline{s}_{\lambda,ij}/2 \right), \end{cases} \tag{2.3} \\ & \text{MAL-Likelihood: } \boldsymbol{Y}_t | \{\alpha_i\}_{i=1}^N, \left\{\boldsymbol{b}(\alpha_i)_{i\cdot}\right\}_{i=1}^N, \{\delta_i\}_{i=1}^N, \tilde{\boldsymbol{\Sigma}}, \boldsymbol{x}_t, w_t \sim \mathcal{N}\left( \mathbf{B}(\boldsymbol{\alpha})\boldsymbol{x}_t + \mathbf{D}\tilde{\boldsymbol{\xi}} w_t, w_t \mathbf{D}\tilde{\boldsymbol{\Sigma}} \mathbf{D} \right), \\ & i= 1,2,\cdots,N, j=1,2,\cdots,N, t=1,2,\cdots, T. \end{align}\]

2.4 Posterior Distribution

2.4.1 AL-likelihood Case

Based on (2.2), the posterior distribution of model parameters are \[\begin{align} & W_{it} | \alpha_i, \boldsymbol{b}(\alpha_i)_{i\cdot}, \delta_i, y_{it} \sim \mathcal{GIG}\left(\frac{1}{2}, d_i + 2, m_{it}\right), \tag{2.4}\\ & \boldsymbol{b}(\alpha_i)_{i\cdot} | \alpha_i, \mathbf{\Lambda}_i, \delta_i, \{w_{it}\}_{t=1}^T, \{y_{it}\}_{t=1}^T, \{\boldsymbol{x}_t\}_{t=1}^T \sim \mathcal{N}\left(\bar{\boldsymbol{b}}_i, \bar{\mathbf{V}}_i\right), \tag{2.5} \\ & \delta_i | \alpha_i, \boldsymbol{b}(\alpha_i)_{i\cdot}, \{v_{it}\}_{t=1}^T, \{y_{it}\}_{t=1}^T, \{\boldsymbol{x}_t\}_{t=1}^T \sim \mathcal{IG}\left(\frac{\bar{n}_{\delta, i}}{2}, \frac{\bar{s}_{\delta,i}}{2}\right), \tag{2.6} \\ & \lambda_{ij}| b(\alpha)_{ij} \sim \mathcal{IG}\left(\frac{\bar{n}_{\lambda, ij}}{2}, \frac{\bar{s}_{\lambda, ij}}{2}\right), \tag{2.7} \\ & i=1,2,\cdots, N, j = 1, 2, \cdots, NP+1, t = 1,2,\cdots, T, \end{align}\] where \(v_{it} = \delta_i w_{it}\), \(\mathcal{GIG}(\alpha, \beta, n)\) represents Generalized Inverse Gaussian distribution. Other quantities in posterior distribution are defined as \[ \begin{aligned} & \bar{\mathbf{V}}_i = \left(\sum_{t=1}^T \frac{1}{w_{it} \delta_i^2 \tilde{\sigma}_i^2} \boldsymbol{x}_t \boldsymbol{x}_t^{\top} + \underline{\mathbf{V}}_i^{-1} \mathbf{\Lambda}_i^{-1}\right)^{-1}, \\ & \bar{\boldsymbol{b}}_i = \bar{\mathbf{V}}_i \left[\sum_{t=1}^T \frac{1}{w_t \delta_i^2 \tilde{\sigma}_i^2}\left(y_{it} - \delta_i\tilde{\xi}_i w_t\right) \boldsymbol{x}_t \right], \\ & \bar{n}_{\delta,i} = \underline{n}_{\delta,i} + 3T, \bar{s}_{\delta,i}=\underline{s}_{\delta,i} + 2 \sum_{t=1}^T v_{it} + \sum_{t=1}^T \frac{\left( y_{it} - \boldsymbol{x}_t^{\top} \boldsymbol{b}(\alpha_i)_{i\cdot} -\tilde{\xi} v_{it} \right)^2}{v_{it} \tilde{\sigma}_i^2}, \\ & i=1,2,\cdots, N, j = 1,2, \cdots, NP+1, t=1,2,\cdots, T. \end{aligned} \]

2.4.2 MAL-likelihood Case

If you adopt MAL-likelihood and prior (2.3), then the posterior distribution of the parameters are \[\begin{align} & W_t|\boldsymbol{\alpha}, \mathbf{B}(\boldsymbol{\alpha}), \tilde{\boldsymbol{\Sigma}}, \boldsymbol{\delta}, \boldsymbol{y}_t, \boldsymbol{x}_t \sim \mathcal{GIG}\left(\frac{2-N}{2}, d+2, m_t\right), \tag{2.8} \\ & \boldsymbol{b}(\alpha_i)_{i\cdot} | \boldsymbol{\alpha}, \boldsymbol{\Lambda}_i, \{\boldsymbol{b}(\alpha_j)_{j\cdot}\}_{j\neq i}, \tilde{\boldsymbol{\Sigma}}, \boldsymbol{\delta}, \{w_t\}_{t=1}^T, \{y_{it}\}_{t=1}^T, \{\boldsymbol{x}_t\}_{t=1}^T \sim \mathcal{N}\left(\bar{\boldsymbol{b}}_{i\cdot}, \bar{\mathbf{V}}_i \right), \tag{2.9} \\ & \tilde{\boldsymbol{\Sigma}} | \boldsymbol{\alpha}, \mathbf{B}(\boldsymbol{\alpha}), \boldsymbol{\delta}, \{w_t\}_{t=1}^T, \{\boldsymbol{y}_t\}_{t=1}^T, \{\boldsymbol{x}\}_{t=1}^T \sim \mathcal{IW}\left(\bar{\nu}, \bar{\boldsymbol{\Sigma}}\right), \tag{2.10} \\ & \delta_i | \alpha_i, \boldsymbol{b}(\alpha_i)_{i\cdot}, \{w_t\}_{t=1}^T, \{y_{it}\}_{t=1}^T, \{\boldsymbol{x}_t\}_{t=1}^T \sim \mathcal{IG}\left(\frac{\bar{n}_{\delta, i}}{2}, \frac{\bar{s}_{\delta,i}}{2}\right), \tag{2.11} \\ & \lambda_{ij} | b(\alpha_i)_{ij} \sim \mathcal{IG}\left(\frac{\bar{n}_{\lambda,ij}}{2}, \frac{\bar{s}_{\lambda,ij}}{2} \right), \tag{2.12} \\ & i = 1,2,\cdots, N, j = 1,2, \cdots, NP+1, t = 1,2,\cdots,T, \end{align}\] where \(d=\tilde{\boldsymbol{\xi}}^{\top}\tilde{\boldsymbol{\Sigma}}^{-1}\tilde{\boldsymbol{\xi}}\), \(m_t = \boldsymbol{e}(\boldsymbol{\alpha})_t^{\top} \left(\boldsymbol{\mathbf{D}}\tilde{\boldsymbol{\Sigma}} \mathbf{D} \right)^{-1} \boldsymbol{e}(\boldsymbol{\alpha})_t\), \(\boldsymbol{e}(\boldsymbol{\alpha})_t = \boldsymbol{y}_t - \mathbf{B}(\boldsymbol{\alpha}) \boldsymbol{x}_t\), and

\[ \begin{aligned} & \bar{\mathbf{V}}_i = \left(\sum_{t=1}^T \frac{\omega_{ii}}{w_t} \boldsymbol{x}_t \boldsymbol{x}_t^{\top} + \underline{\mathbf{V}}_i^{-1} \mathbf{\Lambda}_i^{-1}\right)^{-1}, \\ & \bar{\boldsymbol{b}}_i = \bar{\mathbf{V}}_i \left\{\sum_{t=1}^T \frac{1}{w_t}\left[\omega_{ii} \left(y_{it} - \delta_i\tilde{\xi}_i w_t\right) + \sum_{j\neq i, j =1}^N \omega_{ij} \left(e(\alpha_j)_{jt} - \delta_j \tilde{\xi}_j w_t\right) \right] \right\}, \\ & \bar{\boldsymbol{\Sigma}} = \sum_{t=1}^T \frac{1}{w_t} \mathbf{D}^{-1} \left( \boldsymbol{e}(\boldsymbol{\alpha})_t - \mathbf{D} \tilde{\boldsymbol{\xi}} w_t \right) \left( \boldsymbol{e}(\boldsymbol{\alpha})_t - \mathbf{D} \tilde{\boldsymbol{\xi}} w_t \right)^{\top} \mathbf{D}^{-1} + \underline{\boldsymbol{\Sigma}}, \bar{\nu} = \underline{\nu} + T - P, \\ & \bar{n}_{\delta,i} = \underline{n}_{\delta,i} + 3T, \bar{s}_{\delta,i}=\underline{s}_{\delta,i} + 2 \sum_{t=1}^T v_{it} + \sum_{t=1}^T \frac{\left( y_{it} - \boldsymbol{x}_t^{\top} \boldsymbol{b}(\alpha_i)_{i\cdot} -\tilde{\xi} v_{it} \right)^2}{v_{it} \tilde{\sigma}_i^2}, \end{aligned} \] where \(v_{it} = \delta_i w_t\), \(\omega_{ij}\) is the \((i,j)\) element of \(\left(\mathbf{D}\tilde{\boldsymbol{\Sigma}} \mathbf{D}\right)^{-1}\).

2.5 How to estimate BQVAR using estBQVAR

estBQVAR is the function to conduct Bayesian estimation of QVAR. Up to now, estBQVAR provides MCMC algorithm of Bayesian estimation, which bases the core sampling algorithm on Rcpp and RcppEigen pacakge.

2.5.1 Usage

estBQVAR(
    data_end,               # data frame of endogenous variable in autoregressive system
    lag,                    # lag order(s) of QVAR
    alpha,                  # tail probabilities at which your QVAR is estimated
    data_exo = NULL,        # data frame of exogenous variables, optional
    prior = NULL,           # prior setting, optional
    samplerSetting = NULL,  # sampler setting, optional
    method = "bayes-al",    # likelihood setting, ALD or MALD
    printFreq = 10,         # frequency of print message during estimation
    mute = FALSE            # whether to print message when estimation
)

2.5.1.1 Minimal inputs: data_end, data_exo, lag and alpha

If you are to estimate an \(N\)-dimensional \(\mathrm{QVAR}(P, Q)\) that takes the form of \[ \boldsymbol{Y}_t = \boldsymbol{q}(\boldsymbol{\alpha}) + \sum\limits_{p=1}^P \mathbf{A}(\boldsymbol{\alpha})_p \boldsymbol{Y}_{t-p} + \sum\limits_{q=1}^Q \mathbf{\Gamma}(\boldsymbol{\alpha})_q \boldsymbol{X}_{t-q} + \boldsymbol{u}(\boldsymbol{\alpha})_t, \tag{2.13} \] where \(\boldsymbol{X}_t\) is \(K\)-dimensional vector of exogenous variable, then data_end should be the \(\left(T + \max(P, Q)\right) \times N\) data frame of \(\boldsymbol{Y}_t\), data_exo is the \(\left(T + \max(P, Q)\right) \times K\) data frame of exogenous variables \(\boldsymbol{X}_t\). The time dimension of data is sorted by ascending order, and the first \(\max(P, Q)\) rows of data_end and data_exo will be removed in estimation. To estimate a QVAR model without exougenous variable, you can either pass NULL to the data_exo explicitly or ignore the argument.

The argument lag should be an int object of length 1 or 2. If you pass a scalar to lag, then estBQVAR fucntion will estimate either a QVAR model either with only endogenous variables, of which the lag order equals the value of lag, or one whose lag orders of endogenous and exogenous variables equals the scalar, depending on if there is exougenous variable in your model. If you pass a vector of length 2 to lag, then the first and second entry will be viewed as the lag order of endogenous and exogenous variables, respectively. Once data_exo = NULL, then only the first element of lag will take effect. Only the lag order of \(\boldsymbol{Y}_t\) will be specified, and all other elemnts will be ignored automatically.

alpha corresponds to the notation \(\boldsymbol{\alpha}\) in model (2.13), which should be an numeric object of length 1 or \(N\). The value of each entry of alpha should fall in the range from 0 to 1. If all quantile equations of QVAR are to be estimated at the same tail probability, then you just need to assign alpha a scalar, e.g. alpha = 0.95. If a QVAR model whose each quantile equation is estimated at different tail probability is considered, then you should pass an vector of length \(N\). Take a 3-dimnsional QVAR as example, of which the tail probabilities of three quantile eqautions are 0.25, 0.50, 0.75 respectively, then the correct way is to pass alpha = c(0.25, 0.50, 0.75).

2.5.1.2 method

bayes-al and bayes-mal are available values for argument method. bayes-al represents the Bayesian method based on AL likelihood, which estimate BQVAR based on the posteriors from (2.4) to (2.7), while bayes-mal method executes MCMC algorithm according to the posteriors from (2.8) to (2.12).

2.5.1.3 Prior and sampler setting: prior, samplerSetting

The arguments prior and smaplerSetting are intended for customizing prior distribution of model parameters and MCMC sampler. To simpify the usage in some case, all components of prior and samplerSetting have default values. Once any component necessary is not specified explicitly, then the default value will be adopted as alternative. A complete setting of prior should be a named list object that contains following components:

Table 2.1: Components of prior arguments

Components	Type/Shape	Default values	Notes
mu_A	\(N \times M\) matrix	\(\mathbf{0}_{N\times M}\)	prior mean of \(\mathbf{B}(\boldsymbol{\alpha})\)
Sigma_A	list contains \(N\) positive definite \(M \times M\) matrix	list contains \(N\) \(100 \times \mathbf{I}_{M}\)	prior covariance matrices of each row of \(\mathbf{B}(\boldsymbol{\alpha})\)
Sigma	\(N\times N\) positive definite matrix	\(\mathrm{diag}\left(\tilde{\sigma}_1^2, \tilde{\sigma}_2^2, \cdots, \tilde{\sigma}_N^2\right)\)	matrix parameter of Inverse Wishart distribution of \(\tilde{\boldsymbol{\Sigma}}\), which only takes effect when method = 'bayes-mal'
nu	positive numeric	\(N+1\)	degree of freedom of Inverse Whishart distribution of \(\tilde{\boldsymbol{\Sigma}}\), which only takes effect when method = 'bayes-mal'
n_delta	\(N\times 1\) positive numeric	\(\boldsymbol{1}_N\)	vector whose \(i\)-th entry is the shape parameter \(\underline{n}_{\delta,i}\) of the prior distribution of the scale parameter \(\delta_i\)
s_delta	\(N \times 1\) positive numeric	\(\boldsymbol{1}_N\)	vector whose \(i\)-th entry is the scale parameter \(\underline{s}_{\delta,i}\) of the prior distribution of the scale parameter \(\delta_i\)
n_lambda	\(N \times M\) matrix	-	matrix whose \((i,j)\) entry is the shape parameter of the prior distribution of penalty parameter \(\lambda_{ij}\)
s_lambda	\(N \times M\) matrix	-	matrix whose \((i,j)\) entry is the scale parameter of the prior distribution of penalty parameter \(\lambda_{ij}\)

Where \(M = N P + K Q + 1\). Note that if either n_lambda or s_lambda is not contained in prior argument, then no penalty will be imposed on \(\mathbf{B}(\boldsymbol{\alpha})\).

Complete specification of samplerSetting include: initial values of parameter, the number of sampling (including burn-in and valid sampling number) and the thinning interval, as shown below:

Table 2.2: Components of samplerSetting argument

Components	Type/Shape	Default value	Notes
init_A	\(N\times M\) matrix	\(\mathbf{0}_{N\times M}\)	initial value of \(\mathbf{B}(\boldsymbol{\alpha})\)
init_Sigma	\(N\times N\) positive definite matrix	\(\mathrm{diag}\left(\tilde{\sigma}_1^2, \tilde{\sigma}_2^2, \cdots, \tilde{\sigma}_N^2\right)\)	initial value of \(\tilde{\boldsymbol{\Sigma}}\)
init_delta	\(N\times 1\) positive numeric	\(0.1 \times \boldsymbol{1}_{N}\)	initial value of \(\boldsymbol{\delta}\)
n_sample	positive int	500	number of valid sampling
n_burn	positive int	500	number of burn-in sampling
n_thin	positive int	1	thinning interval

The total sampling number is n_sample * n_thin + n_burn.

2.5.2 Examples

library(bayesQVAR)
# simulate data
set.seed(810)
n <- 5
alpha <- rep(0.95, n)
simuData(n, alpha, 300)  # internal function to generate data
# visualize data
library(ggplot2)
plot(data_end[, 1], type = "l")
for(i in 2:ncol(data_end)){
    lines(data_end[, i], col = i)
}

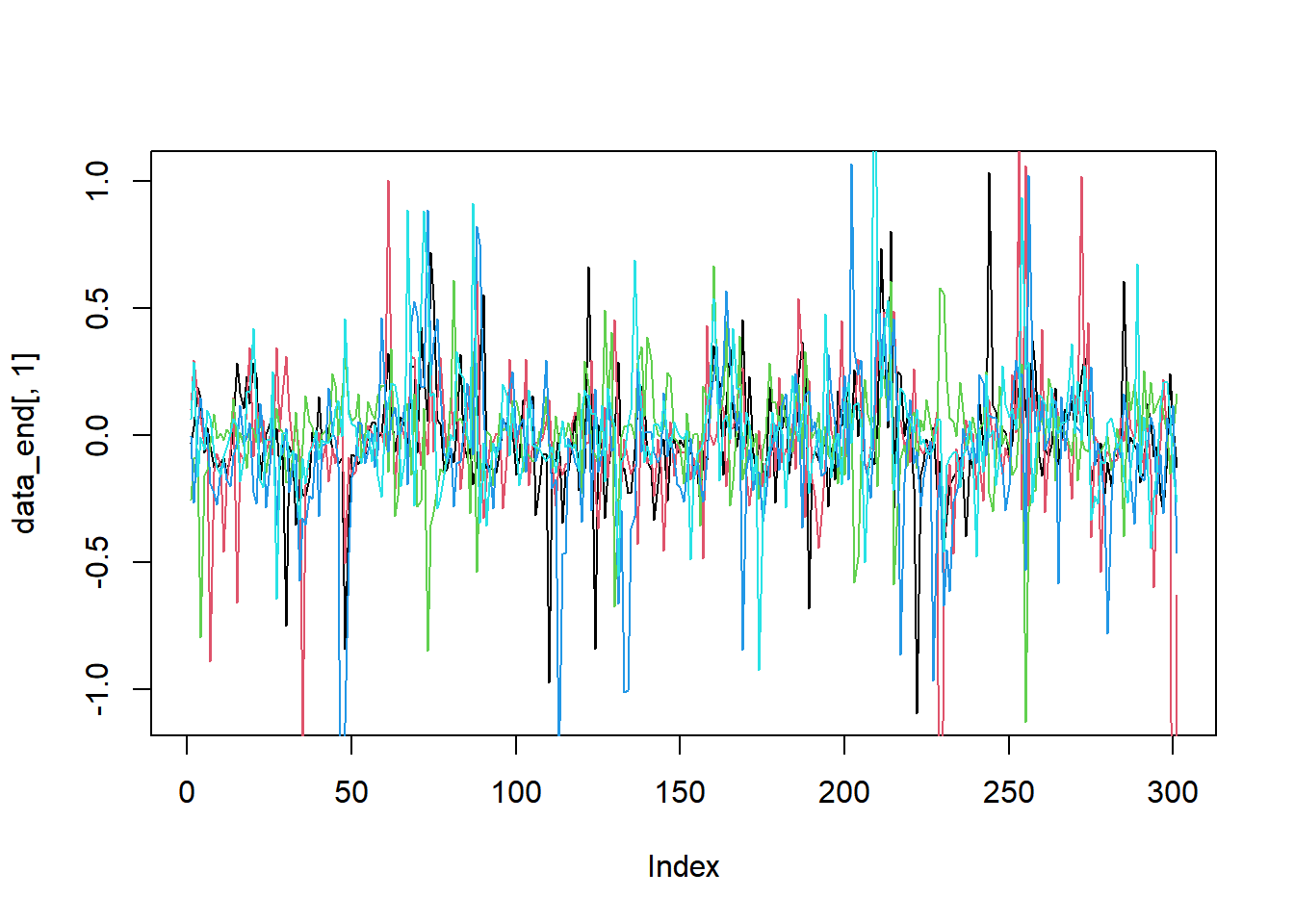
Figure 2.1: Simulated data

# set prior, samplerSetting
n_end <- ncol(data_end)
n_exo <- ncol(data_exo)
lag_end <- 1
lag_exo <- 1
n_x <- n_end * lag_end + n_exo * lag_exo + 1
alpha <- rep(rep(0.95, 5), n / 5)
s <- sqrt(2 / alpha / (1 - alpha))
xi <- (1 - 2 * alpha) / alpha / (1 - alpha)
Sigma <- diag(s^2)
Sigma_A <- list()
for(i in 1:n){
    Sigma_A[[i]] = 100 * diag(n_x)
}
prior <- list(
    mu_A = matrix(0, n_end, n_x),
    Sigma_A = Sigma_A,
    Sigma = Sigma,
    nu = 100 * n_end + 1,
    n_delta = rep(1, n_end),
    s_delta = rep(1, n_end)
)
samplerSetting <- list(
    # initial value
    init_A = matrix(0, n_end, n_x),
    init_Sigma = Sigma,
    init_delta = rep(0.1, n_end),
    n_sample = 250,
    # burn-in, thinning, step size of delta
    n_burn = 250,
    n_thin = 2
)
# estimate QVAR model
BQVAR_mal <- bayesQVAR::estBQVAR(
    data_end = data_end,
    data_exo = data_exo,
    alpha = alpha,
    lag = c(lag_end, lag_exo),
    method = "bayes-mal",
    prior = prior,
    samplerSetting = samplerSetting,
    printFreq = 250,
    mute = FALSE
)
BQVAR_al <- bayesQVAR::estBQVAR(
    data_end = data_end,
    data_exo = data_exo,
    alpha = alpha,
    lag = c(lag_end, lag_exo),
    method = "bayes-al",
    prior = prior,
    samplerSetting = samplerSetting,
    printFreq = 1,
    mute = FALSE
)
# Extract estimate matrices, and calculate quantile of interest
Y <- BQVAR_mal@designMat[["Y"]]
X <- BQVAR_mal@designMat[["X"]]
Ap_est_mal <- BQVAR_mal@estimates[["A"]]
Ap_est_al <- BQVAR_al@estimates[["A"]]
quant_est_mal <- Ap_est_mal %*% X
quant_est_al <- Ap_est_al %*% X
# plot the estimated quantile
par(mfrow = c(3, 2))
for(i in 1:n_end){
    plot(Y[i, ], type = "l")
    lines(quant_alpha[-1, i], col = "blue")
    lines(quant_est_al[i, ], col = "orange")
    lines(quant_est_mal[i, ], col = "red")
}
# performance evaluation
mse_a_al <- sqrt(sum((Ap_est_al[, 1:(n_x - 1)] - cbind(A_alpha, gamma_alpha))^2))
mse_a_mal <- sqrt(sum((Ap_est_mal[, 1:(n_x - 1)] - cbind(A_alpha, gamma_alpha))^2))
mse_quant_al <- sqrt(sum((quant_est_al - quant_alpha[-1, ])^2))
mse_quant_mal <- sqrt(sum((quant_est_mal - quant_alpha[-1, ])^2))
mse_quant_al; mse_quant_mal
mse_a_al; mse_a_mal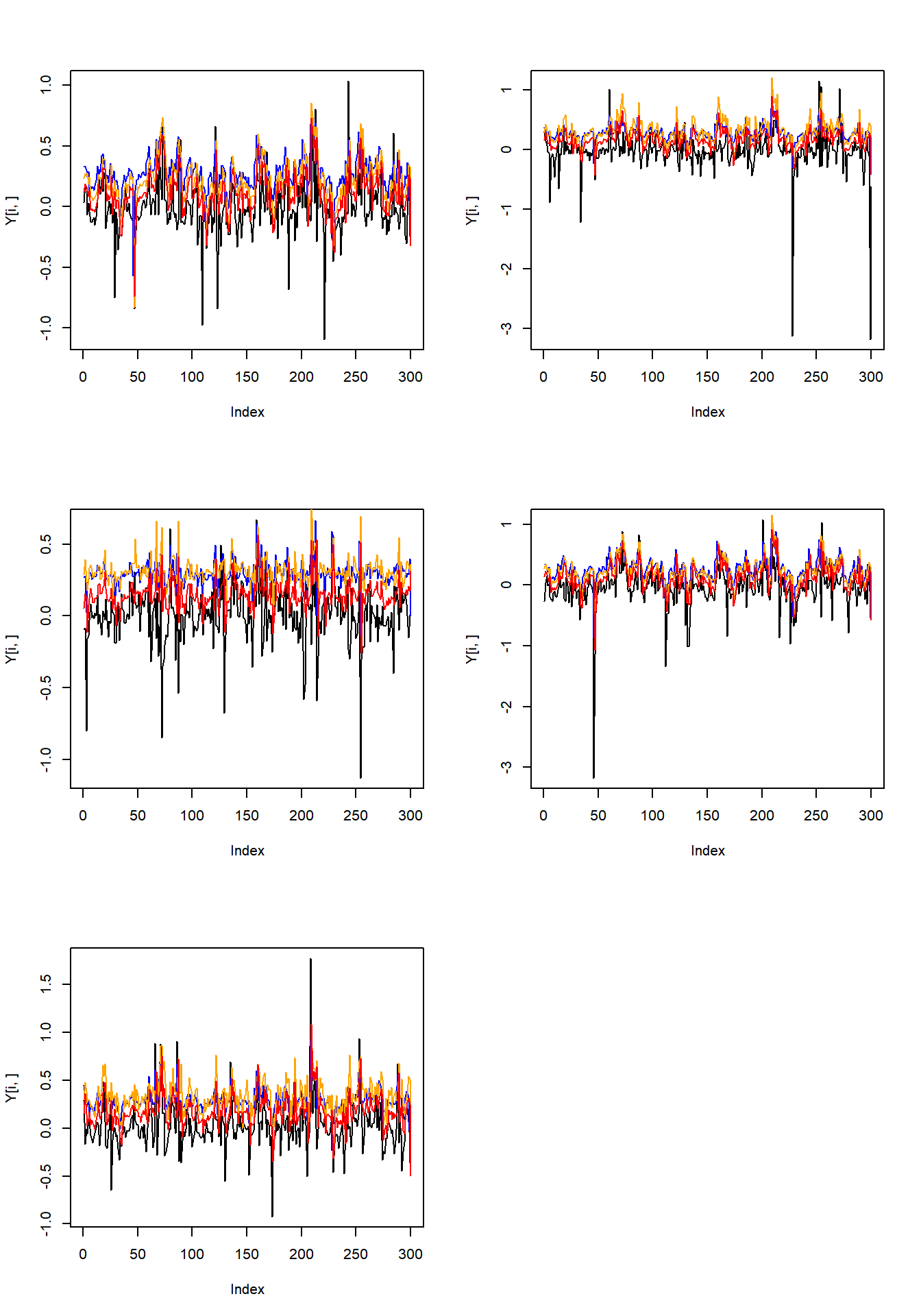

Figure 2.2: Time series, true and estimated quantiles

## Gibbs sampling started at Tue Oct  1 11:12:03 2024
## 
## Iterations 250: 0.21s
## Iterations 500: 0.39s
## Iterations 750: 0.57s
## Gibbs sampling finished at Tue Oct  1 11:12:03 2024
## 
## Estimation started at Tue Oct  1 11:12:03 2024
## 
## 1 equations have been estimated: 0.37s
## 2 equations have been estimated: 0.74s
## 3 equations have been estimated: 1.1s
## 4 equations have been estimated: 1.46s
## 5 equations have been estimated: 1.87s
## Estimation finished at Tue Oct  1 11:12:05 2024
## 
## [1] 8.944108
## [1] 10.03759
## [1] 1.090966
## [1] 0.5611823

As printed above, the method based on MAL-likelihood takes advantages over that based on AL-likelihood in coefficient matrix accuracy, while it has greater quantile estimation error.