Capítulo 3 Análisis Estructural
3.1 Introducción
La pregunta central de este capítulo es: ¿cómo expresar mediante una función la estructura de la dependencia o correlación espacial observada en una realización?
En la literatura geoestadística, esto se conoce como análisis estructural de la dependencia espacial y constituye un paso importante para la predicción óptima (kriging).
La eficacia del kriging depende directamente de las funciones que describen la dependencia espacial detectada.
Las funciones principales son:
- Funciones de covarianza (covariogramas)
- Semivariogramas
Sin embargo, los semivariogramas y covariogramas empíricos calculados a partir de los datos observados no siempre cumplen con las propiedades teóricas necesarias.
Por esta razón, se ajustan modelos teóricos válidos (modelos de covarianza o semivariogramas).
En este capítulo nos enfocaremos en:
- Los modelos teóricos de covarianza y semivariogramas más utilizados.
- La construcción de sus contrapartes empíricas o experimentales.
- El ajuste de un modelo válido a los datos observados.
Daremos mayor atención a los semivariogramas, ya que abarcan un espectro más amplio de variables regionalizadas que los modelos de covarianza.
Finalmente, todo conocimiento adicional sobre el fenómeno regionalizado estudiado es de gran utilidad para orientar el análisis. Aunque algunos autores incluyen técnicas de análisis exploratorio, aquí nos centraremos en la detección de dependencia espacial en la realización observada y su representación mediante un semivariograma o una función de covarianza, según la hipótesis de estacionariedad asumida.
3.2 Función de covarianza
3.2.1 Definición y propiedades
La función de covarianza de un campo aleatorio espacial se define como:
\[ C(s_i, s_j) = C(Z(s_i), Z(s_j)) = E \big[ (Z(s_i) - \mu(s_i))(Z(s_j) - \mu(s_j)) \big], \quad \forall s_i, s_j \in D. \quad \tag{3.1} \]
Bajo la hipótesis de estacionariedad de segundo orden, la función de covarianza cumple las siguientes propiedades:
- Depende únicamente del vector de separación \(h\), no de las posiciones absolutas:
\[ C(h) = E[(Z(s+h) - \mu)(Z(s) - \mu)], \quad \forall s, s+h \in D \subset \mathbb{R}^d. \quad \tag{3.2} \]
Definición 3.1 (Isotropía/Anisotropía).
- Si \(C(h)\) depende solo de la distancia \(|h|\), se dice que el
proceso es isotrópico.
- Si también depende de la dirección de \(h\), se dice que es
anisotrópico.
Definición 3.2 (Homogeneidad).
Un campo aleatorio es homogéneo si es intrínsecamente estacionario e
isotrópico.
- Está acotada por su valor en el origen:
\[ |C(h)| \leq C(0) = V(Z(s)). \quad \tag{3.3} \]
Esto se deduce de la desigualdad de Cauchy-Schwarz y de la definición de varianza.
- Es una función par:
\[ C(h) = C(-h). \quad \tag{3.4} \]
Esto se debe a la simetría en la definición de la covarianza.
- Es una función definida positiva:
Para cualquier combinación lineal \(\sum_{i=1}^n \lambda_i Z(s_i)\):
\[ V\!\left(\sum_{i=1}^n \lambda_i Z(s_i)\right) = \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j C(s_i - s_j) \geq 0, \quad \forall n, \lambda_i \in \mathbb{R}. \quad \tag{3.5} \]
Esto implica que \(C(h)\) es una función positiva definida en \(\mathbb{R}^d\).
Es la condición esencial para que una función sea un covariograma válido.
- Propiedades de estabilidad (Chilès y Delfiner, 1999):
- Si \(C_k(h)\) son funciones de covarianza y \(C_k(h) \to C(h)\) cuando \(k \to \infty\), entonces \(C(h)\) es también un covariograma válido.
- Cualquier combinación lineal de funciones de covarianza con coeficientes positivos es también una función de covarianza.
- En general, si \(C(h, \theta)\) es válido y \(\mu(d\theta)\) es una medida positiva, entonces
\[ \int_A C(h,\theta)\,\mu(d\theta) \quad \tag{3.6} \]
es también un covariograma, siempre que la integral exista.
- El producto de funciones de covarianza es también una función de covarianza.
3.2.2 Funciones de covarianza isotrópicas teóricas
En esta sección nos enfocamos en funciones de covarianza isotrópicas, ya que los modelos anisotrópicos muchas veces pueden reducirse a una forma isotrópica.
Recordemos:
- Sea \(h \in \mathbb{R}^d\) el vector de separación.
- En el caso isotrópico, la covarianza solo depende de su norma \(|h|\).
Advertencia: una función positiva definida en \(\mathbb{R}^{d_1}\) también lo es en \(\mathbb{R}^{d_2}\) si \(d_2 \leq d_1\), pero no necesariamente al revés.
3.2.2.1 Ejemplo (Covariograma triangular o tent)
\[ C(h) = \begin{cases} \sigma^2 \left(1 - \frac{|h|}{a}\right), & 0 \leq |h| \leq a, \\ 0, & |h| > a, \end{cases} \quad \tag{3.7} \]
Este covariograma es válido en \(\mathbb{R}^1\), pero no es positivo definido en \(\mathbb{R}^2\).
De hecho, para ciertos valores de \(k\) (\(k=8\) por ejemplo), se cumple que:
\[ V\left(\sum_{i=1}^{k\times k} \lambda_i Z(s_i)\right) < 0, \]
lo que invalida la positividad requerida.
Aspectos a considerar en cualquier covariograma:
- Comportamiento en el origen: garantiza continuidad y regularidad espacial. En \(h=0\), el valor coincide con la varianza \(C(0)\).
- Comportamiento a grandes distancias: la covarianza tiende a 0 al aumentar \(|h|\). El punto donde se anula se denomina rango.
3.2.2.2 Modelo esférico
\[ C(|h|) = \begin{cases} m\left(1 - \frac{3}{2}\frac{|h|}{a} + \frac{1}{2}\left(\frac{|h|}{a}\right)^3\right), & 0 \leq |h| \leq a, \\ 0, & |h| > a, \end{cases} \quad \tag{3.8} \]
- Válido en \(\mathbb{R}^1, \mathbb{R}^2, \mathbb{R}^3\).
- Muy usado en aplicaciones prácticas.
- Disminuye casi linealmente hasta anularse en \(a\).
- Representa fenómenos continuos pero no diferenciables.
3.2.2.3 Modelo exponencial
\[ C(|h|) = m \exp\!\left(-\frac{|h|}{a}\right), \quad a > 0. \quad \tag{3.9} \]
- Válido en \(\mathbb{R}^d, d \geq 1\).
- Continuo pero no diferenciable en el origen.
- El rango práctico es \(a' = 3a\) (donde la covarianza cae al 5% de \(C(0)\)).
3.2.2.4 Modelo gaussiano
\[ C(|h|) = m \exp\!\left(-\frac{|h|^2}{a^2}\right), \quad a > 0. \quad \tag{3.10} \]
- Válido en \(\mathbb{R}^d, d \geq 1\).
- Infinitamente diferenciable (muy suave).
- El rango práctico es \(a' = a\sqrt{3}\).
3.2.2.5 Modelo Matérn
Tomado de Bevilacqua et al. (2019):
\[ C(h) \;=\; 2^{\,1-\kappa} \, \Gamma(\kappa)^{-1} \, h^{\kappa} \, K_{\kappa}(h) \] donde \(F(\cdot,\cdot,\cdot,\cdot)\) es la función hipergeométrica Gaussiana, \(\Gamma(\cdot)\) es la función Gamma y \(K_{\kappa}(\cdot)\) la función modificada de Bessel de segundo tipo de orden \(\kappa\).
Si \(h\) es la distancia geodésica, entonces \(\kappa \in (0,0.5]\).
3.2.2.6 Wendland Generalizada
Tomado de Bevilacqua et al. (2019):
\[ C(h) \;=\; A \,(1-h^2)^{\beta+\kappa} \, F\!\left(\tfrac{\beta}{2}, \tfrac{\beta+1}{2}, 2\beta+\kappa+1, 1-h^2\right)\, 1(h \in [0,1]) \]
donde \(\mu \ge 0.5(d+1)+\kappa\),
y
\[ A \;=\; \frac{\Gamma(\kappa)\,\Gamma(2\kappa+\beta+1)}{\Gamma(2\kappa)\,\Gamma(\beta+1-\kappa)\,2^{\beta+1}} \]
y \(F(\cdot,\cdot,\cdot,\cdot)\) es la función hipergeométrica Gaussiana.
Los casos \(\kappa=0,1,2\) corresponden respectivamente a los modelos Wend0, Wend1 y Wend2 en GeoModels.
3.2.2.7 Familia estable
Tanto el modelo exponencial como el gaussiano se engloban en la familia:
\[ C(|h|) = \exp\!\left(-\left(\frac{|h|}{a}\right)^{\alpha}\right), \quad a > 0, \; 0 < \alpha \leq 2. \quad \tag{3.11} \]
- Para \(\alpha = 1\): modelo exponencial.
- Para \(\alpha = 2\): modelo gaussiano.
3.2.2.8 Figuras comparativas
En las Figuras 3.1 y 3.2 se muestran las diferencias entre modelos:
- El esférico y el exponencial son lineales cerca del origen.
- El gaussiano presenta un comportamiento parabólico (suave).
- Cuanto menor es el parámetro de escala \(a\), más rápida es la caída de la covarianza.
Los parámetros de suavizamiento (\(\kappa\)) en la Wendland generalizada y Matérn son \(0\) y \(1.5\) respectivamente. El exponente \(\beta\)) en la Wendland generalizada es \(2\).
Code
# GeoCorrFct: Devuelve C(h) para un modelo de GeoModels usando una distancia
library(GeoModels)
# --- Curvas C(h) para distintos 'scale' (rango) con modelo esférico ---
parms1 <- list(mean=0, sill=1, nugget=0, scale=0.2)
parms2 <- list(mean=0, sill=1, nugget=0, scale=0.3)
parms3 <- list(mean=0, sill=1, nugget=0, scale=0.5)
par(mfrow=c(2,3), family="serif")
curve(GeoCorrFct(x, corrmodel="Exponential", param=parms1)$corr,
from=0, to=1, xlab="distancia (h)", ylab="C(h)",
main="Exponencial", lwd=2, lty=2, col=1)
curve(GeoCorrFct(x, corrmodel="Exponential", param=parms2)$corr,
from=0, to=1, add=TRUE, lwd=2, lty=3, col=1)
curve(GeoCorrFct(x, corrmodel="Exponential", param=parms3)$corr,
from=0, to=1, add=TRUE, lwd=2, lty=1, col=1)
par(family="serif")
legend("topright",
legend=c(expression(italic(scale)==0.2),
expression(italic(scale)==0.3),
expression(italic(scale)==0.5)),
lty=c(2,3,1), lwd=2, col=1, bty="n")
curve(GeoCorrFct(x, corrmodel="Spherical", param=parms1)$corr,
from=0, to=1, xlab="distancia (h)", ylab="C(h)",
main="Esférica", lwd=2, lty=2, col=1)
curve(GeoCorrFct(x, corrmodel="Spherical", param=parms2)$corr,
from=0, to=1, add=TRUE, lwd=2, lty=3, col=1)
curve(GeoCorrFct(x, corrmodel="Spherical", param=parms3)$corr,
from=0, to=1, add=TRUE, lwd=2, lty=1, col=1)
par(family="serif")
legend("topright",
legend=c(expression(italic(scale)==0.2),
expression(italic(scale)==0.3),
expression(italic(scale)==0.5)),
lty=c(2,3,1), lwd=2, col=1, bty="n")
curve(GeoCorrFct(x, corrmodel="Gaussian", param=parms1)$corr,
from=0, to=1, xlab="distancia (h)", ylab="C(h)",
main="Gausiana", lwd=2, lty=2, col=1)
curve(GeoCorrFct(x, corrmodel="Gaussian", param=parms2)$corr,
from=0, to=1, add=TRUE, lwd=2, lty=3, col=1)
curve(GeoCorrFct(x, corrmodel="Gaussian", param=parms3)$corr,
from=0, to=1, add=TRUE, lwd=2, lty=1, col=1)
par(family="serif")
legend("topright",
legend=c(expression(italic(scale)==0.2),
expression(italic(scale)==0.3),
expression(italic(scale)==0.5)),
lty=c(2,3,1), lwd=2, col=1, bty="n")
parms1 <- list(mean=0, sill=1, nugget=0, scale=0.2,power2=2,smooth=0)
parms2 <- list(mean=0, sill=1, nugget=0, scale=0.3,power2=2,smooth=0)
parms3 <- list(mean=0, sill=1, nugget=0, scale=0.5,power2=2,smooth=0)
curve(GeoCorrFct(x, corrmodel="GenWend", param=parms1)$corr,
from=0, to=1, xlab="distancia (h)", ylab="C(h)",
main="Wendland Generalizada", lwd=2, lty=2, col=1)
curve(GeoCorrFct(x, corrmodel="GenWend", param=parms2)$corr,
from=0, to=1, add=TRUE, lwd=2, lty=3, col=1)
curve(GeoCorrFct(x, corrmodel="GenWend", param=parms3)$corr,
from=0, to=1, add=TRUE, lwd=2, lty=1, col=1)
par(family="serif")
legend("topright",
legend=c(expression(italic(scale)==0.2),
expression(italic(scale)==0.3),
expression(italic(scale)==0.5)),
lty=c(2,3,1), lwd=2, col=1, bty="n")
parms1 <- list(mean=0, sill=1, nugget=0, scale=0.2,smooth=1.5)
parms2 <- list(mean=0, sill=1, nugget=0, scale=0.3,smooth=1.5)
parms3 <- list(mean=0, sill=1, nugget=0, scale=0.5,smooth=1.5)
curve(GeoCorrFct(x, corrmodel="Matern", param=parms1)$corr,
from=0, to=1, xlab="distancia (h)", ylab="C(h)",
main="Matérn", lwd=2, lty=2, col=1)
curve(GeoCorrFct(x, corrmodel="Matern", param=parms2)$corr,
from=0, to=1, add=TRUE, lwd=2, lty=3, col=1)
curve(GeoCorrFct(x, corrmodel="Matern", param=parms3)$corr,
from=0, to=1, add=TRUE, lwd=2, lty=1, col=1)
par(family="serif")
legend("topright",
legend=c(expression(italic(scale)==0.2),
expression(italic(scale)==0.3),
expression(italic(scale)==0.5)),
lty=c(2,3,1), lwd=2, col=1, bty="n")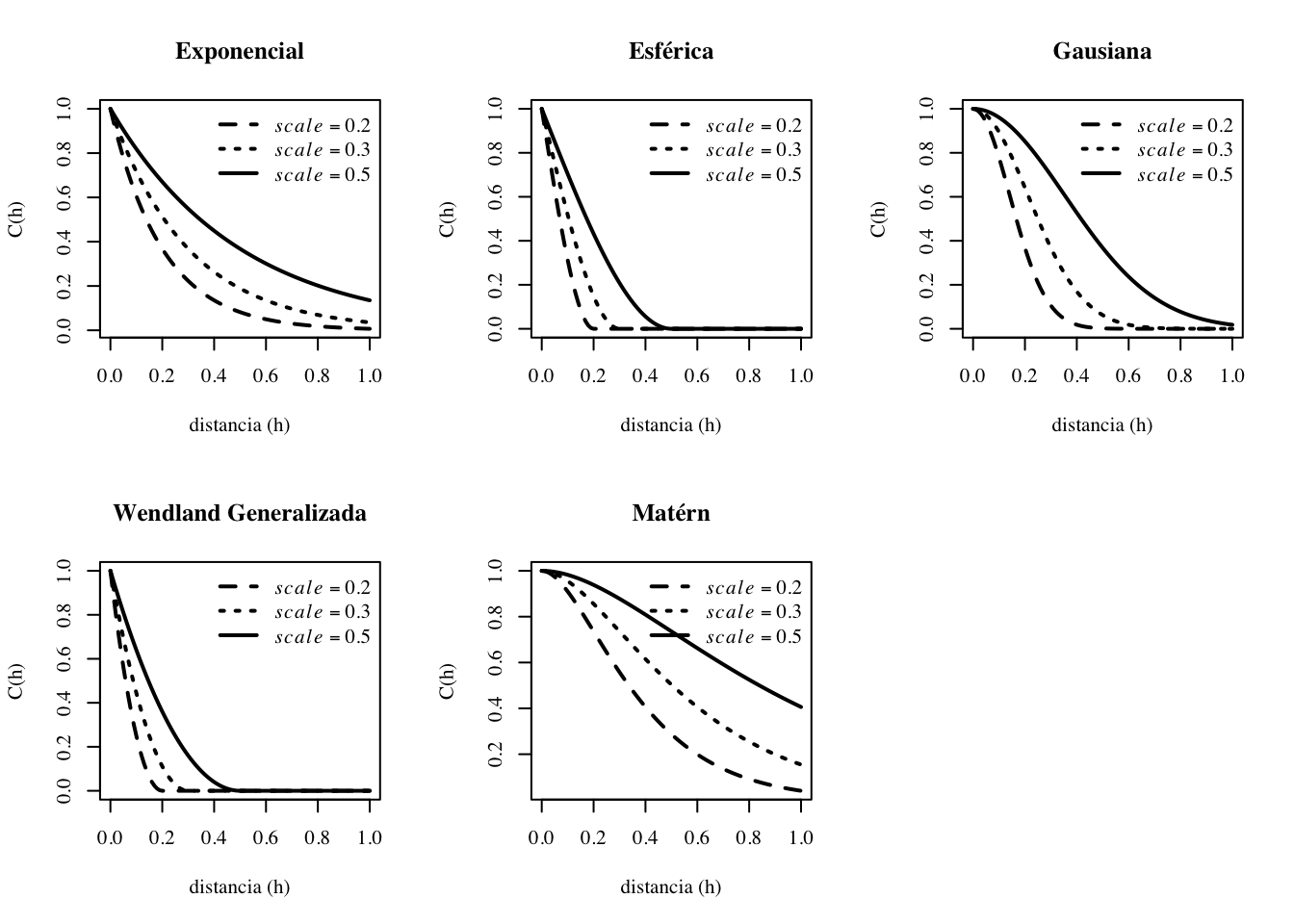
Figura 3.1: Covariogramas esférico, exponencial, gaussiano, genland generalizada y matern con distintos valores de parámetro de escala a.
Code
# Devuelve C(h) para un modelo de GeoModels usando la matriz de covarianza 2x2
parms_exp <- list(mean=0, sill=1, nugget=0, scale=0.3)
parms_gw <- list(mean=0, sill=1, nugget=0, scale=0.3,power2=2,smooth=0)
parms_mat <- list(mean=0, sill=1, nugget=0, scale=0.3,smooth=1.5)
# Exponencial
curve(GeoCorrFct(x, corrmodel="Exponential", param=parms_exp)$corr,
from=0, to=1, xlab="distance (h)", ylab="C(h)",
lwd=2, lty=2, col="red")
# Esférica
curve(GeoCorrFct(x, corrmodel="Spherical", param=parms_exp)$corr,
from=0, to=1, add=TRUE,
lwd=2, lty=4, col="blue")
# Gaussiana
curve(GeoCorrFct(x, corrmodel="Gaussian", param=parms_exp)$corr,
from=0, to=1, add=TRUE,
lwd=2, lty=6, col="darkgreen")
# Wendland Generalizada
curve(GeoCorrFct(x, corrmodel="GenWend", param=parms_gw)$corr,
from=0, to=1, add=TRUE,
lwd=2, lty=3, col="purple")
# Matérn
curve(GeoCorrFct(x, corrmodel="Matern", param=parms_mat)$corr,
from=0, to=1, add=TRUE,
lwd=2, lty=1, col="orange")
# Leyenda
par(family="serif")
legend("topright",
legend=c("Exponencial",
"Esférica",
"Gaussiana",
"Wendland Generalizada",
"Matérn"),
col=c("red","blue","darkgreen","purple","orange"),
lty=c(2,4,6,3,1), lwd=2, bty="n")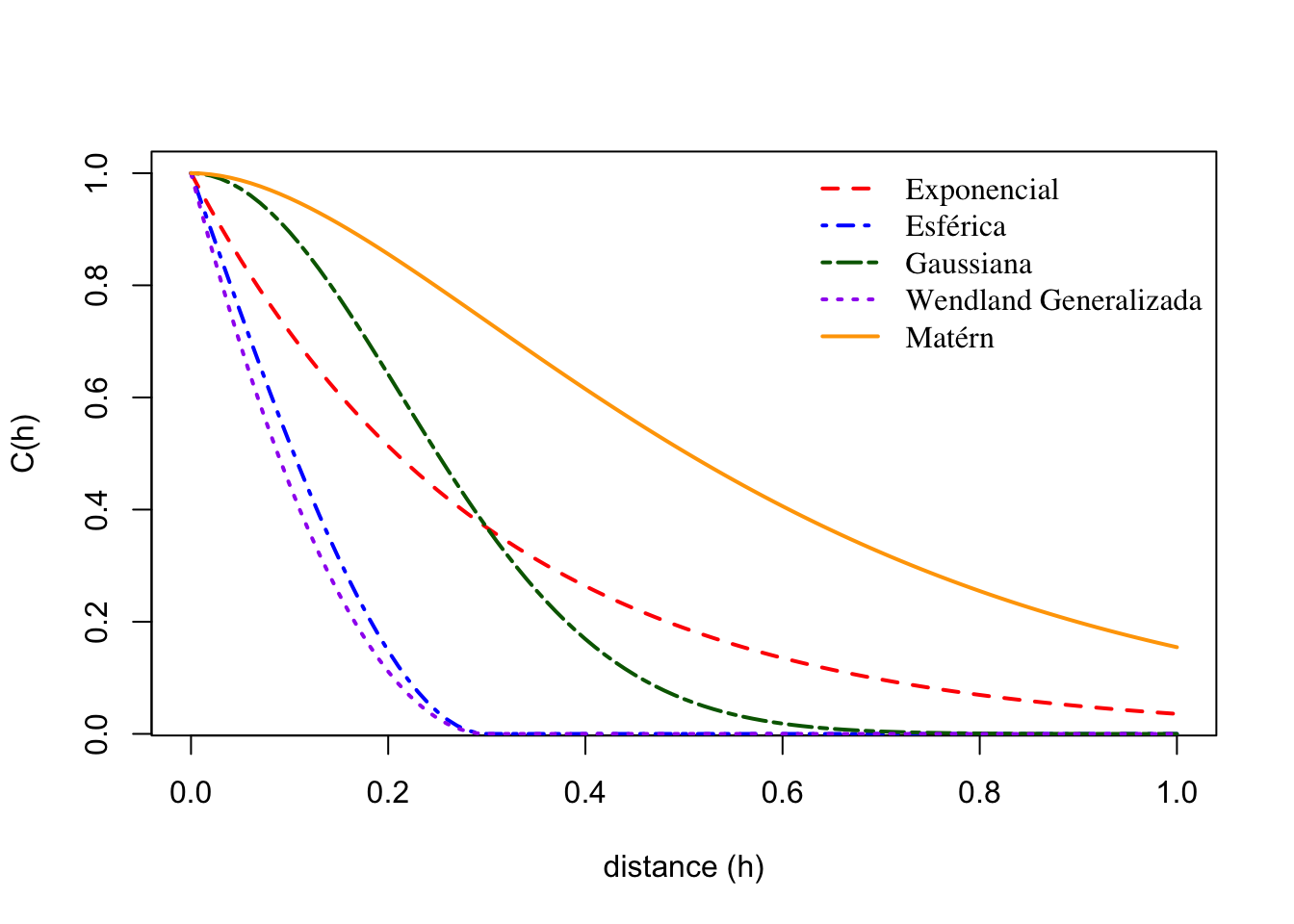
Figura 3.2: Covariogramas esférico, exponencial, gaussiano, genland generalizada y matern con distintos valores de parámetro de escala a.
3.3 Covariograma empírico
En el marco de estacionariedad de segundo orden, el estimador de momentos (MoM) del covariograma es
\[ \hat C(h) \;=\; \frac{1}{\#N(h)} \sum_{(i,j)\in N(h)} \big(Z(s_i)-\bar Z\big)\big(Z(s_j)-\bar Z\big), \quad \tag{3.12} \]
donde \(N(h)=\{(i,j): \|s_i-s_j\|\approx h\}\) es el conjunto de pares separados por la distancia \(h\) (o el bin correspondiente), \(\#N(h)\) su cardinalidad, y \(\bar Z=\tfrac{1}{n}\sum_{i=1}^n Z(s_i)\) la media muestral.
Observaciones:
- \(\hat C(h)\) es sesgado en presencia de dependencia espacial (\(E[\hat C(h)] \neq C(h)\)); el sesgo crece cuando \(\#N(h)\) es pequeño.
- El covariograma empírico puede no ser definido-positivo y, por ello, no debe usarse directamente para predicción.
- Suele definirse sólo en unos pocos lags y carece de significado físico.
- Se recomienda ajustar un modelo teórico válido \(C_\theta(h)\) a \(\hat C(h)\).
3.4 Semivariograma
3.4.1 Definición y propiedades
Definición. El semivariograma se define como
\[ \gamma(s_i-s_j)=\tfrac12\,\mathrm{V}\!\big(Z(s_i)-Z(s_j)\big) \; \tag{3.13} \]
Bajo estacionariedad de segundo orden / hipótesis intrínseca (sin deriva),
\[ \gamma(h)=\tfrac12\,\mathrm{V}\!\big(Z(s+h)-Z(s)\big) =\tfrac12\,\mathrm{E}\!\left[\big(Z(s+h)-Z(s)\big)^2\right] \; \tag{3.14} \]
La relación con la covarianza es
\[ C(h)=C(0)-\gamma(h) \; \tag{3.15} \]
Propiedades:
- \(\gamma(0)=0\) (con posible discontinuidad práctica: nugget).
- Función par: \(\gamma(h)=\gamma(-h)\).
- No negatividad: \(\gamma(h)\ge 0\).
- Definida-negativa condicional (estacionariedad intrínseca):
\[ \sum_{i=1}^n\sum_{j=1}^n \lambda_i\lambda_j\,\gamma(s_i-s_j)\le 0, \quad \text{si } \sum_{i=1}^n\lambda_i=0 \; \tag{3.16} \] 5. Crecimiento asintótico controlado (intrínseca, sin deriva):
\[ \lim_{\|h\|\to\infty}\frac{\gamma(h)}{\|h\|^2}=0. \; \tag{3.17} \]
Comentario. El semivariograma es preferible para inferencia porque no exige conocer \(\mu\). Para campos intrínsecos, es en general anisotrópico (depende del vector \(h\)); cuando depende solo de \(\|h\|\), es isotrópico.
Detalle de las propiedades:
- Nulo en el origen. Por definición,
\[ \gamma(0)=0. \; \tag{3.18} \]
En la práctica puede observarse una discontinuidad en el origen (efecto nugget), pero la definición teórica mantiene \(\gamma(0)=0\).
- Función par. El semivariograma satisface
\[ \gamma(h)=\gamma(-h). \; \tag{3.19} \]
En efecto, tomando \(r=s+h\), se tiene
\[ \gamma(h) =\tfrac12\,\mathrm{V}\!\big(Z(r)-Z(r-h)\big) =\gamma(-h). \]
- No negatividad. Al ser la mitad de una varianza de incrementos,
\[ \gamma(h)=\tfrac12\,\mathrm{V}\!\big(Z(s+h)-Z(s)\big)\;\ge\;0. \; \tag{3.20} \]
- Definida-negativa condicional (estacionariedad intrínseca).
Para cualquier conjunto de ubicaciones \(s_1,\ldots,s_n\) y reales \(\lambda_1,\ldots,\lambda_n\) tales que \(\sum_{i=1}^n \lambda_i=0\),
\[ \sum_{i=1}^n\sum_{j=1}^n \lambda_i\lambda_j\,\gamma(s_i-s_j)\;\le\;0. \; \tag{3.16} \]
Bosquejo de prueba. En el caso estacionario de segundo orden,
\[ 0\le \mathrm{V}\!\Big(\sum_{i=1}^n \lambda_i Z(s_i)\Big) =\sum_{i=1}^n\sum_{j=1}^n \lambda_i\lambda_j\,C(s_i-s_j) =\;C(0)\!\sum_{i=1}^n\sum_{j=1}^n \lambda_i\lambda_j -\sum_{i=1}^n\sum_{j=1}^n \lambda_i\lambda_j\,\gamma(s_i-s_j). \]
Imponiendo \(\sum_i \lambda_i=0\) (caso intrínseco), se obtiene \(\sum_{i,j}\lambda_i\lambda_j\,\gamma(s_i-s_j)\le 0\), como en (3.16).
3.4.2 Comportamiento a distancias intermedias y grandes
El semivariograma es, en general, una función monótona no decreciente, por lo que la variabilidad de los incrementos del campo aumenta con la distancia.
En campos estacionarios de segundo orden, el semivariograma (Figura 3.3):
- parte del origen y crece monótonamente con \(h\);
- se aproxima (exacta o asintóticamente) a su valor límite \(C(0)\), la meseta \(m\).
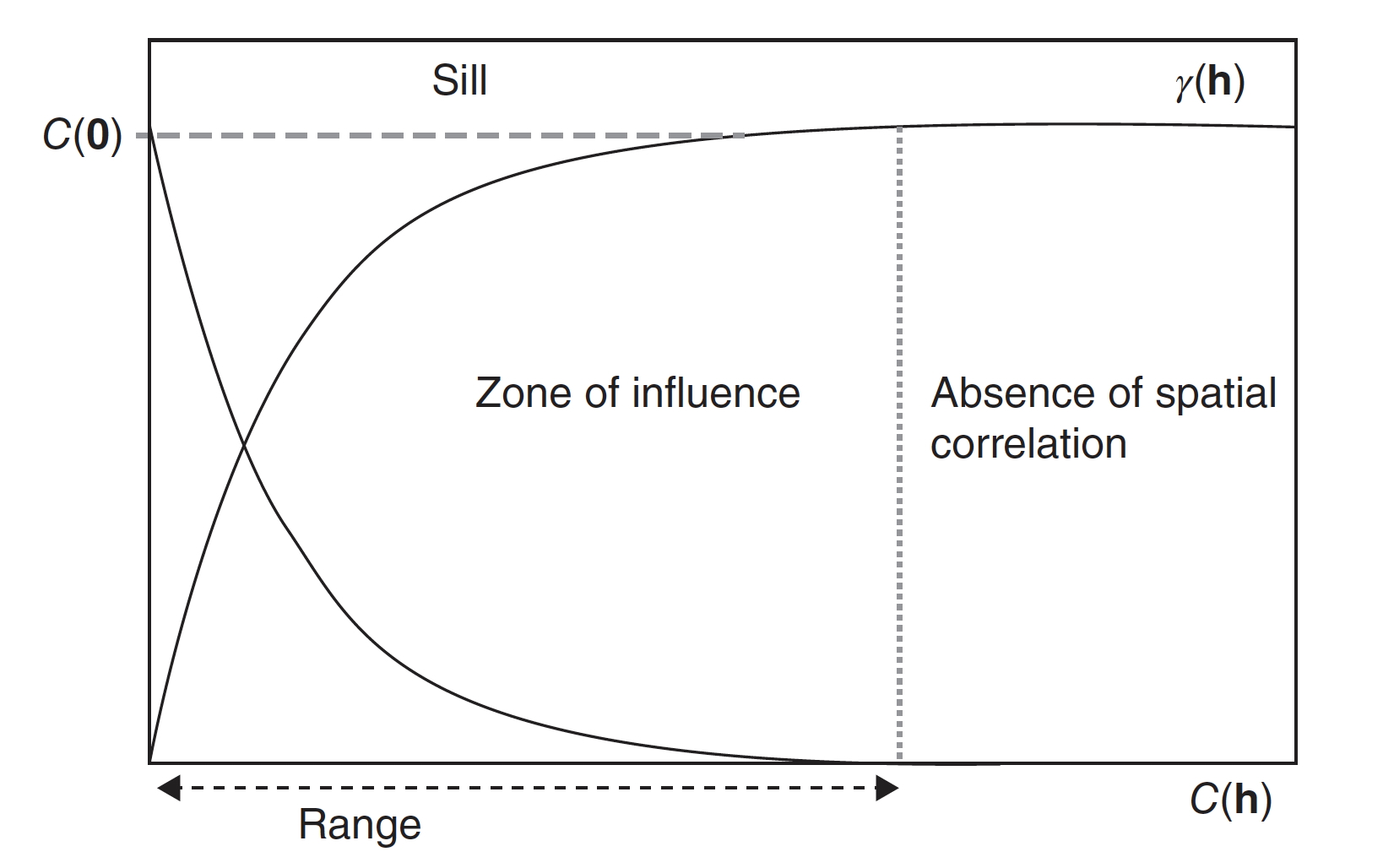
Figura 3.3: Semivariograma acotado y el covariograma como contraparte.
La pendiente indica el cambio en disimilitud con la distancia.
La distancia a la que se alcanza la meseta es el rango, que define el umbral de dependencia espacial (zona de influencia). Cuanto mayor sea el rango, mayor la zona de influencia (Figura 3.4).
Code
library(GeoModels); library(fields)
set.seed(199)
x <- seq(0,1,by=0.01); y <- x
corrmodel = "Spherical"
mean=0;sill=1;nugget=0
f1 <- GeoSim(corrmodel=corrmodel, param=list(mean=mean,sill=sill,nugget=nugget,scale=0.15),coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
f2 <- GeoSim(corrmodel=corrmodel, param=list(mean=mean,sill=sill,nugget=nugget,scale=0.33),coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
f3 <- GeoSim(corrmodel=corrmodel, param=list(mean=mean,sill=sill,nugget=nugget,scale=0.66),coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
op <- par(mfrow=c(1,3), mar=c(2,2,2,1))
image(x,y,f1,col=tim.colors(),main="(a)")
image(x,y,f2,col=tim.colors(),main="(b)")
image(x,y,f3,col=tim.colors(),main="(c)")
Figura 3.4: Realizaciones de un campo gaussiano con covarianza esférica para distintos valores de escala (0.15, 0.33, 0.66).
Si la meseta se alcanza asintóticamente, se usa el rango práctico: la distancia donde \(\gamma(h)=0.95\,m\). Este rango práctico se relaciona estrechamente con el parámetro de escala \(a\) del semivariograma; si la meseta se alcanza exactamente (meseta plana), entonces \(a\) coincide con el rango.1
Es frecuente observar semivariogramas sin meseta: - en presencia de no estacionariedad (p. ej., deriva), - en campos intrínsecamente estacionarios (ver 3.4 punto (v)), - o incluso en campos estacionarios de segundo orden cuando el rango excede la máxima distancia estimable.
3.4.3 Comportamiento cerca del origen
El comportamiento del semivariograma cerca del origen está directamente relacionado con la continuidad y el grado de regularidad del campo aleatorio (rf).
Cuanto más continuo y regular sea el rf en el espacio, más suave y estructurado será su semivariograma cerca de \(h = 0\).
3.4.3.1 Continuidad cuadrática media
Un rf es cuadráticamente medio continuo en un punto \(s\) si se cumple:
\[ \lim_{h \to 0} E\big((Z(s+h) - Z(s))^2\big) = 0. \quad \tag{3.21} \]
Esto implica que:
\[ \lim_{h \to 0} 2V(Z(s)) - 2C(h) = \lim_{h \to 0} \gamma(h) = 0. \quad \tag{3.22} \]
En otras palabras, para que un rf sea continuo en \(s\), el semivariograma debe tender a 0 cuando \(h \to 0\).
3.4.3.2 Suavidad del campo aleatorio
La suavidad está ligada al número de veces que el rf es diferenciable en media cuadrática.
Se mide mediante el orden del semivariograma en el origen, definido como el real \(\alpha\) tal que:
\[ \lim_{|h| \to 0} \frac{\gamma(h)}{|h|^{\alpha}} = c, \quad c \in \mathbb{R}. \quad \tag{3.23} \]
- Si \(\alpha > 1\): el comportamiento es parabólico (suave).
- Si \(\alpha \leq 1\): el comportamiento es lineal (menos regular).
- El caso más común es \(\alpha = 1\).
3.4.3.3 Casos típicos de comportamiento cerca del origen
- Comportamiento lineal:
\(\gamma(h) \sim f(|h|)\).
Común en variables regionalizadas continuas pero no diferenciables.
Las realizaciones muestran picos y gran variabilidad a pequeña escala.
- Comportamiento parabólico:
\(\gamma(h) \sim f(|h|^2)\).
Común en variables altamente regulares. Las realizaciones se ven más suaves y estructuradas. Puede indicar la presencia de una deriva fuerte.
- Discontinuidad en el origen:
El semivariograma presenta un salto en \(h = 0\). Este caso se estudia más adelante (efecto nugget).
Interpretación:
Un semivariograma lineal en el origen implica procesos más irregulares (ruidosos), mientras que uno parabólico indica fenómenos suaves y menos fuzzy.
Esto puede observarse en simulaciones comparativas de campos con distinto grado de regularidad.
La Figura 3.5 muestra que una simulación proveniente de un campo aleatorio con un semivariograma (Matérn en la Figura 3.5) que exhibe un comportamiento parabólico cerca del origen es más suave o menos difuso (nota el parámetros de suavizamiento smooth=1.5), es decir, más estructurado, que otra proveniente de un campo aleatorio con un semivariograma con las mismas características, excepto que presenta un comportamiento lineal cerca del origen (smooth=0.5).
Code
x <- seq(0,1,by=0.01); y <- x
mean=0; sill=1; nugget=0; scale=0.33
f1 <- GeoSim(corrmodel="Matern", param=list(mean=mean,sill=sill,nugget=nugget,scale=scale,smooth=0.5),coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
f2 <- GeoSim(corrmodel="Matern", param=list(mean=mean,sill=sill,nugget=nugget,scale=scale,smooth=1.5),coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
op <- par(mfrow=c(1,2), mar=c(2,2,2,1))
image(x,y,f1,col=tim.colors(),main="(a)")
image(x,y,f2,col=tim.colors(),main="(b)")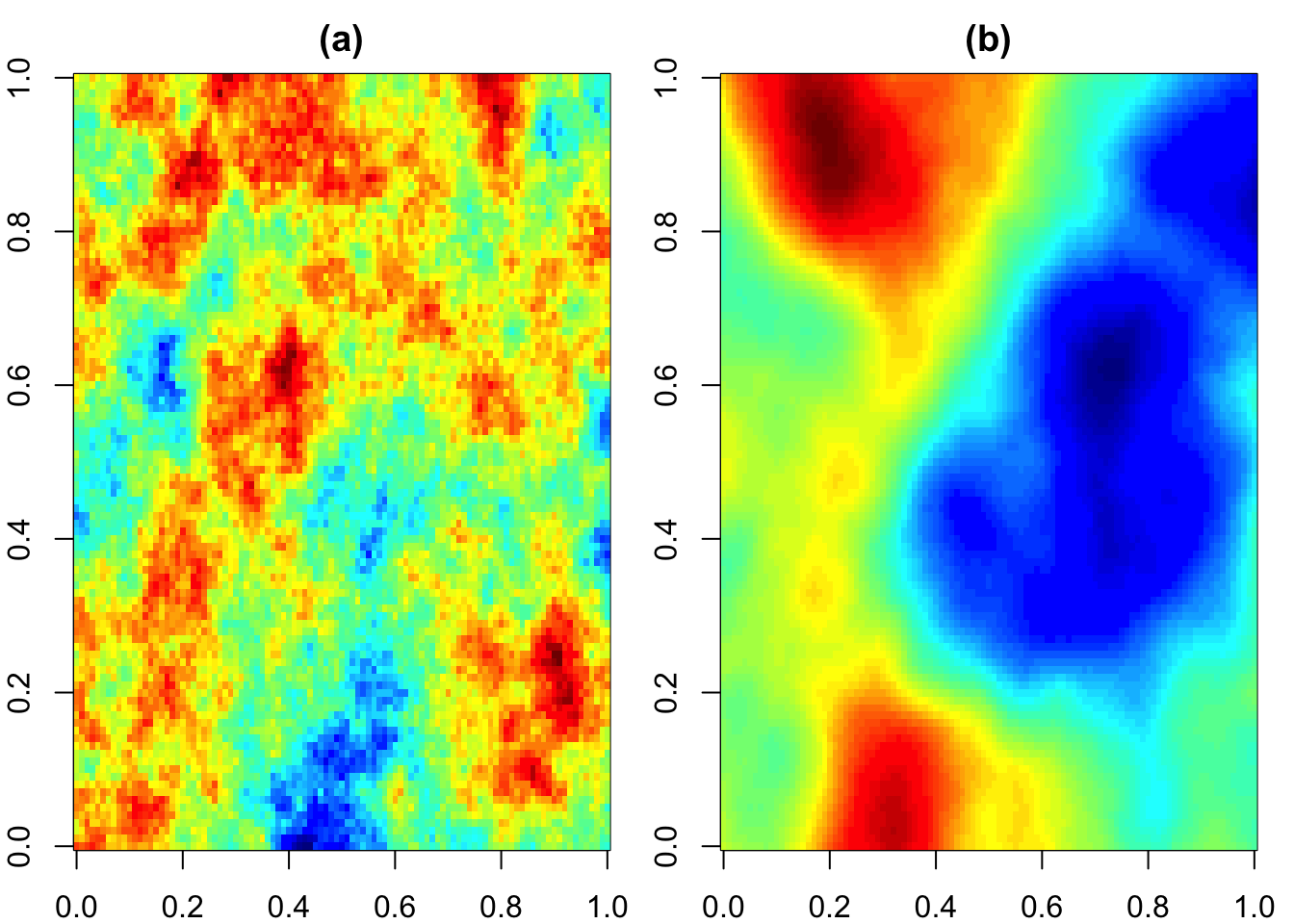
Figura 3.5: Representación en 2D de simulaciones de dos campos aleatorios con un semivariograma que solo difiere en el comportamiento cerca del origen: (a) lineal, (b) parabólico.
3.4.4 Discontinuidad en el origen
Aunque teóricamente el semivariograma debería anularse en el origen, en la práctica esto no siempre ocurre.
Esta discontinuidad en \(h = 0\) se conoce como efecto nugget y suele indicar que la variable regionalizada es muy irregular o incluso discontinua.
Para modelar un semivariograma con efecto nugget basta con sumarlo a cualquier modelo válido como se observa en la Figura
3.6 (nugget=3).
Code
x <- seq(0,1,by=0.01); y <- x
mean=0; sill=1; scale=0.33;smooth=1.5
f1 <- GeoSim(corrmodel="Matern", param=list(mean=mean,sill=sill,nugget=0,scale=scale,smooth=smooth),coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
f2 <- GeoSim(corrmodel="Matern", param=list(mean=mean,sill=sill,nugget=0.25,scale=scale,smooth=smooth),coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
op <- par(mfrow=c(1,2), mar=c(2,2,2,1))
image(x,y,f1,col=tim.colors(),main="(a)")
image(x,y,f2,col=tim.colors(),main="(b)")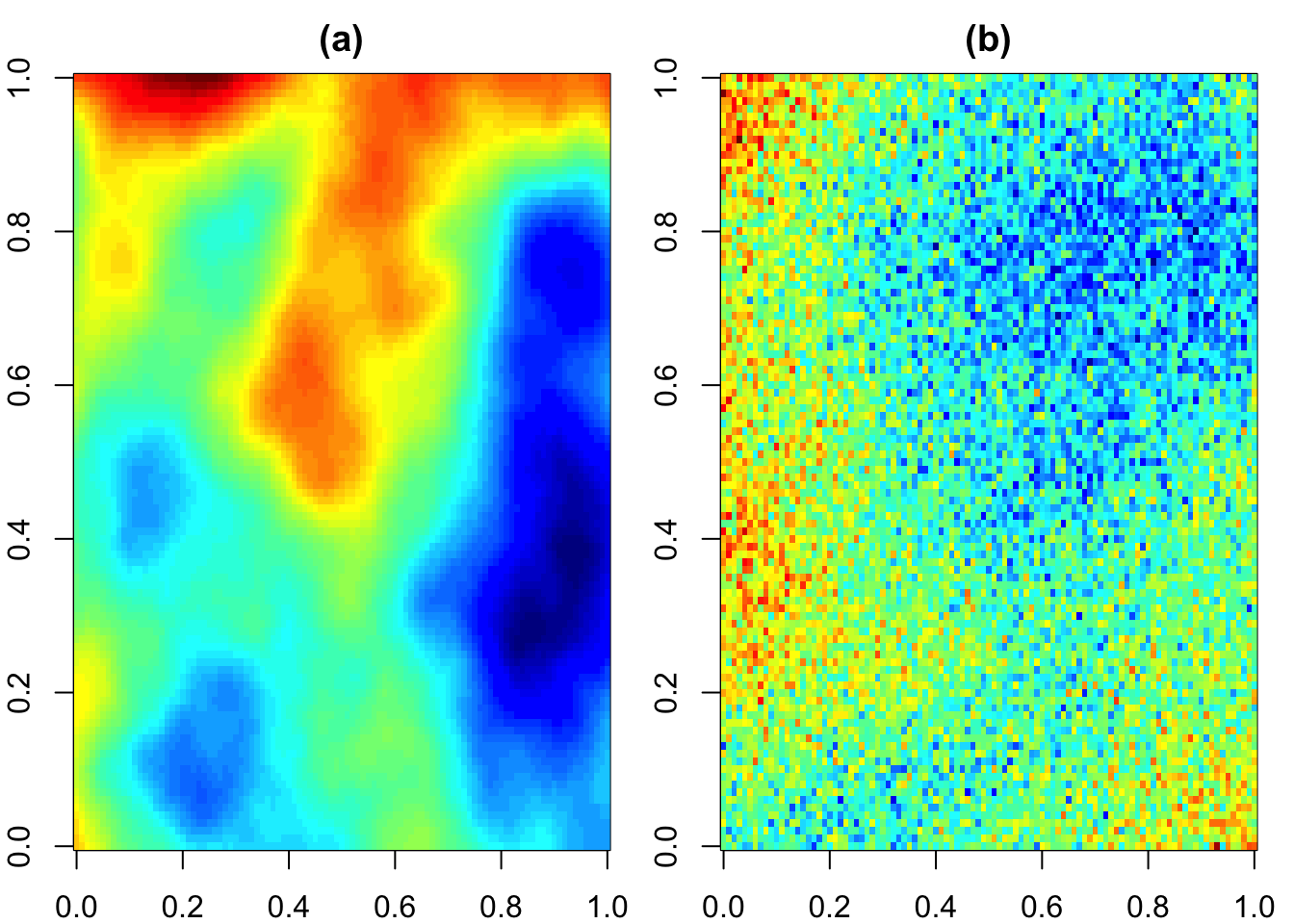
Figura 3.6: Campos simulados de valores usando un semivariograma con parámetro de escala a=0.33: (a) efecto nugget = 0; (b) efecto nugget = 0.25.
En este caso, la meseta total (sill) se divide en dos componentes:
- sill parcial: la parte explicada por la estructura espacial.
- efecto nugget: la discontinuidad en el origen.
La proporción entre el nugget y el sill total se denomina efecto nugget relativo, mientras que la proporción entre el sill parcial y el sill total se llama variabilidad estructurada relativa.
El efecto nugget reduce la suavidad del campo aleatorio e indica una menor estructura espacial.
Esto se observa claramente en simulaciones: un campo sin nugget aparece más estructurado, mientras que uno con nugget luce más irregular. En particular, nota en la Figura 3.6 que pese a que el suavizamiento es alto (smooth=1.5), un nugget de \(0.25\) reduce el suavizamiento.
3.4.4.1 Posibles causas del efecto nugget
Siguiendo a Chiles and Delfiner (2012), las causas pueden ser:
- Microestructuras más pequeñas que el soporte de muestreo.
- Estructuras con rango menor a la distancia mínima entre puntos.
- Errores de medición o de posicionamiento.
En la práctica, el efecto nugget puede confundirse con la presencia de estructuras a microescala o con errores.
Por ejemplo:
- Si existe una microestructura con rango muy pequeño, el semivariograma puede presentar una discontinuidad inicial difícil de distinguir.
- En el caso de errores de medición, se suele modelar como una componente adicional con varianza constante \(\sigma^2_\varepsilon\).
En el primer caso, Figura 3.7, se ha considerado un semivariograma anidado compuesto por dos estructuras.
La primera representa la estructura a microescala y tiene un umbral \(m\), que se alcanza a una distancia de separación de algunos pocos centímetros (Figura 3.7 a).
La segunda representa la macroescala (en kilómetros).
El semivariograma anidado (Figura 3.7 b) alcanzará el umbral de la estructura a microescala en solo unos pocos centímetros, de modo que este umbral se confundirá con una discontinuidad en el origen de magnitud \(m\).
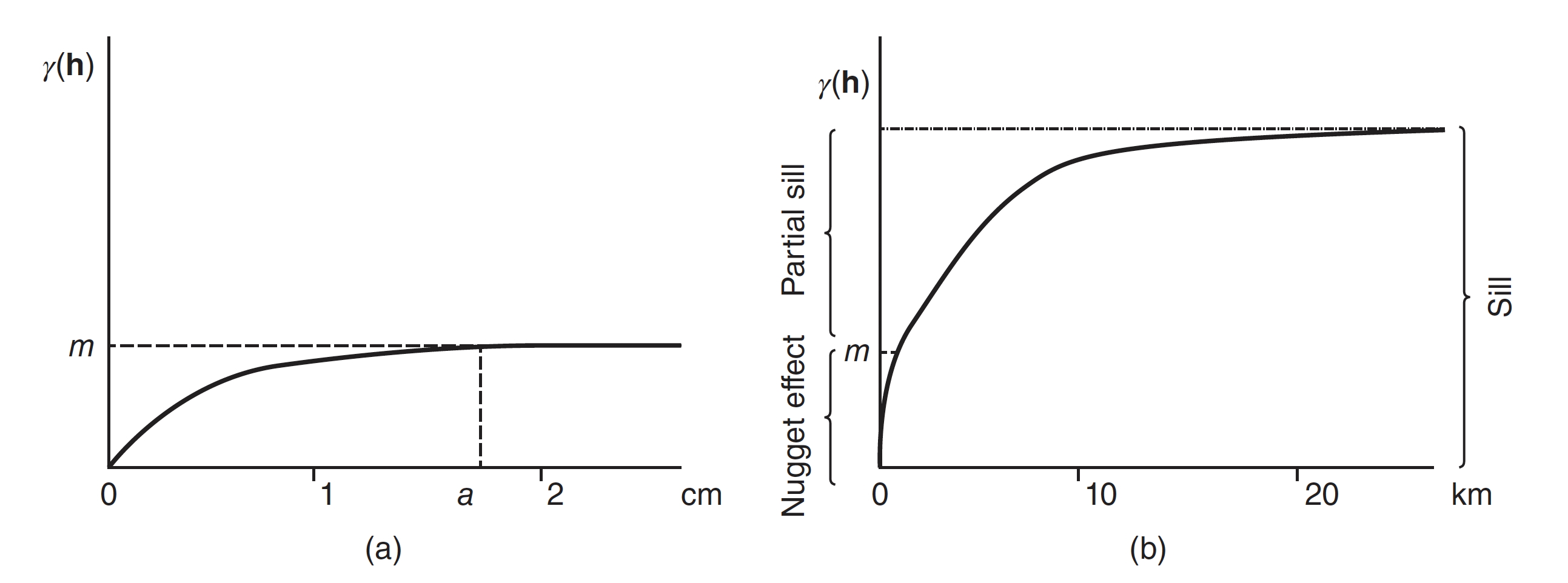
Figura 3.7: Variograma anidado.
Formalmente, si \(Z^*(s) = Z(s) + \varepsilon(s)\), con errores independientes y no correlacionados espacialmente:
\[ \gamma_{Z^*(s)}(h) = \gamma_{Z(s)}(h) + \gamma_{\varepsilon}(h), \quad h \neq 0 \tag{3.23} \]
y si los errores tienen varianza constante:
\[ \gamma_{Z^*(s)}(h) = \gamma_{Z(s)}(h) + \sigma^2_\varepsilon. \tag{3.24} \]
El caso límite corresponde al nugget puro, en el cual el semivariograma es constante para todas las distancias, indicando ausencia total de dependencia espacial.
3.5 Modelos teóricos de semivariogramas
En geostatística, los semivariogramas teóricos son funciones que cumplen con ciertas propiedades matemáticas (como la condición de no-negatividad condicional) y que permiten representar semivariogramas empíricos observados en los datos. Aunque no provienen de hipótesis específicas sobre un proceso aleatorio, son indispensables para que los procedimientos de kriging sean matemáticamente consistentes.
Se suelen distinguir tres grandes tipos: - Semivariogramas con umbral (sill) o de transición. - Semivariogramas con umbral y efecto de cavidad (hole-effect). - Semivariogramas sin umbral.
3.5.1 Semivariogramas con umbral
Estos modelos se asocian a la hipótesis de estacionariedad de segundo orden y tienen un equivalente en términos de funciones de covarianza. El valor del umbral representa la varianza del proceso una vez que se pierde la correlación espacial.
3.5.1.1 Modelo esférico
Válido en \(\mathbb{R}^1\), \(\mathbb{R}^2\) y \(\mathbb{R}^3\):
\[ \gamma(|h|) = \begin{cases} m \left( 1.5 \frac{|h|}{a} - 0.5 \left(\frac{|h|}{a}\right)^3 \right), & |h| \leq a \\ m, & |h| > a \end{cases} \]
Presenta un crecimiento casi lineal hasta el rango \(a\) (scale), donde alcanza el umbral \(m\) (sill) que se suele observar en aplicaciones. Es continuo pero no infinitamente diferenciable, lo que lo hace adecuado para fenómenos con cierta irregularidad.
El modelo esférico representa características de transición con una extensión común que aparecen como zonas (manchas) —algunos con valores altos y otros con valores bajos—. La Figura 3.8 muestra la curva del modelo esférico y las representaciones 2D y 3D de una simulación de un campo aleatorio con este semivariograma, manteniendo el mismo umbral (sill), \(m = 1\), y dos alcances (range o ´scale´) distintos: \(a = 0.15\) (izquierda) y \(a = 0.5\) (derecha).
En las vistas 2D se observa que el diámetro promedio de las zonas de valores altos y bajos está determinado por el alcance del modelo. Esta misma relación también se aprecia en la representación 3D de los valores simulados.
Code
# -------- Parámetros (Spherical) --------
parms_sph1 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.15)
parms_sph2 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.50)
nx <- 100
x <- y <- seq(0, 1, length.out = nx)
corrmodel = "Spherical"
set.seed(851)
# -------- Layout 2x3 --------
op <- par(mfrow = c(3,2), family = "serif", mar = c(4,4,2,1), mgp = c(2,0.7,0))
## (1) Semivariograma teórico (Spherical, escala 0.15)
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_sph1)$corr,
from = 0, to = 1, xlab = "distance", ylab = expression(gamma("|h|")),
lwd = 2, lty = 1, col = 1)
legend("bottomright", "Spherical (scale=0.15)", lty = 1, lwd = 2, col = 1, bty = "n")
## (4) Semivariograma teórico (Spherical, escala 0.50)
par(mar = c(4,4,2,1))
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_sph2)$corr,
from = 0, to = 1, xlab = "distance", ylab = expression(gamma("|h|")),
lwd = 2, lty = 1, col = 1)
legend("bottomright", "Spherical (scale=0.50)", lty = 1, lwd = 2, col = 1, bty = "n")
## (2) Imagen del campo simulado (escala 0.15)
g1 <- 1-GeoSim(corrmodel=corrmodel, param=parms_sph1,coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
image(x, y, g1, col = rainbow(128), xlab = "", ylab = "", main = "Simulación (scale=0.15)")
## (5) Imagen del campo simulado (escala 0.50)
g2 <- 1-GeoSim(corrmodel=corrmodel, param=parms_sph2,coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
image(x, y, g2, col = rainbow(128), xlab = "", ylab = "", main = "Simulación (scale=0.50)")
## (3) Superficie 3D (escala 0.15)
par(mar = c(0,0,2,0))
persp(x, y, g1, theta = 40, phi = 40, col = rainbow(128),
border = NA, shade = 0.5, main = "Superficie 3D (0.15)")
## (6) Superficie 3D (escala 0.50)
par(mar = c(0,0,2,0))
persp(x, y, g2, theta = 40, phi = 40, col = rainbow(128),
border = NA, shade = 0.5, main = "Superficie 3D (0.50)")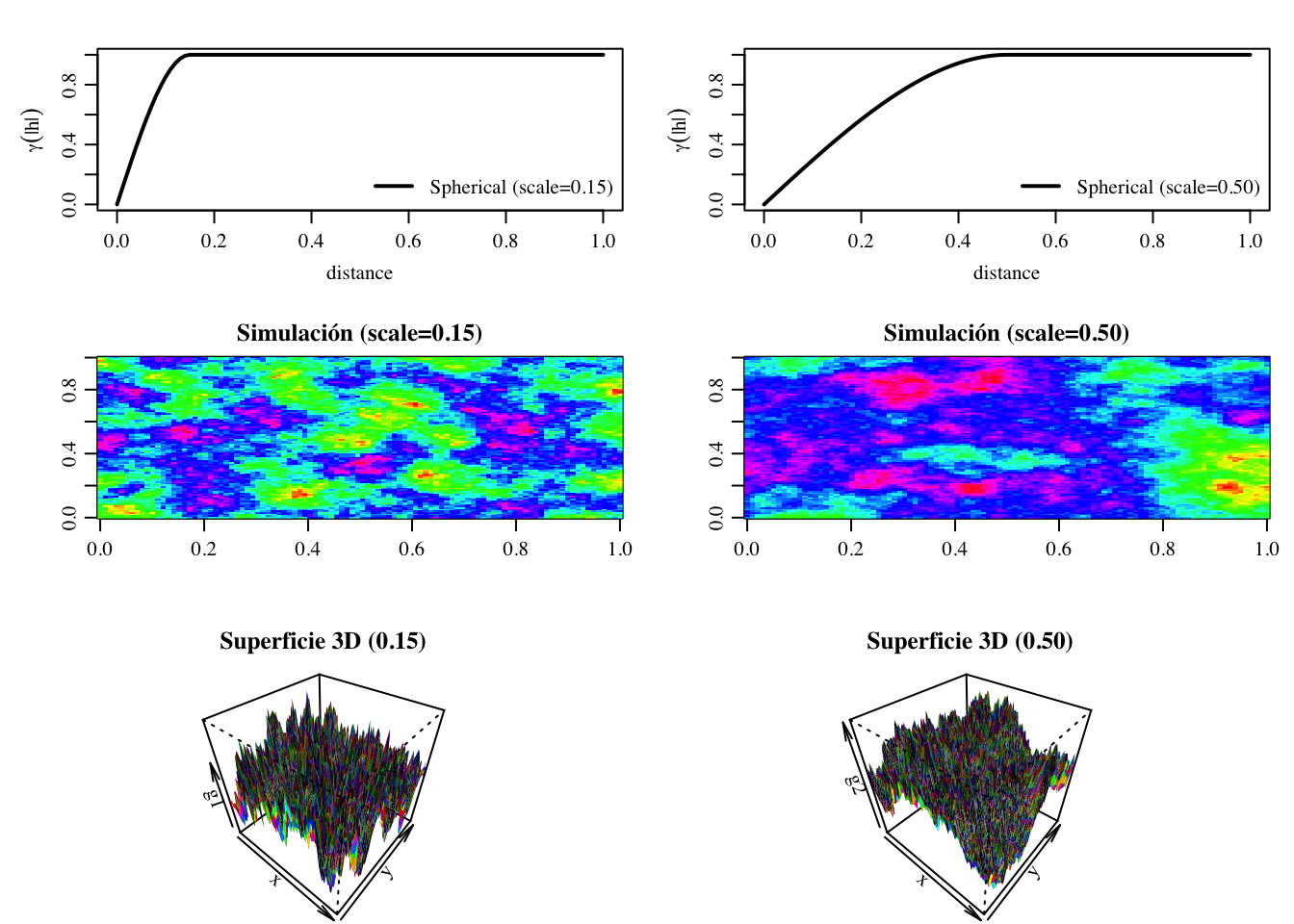
Figura 3.8: Panel superior: Modelo esférico. Izquierda: \(a = 0.15, \, m = 1\). Derecha: \(a = 0.50, \, m = 1\). Panel central: Simulación de un campo aleatorio con un semivariograma esférico (representación 2D). Izquierda: \(a = 0.15, \, m = 1\). Derecha: \(a = 0.50, \, m = 1\). Panel inferior: Simulación de un campo aleatorio con un semivariograma esférico (representación 3D). Izquierda: \(a = 0.15, \, m = 1\). Derecha: \(a = 0.50, \, m = 1\).
Un caso particular es el efecto nugget puro, que se obtiene cuando \(a \to 0\) y representa la ausencia total de correlación espacial como se muestra en la Figura 3.9.
Code
# -------- Parámetros (Spherical) --------
parms_sph1 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.0001)
nx <- 100
x <- y <- seq(0, 1, length.out = nx)
corrmodel = "Spherical"
set.seed(851)
op <- par(mfrow = c(1,3), family = "serif", mar = c(4,4,2,1), mgp = c(2,0.7,0))
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_sph1)$corr,
from = 0, to = 1, xlab = "distance", ylab = expression(gamma("|h|")),
lwd = 2, lty = 1, col = 1)
legend("bottomright", "Pure nugget (scale=0.0001)", lty = 1, lwd = 2, col = 1, bty = "n")
## (2) Imagen del campo simulado (escala 0.15)
g1 <- 1-GeoSim(corrmodel=corrmodel, param=parms_sph1,coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
image(x, y, g1, col = rainbow(128), xlab = "", ylab = "", main = "Simulación (scale=0.0001)")
## (3) Superficie 3D (escala 0.15)
par(mar = c(0,0,2,0))
persp(x, y, g1, theta = 40, phi = 40, col = rainbow(128),
border = NA, shade = 0.5, main = "Superficie 3D (0.0001)")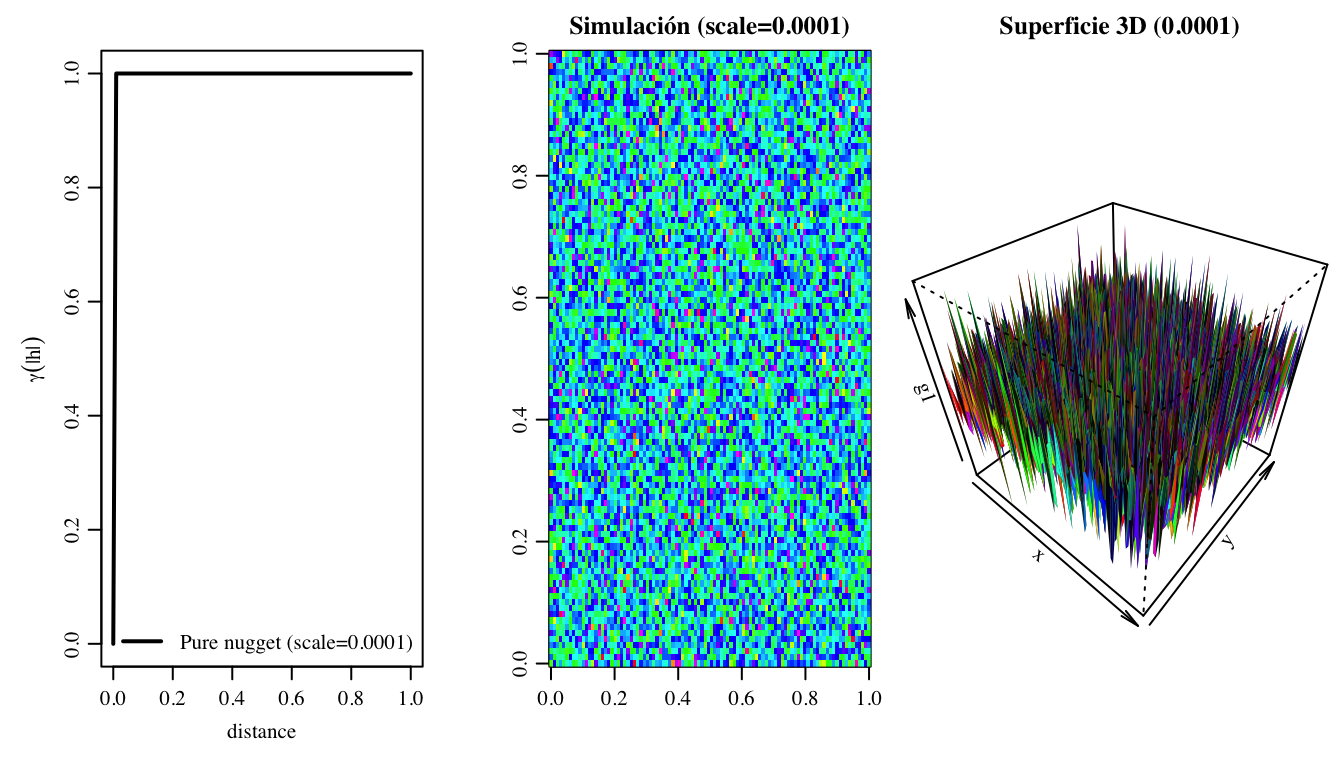
Figura 3.9: Modelo esférico. Simulación 2D y representación 3D. \(a = 0.0001, \, m = 1\).
3.5.1.2 Modelo exponencial
\[ \gamma(|h|) = m \left( 1 - \exp\left(-\frac{|h|}{a}\right)\right). \]
Este modelo es válido en \(\mathbb{R}^d\) y crece linealmente cerca del origen, pero alcanza el umbral sólo de manera asintótica. Su rango práctico es aproximadamente \(a' \approx 3a\). Refleja estructuras de transición aleatorias.
La Figura 3.10 muestra la gráfica del modelo exponencial, junto con las representaciones 2D y 3D de una simulación de un campo aleatorio con este modelo de semivariograma, manteniendo el mismo umbral (sill) pero con diferente parámetro de escala.
Code
# -------- Parámetros (Exponencial) --------
parms_sph1 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.1)
parms_sph2 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.25)
nx <- 100
x <- y <- seq(0, 1, length.out = nx)
corrmodel = "Exponential"
set.seed(851)
# -------- Layout 2x3 --------
op <- par(mfrow = c(3,2), family = "serif", mar = c(4,4,2,1), mgp = c(2,0.7,0))
## (1) Semivariograma teórico (Exponencial, escala 0.1)
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_sph1)$corr,
from = 0, to = 1, xlab = "distance", ylab = expression(gamma("|h|")),
lwd = 2, lty = 1, col = 1)
legend("bottomright", "Exponencial (scale=0.1)", lty = 1, lwd = 2, col = 1, bty = "n")
## (4) Semivariograma teórico (Exponencial, escala 0.25)
par(mar = c(4,4,2,1))
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_sph2)$corr,
from = 0, to = 1, xlab = "distance", ylab = expression(gamma("|h|")),
lwd = 2, lty = 1, col = 1)
legend("bottomright", "Exponencial (scale=0.25)", lty = 1, lwd = 2, col = 1, bty = "n")
## (2) Imagen del campo simulado (escala 0.1)
g1 <- 1-GeoSim(corrmodel=corrmodel, param=parms_sph1,coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
image(x, y, g1, col = rainbow(128), xlab = "", ylab = "", main = "Simulación (scale=0.1)")
## (5) Imagen del campo simulado (escala 0.25)
g2 <- 1-GeoSim(corrmodel=corrmodel, param=parms_sph2,coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
image(x, y, g2, col = rainbow(128), xlab = "", ylab = "", main = "Simulación (scale=0.25)")
## (3) Superficie 3D (escala 0.1)
par(mar = c(0,0,2,0))
persp(x, y, g1, theta = 40, phi = 40, col = rainbow(128),
border = NA, shade = 0.5, main = "Superficie 3D (0.1)")
## (6) Superficie 3D (escala 0.25)
par(mar = c(0,0,2,0))
persp(x, y, g2, theta = 40, phi = 40, col = rainbow(128),
border = NA, shade = 0.5, main = "Superficie 3D (0.25)")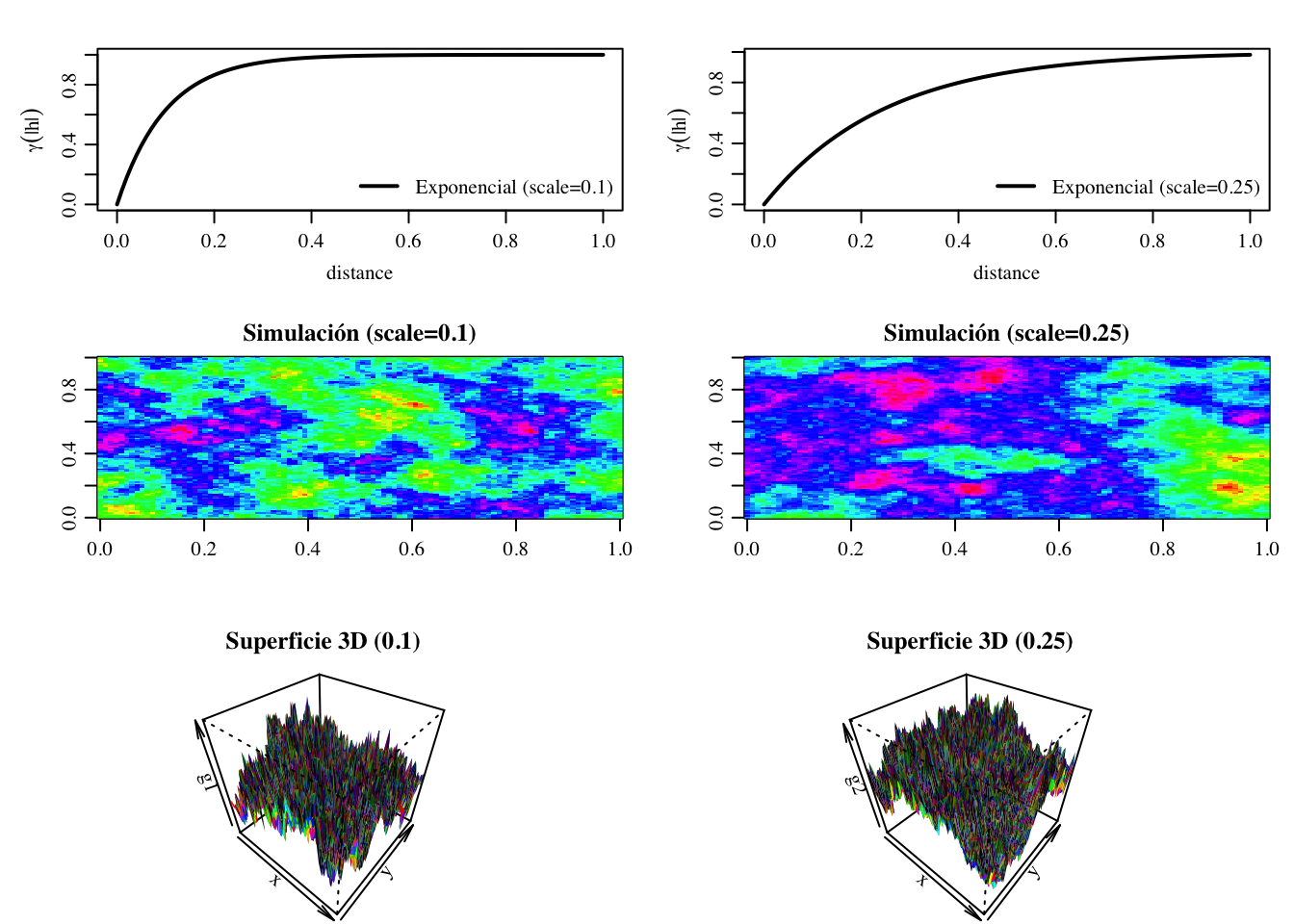
Figura 3.10: Panel superior: Modelo exponencial. Izquierda: \(a = 0.10, \, m = 1\). Derecha: \(a = 0.25, \, m = 1\). Panel central: Simulación de un campo aleatorio con un semivariograma exponencial (representación 2D). Izquierda: \(a = 0.10, \, m = 1\). Derecha: \(a = 0.25, \, m = 1\). Panel inferior: Simulación de un campo aleatorio con un semivariograma exponencial (representación 3D). Izquierda: \(a = 0.10, \, m = 1\). Derecha: \(a = 0.25, \, m = 1\).
Se observa que las zonas de valores altos y bajos presentan una irregularidad similar en ambos casos. Esto se debe a que el modelo exponencial está estrechamente relacionado con características de transición en las que las estructuras tienen extensiones aleatorias. El tamaño promedio de las zonas indica la magnitud del parámetro de escala y, en consecuencia, del alcance práctico.
3.5.1.3 Modelo gaussiano
Este modelo es válido en \(\mathbb{R}^d\), \(d\geq 1\)
\[ \gamma(|h|) = m \left( 1 - \exp\left(-\frac{|h|^2}{a^2}\right)\right). \]
Presenta un comportamiento parabólico cerca del origen (\(\alpha = 2\)), lo que implica gran suavidad y diferenciabilidad. Sin embargo, esta regularidad es poco realista en la práctica y rara vez se ajusta bien a datos reales.
Code
# -------- Parámetros (Gaussiano) --------
parms_sph1 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.1)
parms_sph2 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.25)
nx <- 100
x <- y <- seq(0, 1, length.out = nx)
corrmodel = "Gaussian"
set.seed(851)
# -------- Layout 2x3 --------
op <- par(mfrow = c(3,2), family = "serif", mar = c(4,4,2,1), mgp = c(2,0.7,0))
## (1) Semivariograma teórico (Gaussiano, escala 0.1)
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_sph1)$corr,
from = 0, to = 1, xlab = "distance", ylab = expression(gamma("|h|")),
lwd = 2, lty = 1, col = 1)
legend("bottomright", "Gaussiano (scale=0.1)", lty = 1, lwd = 2, col = 1, bty = "n")
## (4) Semivariograma teórico (Gaussiano, escala 0.25)
par(mar = c(4,4,2,1))
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_sph2)$corr,
from = 0, to = 1, xlab = "distance", ylab = expression(gamma("|h|")),
lwd = 2, lty = 1, col = 1)
legend("bottomright", "Gaussiano (scale=0.25)", lty = 1, lwd = 2, col = 1, bty = "n")
## (2) Imagen del campo simulado (escala 0.1)
g1 <- 1-GeoSim(corrmodel=corrmodel, param=parms_sph1,coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
image(x, y, g1, col = rainbow(128), xlab = "", ylab = "", main = "Simulación (scale=0.1)")
## (5) Imagen del campo simulado (escala 0.25)
g2 <- 1-GeoSim(corrmodel=corrmodel, param=parms_sph2,coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
image(x, y, g2, col = rainbow(128), xlab = "", ylab = "", main = "Simulación (scale=0.25)")
## (3) Superficie 3D (escala 0.1)
par(mar = c(0,0,2,0))
persp(x, y, g1, theta = 40, phi = 40, col = rainbow(128),
border = NA, shade = 0.5, main = "Superficie 3D (0.1)")
## (6) Superficie 3D (escala 0.25)
par(mar = c(0,0,2,0))
persp(x, y, g2, theta = 40, phi = 40, col = rainbow(128),
border = NA, shade = 0.5, main = "Superficie 3D (0.25)")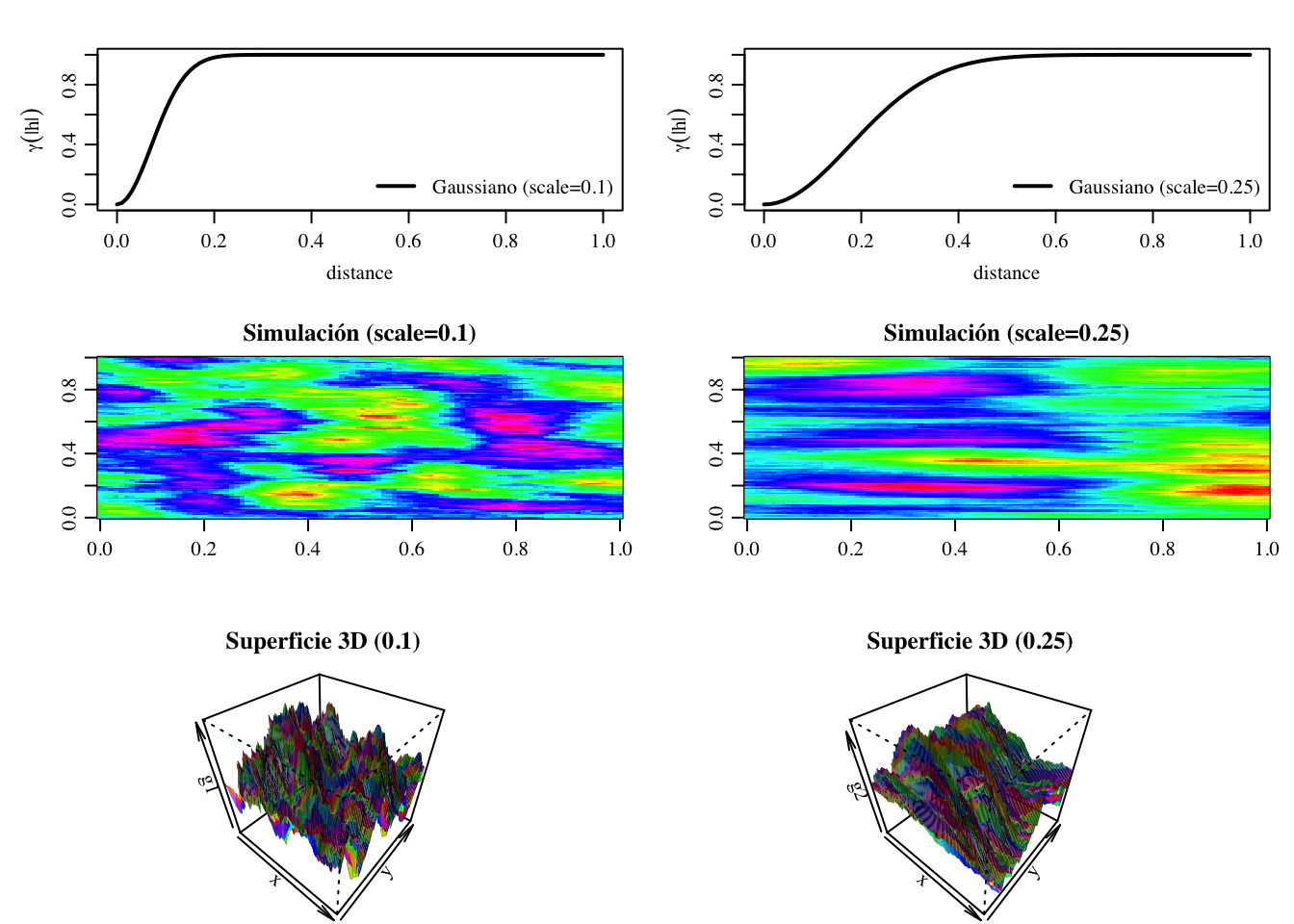
Figura 3.11: Panel superior: Modelo gaussiano. Izquierda: \(a = 0.15, \, m = 1\). Derecha: \(a = 0.25, \, m = 1\). Panel central: Simulación de un campo aleatorio con un semivariograma gaussiano (representación 2D). Izquierda: \(a = 0.10, \, m = 1\). Derecha: \(a = 0.25, \, m = 1\). Panel inferior: Simulación de un campo aleatorio con un semivariograma gaussiano (representación 3D). Izquierda: \(a = 0.10, \, m = 1\). Derecha: \(a = 0.25, \, m = 1\).
La Figura 3.11 (panel superior) muestra la gráfica de dos modelos gaussianos con el mismo umbral asintótico (sill) y diferentes alcances.
A partir de las representaciones 2D y 3D de una simulación de un campo aleatorio con un semivariograma gaussiano (paneles central e inferior, respectivamente), puede apreciarse fácilmente por qué este modelo no se utiliza en la práctica.
3.5.1.4 Modelo de Cauchy generalizado
Este modelo es válido en \(\mathbb{R}^d\), \(d\geq 1\) (Gneiting and Schlather (2004)):
\[ \gamma(|h|) = m \left( 1 - \frac{1}{\left(1 + \left(\tfrac{|h|}{a}\right)^{\alpha}\right)^{\beta/\alpha}}\right). \]
Para \(\alpha = 2\) se obtiene el modelo de Cauchy clásico, cualquier combinación de \(\alpha \in (0,2]\) (controla la suavidad power1) y \(\beta \geq 0\) (controla la rapidez del decaimiento power2) es permitida. Se caracteriza por alcanzar el umbral muy lentamente, lo que refleja dependencias de largo alcance.
Code
# -------- Parámetros (Cauchy) --------
parms_1 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.33,power1=0.1,power2=0.3)
parms_2 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.33,power1=1.5,power2=0.3)
nx <- 100
x <- y <- seq(0, 1, length.out = nx)
corrmodel = "GenCauchy"
set.seed(851)
# -------- Layout 2x3 --------
op <- par(mfrow = c(3,2), family = "serif", mar = c(4,4,2,1), mgp = c(2,0.7,0))
## (1) Semivariograma teórico (Cauchy, alpha=0.1,beta=0.3)
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_1)$corr,
from = 0, to = 1, xlab = "distance", ylab = expression(gamma("|h|")),
lwd = 2, lty = 1, col = 1)
legend("bottomright", "Cauchy (alpha=0.1,beta=0.3)", lty = 1, lwd = 2, col = 1, bty = "n")
## (4) Semivariograma teórico (Cauchy, escala 0.33)
par(mar = c(4,4,2,1))
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_2)$corr,
from = 0, to = 1, xlab = "distance", ylab = expression(gamma("|h|")),
lwd = 2, lty = 1, col = 1)
legend("bottomright", "Cauchy (alpha=1.5,beta=0.3)", lty = 1, lwd = 2, col = 1, bty = "n")
## (2) Imagen del campo simulado (alpha=0.1,beta=0.3)
g1 <- 1-GeoSim(corrmodel=corrmodel, param=parms_1,coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
image(x, y, g1, col = rainbow(128), xlab = "", ylab = "", main = "Simulación (alpha=0.1,beta=0.3)")
## (5) Imagen del campo simulado (alpha=1.5,beta=0.3)
g2 <- 1-GeoSim(corrmodel=corrmodel, param=parms_2,coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
image(x, y, g2, col = rainbow(128), xlab = "", ylab = "", main = "Simulación (alpha=1.5,beta=0.3)")
## (3) Superficie 3D (alpha=0.1,beta=0.3)
par(mar = c(0,0,2,0))
persp(x, y, g1, theta = 40, phi = 40, col = rainbow(128),
border = NA, shade = 0.5, main = "Superficie 3D (alpha=0.1,beta=0.3)")
## (6) Superficie 3D (alpha=1.5,beta=0.3)
par(mar = c(0,0,2,0))
persp(x, y, g2, theta = 40, phi = 40, col = rainbow(128),
border = NA, shade = 0.5, main = "Superficie 3D (alpha=1.5,beta=0.3)")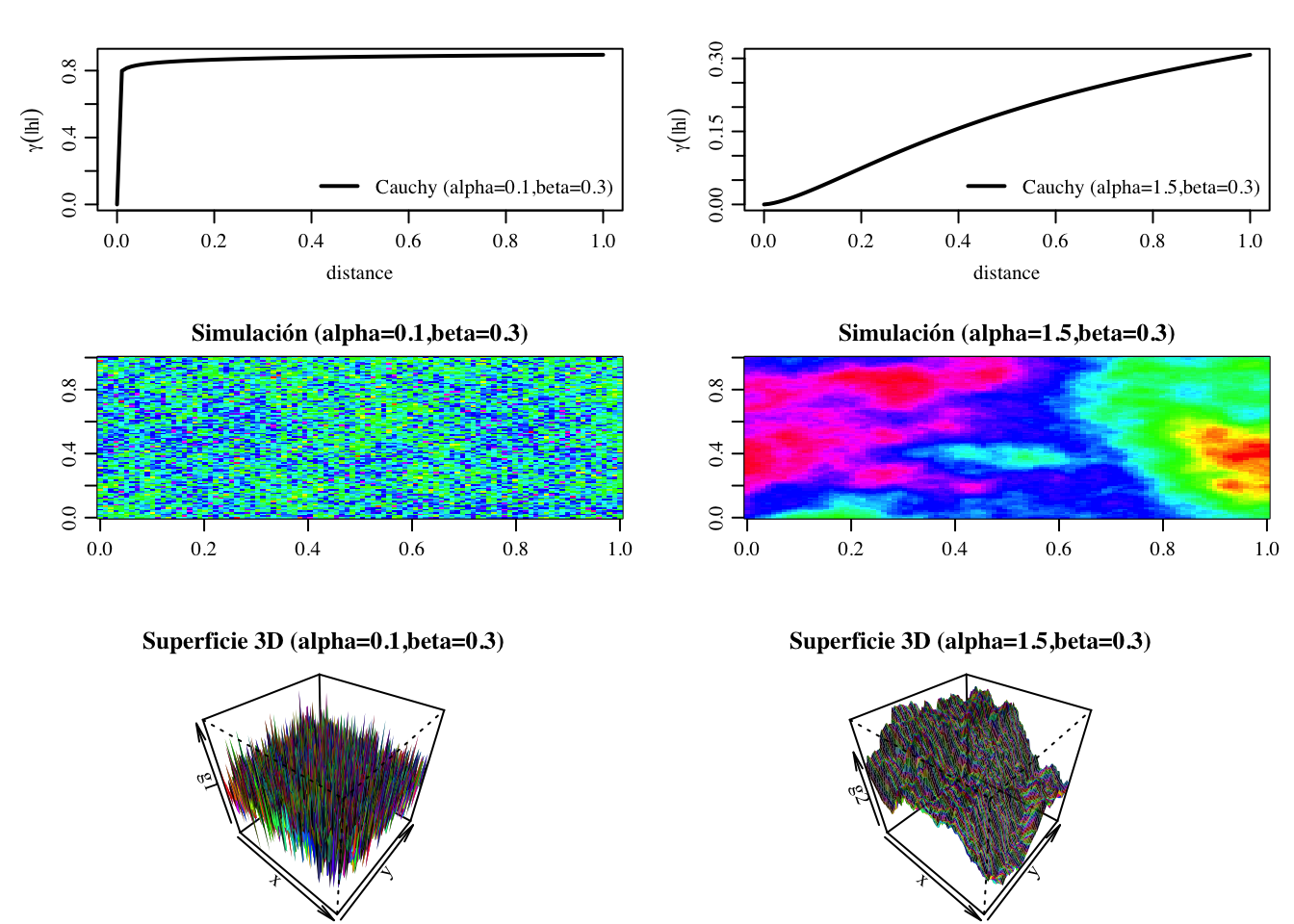
Figura 3.12: Panel superior: Modelo Cauchy Izquierda: \(a = 0.33, m = 1, \alpha = 0.1,\beta = 0.5\). Derecha: \(a = 0.33, m = 1, \alpha = 1.5, \beta = 0.5\). Panel central: Simulación de un campo aleatorio con un semivariograma gaussiano (representación 2D). Panel inferior: Simulación de un campo aleatorio con un semivariograma gaussiano (representación 3D).
La Figura 3.12 (panel superior) muestra la gráfica de dos modelos gaussianos con el mismo umbral asintótico (sill), alcances (scale), decaimiento (power2) con diferentes
suavidades (power1).
A partir de las representaciones 2D y 3D de una simulación de un campo aleatorio con un semivariograma gaussiano (paneles central e inferior, respectivamente), las propiedades del modelo.
3.5.1.5 Modelo Wendland Generalizado
El modelo de covarianza Wendland generalizado (Bevilacqua et al. (2019)) se define como:
\[ \gamma(|h|) = m \, A \, \left(1 - \left(\frac{|h|}{a}\right)^2\right)^{\beta + \kappa} \, {}_2F_1\!\left( \frac{\beta}{2}, \frac{\beta + 1}{2}; 2\beta + \kappa + 1; 1 - \left(\frac{|h|}{a}\right)^2 \right) \, \mathbf{1}\!\left(\frac{|h|}{a} \in [0,1]\right), \]
donde \(h = \|x - x'\|\) es la distancia euclidiana, \({}_2F_1(\cdot)\) denota la función hipergeométrica gaussiana, y el coeficiente de normalización \(A\) está dado por:
\[ A = \frac{\Gamma(\kappa)\,\Gamma(2\kappa + \beta + 1)} {\Gamma(2\kappa)\,\Gamma(\beta + 1 - \kappa)\,2^{\beta + 1}}, \qquad \mu \ge 0.5(d + 1) + \kappa. \]
El parámetro \(m\) representa la varianza o sill del proceso, y \(a > 0\) corresponde al parámetro de escala o rango espacial.
Los casos particulares \(\kappa = 0, 1, 2\) corresponden respectivamente a los modelos clásicos Wend0, Wend1 y Wend2.
Este modelo es de soporte compacto, ya que \(\gamma(|h|) = 0\) para \(|h| > a\).
En GeoModelos, los parámetros son:
power2: \(\beta\)scale: \(a\)smooth: \(\kappa\)sill: \(m\)
Code
# -------- Parámetros (GenWend) --------
parms_1 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.33,smooth=3,power2=0.1)
parms_2 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.33,smooth=3,power2=2.5)
nx <- 100
x <- y <- seq(0, 1, length.out = nx)
corrmodel = "GenWend"
set.seed(851)
# -------- Layout 2x3 --------
op <- par(mfrow = c(3,2), family = "serif", mar = c(4,4,2,1), mgp = c(2,0.7,0))
## (1) Semivariograma teórico (kappa=3,beta=0.1)
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_1)$corr,
from = 0, to = 1, xlab = "distance", ylab = expression(gamma("|h|")),
lwd = 2, lty = 1, col = 1)
legend("bottomright", "GenWend (kappa=3,beta=0.1)", lty = 1, lwd = 2, col = 1, bty = "n")
## (4) Semivariograma teórico (GenWend, kappa=3,beta=2.5)
par(mar = c(4,4,2,1))
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_2)$corr,
from = 0, to = 1, xlab = "distance", ylab = expression(gamma("|h|")),
lwd = 2, lty = 1, col = 1)
legend("bottomright", "GenWend (kappa=3,beta=2.5)", lty = 1, lwd = 2, col = 1, bty = "n")
## (2) Imagen del campo simulado (kappa=3,beta=0.1)
g1 <- 1-GeoSim(corrmodel=corrmodel, param=parms_1,coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
image(x, y, g1, col = rainbow(128), xlab = "", ylab = "", main = "Simulación (kappa=3,beta=0.1)")
## (5) Imagen del campo simulado (kappa=3,beta=2.5)
g2 <- 1-GeoSim(corrmodel=corrmodel, param=parms_2,coordx = x,coordy = y,grid = TRUE, progress = FALSE)$data
image(x, y, g2, col = rainbow(128), xlab = "", ylab = "", main = "Simulación (kappa=3,beta=2.5)")
## (3) Superficie 3D (kappa=3,beta=0.1)
par(mar = c(0,0,2,0))
persp(x, y, g1, theta = 40, phi = 40, col = rainbow(128),
border = NA, shade = 0.5, main = "Superficie 3D (kappa=3,beta=0.1)")
## (6) Superficie 3D (kappa=3,beta=2.5)
par(mar = c(0,0,2,0))
persp(x, y, g2, theta = 40, phi = 40, col = rainbow(128),
border = NA, shade = 0.5, main = "Superficie 3D (kappa=3,beta=2.5)")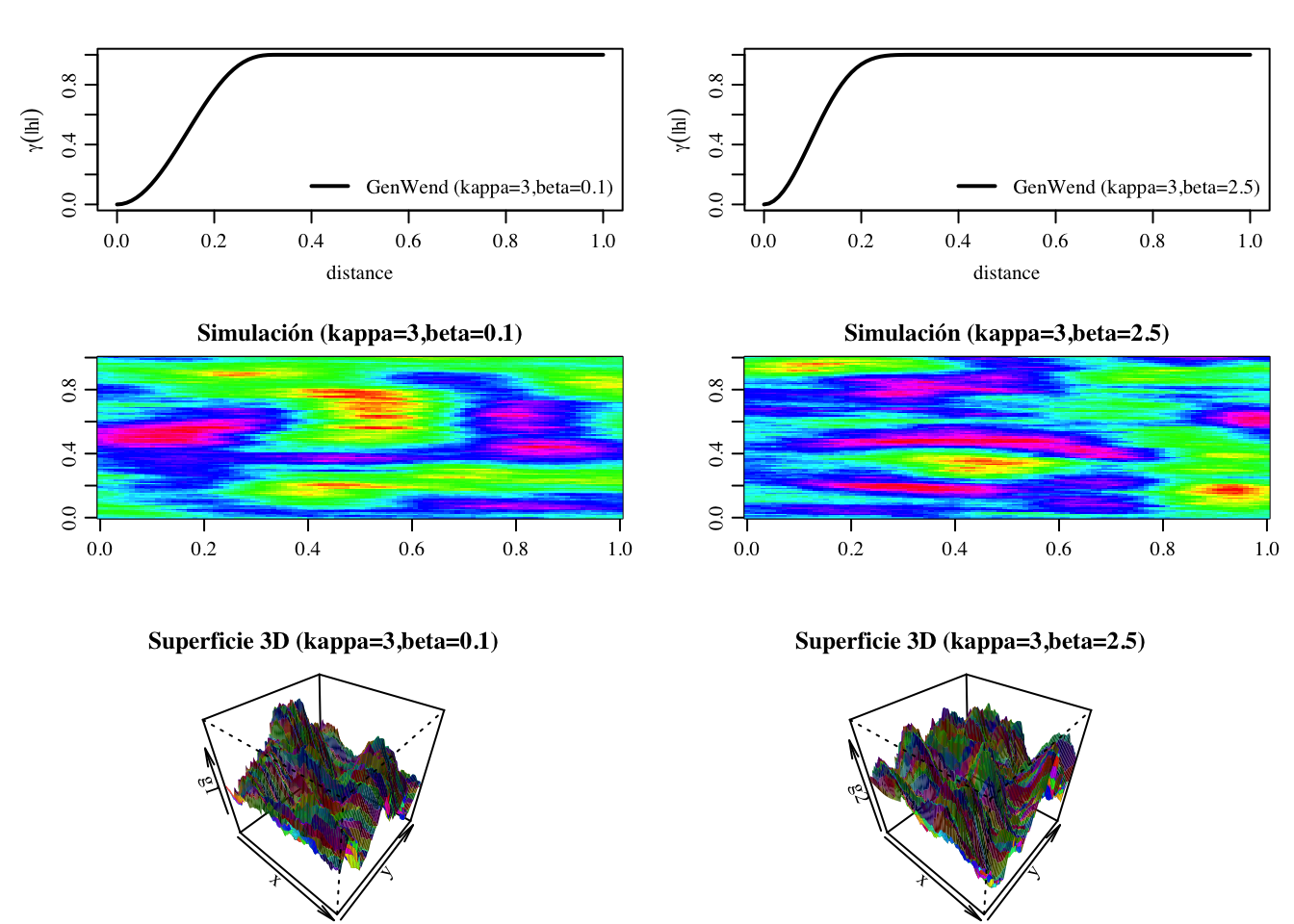
Figura 3.13: Panel superior: Modelo Wendland. Izquierda: \(a = 0.33, m = 1, \beta = 0.1, \kappa = 3\). Derecha: \(a = 0.33, m = 1,\beta = 2.5,\kappa = 3\). Panel central: Simulación de un campo aleatorio con un semivariograma gaussiano (representación 2D). Panel inferior: Simulación de un campo aleatorio con un semivariograma gaussiano (representación 3D).
La Figura 3.13 (panel superior) muestra la gráfica de dos modelos gaussianos con el mismo umbral asintótico (sill), alcances (scale), suavizamiento (smooth) con diferentes decaimientos
(power2).
A partir de las representaciones 2D y 3D de una simulación de un campo aleatorio con un semivariograma gaussiano (paneles central e inferior, respectivamente), las propiedades del modelo.
3.5.2 Semivariogramas con efecto de cavidad (hole effect)
Los modelos descritos previamente representan funciones que aumentan de manera monótona con la distancia entre dos puntos, reflejando una dependencia espacial positiva.
Sin embargo, existen procesos en los que la correlación no crece de forma uniforme, sino que oscila entre valores positivos y negativos.
En tales casos, el semivariograma no es monótono, sino que presenta ondas u oscilaciones conocidas como efecto de cavidad (hole effect).
Estos modelos se utilizan para describir dependencias espaciales alternantes, en las que los incrementos de la variable muestran una secuencia de correlaciones positivas y negativas a distintas escalas espaciales. Se aplican a fenómenos con componentes oscilatorios o patrones periódicos que poseen significado físico, como variaciones cíclicas en el subsuelo o estructuras repetitivas en materiales.
Los semivariogramas con efecto de cavidad pueden: - Mostrar un comportamiento lineal o parabólico cerca del origen. - Presentar o no un umbral (sill). - Ser periódicos o pseudo-periódicos, según la regularidad de la oscilación.
En la práctica, cuando se identifica una periodicidad clara, se recomienda filtrarla o modelarla explícitamente. Si los datos no son suficientes para confirmar su existencia, las oscilaciones deben interpretarse con precaución, ya que pueden deberse a otras causas, como correlaciones residuales o ruido en los datos empíricos.
En GeoModels se tiene las siguientes opciones en este tipo:
SchoenbergWaveMatern_HoleGenWend_HoleGenWend_Matern_Hole
3.5.2.1 Modelo de covarianza de Schoenberg
El modelo de covarianza de Schoenberg se define, para dimensión \(d\) (Schoenberg (1938)), como:
\[ \gamma(|h|) = m \, \Gamma\!\left(\frac{d}{2}\right) \left(\frac{|h|}{2a}\right)^{1 - \frac{d}{2}} J_{\frac{d}{2} - 1}\!\left(\frac{|h|}{a}\right), \quad |h| \ge 0, \]
donde:
- \(|h| = \|x - x'\|\) es la distancia euclidiana,
- \(m\) representa la varianza o sill,
- \(a > 0\) es el parámetro de escala o rango espacial,
- \(\Gamma(\cdot)\) es la función Gamma, y
- \(J_{\nu}(\cdot)\) es la función de Bessel de primer tipo de orden \(\nu\).
Caso particular: dimensión \(d = 2\)
Para \(d = 2\), se tiene \(\Gamma(1) = 1\) y \(J_{0}(\cdot)\) es la función de Bessel de orden cero.
Por lo tanto, la covarianza se simplifica a:
\[ \gamma(|h|) = m \, J_{0}\!\left(\frac{|h|}{a}\right). \]
Este modelo genera una función oscilante, positiva definida en \(\mathbb{R}^2\), y es frecuentemente utilizado para representar campos aleatorios con comportamiento periódico o con estructura radial. Su representación gráfica se muestra en la Figura 3.14 con diferentes valores para la escala.
Code
library(GeoModels)
parms_1 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.1)
parms_2 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.5)
parms_3 <- list(mean = 0, sill = 1, nugget = 0, scale = 1)
parms_4 <- list(mean = 0, sill = 1, nugget = 0, scale = 1.5)
corrmodel <- "Schoenberg"
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_1)$corr, from = 0, to = 1,
main = "Modelo Schoenberg", lwd = 2, lty = 4,xlab = "distancia",
ylab = expression(gamma("|h|")))
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_2)$corr, from = 0, to = 1,add = TRUE,lwd = 2, lty = 2)
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_3)$corr, from = 0, to = 1,add = TRUE,lwd = 2, lty = 3)
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_4)$corr, from = 0, to = 1,add = TRUE,lwd = 2, lty = 1)
legend("bottomright", c(expression(paste(alpha == 0.1)), expression(paste(alpha ==
0.5)), expression(paste(alpha == 1)), expression(paste(alpha == 1.5))),
lty = c(4, 2, 3, 1), lwd = c(2, 2, 2, 2), col = 1)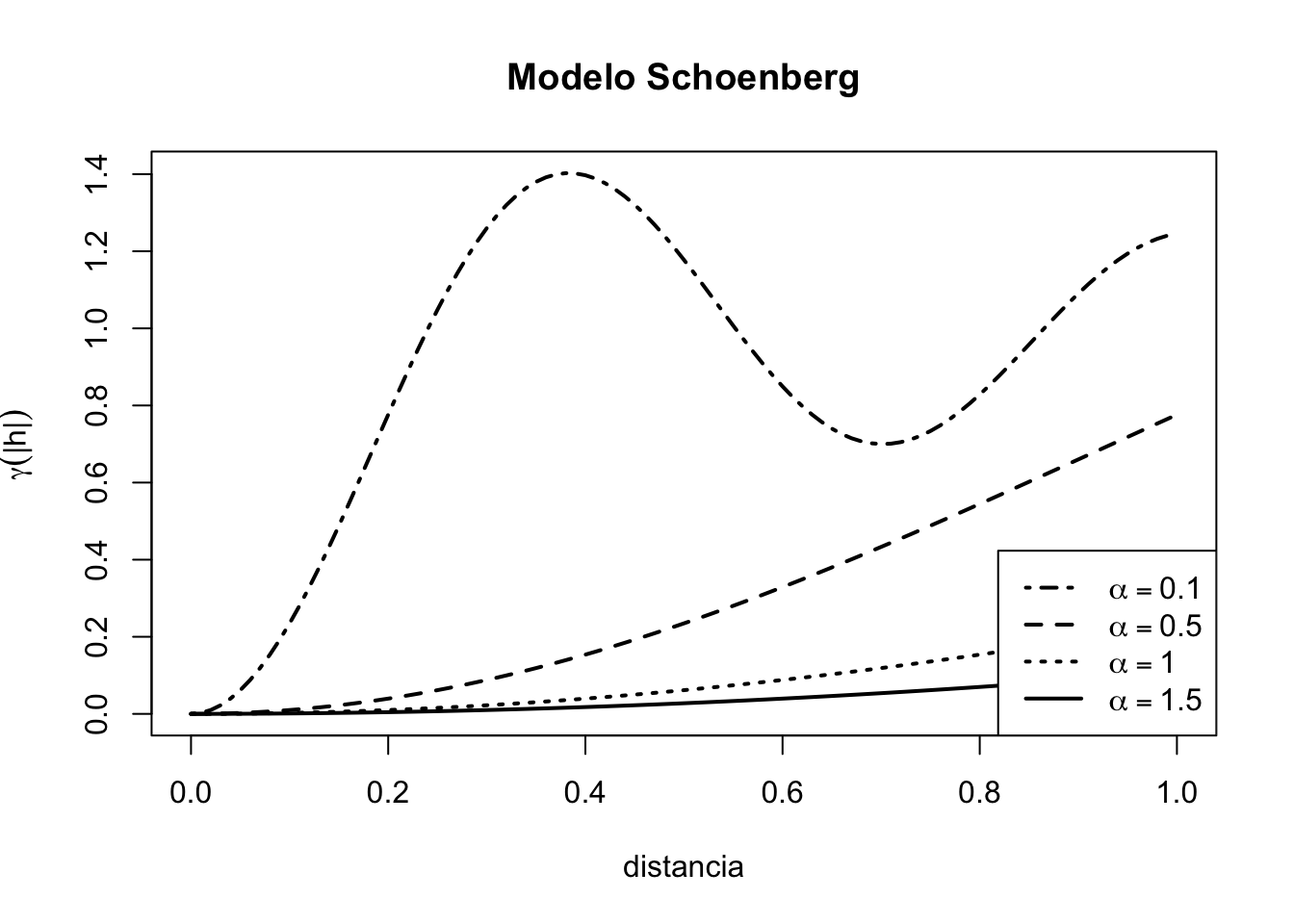
Figura 3.14: Modelo Schoenberg para diferentes valores de escala \(a = 0.1, a = 0.5, a = 1, a = 1.5\).
3.5.2.2 Modelo de covarianza Wave
El modelo Wave (u oscilatorio) se define como:
\[ \gamma(|h|) = m \, \frac{a}{|h|} \, \sin\!\left(\frac{|h|}{a}\right), \]
donde:
- \(|h| = \|x - x'\|\) es la distancia euclidiana,
- \(m\) representa la varianza o sill,
- \(a > 0\) es el parámetro de escala o rango espacial.
Propiedades
- Para \(|h| = 0\) se tiene \(\gamma(0) = m\).
- Para \(|h| > 0\), la función presenta un comportamiento oscilante, alternando entre valores positivos y negativos conforme aumenta la distancia.
- El modelo no es estrictamente positivo definido en todas las dimensiones, pero se utiliza en geostatística unidimensional o para representar procesos periódicos u ondulatorios.
Forma de correlación normalizada
Dividiendo por el sill \(m\), la función de correlación se expresa como:
\[ \rho(|h|) = \frac{a}{|h|}\,\sin\!\left(\frac{|h|}{a}\right), \]
con \(\rho(0)=1\). Su representación gráfica se muestra en la Figura 3.15 con diferentes valores para la escala.
Code
library(GeoModels)
parms_1 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.1)
parms_2 <- list(mean = 0, sill = 1, nugget = 0, scale = 0.5)
parms_3 <- list(mean = 0, sill = 1, nugget = 0, scale = 1)
parms_4 <- list(mean = 0, sill = 1, nugget = 0, scale = 1.5)
corrmodel <- "Wave"
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_1)$corr, from = 0, to = 1,
main = "Modelo Wave", lwd = 2, lty = 4,xlab = "distancia",
ylab = expression(gamma("|h|")))
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_2)$corr, from = 0, to = 1,add = TRUE,lwd = 2, lty = 2)
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_3)$corr, from = 0, to = 1,add = TRUE,lwd = 2, lty = 3)
curve(1-GeoCorrFct(x,corrmodel=corrmodel ,param = parms_4)$corr, from = 0, to = 1,add = TRUE,lwd = 2, lty = 1)
legend("bottomright", c(expression(paste(alpha == 0.1)), expression(paste(alpha ==
0.5)), expression(paste(alpha == 1)), expression(paste(alpha == 1.5))),
lty = c(4, 2, 3, 1), lwd = c(2, 2, 2, 2), col = 1)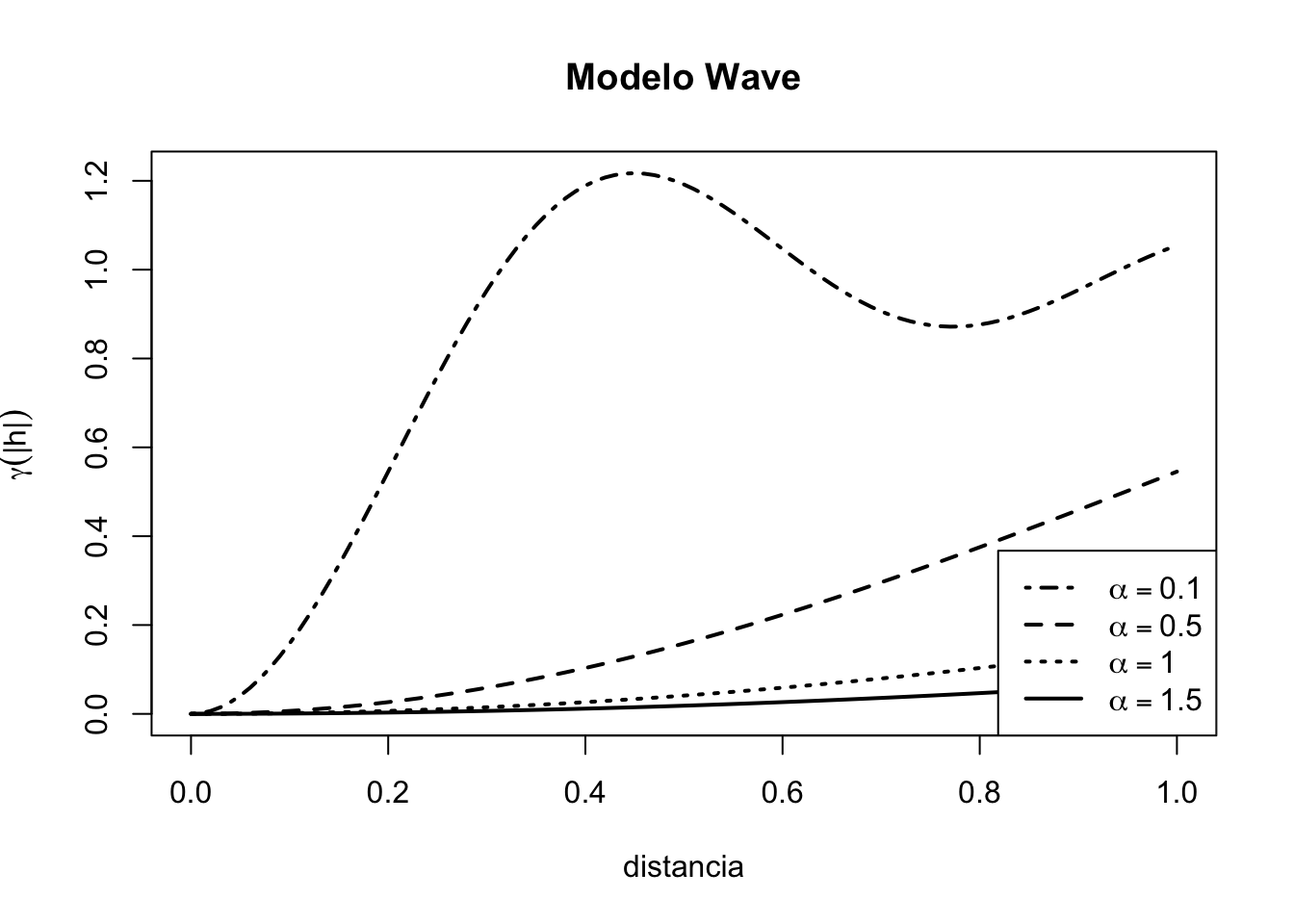
Figura 3.15: Modelo Schoenberg para diferentes valores de escala \(a = 0.1, a = 0.5, a = 1, a = 1.5\).
3.6 Semivariograma empírico
En la práctica, los datos que disponemos son un conjunto finito de observaciones georreferenciadas en un dominio espacial. A partir de estas observaciones se busca inferir la estructura de dependencia espacial del fenómeno estudiado.
El semivariograma es el instrumento fundamental para describir dicha dependencia, pues capta la variabilidad espacial de una variable regionalizada. En la práctica, se utiliza su versión empírica o experimental, la cual constituye el principal estimador de la estructura de variabilidad espacial del fenómeno de interés.
Nota: El semivariograma empírico es el instrumento utilizado para estimar la variabilidad espacial de un fenómeno.
3.6.0.1 Estimación clásica (Método de los Momentos)
Bajo el supuesto de estacionariedad intrínseca, el estimador clásico del semivariograma (propuesto por Matheron (1962)) se define como:
\[ \hat{\gamma}(\mathbf{h}) = \frac{1}{2\,\#N(\mathbf{h})} \sum_{N(\mathbf{h})} \left[ Z(\mathbf{s}_i + \mathbf{h}) - Z(\mathbf{s}_i) \right]^2, \]
donde:
- \(Z(\mathbf{s}_i)\) son los valores observados de la variable,
- \(\mathbf{h}\) es el vector de separación espacial entre dos puntos, y
- \(\#N(\mathbf{h})\) es el número de pares de puntos separados por esa distancia.
El gráfico de \(\hat{\gamma}(\mathbf{h})\) frente a \(|\mathbf{h}|\) constituye el semivariograma empírico.
Este estimador es insesgado, ya que:
\[ E[\hat{\gamma}(\mathbf{h})] = \gamma(\mathbf{h}). \]
En la práctica, el semivariograma empírico se calcula para distancias menores a la mitad del diámetro del dominio, ya que el número de pares disponibles disminuye con la distancia, haciendo las estimaciones menos confiables para grandes separaciones.
3.6.0.2 Relación con la covarianza empírica
Mientras que el covariograma empírico suele ser un estimador sesgado de la covarianza verdadera, el semivariograma empírico es un estimador insesgado de la semivarianza bajo la hipótesis intrínseca.
En el caso de estacionariedad de segundo orden, se cumple que:
\[ \hat{\gamma}(\mathbf{h}) \neq \hat{C}(0) - \hat{C}(\mathbf{h}), \]
ya que el cálculo del semivariograma no depende del promedio global \(\bar{Z}\), lo cual evita sesgos derivados de una media desconocida.
3.6.0.3 Regiones de tolerancia y direccionalidad
Para mejorar la estimación, especialmente cuando las distancias entre puntos son irregulares, se agrupan los pares dentro de regiones de tolerancia (ver Figura 3.16).
Estas regiones se definen por: - un intervalo de distancia \(|\mathbf{h}| \pm \Delta|\mathbf{h}|\), y
- un ángulo de tolerancia en torno a la dirección de \(\mathbf{h}\).

Figura 3.16: Región de tolerancia en \(\mathbb{R}\).
El valor promedio de las semidiferencias cuadradas dentro de cada región se asigna al vector \(\mathbf{h}\) representativo del intervalo.
Para detectar anisotropías, se recomienda construir el semivariograma empírico en varias direcciones (por ejemplo, \(0, \pi/4, \pi/2, 3\pi/4\)).
A medida que aumenta la longitud de los intervalos y el ángulo de tolerancia, las fluctuaciones en el semivariograma disminuyen, aunque se incrementa el error de discretización (ver Figura 3.17).
Code
library(GeoModels)
set.seed(3132)
coords <- cbind(runif(50),runif(50))
# Simulación de un campo aleatorio gaussiano con modelo esférico anisotrópico
sim1 <- GeoSim(coordx = coords[,1], coordy =coords[,2],
corrmodel = "Spherical",
param = list(mean =0,sill = 5, nugget = 0, scale = 0.3),
anisopars = list(angle = pi/2, ratio = 4),progress = FALSE,grid = TRUE)# anisotropía: dirección y razón
par(mfrow = c(2, 2))
bin1 <- GeoVariogramDir(coordx = cbind(sim1$coordx,sim1$coordy),data=sim1$data,tolerance = 0,directions = c(90))
plot(bin1,type = "b", ylab = "Semivariogram", lwd = 2, pch = 21, bg = "darkgray",
main = "(a)", xlim = c(0, 1))
bin2 <- GeoVariogramDir(coordx = cbind(sim1$coordx,sim1$coordy),data=sim1$data,tolerance = 40,directions = c(90))
plot(bin2,type = "b", ylab = "Semivariogram", lwd = 2, pch = 21, bg = "darkgray",
main = "(b)", xlim = c(0, 1))
bin3 <- GeoVariogramDir(coordx = cbind(sim1$coordx,sim1$coordy),data=sim1$data,tolerance = 50,directions = c(90))
plot(bin2,type = "b", ylab = "Semivariogram", lwd = 2, pch = 21, bg = "darkgray",
main = "(c)", xlim = c(0, 1))
bin4 <- GeoVariogramDir(coordx = cbind(sim1$coordx,sim1$coordy),data=sim1$data,tolerance = 90,directions = c(90))
plot(bin2,type = "b", ylab = "Semivariogram", lwd = 2, pch = 21, bg = "darkgray",
main = "(d)", xlim = c(0, 1))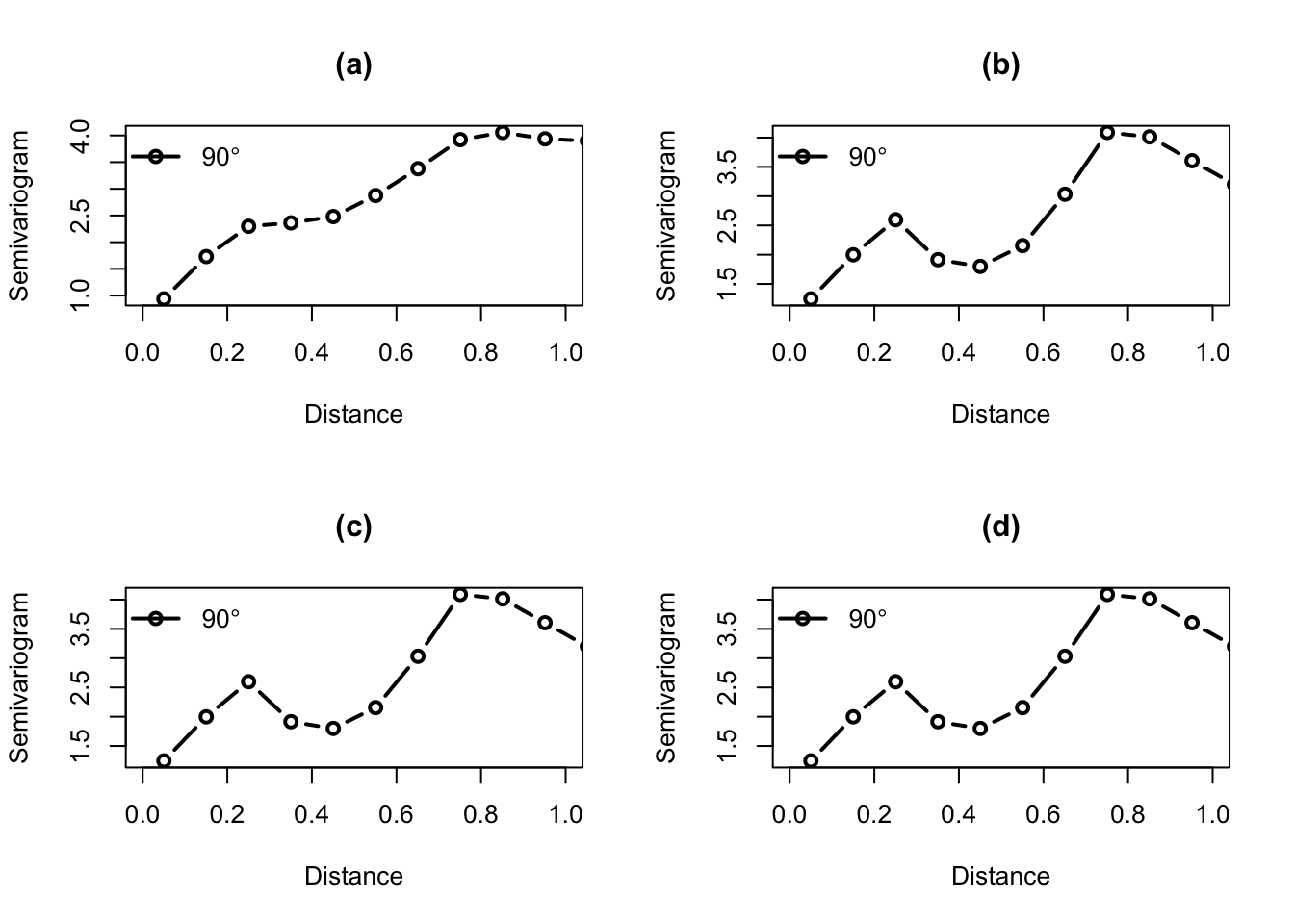
Figura 3.17: Efecto del ángulo de tolerancia en un semivariograma empírico Norte–Sur. Ángulo de tolerancia 0, 40, 50 y 90 grados.
3.6.0.4 Ejemplo (Semivariograma empírico clásico)
Consideremos 25 datos distribuidos en una malla regular de \(100 \times 100\)
Para cada par de puntos separados por una distancia \(h\), se calcula:
\[ \frac{1}{2} \left[ Z(\mathbf{s}_i + \mathbf{h}) - Z(\mathbf{s}_i) \right]^2, \]
y se promedia sobre los pares que cumplen la condición de separación.
Se simulan a continuación los datos de la malla regular y el valor de la variable analizada y se regresenta en la gráfica 3.18:
Code
# Coordenadas del grid:
nd <- 5
x <- y <- seq(0, 100, length.out = nd)
coords <- expand.grid(x,y)
# Se fijan los parametros del modelo:
corrmodel <- "Exponential"
mean <- 0
sill <- 40
nugget <- 0
scale <- 50
# smooth <- 1
set.seed(1)
# Simulacion del campo aleatorio gaussiano:
z <- GeoSim(coordx=coords, corrmodel=corrmodel, param=list(mean=mean,
sill=sill, nugget=nugget, scale=scale),progress = FALSE)$data
kableExtra::kable(head(data.frame(x_coord = coords[,1],y_coord = coords[,2],z_value = round(z,4)),10))| x_coord | y_coord | z_value |
|---|---|---|
| 0 | 0 | -3.9620 |
| 25 | 0 | -1.4797 |
| 50 | 0 | -5.0993 |
| 75 | 0 | 4.9288 |
| 100 | 0 | 4.6464 |
| 0 | 25 | -6.3439 |
| 25 | 25 | -1.4197 |
| 50 | 25 | 2.2361 |
| 75 | 25 | 5.6811 |
| 100 | 25 | 3.1202 |
Code
Figura 3.18: Veinticinco valores observados en una cuadrícula de 100 × 100.
Ahora se calcula el variograma empírico:
Se muestra los resultados principales del cálculo en la siguiente tabla:
Code
| Lag_distances | Num_pais | Semi_values |
|---|---|---|
| 34.70178 | 40 | 13.99547 |
| 44.40356 | 32 | 16.45620 |
| 54.10534 | 30 | 16.39687 |
| 63.80712 | 48 | 14.22640 |
| 73.50890 | 18 | 19.59807 |
| 83.21068 | 52 | 20.91646 |
| 92.91246 | 24 | 18.47733 |
| 102.61424 | 10 | 28.49164 |
| 122.01780 | 36 | 19.64546 |
| 141.42136 | 8 | 13.71256 |
La Figura 3.19 muestra su representación gráfica.
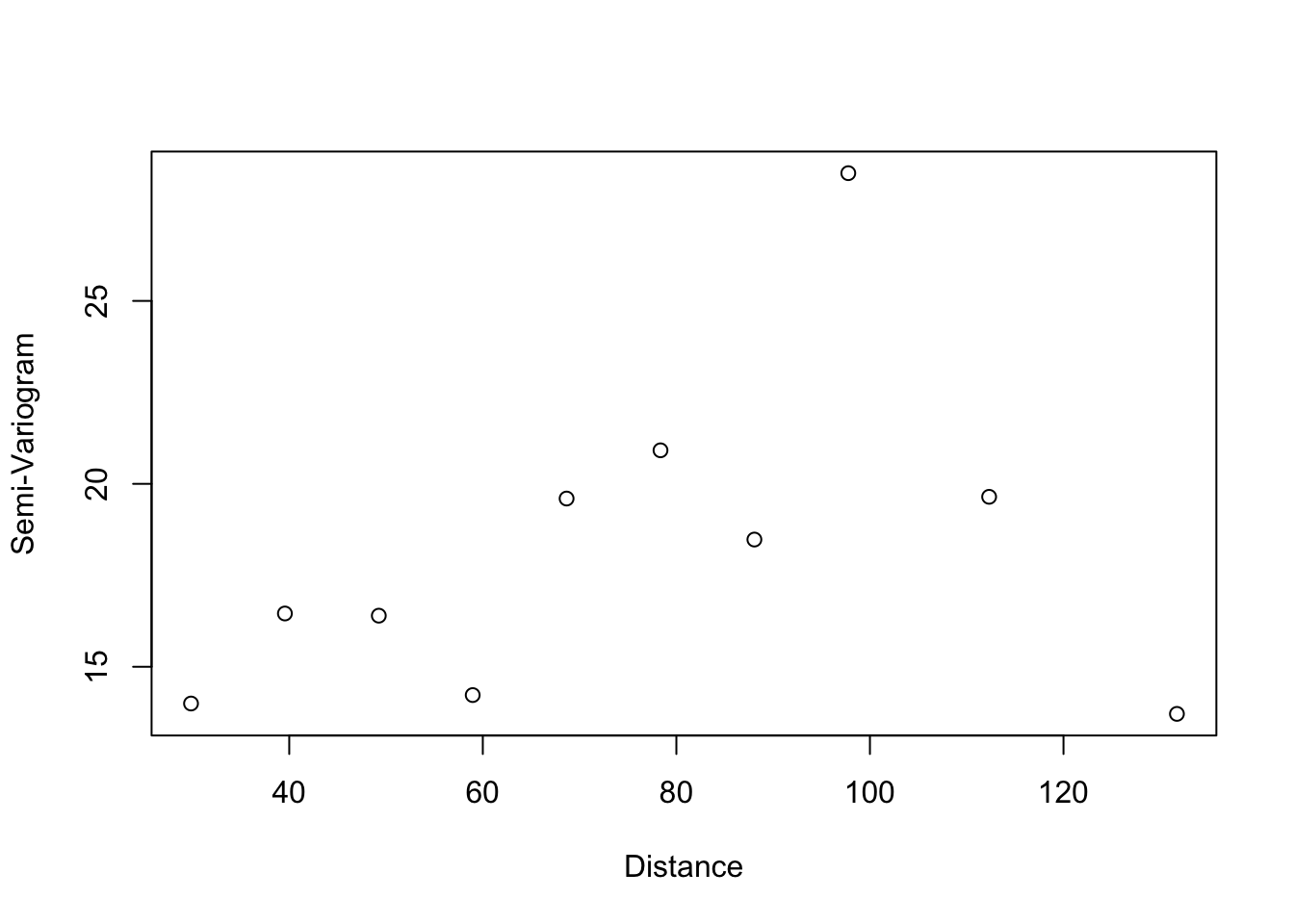
Figura 3.19: Semivariograma empírico (estimador clásico)
Los resultados del cálculo con el estimador clásico (MoM) muestran que:
El número de pares disminuye con la distancia.
Las estimaciones para grandes distancias son menos confiables.
El semivariograma tiende a estabilizarse en torno al valor del sill cuando se alcanza el rango espacial.
3.6.0.5 Ejemplo (Construcción de un semivariograma empírico — Niveles de monóxido de carbono en Madrid (semana 50, 10 pm))
En este ejemplo se analizan los niveles registrados de monóxido de carbono (CO) en la ciudad de Madrid, correspondientes a los días laborables de la semana 50 del año 2008, a las 10 pm.
Los datos proceden de una base geoespacial real y están formateados como:
\[ (x_i, y_i, \log CO_i^*), \quad i = 1, \ldots, 23, \]
donde:
- \((x_i, y_i)\) son las coordenadas UTM de las 23 estaciones de monitoreo, y
- \(\log CO_i^*\) representa el promedio del logaritmo de las concentraciones de CO (mg/cm³) observadas en cada estación.
3.6.0.6 Configuración del análisis
Las distancias mínima y máxima entre estaciones son aproximadamente 820 m y 14 360 m, respectivamente.
Siguiendo la práctica habitual, se fijó:
- una distancia inicial (primer lag) de 800 m, y
- una distancia máxima igual a la mitad de la distancia máxima observada, es decir, unos 7000 m.
El intervalo entre lags se dividió en 10 clases de distancia de 688.9 m cada una.
Además, se aplicó un ángulo de tolerancia de \(\pi/8\), asegurando un número suficiente de pares en cada intervalo.
3.6.0.7 Cálculo y representación
El semivariograma empírico clásico se calculó mediante el estimador de Matheron (MoM).
Este resultado fue obtenido en R usando el paquete GeoModels y se presentan en la Figura 3.19.
3.6.0.8 Interpretación
El análisis gráfico revela:
- Comportamiento lineal cerca del origen, lo que sugiere continuidad espacial del fenómeno.
- Estructura bien definida para distancias menores a 5000 m.
- Una tendencia a estabilizarse en torno a un sill aproximado de 0.14, aunque no es evidente si este se alcanza completamente o de manera asintótica (el rango práctico podría ser considerablemente mayor).
Con base en esta evidencia, los modelos teóricos candidatos para ajustar el semivariograma empírico son:
- Modelo Esférico — recomendado por su linealidad inicial y estabilización clara.
- Modelo Exponencial — alternativa razonable si se asume un comportamiento asintótico.
El conocimiento geográfico de la ciudad —su estructura urbana y patrones de contaminación— apoya el uso del modelo esférico como la representación más adecuada para los niveles de CO en Madrid.
Se obtienen los datos para el análisis:
Code
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/refs/heads/master/SpatialData/MuniMadrid.txt"
Munimadrid <- read.table(uu, header=TRUE)
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/refs/heads/master/SpatialData/Madrid_LOG_co50s10h.txt"
co.50s.10h <- read.table(uu, header=TRUE)La Figura 3.20 muestra los valores observados en las 23 estaciones de monitoreo de la semana 50 a las 10pm en Madrid.
Code
par(mfrow=c(1,2))
# points(co.50s.10h, # pt.divide="equal", #col=grey(seq(1,0,l=21)),
# pch=21, bg=8, lwd=4, cex.max=3, col=cm.colors(12) )
coord <- cbind(co.50s.10h$x,co.50s.10h$y)
plot(coord, pch=21, bg=8, lwd=4,col=cm.colors(12) ,xlab = "X Coord", ylab = "Y Coord",cex = co.50s.10h$co)
library(scatterplot3d)
scatterplot3d(coord[,1], coord[,2], co.50s.10h$co,
highlight.3d=TRUE, xlab="X-coord",ylab="Y-coord",
zlab="logCO*", pch=20, type="h",
cex.axis=.7, mar=c(2,2,2,2), mgp=c(0,0,0),
cex.lab=.6)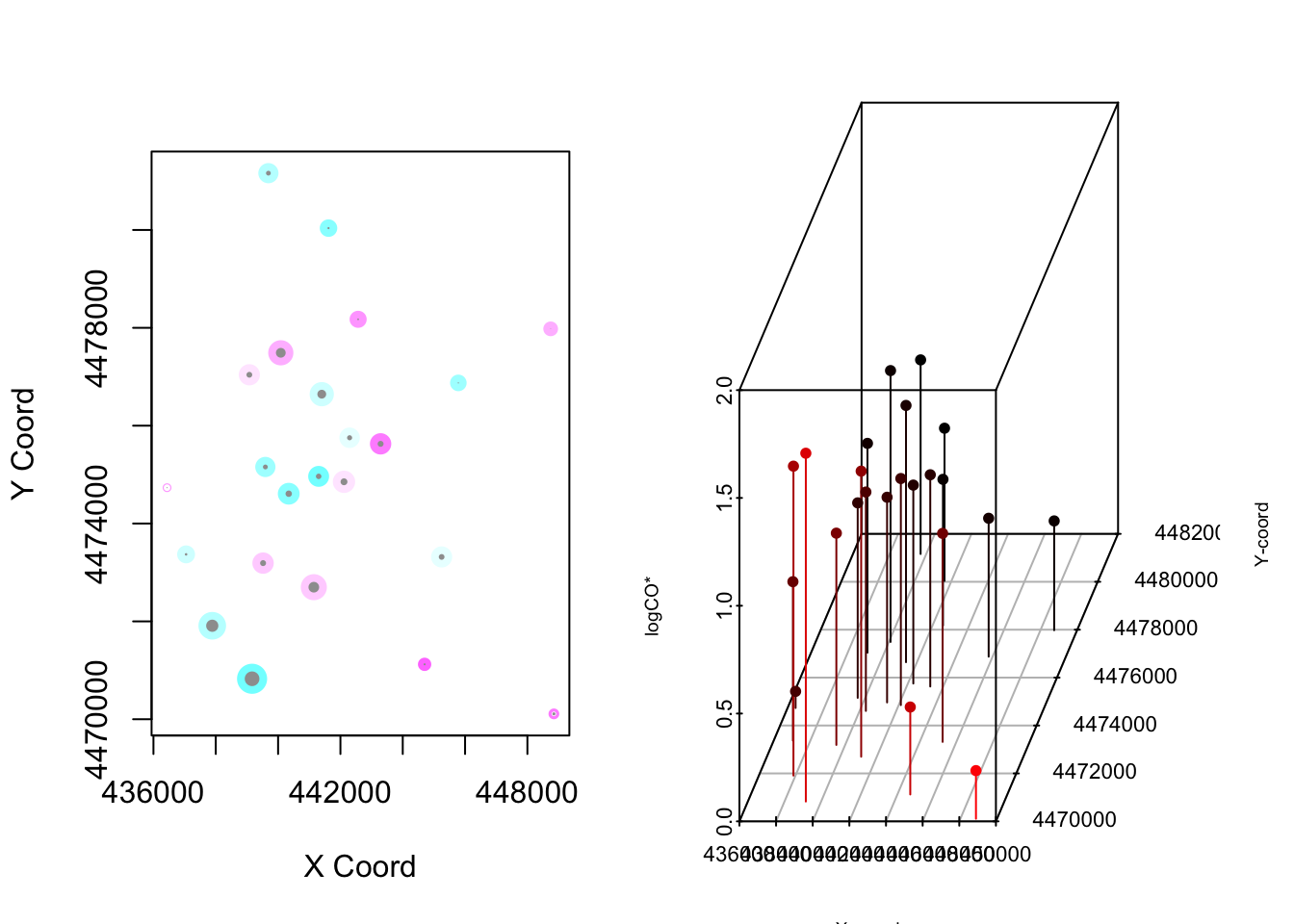
Figura 3.20: 23 estaciones de monitoreo de la semana 50 a las 10pm en Madrid
Semivariograma empírico de los niveles de monóxido de carbono (CO) en Madrid. Se observa en la Figura 3.21 un comportamiento lineal cerca del origen y estabilización alrededor de un sill de 0.14 .
Code
| Lag_distances | Num_pais | Semi_values |
|---|---|---|
| 1335.614 | 8 | 0.0127519 |
| 1850.558 | 10 | 0.0571909 |
| 2365.502 | 17 | 0.0404673 |
| 2880.447 | 14 | 0.0538641 |
| 3395.391 | 16 | 0.1327845 |
| 3910.335 | 23 | 0.1044954 |
| 4425.279 | 18 | 0.0657361 |
| 4940.223 | 16 | 0.2167371 |
| 5455.167 | 16 | 0.1528292 |
| 5970.112 | 20 | 0.1593673 |
| 6485.056 | 11 | 0.1005506 |
| 7000.000 | 13 | 0.1287673 |
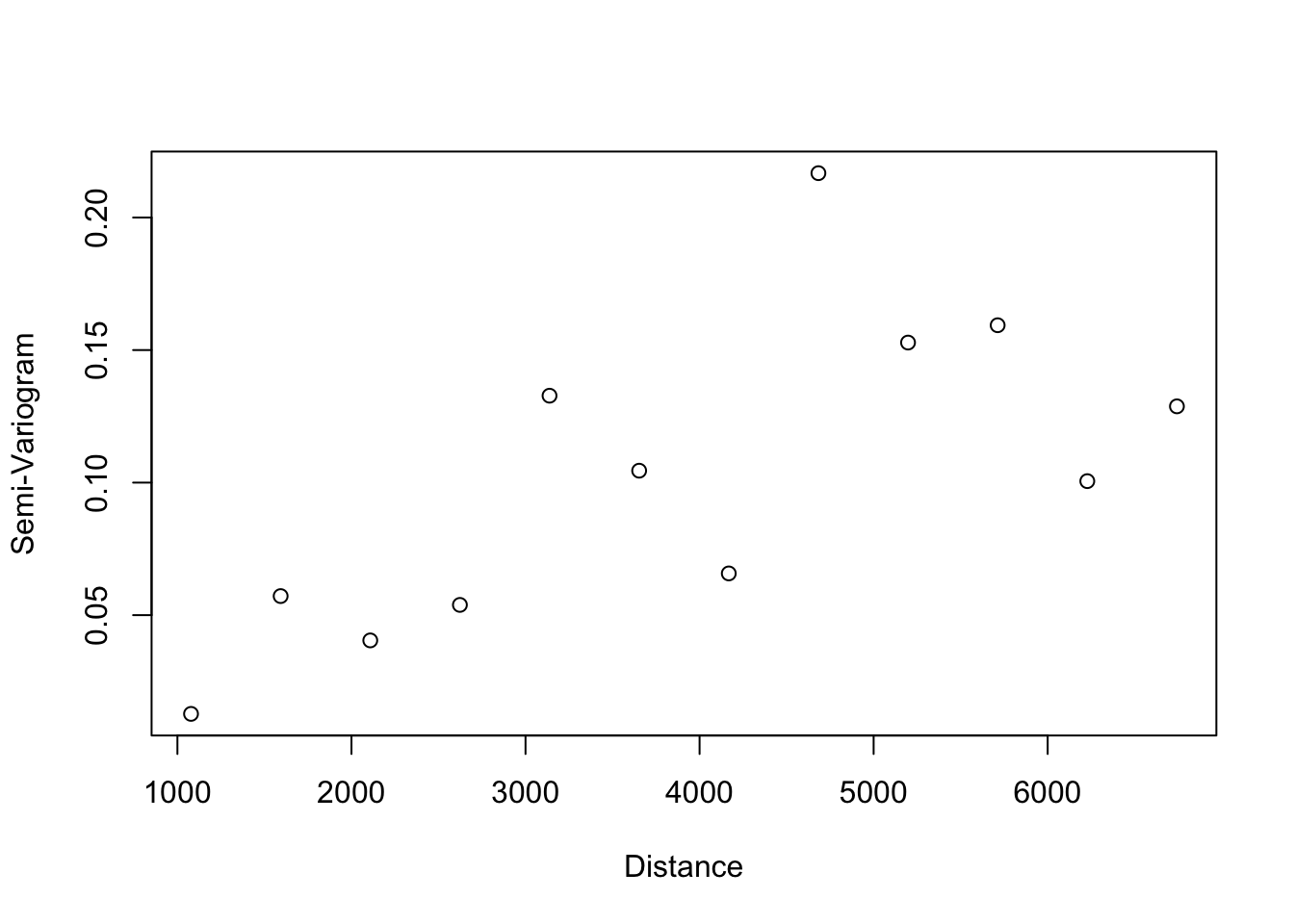
Figura 3.21: Datos de monóxido de carbono en Madrid, semana 50, 10pm