B Métodos Experimentales y Cuasi-experimentales
B.1 Motivación
Evidence-based programs
Statistical methods:
RCTs – promoted by agencies (e.g. J-PAL)
Quasi-experiments – look for situations “simulating” an experiment
Increased access to data and measurement of concepts
B.2 RCTs in practice
Evidence-based science

B.3 Some ideas
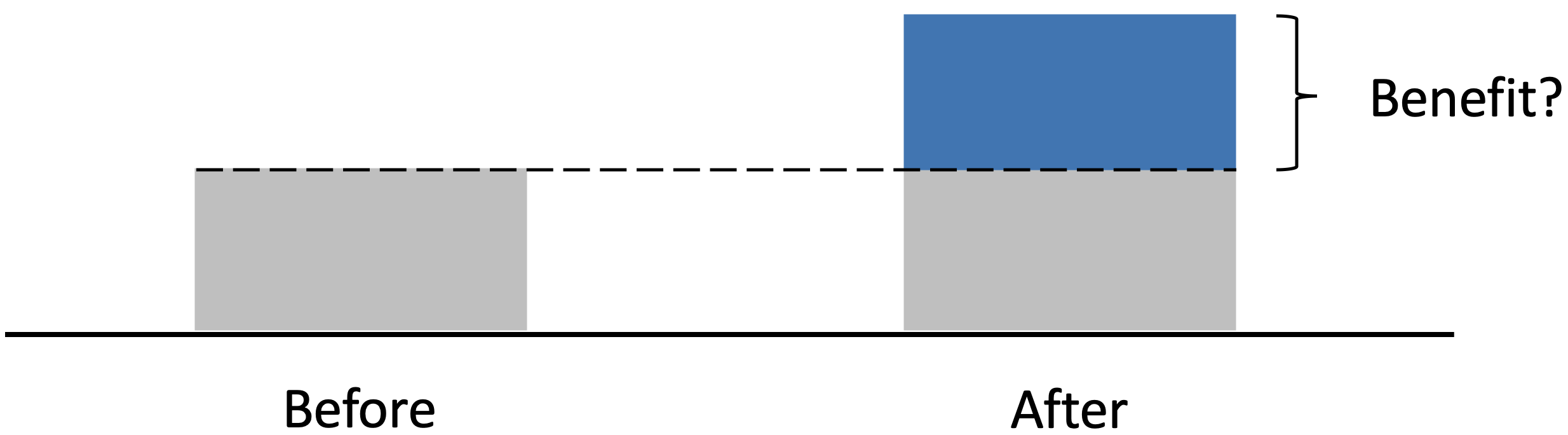
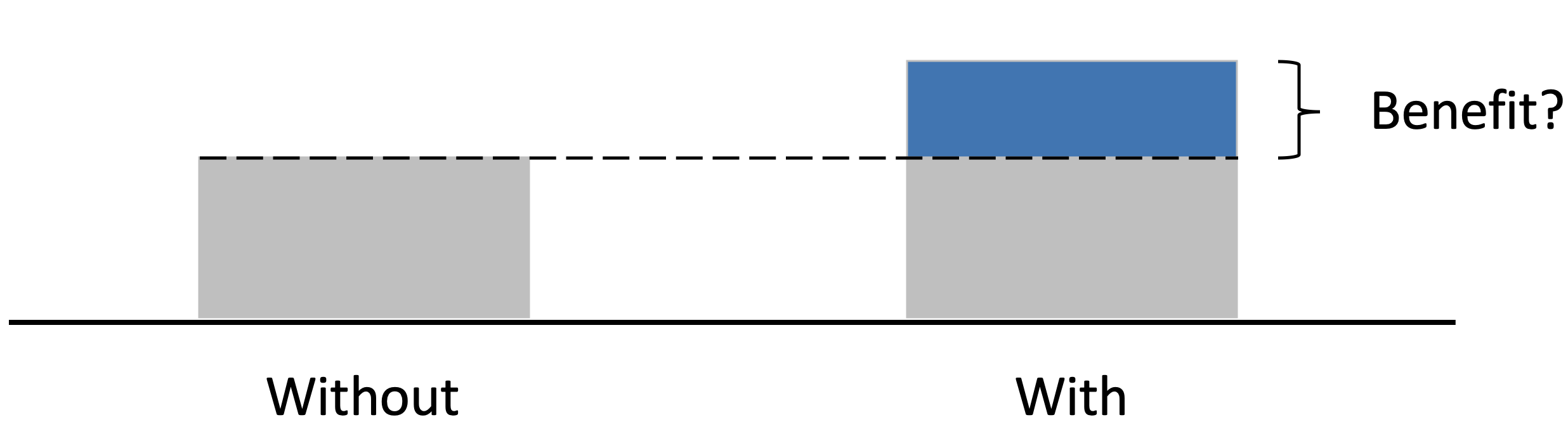
Objective: Measure the benefits (or lack of) that the program gives
Approach #1: Before versus after

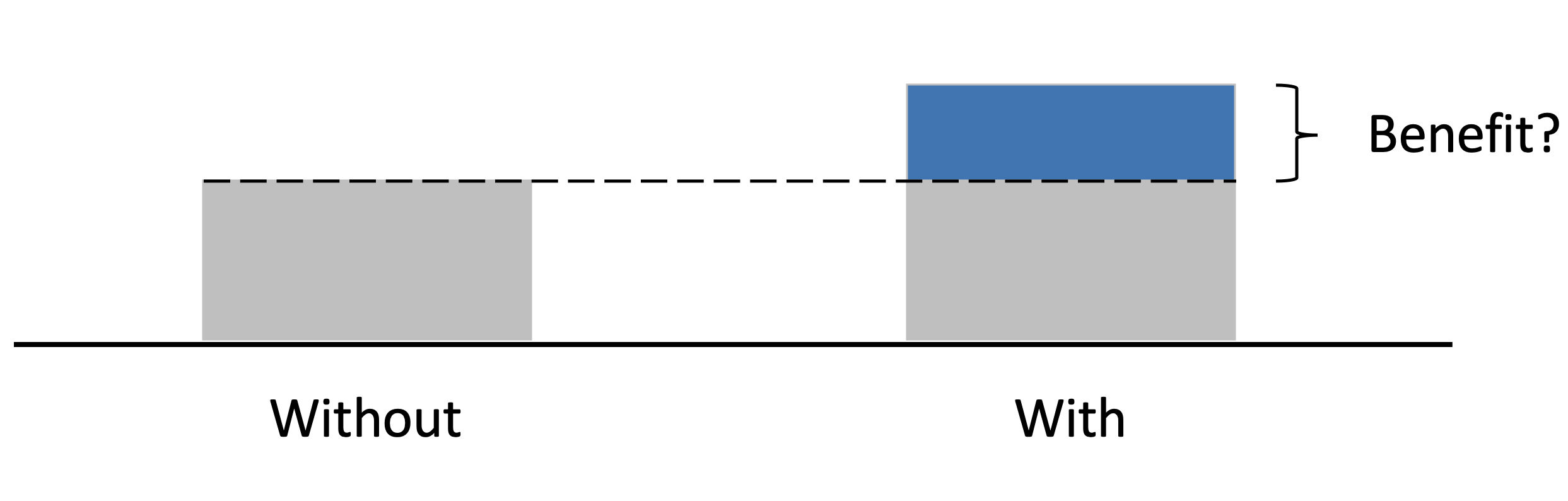
Approach #2: Compare people with and without the program

B.4 Statistical concepts
Objective: Measure the benefits (or lack of) that the program gives
Ideal approach: Compare the same person with and without the program

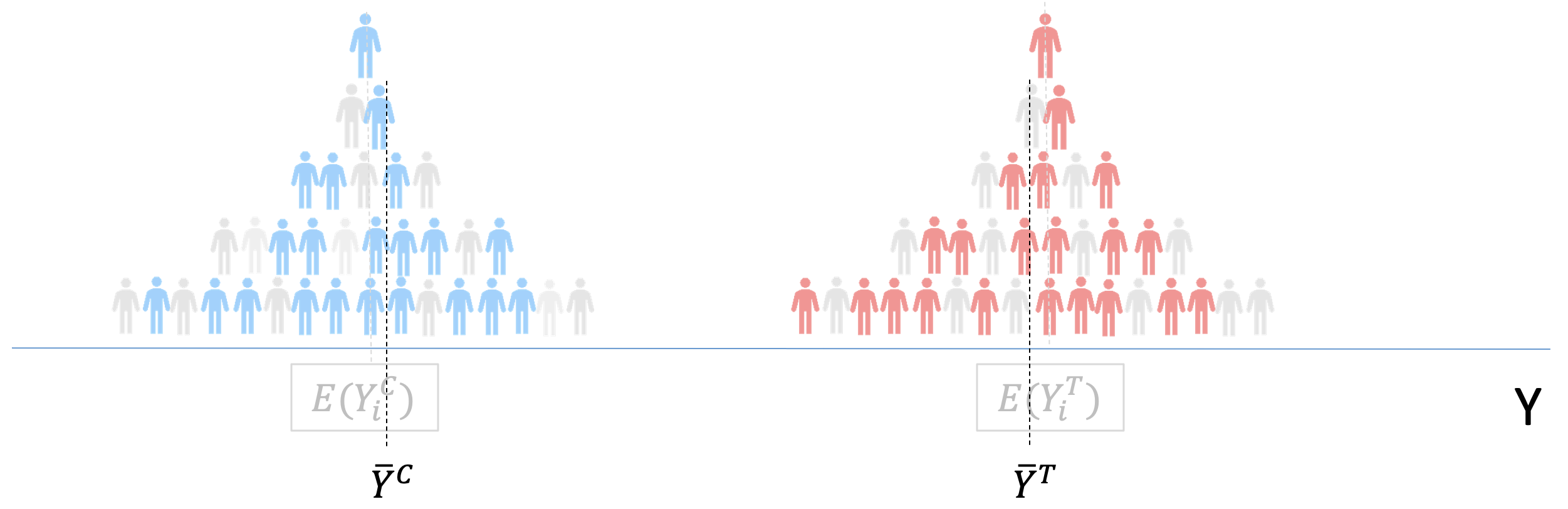
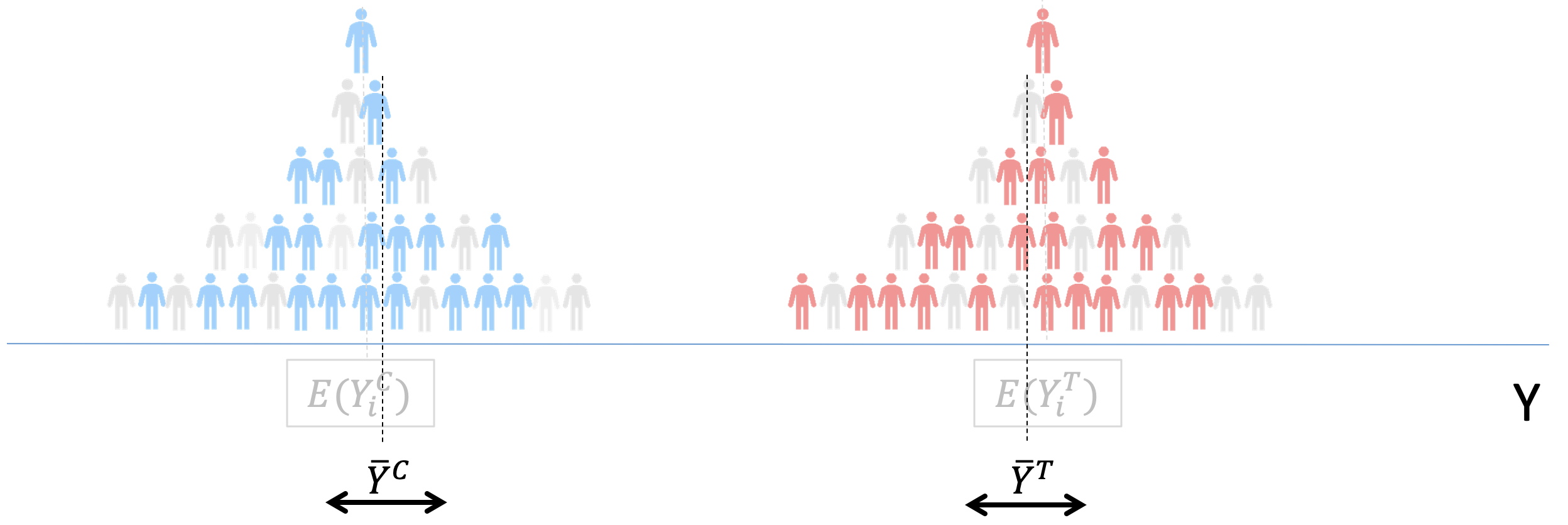
Potential Outcomes

Treatment Effect \[TE=Y_i^T-Y_i^C\] However… we can only observe “one” version of Sofia, not both!
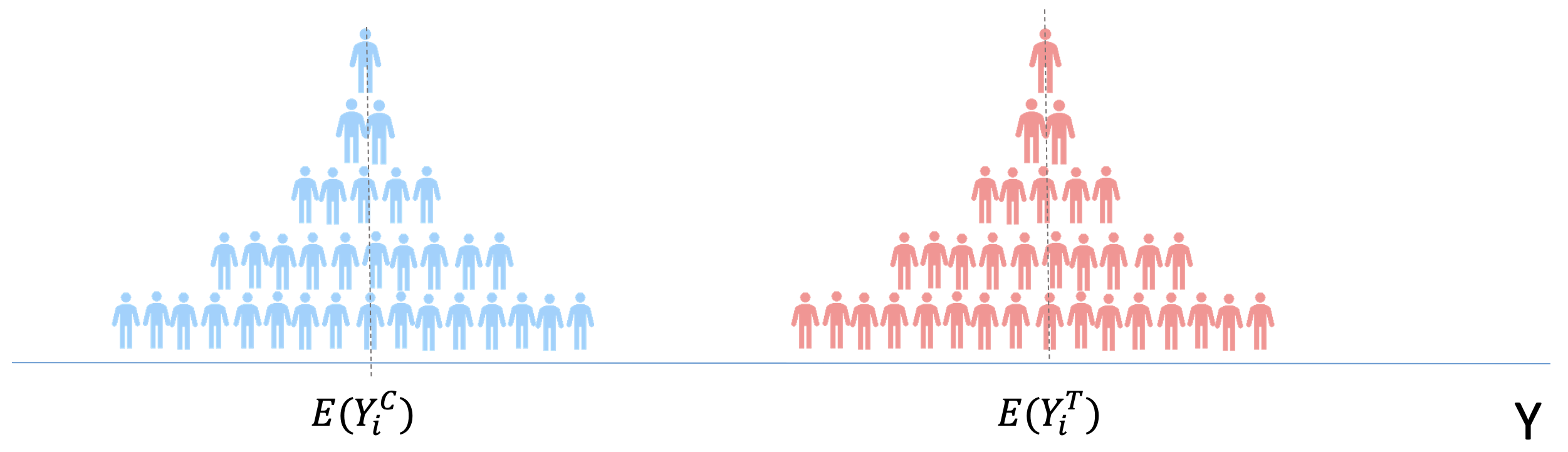
Let’s imagine now that we compare health (Y) in two alternative worlds:
No one gets vaccination: everyone gets their \(Y_i^C\) level of health

Everyone gets vaccination: everyone gets their \(Y_i^T\) level of health
If we could look at both “versions” of the world we could calculate:
Average Treatment Effects: \(ATE=E[Y_i^T]-E[Y_i^C]\)
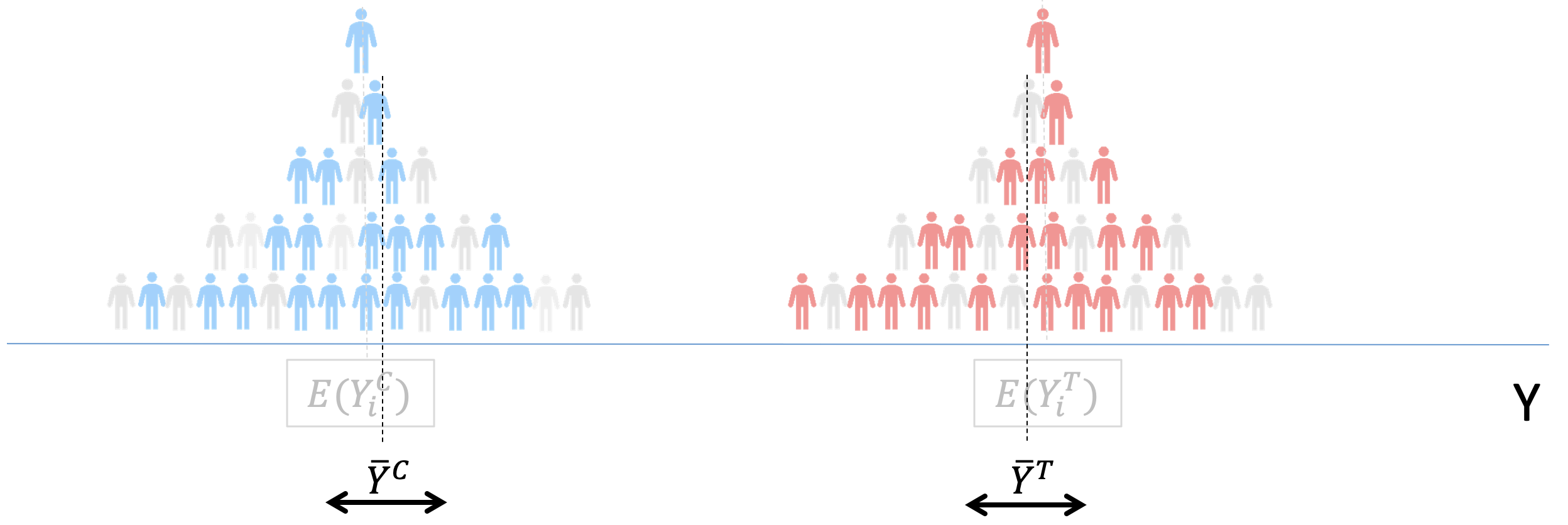
Now it looks impossible + extremely costly
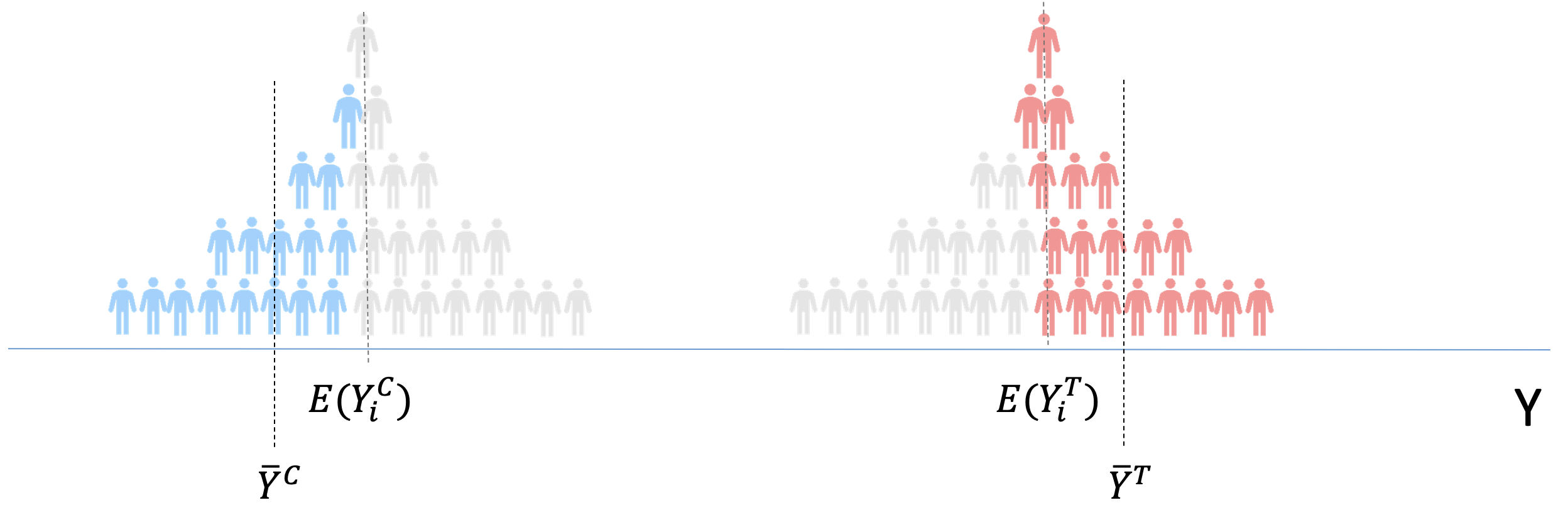
But, what if we take a sample instead of looking at “everyone”
We can still get very close to \(E[Y_i^T]\) and \(E[Y_i^C]\) if we choose “wisely”
Problem with self-selection \(\Longrightarrow\) Bias
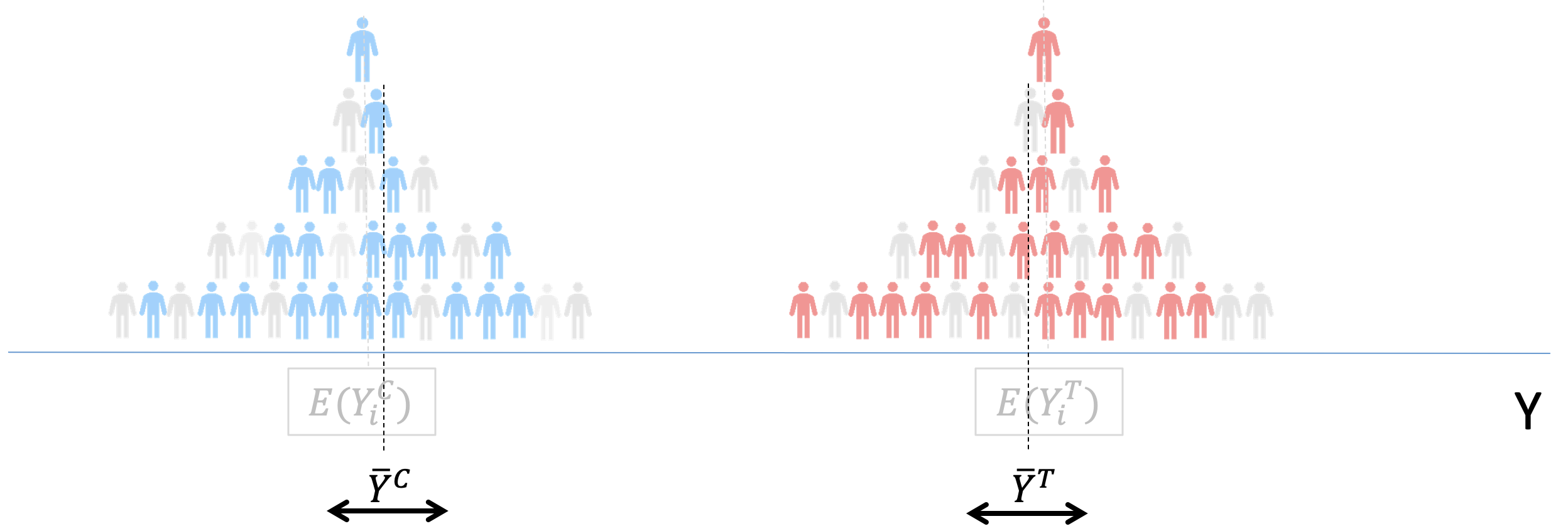
Standard errors. In this case, \(\bar{Y}^T-\bar{Y}^C\) gives us an “estimate” of ATE. Thus we, need to create intervals in which ATE could be.
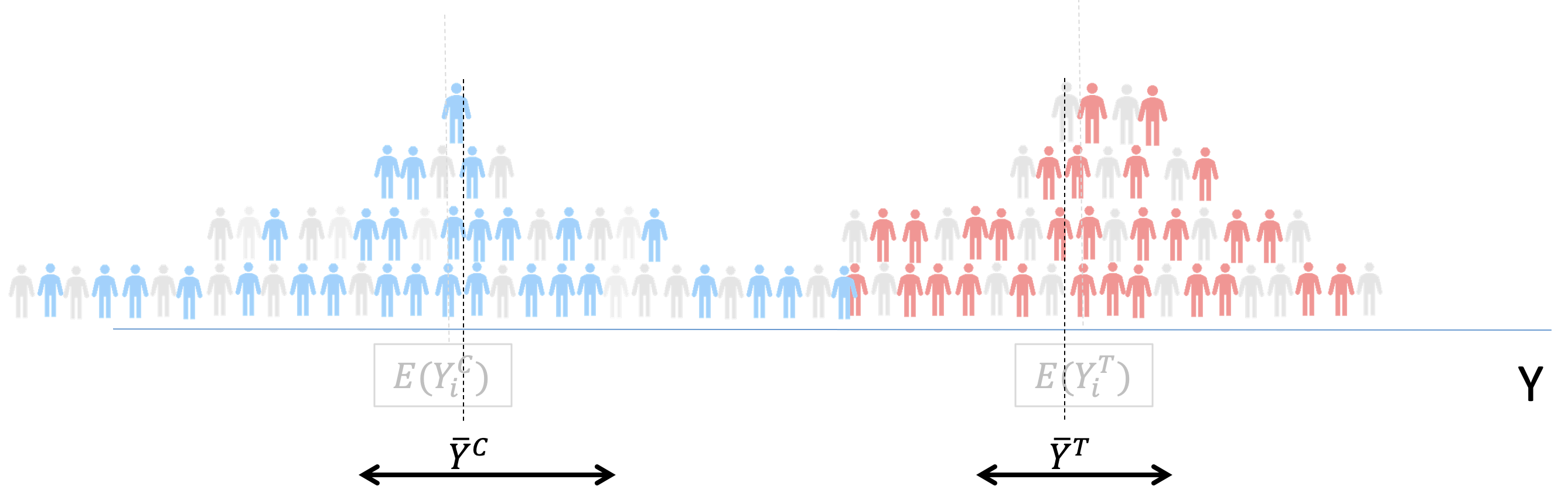
B.5 RCTs
Objective: Measure the benefits (or lack of) that the program gives
- Solution: Randomization
Challenges found on RCTs:
Externalities
John Henry and Hawthrone effects
Attrition
Partial participation
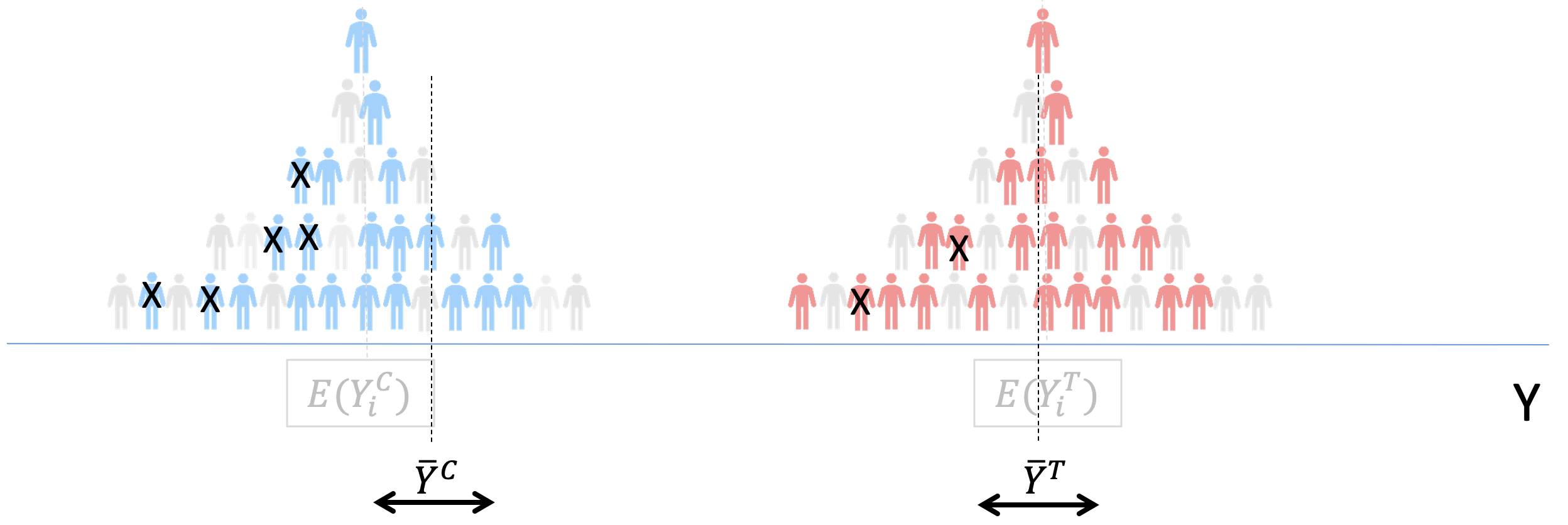
Externalities. Mean that it is not possible to observe “control” in a pure form
Externalities. Depending on the type of externality, we would be over- or under-estimating ATE
 John Henry effects: a legendary American steel driver in the 1870s who, when he heard his output was being compared with that of a steam drill, worked so hard to outperform the machine that he died in the process.
John Henry effects: a legendary American steel driver in the 1870s who, when he heard his output was being compared with that of a steam drill, worked so hard to outperform the machine that he died in the process.
Hawthrone effects: Hawthorne Works (Western Electric factory outside Chicago) commissioned a study to see if their workers would become more productive in higher or lower levels of light. The workers’ productivity seemed to improve when changes were made, and slumped when the study ended.
Attrition. Need to be careful with “selective attrition”
Attrition. Could result from deaths, migration, unwillingness to continue participating
Partial participation: treatment is not always enforceable
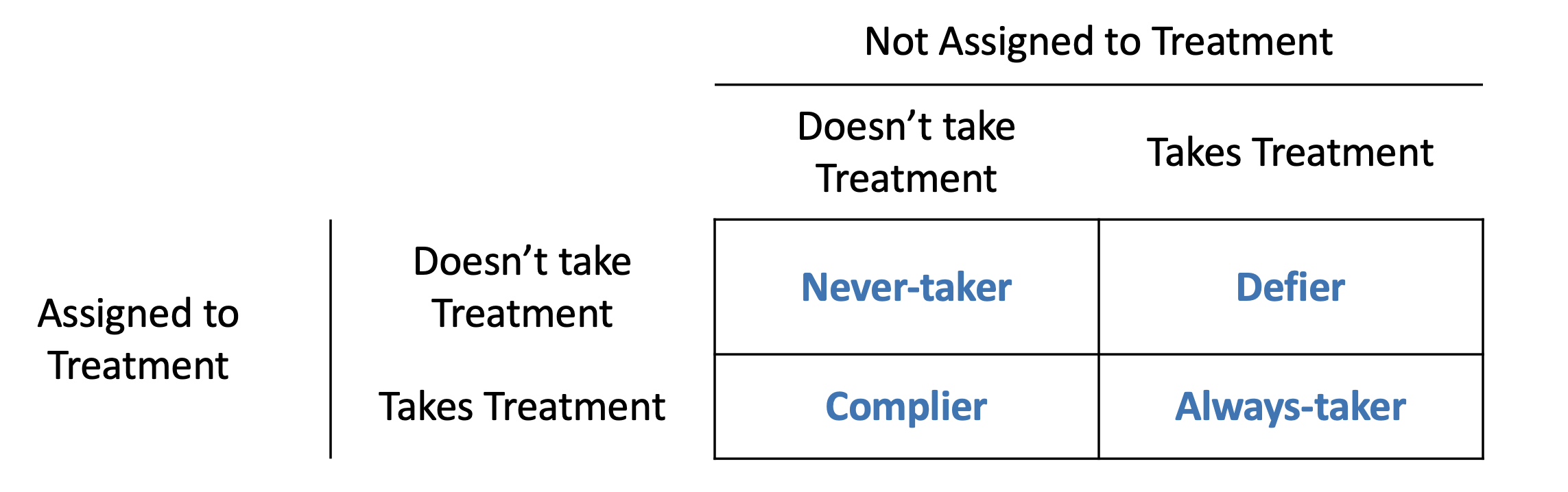
Partial participation
\[Y_1=\gamma_0+\gamma_1Z_i+U_i\] \[T_i=\eta_0+\eta_1Z_i+V_i\] LATE (ATE on compliers) \[\dfrac{\partial Y}{\partial T}=\frac{\dfrac{\partial Y}{\partial Z}}{\dfrac{\partial T}{\partial Z}}=\frac{\gamma_1}{\eta_1}\] ## RCT in practice
Identify the causes of a problem that you want to solve
-Complement this with field work
Build a theory of change
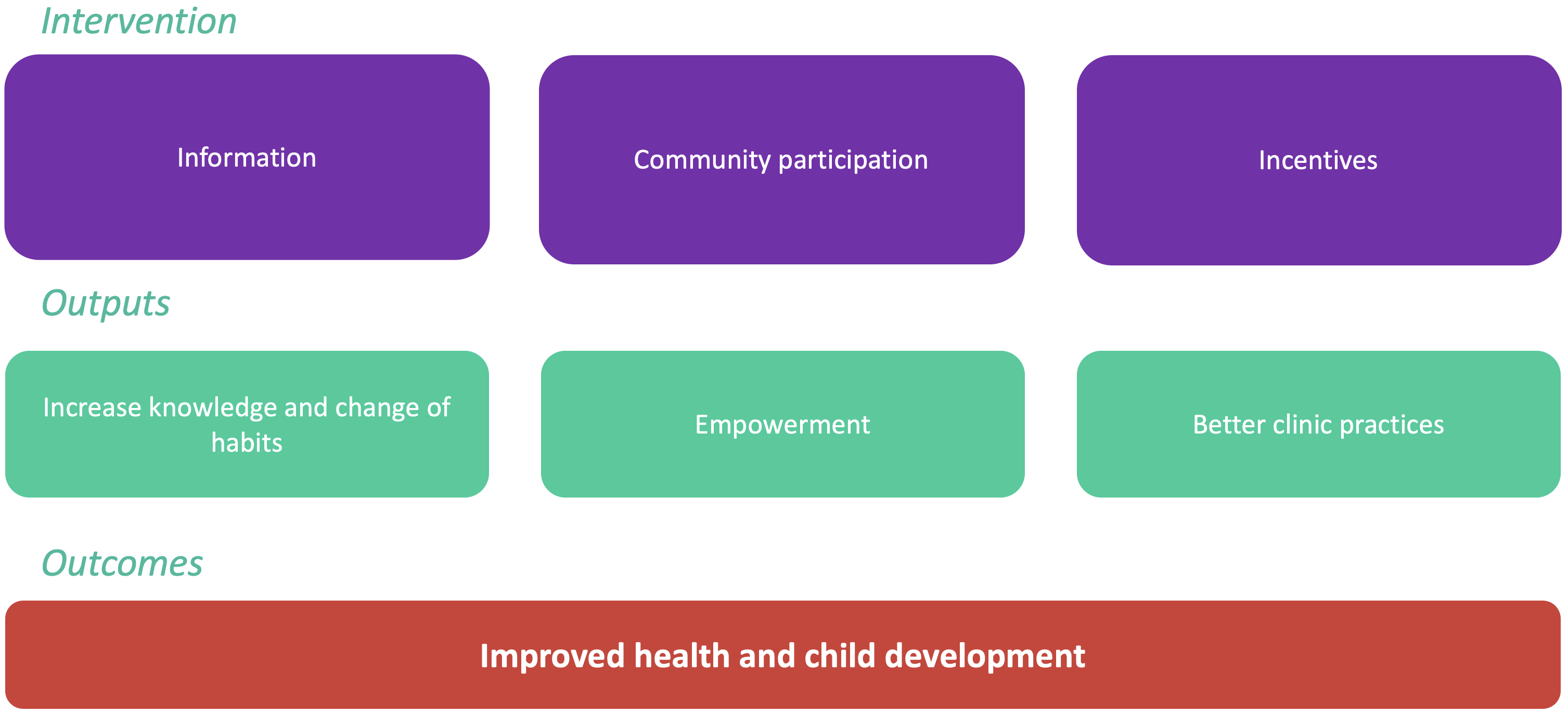
Figure B.1: Theory of change
- Associate your theory of change with a list of indicators
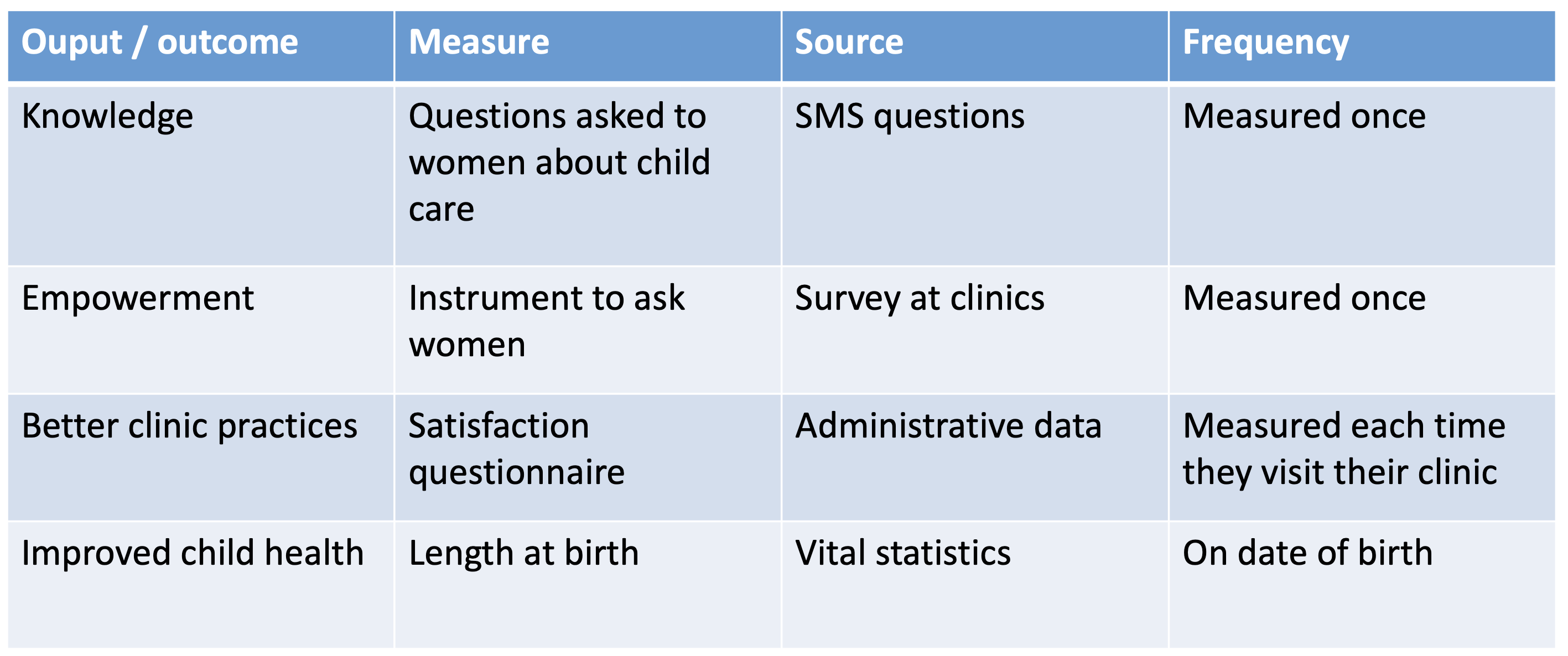
Figure B.2: List of indicators
Trial registry
1. Identify the causes of a problem that you want to solve
2. Build a theory of change
3. Associate your theory of change with a list of indicators
4. IRB / Ethics board (example)
5. Pre-pilot
6. Monitor / FOISelecting your level of treatment
-Individual level
-Group level
-Locality level
Selecting your sample size
What to do if you have several “treatment arms”?
Setup your monitoring tools
Example:
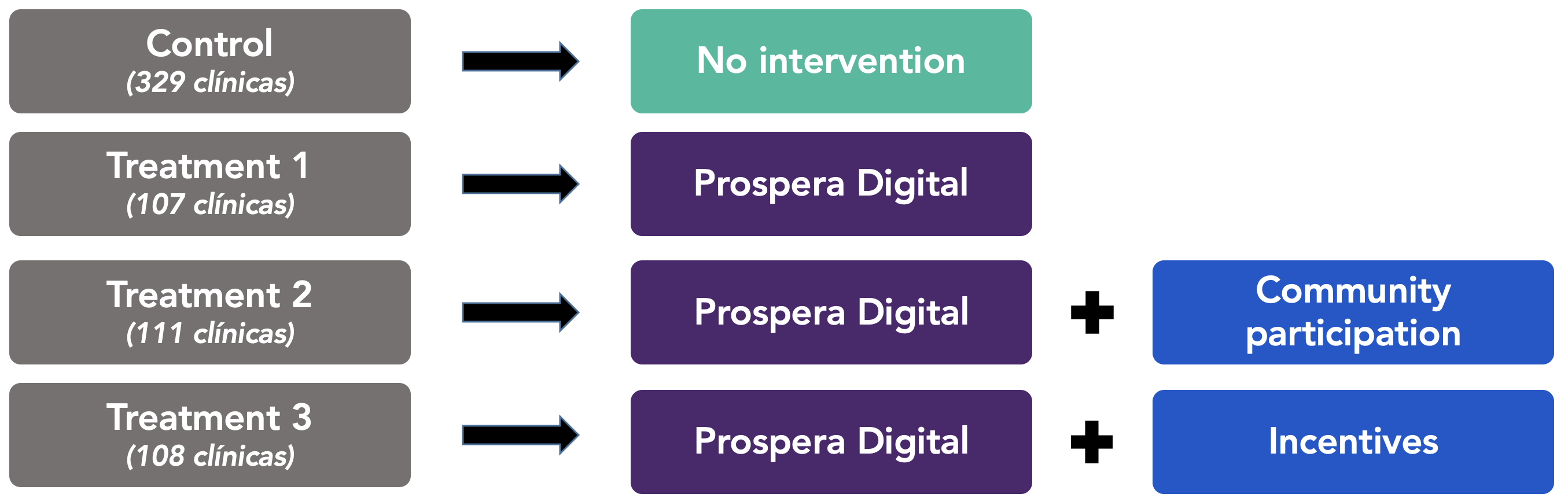
B.6 Quiz
In an educational project some treatment schools decide after you randomize that they cannot participate. Your implementing partner wants to substitute those schools with new schools from the control which really want to receive treatment.
Should you allow for this?
In your financial intervention you gave debit cards to people in treatment localities. You realize that some people in the treatment are not using the debit card at all.
Should you define them as part of the treatment or the control when making your analysis?
In a health intervention you are giving workshops to patients as part of an intervention. Your intervention takes place in two States (one poor and one rich), half of the clinics in each State is treatment and the other half is control.
Your implementing partner tells you that it is very inefficient and expensive doing half and half. That they can only afford to do one full State treatment and the other control. If this is a take-it or leave-it situation, what would you do?
In a gender violence project you are giving one-to-one advisories to victims. Your treatment is distributed at the locality level. Some of your beneficiaries seem to be improving and ask you that they want to invite their friends in the community who have been also victims, but are not receiving “treatment”.
Should you allow for this?
Quasi-experiments
Difference-in-difference
Regression discontinuity
Natural experiments
Matching
Objective: Try to find a credible scenario for the “control”