Capítulo 1 Distribuições de Probabilidade

1.1 Distribuições discretas

1.1.1 Distribuição de Bernoulli

Definição 1.1 Uma variável aleatória \(X\) tem uma distribuição Bernoulli, se assume apenas os valores 0 ou 1. Sua função de probabilidade é dada por:

\[\begin{equation*} P(X=x) = p^x(1-p)^{1-x}, \ \ x=0,1. \end{equation*}\] Notação: \(X \sim Bernoulli(p)\) ou \(X \sim Ber(p)\)

Exemplo 1.1 Seja \(X \sim Ber(0.7)\).

Calcule a \(P(X=1)\) e \(P(X=0)\).

# P(X=1): 
dbinom(1,1,0.7)

## [1] 0.7

#P(X=0)
dbinom(0,1,0.7)

## [1] 0.3

1.1.2 Distribuição Binomial

Definição 1.2 Uma variável aleatória \(X\) tem uma distribuição Binomial com parâmetros \(n\) e \(p\) se sua função de probabilidade é dada por:

\[\begin{equation*} P(X=x) = \binom{n}{p}p^x(1-p)^{n-x}, \ \ x=0,1,\ldots,n. \end{equation*}\] Notação: \(X \sim Binomial(n,p)\).

Exemplo 1.2 Um aluno marca ao acaso as respostas em um teste múltipla-escolha com 10 questões e cinco alternativas por questão.

\(X \sim Binomial(n=10,p=0,2)\)

Qual é a probabilidade dele acertar exatamente 4 questões?

# P(X = 4)
dbinom(4,10,0.2)

## [1] 0.08808038

Qual é a probabilidade dele acertar pelo menos 4 questões?

# P(X >= 4) = 1 - P(X < 4)= 1 - P(X<=3)
1 - pbinom(3,10,0.2)

## [1] 0.1208739

Gráfico da função de probabilidade.

x <- 0:10
fx <- dbinom(x,10,0.2)
plot(x, fx, pch=19, ylab=expression(paste(P(X==x))))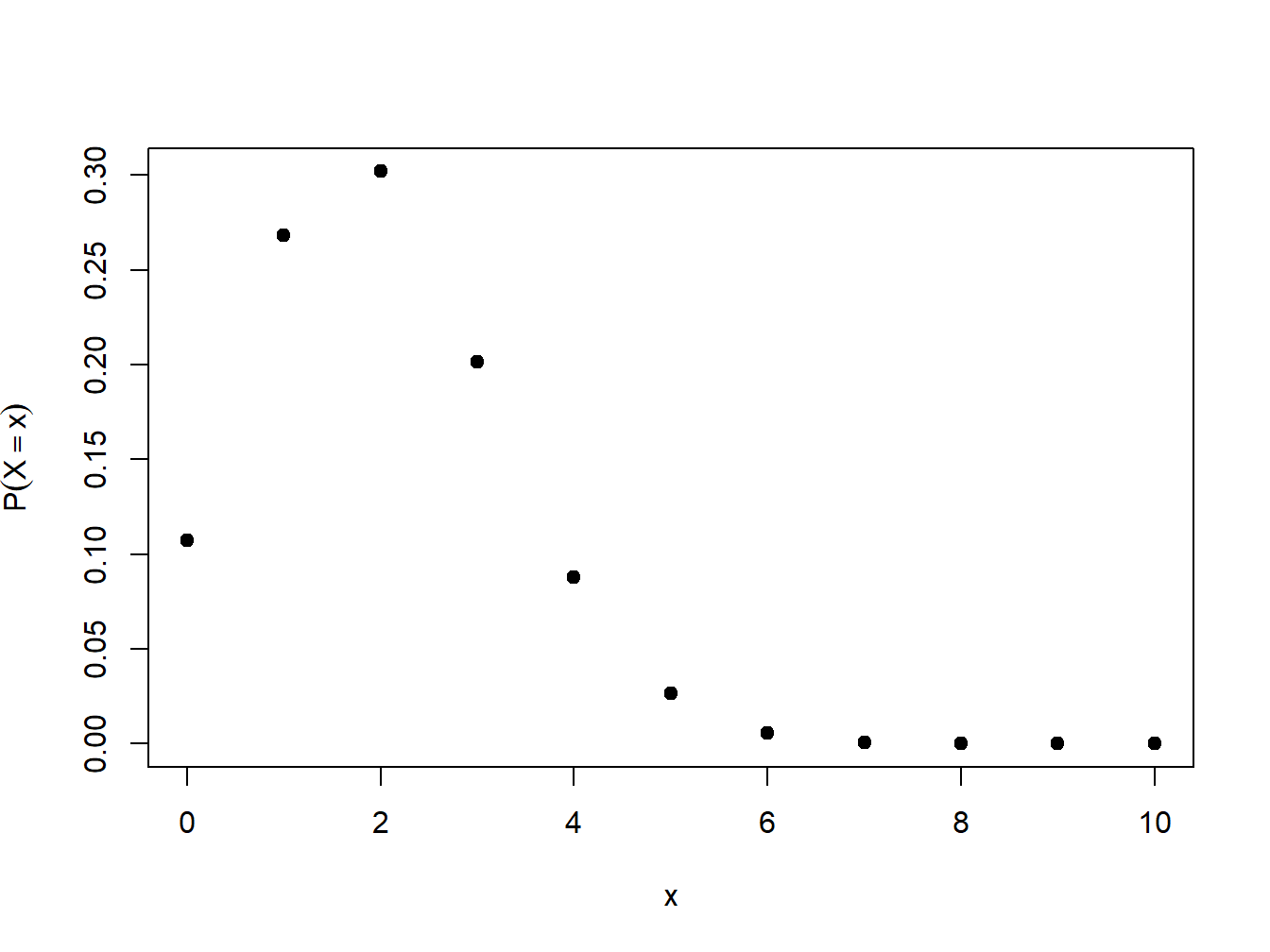

Figura 1.1: Função de probabilidade para Binomial(10,0.2)

Gráfico da função de distribuição.

Fx <- pbinom(x,10,0.2)
plot(x, Fx, type='S', ylab=expression(paste(P(X <= x))), ylim=c(0,1))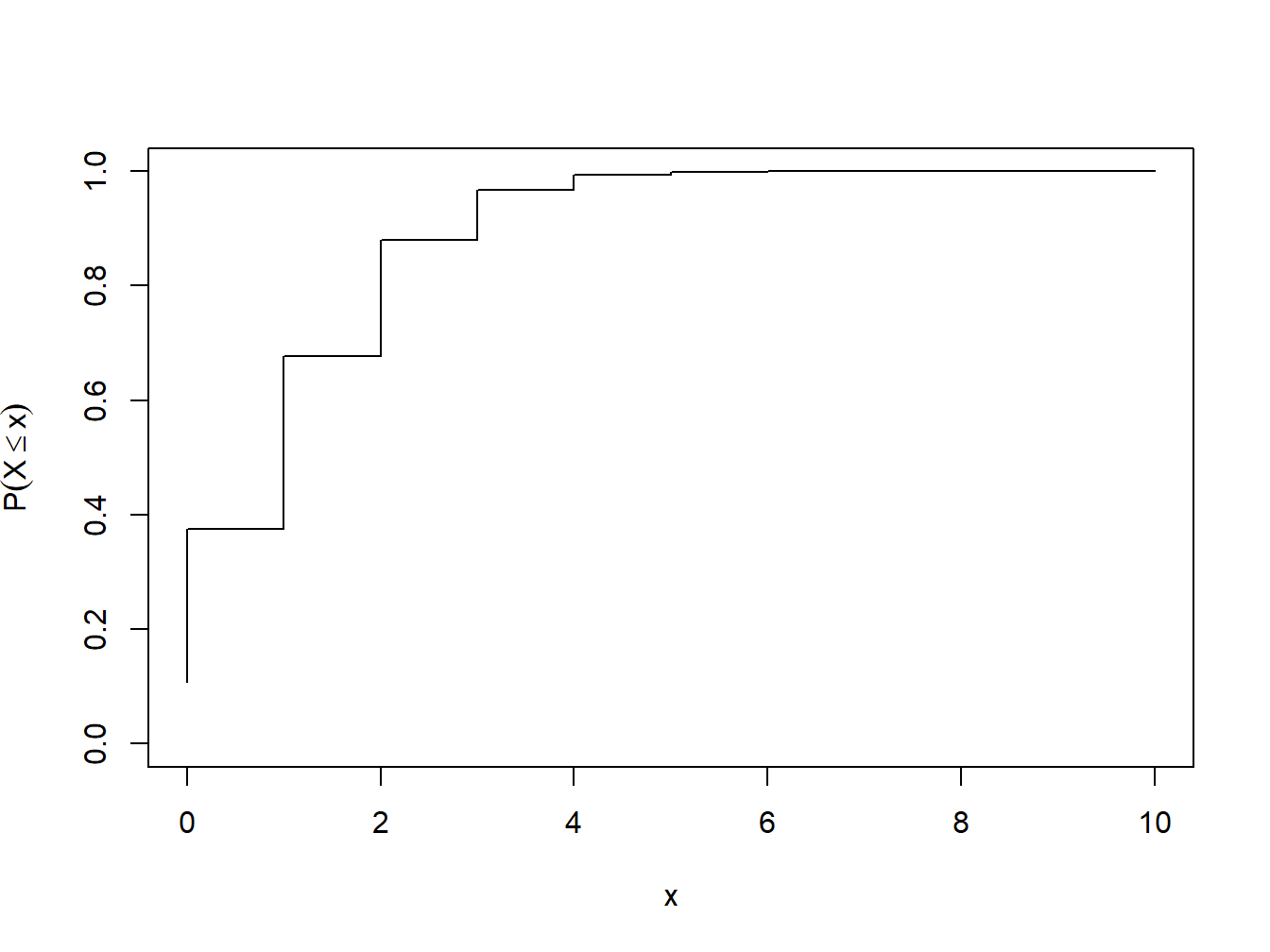

Figura 1.2: Função da distribuição acumulada para Binomial(10,0.2)

1.1.3 Distribuição de Poisson

Definição 1.3 Uma variável aleatória \(X\) tem uma distribuição Poisson de parâmetro \(\lambda\), \(\lambda > 0\), se sua função de probabilidade é dada por:

\[\begin{equation*} P(X=x) = \dfrac{e^{-\lambda}{\lambda}^{x}}{x!}, \ \ x=0,1,\ldots. \end{equation*}\] Notação: \(X \sim Poisson(\lambda)\).

Exemplo 1.3 Considere um processo que têm uma taxa de 0,2 defeitos por unidade.

\(X \sim Poisson(\lambda=0,2)\)

Qual a probabilidade de uma unidade qualquer apresentar dois defeitos?

# P(X=2)
dpois(2,0.2)

## [1] 0.01637462

Qual a probabilidade de 1 a 3 unidades apresentar defeitos?

# P(1 <= X <= 3)
ppois(3,0.2) - ppois(1,0.2)

## [1] 0.01746626

Relação entre Binomial e Poisson

Seja \(X \sim Binomial(n,p)\). Para \(n\) grande e \(p\) pequeno, podemos aproximar essas probabilidades por \[\begin{equation*} P(X = k) \simeq \dfrac{e^{np}(np)^{k}}{k!}, \ \ k=0,1,\ldots,n. \end{equation*}\]

Exemplo 1.4 Seja \(X \sim Binomial(n=20,p=0.007)\). Calcule \(P(X = 3)\).

# Binomial: 
dbinom(3,20,0.007)

## [1] 0.0003470054

# Poisson:
dpois(3,20*0.007)

## [1] 0.0003975865

1.2 Distribuições contínuas

1.2.1 Distribuição Uniforme

Definição 1.4 A variável aleatória \(X\) tem distribuição uniforme no intervalo \([a,b]\) se sua função de densidade é dada por: \[\begin{equation*} f(x) = \dfrac{1}{b-a}, \ \ a \leq x \leq b. \end{equation*}\] Notação: \(X \sim U[a,b]\).

Exemplo 1.5 Um programa de TV dura 1 hora e um telespectador impaciente inicia assistindo, mas vai trocar de canal a qualquer momento durante o programa. Qual a probabilidade de ele assistir à maior parte do programa?

# P(X > 1/2)
1 - punif(1/2,0,1)

## [1] 0.5

Gráfico da função de densidade de probabilidade.

x <- seq(-1,2,length.out = 10000)
fx <- dunif(x,0,1)
plot(x, fx, ylab=expression(paste(f(x))), type="l")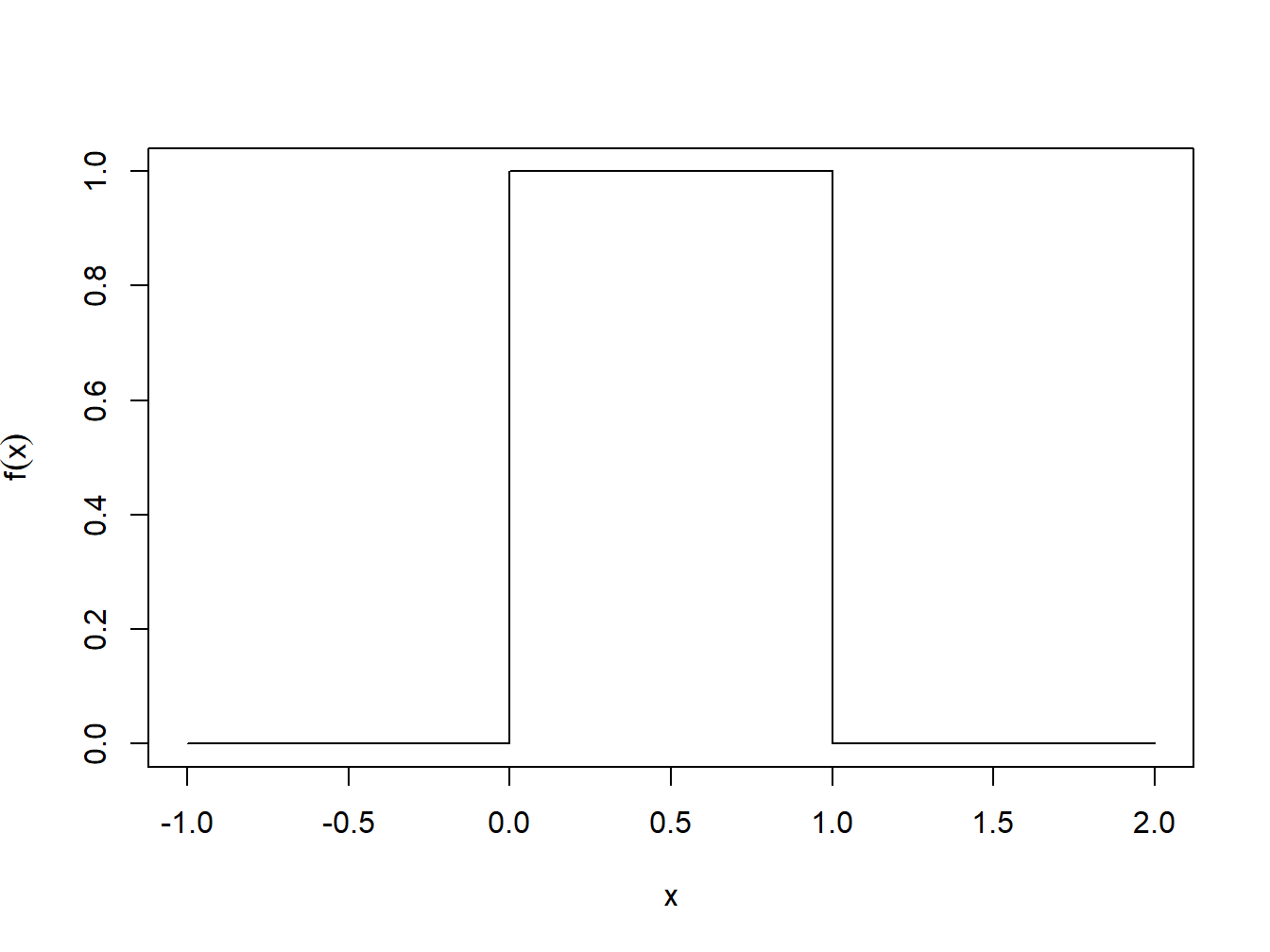

Figura 1.3: Densidade da Uniforme(0,1)

Gráfico da função de distribuição acumulada.

Fx <- punif(x,0,1)
plot(x, Fx, ylab=expression(paste(F(x))), ylim=c(0,1), type="l")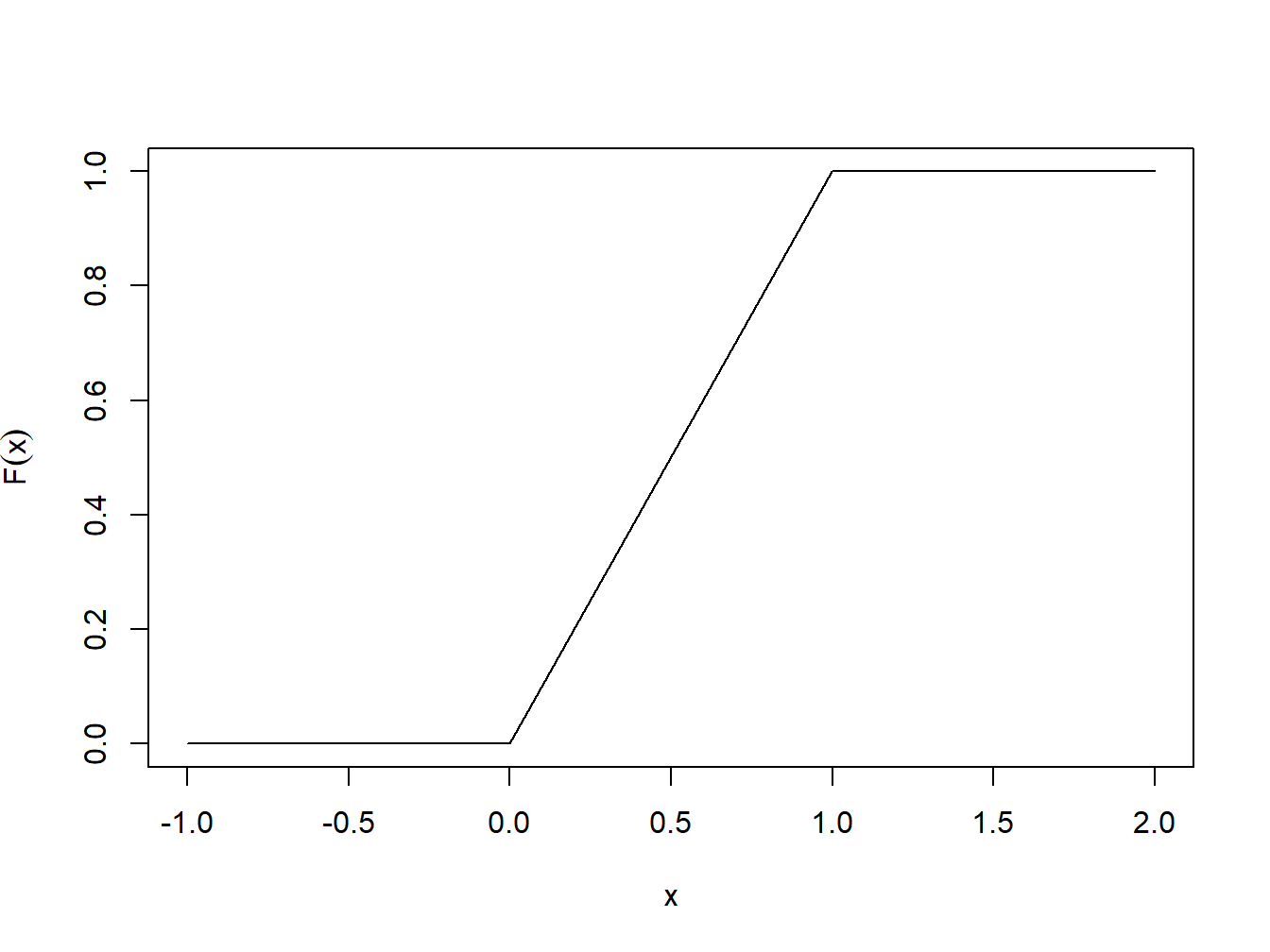

Figura 1.4: Função de distribuição acumulada da Uniforme(0,1)

1.2.2 Distribuição Exponencial

Definição 1.5 A variável aleatória \(X\) tem distribuição exponencial de parâmetro \(\lambda\), \(\lambda > 0\), se tiver densidade dada por:

\[\begin{equation*} f(x) = {\lambda}e^{-{\lambda}x}, \ \ x \geq 0. \end{equation*}\] Notação: \(X \sim Exp(\lambda)\).

Exemplo 1.6 Suponha que a duração de um telefonema, em minutos, seja uma variável aleatória exponencial com parâmetro \(\lambda = 1/5\). Se alguém chega logo na sua frente em uma cabine telefônica, determine a probabilidade de que você tenha que esperar mais de 10 minutos.

# P(X > 10)
1 - pexp(10,1/5)

## [1] 0.1353353

Gráfico da função de densidade de probabilidade.

x <- seq(0,6,length.out = 10000)
fx1 <- dexp(x,1)
fx2 <- dexp(x,2)
fx3 <- dexp(x,5)
plot(x, fx1, ylab=expression(paste(f(x))), type = "l", ylim=c(0,5))
lines(x,fx2,type = "l", col="red")
lines(x,fx3,type="l", col="blue")
legend("topright", c(expression(paste(Exp(1))), expression(paste(Exp(2))), expression(paste(Exp(5)))), col = c("black", "red", "blue"), bty="n", lty=c(1,1,1), inset = 0.05 )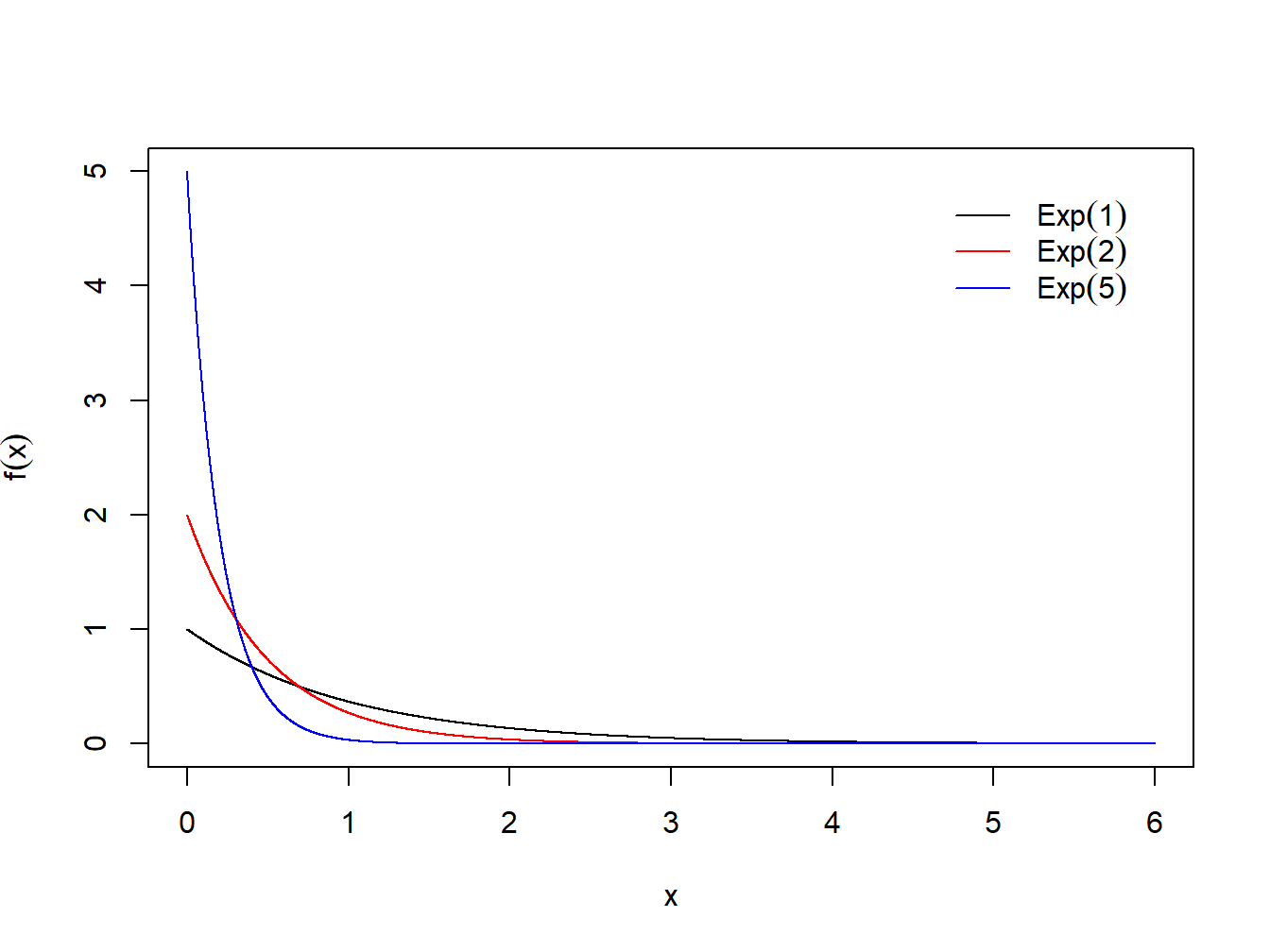

Figura 1.5: Densidade da Exponencial

Gráfico da função de distribuição acumulada.

Fx1 <- pexp(x,1)
Fx2 <- pexp(x,2)
Fx3 <- pexp(x,5)
plot(x, Fx1, ylab=expression(paste(F(x))), type = "l", ylim=c(0,1))
lines(x,Fx2,type = "l", col="red")
lines(x,Fx3,type="l", col="blue")
legend("bottomright", c(expression(paste(Exp(1))), expression(paste(Exp(2))), expression(paste(Exp(5)))), col = c("black", "red", "blue"), bty="n", lty=c(1,1,1), inset = 0.05 )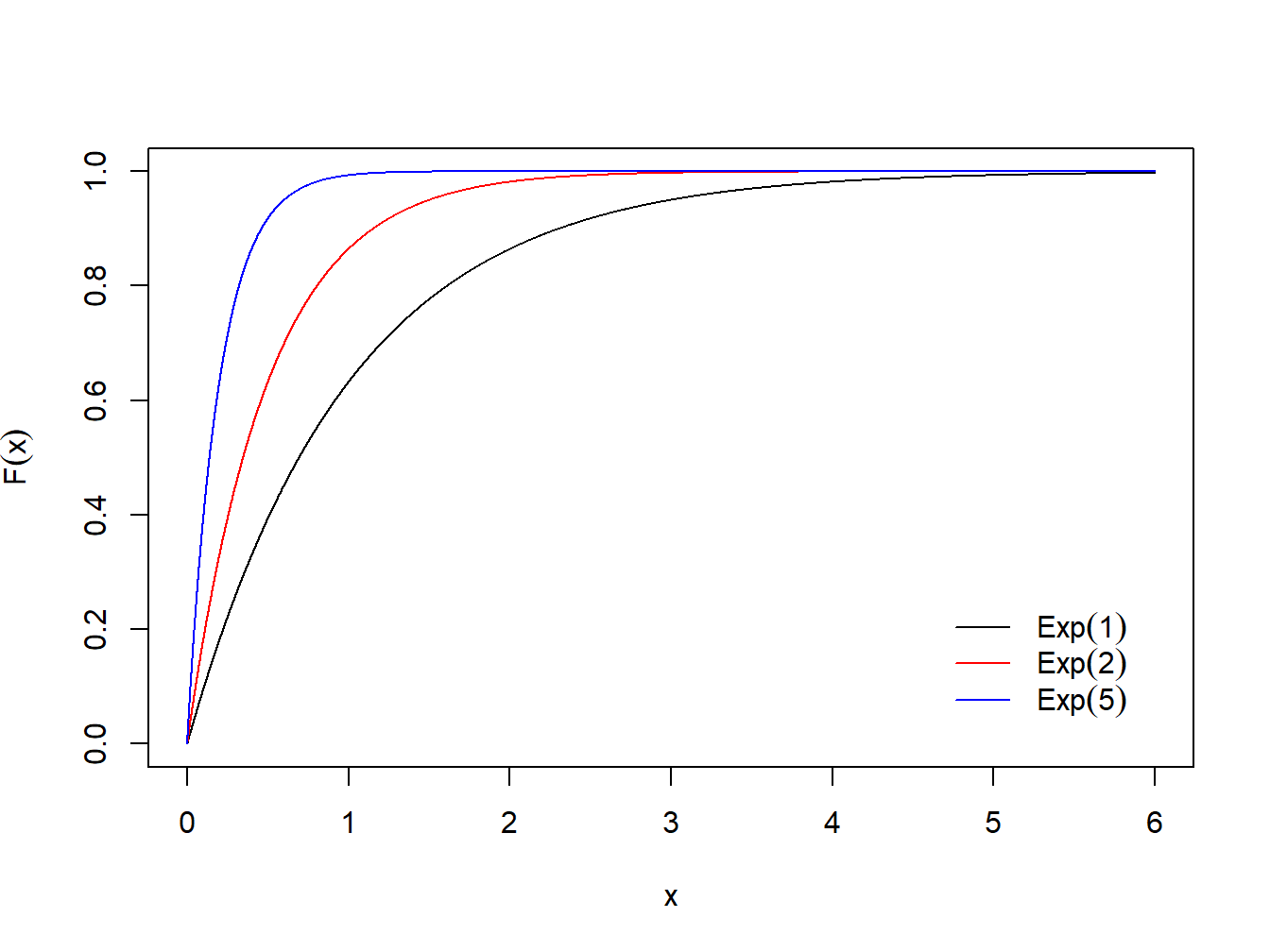

Figura 1.6: Função de distribuição acumulada da Exponencial

1.2.3 Distribuição Gama

Definição 1.6 A variável aleatória \(X\) tem distribuição Gama, se sua densidade for dada por \[\begin{equation*} f(x) = \dfrac{\beta}{\Gamma(\alpha)}x^{\alpha - 1}e^{-\beta{x}}, \ \ x \geq 0, \end{equation*}\] sendo \(\alpha\) e \(\beta\) dois parâmetros positivos e \(\Gamma(\alpha)\) sendo a função matemática Gama, definida por \[\begin{equation*} \Gamma(\alpha) = \int_{0}^{\infty}{x^{\alpha - 1}e^{-x}dx}, \ \ \alpha > 0. \end{equation*}\]

Notação: \(X \sim Gama(\alpha,\beta)\).

Resultados:

\(\Gamma(\alpha + 1) = \alpha\Gamma(\alpha), \ \ \alpha > 0\);
\(\Gamma(n) = (n-1)!\), \(n\) inteiro positivo;
\(\Gamma(1/2) = \sqrt{\pi}\).

  gamma(4) == 3*gamma(3)

## [1] TRUE

  gamma(4)

## [1] 6

  gamma(1/2)

## [1] 1.772454

Gráfico da função de densidade de probabilidade.

x <- seq(0,6,length.out = 10000)

fx1 <- dgamma(x,2,2)
fx2 <- dgamma(x,3,2)
fx3 <- dgamma(x,2,1)
plot(x, fx1, ylab=expression(paste(f(x))), type = "l", ylim=c(0,1))
lines(x,fx2,type = "l", col="red")
lines(x,fx3,type="l", col="blue")
legend("topright", c(expression(paste(alpha, "=", 2,",",beta, "=", 2)),
                     expression(paste(alpha, "=", 3,",",beta, "=", 2)),
                     expression(paste(alpha, "=", 2,",",beta, "=", 1))), 
       col = c("black", "red", "blue"), bty="n", lty=c(1,1,1), inset = 0.08)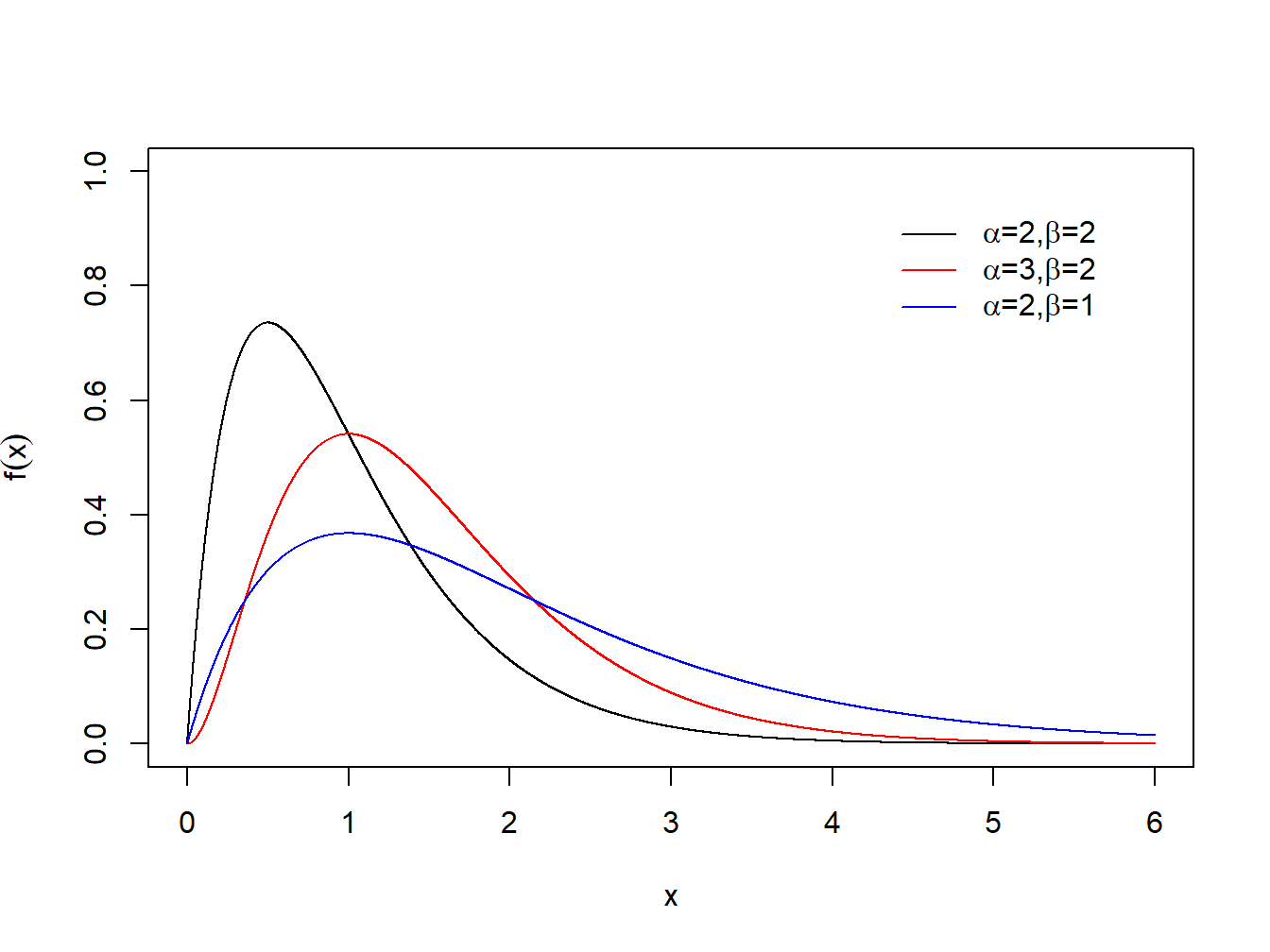

Figura 1.7: Densidade da Gama

Gráfico da função de distribuição acumulada.

Fx1 <- pgamma(x,2,2)
Fx2 <- pgamma(x,3,2)
Fx3 <- pgamma(x,2,1)
plot(x, Fx1, ylab=expression(paste(F(x))), type = "l", ylim=c(0,1))
lines(x,Fx2,type = "l", col="red")
lines(x,Fx3,type="l", col="blue")
legend("bottomright", c(expression(paste(alpha, "=", 2,",",beta, "=", 2)),
                     expression(paste(alpha, "=", 3,",",beta, "=", 2)),
                     expression(paste(alpha, "=", 2,",",beta, "=", 1))), 
       col = c("black", "red", "blue"), bty="n", lty=c(1,1,1), inset = 0.08)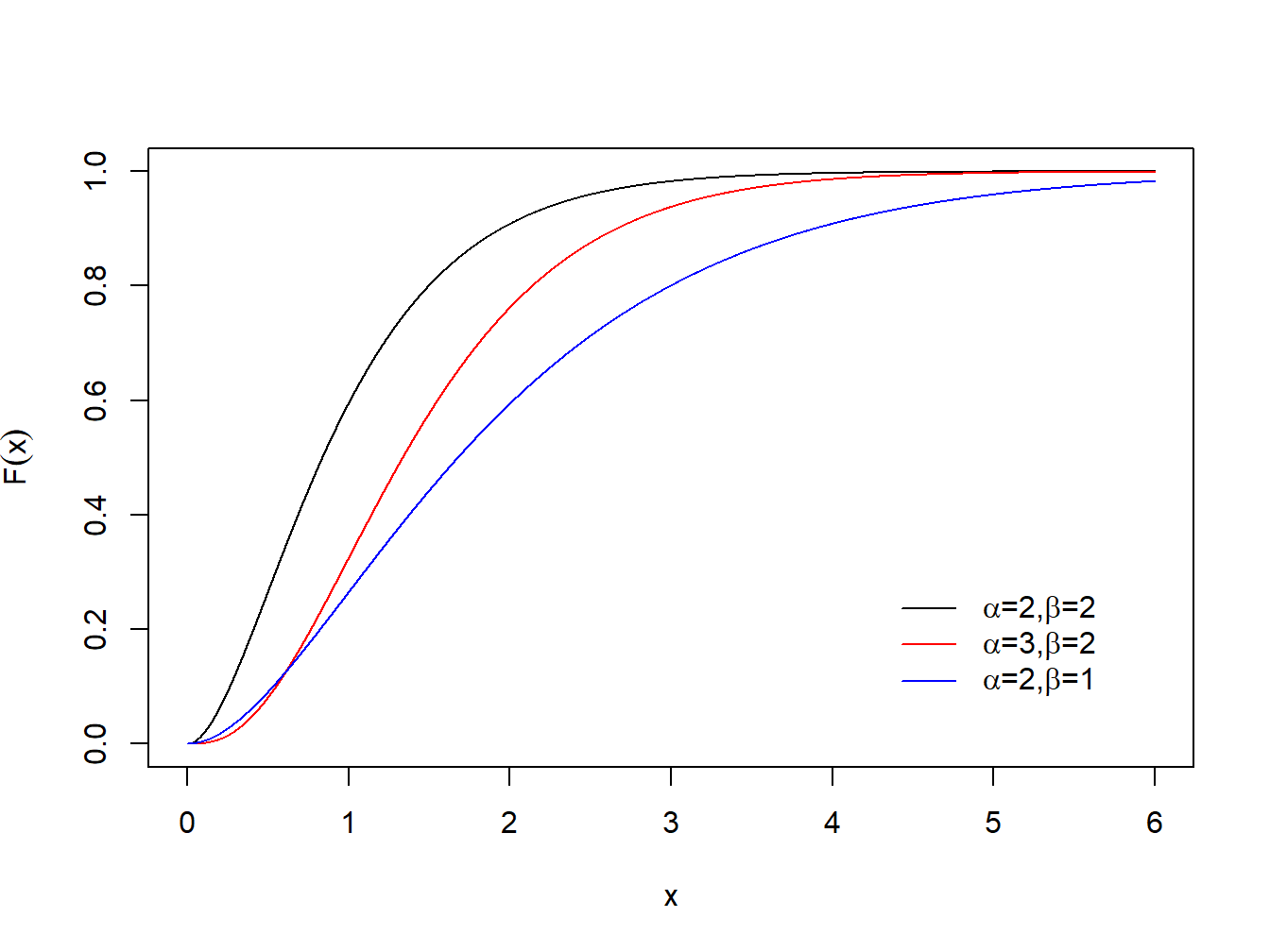

Figura 1.8: Função de distribuição acumulada da Gama

1.2.4 Distribuição Normal

Definição 1.7 Uma variável aleatória \(X\) tem distribuição Normal se sua densidade é dada por

\[\begin{equation*} f(x) = \dfrac{1}{\sigma\sqrt{2\pi}}e^{-\dfrac{(x - \mu)^2}{2\sigma^2}}, \ \ -\infty < x < \infty, \end{equation*}\]

com \(\mu \in \mathbb{R}, \sigma > 0\).

Notação: \(X \sim N(\mu,\sigma^2)\).

Gráfico da função de densidade de probabilidade.

x <- seq(-5,10,length.out = 10000)

fx <- dnorm(x,2,2)
plot(x, fx, ylab=expression(paste(f(x))), type = "l", ylim=c(0,0.5), xlim=c(-5,10), axes=FALSE)
axis(1,-5:10); axis(2)
segments(2,0,2,dnorm(2,2,2), lty=3)

fz <- dnorm(x,0,1)
lines(x,fz,col="blue")
segments(0,0,0,dnorm(0), lty=3, col="blue")

fy <- dnorm(x,2,3)
lines(x,fy,col="red")
segments(2,0,2,dnorm(2,2,3), lty=3, col="red")

legend("topright", c(expression(N(2,4),N(0,1),N(2,9))), col=c("black", "blue", "red"), lty=c(1,1,1), bty="n", inset=0.05)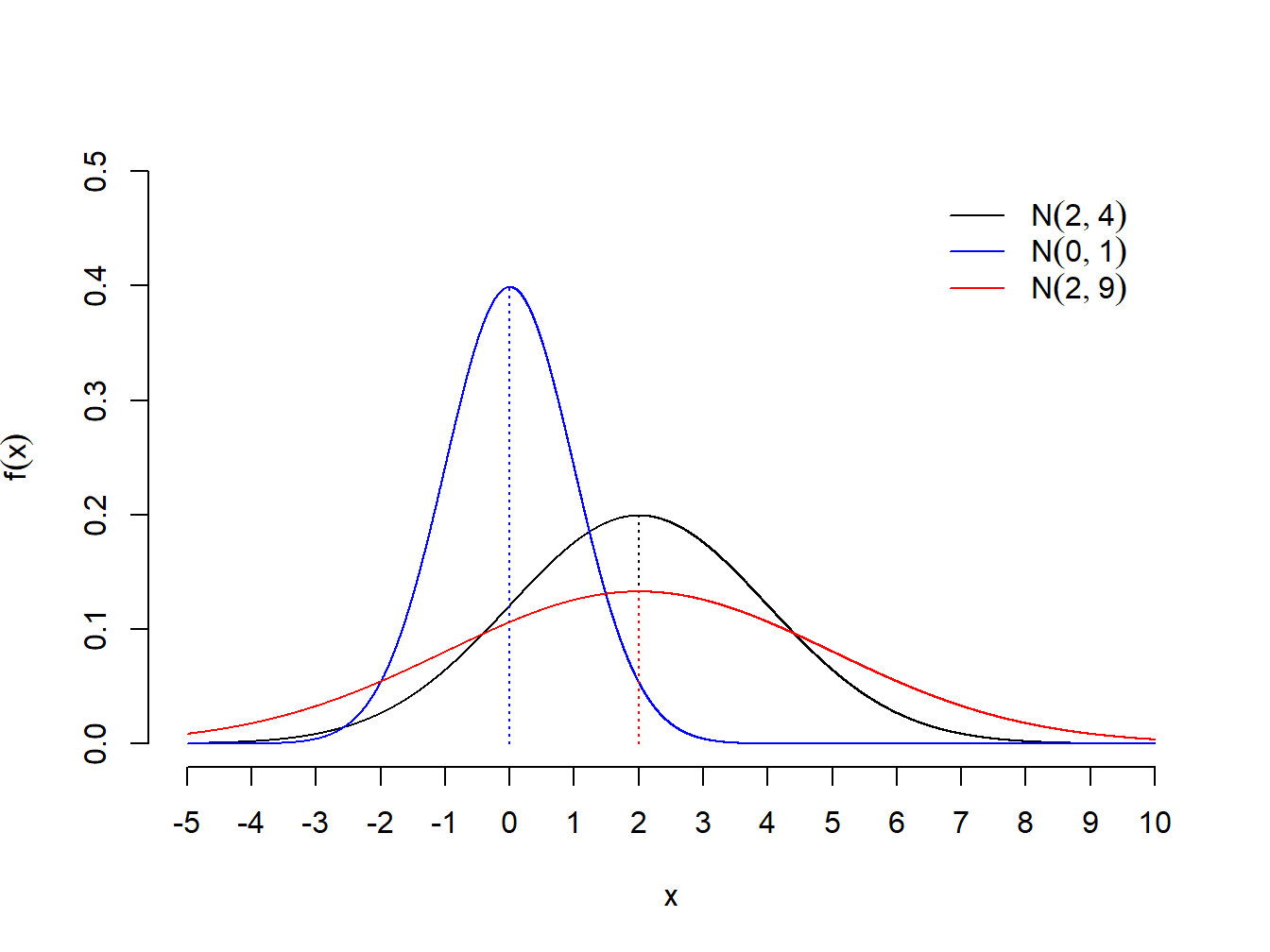

Figura 1.9: Densidade da Normal

Gráfico da função de distribuição acumulada.

Fx <- pnorm(x,2,2)
plot(x, Fx, ylab=expression(paste(F(x))), type = "l", ylim=c(0,1), xlim=c(-5,10), xaxt="n", yaxt="n")
axis(1,-5:10); axis(2,seq(0,1,by = 0.1))
segments(2,0,2,pnorm(2,2,2), lty=3)
segments(-6,pnorm(2,2,2),2,pnorm(2,2,2), lty=3)
Fz <- pnorm(x,0,1)
lines(x,Fz,col="blue")
segments(0,0,0,pnorm(0), lty=3)
Fy <- pnorm(x,2,3)
lines(x,Fy,col="red")
legend("bottomright", c(expression(N(2,4),N(0,1),N(2,9))), col=c("black", "blue", "red"), lty=c(1,1,1), bty="n", inset=0.05)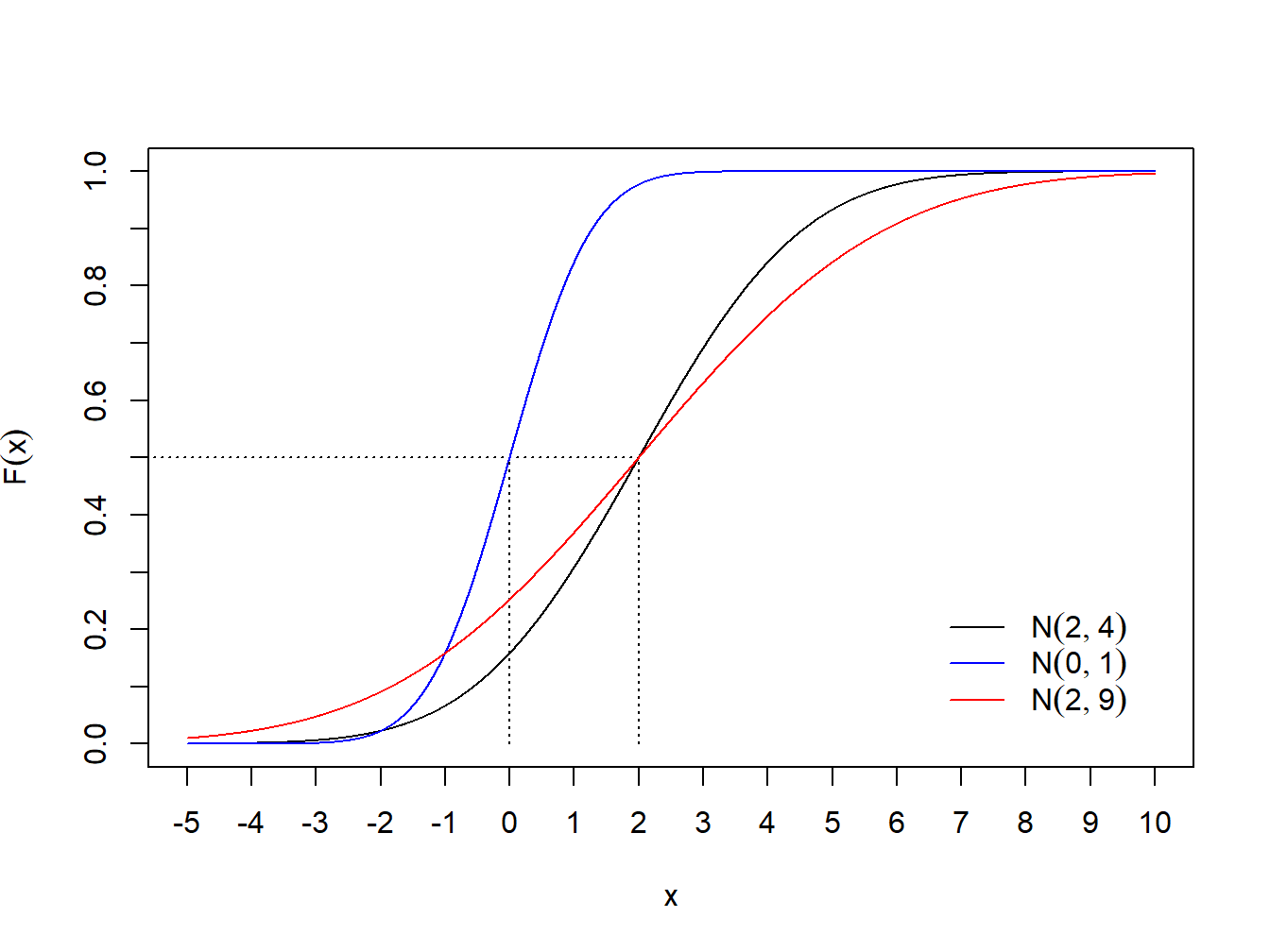

Figura 1.10: Função de distribuição acumulada da Normal

Exemplo 1.7 Suponha que \(X \sim N(10,4)\).

Determine o primeiro quartil, isto é, \(x_{0,25}\) tal que \(P(X \leq x_{0,25}) = 0,25\).
Calcule a seguinte probabilidade \(P(9 \leq X \leq 12)\).

# a) 
qnorm(0.25,10,4)

## [1] 7.302041

#b)
pnorm(12,10,4) - pnorm(9,10,4)

## [1] 0.2901688

1.3 Relações entre distribuições comuns

Resultado: Se \(X \sim Gama(1,\beta)\), então \(X \sim Exp(\beta)\).

set.seed(789)
# X ~ Gama(1,3)
x <- rgamma(6000,1,3)
hist(x, prob=T, breaks=30, ylim=c(0,3), main="", ylab="Densidade")
# X ~ Exp(3)
curve(dexp(x,3), 0, 3, add=T, col="red")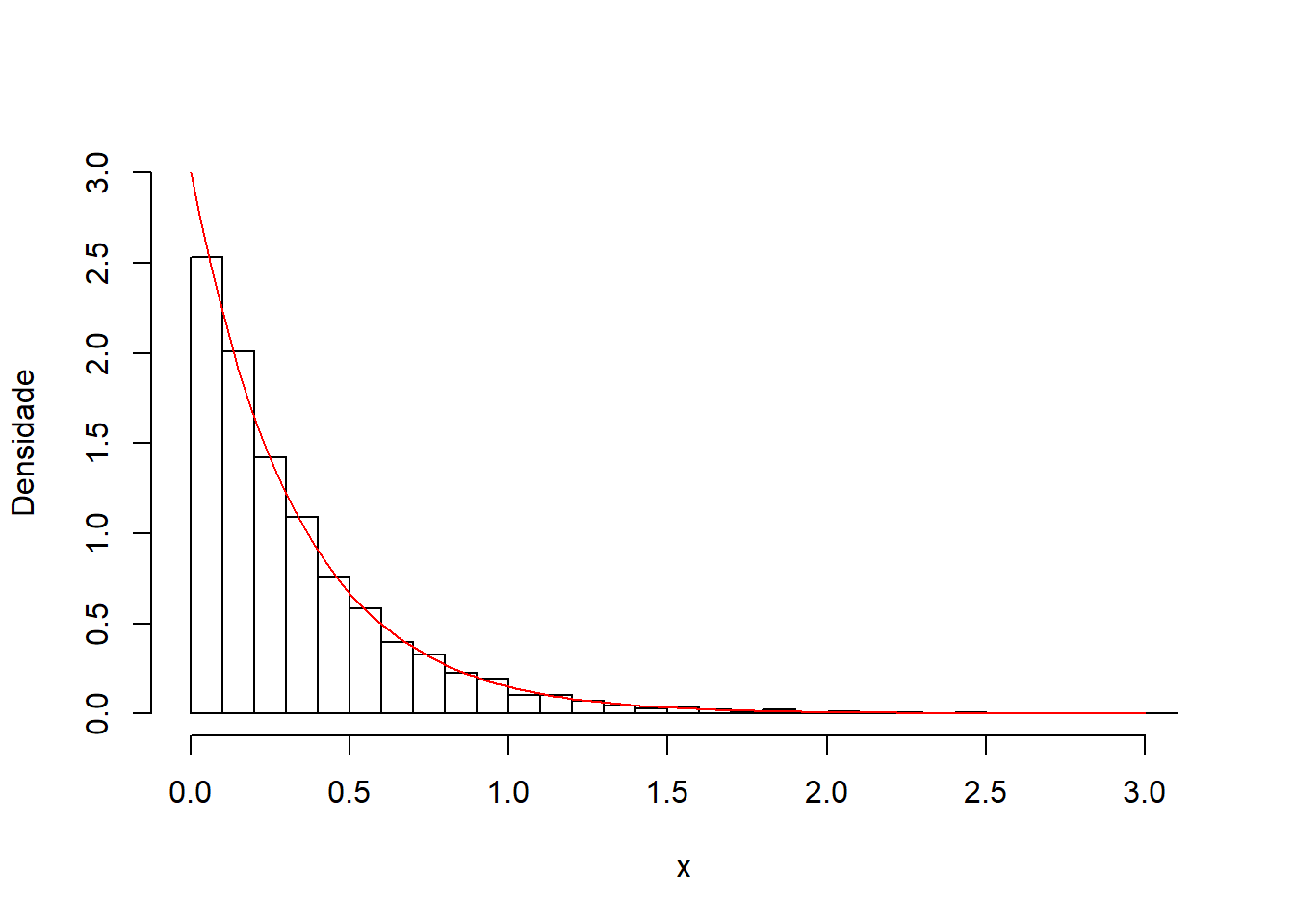

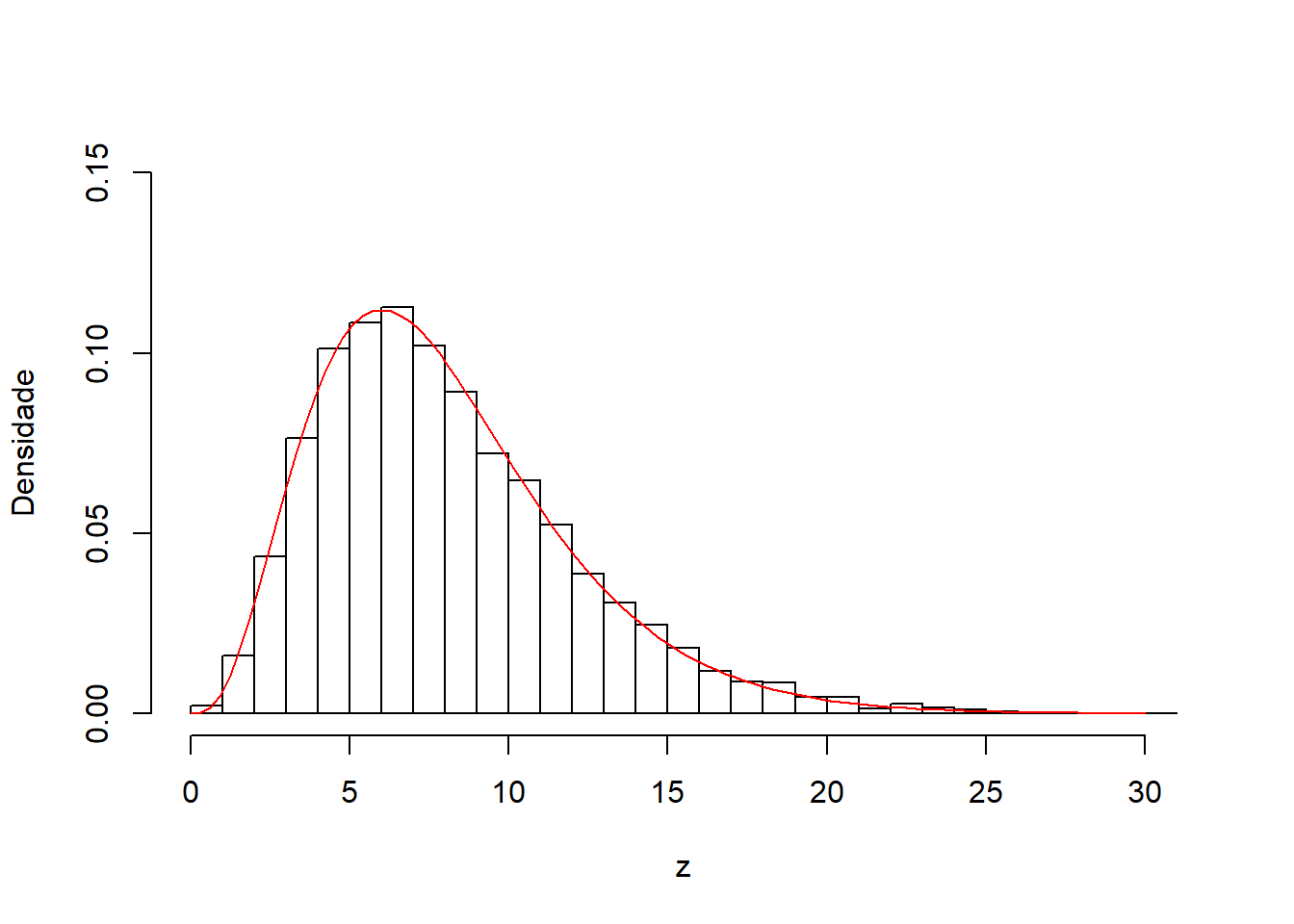
Resultado: Se \(X \sim Gama(n/2,1/2)\), então \(X \sim \chi^{2}_{n}\).

# X ~ Gama(5/2, 1/2)
x <- rgamma(6000,5/2,1/2)
hist(x, prob=T, breaks=20, main="", ylim=c(0,0.17), ylab="Densidade")
# X ~ Qui-quadrado(5)
curve(dchisq(x,5), 0, 15, add=T, col="red")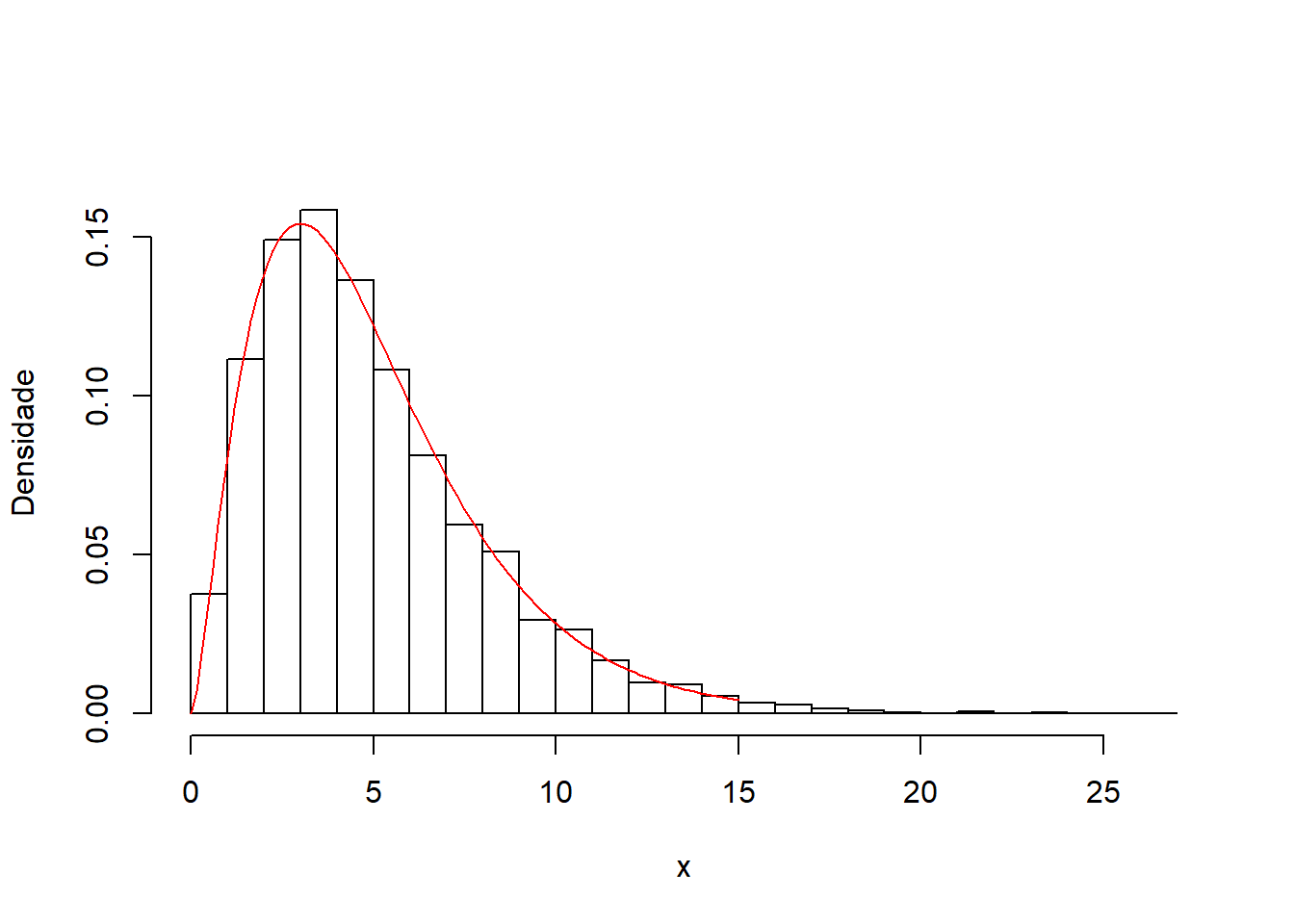

Resultado: Se \(X_{i} \sim Exp(\lambda)\) então \(\sum_{i=1}^{n}{X_{i}} \sim Gama(n,\lambda)\).

# X1 ~ Exp(2) ; X2 ~ Exp(2); X3 ~ Exp(2)
x <- matrix(rexp(6000,2), ncol=3)
# Z = X1 + X2 + X3
z <- apply(x,1,sum)
# Z ~ Gama(3,2)
hist(z, prob=T, breaks= 30, main="", ylab="Densidade", ylim=c(0,0.7))
curve(dgamma(x,3,2),0,10,add=T, col="red")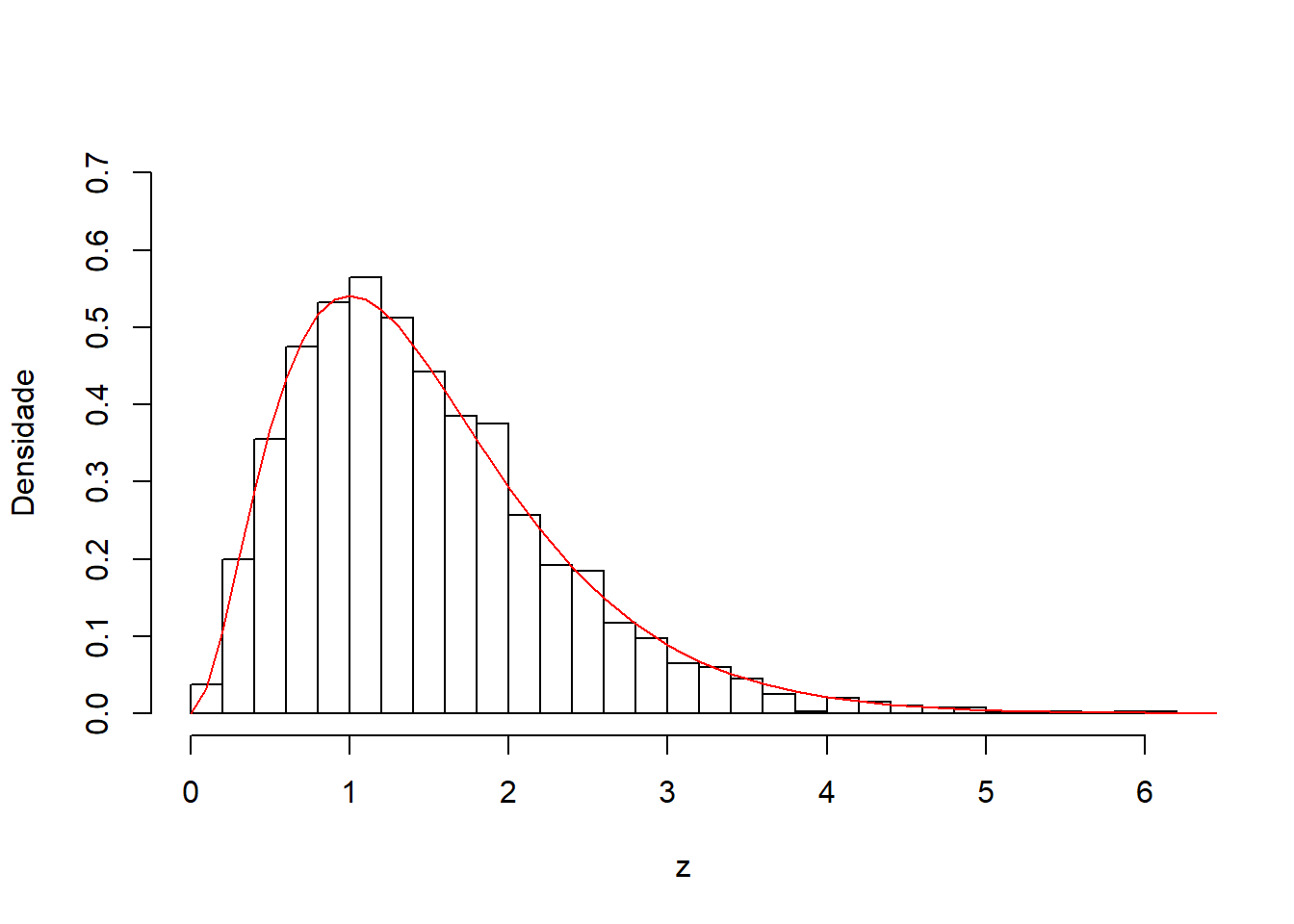

Resultado: Se \(X_{i} \sim N(\mu,\sigma^2)\), independentes, então \(\sum_{i=1}^{n}{X_{i}} \sim N(n\mu,n\sigma^2)\).

# X1, X2, X3, X4 ~ N(2,4)
x <- matrix(rnorm(6000,2,sqrt(4)), ncol=4)
# Z <- X1 + X2 + X3 + X4 
z <- apply(x,1,sum)
# Z ~ N(4*2,4*4)
hist(z,prob=T, breaks=20, main="", ylab="Densidade", ylim=c(0,0.12))
curve(dnorm(x,4*2,sqrt(4*4)),-10,25, add=T, col="red")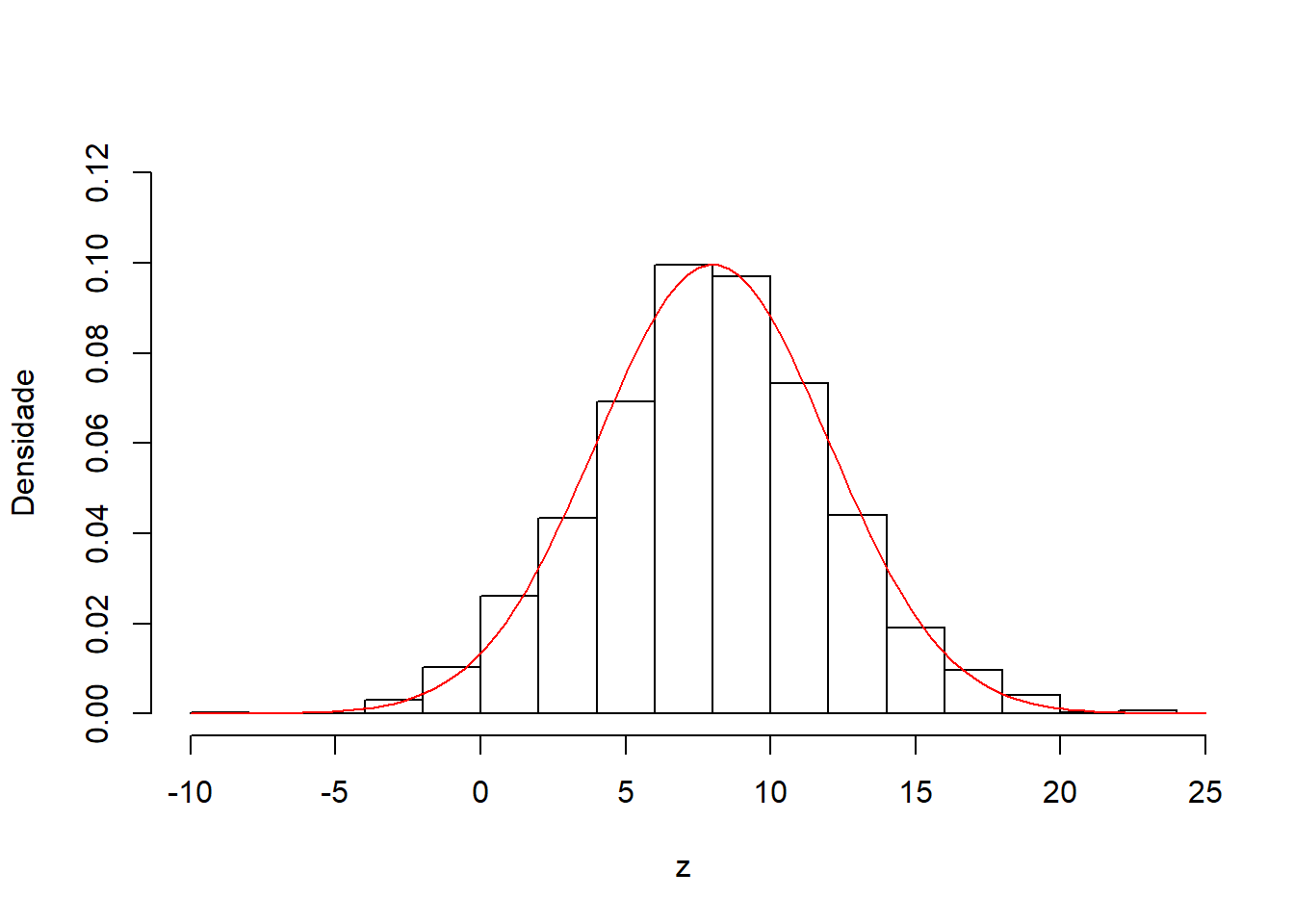

Resultado: Se \(X \sim N(0,1)\) então \(X^{2} \sim \chi^{2}_{1}\).

# X ~ N(0,1)
x <- rnorm(6000)
par(mfrow=c(1,2))
hist(x, prob=T, breaks=20, main="", ylab="Densidade")
curve(dnorm(x), -4, 4, add=T, col="red")
# X^2 
hist(x^2, prob=T, breaks=20, main="", ylab="Densidade")
curve(dchisq(x, df=1), 0, 10, add=T, col="red")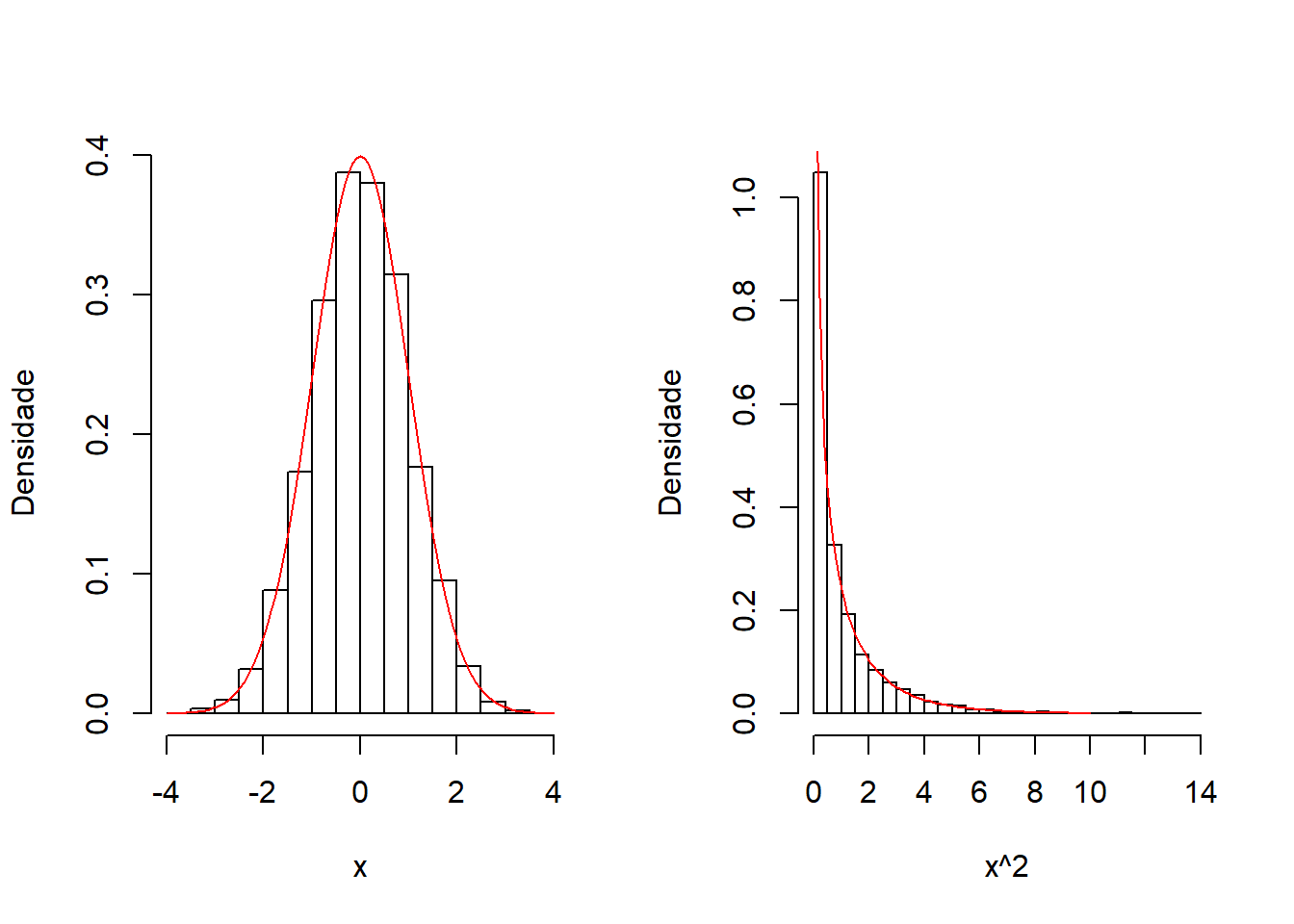

Resultado: Se \(X_{i} \sim N(0,1)\), independentes, então \(\sum_{i=1}^{n}{X^{2}} \sim \chi^{2}_{n}\).

# X1, X2, X3, X4, X5 ~ N(0,1)
x <- matrix(rnorm(10000), ncol=5)
# Z = X1^2 + X2^2 + X3^2 + X4^2 + X5^2
z <- apply(x^2, 1, sum)
# Z ~ Qui-quadrado(5)
hist(z, prob=T, breaks=30, main="", ylab="Densidade", ylim=c(0,0.17))
curve(dchisq(x, 5), 0, 30, add=T, col="red")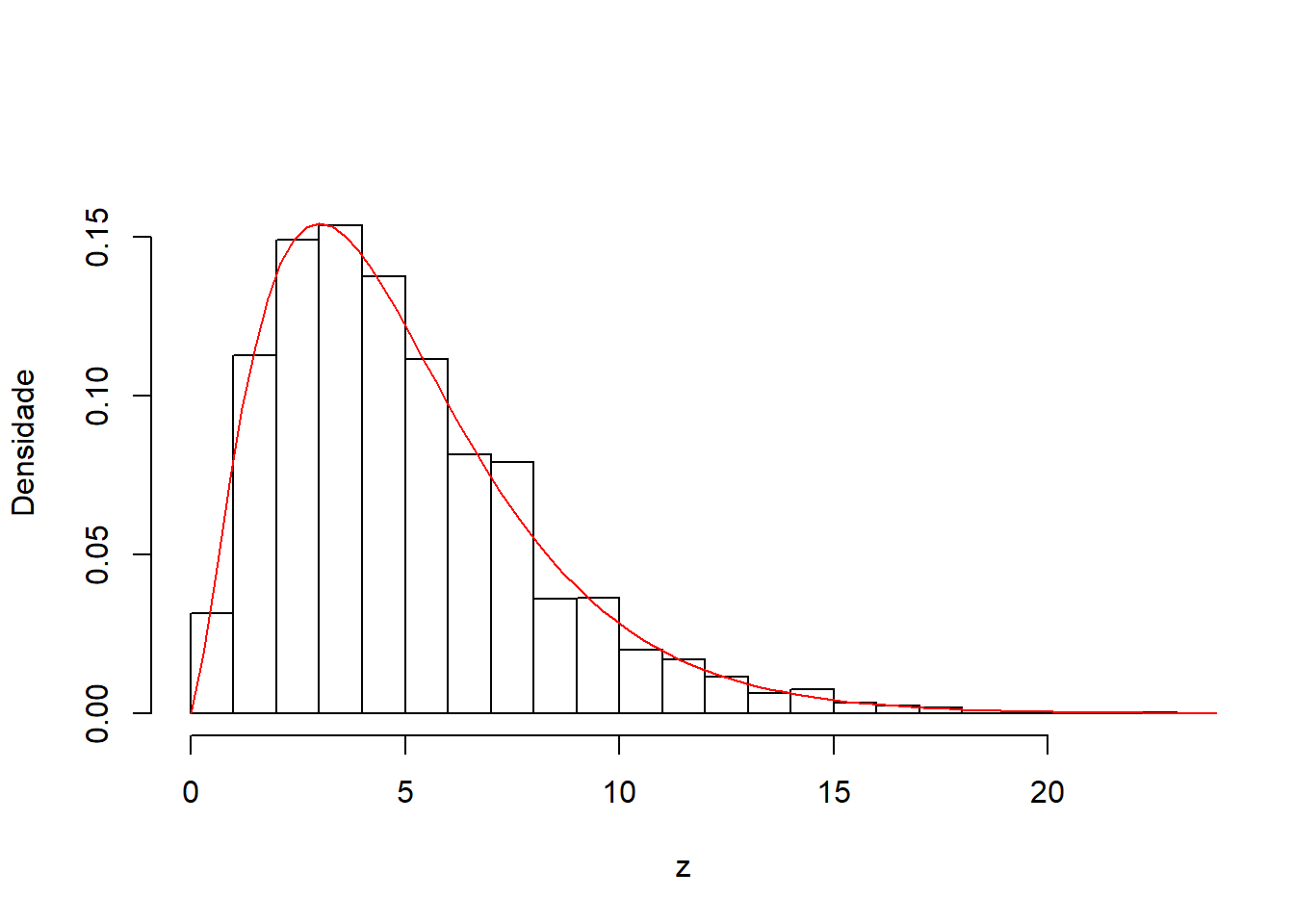

Resultado: Se \(X_{i} \sim \chi^{2}_{k_{i}}\), independentes, então \(\sum_{i=1}^{n}{X_{i}} \sim \chi^{2}_{k_{1}+\ldots+k_{n}}\).

# X1 ~ Qui-quadrado(2) ; X2 ~ Qui-quadrado(1); X3 ~ Qui-quadrado(5)
x <- matrix(c(rchisq(6000,2),rchisq(6000,1),rchisq(6000,5)), ncol=3)
# Z = X1 + X2 + X3 
z <- apply(x,1,sum)
# Z ~ Qui-quadrado(2+1+5)
hist(z,breaks=30, main="", ylab="Densidade" , ylim=c(0,0.15), prob="T")
curve(dchisq(x, df=8), 0, 30, add=T, col="red")