1 R amb RStudio
Autors: Muñoz R. & Gascón S.
En aquesta secció d’introducció a R amb RStudio veureu com carregar dades, comprovar que s’ha fet correctament i exploració incial de les dades. A més veurem com adequar i comprovar que les dades tenen el format necessari per a realitzar una anàlisi d’ANOVA1.
A l’exemple que anem a treballar farem una ANOVA per saber si hi ha diferències d’alçada (height; numèric continu) en funció del sexe (sex; categòric i binari).
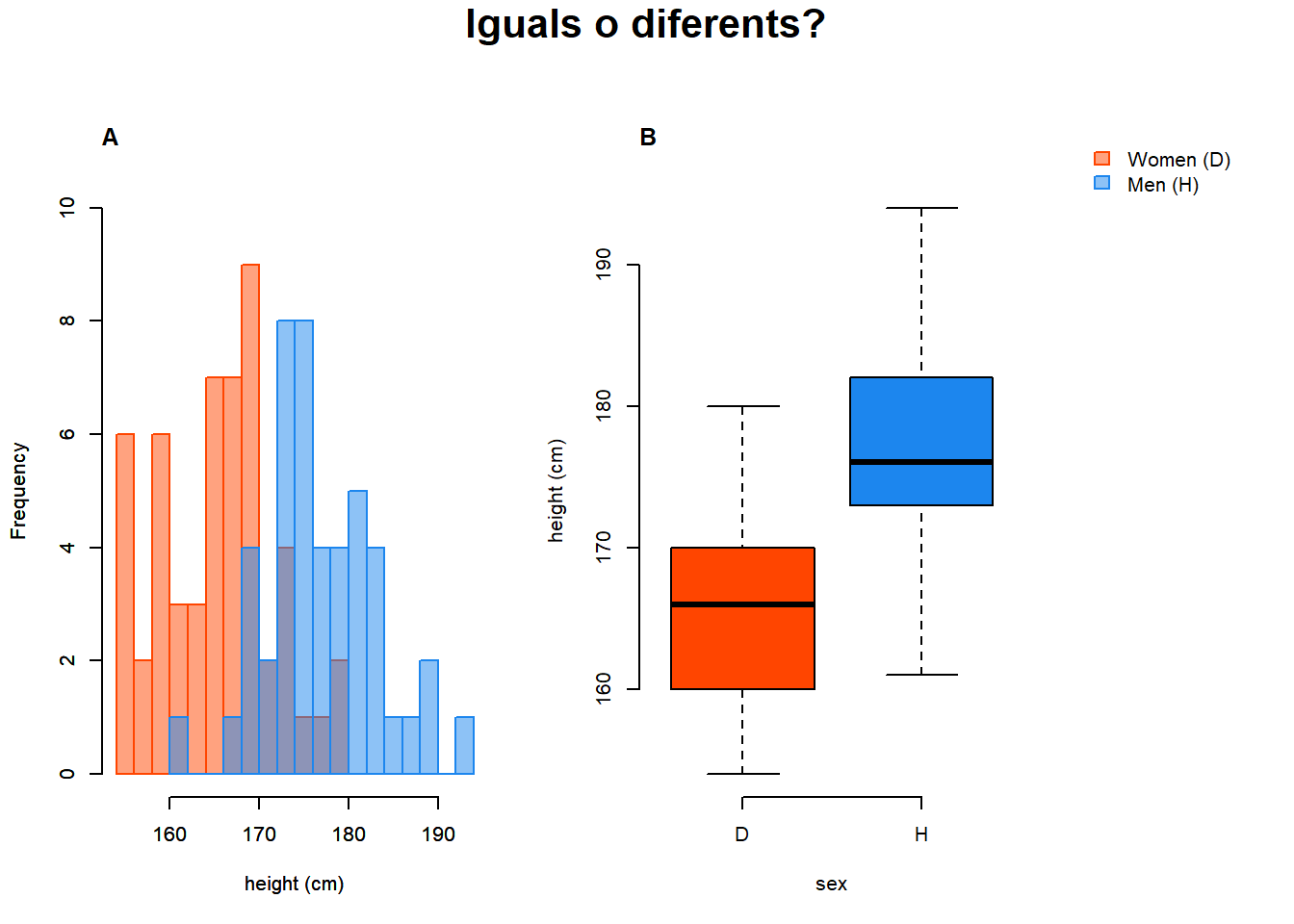
Figure 1.1: A) histograma de les alçades per gènere (binari). B) boxplots de les alçades per gènere (binari).
Abans de començar a treballar cal fer algunes passos:
Establir el que s’anomena directori de treball o alternativament també podeu utlitzar Projecte d’RStudio: L’espai on l’R efectuarà tota la feina. És on heu de guardar les dades, perquè R les trobi i les pugui carregar
Carregar les dades a l’R
1.1 Establir directori de treball
Per tal que R trobe l’arxiu a cada sessió cal definir quina és la nostra carpeta/directori de treball o bé generar un projecte d’Rstudio.
Podeu saber, en quin directori de treball està funcionant l’R si piqueu getwd(). Llavors, R us retorna la ruta del directori de treball actual.
La carpeta/directori de treball es defineix mitjançant la funció set working directory setwd() o bé pel menú superior d’RStudio (allà on posa, File,Edit,Code) on posa Session> Set Working directory>Choose Directory
Ull !!!! al establir la ruta (el camí de carpetes fins arribar a la carpeta que voleu utilitzar com a directori de treball), heu de vigilar de no tenir carpetes amb símbols estranys (per R els accents són símbols estranys) i **tampoc espais en els noms de les carpetes. Si us passa això, heu de canviar el nom d ela carpeta, ja que sinó teniu moltes probabilitats de que R no pugui trobar el camí* fins la vostra carpeta que serà el directori de treball.
Per solucionar problemes amb els path o rutes, l’RStudio té la opció de definir Projectes. Això permet que tot el que poseu dins la carpeta del projecte directament la podreu llegir sense haver d’anar canviant el directori de treball.
1.1.1 Per Windows
En el vostre cas haureu de substituir: “C:/Documents/AAD” per la vostra ruta. Alerta! Els símbols / han d’estar orientats cap a la dreta.
1.2 Crear i treballar amb Projecte d’RStudio
Quan es crea un Projecte tots els arxius queden vinculats al projecte, i per tant no cal establir cap directori de treball.
Com crear un nou Projecte:
Heu de seleccionar al menú File > New Project
S’obrirà una finestra demanant si es vol:
New Directory (creeu el projecte en una carpeta nova). Llavors seleccioneu el tipus de Projecte, en el nostre cas Empty Projecti assignem un nom al directori (carpeta) que es crearà i que serà el nom del Projecte. Per acabar, heu de fer clic a Create Project. Això, crea una carpeta i a dins un fitxer amb el mateix nom que la carpeta però amb extensió .Rproj
Existing Directory (creeu el projecte en una carpeta que ja existeix). Sel·leccioneu la carpeta on voleu posar el vostre projecte utilitzant el botó Browse. Un cop escollida feu clic a Create Project.
Version Control (no la escolliu)
Per obrir un projecte feu doble clic al arxiu amb extensió .Rproj, o el podeu obrir des del menú d’RStudio seleccionant la opció de File>Open Project
AVANTATGE de treballar amb Projectes, qualsevol arxiu o fitxer que creem queda vinculat automàticament a la carpeta del Projecte i quan guardem es guardarà allà.
1.3 Carregar dades per a l’anàlisi
1.3.1 format dades d’Excel .csv
Per obtenir dades d’Excel en format .csv, cal que guardeu el vostre arxiu d’excel com a text delimitat per comes, trobareu la opció si feu Guardar com
Un cop guardades en aquest format ja podeu utilitzar les següents instruccions per carregar les dades.
Les dades per aquest exercici les trobareu a l’Excel “dades_base.csv”. Cal comprovar/preparar les dades com en vist anteriorment.
- Cada columna serà una variable.
- Eviteu barrejar nombres i text dintre d’una columna.
- Quan una dada és desconeguda, es deixa la cel·la en blanc o bé s’escriu NA (Not Available).
- Eviteu apòstrofs (’), espais, #, etc. als encapçalaments.
- Cada columna ha de tindre únicament una cel·la com a encapçalaments/nom.
- No deixeu files en blanc entre fila de encapçalament i els valors.
Pel que fa als arguments:
- pes_alumnes.data és el nom (objecte) que li donem a la taula de dades o data frame (Nom amb que és designen aquest tipus de taules a R).
- <- és el símbol d’assignació. Assignem el què apareix a la dreta a un objecte (nom) que apareix a l’esquerre. Podeu comprovar que l’objecte ha estat assignat mirant si apareix a la finestra superior dreta d’RStudio anomenada Global Environment.
- read.csv() és el nom de la funció que usem per a llegir l’arxiu de dades “dades_base.csv”.
- header=T indica que la nostra taula de dades té una fila a dalt indicant el nom de cada columna/variable.
- sep=“;” indica quin és el separador entre columnes de dades. Depenent de com tingueu configurat l’Excel pot ser “;” o “,”.
Podeu accedir a l’ajuda d’una funció (e.g. read.csv()), per veure quins arguments té, picant a la consola:
o
També podeu picar sobre la funció a l’script i després picar F1.
1.3.2 format dades d’R .RData
Si teniu dades en format R, les reconeixereu per l’extensió .RData, també les podeu carregar molt fàcilment.
Passos a seguir:
Guardeu l’arxiu al vostre directori de treball o en una carpeta coneguda2
Escriviu load i entre () el nom de l’arxiu. Recordeu posar el nom entre cometes
I ja ho teniu carregat. Si s’ha carregat us apareixerà a la Pestanya d’Environment de l’RStudio (part superior dreta), sota el títol Data
1.4 Comprovar que s’ha fet correctament
Una vegada han estat carregades i assignades les dades cal comprovar que no ens hem equivocat. Existeixen diverses formes de saber si les dades han estat carregades correctament. A banda de mirar les característiques de l’objecte a la finestra superior dreta d’RStudio ,com hem comentat abans, des de la consola R tenim diverses opcions.
Podem usar la força bruta i picar (o bé copiar i enganxar) el nom de l’objecte (en aquest cas un data frame) pes_alumnes.data a la consola:
## weight height shoe.size exercise diet sex
## 1 42.0 156 35.0 2.0 3 D
## 2 44.0 155 35.0 5.0 1 D
## 3 45.0 154 35.0 5.0 2 D
## 4 45.0 157 37.0 4.0 2 D
## 5 45.0 156 37.0 2.0 0 D
## 6 48.0 160 37.0 7.0 2 D
## 7 48.0 165 39.0 3.0 1 D
## 8 48.0 166 39.0 3.0 1 D
## 9 49.0 164 39.0 2.0 1 D
## 10 50.0 170 39.0 2.0 2 D
## 11 50.0 162 36.0 0.0 3 D
## 12 51.0 160 38.0 8.0 1 D
## 13 51.0 167 37.0 1.0 6 D
## 14 51.5 164 38.0 2.0 0 D
## 15 52.0 168 37.0 5.0 1 D
## 16 52.0 165 39.0 4.0 1 D
## 17 52.0 163 39.0 3.0 2 D
## 18 53.0 162 36.0 0.0 5 D
## 19 54.0 170 40.0 0.0 0 H
## 20 54.0 160 37.0 4.0 3 D
## 21 55.0 169 39.0 1.0 2 D
## 22 55.0 156 37.0 2.0 0 D
## 23 55.0 168 39.0 7.0 0 D
## 24 56.0 166 37.0 5.0 3 D
## 25 56.0 170 40.0 0.0 0 D
## 26 57.0 160 39.0 5.0 0 D
## 27 58.0 175 40.0 4.0 1 D
## 28 58.0 161 41.0 3.0 5 H
## 29 58.0 172 38.0 5.0 0 D
## 30 58.5 175 43.0 5.3 2 H
## 31 60.0 170 39.0 6.0 2 D
## 32 60.0 178 42.0 2.0 4 H
## 33 60.0 161 38.0 0.0 0 D
## 34 60.0 173 43.0 3.0 0 H
## 35 60.0 178 42.0 4.0 2 D
## 36 61.0 168 39.0 2.0 0 D
## 37 61.5 179 41.5 6.0 2 D
## 38 62.0 165 38.0 5.0 0 D
## 39 62.0 170 39.0 5.0 0 D
## 40 63.0 175 40.5 9.0 3 H
## 41 63.0 167 37.0 0.0 0 D
## 42 63.0 180 39.0 5.0 0 D
## 43 63.0 169 38.0 4.5 0 D
## 44 64.0 174 40.0 5.0 1 D
## 45 64.0 174 41.0 5.0 3 D
## 46 65.0 170 41.0 5.0 0 D
## 47 65.0 170 40.0 3.0 0 D
## 48 65.0 173 42.0 8.0 0 H
## 49 65.0 169 40.0 0.0 3 H
## 50 66.0 174 42.0 9.0 0 H
## 51 66.0 179 45.0 5.0 4 H
## 52 66.0 175 42.0 4.0 5 H
## 53 67.0 190 43.0 6.0 2 H
## 54 67.0 175 42.0 0.0 1 H
## 55 67.0 173 40.0 3.5 4 D
## 56 67.0 182 44.0 6.0 2 H
## 57 67.0 175 43.0 3.0 3 H
## 58 68.0 160 37.0 1.0 3 D
## 59 69.0 173 41.0 4.0 0 H
## 60 70.0 181 43.0 6.0 2 H
## 61 70.0 172 41.0 0.0 0 H
## 62 70.0 170 43.0 8.0 3 H
## 63 70.0 160 39.0 2.0 0 D
## 64 70.0 155 36.0 2.0 1 D
## 65 70.0 176 43.0 15.0 0 H
## 66 70.0 158 38.0 4.0 1 D
## 67 70.0 171 40.0 5.0 0 D
## 68 70.0 172 41.0 0.0 2 H
## 69 70.0 174 42.0 5.0 0 H
## 70 71.0 167 42.0 0.0 0 H
## 71 72.0 182 43.0 3.0 0 H
## 72 72.0 165 38.0 3.0 0 D
## 73 72.0 179 43.0 0.0 0 H
## 74 73.0 187 43.0 3.0 0 H
## 75 74.0 176 41.0 0.0 0 H
## 76 74.0 178 45.0 7.0 2 H
## 77 75.0 167 39.0 0.0 0 D
## 78 75.0 178 42.0 0.0 0 H
## 79 75.0 184 44.0 4.0 2 H
## 80 75.0 170 40.0 2.0 0 D
## 81 76.0 177 44.0 15.0 7 H
## 82 76.0 170 41.0 0.0 0 H
## 83 77.0 182 44.0 3.0 1 H
## 84 78.0 185 44.0 4.0 1 H
## 85 78.0 182 44.0 0.0 0 H
## 86 78.0 190 47.0 4.0 0 H
## 87 79.0 165 40.0 0.0 4 D
## 88 80.0 174 43.0 1.0 0 H
## 89 80.0 194 45.0 2.0 0 H
## 90 80.0 183 45.0 2.0 2 H
## 91 80.0 179 42.0 5.0 0 H
## 92 82.0 168 39.0 3.0 0 D
## 93 82.0 183 46.0 8.0 2 H
## 94 82.0 174 42.0 2.0 6 H
## 95 85.0 173 41.0 1.0 2 D
## 96 85.0 176 43.0 0.0 0 H
## 97 85.0 183 46.0 3.0 0 H
## 98 90.0 180 45.0 0.0 1 H
## 99 101.0 173 43.0 7.0 0 HTambé podem seleccionar l’objecte a l’script i picar CTR + Intro. Aquesta opció mostra l’objecte (i.e. taula de dades) complet però no resulta massa pràctic quan les taules de dades són grans.
La taula de dades (data.frame) pes_alumnes.data conté 6 columnes anomenades:
- pes
- height
- shoe.size
- exercici
- dieta
- sex
i 99 dades.
Per veure solament al nom de les columnes/variables de la taula podem usar la funció names():
## [1] "weight" "height" "shoe.size" "exercise" "diet" "sex"No obstant però, aquesta opció sols ens indica el nom de les columnes/variables i no sabem si les dimensions de la taula són les correctes. Tampoc veiem el contingut/natura de la informació de cada columna. Per a conèixer les dimensions podem usar la funció dim():
## [1] 99 6El primer valor correspon al nombre de files (99) i el segon de columnes (6). Es recomanable comprovar a l’Excel (dades_base.csv) si aquestes són les dimensions que ha de tindre la taula de dades (recordeu que l’encapçalament no conta com a línia una vegada carregada la taula a R). El nom de les columnes i les dimensions de la taula poden ser correctes però per a saber si la natura de la informació que hi conté és la correcta cal usar altres funcions. Entre les diferents opcions disponibles summary() i str() són les més habituals.
## 'data.frame': 99 obs. of 6 variables:
## $ weight : num 42 44 45 45 45 48 48 48 49 50 ...
## $ height : int 156 155 154 157 156 160 165 166 164 170 ...
## $ shoe.size: num 35 35 35 37 37 37 39 39 39 39 ...
## $ exercise : num 2 5 5 4 2 7 3 3 2 2 ...
## $ diet : int 3 1 2 2 0 2 1 1 1 2 ...
## $ sex : Factor w/ 2 levels "D","H": 1 1 1 1 1 1 1 1 1 1 ...## weight height shoe.size exercise
## Min. : 42.00 Min. :154.0 Min. :35.00 Min. : 0.000
## 1st Qu.: 56.50 1st Qu.:165.0 1st Qu.:39.00 1st Qu.: 1.500
## Median : 66.00 Median :171.0 Median :40.00 Median : 3.000
## Mean : 65.35 Mean :171.2 Mean :40.52 Mean : 3.508
## 3rd Qu.: 73.50 3rd Qu.:176.5 3rd Qu.:43.00 3rd Qu.: 5.000
## Max. :101.00 Max. :194.0 Max. :47.00 Max. :15.000
## diet sex
## Min. :0.000 D:53
## 1st Qu.:0.000 H:46
## Median :1.000
## Mean :1.343
## 3rd Qu.:2.000
## Max. :7.000En general str() dóna una informació més acurada de l’estructura de la informació i no tant del contingut, però per a nouvinguts pot ser difícil d’interpretar. És per això que, en el context d’AAD, la combinació de dim() i summary() és més recomanable.
La funció summary dóna una descripció de la informació continguda a cada columna que permet deduir la seua natura o classe. Quan per a una columna dona estadístics de posició com el mínim (Min.), el primer quantil (1st Qu.) etc. podem inferir que es tracta d’una variable contínua. Mentre que quan dóna un compte del nombre de vegades que apareix una o més categories podem assumir que és una variable categòrica o factor.
Com veurem a continuació, és molt importat que la variable que defineix els grups que volem comparar siga un factor o l’anàlisi serà incorrecta!!!
1.5 Exploració de les dades
1.5.1 Selecció de dades/files/columnes
Com podeu veure a continuació existeixen diverses formes d’accedir a una única columna d’un data.frame.
La primer usa el nom de l’objecte (data.frame) i el nom de la columna. Entremig cal posar el símbol del dòlar ($).
La segona també usa el nom de l’objecte (data.frame) i el nom de la columna però es basa en l’estructura de les dades. Els símbols [_ i _] amb una coma entremig (,) fan referència a l’estructura de files i columnes de la taula de dades. L’espai abans de la coma ens permet accedir files determinades mentre que el segon ho permet per columnes. Com que les columnes tenen noms, pes_alumnes.data[ ,“sex”] ens permet accedir a la columna sex.
Finalment la tercera forma no usa el nom de la columna i es basa en l’ordre de les columnes. sex és la sisena columna de la taula de dades. Llavors, pes_alumnes.data[ , 6] permet accedir a aquesta columna.
## [1] D D D D D D D D D D D D D D D D D D H D D D D D D D D H D H D H D H D
## [36] D D D D H D D D D D D D H H H H H H H D H H D H H H H D D H D D H H H
## [71] H D H H H H D H H D H H H H H H D H H H H D H H D H H H H
## Levels: D H## [1] D D D D D D D D D D D D D D D D D D H D D D D D D D D H D H D H D H D
## [36] D D D D H D D D D D D D H H H H H H H D H H D H H H H D D H D D H H H
## [71] H D H H H H D H H D H H H H H H D H H H H D H H D H H H H
## Levels: D H## [1] D D D D D D D D D D D D D D D D D D H D D D D D D D D H D H D H D H D
## [36] D D D D H D D D D D D D H H H H H H H D H H D H H H H D D H D D H H H
## [71] H D H H H H D H H D H H H H H H D H H H H D H H D H H H H
## Levels: D HCom a exercici vos recomanem que piqueu:
pes_alumnes.data[1, ]
pes_alumnes.data[1, 6]
pes_alumnes.data[1:3, ]
pes_alumnes.data[ ,5:6]
pes_alumnes.data[1:3, 5:6]Quines dades es mostren?
També es poden seleccionar files i columnes en base als valors d’una altra fila o columna:
## height sex
## 19 170 H
## 28 161 H
## 30 175 H
## 32 178 H
## 34 173 H
## 40 175 H
## 48 173 H
## 49 169 H
## 50 174 H
## 51 179 H
## 52 175 H
## 53 190 H
## 54 175 H
## 56 182 H
## 57 175 H
## 59 173 H
## 60 181 H
## 61 172 H
## 62 170 H
## 65 176 H
## 68 172 H
## 69 174 H
## 70 167 H
## 71 182 H
## 73 179 H
## 74 187 H
## 75 176 H
## 76 178 H
## 78 178 H
## 79 184 H
## 81 177 H
## 82 170 H
## 83 182 H
## 84 185 H
## 85 182 H
## 86 190 H
## 88 174 H
## 89 194 H
## 90 183 H
## 91 179 H
## 93 183 H
## 94 174 H
## 96 176 H
## 97 183 H
## 98 180 H
## 99 173 Ho
## weight sex
## 19 54.0 H
## 28 58.0 H
## 30 58.5 H
## 32 60.0 H
## 34 60.0 H
## 40 63.0 H
## 48 65.0 H
## 49 65.0 H
## 50 66.0 H
## 51 66.0 H
## 52 66.0 H
## 53 67.0 H
## 54 67.0 H
## 56 67.0 H
## 57 67.0 H
## 59 69.0 H
## 60 70.0 H
## 61 70.0 H
## 62 70.0 H
## 65 70.0 H
## 68 70.0 H
## 69 70.0 H
## 70 71.0 H
## 71 72.0 H
## 73 72.0 H
## 74 73.0 H
## 75 74.0 H
## 76 74.0 H
## 78 75.0 H
## 79 75.0 H
## 81 76.0 H
## 82 76.0 H
## 83 77.0 H
## 84 78.0 H
## 85 78.0 H
## 86 78.0 H
## 88 80.0 H
## 89 80.0 H
## 90 80.0 H
## 91 80.0 H
## 93 82.0 H
## 94 82.0 H
## 96 85.0 H
## 97 85.0 H
## 98 90.0 H
## 99 101.0 HEn aquest cas s’han seleccionat totes les dades de les columnes “height” i “sex” que tenen com a sex la categoria “H” (Home).
Alerta! Fixeu-vos que “height” i “sex” i 2 i 3 estan continguts dins d’un vector de dades c(,). De no ser així la selecció no funcionarà perquè poden haver taules de dades amb més de dues dimensions. Llavors pes_alumnes.data[, 2, 6] indica tots els elements en la dimensió 1, la columna 1 de la dimensió 2 i la 6 en la dimensió 3. També és molt important que la categoria vaja entre " " o R tractarà de trobar un objecte al Global Environment de nom H.
1.5.2 Exploració gràfica
La funció summary() ens dóna informació sobre el contingut i natura de cada variable. No obstant però, és habitual realitzar una exploració gràfica de cada variable per separat i de la relació entre variables. L’opció bàsica per a la darrera anàlisi consisteix a realitzar un gràfic, mitjançant la funció plot(), amb dues variables d’interès per observar la presència d’alguna mena de relació entre ambdues:
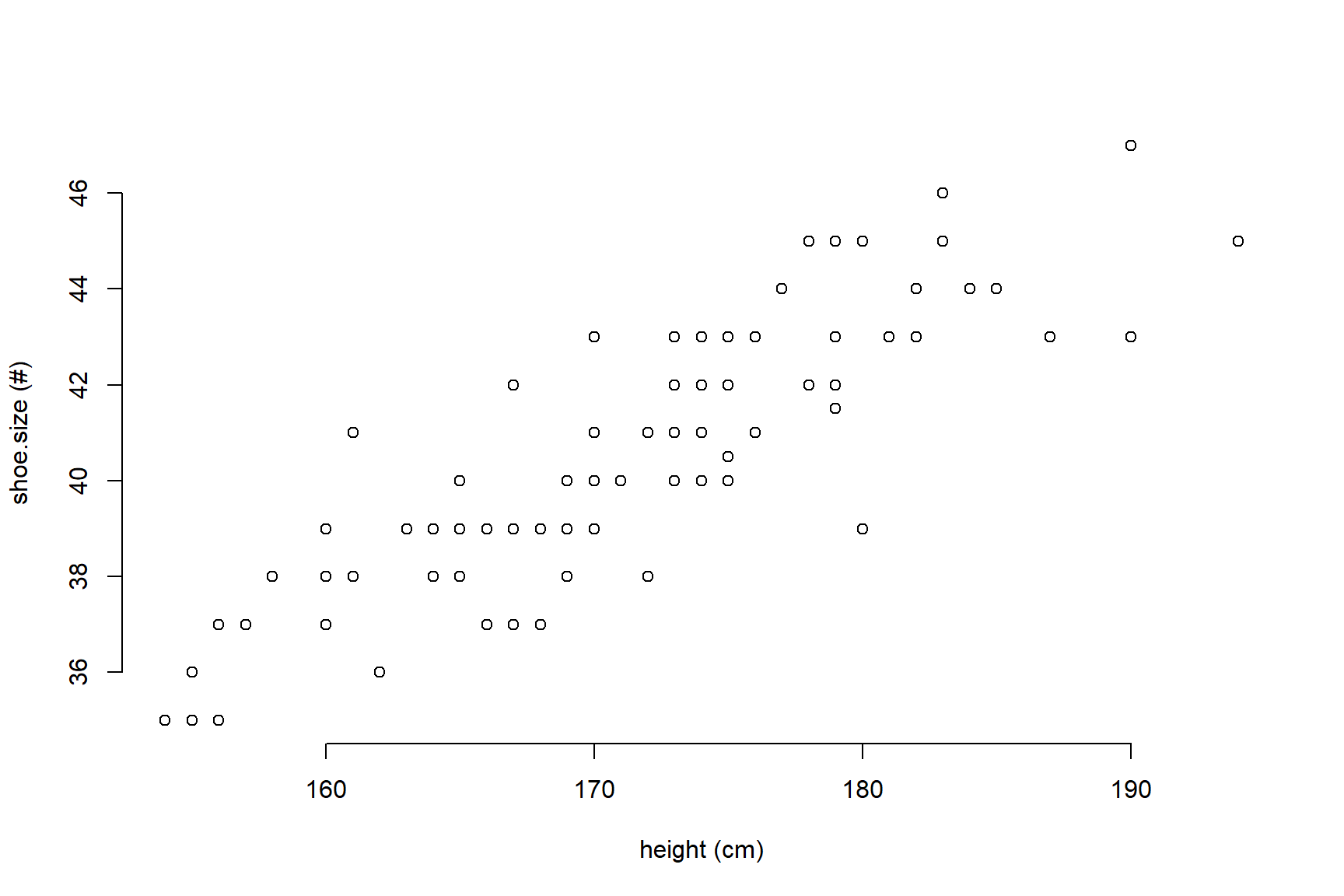
Pel que fa als arguments:
- x és la variable usada a l’eix x.
- y és la variable usada a l’eix y.
- col determina color dels punts, línies, etc.
- xlab determina l’etiqueta (label) usat per a l’eix x.
- ylab determina l’etiqueta (label) usat per a l’eix y.
- bty elimina la caixa que envolta el plot. És un argument merament estètic.
Pel que fa a la relació entre les dues variables, el gràfic mostra una correlació clara entre l’height dels i les alumnes i la mida de shoe.size que tenen.
El gràfic anterior mostra les dues categories emprades juntes. És possible diferenciar-les usant diferents colors i/o tipus de punts per a cadascuna.
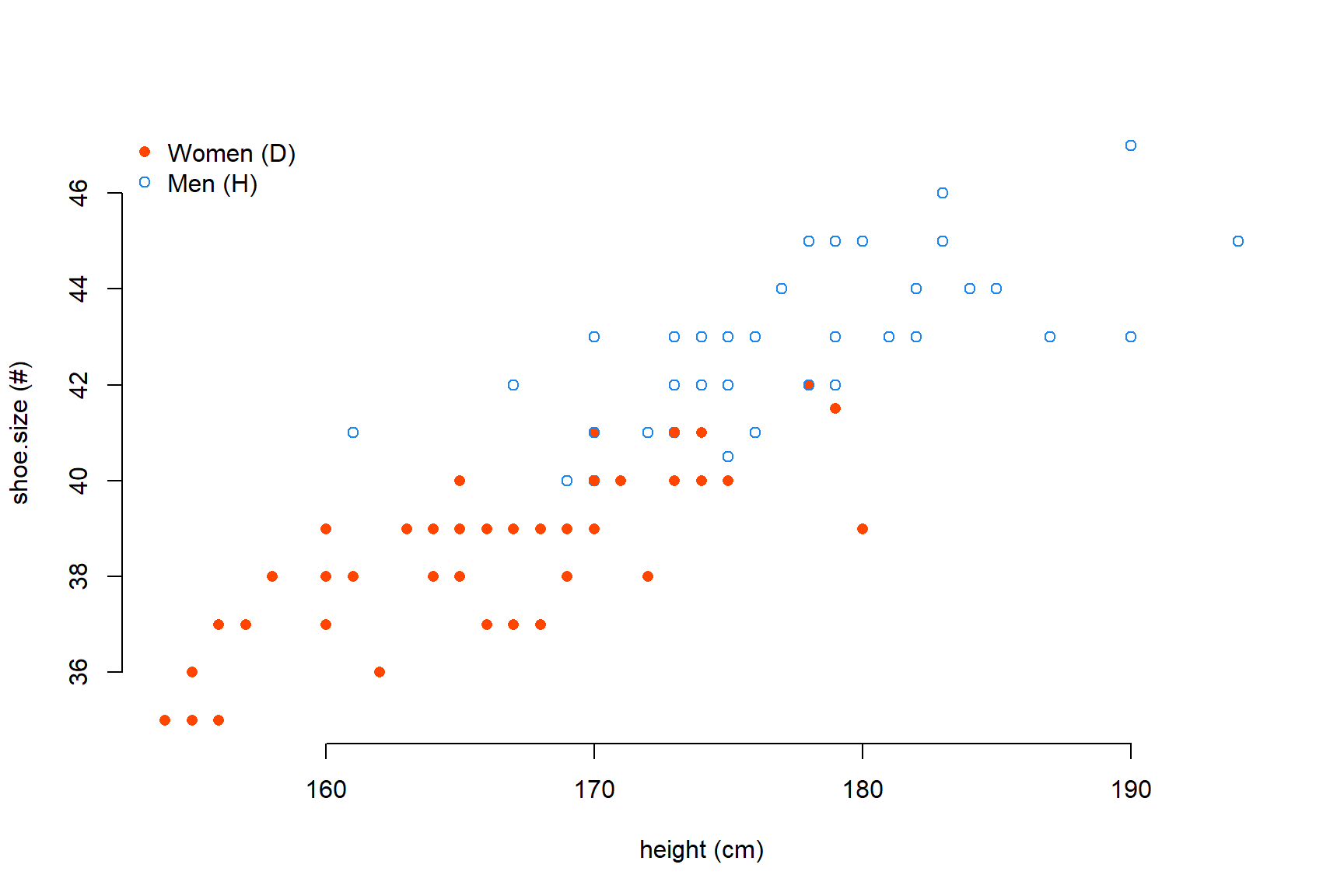
Figure 1.2: Scatter plot entre el height i la mida de shoe.size diferenciat per sex (binari)
Pel que fa als arguments:
- col determina el color dels punts. En aquest cas s’ha usat la funció ifelse() per a modificar els valors segons els valors de la variable sex. ifelse(pes_alumnes.data$sex==“D”, “orangered”, “dodgerblue2”) pot llegir-se com: si (if) pes_alumnes.data$sex és (==) “D” (dona) usa el color “orangered” (carabassa) o bé usa “dodgerblue2” (blau).
- pch determina el tipus de punt utilitzat. ifelse(pes_alumnes.data$sex==“D”, 16, 1) pot llegir-se de forma anàloga com: si (if) pes_alumnes.data$sex és (==) “D” (dona) usa 16 (punts sòlids) o bé usa 1 (buits).
A continuació es mostra un exemple de l’ús de la funció legend(). Serveix per a afegir la llegenda a la cantonada superior esquerre (“topleft”).
Pel que fa als arguments:
- “topleft” indica la posició.
- legend el text/etiquetes.
- col el color dels punts.
- pch determina el tipus de punt utilitzat.
- bty elimina la caixa que envolta el plot. És un argument merament estètic.
Com que sols hi ha dues etiquetes col té dos valors (“orangered” i “dodgerblue2”) i pch també. Fixeu-vos que tots dos es troben indicats mitjançant un vector (c( , )).
La resta d’arguments ha estat explicada al plot anterior.
Quan la variable x és categòrica (pes_alumnes.data$sex), R automàticament genera un boxplot per a cada categoria.
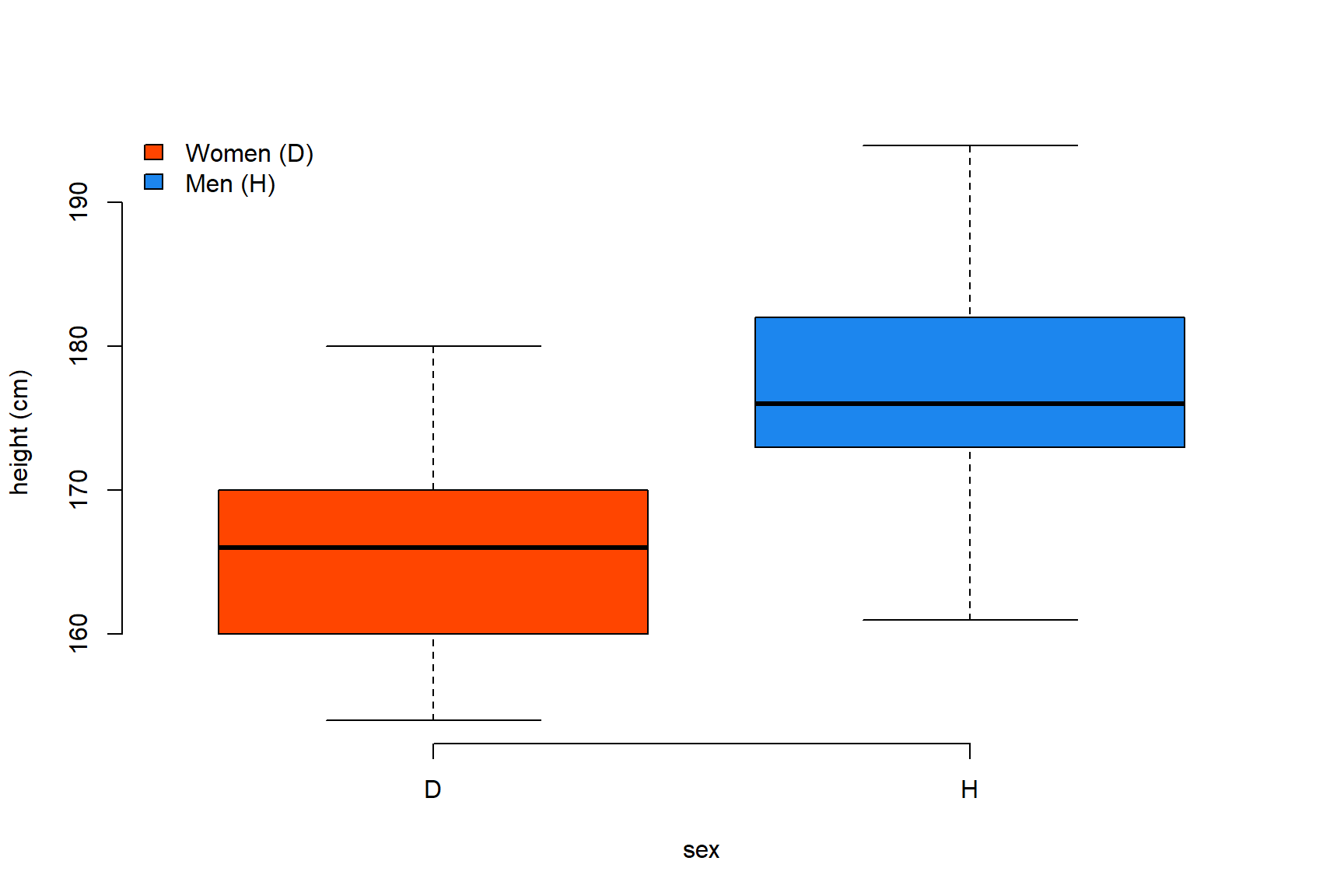
La funció boxplot() permet generar el mateix tipus de plot. Mireu l’ajuda (help(boxplot)) i tracteu de reproduir la mateixa figura usant la funció boxplot().
Els arguments han estat explicats als plots anteriors.
1.5.3 Exploració numèrica
De vegades és necessari conèixer el tipus de distribució que tenen les dades. En moltes ocasions les dades han de ser normals per tal de complir amb els supòsits de les anàlisis estadístiques. Per tal d’investigar si una sèrie de dades s’ajusta a una distribució normal es pot aplicat el test de normalitat de Shapiro-Wilk usant la funció shapiro.test().
##
## Shapiro-Wilk normality test
##
## data: pes_alumnes.data$height
## W = 0.98816, p-value = 0.5278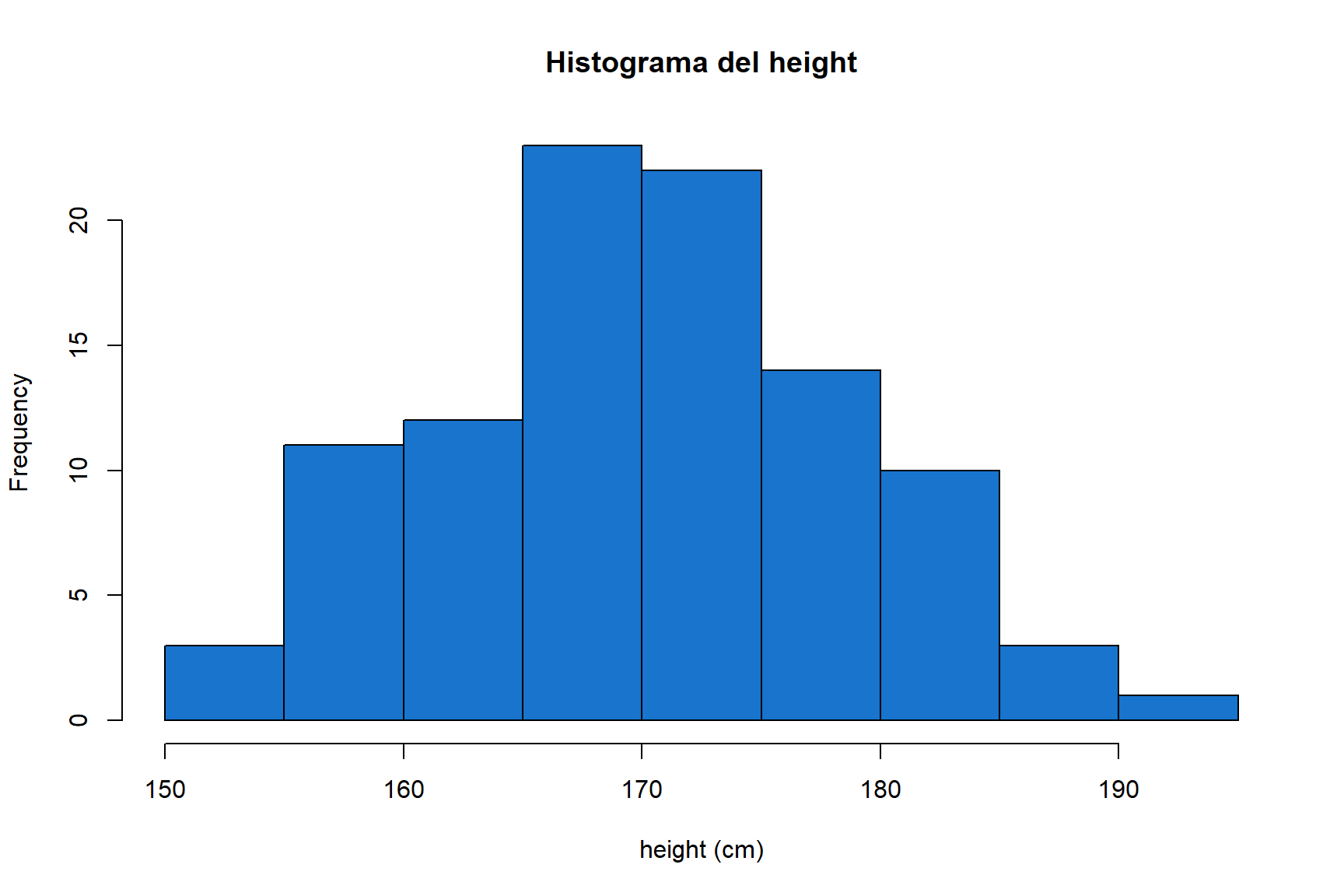
Figure 1.3: Histograma del height dels alumnes
Com que el p-value > 0.05 es pot concloure que la distribució de les alçades és normal. L’histograma de les dades ja ens indicava que amb tota probabilitat el test anava a donar aquest resultat.
En altres ocasions podem estar interessats en la relació entre dues variables continues (e.g. correlació). Per tal de cheightular la correlació entre dues variables la funció més emprada és cor().
## [1] 0.8680414Com era d’esperar la correlació entre l’height dels i les alumnes i la seua mida de shoe.size és molt alta i positiva (i.e. 0.8680414). Es a dir, quan més alt és l’individu, major és la mida de shoe.size. Quan les variables no són normals és millor usar l’índex de correlació Spearman (i.e. method = “spearman”).
Pel que fa als arguments:
- x és la 1a variable.
- y és la 2a variable.
- method és el mètode emprat per cheightular la correlació: “pearson”, “kendall” o “spearman”.
La funció cor() en dóna el valor de la correlació però no indica la significació estadística (i.e. credibilitat) d’aquest valor. Per tal d’obtindre-la podem usar la funció cor.test().
cor.test(x = pes_alumnes.data$height,
y = pes_alumnes.data$shoe.size,
method = "pearson",
alternative = "two.sided",
conf.level = 0.95)##
## Pearson's product-moment correlation
##
## data: pes_alumnes.data$height and pes_alumnes.data$shoe.size
## t = 17.219, df = 97, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.8093152 0.9095852
## sample estimates:
## cor
## 0.8680414Pel que fa als arguments:
- x és la 1a variable.
- y és la 2a variable.
- method és el mètode emprat per cheightular la correlació: “pearson”, “kendall” o “spearman”.
- alternative indica la hipòtesi alternativa.
- conf.level determina el nivell de confiança.
1.6 Adequació de dades
Com veurem a continuació, en alguns casos cal que les variables tinguen una classe específica per a realitzar certes anàlisis. La funció summary() ja ens ha indicat que la variable sex és categòrica. No obstant, podem veure quina classe té usant la funció class(). També podem preguntar si la columna/variable conté factors usant la funció is.factor().
## [1] "factor"o
## [1] TRUELa resposta és TRUE (cert) per la qual cosa sabem que la variable és categòrica (factor).
Si calgués convertir una variable (e.g. continua) a categòrica (factor) s’usa la funció factor().
## [1] 1 2 3 4 5
## Levels: 1 2 3 4 51.7 Principis bàsics de la regressió lineal (RLS)
En ocasions a més del valor de la correlació estem interessats a matematitzar aquesta relació. El model resultant permet explorar numèricament la relació entre ambdues variables obtenint estadístics diferents. També permet fer prediccions sobre valors no observats. Un dels models més simples i habituals és la regressió lineal entre dues variables on s’obtenen els paràmetres corresponents a una fórmula de tipus:
\[y = A \cdot x + B\]
on A és el pendent de la recta i B la intercepció o ordenada a l’origen. El signe d’A pot esser interpretat d’una forma anàloga al signe de la correlació (i.e. relació positiva o negativa) entre les dues variables.
Continuant amb l’exemple anterior, la relació entre l’height (x/variable independent) i la mida de shoe.size dels (y/variable dependent) i les alumnes és positiva i correspon a la línia roja que es pot observar a la figura següent. Com es veurà a la pràctica corresponent, els models lineals han de complir amb una sèrie de supòsits per tal d’ésser considerats vàlids. Una de molt important es bassa en la Homoscedasticitat, Normalitat i manca de no-linealitat dels residus. Els residus corresponen a la diferència entre el valor modelitzat/predit (línia roja) i l’observat (fletxes blaves a la figura següent). Per simplicitat la figura sols inclou 5 fletxes però hi ha tants residus com dades (en aquest cas 99).
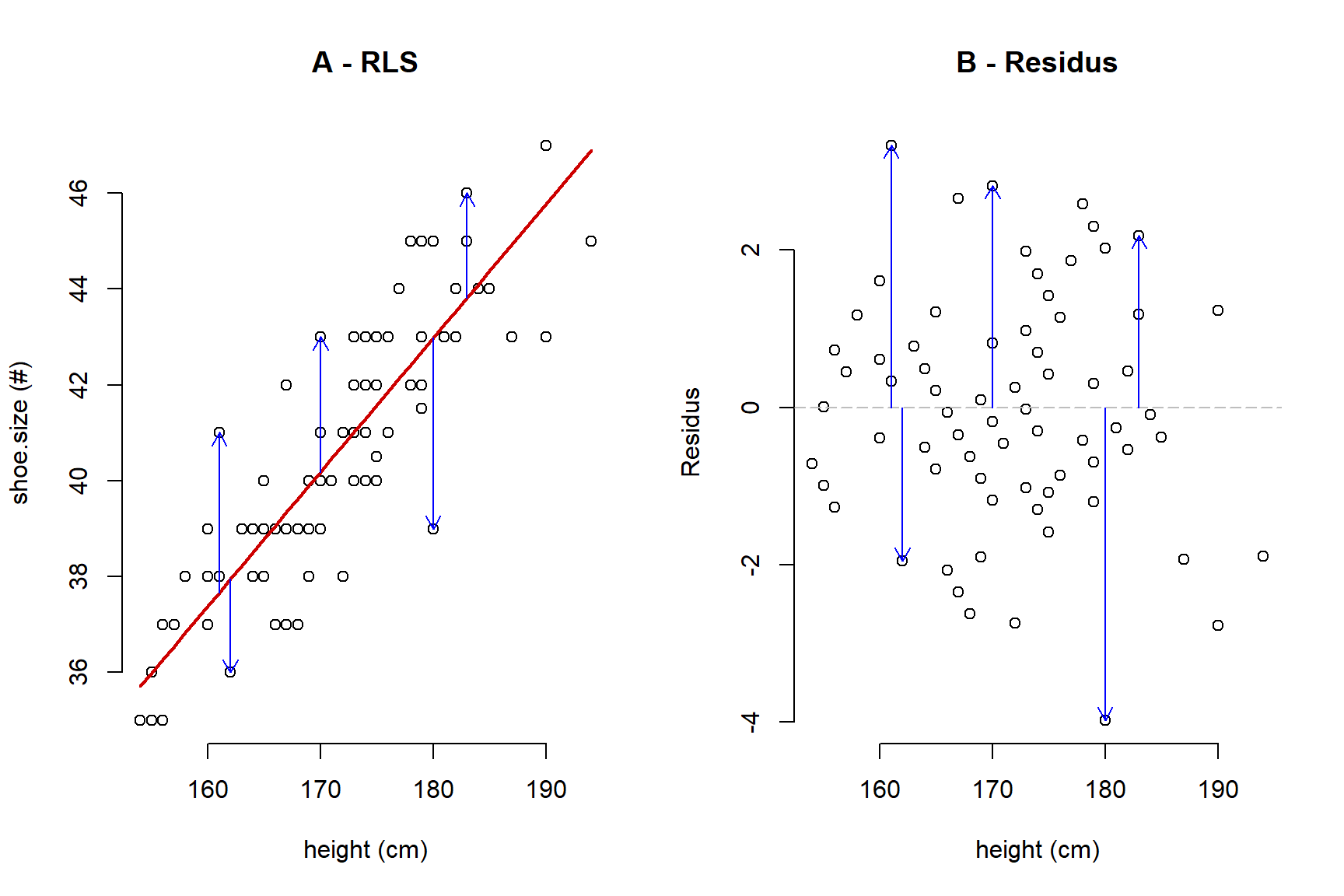
Figure 1.4: A) regressió entre height i la mida de shoe.sizes dels alumnes; B) residus de la RLS
A banda dels tests estadístics que s’apliquen per comprovar l’Homoscedasticitat i la Normalitat és habitual fer un gràfic amb els residus. Quan observem alguna mena de patró als residus, ens indica que el model és incorrecte i que cal fer alguna cosa per millorar-lo (e.g. transformació de les dades). A la figura següent es mostren diferents patrons idealitzats. Únicament la figura A mostra un patró en els residus correcte. Les figures B, E i F mostren biaix, les figures C i F mostren no-linealitat i les figures D, E i F mostren Heteroscedasticitat (no Homoscedasticitat): la variància dels residus és major per als valors superiors del rang de la variable en comparació amb els menors. Fixeu-vos que poden haver combinacions (e.g. la figura E mostra no linealitat i Heteroscedasticitat en els residus).
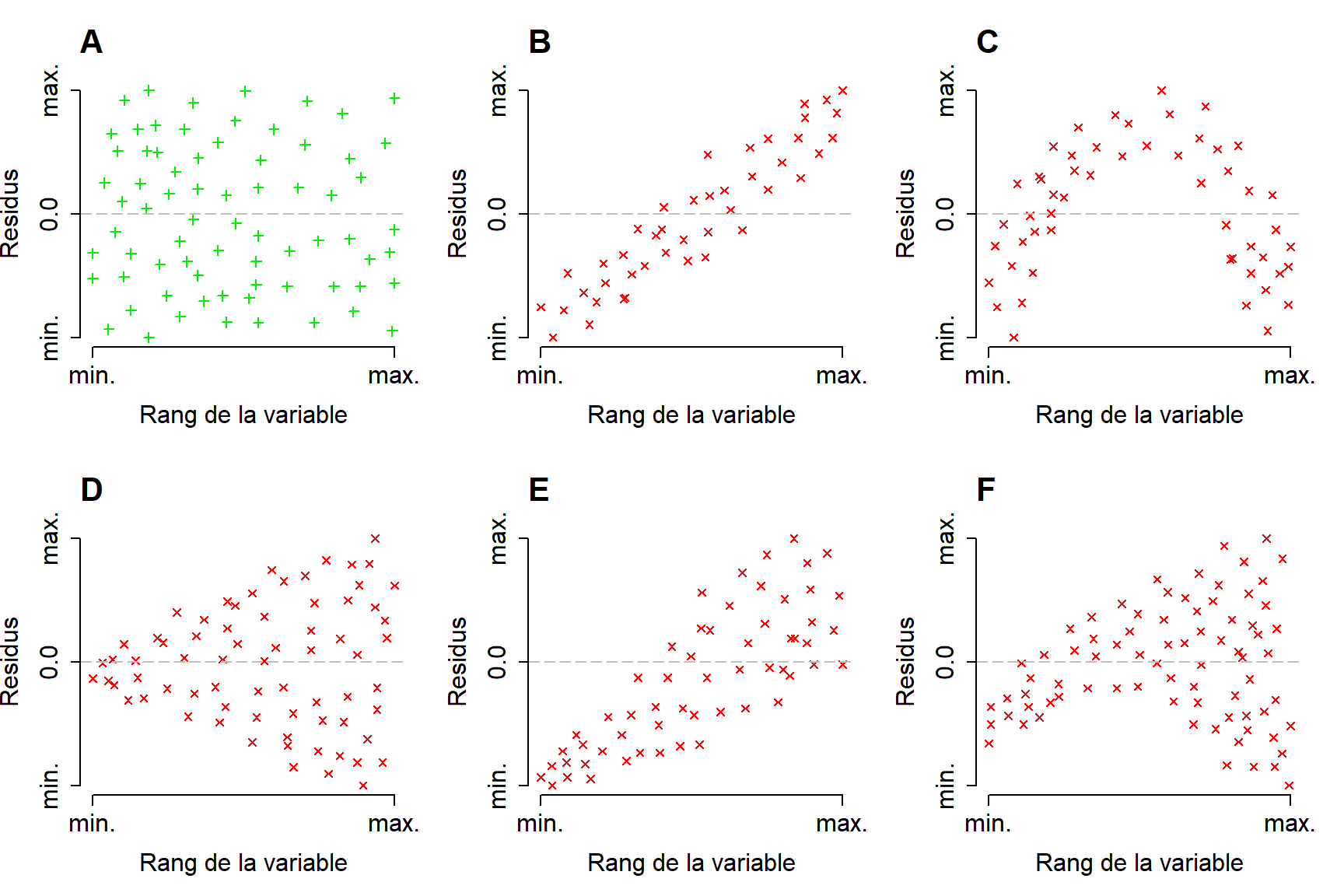
Figure 1.5: Patrons desitjats (verds) i incorrectes (roig) als residus
Tot i que les causes d’eixos patrons poden ser diverses. Per exemple:
- B i C poden ser causats per la manca d’algun predictor. Existeixen models multivariants del tipus: \[z = A \cdot x + B \cdot y + C\]
- B també pot ocórrer per causa d’una mala optimització dels paràmetres del model (i.e. A).
- a banda C pot estar per una mala parametrització del model ja que la relació s’ajusta més a una funció quadràtica.
1.8 Com podem fer una ANOVA
L’anàlisi de la variància (ANOVA) s’utilitza per analitzar les diferències entre les mitjanes d’un seguit de grups (i.e. 2 o 2+ grups). A l’exemple que anem a treballar farem una ANOVA per saber si hi ha diferències en l’height en funció del sex (binari). Com que no tenim el mateix # de casos entre les dues categories de la variable categòrica o factor (i.e. sexe (binari) dels alumnes), per tal de realitzar l’anàlisi d’ANOVA utilitzem la funció lm() (linear model):
Pel que fa als arguments:
- anova_height és l’objecte que contindrà l’anàlisi.
- height és la variable depenent (y).
- ~ és el signe que indica la relació o =.
- sex és la variable independent (x).
- data=pes_alumnes.data indica d’on s’han de extraure les variables (i.e. columnes de dades).
Amb certes particularitats com ara que la variable independent és categòrica (i.e. factor), cal acomplir amb els mateixos supòsits que han estat descrits per a la regressió lineal. Des d’un punt de vista gràfic les distribucions de valors semblen diferents (A - ANOVA). Així els valors modelitzats (i.e. mitjanes) per a cada categoria (i.e. D i H) amb el model de l’ANOVA també semblen diferents (quadrats carabassa i blau) (A - ANOVA). La variància dels residus de totes dues categories (fletxes blaves) són semblants (B - RESIDUS), hi ha Homoscedasticitat, i la distribució dels residus és normal perquè al C - Normal Q-Q Plot els residus s’alineen al llarg de la línia teòrica dels quantils que tindria una distribució normal amb la mitjana i desviació estàndard dels residus de l’ANOVA.
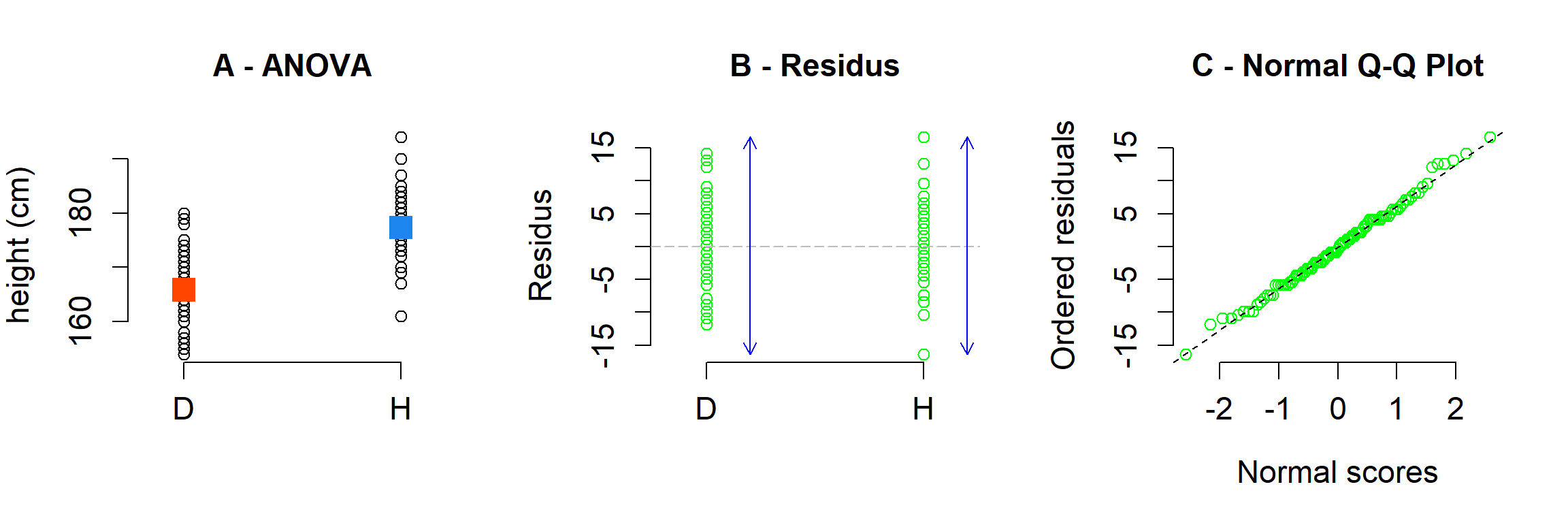
Figure 1.6: A) ANOVA (regressió) entre el gènere (binari) i l’height dels i les alumnes. B) residus de l’ANOVA (regressió). C - Normal Q-Q Plot.
Des d’un punt de vista numèric devem inspeccionar els resultats mitjançant la funció summary(). Ens hem de fixar en els coeficients (Coefficients:). El valor estimat (Estimate) per a la intercepció ((Intercept)) correspon a la mitjana dels valors que alhora correspon al valor predit pel model. El valor calculat és de 165.8491 aquest correspon al punt carbassa de la figura anterior. A la columna Pr(>|t|) podem trobar la significació d’aquest paràmetre. El valor (< 2e-16) i el nombre d’estreles (_***_) ens indiquen que el valor es significatiu i distint de zero.
El valor estimat (Estimate) per a la categoria H (sexH) + el valor calculat per a la categoria D ((Intercept)) correspon a la mitjana dels valors d’H que alhora correspon al valor predit pel model (punt blau de la figura anterior = 165.8491 + 11.4988).
Des del punt de vista de l’objectiu de l’anàlisi, a la columna Pr(>|t|) podem trobar la significació d’aquest paràmetre. El valor (2.93e-14) i el nombre d’estreles (_***_) ens indiquen que el valor es significatiu i distint de zero. El supòsits de l’anàlisi han estat comprovats a la figura anterior per la qual cosa podem concloure que hi ha diferències significatives entre l’alçada (height) de les persones classificades com a Dones (D) i Hòmens (H) i que aquesta té una mitjana d’11.4988 cm.
##
## Call:
## lm(formula = height ~ sex, data = pes_alumnes.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.3478 -4.3478 -0.3478 4.1509 16.6522
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 165.8491 0.8791 188.654 < 2e-16 ***
## sexH 11.4988 1.2897 8.916 2.93e-14 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.4 on 97 degrees of freedom
## Multiple R-squared: 0.4504, Adjusted R-squared: 0.4447
## F-statistic: 79.49 on 1 and 97 DF, p-value: 2.935e-14Com heu observat al llarg de la pràctica programar figures en R no és gaire amigable. R a més d’esser una eina d’anàlisi és un llenguatge de programació. Llavors, quan hem de repetir una anàlisi moltes vegades és recomanable crear una funció que agafant com a argument el nostre model gènere els plots de diagnosi de forma automatitzada.
En aquest exemple anem a generar una funció anomenada mcheck() que tindrà com a argument el nostre model (el.meu.model) i que generarà tots dos plots de diagnosi.
mcheck <- function(el.meu.model){
residus <- el.meu.model$resid # crea un objecte anomenat 'residus' amb els residus del meu model
fitted.values <- el.meu.model$fitted # crea un objecte anomenat 'fitted.values' amb els valors modelitzats pel meu model
par(mfrow=c(1, 2), bty="n") # paràmetres del plot. mfrow=c(1,2) indica dos plots en una única fila. bty="n" elimina la caixa que envolta el plot. És un argument merament estètic.
plot(fitted.values, residus,
xlab="Fitted values", ylab="Residuals") # plot fitted.values vs. residus
abline(h=0, lty="dashed") # genera un línia horitzontal de valor constant 0 (h=0). lty="dashed" indica que la línia ha de ser de punts.
qqnorm(residus,
xlab="Normal scores", ylab="Ordered residuals") # funció que genera un 'Q-Q plot normal'.
qqline(residus, lty="dashed") # funció que genera la línia que tindria una distribució un 'Q-Q plot normal'.
}Ara podem executar la funció i veure els resultats.
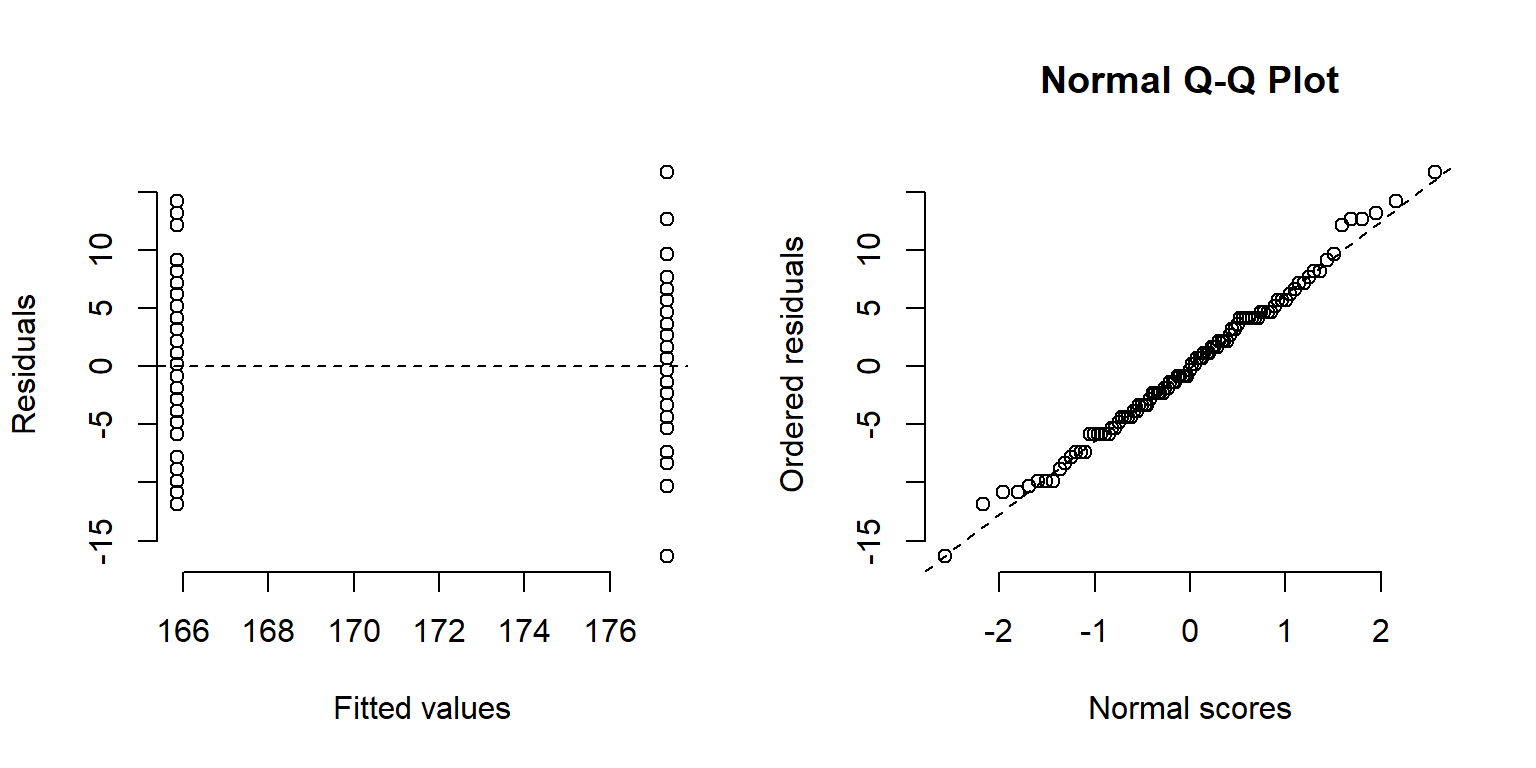
Figure 1.7: Residus de l’ANOVA (esquerra). C - Normal Q-Q Plot (dreta).
A la propera pràctica contrastos no-paramètrics veurem com realitzar una comprovació numèrica dels supòsits de l’ANOVA mitjançant testos estadístics. També veurem quins proves cal utilitzar quan no es compleixen els supòsits de per a realitzar una anàlisi de l’ANOVA.
L’anàlisi de la variància (ANOVA) s’utilitza per analitzar les diferències entre les mitjanes d’un seguit de grups (i.e. 2 o 2+ grups). En la seva forma més simple, ANOVA proporciona una prova estadística indicant si dues o més mitjanes de població són iguals, i per tant generalitza la prova t més enllà de dues mitjanes.↩︎
Si guardeu l’arxiu en una carpeta coneguda, després per RStudio el podeu anar a buscar. Mirant a la part inferior dreta, a la pestanya Files podeu navegar per els vostres arxius. Un cop localitzades les dades que voleu carregar, si cliqueu 2 vegades amb el ratolí, es carreguen automàticament les dades. Ull! si ho feu així, no queda registrat a l’Script d’R, i després podeu tenir problemes per saber quines dades vau utilitzar per fer aquelles anàlisis.↩︎