2 ATE I: Binary treatment
[//] # “Source RMD file: link”
library(lmtest)
library(sandwich)
library(grf)
library(glmnet)
library(splines)
library(ggplot2)
library(reshape2)
library(RColorBrewer)
# discrete colorblind palette
cb_colors <- brewer.pal(n = 8, name = "Dark2")2.1 Notation and definitions
Let’s establish some notation. Each data point will be defined by the triple \((W_i, A_i, Y_i)\). The vector \(W_i\) represents covariates that are observed for individual \(i\). Treatment assignment is indicated by \(A_i \in \{0, 1\}\), with 1 representing treatment, and 0 representing control. The scalar \(Y_i\) is the observed outcome, and it can be real or binary. Each observation is drawn independently and from the same distribution \(P\) of \((W,A,Y)\). We’ll be interested in assessing the causal effect of treatment on outcome.
A difficulty in estimating causal quantities is that we observe each individual in only one treatment state: either they were treated, or they weren’t. Recall the potential outcomes framework seen in class. The observed outcome \(Y_i\) corresponds to whichever potential outcome we got to see: \[\begin{equation} Y \equiv Y(A) = \begin{cases} Y(1) \qquad \text{if }A = 1 \text{ (treated)} \\ Y(0) \qquad \text{if }A = 0 \text{ (control)}\\ \end{cases} \end{equation}\]
Since we can’t observe both \(Y(1)\) and \(Y(0)\), we won’t be able to make statistical claims about the potential individual treatment effect \(Y(1) - Y(0)\). Instead, our goal will be to estimate the average treatment effect (ATE): \[\begin{equation} \tag{2.1} \theta := \mathop{\mathrm{E}}[Y(1) - Y(0)]. \end{equation}\]
Here, when we refer to the randomized setting we mean that we have data generated by a randomized controlled trial. In particular, the treatment assignment \(A\) does not depend on the individual’s potential outcomes: \[\begin{equation} \tag{2.2} Y(1), Y(0) \perp\!\!\!\perp A. \end{equation}\] This precludes situations in which individuals, for example, may self-select into or out of treatment. The canonical failure example is a job training program (where \(A=1\) means enrollment in the job training program and \(A=0\) otherwise) in which workers enroll more often if they are more likely to benefit from treatment because in that case \(A\) and \(Y(1) - Y(0)\) would be positively correlated.
When condition (2.2) is violated, we say that we are in an observational setting. This is a more complex setting encompassing several different scenarios: sometimes it’s still possible to estimate the ATE under the selection under the unconfoundeness assumption, also known as no unmeasured confounders, ignorability or selection on observables: \[\begin{equation} \tag{2.3} Y(1), Y(0) \perp\!\!\!\perp A \ | \ W. \end{equation}\]
It says that all possible sources of self-selection, etc., can be explained by the observable covariates \(W_i\).
As we’ll see below, a key quantity of interest will be the treatment assignment probability, or propensity score \(\pi(W) := P\{A = 1 | W\}\). In an experimental setting this quantity is usually known and fixed, and in observational settings it must be estimated from the data. We will often need to assume that the propensity score is bounded away from zero and one. That is: \[\begin{equation} \tag{2.4} 0 < \pi(w) < 1 \qquad \text{for all }w. \end{equation}\] This assumption is known as overlap, and it means that for all types of people in our population (i.e., all values of observable characteristics) we can find some portion of individuals in treatment and some in control. Intuitively, this is necessary because we’d like to be comparing treatment and control at each level of the covariates and then aggregate those results.
As a running example, in what follows we’ll be using an abridged version of a public dataset from the General Social Survey (GSS) (Smith, 2016). The setting is a randomized controlled trial. Individuals were asked about their thoughts on government spending on the social safety net. The treatment is the wording of the question: about half of the individuals were asked if they thought government spends too much on “welfare” \((A_i = 1)\), while the remaining half was asked about “assistance to the poor” \((A_i = 0)\). The outcome is binary, with \(Y_i = 1\) corresponding to a positive answer. In the data set below, we also collect a few other demographic covariates.
# Read in data
data <- read.csv("https://docs.google.com/uc?id=1AQva5-vDlgBcM_Tv9yrO8yMYRfQJgqo_&export=download")
n <- nrow(data)
# Treatment: does the the gov't spend too much on "welfare" (1) or "assistance to the poor" (0)
treatment <- "w"
# Outcome: 1 for 'yes', 0 for 'no'
outcome <- "y"
# Additional covariates
covariates <- c("age", "polviews", "income", "educ", "marital", "sex")2.2 Difference-in-means estimator
Let’s begin by considering a simple estimator that is available in experimental settings. The difference-in-means estimator is the sample average of outcomes in treatment minus the sample average of outcomes in control. \[\begin{equation} \tag{2.5} \widehat{\theta}_{n}^{DIFF} = \frac{1}{n_1} \sum_{i\in\mathcal{I}_1} Y_i - \frac{1}{n_0} \sum_{i\in\mathcal{I}_0} Y_i \qquad \text{where} \qquad \mathcal{I}_a := \{i \in \{1,\dots,n\} : A_i = a \}, \quad n_w := |\mathcal{I}_a| \end{equation}\]
Here’s one way to compute the difference-in-means estimator and its associated statistics (t-stats, p-values, etc.) directly, assuming asymptotic normality as we saw in class (here, we estimate everything directly, in the class notes, we implement the estimtator using funcitons in R which is usually easier to do in practice):
# Only valid in the randomized setting. Do not use in observational settings.
Y <- data[,outcome]
A <- data[,treatment]
ate.est <- mean(Y[A==1]) - mean(Y[A==0])
ate.se <- sqrt(var(Y[A == 1]) / sum(A == 1) + var(Y[A == 0]) / sum(A == 0))
ate.tstat <- ate.est / ate.se
ate.pvalue <- 2*(pnorm(1 - abs(ate.est/ate.se)))
ate.results <- c(estimate=ate.est, std.error=ate.se, t.stat=ate.tstat, pvalue=ate.pvalue)
print(ate.results)## estimate std.error t.stat pvalue
## -0.346014670 0.004804239 -72.022788469 0.000000000Or, alternatively, via the t.test function, as in class notes:
##
## Welch Two Sample t-test
##
## data: y by w
## t = 72.023, df = 21529, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
## 95 percent confidence interval:
## 0.3365980 0.3554313
## sample estimates:
## mean in group 0 mean in group 1
## 0.43812903 0.09211436We can also compute the same quantity via linear regression as we saw in class, using the fact that \[\begin{equation} Y = Y(0) + A \left[ Y(1) - Y(0) \right], \end{equation}\]
so that taking expectations conditional on treatment assignment, \[\begin{equation} \mathop{\mathrm{E}}[Y | A] = \alpha + A \theta \qquad \text{where} \qquad \alpha := \mathop{\mathrm{E}}[Y(0)] \end{equation}\]
[Exercise: make sure you understand this decomposition. Where is the unconfoundedness assumption (2.2) used?]
This result implies that we can estimate the ATE of a binary treatment via a linear regression of observed outcomes \(Y_i\) on a vector consisting of intercept and treatment assignment \((1, W_i)\).
# Do not use! standard errors are not robust to heteroskedasticity! (See below)
fmla <- formula(paste0(outcome, '~', treatment))
ols <- lm(fmla, data=data)
coef(summary(ols))[2,]## Estimate Std. Error t value Pr(>|t|)
## -0.346014670 0.004639465 -74.580721760 0.000000000The point estimate we get is the same as we got above by computing the ATE “directly” via mean(Y[W==1]) - mean(Y[W==0]). However, the standard errors are different. This is because in R the command lm does not compute heteroskedasticity-robust standard errors. This is easily solvable, as seen in the class notes:
# Use this instead. Standard errors are heteroskedasticity-robust.
# Only valid in randomized setting.
fmla <- formula(paste0(outcome, '~', treatment))
ols <- lm(fmla, data=data)
coeftest(ols, vcov=vcovHC(ols, type='HC2'))[2,]## Estimate Std. Error t value Pr(>|t|)
## -0.346014670 0.004804239 -72.022788469 0.000000000The difference-in-means estimator is a simple, easily computable, unbiased, “model-free” estimator of the treatment effect. It should always be reported when dealing with data collected in a randomized setting. However, as we’ll see later in this chapter, there are other estimators that have smallest variance.
2.3 Turning an experimental dataset into an observational one
In what follows we’ll purposely create a biased sample to show how the difference in means estimator fails in observational settings. We’ll focus on two covariates: age and political views (polviews). Presumably, younger or more liberal individuals are less affected by the change in wording in the question. So let’s see what happens when we make these individuals more prominent in our sample of treated individuals, and less prominent in our sample of untreated individuals.
# Probabilistically dropping observations in a manner that depends on x
# copying old dataset, just in case
data.exp <- data
# defining the group that will be dropped with some high probability
grp <- ((data$w == 1) & # if treated AND...
(
(data$age > 45) | # belongs an older group OR
(data$polviews < 5) # more conservative
)) | # OR
((data$w == 0) & # if untreated AND...
(
(data$age < 45) | # belongs a younger group OR
(data$polviews > 4) # more liberal
))
# Individuals in the group above have a smaller chance of being kept in the sample
prob.keep <- ifelse(grp, .15, .85)
keep.idx <- as.logical(rbinom(n=nrow(data), prob=prob.keep, size = 1))
# Dropping
data <- data[keep.idx,]Let’s see what happens to our sample before and after the change. Figure 2.1 shows the original dataset. Each observation is represented by a point on either the left or right scatterplots. An outcome of \(Y_i=1\) is denoted by a green diamond, and \(Y_i=0\) is denoted by a purple circle, but let’s not focus on the outcome at the moment. For now, what’s important to note is that the covariate distributions for treated and untreated populations are very similar. This is what we should expect in an experimental setting under unconfoundedness.
W <- model.matrix(formula("~ 0 + age + polviews"), data.exp) # old 'experimental' dataset
A <- data.exp$w
Y <- data.exp$y
par(mfrow=c(1,2))
for (a in c(0, 1)) {
plot(W[A==a,1] + rnorm(n=sum(A==a), sd=.1), W[A==a,2] + rnorm(n=sum(A==a), sd=.1),
pch=ifelse(Y, 23, 21), cex=1,
col=ifelse(Y, adjustcolor(cb_colors[1],alpha.f=0.3), adjustcolor(cb_colors[3], alpha.f=0.3)),
bg=ifelse(Y, adjustcolor(cb_colors[1],alpha.f=0.3), adjustcolor(cb_colors[3], alpha.f=0.3)),
main=ifelse(a, "Treated", "Untreated"),
xlab="age", ylab="polviews", las=1)
}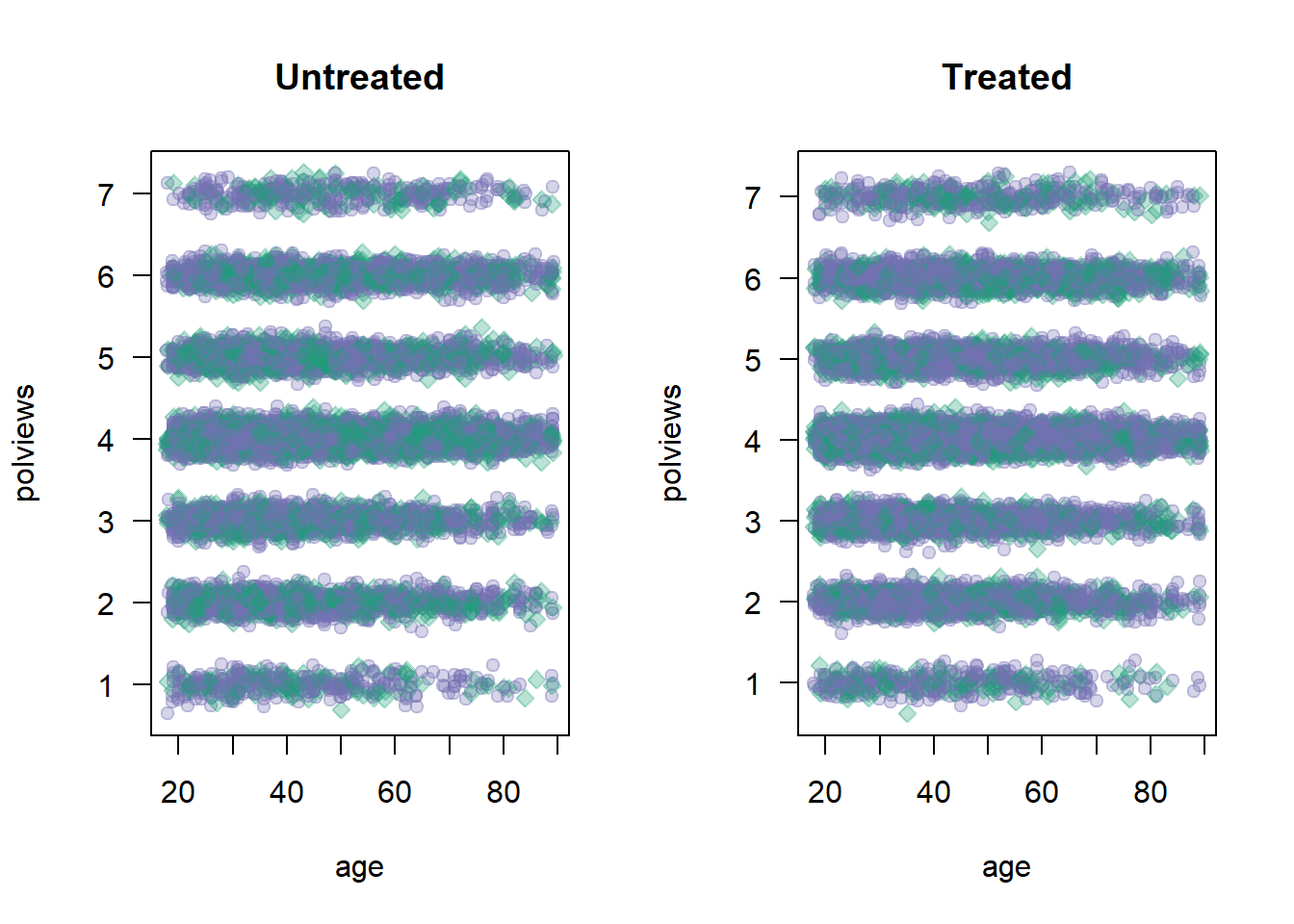
Figure 2.1: Covariate distributions in the original dataset
On the other hand, Figure 2.2 shows what the modified dataset looks like. The treated population is much younger and more liberal, while the untreated population is older and more conservative.
W <- model.matrix(formula("~ 0 + age + polviews"), data)
A <- data$w
Y <- data$y
par(mfrow=c(1,2))
for (a in c(0, 1)) {
plot(W[A==a,1] + rnorm(n=sum(A==a), sd=.1), W[A==a,2] + rnorm(n=sum(A==a), sd=.1),
pch=ifelse(Y, 23, 21), cex=1,
col=ifelse(Y, adjustcolor(cb_colors[1],alpha.f=0.3), adjustcolor(cb_colors[3], alpha.f=0.3)),
bg=ifelse(Y, adjustcolor(cb_colors[1],alpha.f=0.3), adjustcolor(cb_colors[3], alpha.f=0.3)),
main=ifelse(a, "Treated", "Untreated"),
xlab="age", ylab="polviews", las=1)
}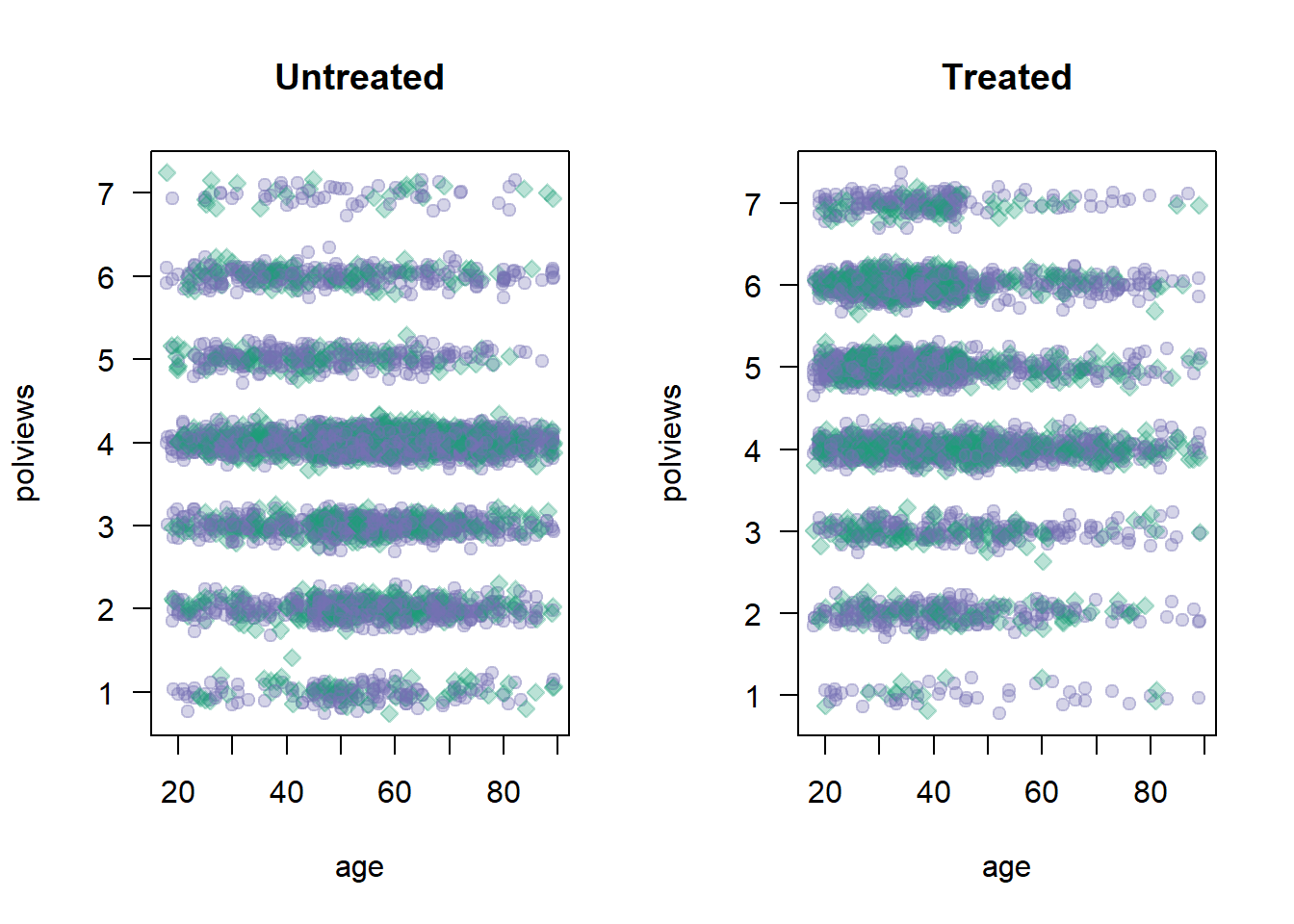
Figure 2.2: Covariate distributions in the modified dataset
As we would expect the difference-in-means estimate is biased toward zero because in this new dataset we mostly treated individuals for which we expect the effect to be smaller.
# Do not use in observational settings.
# This is only to show how the difference-in-means estimator is biased in that case.
fmla <- formula(paste0(outcome, '~', treatment))
ols <- lm(fmla, data=data)
coeftest(ols, vcov=vcovHC(ols, type='HC2'))[2,]## Estimate Std. Error t value Pr(>|t|)
## -3.018997e-01 8.510889e-03 -3.547217e+01 3.091486e-258Note that the dataset created above still satisfies unconfoundedness (2.3), since discrepancies in treatment assignment probability are described by observable covariates (age and polviews). Moreover, it also satisfies the overlap assumption (2.4), since we never completely dropped all treated or all untreated observations in any region of the covariate space. This is important because, in what follows, we’ll consider different estimators of the ATE that are available in observational settings under unconfoundedness and overlap.
2.4 Direct estimation via regression
Our first estimator is suggested by the following decomposition of the ATE, which is possible due to unconfoundedness (2.3).
\[\begin{equation} \mathop{\mathrm{E}}[Y(1) - Y(0)] = \mathop{\mathrm{E}}[\mathop{\mathrm{E}}[Y | W, A=1]] - \mathop{\mathrm{E}}[\mathop{\mathrm{E}}[Y | W, A=0]] \end{equation}\]
[Exercise: make sure you understand this. Where is the unconfoundedness assumption used?]
The decomposition above suggests the following procedure, sometimes called the direct estimate or regression estimtaor (note that is not ``linear regression’’) of the ATE:
- Estimate \(\mu_a(w) := E[Y|A= a, W = w]\), preferably using nonparametric methods, Nadaraya-Watson for example.
- Predict \(\hat{\mu}_{n,1}(W_i)\) and \(\hat{\mu}_{n,0}(W_i)\) for each observation in the data.
- Average out the predictions and subtract them. \[\begin{equation} \hat{\theta}_{n}^{DM} := \frac{1}{n} \sum_{i=1}^{n} \hat{\mu}_{n,1}(W_i) - \hat{\mu}_{n,0}(W_i) \end{equation}\]
# Do not use! We'll see a better estimator below.
# Fitting some model of E[Y|X,W]
fmla <- as.formula(paste0(outcome, "~ ", paste("bs(", covariates, ", df=3)", "*", treatment, collapse="+")))
model <- lm(fmla, data=data)
# Predicting E[Y|X,W=w] for w in {0, 1}
data.1 <- data
data.1[,treatment] <- 1
data.0 <- data
data.0[,treatment] <- 0
muhat.treat <- predict(model, newdata=data.1)
muhat.ctrl <- predict(model, newdata=data.0)
# Averaging predictions and taking their difference
ate.est <- mean(muhat.treat) - mean(muhat.ctrl)
print(ate.est)## [1] -0.3583798This estimator allows us to leverage regression techniques to estimate the ATE, so the resulting estimate should have smaller root-mean-squared error. However, it has several disadvantages that make it undesirable. First, its properties will rely heavily on the model \(\hat{\mu}_{n,a}(w)\) being correctly specified: it will be an unbiased and/or consistent estimate of the ATE provided that \(\hat{\mu}_{n,a}(w)\) is an unbiased and/or consistent estimator of \(\mathop{\mathrm{E}}[Y|X=x, W=w]\). In practice, having a well-specified model is not something we want to rely upon. In general, it will also not be asymptotically normal, which means that we can’t easily compute t-statistics and p-values for it.
A technical note. Step 1 above can be done by regressing \(Y_i\) on \(W_i\) using only treated observations to get an estimate \(\hat{\mu}_{n,1}(w)\) first, and then repeating the same to obtain \(\hat{\mu}_{n,0}(w)\) from the control observations. Or it can be done by regression \(Y_i\) on both covariates \((W_i, A_i)\) together and obtaining a function \(\hat{\mu}_{n,a}(w)\). Both have advantages and disadvantages, and we refer to Künzel, Sekhon, Bickel, Yu (2019) for a discussion.
2.5 Inverse propensity-weighted estimator
To understand this estimator, let’s first consider a toy problem. Suppose that we’d like to estimate the average effect of a certain learning intervention on students’ grades, measured on a scale of 0-100. We run two separate experiments in schools of type C and D. Suppose that, unknown to us, grades among treated students in schools of type C are approximately distributed as \(Y_i(1) | \text{school C} \sim N(60, 5^2)\), whereas in schools of type D they are distributed as \(Y_i(1) | \text{school D} \sim N(70, 5^2)\). Moreover, for simplicity both schools have the same number of students. If we could treat the same number of students in both types of schools, we’d get an unbiased estimate of the population mean grade among treated individuals: \((1/2)60 + (1/2)70 = 65\).
However, suppose that enrollment in the treatment is voluntary. In school C, only 5% enroll in the study, whereas in school D the number is 40%. Therefore, if we take an average of treated students’ grades without taking school membership into account, school D’s students would be over-represented, and therefore our estimate of treated student’s grades would be biased upward.
# Simulating the scenario over a large number of times
C.mean <- 60
D.mean <- 70
pop.mean <- .5 * C.mean + .5 * D.mean # both schools have the same size
# simulating the scenario about a large number of times
sample.means <- replicate(1000, {
school <- sample(c("C", "D"), p=c(.5, .5), size=100, replace=TRUE)
treated <- ifelse(school == 'C', rbinom(100, 1, .05), rbinom(100, 1, .4))
grades <- ifelse(school == 'C', rnorm(100, C.mean, 5), rnorm(100, D.mean, 5))
mean(grades[treated == 1]) # average grades among treated students, without taking school into account
})
hist(sample.means, freq=F, main="", xlim=c(55, 75), col=rgb(0,0,1,1/8),
ylab="", xlab="", las=1)
abline(v=pop.mean, lwd=3, lty=2)
legend("topleft", "truth", lwd=3, lty=2, bty="n")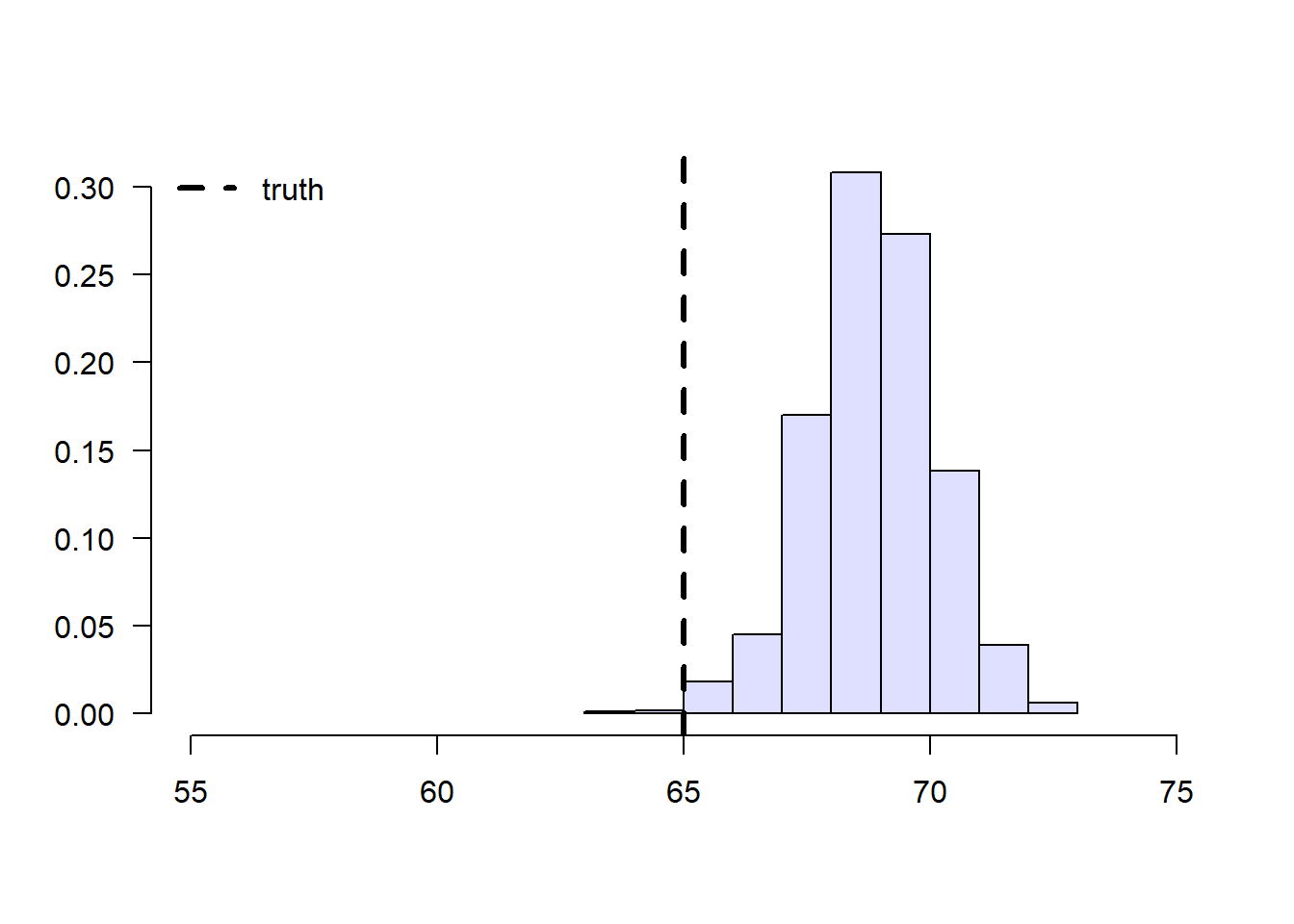
Figure 2.3: Sample means of treated students’ grades
To solve this problem, we can consider each school separately, and then aggregate the results. Denote by \(n_C\) the number of students from school \(C\), and \(n_{C,1}\) denote the number of treated students in that school. Likewise, denote by \(n_D\) and \(n_{D,1}\) the same quantities for school \(D\). Then our aggregated means estimator can be written as: \[\begin{equation} \tag{2.6} \overbrace{ \left( \frac{n_{C}}{n} \right) }^{\text{Proportion of C}} \underbrace{ \frac{1}{n_{C, 1}} \sum_{\substack{i \in \text{school C} \\ i \text{ treated}}} Y_i }_{\text{avg. among treated in C}} + \overbrace{ \left( \frac{n_{D}}{n} \right) }^{\text{Proportion of D}} \underbrace{ \frac{1}{n_{D, 1}} \sum_{\substack{i \in \text{school D} \\ i \text{ treated}}} Y_i }_{\text{avg. among treated in D}}. \end{equation}\]
# simulating the scenario over a large number of times
agg.means <- replicate(1000, {
school <- sample(c("C", "D"), p=c(.5, .5), size=100, replace=TRUE)
treated <- ifelse(school == 'C', rbinom(100, 1, .05), rbinom(100, 1, .4))
grades <- ifelse(school == 'C', rnorm(100, C.mean, 5), rnorm(100, D.mean, 5))
# average grades among treated students in each school
mean.treated.C <- mean(grades[(treated == 1) & (school == 'C')])
mean.treated.D <- mean(grades[(treated == 1) & (school == 'D')])
# probability of belonging to each school
prob.C <- mean(school == 'C')
prob.D <- mean(school == 'D')
prob.C * mean.treated.C + prob.D * mean.treated.D
})
hist(agg.means, freq=F, main="", xlim=c(50, 75), col=rgb(0,0,1,1/8),
ylab="", xlab="", las=1)
abline(v=pop.mean, lwd=3, lty=2)
legend("topright", "truth", lwd=3, lty=2, bty="n")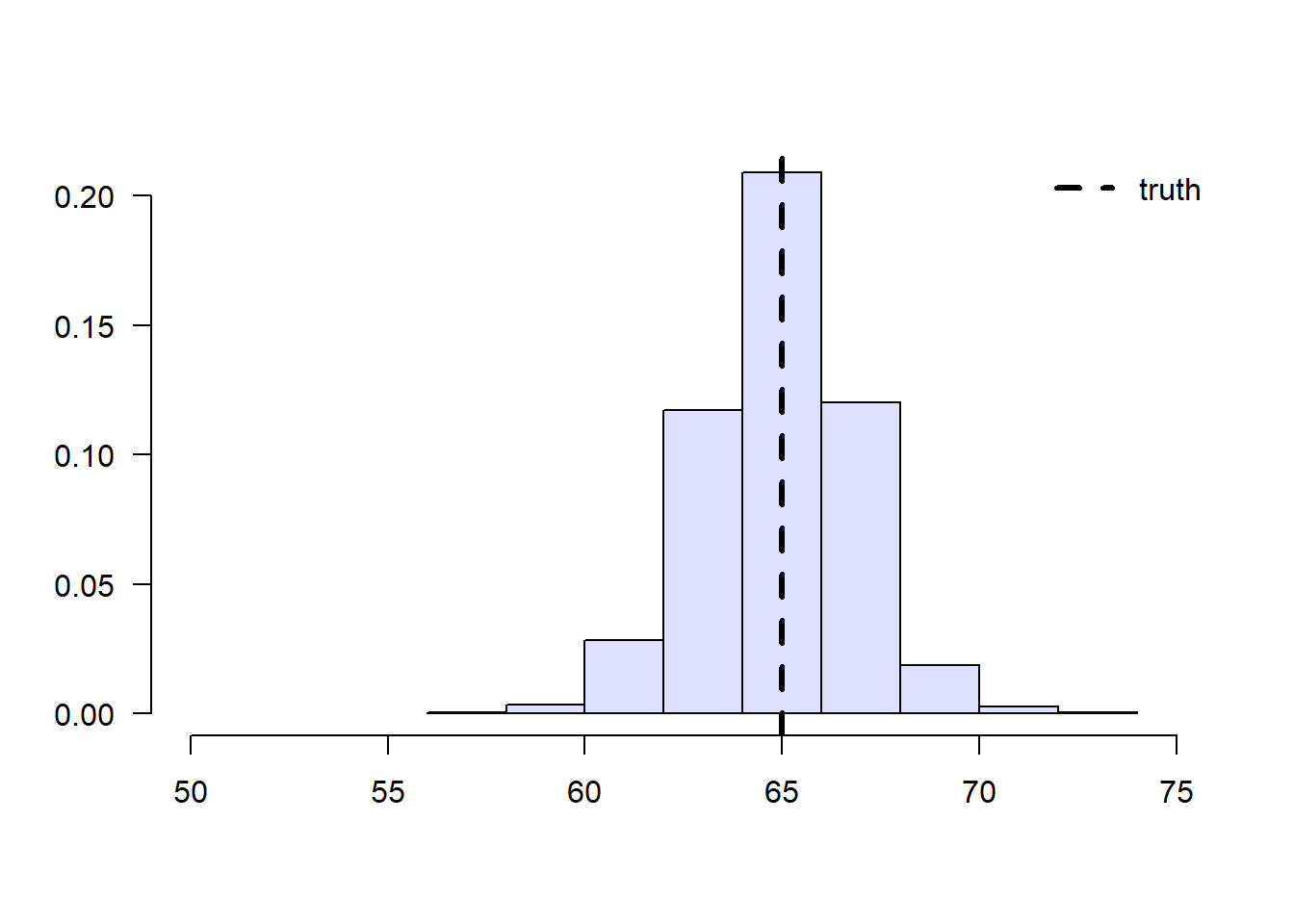
Figure 2.4: Aggregated sample means of treated students’ grades
Next, we’ll manipulate expression (2.6). This next derivation can be a bit overwhelming, but please keep in mind that we’re simply doing algebraic manipulations, as well as establishing some common and useful notation. First, note that we can rewrite the average for school C in (2.6) as \[\begin{equation} \tag{2.7} \frac{1}{n_{C, 1}} \sum_{\substack{i \in \text{school C} \\ i \text{ treated}}} Y_i = \frac{1}{n_C} \sum_{\substack{i \in \text{school C} \\ i \text{ treated}}} \frac{1}{(n_{C,1} / n_C)} Y_i = \frac{1}{n_C} \sum_{i \in \text{school C}} \frac{A_i}{(n_{C,1} / n_C)} Y_i, \end{equation}\]
where \(A_i\) is the treatment indicator. Plugging (2.7) back into (2.6), \[\begin{equation} \left( \frac{n_{C}}{n} \right) \frac{1}{n_C} \sum_{i \in \text{school C}} \frac{A_i}{(n_{C,1} / n_C)} Y_i + \left( \frac{n_{D}}{n} \right) \frac{1}{n_D} \sum_{i \in \text{school D}} \frac{A_i}{(n_{D,1} / n_D)} Y_i. \end{equation}\]
Note that the \(n_C\) and \(n_D\) will cancel out. Finally, if we denote the sample proportion of treated students in school \(C\) by \(\hat{\pi}(C_i) \approx n_{C,1}/n_C\) and similar for school \(D\), (2.6) can be written compactly as \[\begin{equation} \tag{2.8} \frac{1}{n} \sum_{i=1}^{n} \frac{A_i}{\hat{\pi}(W_i)} Y_i, \end{equation}\] where \(W_i \in \{A, B\}\) denotes the school membership. Quantity \(\hat{\pi}(W_i)\) is an estimate of the probability of treatment given the control variable \(\pi(W_i) = \mathop{\mathrm{P}}[A_i=1 | W_i ]\), also called the propensity score. Because (2.8) is a weighted average with weights \(A_i/\hat{\pi}(W_i)\), when written in this form we say that it is an inverse propensity-weighted estimator (IPW).
The IPW estimator is also defined when there are continuous covariates. In that case, we must estimate the assignment probability given some model, for example using logistic regression, forests, etc. With respect to modeling, the behavior of the IPW estimator is similar to the direct estimator: if \(\hat{\pi}(W_i)\) is an unbiased estimate of \(\pi(W_i)\), then (2.8) is an unbiased estimate of \(E[Y(1)]\); and we can show that if \(\hat{\pi}(W_i)\) is a consistent estimator of \(\pi(W_i)\), then (2.8) is consistent for \(E[Y(1)]\), as seen in class.
When the treatment propensity \(\hat{\pi}(W_i)\) is small, the summands in (2.8) can be very large. In particular, if \(\hat{\pi}(w)\) is exactly zero, then this estimator is undefined. That is why, in addition to requiring conditional unconfoundedness (2.3), it also requires the overlap condition (2.4). In any case, when overlap is small (i.e., \(\hat{\pi}(x)\) is very close to zero for many \(x\)), IPW becomes an unattractive estimator due to its high variance. We’ll see in the next section an improved estimator that builds upon IPW but is strictly superior and should be used instead.
Finally, we just derived an estimator of the average treated outcome, but we could repeat the argument for control units instead. Subtracting the two estimators leads to the following inverse propensity-weighted estimate of the treatment effect: \[\begin{equation} \tag{2.9} \widehat{\tau}^{IPW} := \frac{1}{n} \sum_{i=1}^{n} Y_i \frac{A_i}{\hat{\pi}(W_i)} - \frac{1}{n} \sum_{i=1}^{n} Y_i \frac{(1 - A_i) }{1-\hat{\pi}(W_i)}. \end{equation}\]
The argument above suggests the following algorithm:
- Estimate the propensity scores \(\pi(W_i)\) by regressing \(W_i\) on \(X_i\), preferably using a non-parametric method.
- Compute the IPW estimator summand: \[Z_i = Y_i \times \left(\frac{W_i}{\hat{\pi}(X_i)} - \frac{(1-W_i)}{(1-\hat{\pi}(X_i))} \right)\]
- Compute the mean and standard error of the new variable \(Z_i\)
# Available in randomized settings and observational settings with unconfoundedness+overlap
# Estimate the propensity score e(X) via logistic regression using splines
fmla <- as.formula(paste0("~", paste0("bs(", covariates, ", df=3)", collapse="+")))
W <- data[,treatment]
Y <- data[,outcome]
XX <- model.matrix(fmla, data)
logit <- cv.glmnet(x=XX, y=W, family="binomial")
e.hat <- predict(logit, XX, s = "lambda.min", type="response")
# Using the fact that
z <- Y * (W/e.hat - (1-W)/(1-e.hat))
ate.est <- mean(z)
ate.se <- sd(z) / sqrt(length(z))
ate.tstat <- ate.est / ate.se
ate.pvalue <- 2*(pnorm(1 - abs(ate.est/ate.se)))
ate.results <- c(estimate=ate.est, std.error=ate.se, t.stat=ate.tstat, pvalue=ate.pvalue)
print(ate.results)## estimate std.error t.stat pvalue
## -3.561350e-01 1.327492e-02 -2.682766e+01 4.337035e-147