2 Covariance

Les concepts de variance, de covariance, d’écart type et de corrélation linéaire sont très utilisés en statistiques élémentaires, mais ils sont à la vérité, comme tels, un peu difficiles à comprendre.

Pourquoi par exemple utilise-t-on l’écart quadratique moyen plutôt que l’écart absolu moyen, pourquoi additionner des carrés ? Est-il possible de donner un sens intuitif à cela ?

2.1 Moment de force (mécanique)

Le concept de covariance est fortement lié au concept de moment de force en mécanique. Nous en rappelons donc tout d’abord la définition : on appelle moment d’une force \(F\) par rapport à un axe de rotation \(\Delta\) le produit de la masse F de la force et de son bras de levier \(d\).

On note \(M_{F}\) = \(F.d\)

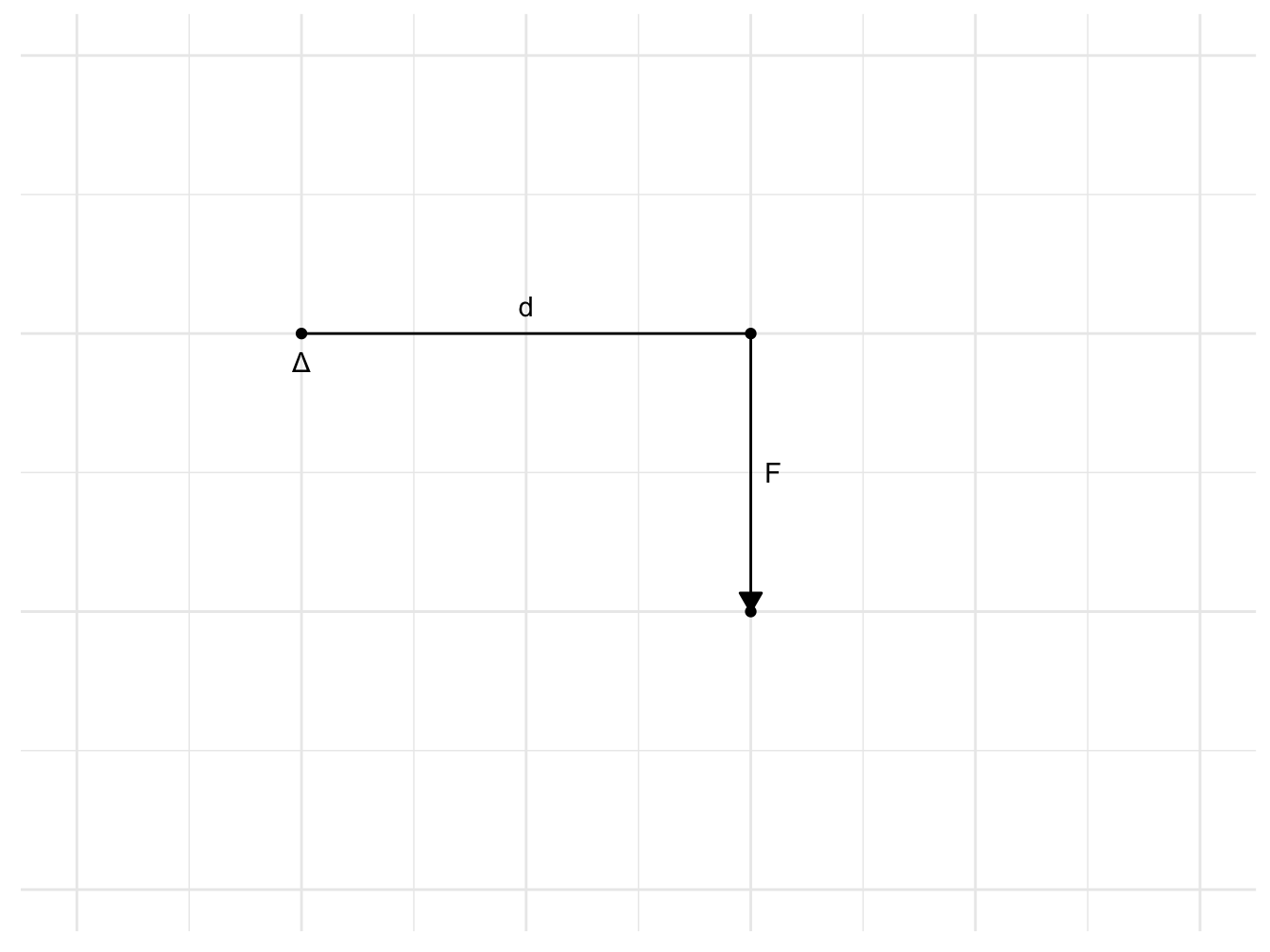
Figure 2.1: Moment de force

2.2 Moment de force (statistique)

Une représentation analogue peut-être donnée en statistique :

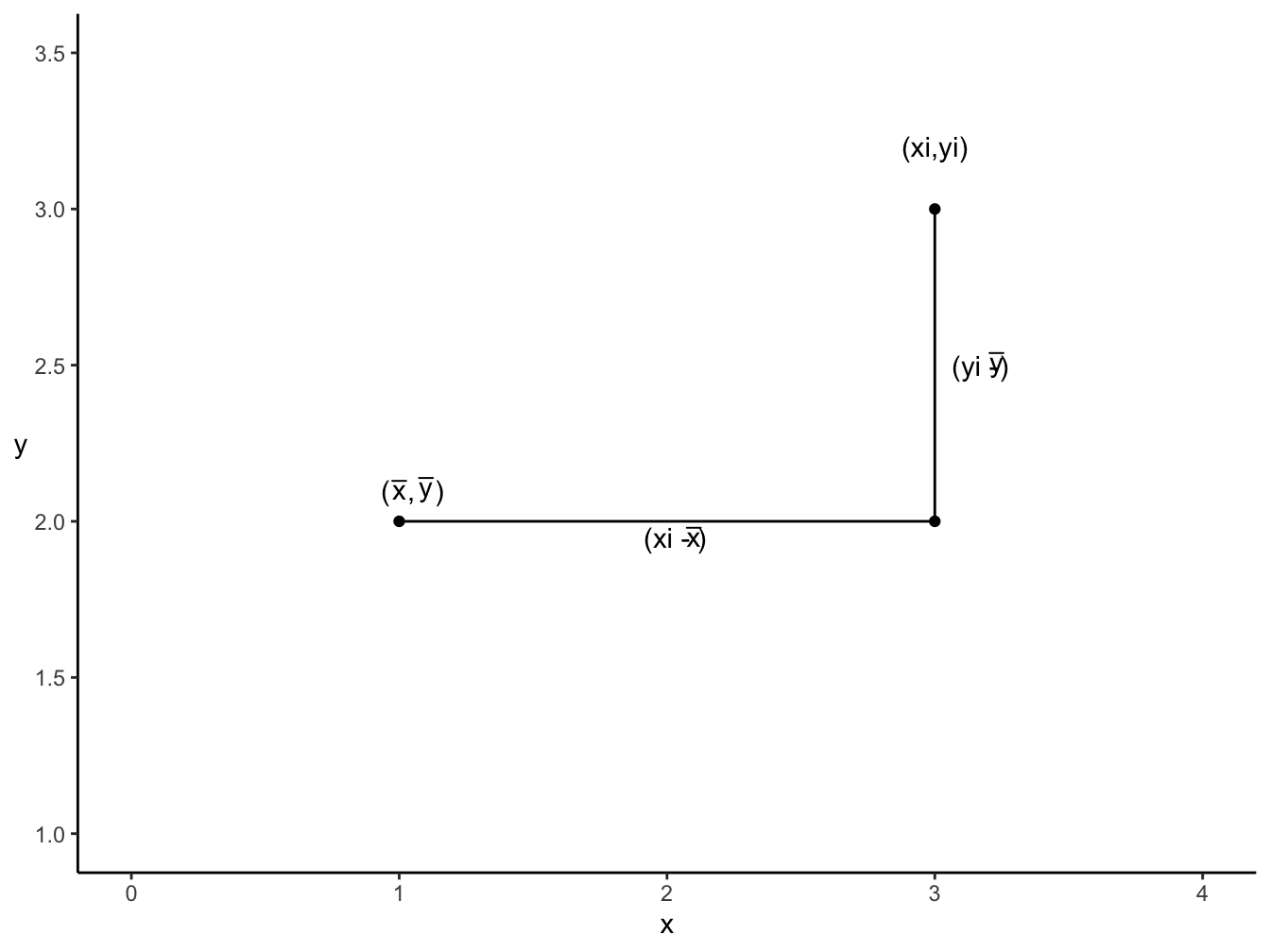
Figure 2.2: Moment de force

Où (\(y_i\) - \(\bar{y}\)) est une force (équivalente à F) et (\(x_i - \bar{x}\)) la distance à l’axe de rotation au point \((\bar{x},\bar{y})\)

2.3 Définition de la covariance

\(Wikipédia\) propose la définition suivante : “En théorie des probabilités et en statistique, la covariance entre deux variables aléatoires est un nombre permettant de quantifier leurs écarts conjoints par rapport à leurs espérances respectives. Elle s’utilise également pour deux séries de données numériques (écarts par rapport aux moyennes). La covariance de deux variables aléatoires indépendantes est nulle, bien que la réciproque ne soit pas toujours vraie.”

Autrement dit la covariance est une mesure de la variabilité conjointe de deux variables aléatoires qui s’obtient par la moyenne des produits des écarts des variables par rapport à leurs moyennes. La covariance indique si, et indirectement dans quelle mesure, les valeurs d’une variable augmentent ou diminuent avec les valeurs croissantes de l’autre variable. La covariance est une valeur qui indique le degré de variation conjointe de deux variables.

Mathématiquement la covariance est définie par :

\[ Cov(X,Y) = \mathbb{E}[(X - \mathbb{E}(X))(Y - \mathbb{E}(Y))] \] Une autre écriture en développant :

\[ Cov(X,Y) = \mathbb(XY - X \mathbb{E}(Y) - Y \mathbb{E}(X) + \mathbb{E}(X)\mathbb{E}(Y))\\ Cov(X,Y) = \mathbb{E}(XY) - \mathbb{E}(X)\mathbb{E}(Y) \] En pratique, le calcul numérique de la covariance utilise l’estimateur sans biais suivant :

\[ {Cov(X,Y)}=\frac{1}{(N-1)} \sum_{i=1}^{N} (x_i-\overline{x})(y_i -\overline{y}) \]

\(\color{red}{\underline{Remarque}}:\) On divise par \((N-1)\) et non pas par \(N\).

D’après Kenney et Keeping (1951) la correction dite de Bessel devrait plutôt être attribuée à GAUSS (1823).

\[ Cov(X,Y)=\frac{N}{N-1}(\overline{xy}-\overline{x}~\overline{y}) \]

La covariance est à un facteur correctif près \(\frac{N}{N-1}\), la moyenne empirique du produit des variables moins le produit des moyennes empiriques de chaque variable.

\(\underline{Preuve}\) : Soit \(S_{xy}\) la variance de l’échantillon :

\[ (n-1) S_{xy} = \sum_{i = 1}^N (x_i- \bar{x})(y_i - \bar{y})\\ = \sum_{i = 1}^N x_iy_i - N \overline{x}~\overline{y} \\ = \sum_{i =1}^N x_iy_i - \frac{1}{N} \sum_{i =1}^N x_i \sum_{i =1}^N y_i \]

Donc

\[ (n-1)~ \mathbb{E} (S_{xy}) = \mathbb{E} (\sum_{i =1}^N x_iy_i) - \frac{1}{N} ~ \mathbb{E} (\sum_{i =1}^N x_i \sum_{i =1}^N y_i)\\ = N \mu x_iy_i - \frac{1}{N}(N\mu xy + N(N-1) \mu x ~ \mu y)\\ = (N-1)~(\mu x_iy_i - \mu x ~ \mu y )\\ = (N-1)~Cov(x,y) \]

Avec \[ \mathbb{E}{(X_iY_i)} = \mu xy\\ \mathbb{E}{(X_iY_j)} = \mu x ~\mu y \]

Donc \(\frac{1}{N-1} \sum_{i =1}^N ( x_i-\bar{x})(y_i - \bar{y})\) est un estimateur sans biais de la covariance de la population.

2.4 Covariance et point(s) de référence

L’expression usuelle de la covariance est définie par rapport à un point de référence particulier : le centre de gravité du nuage de points \((\bar{x}, \bar{y})\)

1. On peut montrer que la covariance est minimale pour ce point de référence plutôt que tout autre point de coordonnées \((a,b)\).

Soit \(C = \frac{1}{N} \sum_{i =1}^N ( x_i-a)(y_i - b)\). On a :

\[ \frac{\delta C}{\delta a} = - \frac{1}{N-1} \sum_{i=1}^{N}(y_i - b) = 0\\ \frac{\delta C}{\delta b} = - \frac{1}{N-1} \sum_{i=1}^{N}(y_i - a) = 0 \]

On voit trivialement que \(a = \bar{x}\) et \(a = \bar{y}\) minimise l’expression \(C\).

2. On peut montrer que la covariance peut également se définir à partir de la moyenne de tous les rectangles (\(x_i - x_j\))(\(y_i - y_j\)).

\[Cov(X,Y) = \frac{1}{N-1} \sum_{i =1}^N ( x_i-\bar{x})(y_i - \bar{y})\]

\[Cov(X,Y) = \frac{1}{2(N-1)}(\sum_{i=1}^N(x_i -\bar{x})(y_i - \bar{y}) + \sum_{j=1}^N(x_j - \bar{x})(y_i - \bar{y}))\]

\[= \frac{1}{2N(N-1)} \sum_{i=1}^N \sum_{j=1}^N ((x_i - \bar{x})(y_i - \bar{y}) + (x_j - \bar{x})(y_j - \bar{y}))\]

\[= \frac{1}{2N(N-1)} \sum_{i=1}^N \sum_{j=1}^N (x_iy_i - x_i\bar{y} - y_i\bar{x} + \bar{x}\bar{y} + x_jy_i - x_j\bar{y}- y_i\bar{x} + \bar{x}\bar{y})\]

\[= \frac{1}{2N(N-1)} \sum_{i=1}^N \sum_{j=1}^N ((x_i - x_j)(y_i - y_j) + x_iy_j + x_jy_i - x_i\bar{y} - y_i\bar{x} + \bar{x}\bar{y} - x_j\bar{y} - y_i\bar{x} + \bar{x}\bar{y})\]

\[Cov(X,Y) = \frac{1}{2N(N-1)} \sum_{i=1}^N \sum_{j=1}^N (x_i - x_j)(y_i - y_j)\]

On peut ainsi, en partant de la définition usuelle de la covariance considérer le centre de gravité (\(\bar{x},\bar{y}\)) comme le point de référence d’une une expression équivalente de la covariance faisant intervenir une construction basée sur toutes les paires de points \(i,j\) de l’échantillon de N points.

2.5 Covariance définie en fonction de la comparaison de couples de points

2.5.1 Un peu de théorie

Il existe un moyen plus direct de parvenir à l’écriture de la covariance faisant intervenir dans le calcul tous les rectangles formés par les paires de points (\(i,j\)) : \((x_i - x_j)(y_j - y_i)\).

Considérons deux variables aléatoires \(X\) et \(Y\) ainisi qu’un échantillon simple bivarié \(i=1,2,...,N\) {\((x_1, y_1), (x_2, y_2), ... (x_N, y_N)\)}

Considérons les hypothèses :

• Les observations sont indépendantes ;

• Les variables X et Y ne sont pas nécessairement indépendantes.

Prenons deux points au hasard désignés par les indices \(k\) et \(l\) et calculons :

\[ \mathbb E ((x_k - x_l)(y_k - y_l)) \] On a :

\[ \mathbb E (x_ky_k - x_ky_l - x_ly_k + x_ly_l) \\ \mathbb E (x_ky_k) - \mathbb E (x_k) \mathbb E(y_l) - \mathbb E(x_l)(y_k) + \mathbb E(x_ly_l) \\ = 2 \mathbb E (XY) - 2 \mathbb E(X)\mathbb E(Y) \\ = \color{red}{2 Cov(X,Y)} \]

Autrement dit l’espérance mathématique de l’aire du rectangle formé par deux points tirés au hasard équivaut au double de la covariance.

Remarquons tout d’abord, qu’à l’échelle de \(\frac{1}{\sqrt{2}}\) le rectangle considéré est une représentation de la covariance.

Remarquons ensuite que pour le calcul de la covariance empirique, le résultat précédent théorique de \(\mathbb E((x_k - x_l)(y_k - y_l))\) va nous conduire à calculer la moyenne empirique de tous les rectangles formés par les couples de points \(i,j = 1,2,..,N\).

Une définition équivalente de la covariance consiste donc à poser :

\[ Cov(X,Y) = \frac{1}{2N(N-1)} \sum_{i=1}^{N-1} \sum_{j=i+1}^N (x_i - x_j)(y_i - y_j) \]

ou en raison de la symétrie :

\[ Cov(X,Y) = \frac{1}{N(N-1)} \sum_{i=1}^{N} \sum_{j=1}^N(x_i - x_j)(y_i - y_j) \]

Il est utile de remarquer que les \(N^2\) associations de points \(i,j =1,2,...N\), evidemment \((x_i - x_j)(y_i - y_j) = 0\) pour \(i=j\). On a donc en fait exactement et seulement \(N^2\)-\(N\) rectangles à considérer dans le calcul ce la covariance.

D’ailleurs nous trouvons de la sorte directement un estimateur sans biais de la covariance intégrant la correction de Bessel.

\(\underline{Preuve}\) :

\[ \frac{1}{2N(N-1 )} \sum_{i=1}^N \sum_{j=1}^N (x_i - x_j)(y_i - y_j) \\ = \frac{1}{N(N-1)} \sum_{i=1}^{N} Nx_iy_i - x_i N \bar{y} - y_iN\bar{x} + N\bar{xy} \\ = \frac{2N^2}{2N(N-1)}(\bar{xy} - \bar{x}\bar{y}) \\ = \frac {N}{N-1}(\bar{xy} - \bar{x}\bar{y}) \\ = \color{red}{Cov(X,Y)} \]

2.6 Le cas particulier de la Variance

La variance étant le cas particulier de la covariance entre deux variables identiques on peut très rapidement décliner les résultats précédents :

\[ Var(X) = Cov(X,X) = \mathbb E (X - \mathbb E(X))^2 = \mathbb E(X^2) - \mathbb E(X)^2 \]

Un estimateur sans biais de la variance de la population sur un echantillon \(x_i, i = 1,2, ..., N\) s’écrit :

\[ Var(X) = \frac{1}{N-1} \sum_{i=1}^N(x_i - \bar{x})^2 \] ou \[ Var(X) = \frac{1}{N(N-1)} \sum_{i=1}^{N-1} \sum_{j=i+1}^{N}(x_i - x_j)^2 \] ou \[ Var(X) = \frac{1}{2N(N-1)} \sum_{i=1}^{N} \sum_{j=1}^{N}(x_i - x_j)^2 \]

2.7 Représentations graphiques :

2.7.1 Proposition de Kevin HAYES (2011)

Considérons deux variables aléatoires \(X,~Y,\) et un échantillon simple bivarié \({(x_1,~y_1),(x_2,~y_2),\dotsi (x_N,~y_N)}\).

Hayes choisit de représenter la covariance entre deux points \((x,y)\) par le triangle au-dessus (en-dessous) de l’hypoténuse selon que la pente entre les deux points est positive ou négative. Mais, il ne propose pas une représentation générale pour un nuage de points mais plutôt uniquement une représentation pour deux points, sans effectuer toutes les superpositions dans le cas de N points. De plus, il est important de souligner que, lorsque nous sommes confrontés à des points ex aequo, le triangle est dégénéré et est représenté par une droite.

Pour illustrer, Hayes (2011), utilise un échantillon constitué de 6 observations bivariées :

Point	a	b	c	d	e	f
x	1	2	3	3	1	5
y	1	2	3	2	4	5

Hayes (2011) propose la représentation suivante :

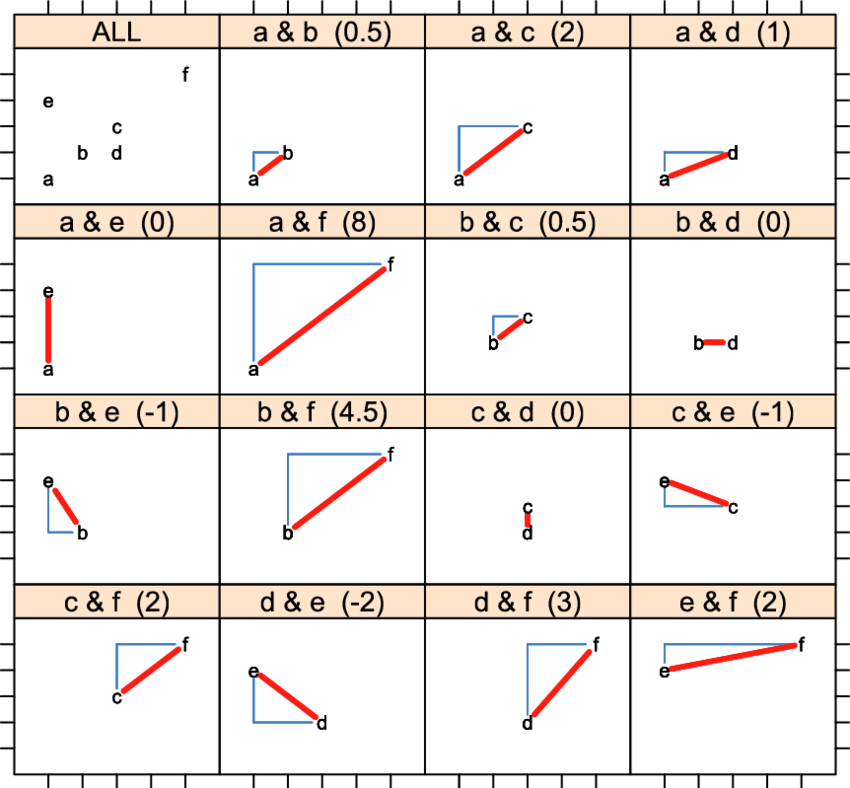
Comme évoqué précédemment Hayes (2011) semble représenter la covariance par le triangle au-dessus (au-dessous) de l’hypoténuse selon que la pente entre les deux points est positive (négative). Aussi, il est important de noter qu’Hayes (2011) ne propose pas de représentation pour l’ensemble des couples de points et enfin, en cas d’ex aequo entre deux points le triangle formé par ces deux points est dégénéré.

2.7.2 Représentation graphique de la covariance

Nous allons, pour cette représentation de la covariance conserver la forme du rectangle comme vu précédemment et considérer que cette représentation est vraie à l’échelle \(\frac{1}{\sqrt(2)}\).

2.7.3 Principe de construction

Nous considérons un exemple simple constitué d’un échantillon comportant 4 observations. Pour représenter la covariance nous comparons les points deux à deux. La contribution à la covariance consiste à représenter chacun des rectangles ainsi formés par les couples de points. Enfin nous adoptons la convention suivante si deux points sont tels que la relation entre x et y est positive (négative) alors le rectangle est représenté en bleu (rouge).

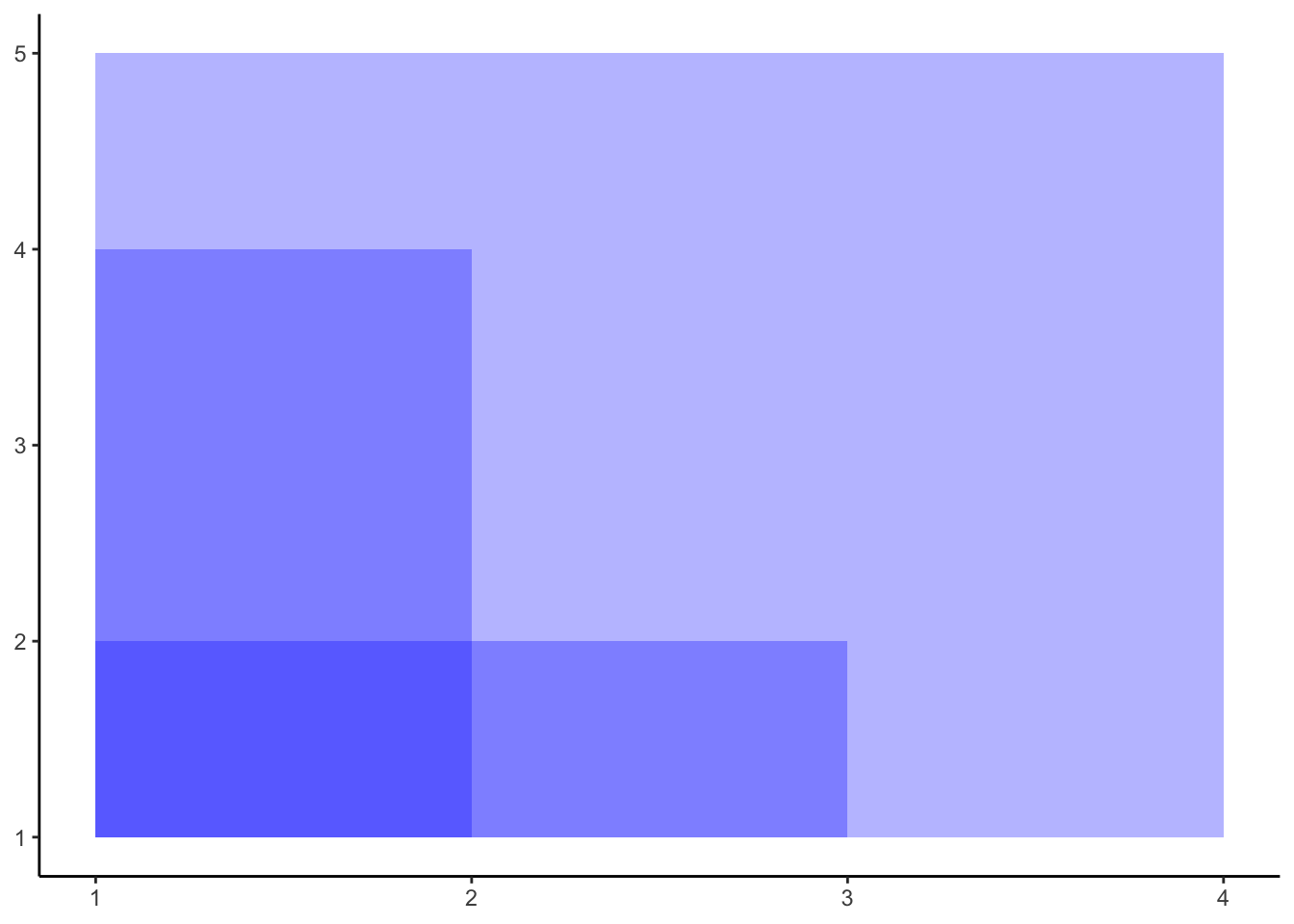
Commençons par le point A, comparé successivement aux points B, C puis D.

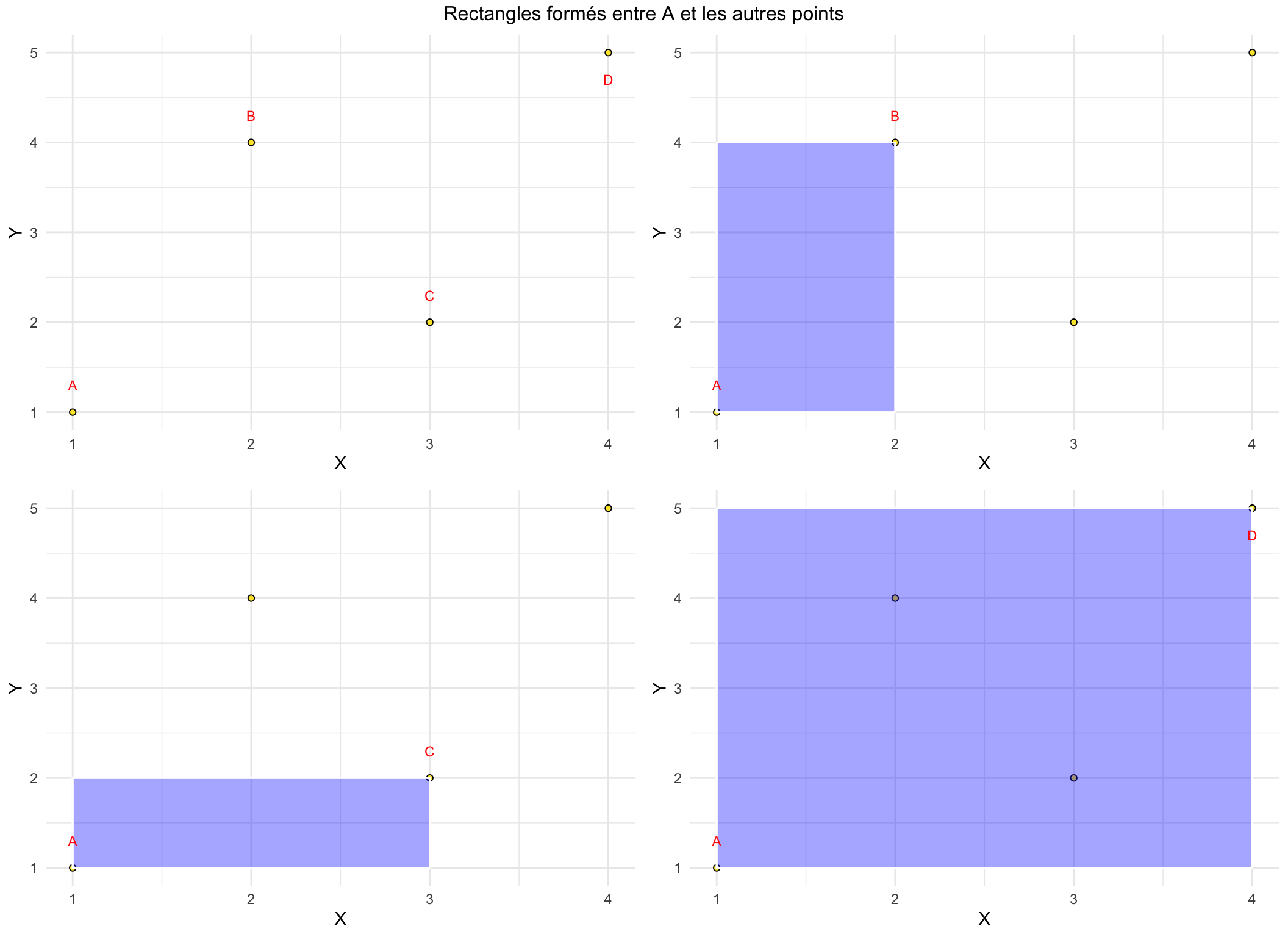
L’étape suivante, consite à superposer ces différents rectangles, ce qui donne pour notre premier point A :

 

Nous répétons l’opération en prenant à présent le point B que nous comparons aux points C et D.

Le dernier cas consiste à comparer le point C au point D.

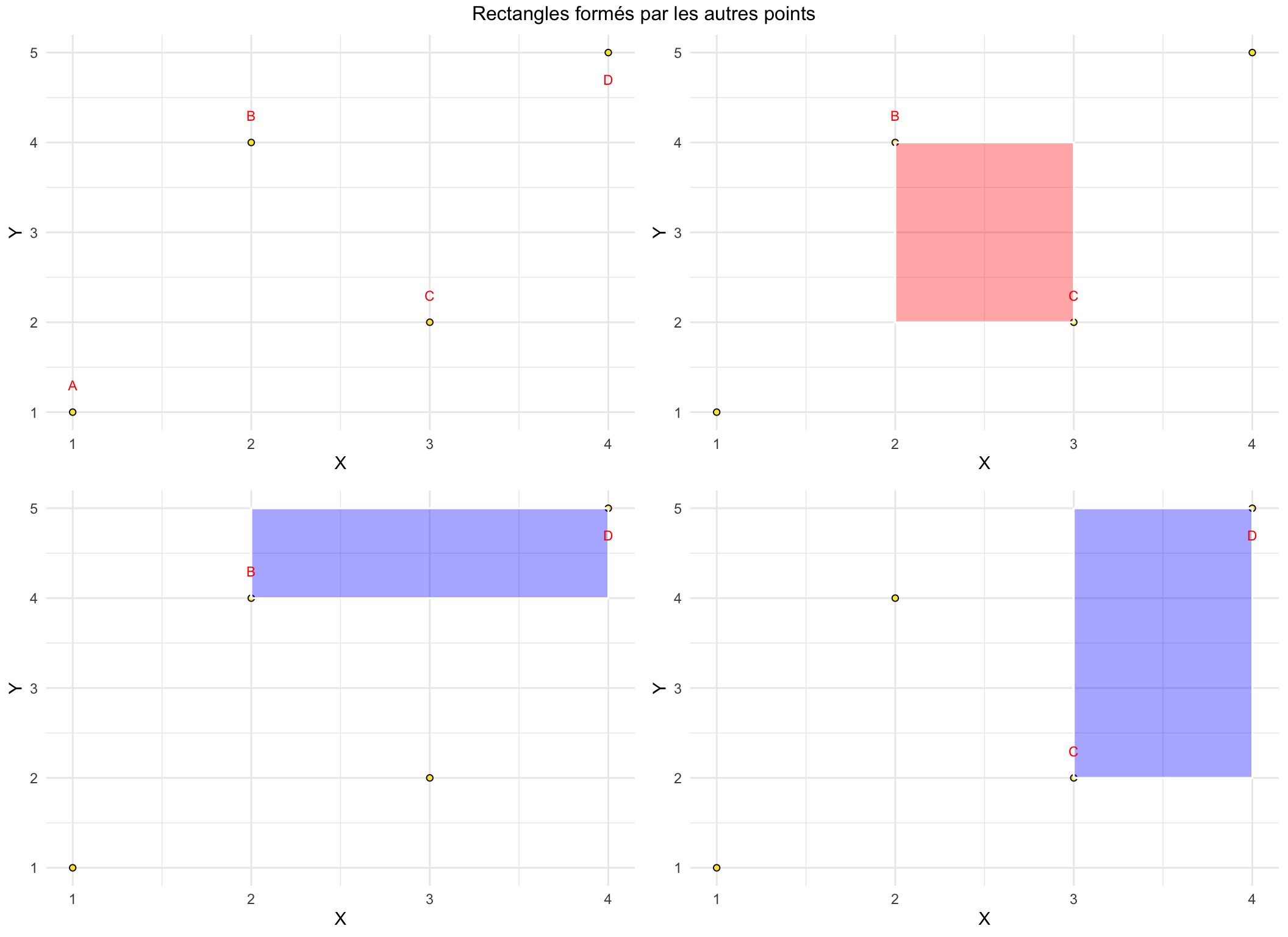
Remarques : On a vu précédemment que la moyenne de toutes les aires représentées était égale au double de la covariance, soit : \(2Cov(X,Y)\). Nous avons représenté la covariance entre chaque couple de points, le plan (\(X\), \(Y\)) a ainsi été séparé en plusieurs quadrillages en fonction des différentes covariances susmentionnées.

L’étape finale consiste à superposer toutes ces contributions à la covariance.

On obtient ainsi le graphique suivant :

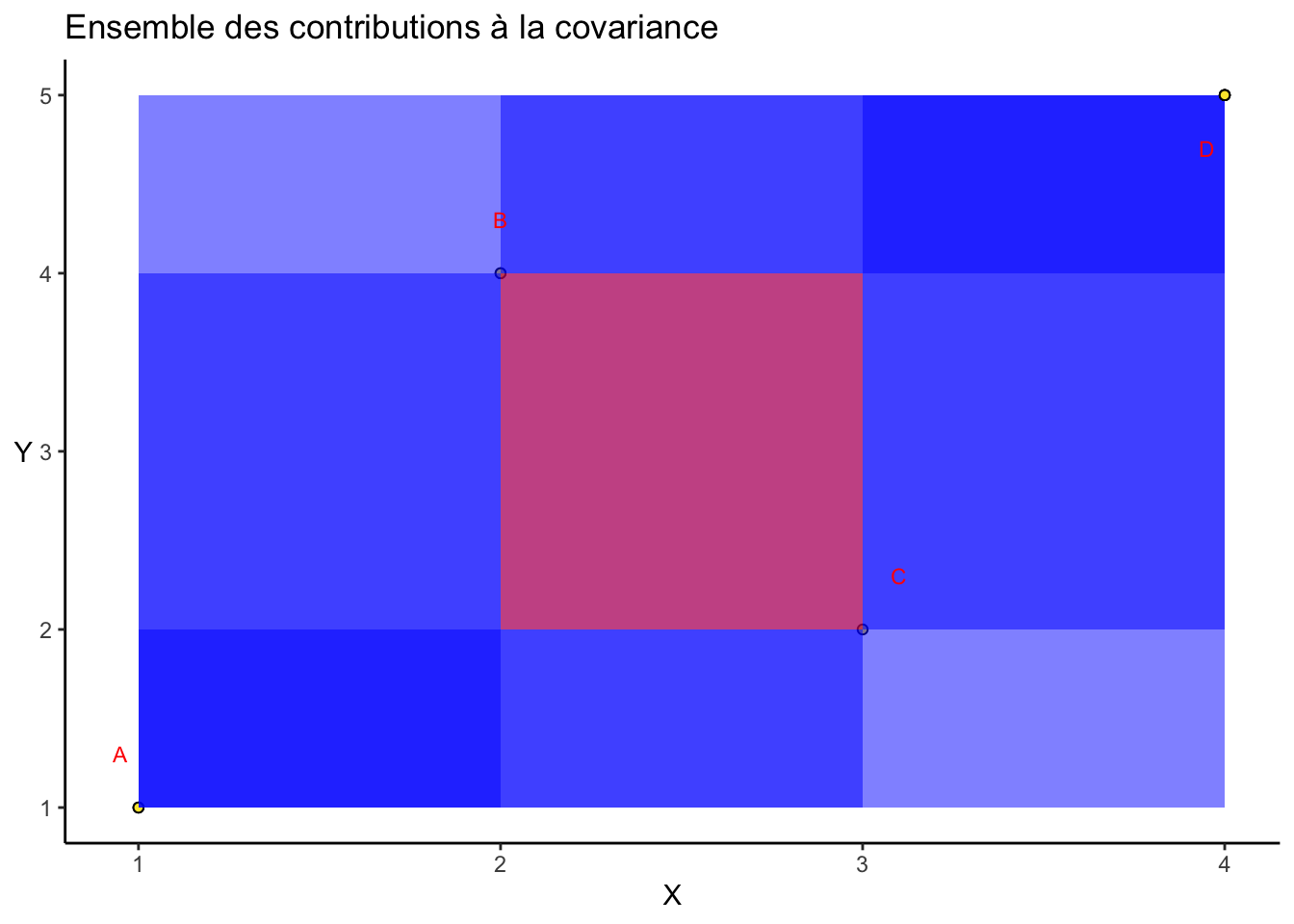
2.7.4 Nouvelle représentation de la covariance

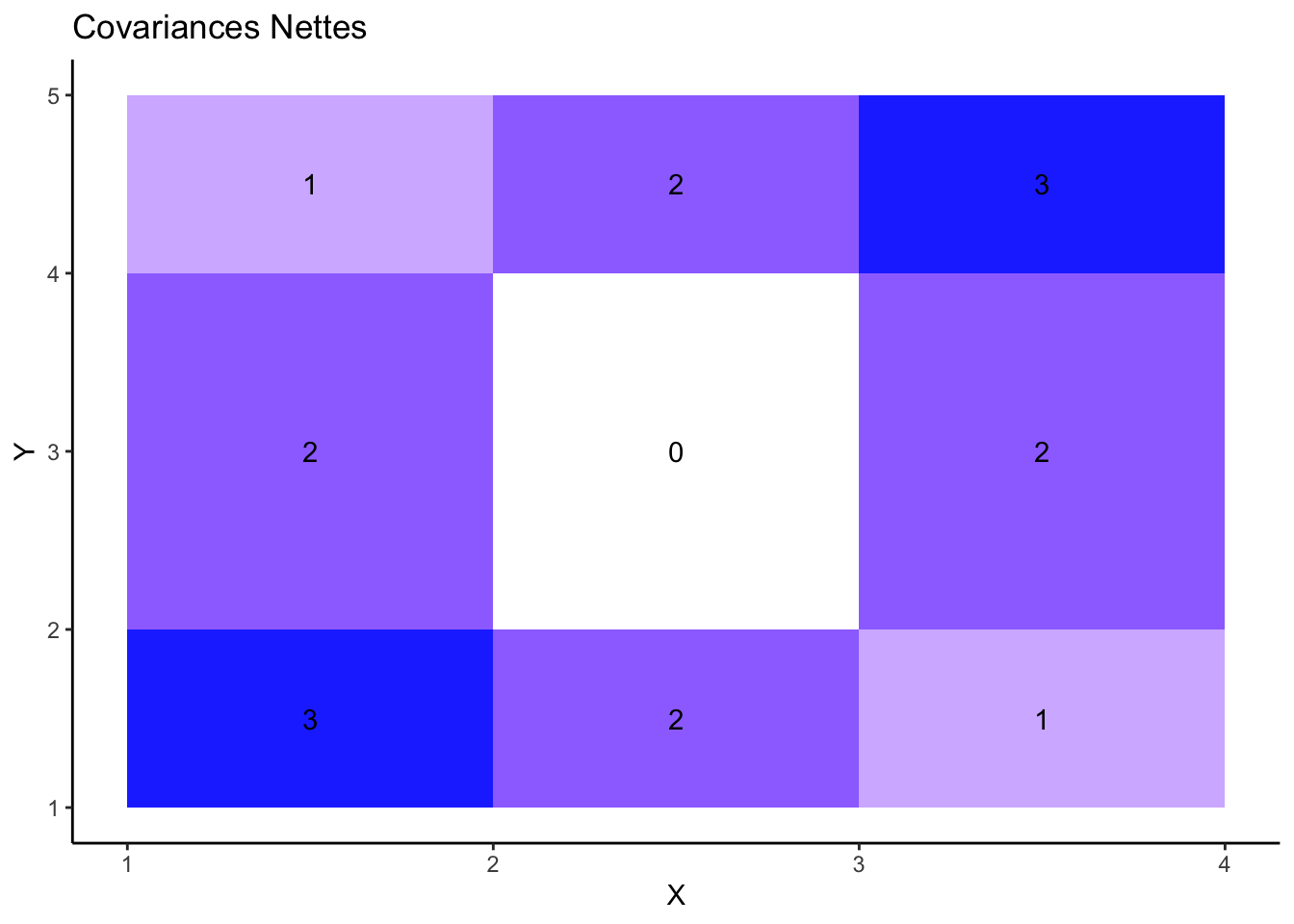
La représentation de la covariance dans le graphique précédent présente un défaut majeur. En effet, le rectangle formé des points B et C est en fait rempli une fois en bleu et une fois en rouge. Le résultat de ces superpositions devrait par conséquent être en blanc (par exemple) pour indiquer clairement que la contribution à la covariance de ces deux points est globalement nulle.

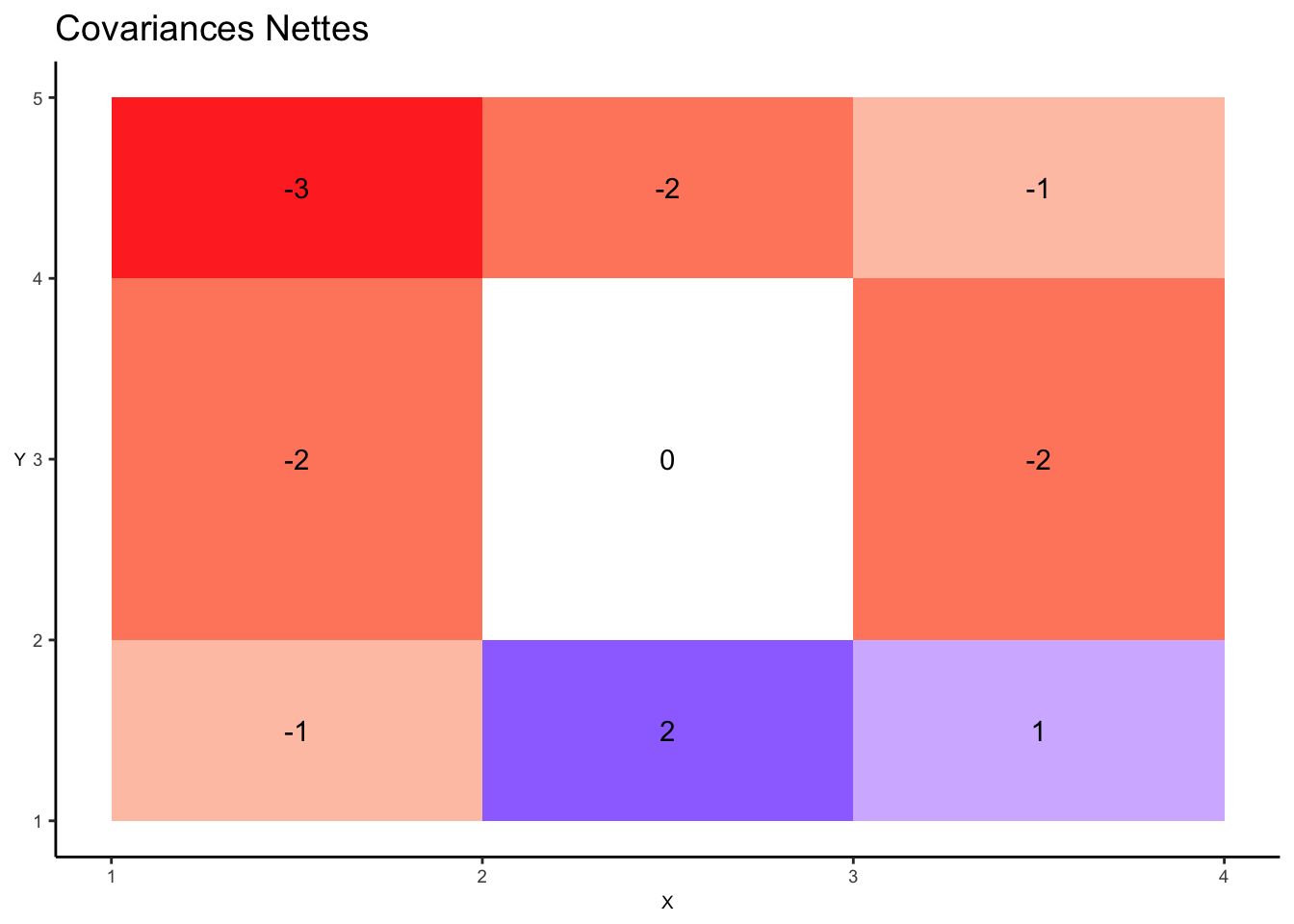
Dans le graphique suivant nous corrigeons cette difficulté en procédant au comptage net, pour chaque zone du pavage, entre les contributions positives et négatives à la covariance. Nous indiquons précisément dans le graphique ce nombre net de couches qui se superposent.

2.7.5 Représentation de la covariance sur un autre exemple

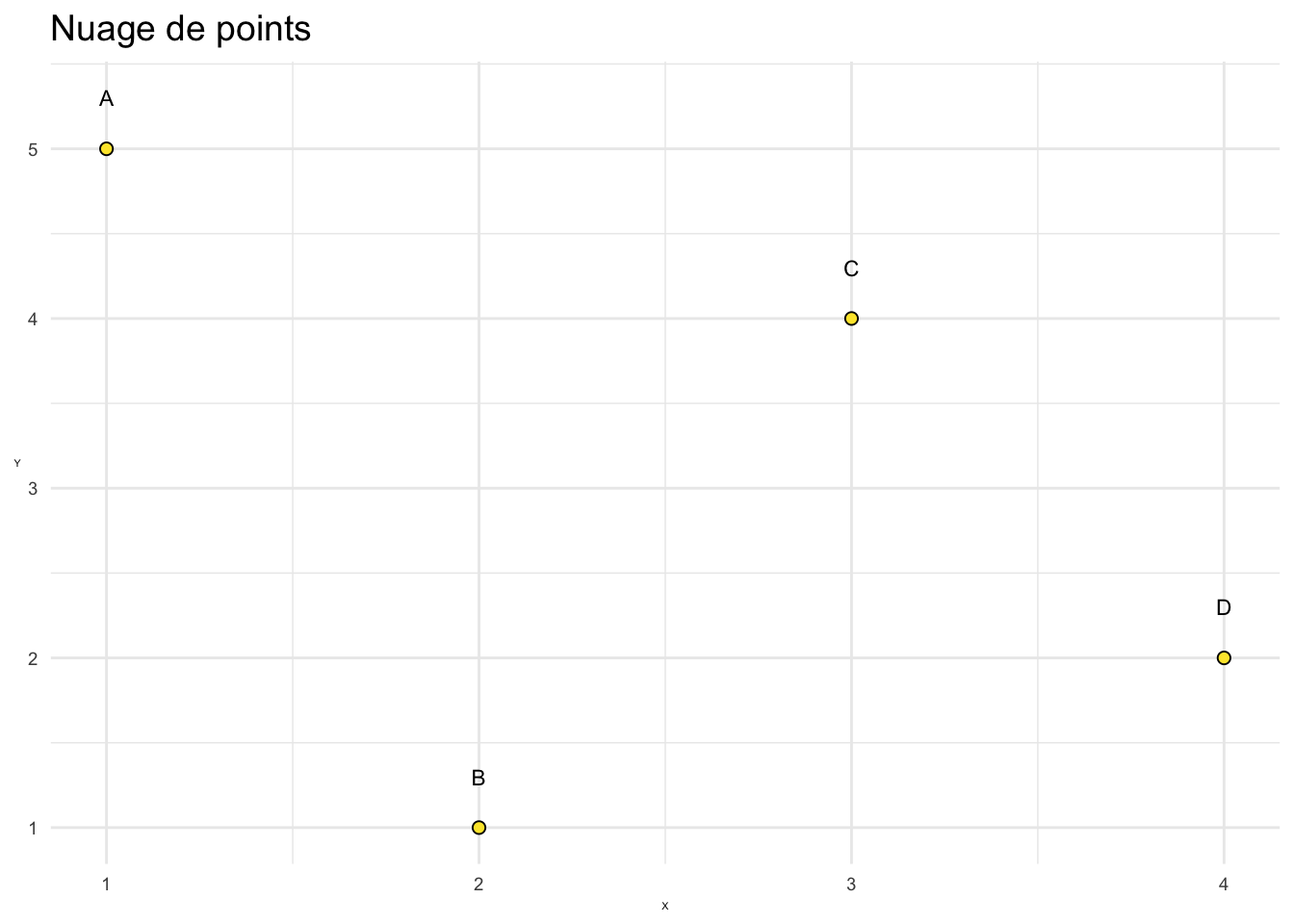
En supperposant les différentes contributions à la covariance, nous obtenons le graphique suivant :

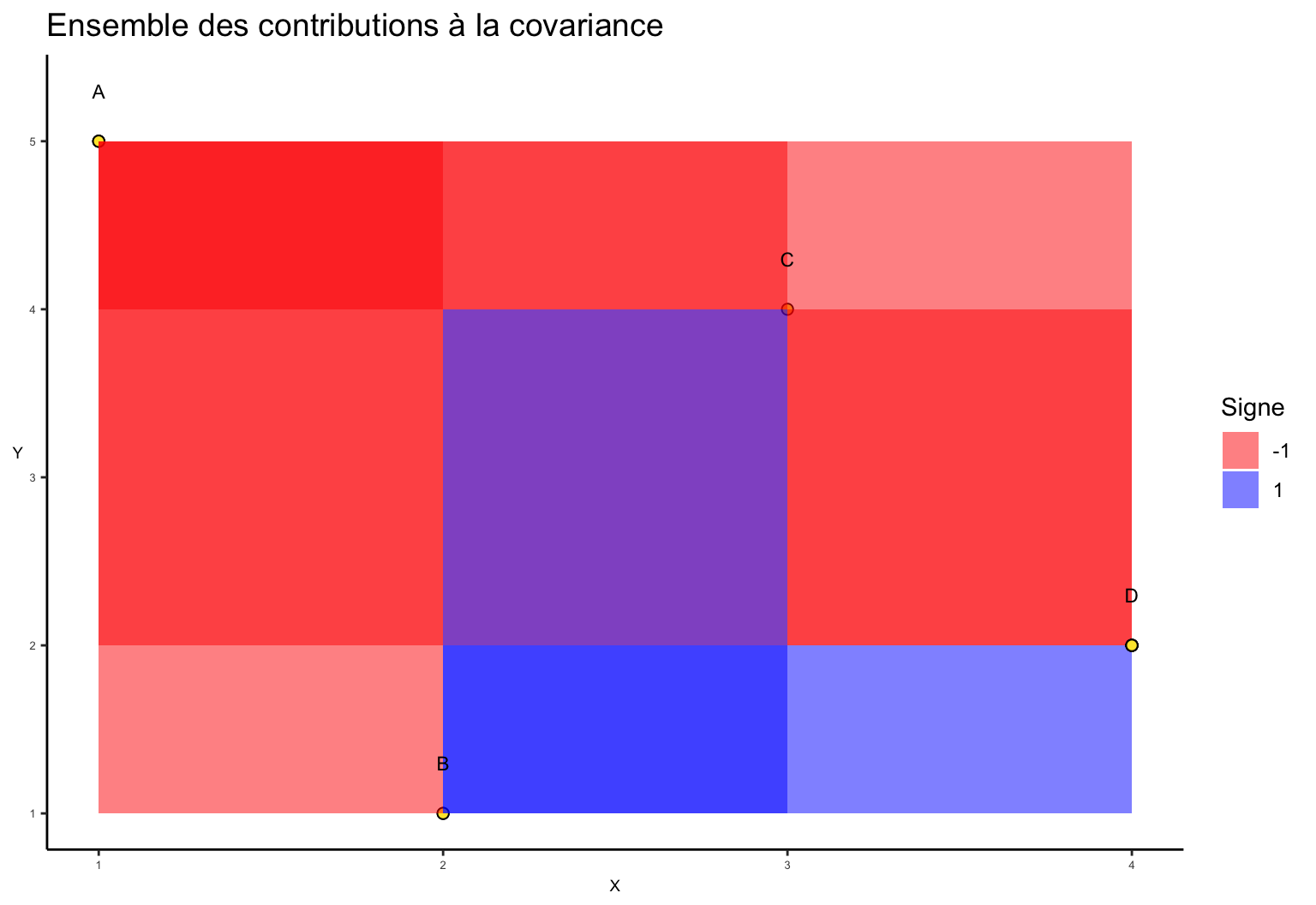
Enfin, en faisant la somme nette des différentes couches nous obtenons :

2.8 Extension

Le principe de construction graphique de la représentation de la covariance ayant été présenté, notre objectif est à présent d’utiliser ce schéma de construction pour des échantillons quelconques comportant un grand nombre de points.

Par ailleurs nous voulons présenter l’intérêt de cette représentation graphique en fonction du signe et de l’intensité de la corrélation entre les variables notamment.

Cas 1 : Tendance croissante

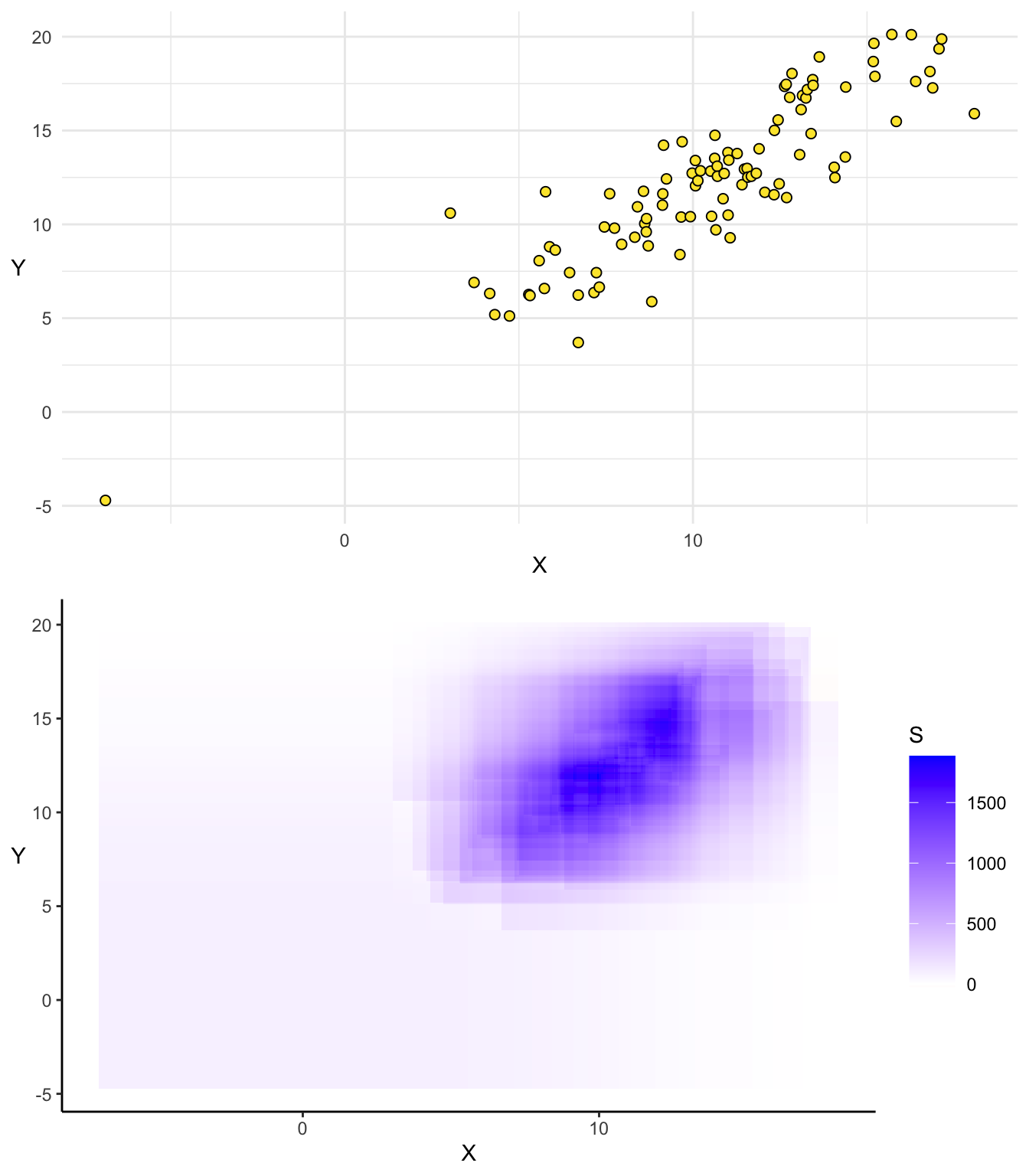
Cas 2 : Tendance décroissante

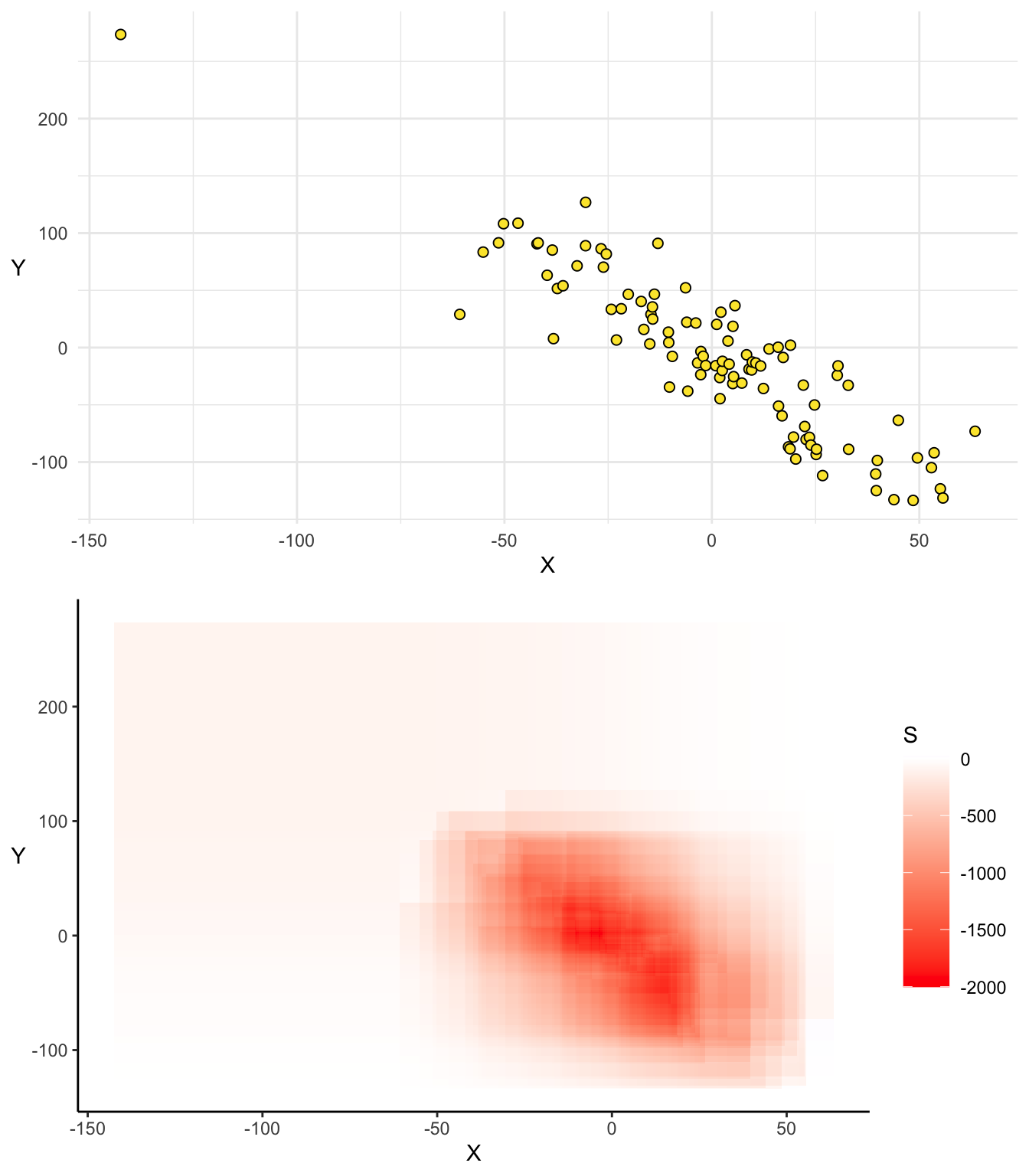
Dans les cas polaires dans lesquels la tendance du nuage du point est clairement identifiée, ce graphique permet une très bonne lisibilité de la relation entre les points en particulier et en général. Qu’en est-il lorsque les tendances du nuage de points sont multiples ?

Cas 3 : Tendance multiples

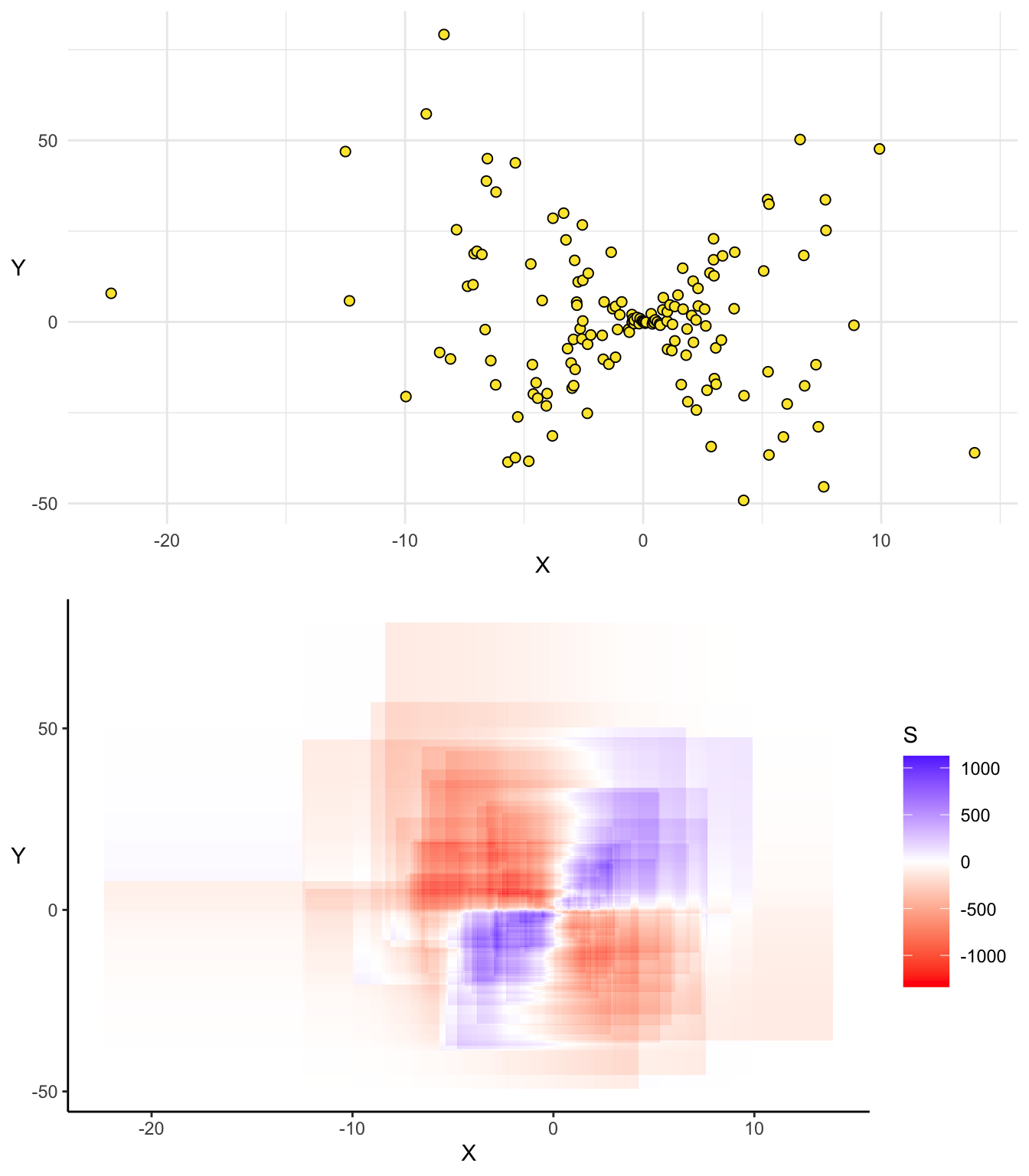
Dans le cas de tendances multiples ce type de représentation est encore plus intéressante. En effet, elle nous permet de déceler visualement le comportement du nuage de points et d’en détecter les éventuelles anomalies.

2.8.1 Alternatives

 

Nous pouvons, pour représenter la covariance, utiliser d’autres types de graphiques basés sur les mêmes principes mais mobilisant des techniques de représentation différentes (contours, 3D, etc…), tels que :

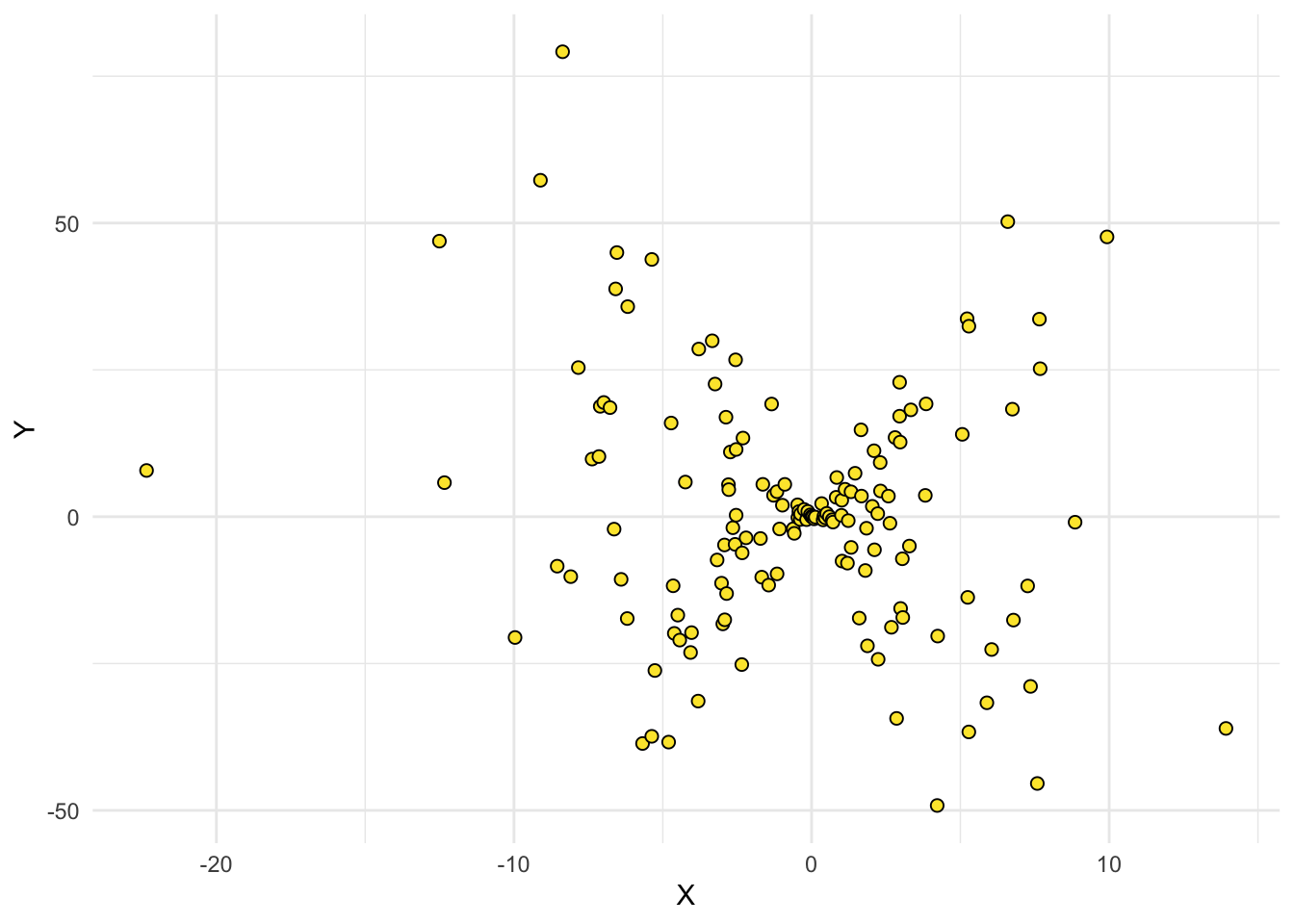
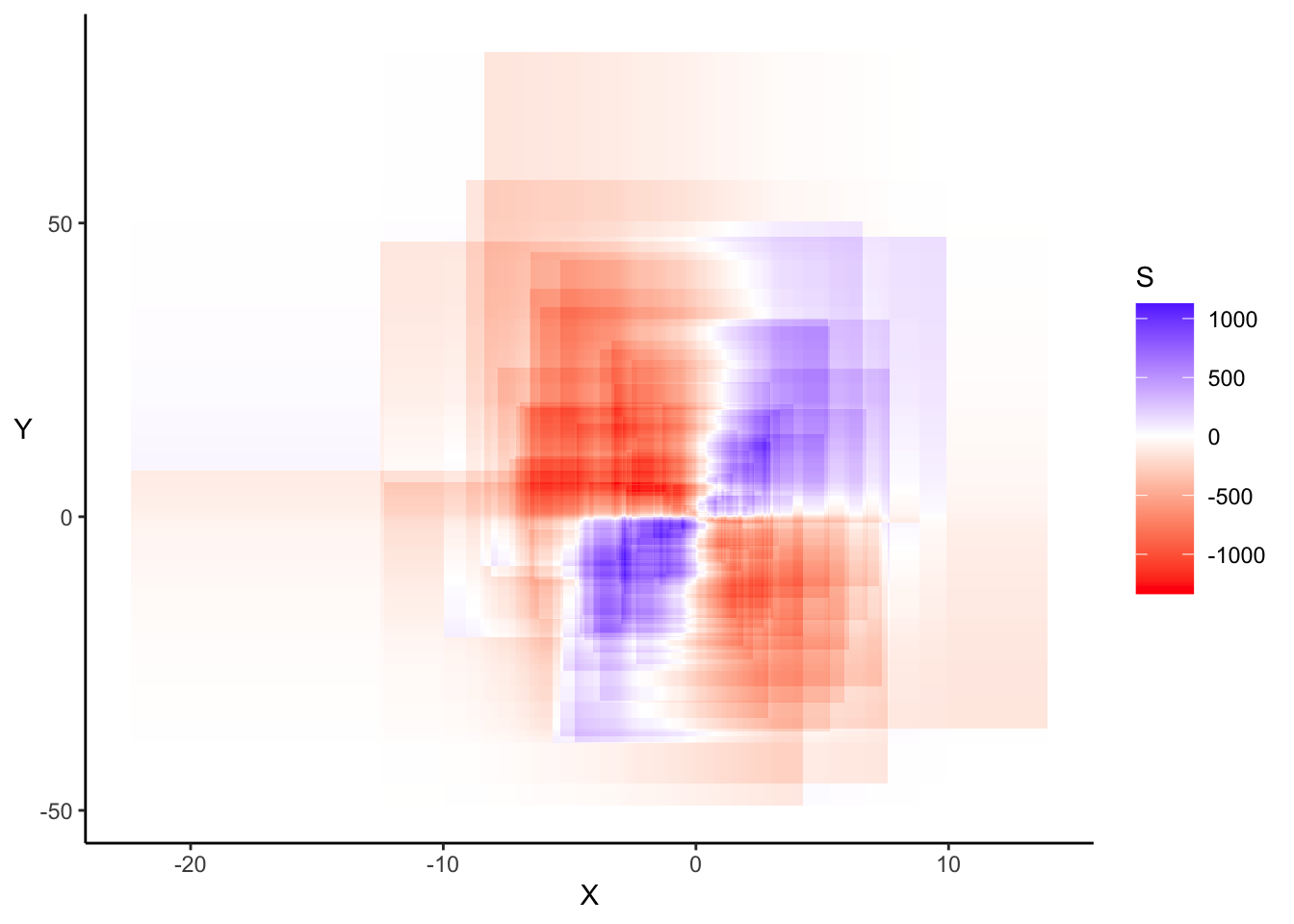
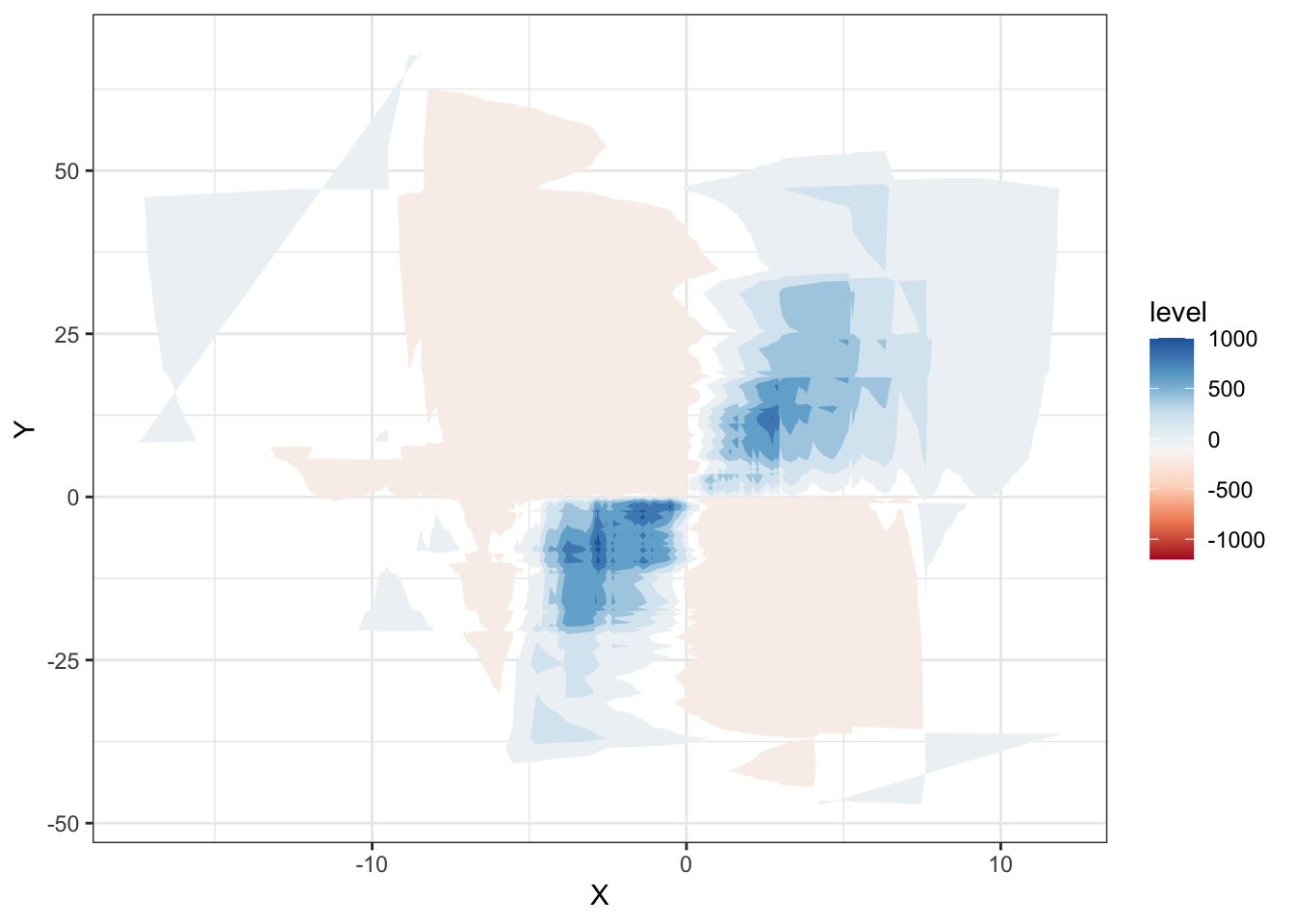
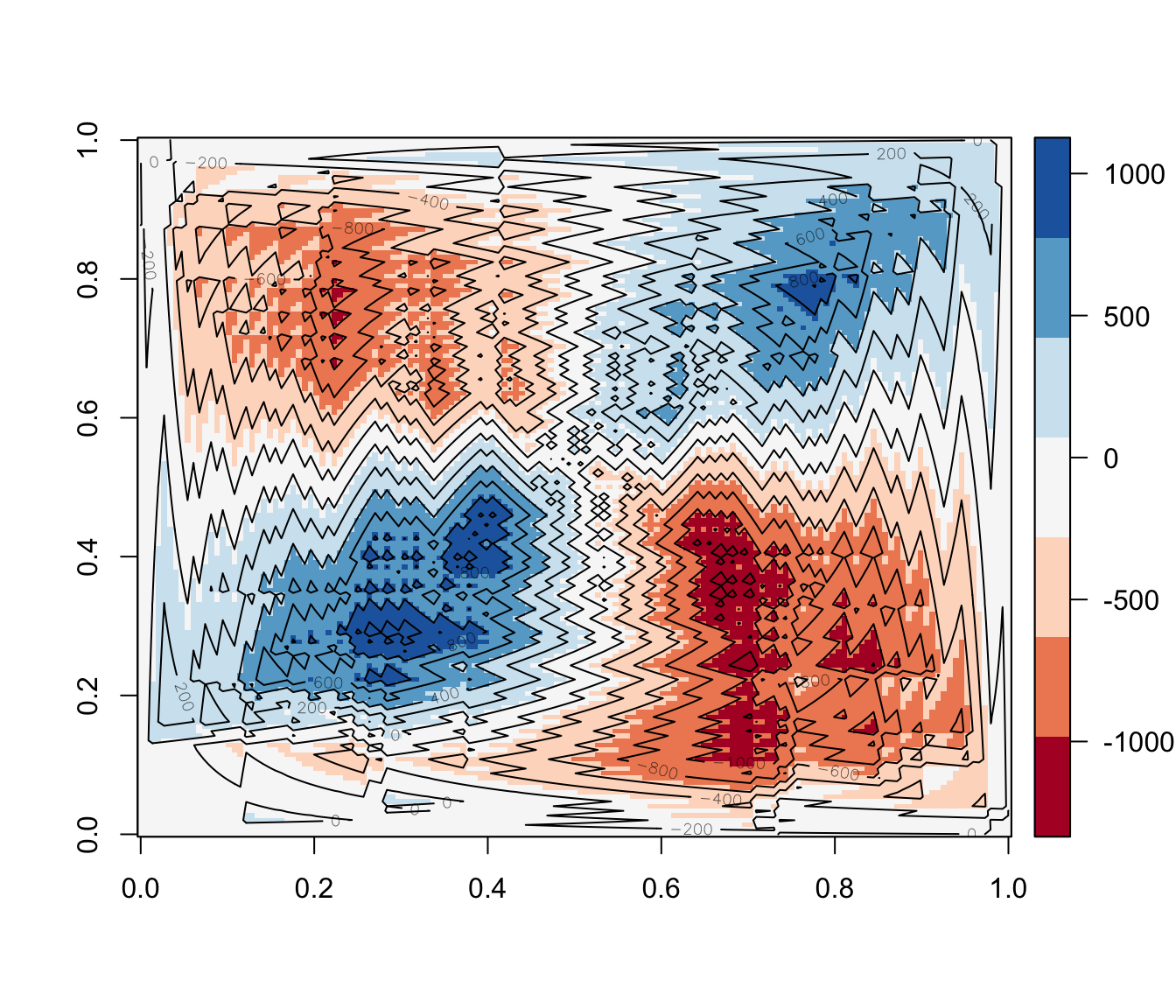
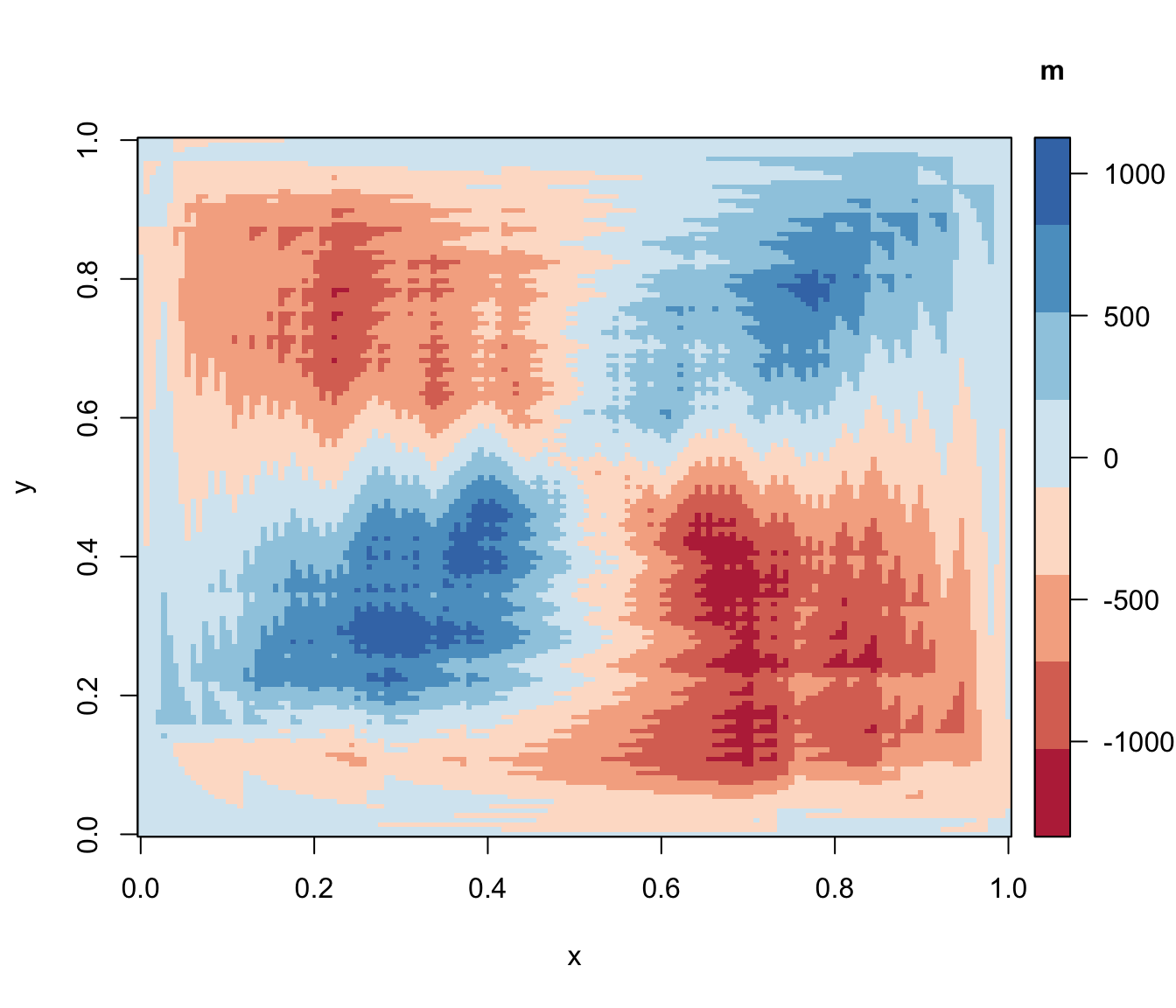
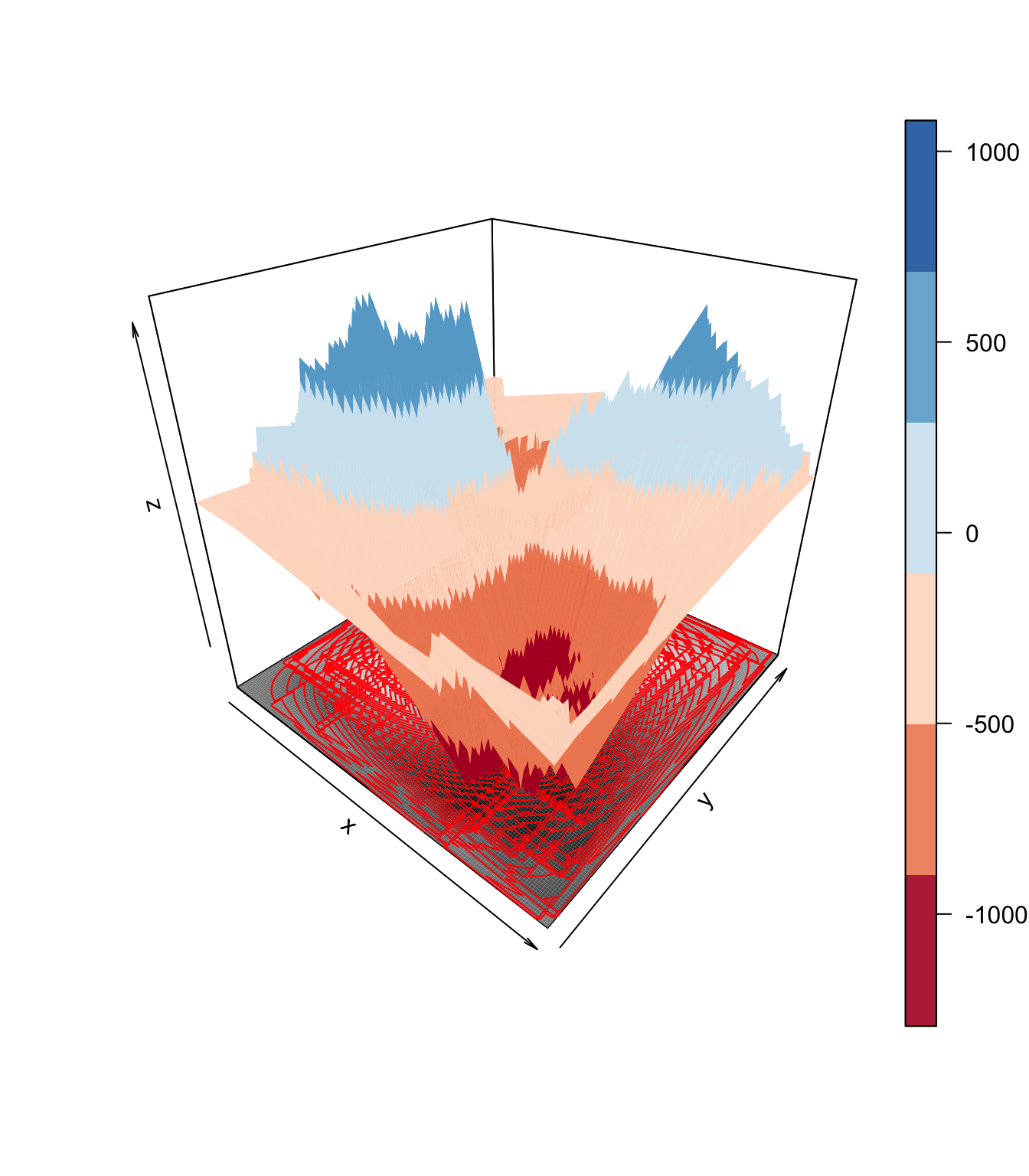
Les quelques exemples montrés ci-dessous nous ont permis de montrer les différentes déclinaisons de cette représentation de la covariance.

Nous avons rencontré de nombreuses difficultés techniques dans le développement de ces graphiques . En résumé, cette représentation consiste à compter le nombre net de couches de covariance former par toutes les paires de points dans un quadrillage précis du plan et d’attribuer une couleur à celui-ci. De ce fait, lorsque le nombre de points est élevé cela pose un problème matériel car le nombre de couches à représenter est trop élevé. Aussi, le choix des couleurs pour la représentation est une question délicate car la convention de couleur utilisée (bleue pour les covariances positive et rouge pour les négatives) ne permet pas une grande lisibilité lorsque le nombre de points est important car il est difficile de régler le contraste des couleurs sur R. Peut-être devrions nous choisir une palette de couleurs comme dans les graphiques précédents. Certaines alternatives comme la représentation en 3D ou l’utilisation des contours permettent de contourner certaines des difficultés évoquées mais ont l’inconvénient majeur d’être moins intuitives.