1 Unidad 1. Elementos de un programa informatico.

1.1 Resumen del contenido teórico.

PENDIENTE

1.2 Ejercicios prácticos.

En esta primera unidad los ejercicios se hacen con pseudocódigo. En la Unidad 2 ya cambiamos a Java.

1.2.1 Ejercicios-I. Algoritmos iniciales (pseudocódigo)

1.- Construir un algoritmo que tome como dato de entrada un número que corresponde a la longitud de un radio y nos calcula y escribe la longitud de la circunferencia, el área del círculo y el volumen de la esfera.

\(l=2*pi*r\)
\(a=pi*r2\)
\(v=4/3*pi*r3\)

Solución con pseudocódigo

“/pseudo_code_exercises/ud_1_ejercicio_1.psc”

Algoritmo calculos_radio
    
    Escribir "Ingrese la longitud del radio:"
    Leer A
    
    l <- 2*3.1416*A
    a <- 3.1416*A^2
    v <- (4/3)*3.1416*A^3
    
    Escribir "La longitud de la circunferencia es: ",l
    Escribir "El área de la circunferencia es: ",a
    Escribir "El volumen de la esfera es: ",v
    
FinAlgoritmo

Solución con R

calculos_radio <- function(r) {
  
  l = 2*pi*r
  a = pi*r**2
  v = (4/3)*pi*r**3
  
  print(c(l, a, v))
}

calculos_radio(3)

## [1]  18.84956  28.27433 113.09734

Solución con Python


import math

def calculos_radio(r):
  
  l = 2*math.pi*r
  a = math.pi*r**2
  v = (4/3)*math.pi*r**3
  
  print(l, a, v)


calculos_radio(3)

## 18.84955592153876 28.274333882308138 113.09733552923254

2.- Construir un algoritmo que leído un número por teclado nos diga si es positivo, negativo o nulo.

Solución con pseudocódigo

“/pseudo_code_exercises/ud_1_ejercicio_1.psc”

Algoritmo numero_signo
    Escribir "Introduzca un número entero:"
    Leer A
    Si A > 0 Entonces
        Escribir "El número introducido es positivo."
    SiNo
        Si A < 0 Entonces
            Escribir "El número introducido es negativo."
        SiNo
            Escribir "El número introducido es nulo."   
        Fin Si  
    Fin Si
    
FinAlgoritmo

Solución con R

numero_signo <- function(num) {
  
  if (num > 0) {
    
    print("El número introducido es positivo.")
    
  } else if (num < 0) {
    
    print("El número introducido es negativo.")
 
  } else {
    
    print("El número introducido es nulo.")
    
  } 
}

numero_signo(-2)

## [1] "El número introducido es negativo."

Solución con Python


def numero_signo(num):

    if num > 0:
    
      print("El numero introducido es positivo.")
      
    elif num == 0:
    
      print("El numero introducido es nulo.")
      
    else:
    
      print("El numero introducido es negativo.")

  
numero_signo(-8)

## El numero introducido es negativo.

3.- Construir un algoritmo para calcular y escribir la suma de los 100 primeros números naturales. Utilizar las estructuras PARA, MIENTRAS Y REPETIR.

Solución con pseudocódigo

Estructura “MIENTRAS”

“/pseudo_code_exercises/ud_1_ejercicio_3_1.psc”

Proceso Ejercicio_3_1
    n<-1
    suma<-0
    Mientras n<=100 Hacer
        suma<-suma+n
        n<-n+1
    Fin Mientras
    Escribir "Suma: ", suma
    
FinProceso

Estructura “PARA”

“/pseudo_code_exercises/ud_1_ejercicio_3_2.psc”

Proceso Ejercicio_3_2
    suma<-0
    Para n<-1 Hasta 100 Con Paso 1 Hacer
        suma<-suma+n
    Fin Para
    Escribir "Suma: ", suma
    
FinProceso

Estructura “REPETIR”

“/pseudo_code_exercises/ud_1_ejercicio_3_3.psc”

Proceso Ejercicio_3_3
    n<-1
    suma<-0
    Repetir
        suma<-suma+n
        n<-n+1
    Hasta Que n>100
    Escribir "Suma: ", suma
FinProceso

Solución con R

Solución con Python

4.- Construir un algoritmo para sumar independientemente los números pares y los impares comprendidos entre 1 y 100. Visualizar los resultados.

Solución con pseudocódigo

“/pseudo_code_exercises/ud_1_ejercicio_4.psc”

Proceso suma_pares_impares
    suma_par<-0
    suma_impar<-0
    Para i<-1 Hasta 100 Con Paso 1 Hacer
        Si i%2=0 Entonces
            suma_par<-suma_par+i
        SiNo
            suma_impar<-suma_impar+i
        FinSi
    FinPara
        
    Escribir "Suma par: ", suma_par
    Escribir "Suma impar: ", suma_impar
FinProceso

Solución con R

Solución con Python

5.- Construir un algoritmo que leídos tres números introducidos por teclado me visualice el mayor.

Solución con pseudocódigo

“/pseudo_code_exercises/ud_1_ejercicio_5.psc”

Proceso numero_mayor
    Definir n1,n2,n3 como entero
    Escribir "Introduce el primer número"
    Leer n1
    Escribir "Introduce el segundo número"
    Leer n2 
    Escribir "Introduce el tercer número"
    Leer n3
    // guardo en una variable el  primer número para comparar el resto
    // de números con él, de modo que si son mayores sustituyo su valor
    mayor<-n1
    Si n2>n1 Entonces
        mayor<-n2
    Fin Si
    Si n3>mayor Entonces
        mayor<-n3
    Fin Si
    Escribir "El mayor es: ",mayor
FinProceso

Solución con R

Solución con Python

6.- Construir un algoritmo para visualizar los N primeros múltiplos de 4, donde N es un número que se lee por teclado.

Solución con pseudocódigo

“/pseudo_code_exercises/ud_1_ejercicio_6.psc”

Proceso multiplos_de_4
    Escribir "¿Cuántos múltiplos de 4 quieres?"
    Leer n
    Para i<-1 Hasta n Con Paso 1 Hacer
        multiplo<-4*i
        Escribir multiplo
    FinPara
FinProceso

Solución con R

Solución con Python

7.- Construir un algoritmo para introducir una serie de números, que finaliza al leer el número 0. Una vez que ha finalizada la captura de números queremos saber cuantos había mayores, iguales y menores que 50.

Solución con pseudocódigo

“/pseudo_code_exercises/ud_1_ejercicio_7.psc”

Proceso comparacion_numero_50
    mayores<-0
    menores<-0
    iguales<-0
    Escribir "Introduce un número"
    Leer n
    Mientras n<>0 Hacer
        
        Si n>50 Entonces
            mayores<-mayores+1
        Sino
            Si n<50 Entonces
                menores<-menores+1
            Sino
                iguales<-iguales+1
                
            Fin Si
        Fin Si
        Escribir "Introduce un número"
        Leer n
    Fin Mientras
    Escribir "Mayores de 50: ",mayores
    Escribir "Menores de 50: ",menores
    Escribir "Iguales 50: ",iguales
FinProceso

Solución con R

Solución con Python

__8.- Escribir un algoritmo que lea una temperatura en grados Fahrenheit y escriba su equivalente en grados centígrados C=(F-32)*5/9__

Solución con pseudocódigo

“/pseudo_code_exercises/ud_1_ejercicio_8.psc”

Proceso convertidor_fahrenheit_centigrados
    Escribir "Introduce temperatura en ºF"
    Leer F
    C <- (F-32)*5/9
    Escribir "Son " C " ºC"
FinProceso

Solución con R

Solución con Python

9.- Hacer un algoritmo que calcule el sueldo neto semanal de un trabajador a partir de la lectura de las horas trabajadas y el precio por hora. Para el cálculo del sueldo neto hay que tener en cuenta los siguientes datos:

Las primeras 35 horas se pagan al precio dado (precio normal).
Las horas que pasen de 35 se pagan a 1,5 de la tarifa normal.
Las tasas de impuestos son:

o Los primeras 5000€ son libres de impuestos.
o Entre 5000€ u 10000€ tienen un impuesto del 5%.
o Lo que sobrepase de 10000€ tiene un impuesto del 15%.

Solución con pseudocódigo

En este caso he incluido dos soluciones con pseudocódigo. La primera con el sufijo "_SBN“, que indica que es la solución a la que yo llegué. Y una segunda, con el sufijo”_CORRECCION", que es la solución que nos dio el profesor.

“/pseudo_code_exercises/ud_1_ejercicio_9_SBN.psc”

Proceso salario_semanal
    Escribir "¿Cuántas horas trabajó el empleado durante la semana?"
    Leer horas_trabajadas
    Escribir "¿Cuál es el precio por hora trabajada?"
    Leer precio_hora
    Si horas_trabajadas<35 Entonces
        sueldo_bruto<-horas_trabajadas*precio_hora
    SiNo
        sueldo_bruto<-35*precio_hora + (horas_trabajadas-35)*precio_hora*1.5
    Fin Si
    Si sueldo_bruto<=5000 Entonces
        Escribir "Salario semanal: ", sueldo_bruto
    SiNo
        Si sueldo_bruto>5000 Y sueldo_bruto<=10000 Entonces
            salario<-5000+0.95*(sueldo_bruto-5000)
            Escribir "Salario semanal: ", salario
        SiNo 
            salario<-5000+0.95*(5000)+0.85*(sueldo_bruto-10000)
            Escribir "Salario semanal: ", salario
        FinSi
    FinSi
FinProceso

“/pseudo_code_exercises/ud_1_ejercicio_9_CORRECCION.psc”

Proceso Ejercicio_9
    Escribir "Introduce horas trabajadas esta semana"
    Leer horas
    Escribir "Introduce el precio por hora"
    Leer precioHora
    Si horas<35 Entonces
        horasNormales<-horas
        horasExtras<-0
    SiNo
        horasNormales<-35
        horasExtras<-horas-35
    Fin Si
    bruto<-horasNormales*precioHora+horasExtras*(precioHora*1.5)
    Si bruto<=5000 Entonces
        tasas<-0
    SiNo
        Si bruto>5000 Y bruto<=10000 Entonces
            tasas<-(bruto-5000)*5/100
        SiNo 
            //sueldo bruto semanal de más de 10000
            tasas<-((10000-5000)*5/100)+((bruto-10000)*15/100)
        Fin Si
    Fin Si
    neto<-bruto-tasas
    Escribir "Salario semanal bruto: ", bruto
    Escribir "Tasas: ", tasas
    Escribir "Salario semanal neto: ", neto
FinProceso

Solución con R

Solución con Python

10.- Diseñar el algoritmo de un programa que lee un número entero positivo y determina el número de dígitos necesarios para la representación de ese valor.

Solución con pseudocódigo

“/pseudo_code_exercises/ud_1_ejercicio_10.psc”

Proceso digitos_numero
    Escribir "Introduce un número entero"
    Leer n
    c<-0
    Mientras n>=1 Hacer
        n<-n/10
        c<-c+1
    Fin Mientras
    Escribir "Son necesaros " c " dígitos."
FinProceso

Solución con R

Solución con Python

1.2.2 Ejercicios-II. Algoritmos - Pseudocódigo

11.- Imaginemos que queremos desarrollar un algoritmo tal que al escribir un día de la semana aparezca por pantalla la actividad extraescolar a la que debe acudir nuestro hijo. Por ejemplo, si ejecutamos el programa y escribimos martes que aparezca “natación”.

Las actividades que se realizan por días son: lunes: psicomotricidad jueves: natación martes: natación viernes: descanso miércoles: música

Los días sábado y domingo no se realizan actividades con lo que si el usuario escribe por error alguno de estos días de la semana se debe mostrar el mensaje: “Día sin actividades”. Si por equivocación, además se escribe un día inexistente se debe mostrar en pantalla “Día erróneo”. Tener en cuenta las mayúsculas, minúsculas y tildes. No es lo mismo lunes que Lunes, ni miércoles que miercoles. Esto es así porque el carácter ‘l’ es distinto del carácter ‘L’ en el código ASCII que es el que se usa para representarlos.

Solución con pseudocódigo

Solución con R

Solución con Python

12.- Para realizar la traza se ha de hacer un seguimiento de los valores que toman las variables simulando manualmente la ejecución del algoritmo, es decir, siguiendo el flujo de ejecución del mismo. Haz la traza del siguiente programa e indica qué valores toman las variables y qué escribe, suponiendo que a “a” se le da el valor 5. Continúa rellenando la tabla.

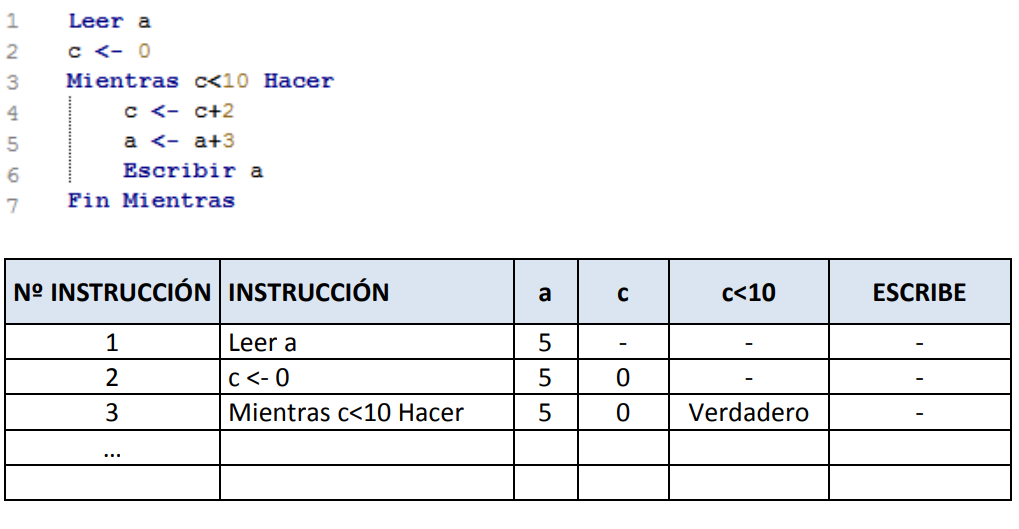
include_graphics("./imgs/ud_1_exercise_11_img.png")

Solución con pseudocódigo

Solución con R

Solución con Python

13.- Realiza un algoritmo que nos indique si un año determinado es bisiesto, debemos pedir al usuario el año. Un año es bisiesto si es múltiplo de 4, a excepción de los que siendo múltiplos de 4 también son múltiplos de 100 pero no de 400.

Solución con pseudocódigo

Solución con R

Solución con Python

14.- Realiza un algoritmo que pida al usuario una hora en elementos separados (hora 0-23, minutos 0-59 y segundos 0-59). A continuación se debe mostrar por pantalla qué hora será pasado un minuto.

Solución con pseudocódigo

Solución con R

Solución con Python

15.- Realiza la traza de seguimiento del ejercicio anterior. Usa valores extremos, por ejemplo 23 horas 59 minutos 10 segundos, o 0 horas 3 minutos y 59 segundos o las 5 horas 59 minutos 24 segundos.

Solución con pseudocódigo

Solución con R

Solución con Python

16.- Realiza un algoritmo que dé solución al cálculo del factorial de un número entero. n! = n x (n-1) x (n-2) x … x 1 Realiza una versión con un bucle PARA y otra con un bucle MIENTRAS.

Solución con pseudocódigo

Solución con R

Solución con Python

17.- Realiza un algoritmo que dé solución al problema de calcular la multiplicación de dos números mediante el uso de sumas sucesivas.

Solución con pseudocódigo

Solución con R

Solución con Python

18.- Realiza un algoritmo que pida dos números X e Y de forma que se pretende calcular \(X^Y\) suponiendo que no existe el operador de potencia. X puede ser cualquier número entero distinto de 0. Y puede ser cualquier entero positivo, negativo o nulo.

(Recuerda que \(X^0 =1, X-Y=1/X^Y\))

Solución con pseudocódigo

Solución con R

Solución con Python

19.- Algoritmo que lea un valor entero que represente la posición ordinal de un mes (1,2,…12) y nos diga cuantos días tiene ese mes, o un mensaje de error si el valor del mes es incorrecto. Para febrero se indicará 28 o 29 días.

Solución con pseudocódigo

Solución con R

Solución con Python

20.- Diseñar un algoritmo para jugar a la adivinanza de números. El ordenador generará un número al azar, entre 0 y 15, y el usuario tendrá que adivinar cuál es. Se dispondrá de todas las oportunidades que quiera y el programa tendrá que ir diciendo si se ha pasado o se quedó corto en cada intento. Finalmente cuando consiga acertarlo se deberá mostrar un mensaje de felicitación y el número de intentos que necesitó. Para generar el número al azar supondremos una función AZAR(x) que genera un número aleatorio entre 0 y x-1.

Como al menos se deberá de repetir una vez el intento de acierto, es más adecuado una estructura REPETIR ..HASTA/MIENTRAS. En cada repetición se pide al usuario el número y se compara con el que hay que acertar, incrementando el número de intentos. Con una estructura SI se comprueba si se pasó, se quedó corto o lo acertó. La condición de salida de REPETIR será que se haya acertado.

Solución con pseudocódigo

Solución con R

Solución con Python

1.2.3 Ejercicios-III. Programación modular.

21.- Dados dos valores numéricos reales almacenados en dos variables de nombre a y b, hacer un programa que llame a una función de nombre Cambiar(v1, v2) a la que se le pasan como parámetros dichas variables e intercambia sus valores, mostrando el resultado.

Solución con pseudocódigo

Solución con R

Solución con Python

22.- Escribe un programa con diseño modular que recoja por teclado dos números reales y presente una serie de opciones correspondientes a operaciones aritméticas a realizar con las mismas:

Sumar
Restar
Multiplicar
Dividir En función de la operación elegida, se llama a la función correspondiente que retorna el valor del resultado de dicha operación, que se muestra en el programa principal.

Solución con pseudocódigo

Solución con R

Solución con Python

23.- Escribir un programa que utilice una función recursiva para calcular y retornar la potencia de un número real distinto de cero, siendo su exponente entero y positivo.

Xn = X * X n-1 X0 = 1

Solución con pseudocódigo

Solución con R

Solución con Python

24.- Realizar un programa que disponga de una función llamada esBisiesto que reciba un año y devuelva cierto si es bisiesto y falso si no lo es. Realizado en el Ejercicio 13: Los años que sean divisibles por 4 serán bisiestos; aunque no serán bisiestos si son divisibles entre 100 (como los años 1700, 1800, 1900, 2100) a no ser que sean divisibles por 400 (como los años 1600, 2000, 2400).

Solución con pseudocódigo

Solución con R

Solución con Python

25.- Construir un algoritmo que calcule el número “e”, la base de los logaritmos neperianos, calcular a partir de la siguiente aproximación: e= 1 + 1/1! + 1/2! +1/3! + …… + 1/N! siendo N un número entero positivo mayor que 10 que se pedirá por teclado. Utilizar una función para calcular los factoriales correspondientes a los denominadores de los términos.

Solución con pseudocódigo

Solución con R

Solución con Python