C Real Data Analysis
We applied the SpaceX method on two spatial transcriptomics datasets which are obtained from the preoptic region of the mouse hypothalamus (Moffitt et al. 2018) and the human breast cancer dataset (Ståhl et al. 2016). Here we provide details of preprocessing and exploratory analysis of both datasets in section C.1. We illustrate the detailed application of the community detection algorithm on those two datasets in section C.2.
C.1 Exploratory analysis of the datasets
C.1.1 Merfish Data
The MERFISH dataset is obtained from the preoptic area of the mouse hypothalamus (Moffitt et al. 2018). The dataset consists of \(160\) genes and corresponding gene expressions are measured in \(4975\) spatial locations. There are \(7\) pre-determined spatial clusters in the dataset named Astrocyte, Endothelial, Ependymal, Excitatory, Inhibitory, Immature, Mature, and the corresponding sizes are \(724\), \(503\), \(314\), \(1024\), \(1694\), \(168\), \(385\) respectively. The dataset consists of \(2\) more clusters named Microglia, Pericytes with cluster sizes \(90\), \(73\) respectively which are less than \(100\). Those two clusters are removed from the dataset. After removing those two clusters, we have gene expressions from \(4812\) locations corresponding to \(160\) genes. There are no genes with more than \(95\%\) zeros reads. The left panel of Figure C.1 shows the violin plot of the percentage of zero reads among the genes for each cluster in the MERFISH dataset. The Umap representation of the Merfish data has been provided on the right panel of Figure C.1.
Figure C.1: Left panel shows the violin plot of percentage of zero reads among the genes for each cluster w.r.t. Merfish data and the right panel shows the Umap.
C.1.2 Breast Cancer Data
The human breast cancer dataset contains expression levels from \(5262\) genes measured at \(250\) locations (Ståhl et al. 2016). We use the SPARK method with \(5\%\) FDR cut-off on p-values to detect \(290\) spatially expressed genes to carry forward our analysis. The violin plot of the percentage of zero reads among the genes for each spatially contiguous cluster in the Breast cancer dataset is shown in the left panel of Figure C.2. On the right panel of Figure C.2, we have provided the Umap.
Figure C.2: On the left panel, we have violin plot of percentage of zero reads among the genes for each cluster w.r.t. Breast Cancer data and the Umap is shown on the right panel.
C.2 Community detection
The community detection is a downstream analysis of the shared and cluster-specific networks which are obtained from the SpaceX method. The communities are detected by optimizing modularity over partitions in a network structure (Brandes et al. 2007). Figure C.3 and C.4 show the detected community modules from shared and cluster-specific co-expression networks for MERFISH and breast cancer data respectively.
Figure C.3: Shared and cell-type specific community detection for Merfish data
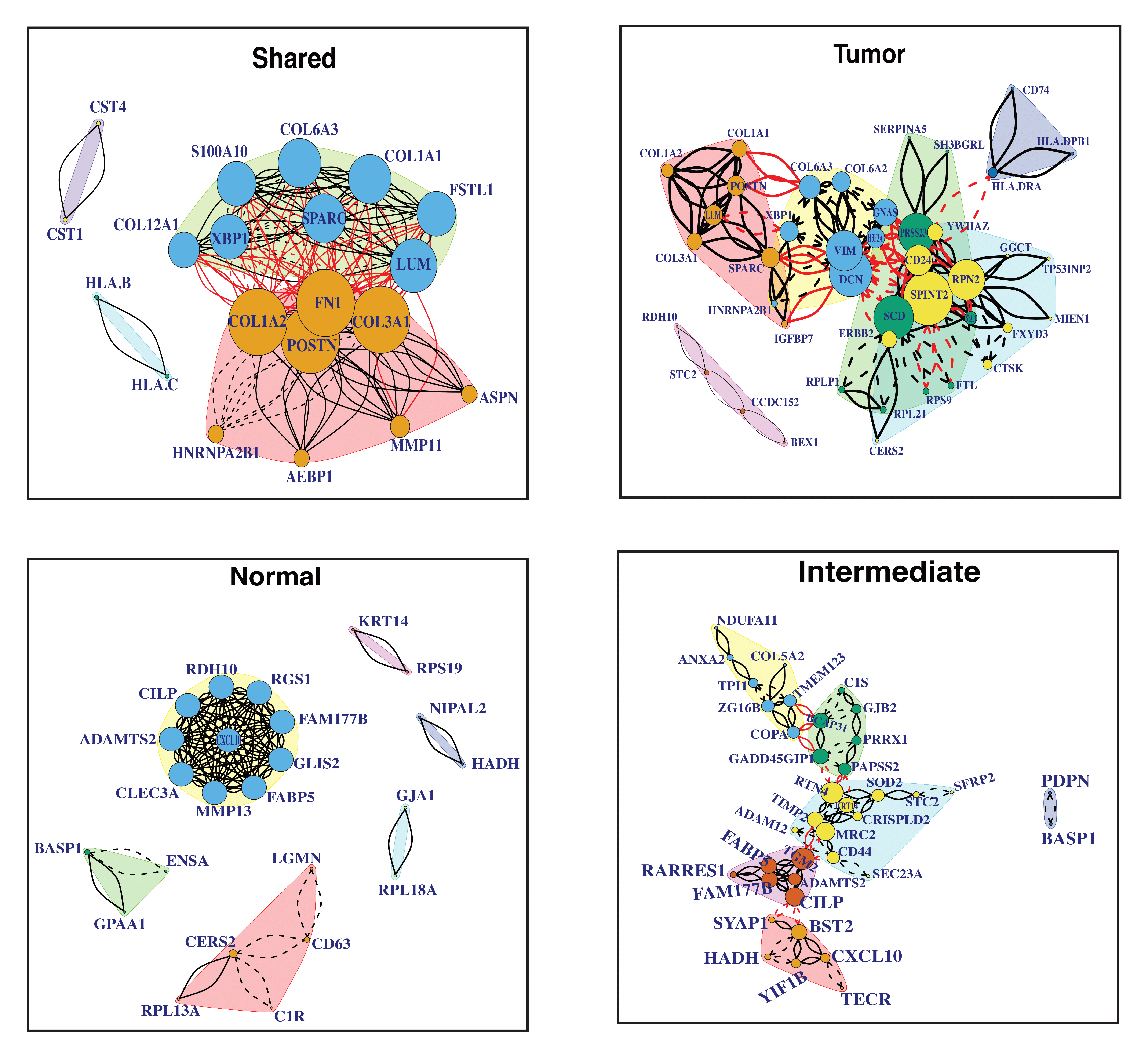
Figure C.4: Shared and cell-type specific community detection for Breast cancer data
C.3 Benchmarking on real spatial transcriptomics data
In this section, we benchmark our models on two real spatial transcriptomics datasets based on model fitting criteria. To this end, we use information-based criteria – a standard and well-established technique to compare the model fits between hierarchical Bayesian models (Gelman, Hwang, and Vehtari 2014). In this case, we use two information criteria-based metrics to assess our model fitting: (i) Bayesian analogue of AIC (Akaike 1998), defined as the Bayesian information criteria (BIC, Watanabe (2013)); and (ii) Watanabe-Akaike information criterion (WAIC) (Watanabe 2010), an improvement on the AIC and a fully Bayesian approach to measure model accuracy computed with log pointwise posterior predictive density and then adding a correction for the effective number of parameters to adjust for over-fitting. These criterion based methods are often used for model selection and specifically for spatial datasets (Banerjee, Wall, and Carlin 2003; Banerjee, Gelfand, and Polasek 2000; Lee and Ghosh 2009). In both cases, lower (relative) values indicate better model fits.
Table C.1 shows the BIC and WAIC values for the SpaceX and non-spatial Poisson model for both the mouse hypothalamus and breast cancer data. Based on the criteria based values from the Table C.1, we can conclude that the SpaceX model is a better fit to both spatial transcriptomics datasets than the non-spatial Poisson model. For example, there is 64.7% and 46.6% of relative gain in accuracy of model fitting of the SpaceX model and non-spatial model w.r.t. BIC and WAIC respectively in case of Merfish data. A similar inference can be drawn for the breast cancer data where the relative gains are 66.4% and 45.5% for BIC and WAIC respectively in case of model fitting.
| BIC (Merfish) | WAIC (Merfish) | BIC (Breast cancer) | WAIC (Breast cancer) | |
| SpaceX Model | 13520 | 43783 | 24346 | 54179 |
| Non-spatial Poisson model | 38274 | 82045 | 72523 | 99474 |
C.4 List of hub genes and edges
A detailed list of hub genes and top edges for both the datasets can be found at https://github.com/SatwikAch/SpaceX.
C.5 Corroboration with TCGA Breast Cancer Data
To corroborate some of our findings, we consider the TCGA-based gene expression from 67 breast cancer tissues and 20,000 genes using parallel high-throughput sequencing (Wirth et al. 2011; Weinstein et al. 2013). To make a fair “apples-to-apples” comparison, we used the same intersecting gene set from the spatial transcriptomics based breast cancer data used in our paper . We used a network-based algorithm: personalized cancer-specific integrated network estimation (PRECISE, Ha et al. (2018)) to obtain gene networks. PRECISE is Bayesian method for gene-network reconstruction for bulk-sequencing data that uses a regression-based approach. The PRECISE method detected \(77\) hub genes out of total \(290\) genes compared to the SpaceX method, which detected \(59\) hub genes – with \(19\) intersecting hub genes using both methods. The list of all the hub genes detected from each method and intersection hub genes from both method can be found at the webiste mentioned below under the name BC_Hub_genes_TCGA.csv (https://github.com/SatwikAch/SpaceX/tree/main/Hub%20genes).
Interestingly, multiple collagens genes (COL16A1, COL6A2, COL5A1) are detected as hub genes by both methods. Collagen biosynthesis can be regulated by cancer cells through mutated genes, transcription factors and signaling pathways (Xu et al. 2019). Understanding of the structural properties and functions of collagen in cancer will lead to anticancer therapy. The LUM gene is associated with collagen genes and effectively regulates estrogen receptors and function properties of breast cancer cells (Karamanou et al. 2017). Upregulation in FN1 gene indicates development various types of tumors (Y. Sun et al. 2020). XBP1 can induce cell invasion and metastasis in breast cancer cells by promoting high expression (S. Chen et al. 2020). VIM gene is used as a biomarker for the early detection of cancer (Mohebi et al. 2020).
C.6 Application of SpaceX method on Spatial Transcriptomics data from Alzheimer’s Disease
W. T. Chen et al. (2020) (C2020, henceforth) used spatial transcriptomics techniques to measure spatial gene expression from small tissue domains related to Alzheimer’s disease to characterize the molecular changes and cellular interactions. The study collected gene expression data from a total of \(9,957\) spots that were annotated into \(14\) brain regions in the original study (as shown in Figure 1B of C2020). The tissue domains and their contained number of spots are provided in Table C.2.| RSP | PTL | SSp | AUD | TEP | ENTI | OLF |
| 262 | 585 | 532 | 860 | 150 | 112 | 749 |
| CNU | CTXsp | FB | TH | HY | HPs | HPd |
| 136 | 709 | 1155 | 2114 | 1097 | 437 | 1059 |
For the network analyses and corresponding biological interpretations C2020 focused on \(57\) plaque-induced genes (PIGs) which are highly responsive towards \(\beta\)-amyloid (A\(\beta\)) plaques deposition as highlighted in the several studies (Krasemann et al. 2017; Sala Frigerio et al. 2019). PIGs are gradually co-expressed with increase in A\(\beta\) load and responsible for endosomes and lysosomes, oxidation-reduction, and inflammation. We obtained the data from their data repository mentioned in the data and code availability Section of C2020. The authors of C2020 used a WGCNA based analysis to discover gene modules consisting of genes with similar co-expression patterns and focused on PIGs which were most responsive to A\(\beta\) as shown in Figure S3B of their paper.
For confirmatory analyses, we analogously apply our SpaceX model to same \(57\) PIGs assessed on the \(9957\) spots divided into \(14\) tissue domains following C2020. SpaceX detects multiple hub genes across tissue domains and their intersections as shown in Figure C.5. In total, we found \(40\) hub genes across the 14 tissue domains among which five (marked in red in Figure C.5) intersect with those found by C2020 who listed 10 top hub genes: Ctsd, C4b, Cst3, Apoe, C4a, Gfap, Tyrobp, Lyz2, Trem2, and B2m (Figure 3D in C2020). Out of these 10 top hub genes, we are able to identify 5 genes: B2m, Lyz2, Ctsd, Trem2, Tyrobp based on a correlation level cut-off \(0.5\). C2020 can only detect them as overall hub genes but our analysis goes a step further to detect hub genes for specific tissue domains and their intersections. The common 5 genes are identified as hub genes across multiple tissue domains e.g. B2m is for HPs; Lyz2 is for PTL, SSp, CTXsp, AUD, FB, HY, TH; Ctsd is for PTL, HPs, HPd, SSp, CTXsp, AUD, FB, HY, TH etc.
We do not detect rest of top 5 hub genes (C4b, C4a, Cst3, Apoe, Gfap) because of the low-correlation levels (\(\le\) \(0.25\)) in the dataset provided. Figure C.6 shows the boxplot of marginal correlations between top 10 hub genes (as detected by C2020) with other genes across all the clusters. In Figure C.6, last 5 genes are not identified as hub genes by the SpaceX method because low level of correlation which can clearly observed by the corresponding boxplots which have spread around \(0\). Furthermore, the differences can be be attributed to different analytical methods since C2020 employed a WGCNA-based network method to detect their hub genes, which to best of our understanding, does not incorporate spatial domain information in their models. In contrast, our SpaceX method uses a factor-model based network reconstruction that effectively leverages the spatial information to construct co-expression networks which as we have shown through simulations has higher power and better signal detection (see Section 3 of the paper). This engenders identification of hub genes across multiple tissue domains such as C1qb, C1qc, Fcrls, Hexb, Mpeg1 which is shared across all \(14\) domains – which is not detected by C2020. We provide further discussion about these hub genes and related functionalities and the shared and tissue specific networks are shown in Figure C.7.
Tyrobp is a top hub gene which is detected across all the tissue domains as shown in Figure C.5 and encodes transmembrane signaling polypeptide which is connected to immune cell responses across multiple tissue domains (Humphrey et al. 2004). Different variants of another hub gene Trem2 (identified as a conserved hub gene across the following tissue domains: RSP, PLT, SSp, AUD, OLF, CTXsp, FB, TH, HY, HPs, HPd as shown in Figure C.5) associated with Alzheimer’s disease induce partial loss of memory and alter the behaviour of microglial cells, including their response to amyloid plaques (Carmona et al. 2018). Ctsd’s function is the processing proteins linked to Alzheimer’s disease, as well as in autophagy (Di Domenico, Tramutola, and Perluigi 2016). Lysozyme 2 (Lyz2) is a microglia gene which is associated with A\(\beta\) plaque phagocytosis (Grubman et al. 2021). B2m regulates age-related cognitive dysfunction and impaired neurogenesis (Smith et al. 2015). These interpretations align with the findings of C2020. Additionally, we have detected C1qb, C1qc, Fcrls, Hexb, Mpeg1 as hub genes across multiple tissue domains as shown in Figure @ref(fig:PIG_upset_plot). C1q genes (C1qb, C1qc) are a classical pathway which is multifunctional protein known to be expressed in brain of AD tissue (Fonseca et al. 2004). Infected mouse brains exhibits downregulation of the Fc receptor-like S, scavenger receptor (Fcrls) gene (Tanaka et al. 2013).
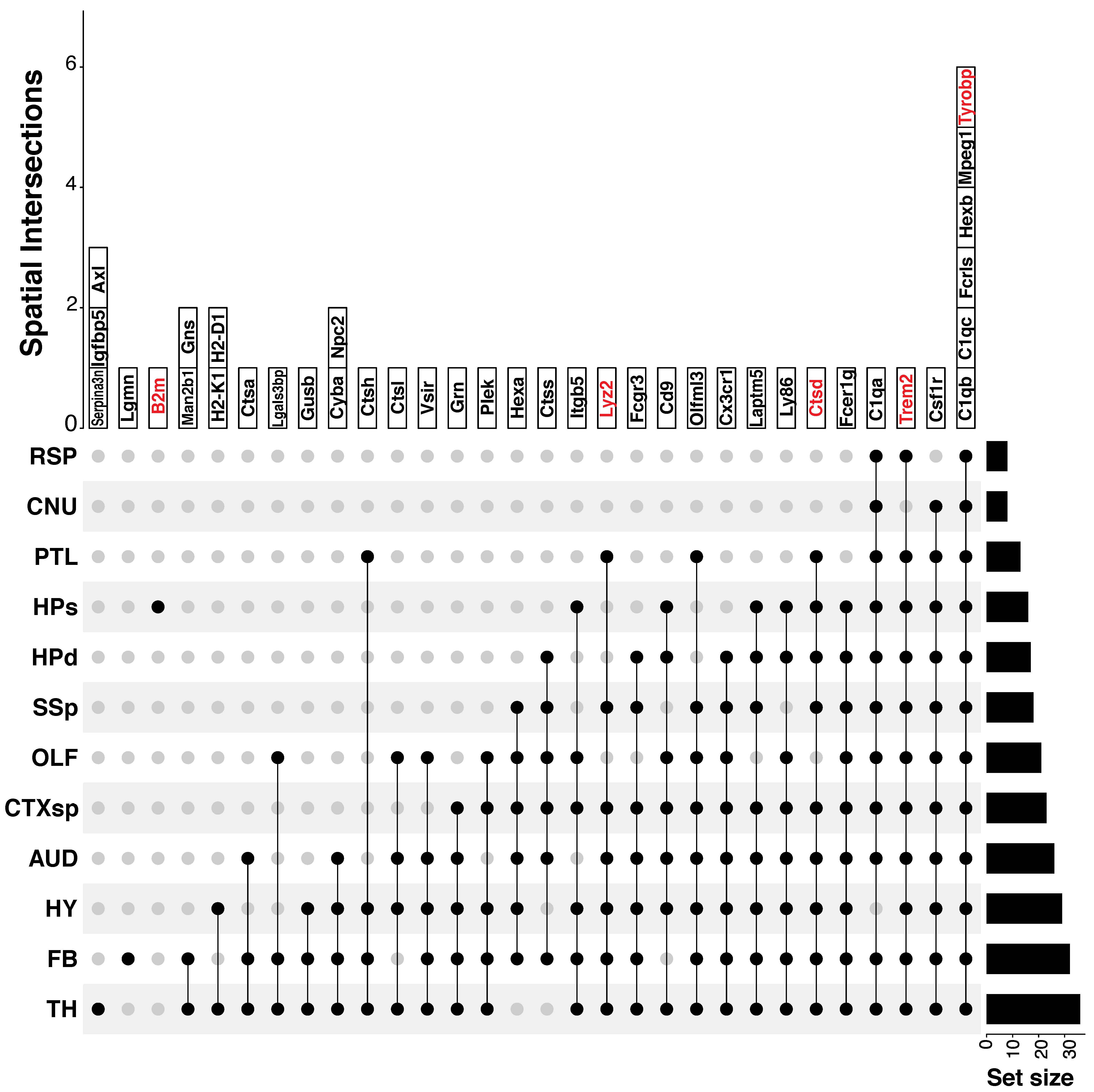
Figure C.5: The upset plot shows hub genes for each tissue domain and different spatial intersections. The red colored hub genes are also detected as top hub genes in W. T. Chen et al. (2020).
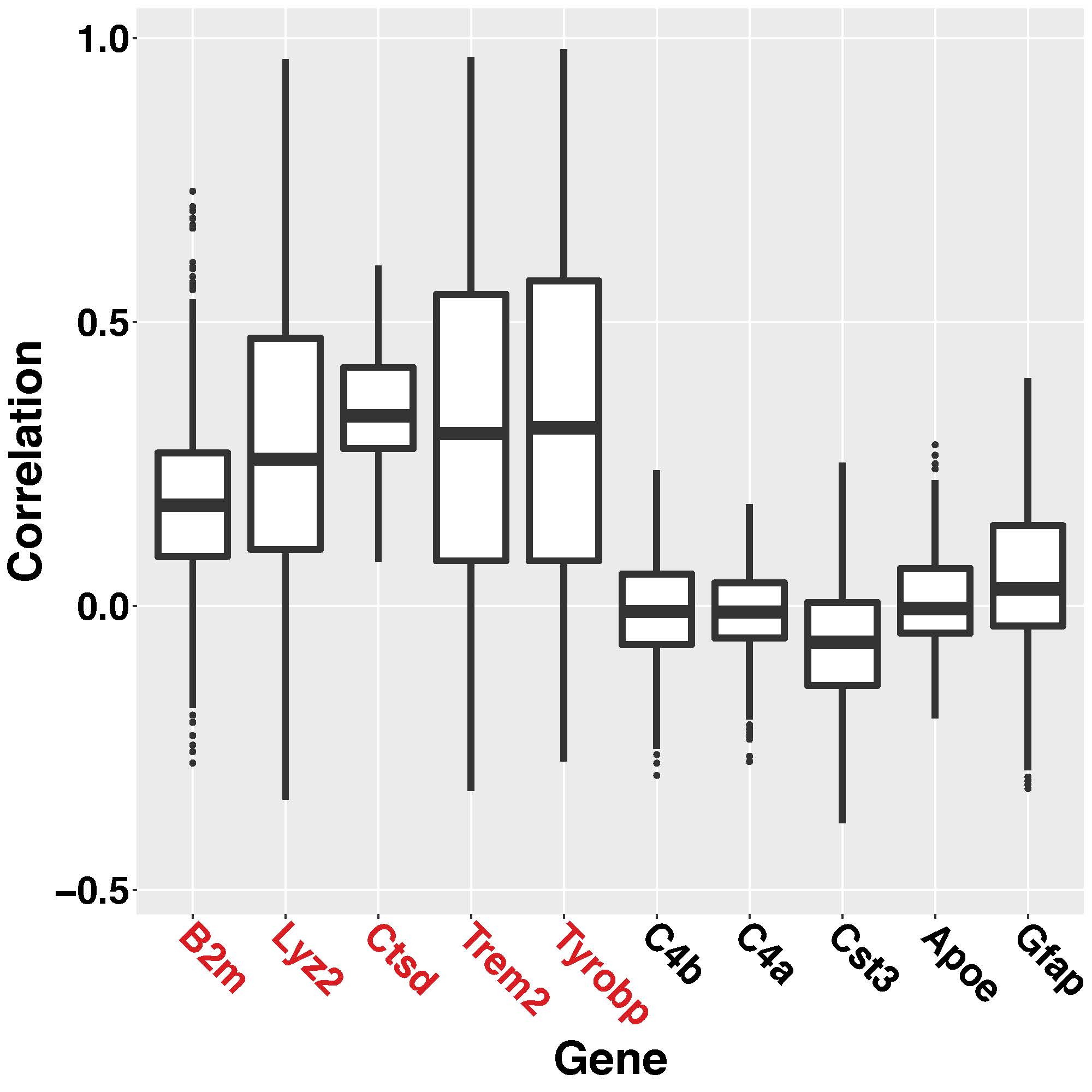
Figure C.6: Boxplot of correlations across all the clusters for top \(10\) hub genes as detected by C2020. First five genes (marked in red) which are also detected as hub genes by SpaceX method. Last five genes are not identified as hub genes by the SpaceX method.
Figure C.7: Shared and tissue domain specific networks.
C.7 Network similarity between cell-type specific networks
We further evaluated the performance of SpaceX to detect similarity between cell-cell interactions. To this end, we used Hamming distance, a well-established similarity measure between two networks, which has been used in several network topology based research studies (Tian and Shen 2005, 2006; Ehounou et al. 2020). In our case, the Hamming distance is equivalent to the distance between their two co-expression networks, i.e., the number of elements having a similar (or different) values in each of the two networks. A low (high) value in Hamming distance between two networks implies those two networks are more (less) similar to each other.
The mouse hypothalamus data consists of 7 cell-type based clusters among 4812 spatial locations. The SpaceX method provides gene co-expression networks specifically for each cell types. Using the Hamming distance as similarity metric, we measure the network similarity between cell-type specific networks obtained from the Mouse hypthalamaous data analyses in Section 4.1 of the paper. The heatmap of the Hamming distances between cell-type specific networks is shown in Figure C.8. We can observe that the co-expression network of immature cell-type is further apart than other cell type specific network in terms of Hamming distance. We rescale the Hamming distance with maximum value such that the distances are in [0,1] interval. Specifically, the Hamming distances of immature cell type network with other cell type (Endothelial, Astrocyte, Mature, Inhibitory, Excitatory, Ependymal) networks are 1, 0.73, 0.83, 0.79, 0.82, 0.73 respectively. Based on Figure C.8, network of endothelial cell type is distant from other cell-type based networks except for the immature cell-type. The distance of Astrocyte cell-type netwrok from Ependymal and Excitatory are 0.27 and 0.32 respectively. The neuronal cell type specific networks have lower distance than others which leads to infer a higher level of similarity between cell-type based networks than others. This similarity and disparity based finding aligns with multiple prior works which discuss about hypothalamic cell diversity (R. Chen et al. 2017; Mickelsen et al. 2020).
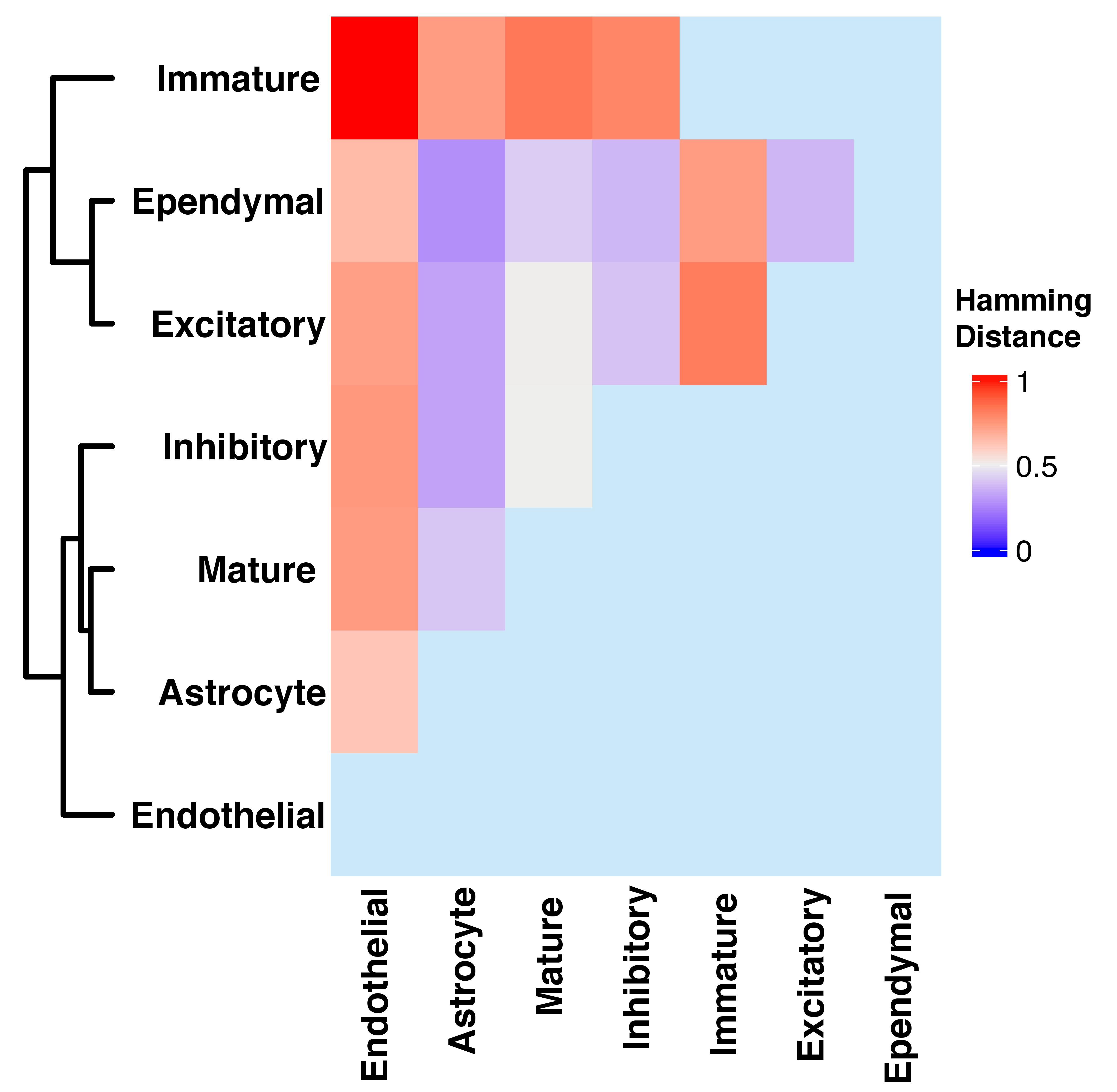
Figure C.8: The Figure shows heatmap of Hamming distances between cell-type specific networks.