Chapter 5 Methods
We describe our methods in this chapter.
5.1 The Algorithm
When we look for interesting connection rules in a huge set of possible rules, the challenge is to develop an efficient algorithm for reducing the number of possibilities.
Such an algorithm has two steps.
- In the first step, we only consider those items and item sets that occur a minimal number of times.
In our example, we could limit our quest to those comments (items) and combinations of comments that are mentioned in at least 2 out of 10 cases.
The comment "adhd" (which stands for Attention Deficit Hyperactivity Disorder) would then be dropped as it occurs only once. But here's the trick: if "adhd" only occurs once, then all potential combinations of other comments plus "adhd" cannot occur twice or more! In other words: with the exclusion of one item a lot of item sets will go with it.
Examples:
{adhd; drugs}; {adhd; divorced}; {adhd; drugs; divorced}; ...
We refer to the number of occurrences of items and item sets as support.
Support = Frequency Of Item Set / Total
The support for the comment "adhd" is 1 in 10 (0.10, or 10%).
Keep in mind that an item set can consist of 1 or more items. A single comment itself is therefore also an item set, even if the set only contains one item!
- Once we have determined item sets with sufficient support, we can proceed to step 2. Here, we assess association rules on the basis of confidence. This is a tough concept that often leads to confusion. We will explain it using our example.
The formula for confidence is:
Confidence (X→Y) = (Support (X,Y)) / (Support (X))
In words, this formula expresses the probability that item set X (as a condition) leads to item set Y (the consequence).
In the example of the supermarket, the rule that buying bread leads to buying peanut butter has a probability equal to the number of times peanut butter and bread are bought together, divided by the number of times bread is bought.
In a numerical example: imagine a supermarket analyzing 80 shopping baskets.
- In 60 cases, the shopping basket contains bread (the gray shaded part, in the left column of the figure).
- In 50 cases, the shopping basket contains peanut butter (the yellow shaded area in the right column).

The support for bread is 60/80 = 0.75 (or 75%).
The support for peanut butter is 50/80 = 0.625 (or 62.5%).
We can also calculate the support for the item set {bread, peanut butter}: 40/80 = 0.50.
We can now calculate the confidence for the association rules.
{bread} → {peanut butter}
and
{peanut butter} → {bread}
For the first association {bread} → {peanut butter} the confidence can be calculated as:
Confidence (bread → peanut butter) = 0.50 / 0.75 = 0.67
In 2 out of 3 cases (67%), buying bread leads to buying peanut butter.
This seems to be informative. Or is it? What do you think? What exactly is the "value" of this information?
The 67% confidence for this rule is only informative if it deviates from support for peanut butter! Without prior information on buying bread, we would estimate the probability of buying peanut butter at 62.5%.
But if we know that there bread is part of the shopping basket, then the probability of peanut butter in the shopping basket is only slightly higher (67%).
For assessing the value if information, we need - in addition to support and confidence - a third measure, which we call lift. We will come back to that later on.
Note that confidence for {bread} → {peanut butter} is not the same as confidence for {peanut butter} → {bread}!
Confidence (peanut butter → bread) = 0.50 / 0.625 = 0.80
We can interpret the difference.
If peanut butter is bought, chances are very high (80%) that bread will also be bought.
It is more common to buy bread but "no peanut butter, than to buy peanut butter but no bread. How come? Well, not everyone likes peanut butter on their bread; but in reverse, peanut butter cannot be used for many other purposes than on your bread.
Let's apply this to our example.
As an example we can look at the relationship between {parents divorced} and {divorced}.
It may of course happen in incidental cases that your parents divorce after you have been divorced yourself, but much more important in the context of explanations for criminal behavior are the consequences of divorced parents on the lives of their children. A divorce can be related to the loss of a job; job loss can lead to drug use and lack of money; and so on.
So the interesting relationship for us is:
{parents divorced} → {divorced}
In the formula for confidence we have to calculate the support for the item {parents separated} and for the item set {parents separated; divorced}. The support for {divorced} is not important in this relationship.
Because the data file is small, we can easily calculate it, for example in Excel.

In the penultimate column, we indicated with a 1 whether the comment “parents divorced” applies to each of the 10 offendants in our study. This appears to be the case 6 times. The support for {parents divorced} is 6/10 = 0.60.
In the last column we look at the item couple {parents divorced; divorced}. We have entered an “x” if the parents are not divorced. After all, if the parents are not divorced, then the item pair {parents divorced; separated} is certainly not an issue!
We have indicated with a \(0\) or \(1\) whether the person is divorced or not, given that the parents are divorced. This occurs in 3 out of 6 cases. The confidence of the relationship is therefore 3/6 = 0.50.
Self test
In our sample file, you are looking for the relationship between “job loss” and “drugs”.
Write out the connection rule for yourself. Then calculate:
- the support for these two items separately
- the support for the item pair, and
- the confidence associated with the connection rule!
5.1.1 Step 1: Reading the Data
In a large file with many people and many items, it is impossible to make these calculations manually. We will therefore use R.
A powerful package for market basket analysis is the arules package.
If you are going to use arules for the first time, you have to first install it on our computer with install.packages(). If you want to use the functions of arules in your R session, you invoke the package with the library() command.
# install.packages("arules")
library(arules)## Warning: package 'arules' was built under R version 4.0.3## Loading required package: Matrix##
## Attaching package: 'arules'## The following objects are masked from 'package:base':
##
## abbreviate, writeIn the console a warning may appeared that the package was written in a later version of R than the version installed on your computer. Something like:
Warning message: package "arules" was built under R version 3.2.5
Packages are regularly updated (bug fixes, new functions). If it were only for this reason, it is recommended to regularly install the latest version of R, and the latest versions of the packages you used most often.
There is, what we call, “backward compatibility”. In recent versions of R, packages built in older versions will work, but the reverse is not always the case. R gives a warning because it may be that the functions in the package will work under the old R version.
We normally read our data as a rectangular file, in which the rows and columns have a fixed meaning: each row is an object (say, a person or a transaction), and each column is a variable.
We can do the same to our data. Our data read stored in Excel was saved as a csv-file and then read in R. A csv-file is just a text-file, with (here, 10) lines. Each of the 10 lines represents the data for a specific person. Every line consists of up to 5 elements, corresponding to the columns in the Excel-file.
R can read (import) data from Excel directly, but it is more common to store and share data in csv-files, probably because they are plain and simple to use by most software programs.
Below we use Notepad++, to display the csv-file. Notepad++ is a popular free source code editor.

If we read the comma separated values csv-file crime.csv, with read.csv(), we get the following result. The header=F option tells R that the first line does not contain header information, that is, names of variables.
crimitest <- read.csv("crime.csv", header=F)
crimitest## V1 V2 V3 V4 V5
## 1 parents divorced shop lifting
## 2 drug abuse divorced violent crime
## 3 parents divorced lost job drug abuse violent crime tax debt
## 4 adhd parents divorced
## 5 drug abuse divorced
## 6 parents divorced tax debt divorced
## 7 drug abuse lost job
## 8 lost job tax debt
## 9 parents divorced divorced drug abuse
## 10 parents divorced violent crime divorcedApart from missing data for some variables, we do see data in rectangular format - as expected.
Our file does not contain names for the variables in the first row, so we specified that there is no header in the file (header = F; F is a short notation for False). R itself generates names for the variables (V1 to V5).
The number of variables (5) is determined by the maximum number of comments for one person, in this case person 3.
Note that a certain comment, for example "drugs", can occur as a value of V1 (persons 2, 5 and 7), or as V3 (persons 3 and 9). This is not very useful for analyzing, for several reasons:
- If we want to know how often "drugs" are mentioned in interviews, we have to go through all variables V1 to V5. Adding the frequencies of "drugs" in each of those variables, we would still run the risk of double counting, in case the comment "drugs" appears twice or more in a single interview.
- We want to know, basically, whether or not the comment "drugs" appears in an interviews.
Our latter wish would require us to choose a design in which all possible comments ("adhd", "divorced", "drugs", ...) represent variables which are then coded with 0 (does not occur) or one (does occur). But that's the very thing we wanted to prevent, since interviews, and in shopping baskets for that matter, are likely to consists of a limited number of all possible words, comments and products. The number of zeroes in our data set would be tremendous.
5.1.2 Step 2: Preparing the Data
The Sparse Matrix
The arules package has an extremely useful function to read such data in an efficient way: the read.transactions() function.
The data is organized in a so-called sparse matrix, a rectangle that uses space sparingly.
Since we are not going to use the rectangular data frame crimitest created above, we will first delete it using rm().
rm(crimitest)
crimi <- read.transactions("crime.csv",sep=",")
summary(crimi)## transactions as itemMatrix in sparse format with
## 10 rows (elements/itemsets/transactions) and
## 8 columns (items) and a density of 0.3375
##
## most frequent items:
## parents divorced divorced drug abuse lost job
## 6 5 5 3
## tax debt (Other)
## 3 5
##
## element (itemset/transaction) length distribution:
## sizes
## 2 3 5
## 5 4 1
##
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 2.0 2.0 2.5 2.7 3.0 5.0
##
## includes extended item information - examples:
## labels
## 1 adhd
## 2 divorced
## 3 drug abuseYou see that the summary() function in R is smart. You can apply the function to a data frame, as in previous chapters. But you can also use the same function to summarize the object crimi that is not a data frame! Depending on the type of object (in R: the object class) summary() gives a different result.
Let's look at the output step-by-step.
The first line states that it is indeed a matrix in a sparse format. Sparse here means that each line contains only the comments that have been made (the "ones" in the file; not the "zeros" for all comments that have not been made). In a shopping basket analogy: we list all the types of products that are in the shopping basket. We do not list all types of products that are not in the basket!
The matrix has 10 rows and 8 columns.
The 10 rows are the interviews with 10 individuals with criminal behavior.
The 8 columns represent all possible comments (the items) that have been made. You can easily check for yourself, in this small sample file, that indeed 8 different comments have were made.
- ADHD
- Lost job
- Tax liability
- Drugs
- Divorced
- Violent crime
- Parents divorced
- Shoplifting
- The 5 most frequently made comments are listed, as well as frequently they occur.
The remark "parents divorced"" occurs (as we have already calculated in Excel, above) 6 times.
The support can be calculated as 6 divided by the number of rows (10) is 0.60
All remaining comments (3) appear as "other". Check for yourself which these three comments are!
An interesting statistic is the density.
If we think of the sparse matrix as a rectangle of 10 people times 8 comments filled with zeros and ones, then how many of the \(10 * 8 = 80\) cells of the matrix contains a 1?
We can calculate that ourselves in our simple example:

A total of 27 comments were made. In a matrix with \(10*8=80\) cells, gives a density of 27/80 = 0.3375. The output confirms that.
The density in the shopping baskets at a supermarket will of course be very small!
- The next line of output shows the sizes of the shopping baskets, or in our example, the distribution of the number of comments.
In most cases (5 people) the number of comments is limited to two. Three comments are made in four cases, and five comments in one case.
The distribution of comments is shown statistically, including the minimum (2), the mean (\(27/10 = 2.7\)) and the maximum (5).
Finally, a number of examples are given of the values in the matrix.
The labels are the comments in the data file, and sorted alphabetically: column 1 of the matrix, returns a vector of zeros and ones for the comment "adhd". We will rarely use such matrices (for a supermarket with thousands of items, such a matrix would be too large).
5.1.3 Step 3: Inspecting the Sparse Matrix
You can view your data (the 10 lines of the sparse matrix) with the inspect() command.
To show the first three rows we use:
inspect(crimi[1:3])## items
## [1] {parents divorced,
## shop lifting}
## [2] {divorced,
## drug abuse,
## violent crime}
## [3] {drug abuse,
## lost job,
## parents divorced,
## tax debt,
## violent crime}Compare this with the data in the Excel file!
5.1.4 Step 4: Exploring and Visualizing the Data
We can also create a table of the relative frequency of the different items, using the itemFrequency() function.
In the market basket analysis jargon, this function shows the support of the various items.
For example:
- "adhd" occurs in one of the 10 rows, so the support is \(1/10 = 0.1\) (or 10%).
- The support for drugs is 0.5, and so on.
You can see that the items are arranged in alphabetical order. This is not useful if we have a lot of items (products, comments, etc.) in our database. The output will be huge. You can limit the output to, say, the first 3 items, but those are probably not the most important (or most frequent) items!
The output of itemFrequency() is a vector that we can sort. Because we are interested in the items with the highest support, we sort using the option decreasing = TRUE (the default is sort ascending, so decreasing = FALSE).
In the case of a large number of items, it is recommended that you only display the items with the highest support.
To keep the commands short and clear, we first create a sorted vector (xs) below.
- In the first command we print the vector directly by placing it between parentheses “()”.
- In the second command, we only print the first three items.
Much more convenient is the itemFrequencyPlot() function because we can directly indicate the minimum support for items displayed, or the topN (for example the top three) items with the highest support.
Since we only have 8 items in our simple example, a graphical representation is quite possible (see figures below).
itemFrequency(crimi)## adhd divorced drug abuse lost job
## 0.1 0.5 0.5 0.3
## parents divorced shop lifting tax debt violent crime
## 0.6 0.1 0.3 0.3xs <- sort(itemFrequency(crimi), decreasing=TRUE)
xs[1:3]## parents divorced divorced drug abuse
## 0.6 0.5 0.5sort(itemFrequency(crimi), decreasing=TRUE)## parents divorced divorced drug abuse lost job
## 0.6 0.5 0.5 0.3
## tax debt violent crime adhd shop lifting
## 0.3 0.3 0.1 0.1itemFrequencyPlot(crimi)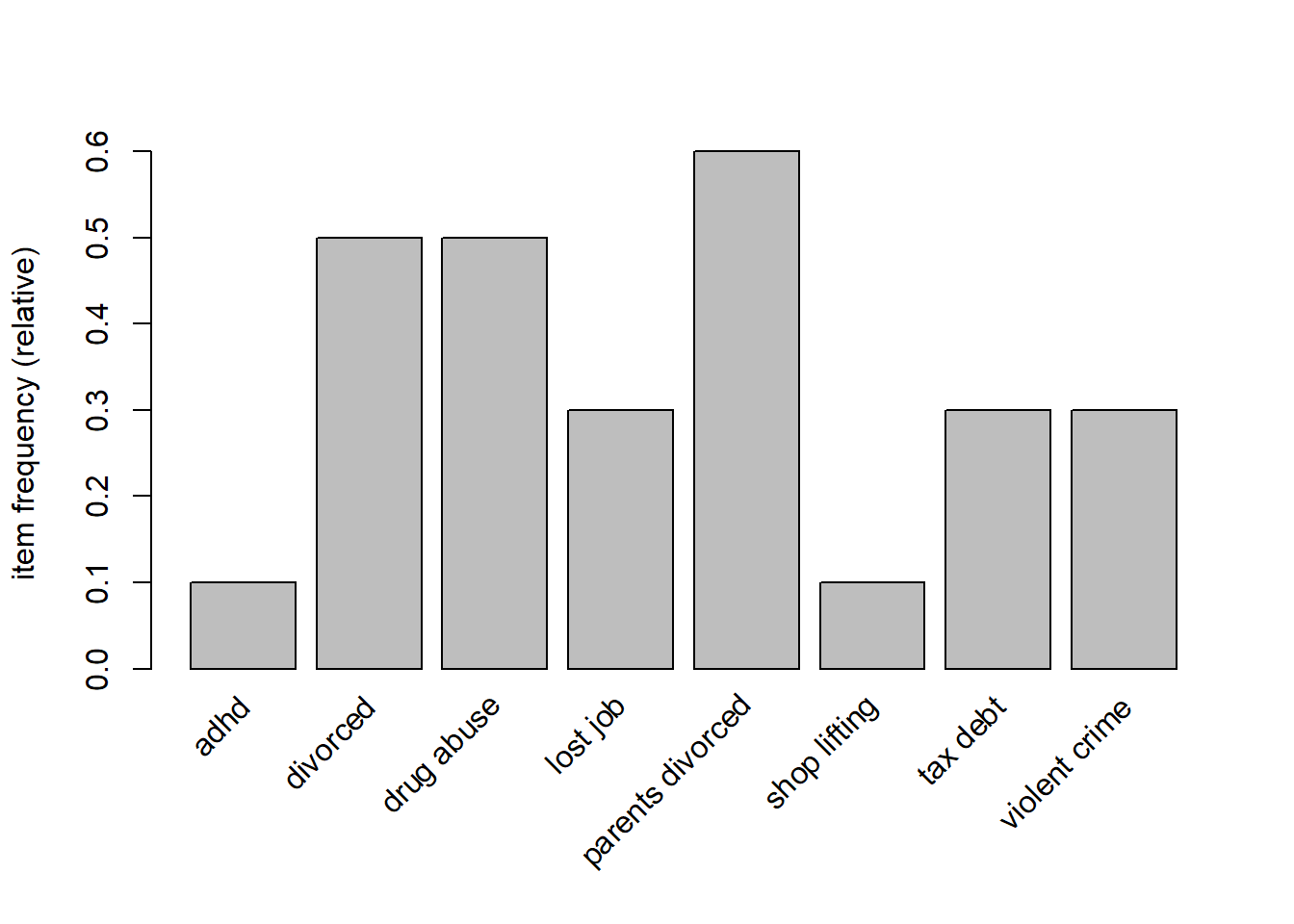
itemFrequencyPlot(crimi, support=.3)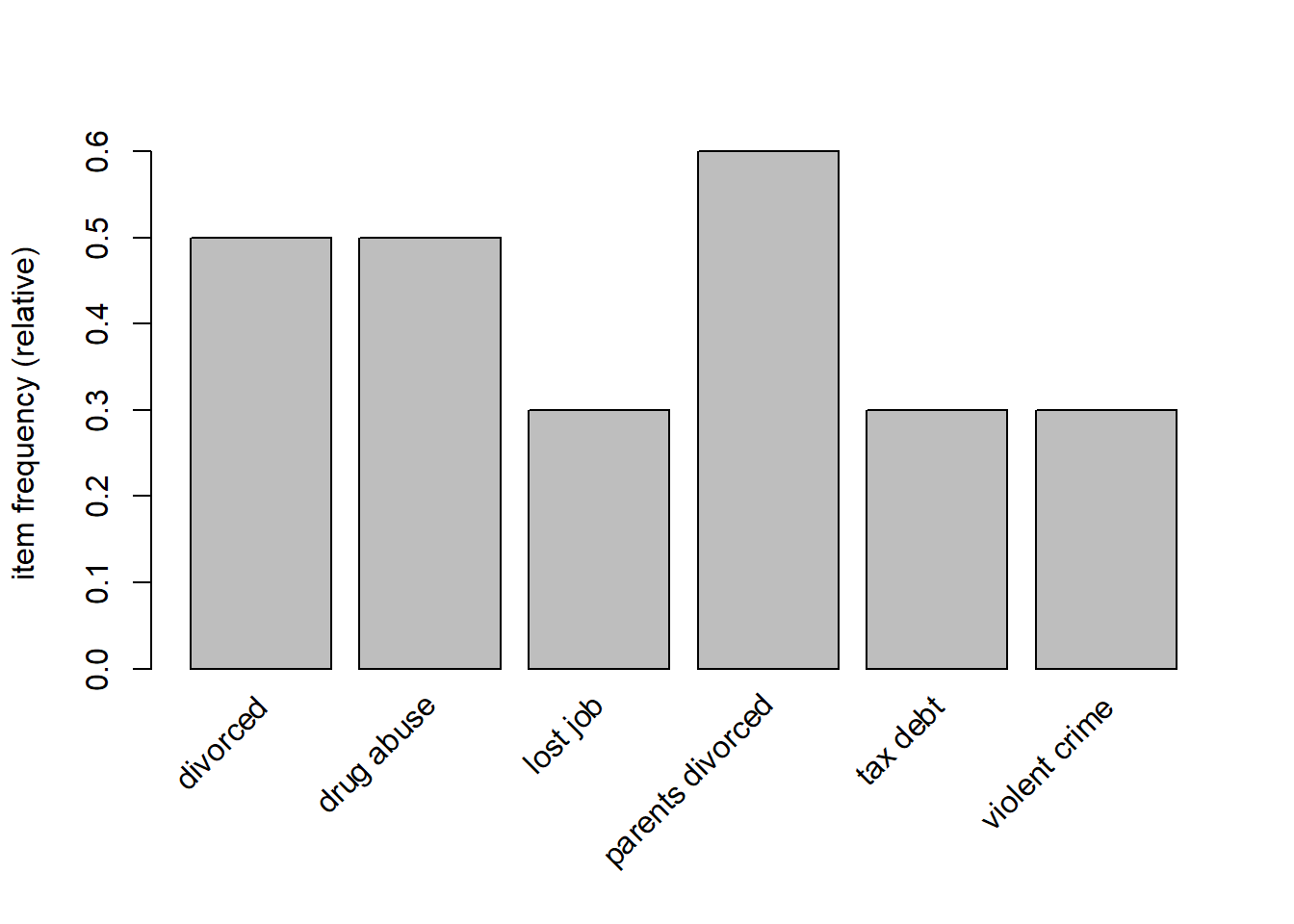
itemFrequencyPlot(crimi, topN=3)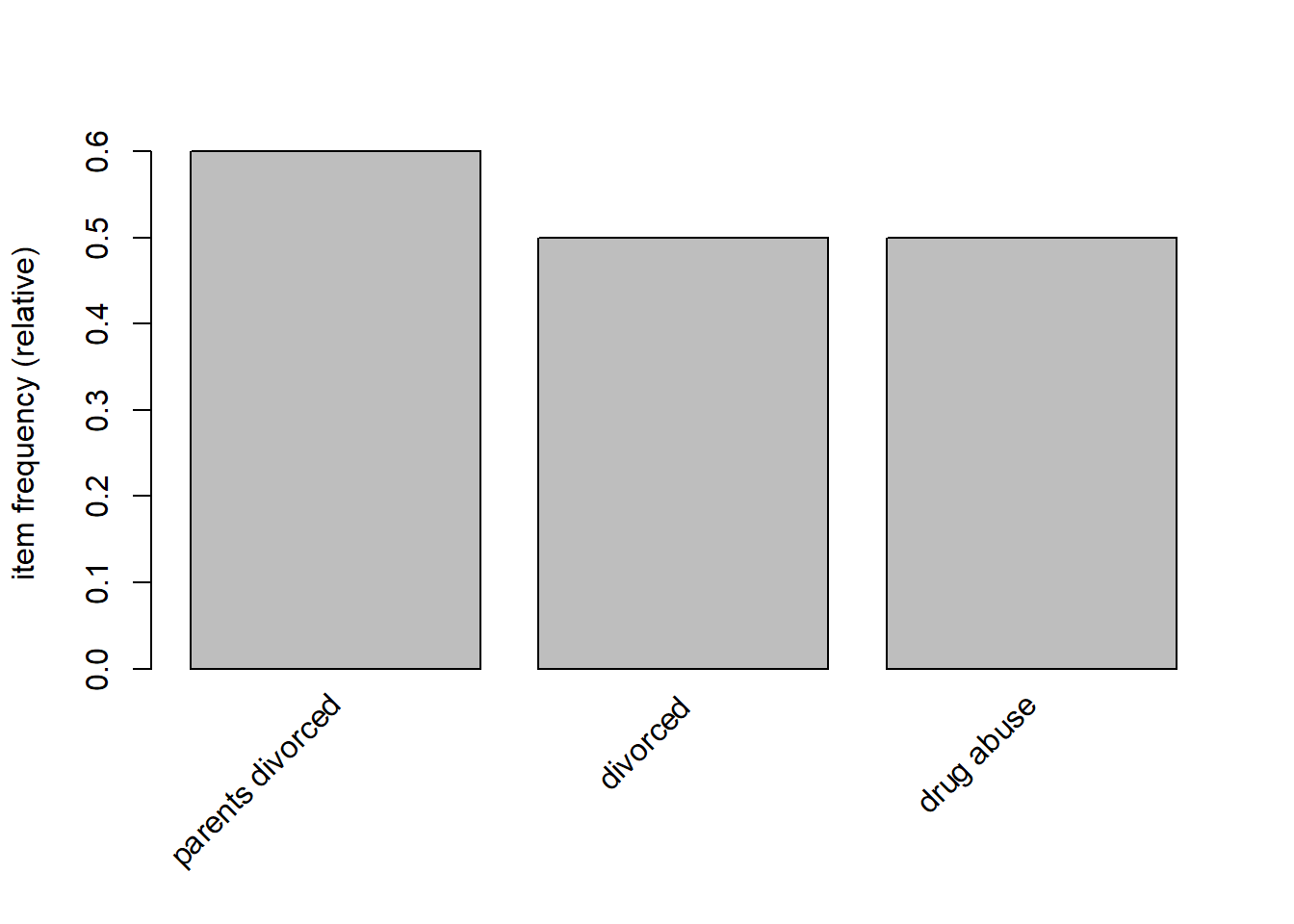
The patterns in the data can visualized with the image() function.
Applied to shopping baskets, this function shows in a matrix diagram (a graph with blocks) which consumers buy which products. This really only makes sense if both the number of rows (in our case, criminals) and the number of items (comments about these criminals) are small.
For large data files, the image() function produces a huge amount of dots in a rectangle that is difficult to interpret.
In our example:
image(crimi) # all data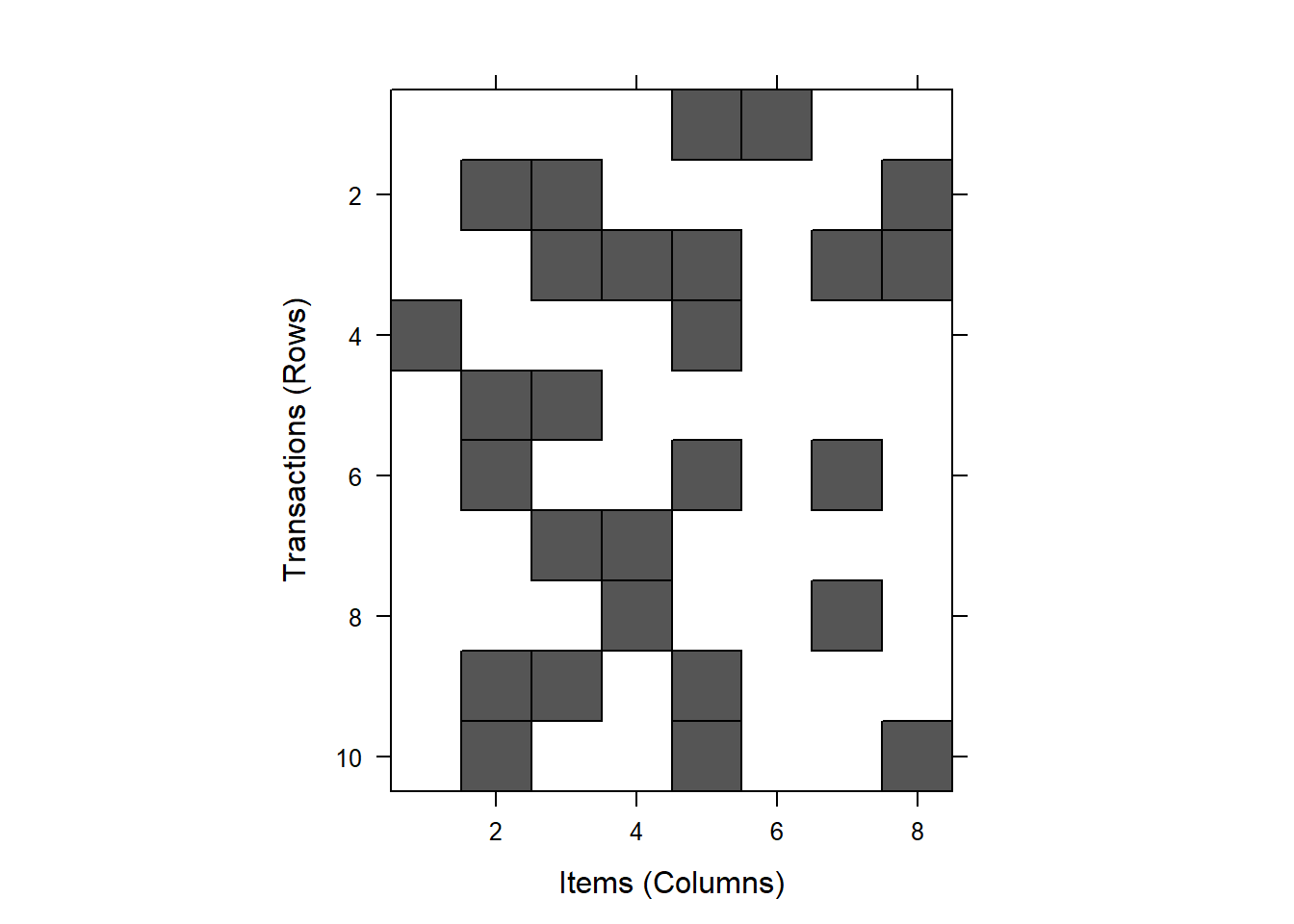
image(crimi[1:3,]) # first 3 cases (rows)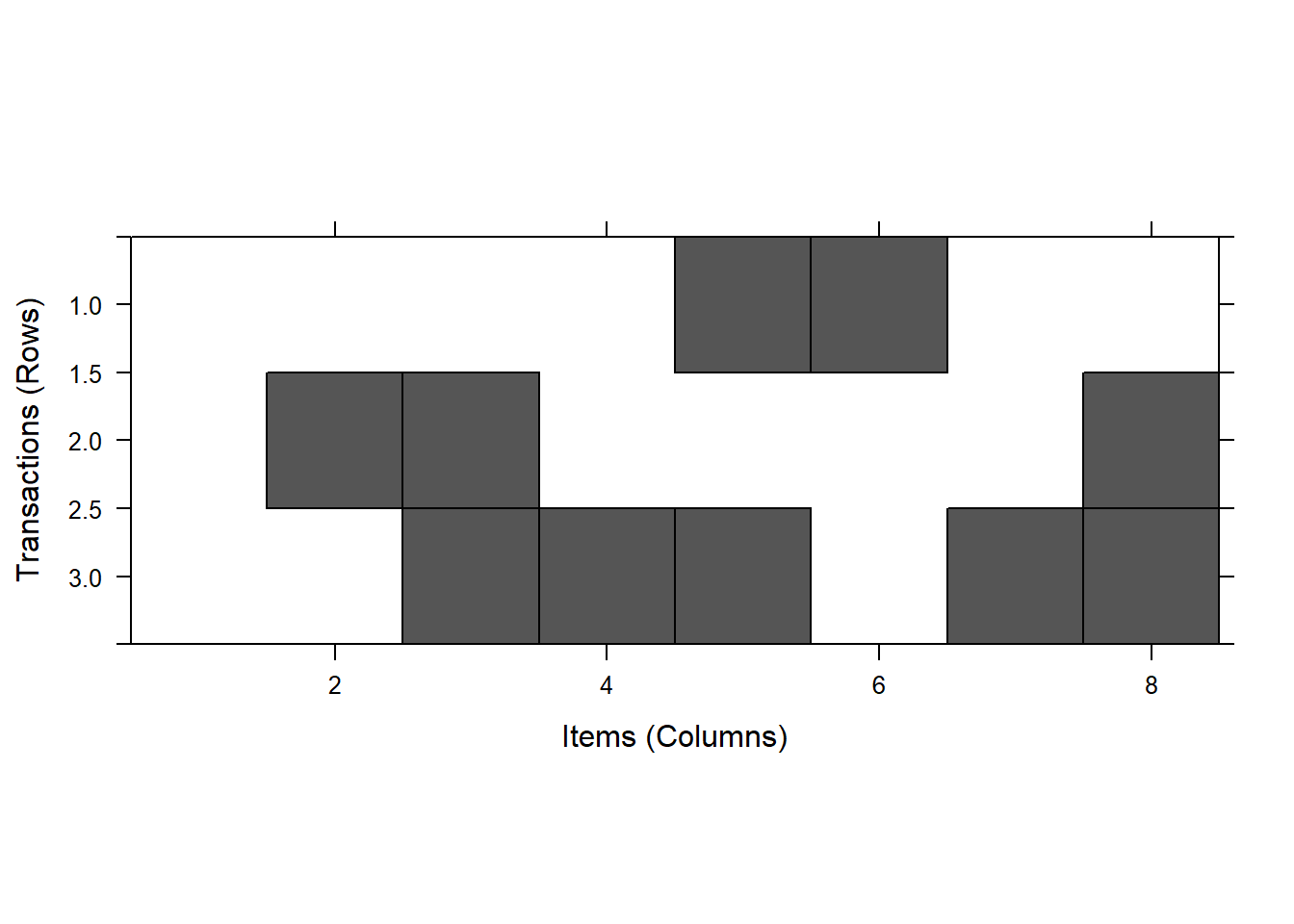
image(crimi[,6:8]) # rows 6 to 8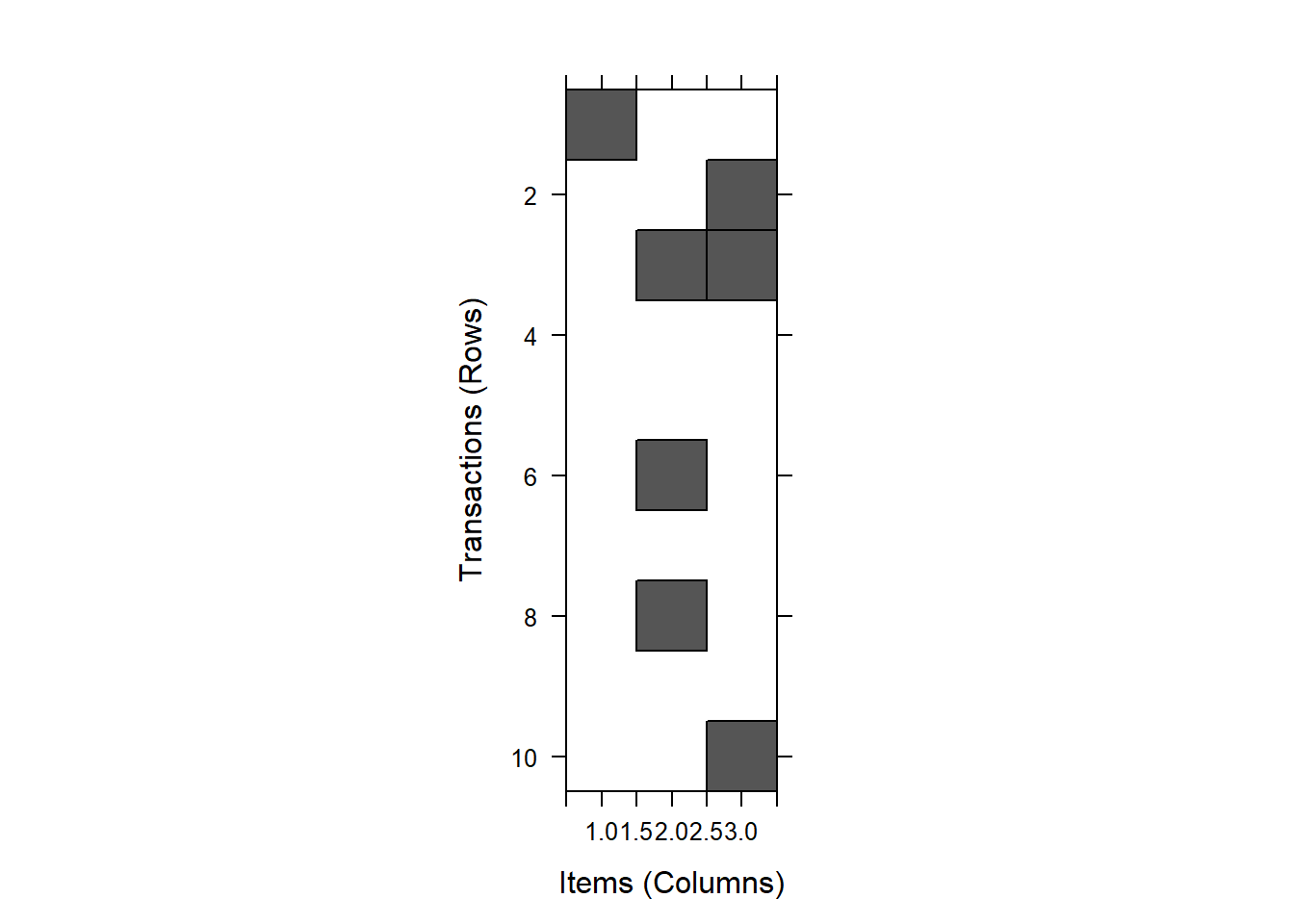
Try to discover patterns yourself on the basis of the figure.
- Which items are common?
- And which items often appear in combination with other items?
5.1.5 Step 5: Training the model
Now that we have read and explored the data, we are ready for the next step: analyzing the connections between the items.
We have already started with this in the image() function in step 3, but it will be clear that the graph is not easy to interpret - especially if we have a lot of data.
We can efficiently trace relationships (or associations) in the file with the apriori() function.
The apriori() function uses the following arguments, in brackets:
- the sparse matrix
- the minimum support
- the minimum confidence, and
- the minimum number of items (minlen) in a connection rule (or association rule).
By indicating a minimum support, we can filter out item sets that are rare.
The same applies to the minimum confidence: we are interested in the relationship between items, and in the probability that the presence of one item predicts the presence of other items.
Some examples:
cr1 <- apriori(crimi)## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.8 0.1 1 none FALSE TRUE 5 0.1 1
## maxlen target ext
## 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 1
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[8 item(s), 10 transaction(s)] done [0.00s].
## sorting and recoding items ... [8 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 done [0.00s].
## writing ... [40 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].inspect(cr1)## lhs rhs support confidence coverage lift count
## [1] {shop lifting} => {parents divorced} 0.1 1 0.1 1.666667 1
## [2] {adhd} => {parents divorced} 0.1 1 0.1 1.666667 1
## [3] {lost job,
## violent crime} => {tax debt} 0.1 1 0.1 3.333333 1
## [4] {tax debt,
## violent crime} => {lost job} 0.1 1 0.1 3.333333 1
## [5] {drug abuse,
## tax debt} => {lost job} 0.1 1 0.1 3.333333 1
## [6] {lost job,
## parents divorced} => {tax debt} 0.1 1 0.1 3.333333 1
## [7] {lost job,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [8] {lost job,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [9] {lost job,
## parents divorced} => {violent crime} 0.1 1 0.1 3.333333 1
## [10] {lost job,
## parents divorced} => {drug abuse} 0.1 1 0.1 2.000000 1
## [11] {tax debt,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [12] {drug abuse,
## tax debt} => {violent crime} 0.1 1 0.1 3.333333 1
## [13] {tax debt,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [14] {divorced,
## tax debt} => {parents divorced} 0.1 1 0.1 1.666667 1
## [15] {drug abuse,
## tax debt} => {parents divorced} 0.1 1 0.1 1.666667 1
## [16] {lost job,
## tax debt,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [17] {drug abuse,
## lost job,
## tax debt} => {violent crime} 0.1 1 0.1 3.333333 1
## [18] {drug abuse,
## lost job,
## violent crime} => {tax debt} 0.1 1 0.1 3.333333 1
## [19] {drug abuse,
## tax debt,
## violent crime} => {lost job} 0.1 1 0.1 3.333333 1
## [20] {lost job,
## tax debt,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [21] {lost job,
## parents divorced,
## tax debt} => {violent crime} 0.1 1 0.1 3.333333 1
## [22] {lost job,
## parents divorced,
## violent crime} => {tax debt} 0.1 1 0.1 3.333333 1
## [23] {parents divorced,
## tax debt,
## violent crime} => {lost job} 0.1 1 0.1 3.333333 1
## [24] {drug abuse,
## lost job,
## tax debt} => {parents divorced} 0.1 1 0.1 1.666667 1
## [25] {lost job,
## parents divorced,
## tax debt} => {drug abuse} 0.1 1 0.1 2.000000 1
## [26] {drug abuse,
## lost job,
## parents divorced} => {tax debt} 0.1 1 0.1 3.333333 1
## [27] {drug abuse,
## parents divorced,
## tax debt} => {lost job} 0.1 1 0.1 3.333333 1
## [28] {drug abuse,
## lost job,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [29] {lost job,
## parents divorced,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [30] {drug abuse,
## lost job,
## parents divorced} => {violent crime} 0.1 1 0.1 3.333333 1
## [31] {drug abuse,
## parents divorced,
## violent crime} => {lost job} 0.1 1 0.1 3.333333 1
## [32] {drug abuse,
## tax debt,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [33] {parents divorced,
## tax debt,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [34] {drug abuse,
## parents divorced,
## tax debt} => {violent crime} 0.1 1 0.1 3.333333 1
## [35] {drug abuse,
## parents divorced,
## violent crime} => {tax debt} 0.1 1 0.1 3.333333 1
## [36] {drug abuse,
## lost job,
## tax debt,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [37] {lost job,
## parents divorced,
## tax debt,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [38] {drug abuse,
## lost job,
## parents divorced,
## tax debt} => {violent crime} 0.1 1 0.1 3.333333 1
## [39] {drug abuse,
## lost job,
## parents divorced,
## violent crime} => {tax debt} 0.1 1 0.1 3.333333 1
## [40] {drug abuse,
## parents divorced,
## tax debt,
## violent crime} => {lost job} 0.1 1 0.1 3.333333 1The first specification uses the default values and results in a large number of lines.
If the optional parameters are omitted, then the default values for support, confidence, and minuses are:
- Support = .1
- Confidence = .8, and
- minlen = 1.
The associaion rules are stored in a new object (cr1).
Default values are usually not the best ones. The optimal values vary from case to case.
In our case, we can use a fairly high value for support, say 0.2 or 0.3, because an item or item pair must appear at least 2 out of 10 times.
In a supermarket with thousands of items, we set the support at a much lower level, as it is unlikely for combinations of products to have support levels as high as 0.2.
Anyway, we only want to see relationships between items, and then we need to have at least 2 items (minlen=2).
We want to have a manageable set of meaningful relationships. If we set the thresholds too low, we will have a lot of rules which makes it hard to digest. If we set the thresholds too high then the number of lines is small, or even zero.
Especially in large data files, we are forced to use trial and error to see what gives the best result. You can compare it to googling. If you are google for information about the presidential elections in the US, then the search string "presidential elections" yields over 300 million hits (including presidential elections in other countries than the US).
Adding "amsterdam" to your search string reduces the number of hits substantially to less than 3 million, still not something you can digest within a short time. The hits include a lot of documents linked to the University of Amsterdam.
Replacing "amsterdam" by "tietjerksteradeel" (a small municipality in the north of the Netherlands) yields 1 hit only. Very manageable, but not necessarily relevant. It turns out that this hit is a Master thesis by a student on a Dutch right-wing politician who has strong feelings on both the US presidential elections and climate change; his views on climate change were criticized by a Dutch weatherman who was born and raised in Tietjerksteradeel. Probably not what we are looking for.
Let's look at the first association rule in the output.
{shop lifting} => {parents divorced}
Let's focus on the three statistics of interest: support, confidence and lift.
- The support for the item pair {shop lifting; parents divorced}, is 0.10.
By now, you should be able to check that yourself from the small data set presented before. There is only one interviewee with indications of both "shop lifting" and "parents divorced". It's the very first case, out of the set of 10. Support is therefore \(1/10=0.10\), as shown in the output.
- The output also tells us that the confidence of the association rule {shop lifting} => {parents divorced} is 1.
The confidence can be calculated as:
Confidence (X→Y) = (Support (X,Y)) / (Support (X))
or here:
X = Shop Lifting, and Y = Parents Divorced
Confidence (X→Y) = 0.10 / 0.10 = 1
This reflects the fact that in all cases of shop lifting, the parents turn out to be divorced. There's only one case of shop lifting, and the only other comment in the interview was about the parents being divorced, resulting is this finding. Obviously, the evidence is quite thin, with only 10 cases in total, and 1 case in support of this finding.
Moreover, it is questionable that this order of events (shop lifting causing parents to divorce) makes a lot of sense. And, since parents often got divorced in our sample (6 out of 10 cases), it may not be that informative anyway.
- Whether a finding is informative, is indicated by lift.
The formula for lift is:
Lift (X→Y) = (Confidence (X,Y)) / (Support (Y))
The outcome of the formula is:
(X = Shop Lifting, and Y = Parents Divorced)
Lift (X→Y) = 1 / (6/10) = 1 / 0.6 = 1.67
The reasoning is as follows.
If the chance of divorced parents occurs more often with prior information about shoplifting, then this this is informative.
In our example, shoplifting is always associated with divorced parents (even if we only have one case): the chance is therefore 100%. Without prior information on shoplifting, the probability of divorced parents is 6/10 = 60% (the support for {parents divorced}). Lift is the ratio between these probabilities: 100% / 60% = 1.67.
5.1.6 More on Lift, and the Formulas for Support, Confidence and Lift Revisited
Note that items with 100% support can never be informative!
This applies to (combinations of) items on the left (LHS) and the right (RHS)!
- If the LHS (the condition, {X}) of the association rule holds for all cases, then the confidence of the item pair {X,Y} is equal to the support for item {y}.
In an example:
If every consumer has bread in his or her shopping basket, and 30% of all consumers also have peanut butter, then the confidence of {bread, peanut butter} is also 30%. 30% buys peanut butter, and 30% buys both peanut butter and bread (since everybody buys bread)!
The lift, then, for Bread → Peanut Butter can be computed as:
Lift(X→Y) = 30% (confidence of item pair), divided by 30% (support for peanut butter) = 1
- If the RHS always holds, the lift equals the confidence for the item pair equal to 1
In our example {peanut butter} → {bread}.
If everyone buys bread and 30% buys peanut butter, the confidence for the item pair {bread, peanut butter} can be computed as support for the item pair {bread, peanut butter} (30%), divided by the support for {peanut butter} (30%); and 30%/30% = 1.
The lift then is confidence (1) divided by support for bread (1): and 1/1 = 1.
This is a complicated way of stating that items that always occur, provide no information for predicting other items. And predicting them is pointless, since they always oocur anyway.
While confidence(X→Y) ≠ confidence(Y→X), by definition lift(X→Y) = lift(Y→X)!
5.1.6.1 Advanced: Why lift(X→Y) = lift(Y→X)
To recap:
- Support is a measure that gives an idea of how frequent an itemset is in all the transactions.
- Confidence measures the likelihood of items given that the shopping cart already has other items.
- Lift controls for the support (frequency) while calculating the conditional probability of occurrence of {Y} given {X}.

To control our output, we can use the various opitions, in brackets. If we set these values to the default values, then obviously the output will be identical to what we have above.
Run both sets of commands and verify that the result is indeed the same! Just to make sure.
cr2 <- apriori(crimi, parameter = list(support=.1, confidence=.8, minlen=1))## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.8 0.1 1 none FALSE TRUE 5 0.1 1
## maxlen target ext
## 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 1
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[8 item(s), 10 transaction(s)] done [0.00s].
## sorting and recoding items ... [8 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 done [0.00s].
## writing ... [40 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].inspect(cr2)## lhs rhs support confidence coverage lift count
## [1] {shop lifting} => {parents divorced} 0.1 1 0.1 1.666667 1
## [2] {adhd} => {parents divorced} 0.1 1 0.1 1.666667 1
## [3] {lost job,
## violent crime} => {tax debt} 0.1 1 0.1 3.333333 1
## [4] {tax debt,
## violent crime} => {lost job} 0.1 1 0.1 3.333333 1
## [5] {drug abuse,
## tax debt} => {lost job} 0.1 1 0.1 3.333333 1
## [6] {lost job,
## parents divorced} => {tax debt} 0.1 1 0.1 3.333333 1
## [7] {lost job,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [8] {lost job,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [9] {lost job,
## parents divorced} => {violent crime} 0.1 1 0.1 3.333333 1
## [10] {lost job,
## parents divorced} => {drug abuse} 0.1 1 0.1 2.000000 1
## [11] {tax debt,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [12] {drug abuse,
## tax debt} => {violent crime} 0.1 1 0.1 3.333333 1
## [13] {tax debt,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [14] {divorced,
## tax debt} => {parents divorced} 0.1 1 0.1 1.666667 1
## [15] {drug abuse,
## tax debt} => {parents divorced} 0.1 1 0.1 1.666667 1
## [16] {lost job,
## tax debt,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [17] {drug abuse,
## lost job,
## tax debt} => {violent crime} 0.1 1 0.1 3.333333 1
## [18] {drug abuse,
## lost job,
## violent crime} => {tax debt} 0.1 1 0.1 3.333333 1
## [19] {drug abuse,
## tax debt,
## violent crime} => {lost job} 0.1 1 0.1 3.333333 1
## [20] {lost job,
## tax debt,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [21] {lost job,
## parents divorced,
## tax debt} => {violent crime} 0.1 1 0.1 3.333333 1
## [22] {lost job,
## parents divorced,
## violent crime} => {tax debt} 0.1 1 0.1 3.333333 1
## [23] {parents divorced,
## tax debt,
## violent crime} => {lost job} 0.1 1 0.1 3.333333 1
## [24] {drug abuse,
## lost job,
## tax debt} => {parents divorced} 0.1 1 0.1 1.666667 1
## [25] {lost job,
## parents divorced,
## tax debt} => {drug abuse} 0.1 1 0.1 2.000000 1
## [26] {drug abuse,
## lost job,
## parents divorced} => {tax debt} 0.1 1 0.1 3.333333 1
## [27] {drug abuse,
## parents divorced,
## tax debt} => {lost job} 0.1 1 0.1 3.333333 1
## [28] {drug abuse,
## lost job,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [29] {lost job,
## parents divorced,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [30] {drug abuse,
## lost job,
## parents divorced} => {violent crime} 0.1 1 0.1 3.333333 1
## [31] {drug abuse,
## parents divorced,
## violent crime} => {lost job} 0.1 1 0.1 3.333333 1
## [32] {drug abuse,
## tax debt,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [33] {parents divorced,
## tax debt,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [34] {drug abuse,
## parents divorced,
## tax debt} => {violent crime} 0.1 1 0.1 3.333333 1
## [35] {drug abuse,
## parents divorced,
## violent crime} => {tax debt} 0.1 1 0.1 3.333333 1
## [36] {drug abuse,
## lost job,
## tax debt,
## violent crime} => {parents divorced} 0.1 1 0.1 1.666667 1
## [37] {lost job,
## parents divorced,
## tax debt,
## violent crime} => {drug abuse} 0.1 1 0.1 2.000000 1
## [38] {drug abuse,
## lost job,
## parents divorced,
## tax debt} => {violent crime} 0.1 1 0.1 3.333333 1
## [39] {drug abuse,
## lost job,
## parents divorced,
## violent crime} => {tax debt} 0.1 1 0.1 3.333333 1
## [40] {drug abuse,
## parents divorced,
## tax debt,
## violent crime} => {lost job} 0.1 1 0.1 3.333333 1Great! Nothing changed.
Below, we set the bar a bit higher. We only want rules with support levels of .3 or higher.
This leaves only 7 rules, but some of them have a length of 1 (with just right hand sides, and no left hand sides). Not rules at all, really.
cr3 <- apriori(crimi, parameter = list(support=.3, confidence=.5))## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.5 0.1 1 none FALSE TRUE 5 0.3 1
## maxlen target ext
## 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 3
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[8 item(s), 10 transaction(s)] done [0.00s].
## sorting and recoding items ... [6 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 done [0.00s].
## writing ... [7 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].inspect(cr3)## lhs rhs support confidence coverage lift
## [1] {} => {divorced} 0.5 0.5 1.0 1.0
## [2] {} => {drug abuse} 0.5 0.5 1.0 1.0
## [3] {} => {parents divorced} 0.6 0.6 1.0 1.0
## [4] {divorced} => {drug abuse} 0.3 0.6 0.5 1.2
## [5] {drug abuse} => {divorced} 0.3 0.6 0.5 1.2
## [6] {divorced} => {parents divorced} 0.3 0.6 0.5 1.0
## [7] {parents divorced} => {divorced} 0.3 0.5 0.6 1.0
## count
## [1] 5
## [2] 5
## [3] 6
## [4] 3
## [5] 3
## [6] 3
## [7] 3And we can set minlen at 2. This leaves out the one-item rules.
From rules 1 versus 2, and rules 3 versus 4, you note that the support levels are the same (as the item pairs are the same), and that the lift levels are the same, by definition: lift(X→Y) = lift(Y→X).
cr4 <- apriori(crimi, parameter = list(support=.3, confidence=.4, minlen=2))## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.4 0.1 1 none FALSE TRUE 5 0.3 2
## maxlen target ext
## 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 3
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[8 item(s), 10 transaction(s)] done [0.00s].
## sorting and recoding items ... [6 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 done [0.00s].
## writing ... [4 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].inspect(cr4)## lhs rhs support confidence coverage lift
## [1] {divorced} => {drug abuse} 0.3 0.6 0.5 1.2
## [2] {drug abuse} => {divorced} 0.3 0.6 0.5 1.2
## [3] {divorced} => {parents divorced} 0.3 0.6 0.5 1.0
## [4] {parents divorced} => {divorced} 0.3 0.5 0.6 1.0
## count
## [1] 3
## [2] 3
## [3] 3
## [4] 3Of course, depending on the size of the output, the case at hand and what you want to learn from it, you can play around with the settings.
Remember that, as a data scientist, your challenge is to find meaningful information and to present it in a clear way!
cr5 <- apriori(crimi, parameter = list(support=.2, confidence=.3, minlen=2))## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.3 0.1 1 none FALSE TRUE 5 0.2 2
## maxlen target ext
## 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 2
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[8 item(s), 10 transaction(s)] done [0.00s].
## sorting and recoding items ... [6 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 done [0.00s].
## writing ... [18 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].inspect(cr5)## lhs rhs support confidence coverage
## [1] {lost job} => {tax debt} 0.2 0.6666667 0.3
## [2] {tax debt} => {lost job} 0.2 0.6666667 0.3
## [3] {lost job} => {drug abuse} 0.2 0.6666667 0.3
## [4] {drug abuse} => {lost job} 0.2 0.4000000 0.5
## [5] {tax debt} => {parents divorced} 0.2 0.6666667 0.3
## [6] {parents divorced} => {tax debt} 0.2 0.3333333 0.6
## [7] {violent crime} => {divorced} 0.2 0.6666667 0.3
## [8] {divorced} => {violent crime} 0.2 0.4000000 0.5
## [9] {violent crime} => {drug abuse} 0.2 0.6666667 0.3
## [10] {drug abuse} => {violent crime} 0.2 0.4000000 0.5
## [11] {violent crime} => {parents divorced} 0.2 0.6666667 0.3
## [12] {parents divorced} => {violent crime} 0.2 0.3333333 0.6
## [13] {divorced} => {drug abuse} 0.3 0.6000000 0.5
## [14] {drug abuse} => {divorced} 0.3 0.6000000 0.5
## [15] {divorced} => {parents divorced} 0.3 0.6000000 0.5
## [16] {parents divorced} => {divorced} 0.3 0.5000000 0.6
## [17] {drug abuse} => {parents divorced} 0.2 0.4000000 0.5
## [18] {parents divorced} => {drug abuse} 0.2 0.3333333 0.6
## lift count
## [1] 2.2222222 2
## [2] 2.2222222 2
## [3] 1.3333333 2
## [4] 1.3333333 2
## [5] 1.1111111 2
## [6] 1.1111111 2
## [7] 1.3333333 2
## [8] 1.3333333 2
## [9] 1.3333333 2
## [10] 1.3333333 2
## [11] 1.1111111 2
## [12] 1.1111111 2
## [13] 1.2000000 3
## [14] 1.2000000 3
## [15] 1.0000000 3
## [16] 1.0000000 3
## [17] 0.6666667 2
## [18] 0.6666667 2It is important to interpret the connection rules correctly.
There are two lines with a relatively large lift, (\(lift>2\)).
Both relate to the items {job loss} and {tax debt}.
It is more than twice as likely, for the 10 individuals in our database, to have a tax debt knowing they have lost their jobs, than for the group as a whole. The opposite is also true: it is more than twice as likely to lose your job knowing there is a tax liability than for the group as a whole.
As an analyst, your main interest may be in certain aspects from the interviews, such as the relationships between (comments about) drug abuse and other items.
We can select lines from the object cr5 created above with the subset() command.
After the name of the object with the connection rules, you must indicate which items you want to select.
To select all connection rules with drug abuse in either the LHS or RHS), use the following command. It is handy to save the rules sorted by lift as an object (say, short). The object is a data frame. We can select rules with, for example, \(lift>1.2\) like below. Since lift is a variable in a data frame, we have to refer to it as short$lift.
short <- inspect(sort(cr5, by="lift"))## lhs rhs support confidence coverage
## [1] {lost job} => {tax debt} 0.2 0.6666667 0.3
## [2] {tax debt} => {lost job} 0.2 0.6666667 0.3
## [3] {lost job} => {drug abuse} 0.2 0.6666667 0.3
## [4] {drug abuse} => {lost job} 0.2 0.4000000 0.5
## [5] {violent crime} => {divorced} 0.2 0.6666667 0.3
## [6] {divorced} => {violent crime} 0.2 0.4000000 0.5
## [7] {violent crime} => {drug abuse} 0.2 0.6666667 0.3
## [8] {drug abuse} => {violent crime} 0.2 0.4000000 0.5
## [9] {divorced} => {drug abuse} 0.3 0.6000000 0.5
## [10] {drug abuse} => {divorced} 0.3 0.6000000 0.5
## [11] {tax debt} => {parents divorced} 0.2 0.6666667 0.3
## [12] {parents divorced} => {tax debt} 0.2 0.3333333 0.6
## [13] {violent crime} => {parents divorced} 0.2 0.6666667 0.3
## [14] {parents divorced} => {violent crime} 0.2 0.3333333 0.6
## [15] {divorced} => {parents divorced} 0.3 0.6000000 0.5
## [16] {parents divorced} => {divorced} 0.3 0.5000000 0.6
## [17] {drug abuse} => {parents divorced} 0.2 0.4000000 0.5
## [18] {parents divorced} => {drug abuse} 0.2 0.3333333 0.6
## lift count
## [1] 2.2222222 2
## [2] 2.2222222 2
## [3] 1.3333333 2
## [4] 1.3333333 2
## [5] 1.3333333 2
## [6] 1.3333333 2
## [7] 1.3333333 2
## [8] 1.3333333 2
## [9] 1.2000000 3
## [10] 1.2000000 3
## [11] 1.1111111 2
## [12] 1.1111111 2
## [13] 1.1111111 2
## [14] 1.1111111 2
## [15] 1.0000000 3
## [16] 1.0000000 3
## [17] 0.6666667 2
## [18] 0.6666667 2short[short$lift>1.2,]## lhs rhs support confidence coverage lift
## [1] {lost job} => {tax debt} 0.2 0.6666667 0.3 2.222222
## [2] {tax debt} => {lost job} 0.2 0.6666667 0.3 2.222222
## [3] {lost job} => {drug abuse} 0.2 0.6666667 0.3 1.333333
## [4] {drug abuse} => {lost job} 0.2 0.4000000 0.5 1.333333
## [5] {violent crime} => {divorced} 0.2 0.6666667 0.3 1.333333
## [6] {divorced} => {violent crime} 0.2 0.4000000 0.5 1.333333
## [7] {violent crime} => {drug abuse} 0.2 0.6666667 0.3 1.333333
## [8] {drug abuse} => {violent crime} 0.2 0.4000000 0.5 1.333333
## count
## [1] 2
## [2] 2
## [3] 2
## [4] 2
## [5] 2
## [6] 2
## [7] 2
## [8] 2We can select lines from the object cr5 created above with the subset() command.
After the name of the object with the connection rules, you must indicate which items you want to select.
To select all connection rules with drug abuse in either the LHS or RHS), use the following command. It is handy to save the rules sorted by lift as an object (say, x). The object is a data frame. We can select rules with, for example, \(lift>1.2\) like below.
drugsRules <- subset(cr5, items %in% "drug abuse")
x<-inspect(sort(drugsRules, by="lift"))## lhs rhs support confidence coverage
## [1] {lost job} => {drug abuse} 0.2 0.6666667 0.3
## [2] {drug abuse} => {lost job} 0.2 0.4000000 0.5
## [3] {violent crime} => {drug abuse} 0.2 0.6666667 0.3
## [4] {drug abuse} => {violent crime} 0.2 0.4000000 0.5
## [5] {divorced} => {drug abuse} 0.3 0.6000000 0.5
## [6] {drug abuse} => {divorced} 0.3 0.6000000 0.5
## [7] {drug abuse} => {parents divorced} 0.2 0.4000000 0.5
## [8] {parents divorced} => {drug abuse} 0.2 0.3333333 0.6
## lift count
## [1] 1.3333333 2
## [2] 1.3333333 2
## [3] 1.3333333 2
## [4] 1.3333333 2
## [5] 1.2000000 3
## [6] 1.2000000 3
## [7] 0.6666667 2
## [8] 0.6666667 2x[x$lift>1,]## lhs rhs support confidence coverage lift
## [1] {lost job} => {drug abuse} 0.2 0.6666667 0.3 1.333333
## [2] {drug abuse} => {lost job} 0.2 0.4000000 0.5 1.333333
## [3] {violent crime} => {drug abuse} 0.2 0.6666667 0.3 1.333333
## [4] {drug abuse} => {violent crime} 0.2 0.4000000 0.5 1.333333
## [5] {divorced} => {drug abuse} 0.3 0.6000000 0.5 1.200000
## [6] {drug abuse} => {divorced} 0.3 0.6000000 0.5 1.200000
## count
## [1] 2
## [2] 2
## [3] 2
## [4] 2
## [5] 3
## [6] 3Note that the string value after the %in% operator has to match the item content exactly! Using parts of it ("abuse"), or extensions ("drug abuse and related"), won't do.