3 Eventos

Pela Definição 1.3, tem-se que qualquer subconjunto A de um espaço amostral $\Omega$ é denominado evento aleatório (doravante referido simplesmente como evento), ou seja, se $A$ está contido em $\Omega$, então $A$ é um evento.

Exemplo.3.1 Duas moedas são lançadas, denotemos por C a face cara e por K a face coroa. Vimos que o espaço amostral é dado por: $$\Omega=\{CK, KC,CC,KK\}.$$ Seja o evento $A= \{ (K,K ) ,( K,C )\}$, então A é o evento em que a primeira moeda lançada dá coroa. Quando esse evento ocorre?

O Exemplo 3.1 motiva a seguinte definição.

Definição 3.1 Um evento ocorre quando ocorre qualquer um de seus elementos irredutíveis. Esses elementos são chamados de eventos elementares, e é denotado aqui pela letra grega minúscula $\omega$.

Então, pela Definição o 3.1, um evento elementar (ou unitário) constitui um único resultado possível do experimento, e não pode ser decomposto em eventos “menores”. Além disso, tem-se que um evento ocorre, se ocorre qualquer um de seus eventos elementares, neste caso o evento elementar ocorrido é dito favorável ao evento A.

Exemplo.3.2 Considere o experimento: “lançar duas moedas e verificar a face superior”. Quais são os eventos elementares desse experimento? Quais são favoráveis ao evento A=“cara na primeira moeda”.

Observação: a pergunta acima deverá ser respondida no conjunto de atividades no sistema AME.

Como eventos são conjuntos, são utilizadas notações, definições e propriedades da teoria matemática de conjuntos para os eventos.

3.1 Notações

1. Um ponto amostral (evento elementar) $\omega$ que está “dentro” de um evento $A$ é dito pertencer à $A$, e denota-se $\omega \in A$.

2. Se o evento elementar $\omega$ não pertence ao evento $A$, usa-se a notação $\omega \notin A$

3. Se um evento $B$ contém outro evento $A$, denota-se $B \subset A$.

4. O evento impossível do experimento é o conjunto vazio, que é denotado por $\emptyset$.

5. O conjunto vazio está contido em qualquer evento não vazio, ou seja, $\emptyset \subset A$ para todo $A \subset \Omega$.

6. $\Omega$ é o evento certo do experimento e contém todos os outros eventos.

3.2 Definições

Considere um experimento aleatório com o espaço amostral $\Omega$.

Definição 3.2 O conjunto que contém todos os subconjuntos de $\Omega$ é denominado conjunto das partes de $\Omega$ e é denotado por $\mathcal{P}(\Omega)$.

Exemplo.3.3 Seja o experimento: “laçar duas moedas e observar as faces superiores”. O espaço amostral desse experimento é $\Omega=\{CK, KC,CC,KK\}$, em que C representa cara e K representa coroa. O conjunto das partes de $\Omega$ é:

$$\begin{aligned} \mathcal{P}(\Omega) &= \left\{ \begin{array}{ll} \emptyset &\\ \{CK\}, \{KC\},\{CC\},\{KK\} & \\ \{CK,KC\}, \{CK,CC\}, \{CK,KK\}, \{KC,CC\}, \{KC,KK\}, \{CC,KK\} &\\ \{CK,KC,CC\}, \{CK,KC,KK\}, \{CK,CC,KK\}, \{KC,CC,KK\} \\ \{CK,KC,CC,KK\}. \\ \end{array} \right.\\ \end{aligned}$$

O conjunto das partes de um espaço amostral é um conjunto de conjuntos, sendo chamado de classes de conjuntos. Pode ser mostrado que o conjunto das partes de um espaço amostral tem $2^n$ elementos, em que n denota o número de elementos no espaço amostral, para uma ilustração veja, por exemplo, Morettin (2010).

Considere um experimento aleatório com espaço amostral $\Omega$ em que os eventos $A$ e $B$ são tais que $A \in \mathcal{P}(\Omega)$, deste modo, valem as seguintes definições.

Definição 3.3 A união dos eventos A e B é dada por $\mbox{A} \cup \mbox{B}=\left\{ \omega \in \Omega: \omega \in \mbox{A} \mbox{ ou } \omega \in \mbox{B} \right\}$, como mostra o diagrama de Venn na Figura 3.1.

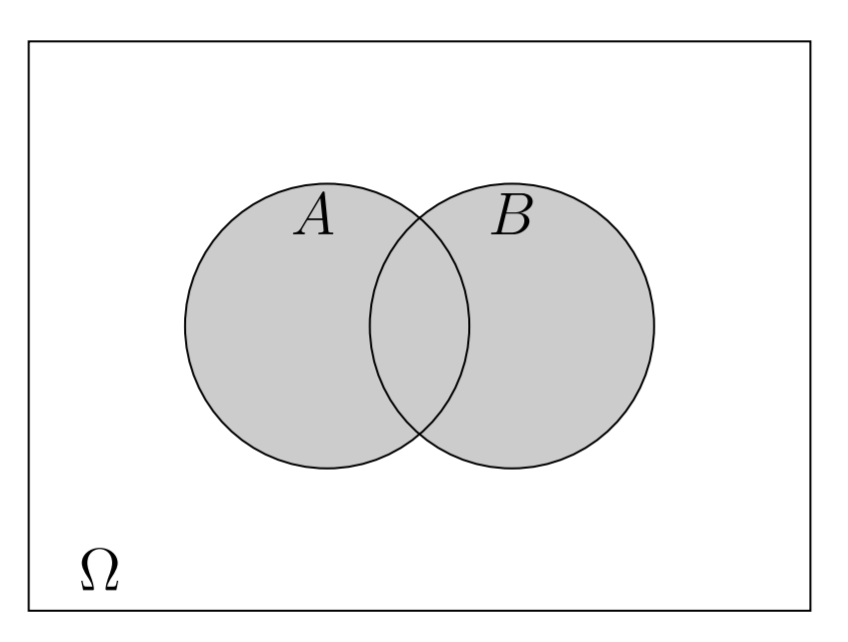
Figura 3.1: :União dos eventos A e B.

Definição 3.4 A interseção dos eventos A e B é dada por: $\mbox{A} \cap \mbox{B}=\left\{ \omega \in \Omega: \omega \in \mbox{A} \mbox{ e } \omega \in \mbox{B} \right\}$, como mostra o diagrama da Figura 3.2.

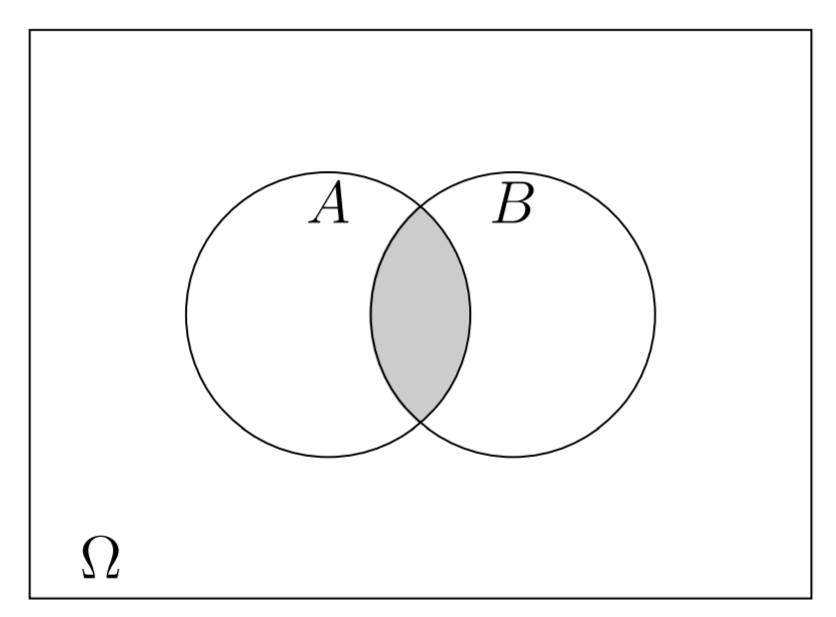
Figura 3.2: :Interseção dos eventos A e B.

Definição 3.5 O complementar de A é dado por: A$^{\mbox{c}}= \Omega -\mbox{A} =\{\omega \in \Omega; \omega \not\in \mbox{A} \}$. Para essa situação veja o diagrama da Figura 3.3.

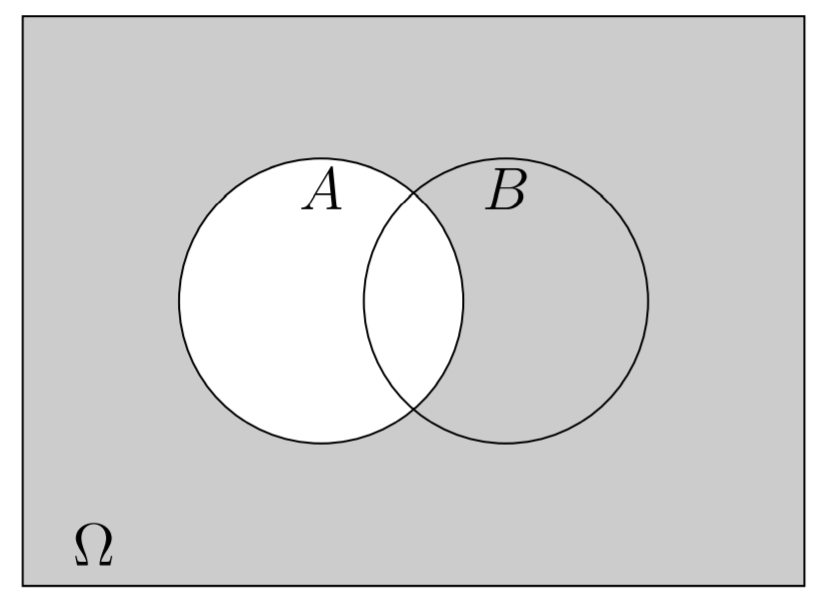
Figura 3.3: : Complementar do evento A.

Definição 3.6 Se $\mbox{A} \cap \mbox{B}=\emptyset$, então dizemos que A e B são eventos disjuntos ou mutuamente excludentes. Veja a representação na Figura 3.4.

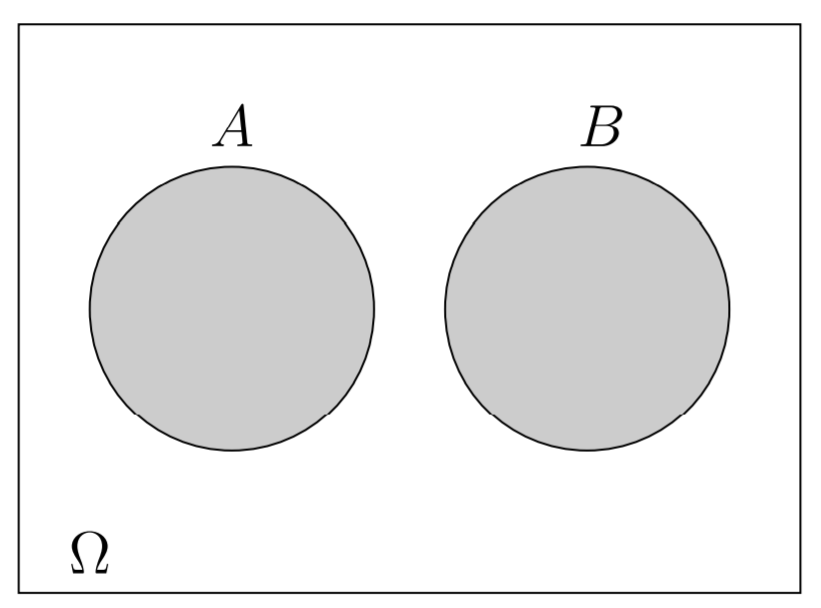
Figura 3.4: : Eventos disjuntos ou mutuamente excludentes.

3.2.1 Generalização das definições

As definições e propriedades apresentadas anteriormente podem ser generalizadas para qualquer quantidade de eventos $A_1,A_2,A_3,...,A_n, n\geq2$ no espaço amostral $\Omega$. Para união e interseção, têm-se:

1. União: $$\displaystyle\bigcup_{i=1}^{n}A_i= A_1 \cup A_2 \cup A_3\cup ...\cup A_n=\{\omega \in A_i \mbox{ para algum } i \}.$$

2. Interseção: $$\displaystyle\bigcap_{i=1}^{n}A_i= A_1\cap A_2 \cap A_3\cap ...\cap A_n=\{\omega \in A_i\mbox{ para todo } i\}.$$

3.3 Propriedades

Propriedade 3.1 (Idempotência) Dado $A \subset \Omega$, tem-se que:

• $(A^c)^c=A$;

• $\Omega^c=\emptyset$;

• $\emptyset^c=\Omega$.

Exemplo.3.4 Seja $\Omega=\{1,6,9,3,8,7\}$ e o evento $A \subset\Omega$ tal que: $A=\{9,7,1\}$. Então, $A^c=\{1,6,3,8\}$ o que implica:

• $(A^c)^c=(\{1,6,3,8\})^c=\{9,7,1\}=A$.

Propriedade 3.2 (Comutatividade) Dados $A,B \subset \Omega$, tem-se:

• $A \cup B = B \cup A$;

• $A \cap B = B \cap A$.

Propriedade 3.3 (Associatividade) Dados $A, B, C \subset \Omega$, tem-se:

• $A \cup (B \cup C)= (A \cup B) \cup C$;

• $A \cap (B \cap C)= (A \cap B) \cap C$.

Propriedade 3.4 (Distributividade) Dados $A, B, C \subset \Omega$, tem-se:

• $A \cup (B \cap C)= (A \cup B) \cap (A \cup C)$;

• $A \cap (B \cup C)= (A \cap B) \cup (A \cap C)$.

Exemplo.3.5 Seja $\Omega=\{a,b,c,d,e,f,g\}$ e o evento $A \subset\Omega$ tal que: $A=\{a,b,c\}$, $B=\{b,c\}$ e $C=\{a,c,g\}$. Observe os eventos:

• $(A \cap B)=\{b,c\}$;

• $(A \cap C)=\{a,c\}$;

• $(B \cup C)=\{a,b,c,g\}$;

• $(A \cap B) \cup (A \cap C)=\{a,b,c\}$;

• $A \cap (B \cup C)=\{a,b,c\} \cap \{a,b,c,g\}=\{a,b,c\}$.

Dos eventos acima, tem-se:

$A \cap (B \cup C)= \{a,b,c\}= (A \cap B) \cup (A \cap C)$.

3.3.1 Leis de De Morgan

Essas leis representam importantes propriedades dos conjuntos para a teoria das probabilidades e são enunciadas a seguir.

Propriedade 3.5 (Lei de De Morgan 1) $$(A \cup B)^c = A^c \cap B^c=\Omega-A \cup B$$

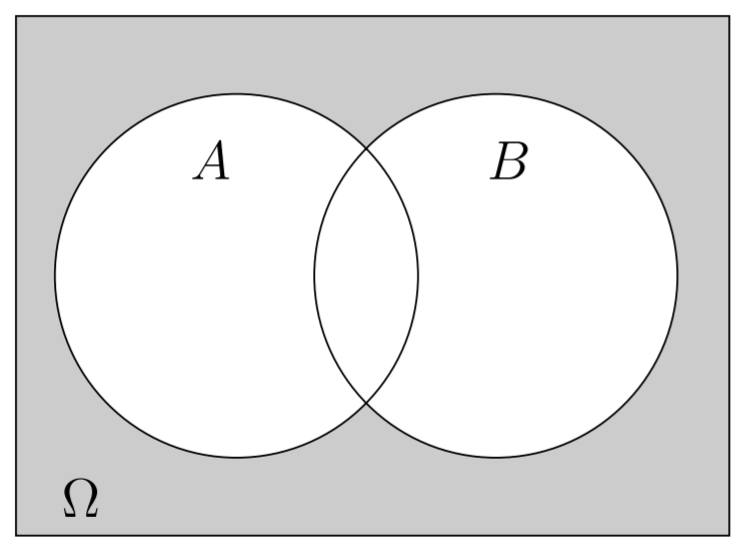
Figura 3.5: : Lei de De Morgan 1.

Propriedade 3.6 (Lei de De Morgan 2) $$(A \cap B)^c = A^c \cup B^c=\Omega-A \cap B$$

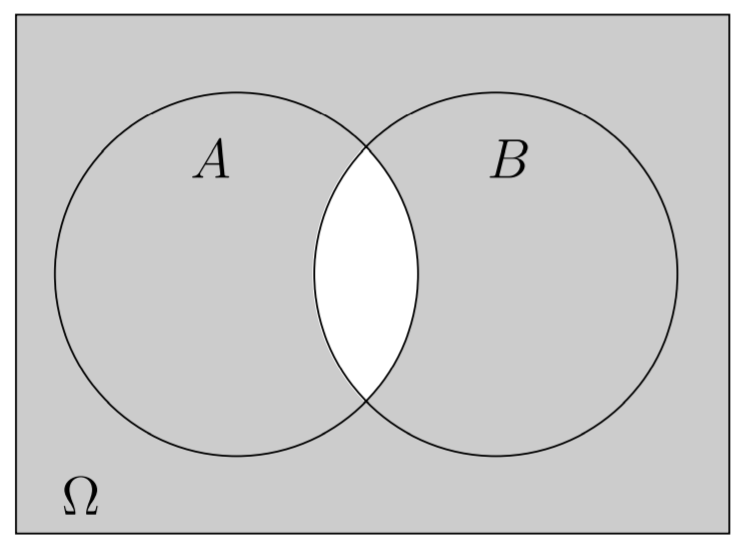
Figura 3.6: : Lei de De Morgan 2.

Tabela 3.1: Dados fornecidos por estudantes ingressantes do ano de 2020 nos cursos de engenharias do Campus da UFC de Russas.

Cidade	UF	Sexo	Curso
Limoeiro do Norte	CE	Feminino	Engenharia Mecânica
Aracati	CE	Feminino	Engenharia de Produção
Limoeiro do Norte	CE	Masculino	Engenharia de Produção
Quixadá	CE	Masculino	Engenharia Mecânica
Russas	CE	Masculino	Engenharia Mecânica
continua …	continua …	continua …	continua …

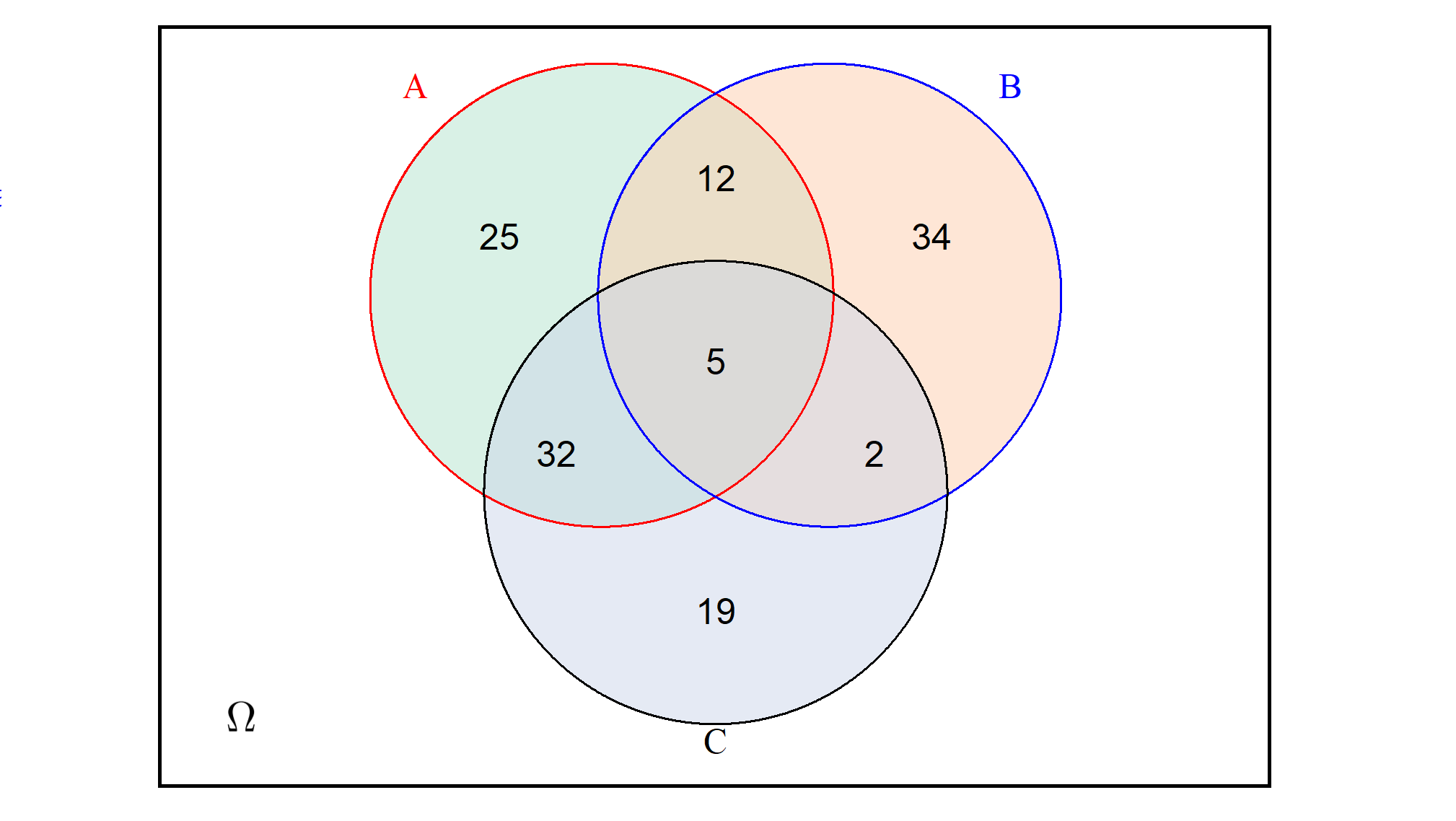
Figura 3.7: : Diagrama de Venn para os conjuntos A, B e C.

Exemplo.3.6 Considere as variáveis “Sexo”, “Curso” e “Cidade” de estudantes do Campus da UFC de Russas, cujas primeiras 5 linhas das observações estão mostradas na Tabela 3.1. Considere, também, os seguintes eventos:

• A= “estudantes do sexo Feminino”

• B= “estudantes que moram e Russas”

• C= “estudantes do curso de Engenharia de Produção”

Suponha ainda que as quantidades de indivíduos para cada um desses eventos estão descritas no diagrama de Venn mostrado na Figura 3.7. Com base nesse diagrama, podem ser obtidas as quantidades de elementos nos seguinte eventos:

1. $\#(A \cup B)=110$

2. $\#(A \cap B \cap C)= 5$

3. $\#((A\cap C)\cup (A\cap B^c))=193$

4. $\#(A\cup B \cup C)=25+12+34+32+5+2+19=129$

5. Sabendo que são 209 estudantes ao todo, $\#((A\cup B \cup C)^c)=80$

6. Dado o item (e) e (d), $\#(A^c \cap C^c)=34+(209-129)=114$

Observação: $\#(A)$ significa número de elementos no conjunto A.

Exemplo.3.7 Suponha uma comunidade e os seguintes eventos:

A= “pessoas que gotam de animais de estimação”

B= “pessoas que gotam de futebol”

C= “pessoas que não gostam de esportes”

Suponha ainda que as quantidades de indivíduos para cada um desses eventos estão descritas no diagrama de Venn mostrado na Figura 3.8.

Com base nesse diagrama, podem ser obtidas as quantidades de elementos nos seguinte eventos:

1. $\#(A \cup B)=150$

2. $\#(A \cap B \cap C^c)=50$

3. $\#(A \cap B \cap C)= \#\emptyset=0$

4. $\#((A\cap C)\cup (A\cap B^c))=\#\emptyset=0$

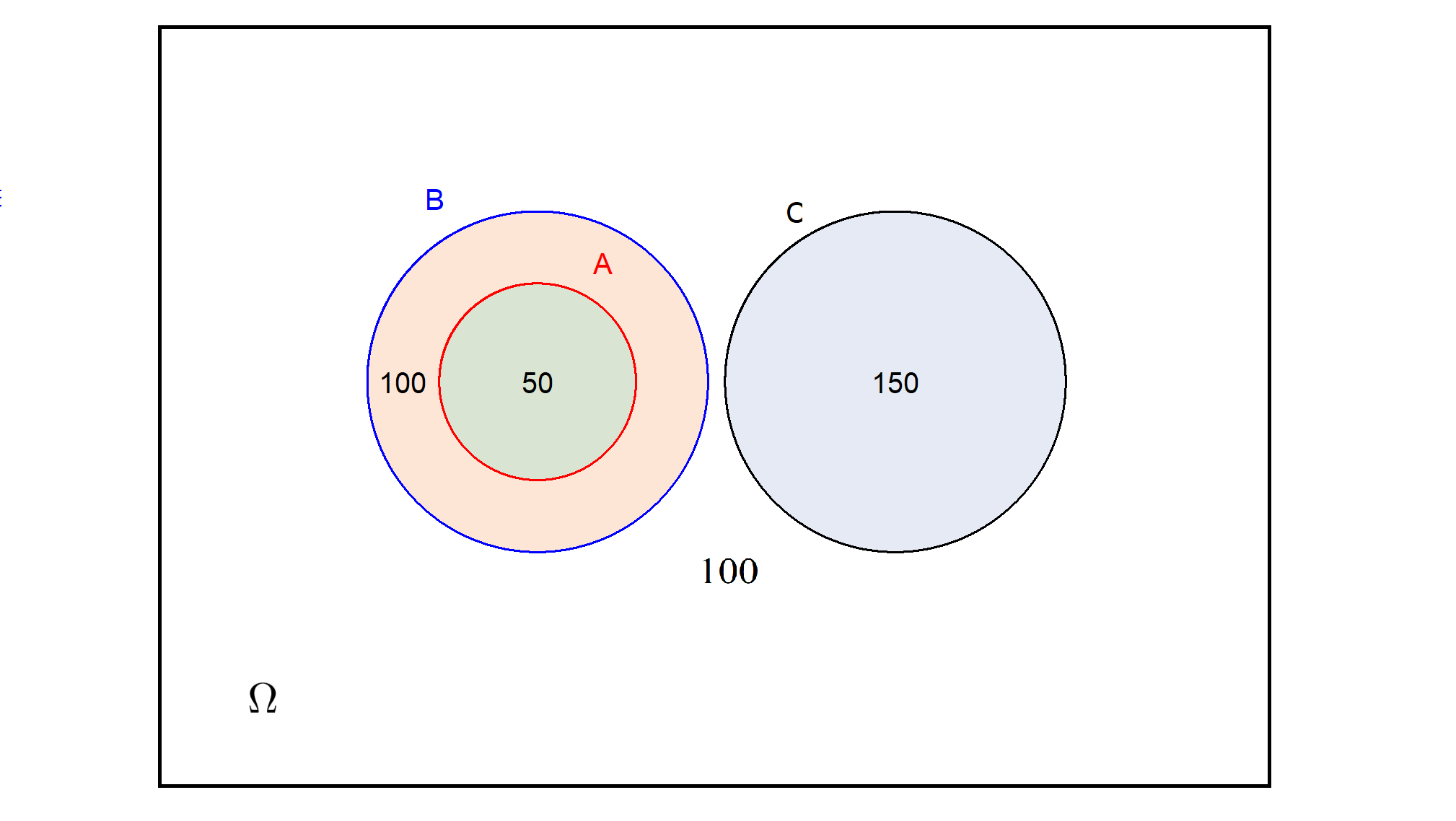
Figura 3.8: : Diagrama de Venn para os conjuntos A, B e C.

Exemplo.3.8 Considere agora o diagrama de Venn mostrado na Figura @fig(fig:diagram3), quais letras minúsculas correspondem aos eventos a seguir:

1. $(A \cup B)^c= (e \cup f)$

2. $A \cap C= b \cup c$

3. $(A \cup B \cup C)^c= f$

4. $B^c=a \cup b \cup e \cup f$

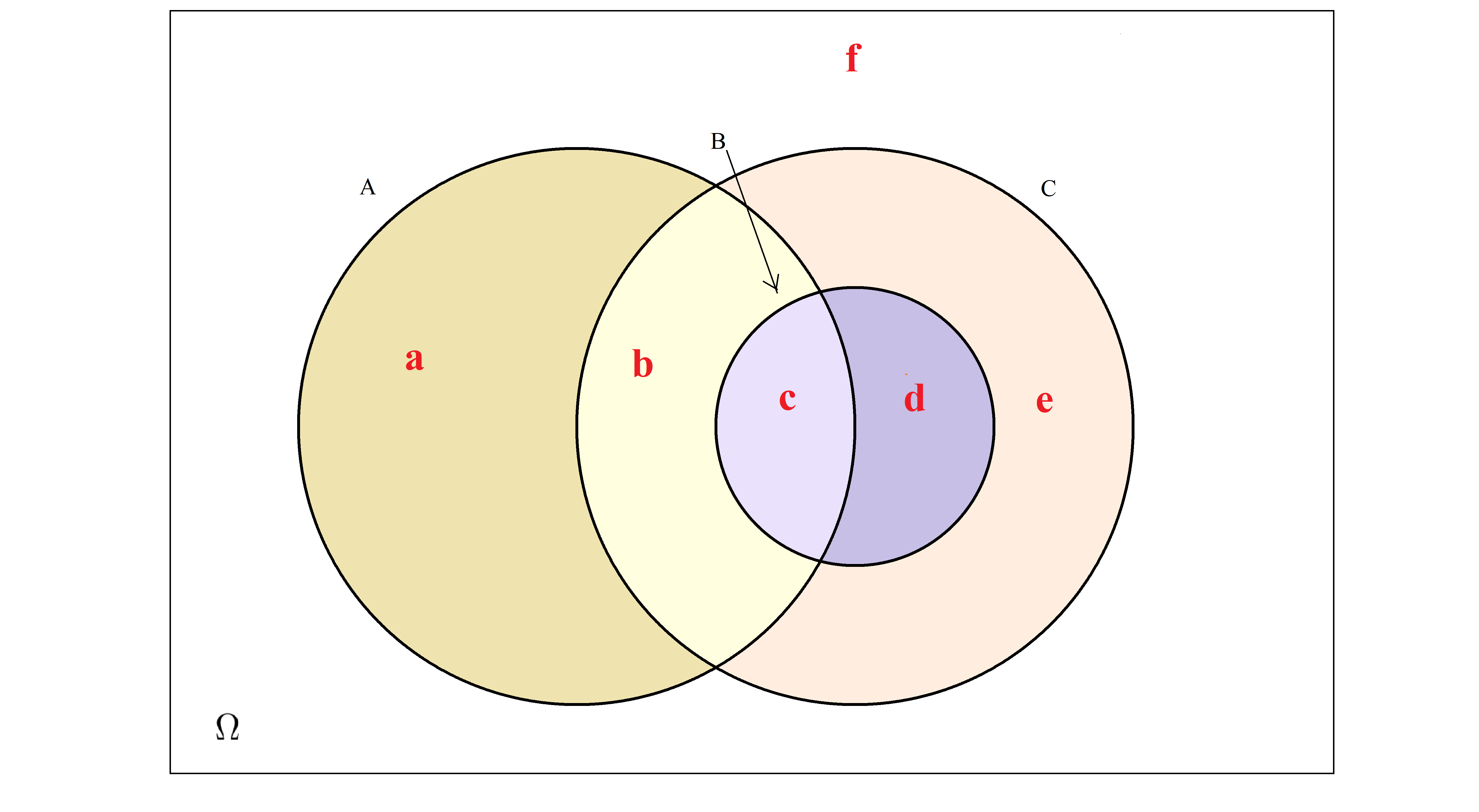
Figura 3.9: : Diagrama de Venn para os conjuntos A, B e C.

Referências

Morettin, Luiz Gonzaga. 2010. Estatı́stica Básica: Probabilidade E Inferência: Volume único. Pearson Prentice Hall.