Chapter 1 Probability Taster Session

1.1 Introduction

This probability taster session provides a brief introduction to the concepts of conditional probability and expectation which are two key concepts in the study of probability. These concepts are studied through two related problems, the birthday problem and the coupon collector problem with collecting of football stickers for the 2022 Fifa World Cup providing a working example throughout. The mathematical concepts introduced in this session are explored further in the Foundations of Statistics module in the MSc in Statistical Science (Distance Learning).

1.2 Motivating Example

For the 2022 Fifa World Cup, Panini produced a sticker album containing 670 distinct stickers.

Assuming that I collect stickers one at a time and each sticker is equally likely to be a copy of any one of the 670 distinct stickers:

How many stickers do I need to collect before I obtain a duplicate sticker?
How many stickers do I need to collect to complete the album?

The first question is known as the birthday problem and the second question is known as the coupon collector problem. In order to answer the questions we need to start with defining probability.

1.3 Probability

We present a brief overview of probability.

The general idea is:

We have a conceptual random experiment $\mathcal{E}$.
We have a list of outcomes $\Omega$, the sample space for the experiment $\mathcal{E}$ but we don’t know which occurs, has occurred or will occur.
We assign to each possible outcome $\omega$ a real number which is the probability of that outcome.

A simple example is rolling a die.

Rolling a die.

The experiment is rolling a fair six-sided die.

The sample space for the roll of the die is

\[\Omega = \{ 1,2,3,4,5,6 \},\]

that is, the set of the six possible outcomes.

The individual outcomes are $\omega = \{1\}, \{2 \}, \ldots, \{6\}$ and we will discuss the probability of each outcome after defining probability.

A probability measure is a real-valued function ${\rm P}$ defined on the events of a sample space, $\Omega$, (set of possible outcomes) which satisfies the following three axioms:

A1. (Positivity) ${\rm P}(A) \geq 0$ for any event $A$.
A2. (Finitivity) ${\rm P}(\Omega) = 1.$
A3. (Additivity) If $A$ and $B$ are disjoint (mutually exclusive) event,
\[ {\rm P} (A \mbox{ or } B) ={\rm P}(A) +{\rm P}(B). \]

Rolling a die. (Revisited)

Let $E_k$ $(k=1,2,\ldots,6)$ be the event that the outcome of the die roll is $\{k\}$. Then \[ {\rm P} (E_k) = \frac{1}{6}.\]

The probability of any event $A$ which consists of $m$ possible outcomes, i.e. numbers between 1 and 6, inclusive, is \[ {\rm P} (A) = \frac{m}{6}.\]

For example, suppose $A$ is the outcome an odd number $\{1,3,5\}$, then \[ {\rm P} (A) = \frac{3}{6} = \frac{1}{2}.\]

1.4 Conditional Probability

Suppose that we have an idea of the probability of some event, but then are given some additional piece of information (a condition). We may be able to adjust the probability of the event given this condition.

Keeping with a football theme:

Suppose we think at the start of the match there is a 60% chance that Brazil will beat France.
At half time we are told that France are winning 4-1.
We would adjust the probability of Brazil winning downwards!

The conditional probability of event $A$, given that event $B$ has occurred, is denoted by ${\rm P}(A \mid B)$ and is defined as \[{\rm P}(A \mid B) = \frac{{\rm P}(A \mbox{ and } B)}{{\rm P}(B)}, \qquad {\rm P}(B) > 0.\]

1.5 Birthday Problem

The traditional birthday problem question is:

How likely is it that, in a group of $M$ individuals two or more people share a birthday?

The complementary question is:

How likely is it that, in a group of $M$ individuals everybody has a distinct birthday?

A related question in the context of sticker collection is:

What is the probability that the first 30 stickers are all different?

Think about the question and then click to reveal the answer.

The probability that the first 30 stickers are all different is: $0.5174$.

There is only just over a $50\%$ chance that they are all different, is that what you expected.

Watch Video 1 for a derivation of the probability that the first 30 stickers are all different.

Video 1: Birthday problem

Alternatively the solutions are available:

Birthday problem derivation

Let $p_k := {\rm P}$(First $k$ stickers are distinct).

Then $p_1 =1$ and $p_2 = 669/670$. There can be no duplicates with a single sticker and the second sticker will be different from the first sticker if it is any of the 669 stickers other than the first sticker.

Suppose that \[ p_{k-1} = \frac{670}{670} \times \frac{669}{670} \times \ldots \times \frac{670 - (k-2)}{670}. \] We define two events: \[A = \{\mbox{First $k$ stickers are distinct} \} \] and \[B = \{\mbox{First $k-1$ stickers are distinct} \}. \] Note that $A$ implies $B$ and this means \[ {\rm P} (A \mbox{ and } B ) = {\rm P} (A).\] Therefore we can use conditional probability to write \[\begin{eqnarray*} {\rm P} (A) &=& {\rm P} (A \mbox{ and } B ) \\ &=& {\rm P} (A \mid B ) {\rm P} (B), \end{eqnarray*}\]

where ${\rm P} (B) = p_{k-1}$.

Now if event $B$ has occurred the first $k-1$ stickers are all different. If the $k^{th}$ sticker is any of the $670 - (k-1)$ stickers that have not been selected in the first $k-1$ stickers then the event $A$ also occurs. Therefore \[ {\rm P} (A \mid B) = \frac{670 -(k-1)}{670}, \] and \[\begin{eqnarray*} p_k ={\rm P} (A) &=& {\rm P} (A \mid B ) {\rm P} (B) \\ &=& \frac{670 -(k-1)}{670} \times \left(\frac{670}{670} \times \frac{669}{670} \times \ldots \times \frac{670 - (k-2)}{670} \right) \\ &=& \frac{670}{670} \times \frac{669}{670} \times \ldots \times \frac{670 - (k-1)}{670}. \end{eqnarray*}\]

The above holds for all $k$ (proof by induction).

Inserting $k=30$ into the above yields: \[\begin{eqnarray*} p_{30} &=& \frac{670}{670} \times \frac{669}{670} \times \ldots \times \frac{641}{670} \\ &=& 0.5174. \end{eqnarray*}\]

Let the random variable $X$ denote how many stickers are collected until the first duplicate occurs. Therefore $X=k$ means that the first $k-1$ stickers are all distinct and the $k^{th}$ sticker is a duplicate of one of the first $k-1$ stickers. Then we can compute the probability mass function (pmf) of $X$, ${\rm P} (X=k)$ and the cumulative distribution function (cdf) of $X$, ${\rm P} (X \leq k)$.

In Figures 1.1 and 1.2, we plot the pmf and cdf of $X$, respectively. We observe that the first duplicate sticker is likely to occur between sticker 20 and sticker 35 with the highest probabilities of the first duplication being for values of $k$ in this range. Note that ${\rm P} (X \leq 77) =0.9906$, so there is a less than $1\%$ chance that the first 77 stickers are all unique.

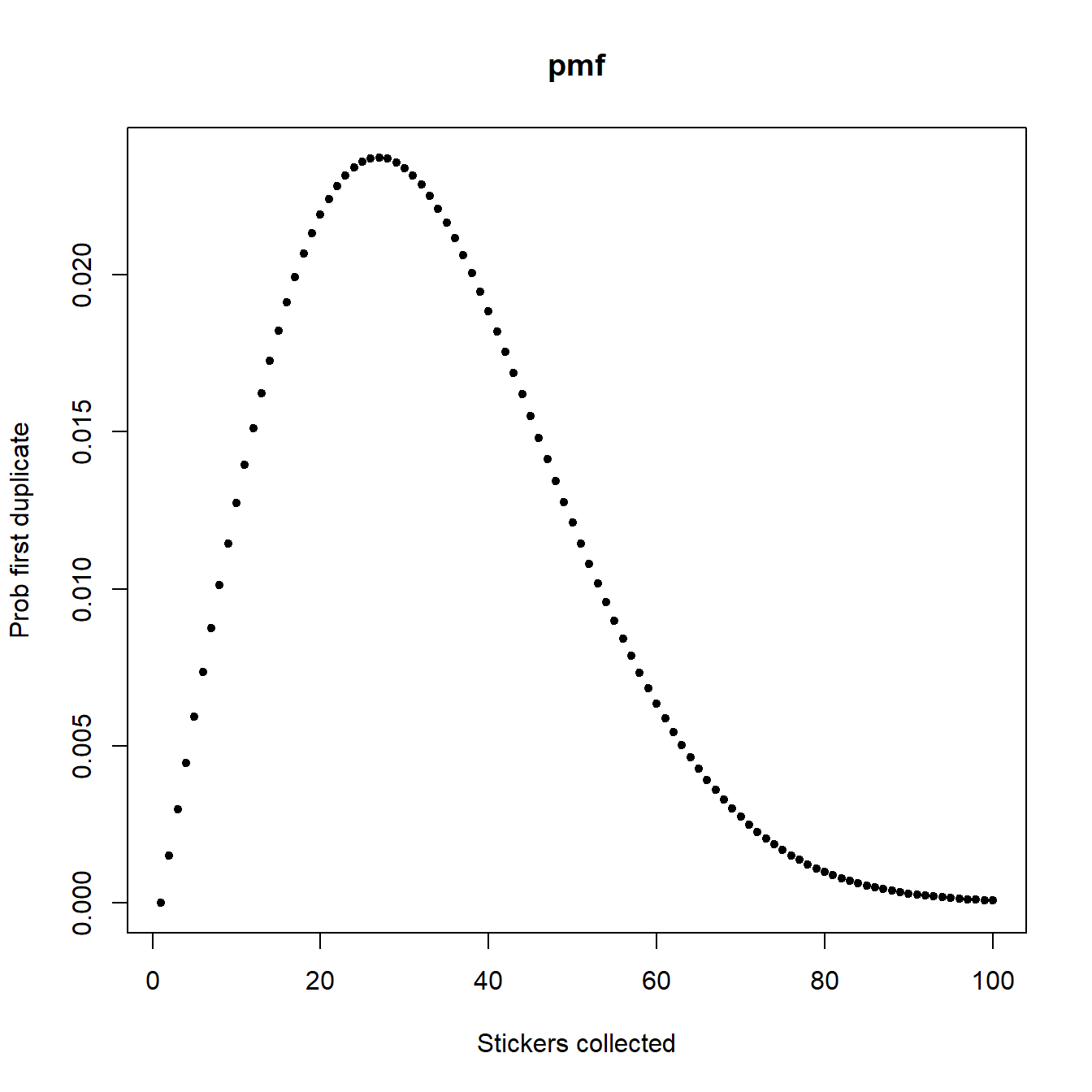
$Probability of first duplicate at the $k^{th}$ sticker$

Figure 1.1: Probability of first duplicate at the $k^{th}$ sticker

$Probability of first duplicate by the $k^{th}$ sticker$

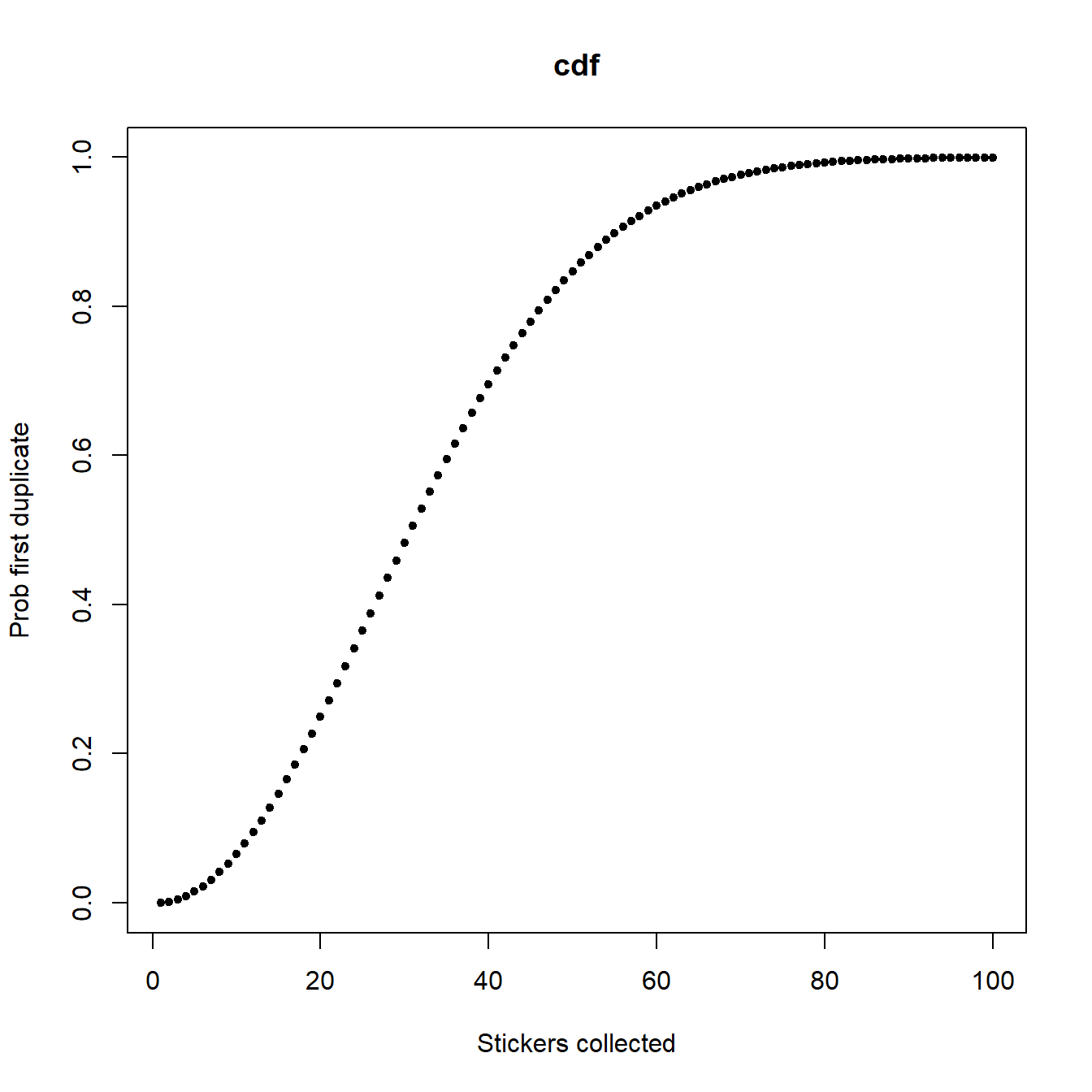
Figure 1.2: Probability of first duplicate by the $k^{th}$ sticker

Discussion of the Birthday problem

The R shiny app sticker birthday allows you to explore how the distribution of many stickers need to be collected until the first duplicate varies as the total number of stickers to be collected varies.

For the classic birthday problem with $N=365$ (birthdays/stickers), there becomes a greater than $50\%$ chance that two people share a birthday once you have a group of size 23. For a typical school class of 30 pupils this rises to a greater than $70\%$ chance.

The assumption that all stickers (birthdays) are equally likely represents the least likely scenario to obtain a duplicate in the first $k$ stickers (individuals). Unless some stickers/dates are very likely/unlikely the assumption that all stickers/dates are equally likely gives a good approximation. In the UK individuals are more likely to be born on a weekday than at a weekend with dates in late September having the most births per day and Boxing Day ($26^{th}$ December) usually having the fewest births.

The question of when a match occurs plays a key role in modelling infectious diseases.

In the early stages of a disease (Covid-19) most infectious contacts are with susceptibles. We can approximate the epidemic process by a (simpler) birth-death process with infection = birth and removal = death. This is effective until we start seeing individuals contacted with the disease for a second time (the birthday problem).

1.6 Expectation

In Section 1.5 we introduced a random variable $X$ for the number of stickers collected until we have the first duplicate. For the random variable $X$, we can define the probability mass function, ${\rm P} (X=k)$ and the cumulative distribution function, ${\rm P} (X \leq k)$.

The first duplicate can occur on the $k^{th}$ sticker where $k=2,3,\ldots,671$ since we must have at least 2 stickers to obtain a duplicate and if we have not seen a duplicate in the first 670 stickers, then we have collected all the stickers and sticker 671 must be a duplicate.

A useful summary for $X$ is its expectation, the average number of stickers collected until a duplication occurs.

The expectation of a discrete random variable $Y$ with probability mass function ${\rm P} (Y=y)$ $(y=0,1,\ldots)$ is given by \[ {\rm E} [Y] = \sum_{y=0}^\infty y {\rm P} (Y=y).\]

First duplicate The expected number of stickers collected until the first duplication occurs, ${\rm E} [X]$, is \[ {\rm E} [X] = \sum_{x=2}^{671} x {\rm P} (X=x) = 33.136. \] Note that the expected (average) number will typically not be a possible (integer) outcome.

1.7 Coupon Collector Problem

There are 670 distinct stickers to collect.

How many stickers, on average, will I need to buy to complete the album?

Think about the question, what do you think the answer is to the nearest 100.

Click to reveal the answer.

The expected number of stickers that are required is $4747.11$, which is $4700$ to the nearest 100.

The first step to answering the question is to answer the following question:

Suppose that I have $K$ ($K=0,1,\ldots,669$) distinct stickers. How many more stickers, on average, do I need to collect to have $K+1$ distinct stickers?

Watch Video 2 for an answer to the question.

Video 2: Coupon Collection problem

Alternatively the details are available:

Coupon collector problem derivation

We can define a random variable $W$ for the number of additional stickers I need to collect.

Consider the next sticker I receive. Either:

The sticker is new to me. Success
It is a sticker I already have. Failure

The probability I am successful at each attempt is \[ p =\frac{670 -K}{670}, \]

and the probability I fail is $1-p =K/670$.

Hence, $W=w$ if we have $w-1$ failures followed by a success and \[ {\rm P} (W=w) =(1-p)^{w-1} p. \hspace{1cm} (w=1,2,\ldots) \] Now $W$ is an example of a geometric random variable and \[\begin{eqnarray*} {\rm E}[W] &=& \sum_{w=1}^\infty w (1-p)^{w-1} p. \end{eqnarray*}\]

What is $\sum_{w=1}^\infty w(1-p)^{w-1}$?

A geometric series with $0 \leq x <1$ satisfies \[ \sum_{n=0}^\infty x^n = 1 + x + x^2 + \ldots = \frac{1}{1-x}. \] Differentiating with respect to $x$ gives \[ \sum_{n=0}^\infty n x^{n-1} = 0 + 1 + 2x + \ldots = \frac{1}{(1-x)^2}. \] Hence, if we take $x=1-p$, \[{\rm E}[W] = p \sum_{w=1}^\infty w (1-p)^{w-1} =\frac{p}{p^2} = \frac{1}{p}. \] Thus \[ {\rm E}[W] = \frac{670}{670-K}. \]

How many stickers do we need to buy in total?

For $k=1,2,\ldots,670$, let $W_k$ denote the number of additional stickers we need to buy after we have the $(k-1)^{st}$ distinct sticker to get the $k^{th}$ distinct sticker.

Then $W_k$ is a geometric random variable with \[ {\rm E}[W_k] = \frac{670}{670-(k-1)}. \]

The total number of stickers we are required to buy to get all 670 stickers is: \[ W_1 + W_2 + \ldots + W_{670}, \] and the expected number is \[ \frac{670}{670-0} + \frac{670}{670-1} + \ldots + \frac{670}{670-669} = 4747.11. \]

At a cost of $90p$ for a packet of 5 stickers ($18p$ per sticker), that is an expected cost of £854.48 to complete the sticker album.

Discussion of the Coupon collector problem

The R shiny app sticker coupon allows you to explore how the distribution of many stickers need to be bought to complete varies with the number of stickers to collect. It also uses simulation to explore the effects on the distribution. For example, knowing the distribution helps answer:

What is the probability it costs over £1000 to complete the album?

Answer

If 5556 or more stickers are required to complete the album is costs over £1000.

Exact calculation is extremely tedious but based on 100,000 simulations, 15,472 simulations required over 5556 stickers to complete the album. That is, we estimate the probability of it costing more than £1000 to complete the album to be $0.15472$.

We can explore how many stickers are we required to buy to collect $K$ distinct stickers, which is given by \[ \frac{670}{670-0} + \frac{670}{670-1} + \ldots + \frac{670}{670-(K-1)}. \]

For what value of $K$ does the expected number of stickers required to collect $K$ stickers first exceed 670?

Answer.
We know $K > 670/2 = 335$ since until we have collected half the stickers we are more likely to get a new sticker than one we already have.
The answer is $K=423$ with $670.44$ stickers on average required to be bought to collect 423 distinct stickers.
Note that it takes on average $670$ stickers to collect the final sticker.
Which requires, on average, more stickers to be bought;

to get the first 650 stickers
or
to get the final 20 stickers?

Answer.
It is close but on average only 2336.62 stickers are required to be bought to get the first 650 stickers, with on average an additional 2410.49 stickers needed to be bought to get the final 20 stickers to complete the album.
The expected number of stickers required to be bought to collect $K$ distinct stickers is given in Figure 1.3.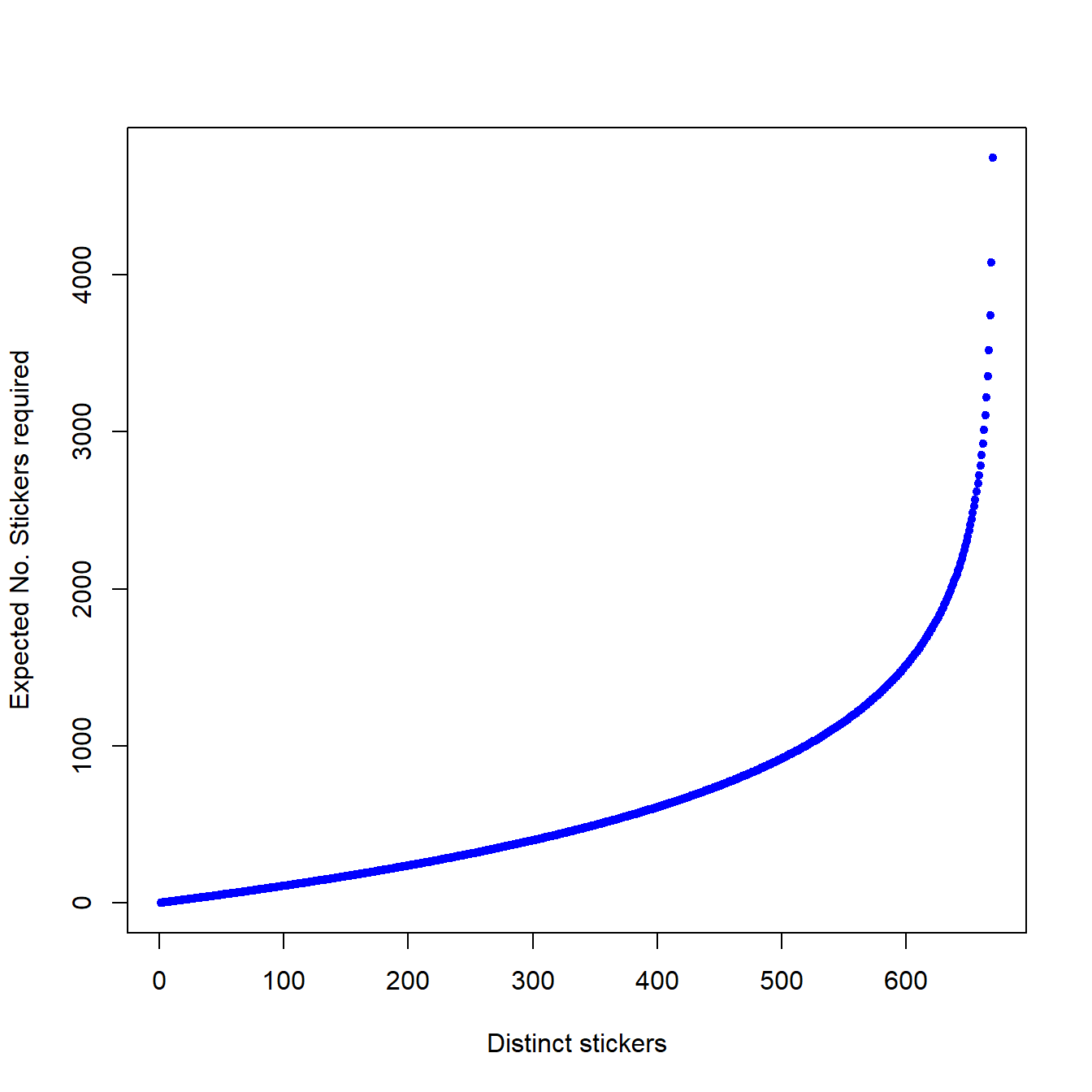

Figure 1.3: Expected number of stickers required to collect $K$ distinct coupons

1.8 Conclusions

This taster session has provided insight into the birthday and coupon collector problems. It has discussed concepts such as:

Conditional Probability.
Expectation.
Geometric Random Variables.

There are numerous extensions of the birthday and coupon collector problems which can be considered such as:

When do we first get a sticker for the third time?
How many stickers do we need to buy to collect 2 complete sets?
What happens if the stickers have unequal probabilities?