Determine whether a relation represents a function.
Find the value of a function.
Determine whether a function is one-to-one.
Use the vertical line test to identify functions.
Graph the functions listed in the library of functions.
1.1 Determining Whether a Relation Represents a Function
Definition 1.1 (Relation - domain - range)
“A relation is a set of ordered pairs. The set of the first components of each ordered pair is called the domain and the set of the second components of each ordered pair is called the range.” (Abramson, 2021, p. 18) (pdf)
Definition 1.2 (Function) “A function is a relation in which each possible input value leads to exactly one output value. We say ‘the output is a function of the input.’ The input values make up the domain, and the output values make up the range.” (Abramson, 2021, p. 18) (pdf)
Procedure
Given a relationship between two quantities, determine whether the relationship is a function.
Identify the input values.
Identify the output values.
If each input value leads to only one output value, classify the relationship as a function. If any input value leads to two or more outputs, do not classify the relationship as a function.
Example 1.1 Are price lists examples of functions?
Each item has its price, so the price is a function of its items. This is even valid if several items have the same price because there is for each item exactly one price.
Several items have the same price, that’s why item is not a function of price.
1.1.1 Using Function Notation
Definition 1.3 (Function Notation: Input value - independent variable & Output value - dependent variable)
“The notation \(y = f(x)\) defines a function named \(f\), This is read as ‘y is a function of x’. The letter \(x\) represents the input value, or independent variable. The letter \(y\) or \(f(x)\) represents the output value, or dependent variable.” (Abramson, 2021, p. 21) (pdf)
1.1.2 Representing Functions Using Tables
“A common method of representing functions is in the form of a table. The table rows or columns display the corresponding input and output values.” (Abramson, 2021, p. 22) (pdf)
1.2 Finding Input and Output Values of a Function
1.2.1 Evaluation of Functions in Algebraic Forms
Procedure
Given the formula for a function & evaluate
Substitute the input variable in the formula with the value provided.
Calculate the result.
Example 6: Evaluating Functions at Specific Values
Given the function \(g(m) = \sqrt{m - 4}\), evaluate g(5)
\[
g(5) = \sqrt{5 - 4} = 1
\]
Example 8: Solving Functions
Given the function \(h(p) = p^2 + 2p\), solve for \(h(p) = 3\)
\[
\begin{align*}
3 = p^2 + 2p\\
p^2 + 2p - 3 = 0 \text{ [substract 3 from each side]} \\
(p + 3) (p - 1) = 0 \text{ [factor]}\\
\text{set each factor equal to 0 and solve for p in each case} \\
p + 3 = 0, p = -3 \\
p - 1 = 0, p = +1
\end{align*}
\tag{1.1}\]
Wach out!
I couldn’t solve Example 8 (Equation 1.1), because I didn’t use the factor transformation of the equation. I came up with only one solution \(p = 1\) after I had transformed to \(p^2 + 2p - 3 = 0\).
For a better understanding I replicated Figure 6 of the book, p.16.
Listing 1.1: Plot function \(h(p) = p^2 + 2p\)
ggplot2::ggplot()+ggplot2::scale_x_continuous(limits =c(-5, 5), breaks =seq(-5, 5, 1))+ggplot2::geom_function(fun =function(x)x^2+(2*x))+ggplot2::geom_hline(yintercept =0, linetype ="solid")+ggplot2::geom_hline(yintercept =3, linetype ="solid", color ="darkgreen", linewidth =1)+ggplot2::geom_segment(ggplot2::aes(x =-3, y =0, xend =-3, yend =+3, color ="orange"), show.legend =FALSE, linewidth =1)+ggplot2::geom_segment(ggplot2::aes(x =1, y =0, xend =1, yend =+3, color ="orange"), show.legend =FALSE, linewidth =1)+ggplot2::geom_point(ggplot2::aes(x =-3, y =+3, fill ="blue"), size =2, show.legend =FALSE)+ggplot2::geom_point(ggplot2::aes(x =1, y =+3, fill ="blue"), size =2, show.legend =FALSE)+ggplot2::theme_bw()+ggplot2::labs( title =expression(paste("Function h(p) = ", p^2+2*p)), x ="p", y ="h(p)")
Graph 1.1: Graph for the function \(h(p) = p^2 + 2p\) showing the solution for \(h(p) = 3\)
Try It 5
Given the function \(g(m) = \sqrt{m - 4}\), solve \(g(m) = 2\)
Given a function in equation form, write its algebraic formula
“Some functions are defined by mathematical rules or procedures expressed in equation form. If it is possible to express the function output with a formula involving the input quantity, then we can define a function in algebraic form.” (Abramson, 2021, p. 26) (pdf)
Solve the equation to isolate the output variable on one side of the equal sign, with the other side as an expression that involves only the input variable.
Use all the usual algebraic methods for solving equations, such as adding or subtracting the same quantity to or from both sides, or multiplying or dividing both sides of the equation by the same quantity. (Abramson, 2021, p. 26)
Example 9: Finding an Equation of a Function
Express the relationship \(2n + 6p = 12\) as a function \(p = f(n)\), if possible.
Example 10: Expressing the Equation of a Circle as a Function
Does the equation \(x^2 + y^2 = 1\) represent a function with \(x\) as input and \(y\) as output? If so, express the relationship as a function \(y = f(x)\).
My solution is wrong as it would mean that \(y = f(x)\) could be represented as function! I did not take into account that there are two solutions: \(y = \pm \sqrt{1 - x^2}\). We get for \(y\) two outputs; the formula is therefore not a function.
Try It 6
If \(x-8y^3=0\), express $y as a function of \(x\):
There are relationships expressed by an equation that do represent a function but cannot be represented by an algebraic formula.
1.2.3 Evaluating a Function Given in Tabular Form
“As we saw above, we can represent functions in tables. Conversely, we can use information in tables to write functions, and we can evaluate functions using the tables.” (Abramson, 2021, p. 27) (pdf)
Procedure
Given is input value, identify output value
Find the given input in the row (or column) of input values.
Identify the corresponding output value paired with that input value.
Given is output value, identify input value
Find the given output values in the row (or column) of output values, noting every time that output value appears.
Identify the input value(s) corresponding to the given output value.
Example 11
Table 1.1: Evaluating and Solving a Tabular Function
\(n\)
1
2
3
4
5
\(g(n)\)
8
6
7
6
8
Evaluate \(g(3)\)Solution: g(3) = 7
Solve \(g(n) = 6\)Solution: n = 2 and n = 4
Wach out!
Again I have not followed exactly the proposed procedure “noting every time that output value appears”. So I have only reported the first part of the solution \(n = 2\)!
Try it 7
Using Table 1.1 to evaluate \(g(1)\). Solution \(g(1) = 8\)
1.2.4 Finding Function Values from a Graph
Note
Don’t forget: Solving a function equation using a graph requires finding all instances of the given output value on the graph and observing the corresponding input value(s).
Definition 1.4 A one-to-one function is a function in which each output value corresponds to exactly one input value.
Example 13: Determining Whether a Relationship Is a One-to-One Function
Is the area of a circle a function of its radius? If yes, is the function one-to-one?
The area = \(\pi \times r^2\). \(\pi\) is a constant, so yes: The area of a circle is a function of its radius. Yes, it is a one-to-one function.
Wach out!
The book answer is more elaborate: It is important to say that both values of the function \(f(r) = \sqrt\frac{{A}}{{\pi}}\) are positive numbers, so that there is only one solution!
Try it 9
Is a balance a function of the bank account number? Yes
Is a bank account number a function of the balance? No
Is a balance a one-to-one function of the bank account number? No
Wach out!
My answer was correct, but in the future I should always add the reason for my solution: For example in this case:
yes, because each bank account has a single balance at any given time
no, because several bank account numbers may have the same balance
no, because the same output may correspond to more than one input
Try it 10
Evaluate the following:
If each percent grade earned in a course translates to one letter grade, is the letter grade a function of the percent grade?: Yes, the letter grade is a function of the percent grade as I can calculate the letter grade from each percent grade.
If so, is the function one-to-one? No, because different percent grades may result in the same letter grade.
1.4 Using the Vertical Line Test
“The vertical line test can be used to determine whether a graph represents a function. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because a function has only one output value for each input value.” (Abramson, 2021, p. 32) (pdf)
Procedure
Given a graph, use the vertical line test to determine if the graph represents a function.
Inspect the graph to see if any vertical line drawn would intersect the curve more than once.
If there is any such line, determine that the graph does not represent a function.
Graph 1.3: Vertical line test: Whenever a vertical line crosses the curve more than once than it is not a function. Only the left graph is a function.
Example 14
Which of the graphs in Graph 1.4 represent(s) a function \(y=f(x)\)?
Graph 1.4: Applying the vertical test
Solution: (a) and (b) are functions. (c) is not a function, because a vertical line would cross twice the curve.
Solution: Yes, you can’t cross with a vertical line the graph twice.
1.5 Using the Horizontal Line Test
“Once we have determined that a graph defines a function, an easy way to determine if it is a one-to-one function is to use the horizontal line test. Draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.” (Abramson, 2021, p. 34) (pdf)
Procedure
Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one function.
Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.
If there is any such line, determine that the function is not one-to-one.
Example 15
Consider the functions shown in Graph 1.4(a) and Graph 1.4(b). Are either of the functions one-to-one?
Solution: Only Graph 1.4(b) is a one-to-one function, because a horizontal line cannot cross the graph twice. Graph 1.4(a) is not a one-to-one function because a horizontal line would cross the curve three times.
Wach out!
The book answer is more detailed: There are places where a horizontal line would only cross once (for example at y = 4 or y = -4), places where it would cross twice (for example y = 3 or y = -3, here the horizontal line is a tangent and a crossing), but there also places (as I have mentioned in my solution) where the horizontal line intersects the graph three times (for instance y = 0).
The important thing is that it is not a one-to-one function if it could cross more than once.
Solution: No, a horizontal line intersects the graph twice.
1.6 Identifying Basic Toolkit Functions
There are some
“toolkit functions,” which form a set of basic named functions for which we know the graph, formula, and special properties.” (Abramson, 2021, p. 35) (pdf)
I will add the full table so that I can consult these different functions with their name and properties.
1.7 Other Resources
Access the following online resources for additional instruction and practice with functions
I will only try odd numbered exercises as only these puzzles have published solutions officially.
1.8.1 Verbal
What is the difference between a relation and a function?
Relation is an umbrella-term signifying a general relationship between two items. A function is a more specialized notion where every input item produces an output item.
Why does the vertical line test tell us whether the graph of a relation represents a function?
If the vertical line test does intersect only once with the graph then it conforms with the definition of a function, where each input is related to one output.
Why does the horizontal line test tell us whether the graph of a function is one-to-one?
If the horizontal line test does only intersect once with the graph then the graph represents a one-to-one function.
1.8.2 Algebraic
Determine whether the relation represents a function.
{\((a,b), (b,c), (c,c)\)}
Yes, this is a function because each input relates to an input, even if two different input items (b and c) relate to the same outcome (c). But if vice versa the same input item would point to two different output item then it would not be a function.
Determine whether the relation represents \(y\) as a function of \(x\).
\(y = x^2\)Yes
Determine whether the relation represents \(y\) as a function of \(x\).
\(3x^2 + y = 14\)Yes
Determine whether the relation represents \(y\) as a function of \(x\).
\(y = -2x^2 + 40\)Yes
Determine whether the relation represents \(y\) as a function of \(x\).
\(x = \frac{3y + 5}{7y - 1}\)Yes
Determine whether the relation represents \(y\) as a function of \(x\).
\(y = \frac{3x + 5}{7x - 1}\)Yes
Determine whether the relation represents \(y\) as a function of \(x\).
\(2xy = 1\)Yes
Determine whether the relation represents \(y\) as a function of \(x\).
\(y = x^3\)Yes
Determine whether the relation represents \(y\) as a function of \(x\).
An additional question: Do I have to solve the equations of all questions of this kind (asking if it is a function or not) and to draw the equation in order to apply the vertical line test?
It is also a good idea to compare the Precalculus exercises with the Math topics of the videos of The Glaser Tutorial Company. There are several hundreds of videos and it seems there is not only an overlap with Precalculus but their videos are following in detail the Precalculus content!
I thought that exercise 23 is not a function because of \(\pm\), signifying that there are two output values. Actually I did not understand why exercise 23 is a function.
So I searched for a solution of the equation in the internet and found exactly my question asked at math.stackexchange!
After reading the question and both answers with all comments several times I believe I understood the problem: Central for my understanding was the start of the answer by Rhys Hughes followed by his comment:
\[
\begin{align*}
x = \pm y \\
x^2 = y^2 (\text{and not }\pm y^2 \text{ because …} ) \\
x^2 = \pm (y^2) \\
x^2 = \pm(1)^2y^2 \\
x^2 = y^2
\end{align*}
\]
Determine whether the relation represents \(y\) as a function of \(x\).
\(y^2 = x^2\)No
Evaluate \(f\) at the indicated values \(f(-3), f(2), f(-a), -f(a), f(a+h)\).
I had no idea how to solve Exercise 33 (Equation 1.2) . Again I found the explication of the solution at math.stackexchange.
Decisive for my understanding were three points:
I had only to substitute for \(g(x)\) and \(g(a)\). So the denominator \(x-a\) remains \(x-a\).
The substitute for \(g(a)\) is equivalent to the substitute for \(g(x)\). Instead of \(g(x) = x^2 + 2x\) I have to use \(g(a) = a^2 + 2a\).
The factorization with \((x-a)\), so that the denominator can be cancelled. I have to confess that I have limited knowledge of polynomial factorization.
I couldn’t solve the second part of the exercise: Solve \(f(x) = 4\). I searched on the internet and discovered Mathepower, a program for solving equation. I entered my problem and got the following correct answer with a detailed explanation of every step of calculation.
My problem: I do not know how to complete the square.
Graph 1.6: Solution of Mathepower for \(x^2 - 3x = 4\) is the solution set {4; 1}
To generate a soluton I could have used also WolframAlpha.
Graph 1.7: Solution of WolframAlpha for \(x^2 - 3x = 4\) is plotting the graph and displays not only the solution {4; 1}, but also alternative forms of the equation formula
TODO
I got the impression that I need to refresh my knowledge about factoring polynomials and solving of quadratic equations. So I registered with the Khan Academy and finished Unit 13 Quadratics:Multiplying & Factoring of Algebra 1.
At first I thought I would need also need Unit 14 Quadratic functions & equation, but after some exercises I got the impression that these skills already overlap with the tutorials of the Precalculus book, so I stopped my excursion for the time being.
Wach out!
Ok, so with that refreshed knowledge I understand now better the factoring solution of Exercise 33 (Equation 1.2) and solving strategy of Exercise 37 (Equation 1.3). But still it was not everything completely clear to me.
1. Given the function \(g(x) = x^2 + 2x\), evaluate \(\frac{g(x) - g(a)}{x-a}, x \ne a\)
In Equation 1.2 I understood that I need to factor out the denominator \(x-a\). But whenever I tried it I got a slightly different result \(x+a+4\) instead of \(x+a+2\). Looking again in the internet I noticed that there is a YouTube video by The Glaser Tutoring Company exactly to the same problem: Evaluate the Given Function: \(g(x) = x2 + 2x\)!!
\[
\begin{align*}
\frac{g(x) - g(a)}{x-a} = \frac{(x^2 + 2x) - (a^2 + 2a)}{x-a} \\
= \frac{x^2 + 2x - a^2 - 2a}{x-a} \\
= \frac{x^2 - a^2 + 2x - 2a}{x-a} \text{ regrouping the nominator!} \\
= \frac{(x+a)(x-a) + (2x - 2a)}{x-a} \text{ a term of the form } (a^2-b^2) \text{ is always} (a+b)(a-b)! \\
= \frac{(x+a)(x-a) +2(x - a)}{x-a} \text{ factor out 2 in the second term}\\
\text{ only now it is save to cancel } (x-a)!\\
= (x+a)+2 \text{ = solution!}
\end{align*}
\]
2. Given the function \(f(x) = x^2 - 3x\) solve for \(f(x) = 4\)
Concerning Equation 1.3 I learned that I have to set quadratic equations to 0. But I didn’t understand why MathePower completed the square by adding \(-(\frac{3}{2})^2\). Finally I solved this exercise again with the help of a YouTube video by The Glaser Tutoring Company.
I knew that I could factor out the equation \(0 = x^2 - 3x - 4\) with +1 and -4 but then I forgot that each product has to be set to zero. (Even I learned this one day before!). So - instead of not using the more complex solution with \(-(\frac{3}{2})^2\) - I got:
\[
\begin{align*}
x^2 - 3x = 4\\
x^2 - 3x - 4 = 0 \\
(x - 4)(x + 1) = 0 \text{ now: set each term to zero} \\
x - 4 = 0; x = 4 \\
x + 1 = 0; x = -1 \\
\text{The solution set is } \{4; -1\}
\end{align*}
\]
# Functions and Function Notation:::::{.my-objectives}:::{.my-objectives-header}Learning Objectives:::::::{.my-objectives-container}- Determine whether a relation represents a function.- Find the value of a function.- Determine whether a function is one-to-one.- Use the vertical line test to identify functions.- Graph the functions listed in the library of functions.:::::::::## Determining Whether a Relation Represents a Function::: {#def-relation-domain-range}##### Relation - domain - range> "A **relation** is a set of ordered pairs. The set of the first> components of each ordered pair is called the **domain** and the set> of the second components of each ordered pair is called the> **range.**" ([Abramson, 2021, p.> 18](zotero://select/library/items/U57DQZPG))> ([pdf](zotero://open-pdf/library/items/68C8JXSW?page=18&annotation=FLKWG5KA)):::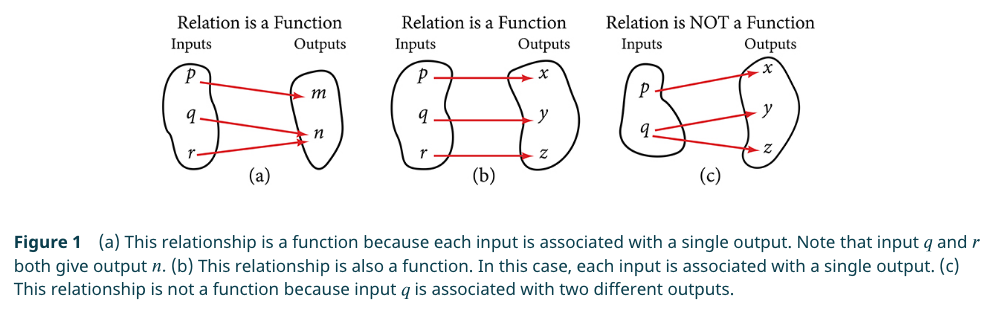{#fig-01-01 fig-alt="" fig-align="center"width="100%"}::: {#def-function}##### Function"A function is a relation in which each possible input value leads toexactly one output value. We say 'the output is a function of theinput.' The input values make up the domain, and the output values makeup the range." ([Abramson, 2021, p.18](zotero://select/library/items/U57DQZPG))([pdf](zotero://open-pdf/library/items/68C8JXSW?page=18&annotation=6PJT7CNS)):::::: callout-important**Given a relationship between two quantities, determine whether therelationship is a function.**1. Identify the input values.2. Identify the output values.3. If each input value leads to only one output value, classify the relationship as a function. If any input value leads to two or more outputs, do not classify the relationship as a function.:::::: {#exm-pricelist}Are price lists examples of functions?- Each item has its price, so the price is a function of its items. This is even valid if several items have the same price because there is for each item exactly one price.- Several items have the same price, that's why item is not a function of price.:::### Using Function Notation::: {#def-function-notation}##### Function Notation: Input value - independent variable & Output value - dependent variable> "The notation $y = f(x)$ defines a function named $f$, This is read as> 'y is a function of x'. The letter $x$ represents the input value, or> independent variable. The letter $y$ or $f(x)$ represents the output> value, or dependent variable." ([Abramson, 2021, p.> 21](zotero://select/library/items/U57DQZPG))> ([pdf](zotero://open-pdf/library/items/68C8JXSW?page=21&annotation=XWZMACMS)):::### Representing Functions Using Tables> "A common method of representing functions is in the form of a table.> The table rows or columns display the corresponding input and output> values." ([Abramson, 2021, p.> 22](zotero://select/library/items/U57DQZPG))> ([pdf](zotero://open-pdf/library/items/68C8JXSW?page=22&annotation=NBNN3GKY))## Finding Input and Output Values of a Function### Evaluation of Functions in Algebraic Forms::: callout-important**Given the formula for a function & evaluate**1. Substitute the input variable in the formula with the value provided.2. Calculate the result.:::::: my-example::: my-example-header**Example 6**: Evaluating Functions at Specific Values:::::: my-example-containerEvaluate $𝑓(𝑥)= x^2 + 3x − 4$ at:**x = 2**$$f(2) = 2^2 + 3 \times 2 - 4 = 6$$ **a**$$f(a) = a^2 + 3a - 4$$ **a + h** $$\begin{align*}f(a + h) = (a + h)^2 + 3(a + h) - 4 \\f(a + h) = a^2 + 2ah + h^2 + 3a + 3h -4\end{align*}$$**evaluate** $\frac{f(a + h) - f(a)}{h}$$$\begin{align*}\frac{f(a + h) - f(a)}{h} = \frac{a^2 + 2ah + h^2 + 3a + 3h -4 - (a^2 + 3a - 4)}{h}\\= \frac{2ah + h^2 + 3h}{h} \\= 2a + h + 3\end{align*}$$::::::::: my-example::: my-example-header**Example 7**: Evaluating Functions:::::: my-example-container**Given the function** $h(p) = p^2 + 2p?, evaluate ?h(4)$\$$$\begin{align*}h(4) = 4^2 + 2 \times 4 \\h(4) = 24\end{align*}$$::::::::: my-example::: my-example-header**Try It 4**::::::: my-example-containerGiven the function $g(m) = \sqrt{m - 4}$, evaluate g(5)$$g(5) = \sqrt{5 - 4} = 1$$::::::::: my-example::: my-example-header**Example 8**: Solving Functions:::::: my-example-containerGiven the function $h(p) = p^2 + 2p$, solve for $h(p) = 3$$$\begin{align*}3 = p^2 + 2p\\p^2 + 2p - 3 = 0 \text{ [substract 3 from each side]} \\(p + 3) (p - 1) = 0 \text{ [factor]}\\\text{set each factor equal to 0 and solve for p in each case} \\p + 3 = 0, p = -3 \\p - 1 = 0, p = +1\end{align*}$$ {#eq-example-8}::::::::: callout-warningI couldn't solve Example 8 (@eq-example-8), because I didn't use thefactor transformation of the equation. I came up with only one solution$p = 1$ after I had transformed to $p^2 + 2p - 3 = 0$.:::::: r-code::: r-code-headerFor a better understanding I replicated [Figure6](https://openstax.org/books/precalculus-2e/pages/1-1-functions-and-function-notation#Figure_01_01_006)of the book, p.16.:::::: r-code-container```{r}#| label: fig-pb-example-8#| fig-cap: "Graph for the function $h(p) = p^2 + 2p$ showing the solution for $h(p) = 3$"#| attr-source: '#lst-fig-pb-example-8 lst-cap="Plot function $h(p) = p^2 + 2p$"'#| fig.align: centerggplot2::ggplot() + ggplot2::scale_x_continuous(limits =c(-5, 5), breaks =seq(-5, 5, 1)) + ggplot2::geom_function(fun =function(x) x^2+ (2* x)) + ggplot2::geom_hline(yintercept =0, linetype ="solid") + ggplot2::geom_hline(yintercept =3, linetype ="solid", color ="darkgreen", linewidth =1) + ggplot2::geom_segment(ggplot2::aes(x =-3, y =0, xend =-3, yend =+3, color ="orange"), show.legend =FALSE, linewidth =1) + ggplot2::geom_segment(ggplot2::aes(x =1, y =0, xend =1, yend =+3, color ="orange"), show.legend =FALSE, linewidth =1) + ggplot2::geom_point(ggplot2::aes(x =-3, y =+3, fill ="blue"), size =2, show.legend =FALSE) + ggplot2::geom_point(ggplot2::aes(x =1, y =+3, fill ="blue"), size =2, show.legend =FALSE) + ggplot2::theme_bw() + ggplot2::labs(title =expression(paste("Function h(p) = ", p^2+2* p)),x ="p",y ="h(p)" )```::::::::: my-example::: my-example-header**Try It 5**:::::: my-example-containerGiven the function $g(m) = \sqrt{m - 4}$, solve $g(m) = 2$$$\begin{align*}2 = \sqrt{m - 4} \\2 = \sqrt{8 - 4} \\m = 8\end{align*}$$::::::### Evaluating Functions Expressed in Formulas::: callout-important**Given a function in equation form, write its algebraic formula**> "Some functions are defined by mathematical rules or procedures> expressed in equation form. If it is possible to express the function> output with a formula involving the input quantity, then we can define> a function in algebraic form." ([Abramson, 2021, p.> 26](zotero://select/library/items/U57DQZPG))> ([pdf](zotero://open-pdf/library/items/68C8JXSW?page=26&annotation=4WB76Q72))1. Solve the equation to isolate the output variable on one side of the equal sign, with the other side as an expression that involves only the input variable.2. Use all the usual algebraic methods for solving equations, such as adding or subtracting the same quantity to or from both sides, or multiplying or dividing both sides of the equation by the same quantity. ([Abramson, 2021, p. 26](zotero://select/library/items/U57DQZPG))::::::::{.my-example}:::{.my-example-header}**Example 9**: Finding an Equation of a Function:::::::{.my-example-container}Express the relationship $2n + 6p = 12$ as a function $p = f(n)$, if possible.$$\begin{align*}2n + 6p = 12 \\6p = 12 - 2n \\p = \frac{12 - 2n}{6} \\p = \frac{6 - n}{3} \\p = 2 - \frac{1}{3}n \\p = f(n) = 2 - \frac{1}{3}n\end{align*}$$::::::::::::::{.my-example}:::{.my-example-header}**Example 10**: Expressing the Equation of a Circle as a Function:::::::{.my-example-container}Does the equation $x^2 + y^2 = 1$ represent a function with $x$ as input and $y$ as output? If so, express the relationship as a function $y = f(x)$. $$\begin{align*}x^2 + y^2 = 1 \\y^2 = 1 - x^2 \\y = \sqrt{1 - x^2} \\\end{align*}$$:::::::::::: {.callout-warning}My solution is wrong as it would mean that $y = f(x)$ could be represented as function! I did not take into account that there are **two solutions**: $y = \pm \sqrt{1 - x^2}$. We get for $y$ two outputs; the formula is therefore not a function. ::::::::{.my-example}:::{.my-example-header}**Try It 6**:::::::{.my-example-container}If $x-8y^3=0$, express $y as a function of $x$:$$\begin{align*}x-8y^3=0 \\-8y^3 = -x \\y^3 = \frac{x}{8} \\y = \frac{\sqrt[3]{x}}{8}\\y = f(x) = \frac{1}{2} \sqrt[3]{x}\end{align*}$$:::::::::::: {.callout-note}There are relationships expressed by an equation that do represent a function but cannot be represented by an algebraic formula.:::### Evaluating a Function Given in Tabular Form> “As we saw above, we can represent functions in tables. Conversely, we can use information in tables to write functions, and we can evaluate functions using the tables.” ([Abramson, 2021, p. 27](zotero://select/library/items/U57DQZPG)) ([pdf](zotero://open-pdf/library/items/68C8JXSW?page=27&annotation=ZJ3WDDHY))::: {.callout-important}**Given is input value, identify output value**1. Find the given input in the row (or column) of input values.2. Identify the corresponding output value paired with that input value.**Given is output value, identify input value**1. Find the given output values in the row (or column) of output values, noting every time that output value appears.2. Identify the input value(s) corresponding to the given output value.::::::::{.my-example}:::{.my-example-header}**Example 11**:::::::{.my-example-container}| $n$ | 1 | 2 | 3 | 4 | 5 ||:----:|---|---|---|---|---|| $g(n)$ | 8 | 6 | 7 | 6 | 8 |: Evaluating and Solving a Tabular Function {#tbl-tabular-function}**Evaluate $g(3)$** **Solution: g(3) = 7****Solve $g(n) = 6$** **Solution: n = 2 and n = 4**:::::::::::: {.callout-warning}Again I have not followed exactly the proposed procedure "noting **every time** that output value appears". So I have only reported the first part of the solution $n = 2$!::::::::{.my-example}:::{.my-example-header}**Try it 7**:::::::{.my-example-container}Using @tbl-tabular-function to evaluate $g(1)$. **Solution $g(1) = 8$**:::::::::### Finding Function Values from a Graph::: {.callout-note}Don't forget: Solving a function equation using a graph requires **finding all instances** of the given output value on the graph and observing the corresponding input value(s).::::::::{.my-example}:::{.my-example-header}**Example 12**: Reading Function Values from a Graph:::::::{.my-example-container}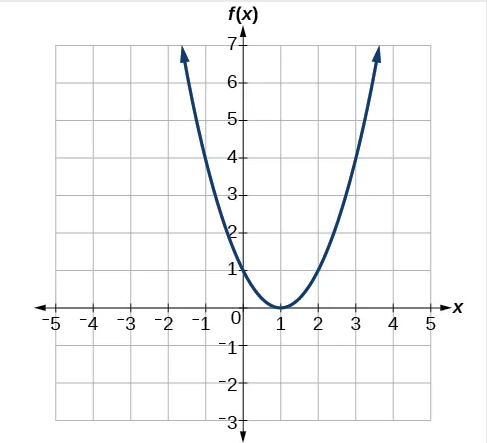{#fig-01-07 fig-alt="parable with f(1) = 0, and f(0) = 1" fig-align="center"width="70%"}***Evaluate $f(2)$: **Solution = f(2) = 1**Solve $f(x)=4$: **Solution = f(3) and f(-1)**::::::::::::::{.my-example}:::{.my-example-header}**Try it 8**:::::::{.my-example-container}Using @fig-01-07 solve $f(x) = 1$ **Solution $f(0)$ and $f(2)$**.:::::::::## Determining Whether a Function is One-to-One:::{#def-one-to-one-function}A one-to-one function is a function in which each output value corresponds to exactly one input value.::::::::{.my-example}:::{.my-example-header}**Example 13**: Determining Whether a Relationship Is a One-to-One Function:::::::{.my-example-container}Is the area of a circle a function of its radius? If yes, is the function one-to-one?The area = $\pi \times r^2$. $\pi$ is a constant, so yes: The area of a circle is a function of its radius. Yes, it is a `r glossary("one-to-one function")`.:::::::::::: {.callout-warning}The book answer is more elaborate: It is important to say that both values of the function $f(r) = \sqrt\frac{{A}}{{\pi}}$ are positive numbers, so that there is only one solution!::::::::{.my-example}:::{.my-example-header}**Try it 9**:::::::{.my-example-container}(a) Is a balance a function of the bank account number? **Yes**(b) Is a bank account number a function of the balance? **No**(c) Is a balance a one-to-one function of the bank account number? **No**:::::::::::: {.callout-warning}My answer was correct, but in the future I should always add the reason for my solution: For example in this case:(a) **yes**, because each bank account has a single balance at any given time(b) **no**, because several bank account numbers may have the same balance(c) **no**, because the same output may correspond to more than one input::::::::{.my-example}:::{.my-example-header}**Try it 10**:::::::{.my-example-container}Evaluate the following:(a) If each percent grade earned in a course translates to one letter grade, is the letter grade a function of the percent grade?: **Yes**, the letter grade is a function of the percent grade as I can calculate the letter grade from each percent grade.(b) If so, is the function one-to-one? **No**, because different percent grades may result in the same letter grade.:::::::::## Using the Vertical Line Test> “The **vertical line test** can be used to determine whether a graph represents a function. If we can draw any vertical line that intersects a graph more than once, then the graph does *not* define a function because a function has only one output value for each input value.” ([Abramson, 2021, p. 32](zotero://select/library/items/U57DQZPG)) ([pdf](zotero://open-pdf/library/items/68C8JXSW?page=32&annotation=R9WLIZBA))::: {.callout-important}Given a graph, use the vertical line test to determine if the graph represents a function.1. Inspect the graph to see if any vertical line drawn would intersect the curve more than once.2. If there is any such line, determine that the graph does not represent a function.:::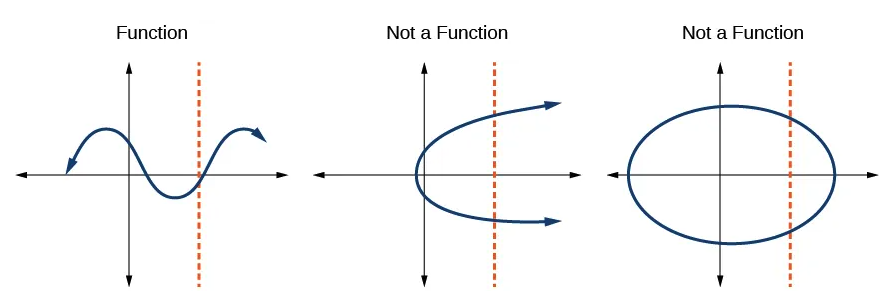{#fig-01-11 fig-alt="Three different functions: Left: a S-curve around the x-axis representing a function, because a vertical line cannot not cross two points of the curve: Middle and right: Half an O open to thre right and an ellipse do not represent a function, because a vertical line intersect two different points of the curves." fig-align="center" width="100%"}:::::{.my-example}:::{.my-example-header}**Example 14**:::::::{.my-example-container}Which of the graphs in @fig-01-12 represent(s) a function $y=f(x)$?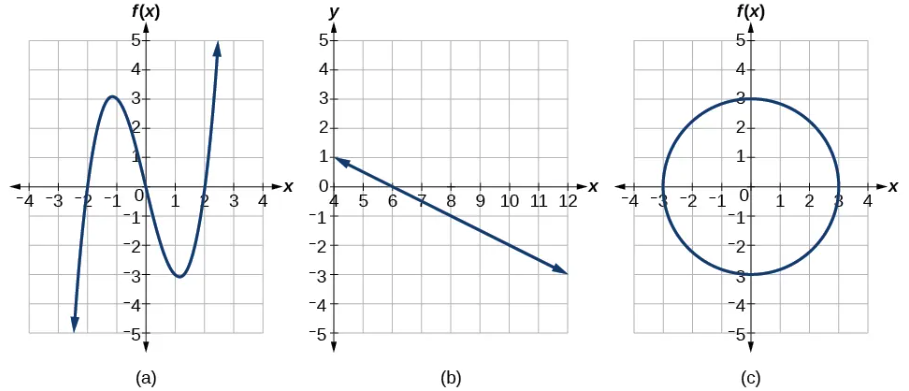{#fig-01-12 fig-alt="Three graphs: Left (a): an inverted S-curve crossing the coordinate axis. Middle (b): A line from (0,1) to (12,-3). Right (c): A circle with radio 3 centered at the the coordinate axis." fig-align="center" width="100%"}**Solution**: (a) and (b) are functions. (c) is not a function, because a vertical line would cross twice the curve.::::::::::::::{.my-example}:::{.my-example-header}**Try it 11**:::::::{.my-example-container}Does the graph in @fig-01-14 represent a function?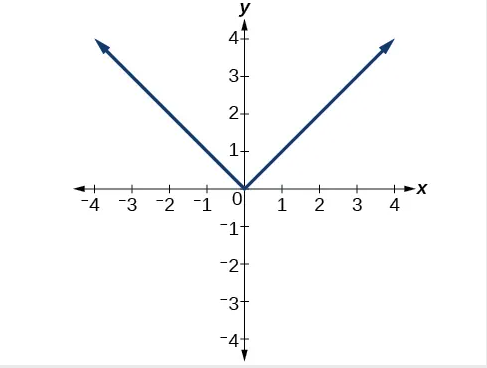{#fig-01-14 fig-alt="Graph shows a V with the deepest point at the coordinate axis." fig-align="center" width="50%"}**Solution:** Yes, you can't cross with a vertical line the graph twice.:::::::::## Using the Horizontal Line Test> “Once we have determined that a graph defines a function, an easy way to determine if it is a one-to-one function is to use the horizontal line test. Draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.” ([Abramson, 2021, p. 34](zotero://select/library/items/U57DQZPG)) ([pdf](zotero://open-pdf/library/items/68C8JXSW?page=34&annotation=L9I5J3YA))::: {.callout-important}Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one function.1. Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.2. If there is any such line, determine that the function is not one-to-one.::::::::{.my-example}:::{.my-example-header}**Example 15**:::::::{.my-example-container}Consider the functions shown in @fig-01-12(a) and @fig-01-12(b). Are either of the functions one-to-one?**Solution**: Only @fig-01-12(b) is a one-to-one function, because a horizontal line cannot cross the graph twice. @fig-01-12(a) is not a one-to-one function because a horizontal line would cross the curve three times.:::::::::::: {.callout-warning}The book answer is more detailed: There are places where a horizontal line would only cross once (for example at y = 4 or y = -4), places where it would cross twice (for example y = 3 or y = -3, here the horizontal line is a tangent and a crossing), but there also places (as I have mentioned in my solution) where the horizontal line intersects the graph three times (for instance y = 0).The important thing is that it is not a one-to-one function if it could cross more than once.::::::::{.my-example}:::{.my-example-header}**Try it 12**:::::::{.my-example-container}Is the graph shown in @fig-01-12(c) one-to-one?**Solution**: No, a horizontal line intersects the graph twice. :::::::::## Identifying Basic Toolkit FunctionsThere are some > “toolkit functions,” which form a set of basic named functions for which we know the graph, formula, and special properties.” ([Abramson, 2021, p. 35](zotero://select/library/items/U57DQZPG)) ([pdf](zotero://open-pdf/library/items/68C8JXSW?page=35&annotation=9UJ2IB3U))I will add the full table so that I can consult these different functions with their name and properties.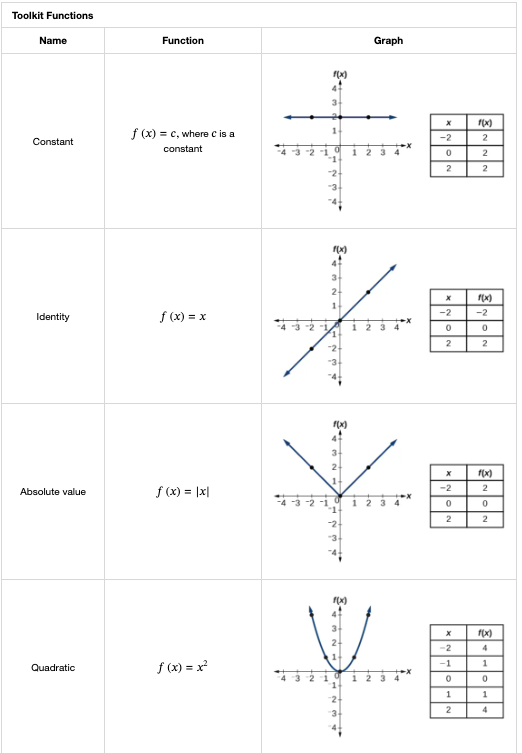{#fig-toolkit-1 fig-alt="alt-text" fig-align="center" width="100%"}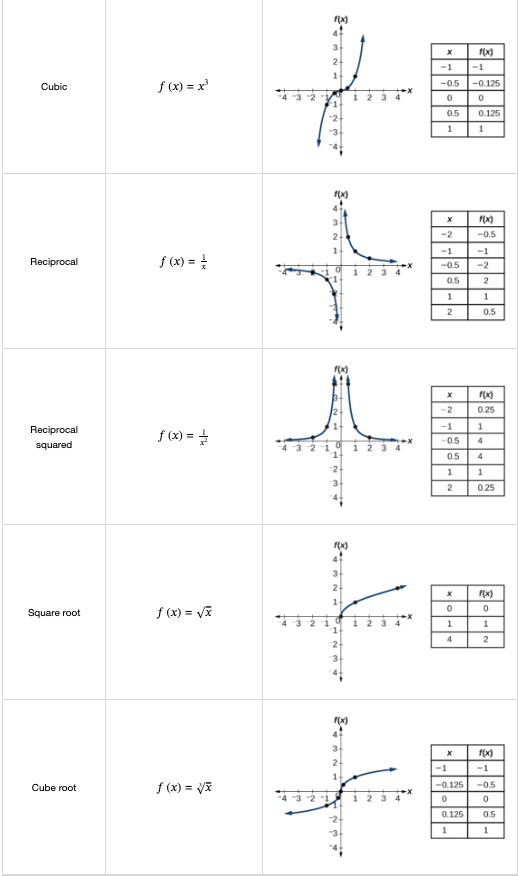{#fig-toolkit-2 fig-alt="alt-text" fig-align="center" width="100%"}## Other Resources:::::{.my-resource}:::{.my-resource-header}Access the following online resources for additional instruction and practice with functions:::::::{.my-resource-container}- [Determine if a Relation is a Function](http://openstax.org/l/relationfunction)- [Vertical Line Test](http://openstax.org/l/vertlinetest)- [Introduction to Functions](http://openstax.org/l/introtofunction)- [Vertical Line Test on Graph](http://openstax.org/l/vertlinegraph)- [One-to-one Functions](http://openstax.org/l/onetoone)- [Graphs as One-to-one Functions](http://openstax.org/l/graphonetoone):::::::::## Section Exercises::: {.callout-note}I will only try odd numbered exercises as only these puzzles have published solutions officially.:::### Verbal:::::{.my-solution}:::{.my-solution-header}1. What is the difference between a relation and a function?:::::::{.my-solution-container}Relation is an umbrella-term signifying a general relationship between two items. A function is a more specialized notion where every input item produces an output item.::::::::::::::{.my-solution}:::{.my-solution-header}3. Why does the vertical line test tell us whether the graph of a relation represents a function?:::::::{.my-solution-container}If the vertical line test does intersect only once with the graph then it conforms with the definition of a function, where each input is related to one output.::::::::::::::{.my-solution}:::{.my-solution-header}5. Why does the horizontal line test tell us whether the graph of a function is one-to-one?:::::::{.my-solution-container}If the horizontal line test does only intersect once with the graph then the graph represents a one-to-one function.:::::::::### Algebraic:::::{.my-solution}:::{.my-solution-header}7. Determine whether the relation represents a function.:::::::{.my-solution-container}{$(a,b), (b,c), (c,c)$}Yes, this is a function because each input relates to an input, even if two different input items (b and c) relate to the same outcome (c). But if vice versa the same input item would point to two different output item then it would not be a function.::::::::::::::{.my-solution}:::{.my-solution-header}9. Determine whether the relation represents $y$ as a function of $x$.:::::::{.my-solution-container}$y = x^2$ **Yes**::::::::::::::{.my-solution}:::{.my-solution-header}11. Determine whether the relation represents $y$ as a function of $x$.:::::::{.my-solution-container}$3x^2 + y = 14$ **Yes**::::::::::::::{.my-solution}:::{.my-solution-header}13. Determine whether the relation represents $y$ as a function of $x$.:::::::{.my-solution-container}$y = -2x^2 + 40$ **Yes**::::::::::::::{.my-solution}:::{.my-solution-header}15. Determine whether the relation represents $y$ as a function of $x$.:::::::{.my-solution-container}$x = \frac{3y + 5}{7y - 1}$ **Yes**::::::::::::::{.my-solution}:::{.my-solution-header}17. Determine whether the relation represents $y$ as a function of $x$.:::::::{.my-solution-container}$y = \frac{3x + 5}{7x - 1}$ **Yes**::::::::::::::{.my-solution}:::{.my-solution-header}19. Determine whether the relation represents $y$ as a function of $x$.:::::::{.my-solution-container}$2xy = 1$ **Yes**::::::::::::::{.my-solution}:::{.my-solution-header}21. Determine whether the relation represents $y$ as a function of $x$.:::::::{.my-solution-container}$y = x^3$ **Yes**::::::::::::::{.my-solution}:::{.my-solution-header}23. Determine whether the relation represents $y$ as a function of $x$.:::::::{.my-solution-container}$x = \pm\sqrt{1-y}$ **Yes**:::::::::::: {.callout-warning}## NEEDS REWRITING (Exercise 23, 33 and 37)I have to rewrite this callout after watching [Does $x = ±sqrt(1 − y)$ represent $y$ as a Function of $x$?](https://www.youtube.com/watch?v=jOlhdHZ39Yk) of The Glaser Tutorial Company!An additional question: Do I have to solve the equations of all questions of this kind (asking if it is a function or not) and to draw the equation in order to apply the vertical line test?It is also a good idea to compare the Precalculus exercises with the [Math topics of the videos](https://www.youtube.com/@GlaserTutoring/playlists?view=50&sort=dd&shelf_id=4) of The Glaser Tutorial Company. There are several hundreds of videos and it seems there is not only an overlap with Precalculus but their videos are following in detail the Precalculus content!***I thought that exercise 23 is not a function because of $\pm$, signifying that there are two output values. Actually I did not understand why exercise 23 is a function.So I searched for a solution of the equation in the internet and found exactly my question asked at [math.stackexchange](https://math.stackexchange.com/questions/4040159/when-x-pm-sqrty-1-is-y-a-function-of-x-how-to-deal-with-the-pm)!After reading the question and both answers with all comments several times I believe I understood the problem: Central for my understanding was the start of the answer by [Rhys Hughes](https://math.stackexchange.com/users/487658/rhys-hughes) followed by his comment: $$\begin{align*}x = \pm y \\x^2 = y^2 (\text{and not }\pm y^2 \text{ because …} ) \\x^2 = \pm (y^2) \\x^2 = \pm(1)^2y^2 \\x^2 = y^2\end{align*}$$::::::::{.my-solution}:::{.my-solution-header}25. Determine whether the relation represents $y$ as a function of $x$.:::::::{.my-solution-container}$y^2 = x^2$ **No**::::::::::::::{.my-solution}:::{.my-solution-header}27. Evaluate $f$ at the indicated values $f(-3), f(2), f(-a), -f(a), f(a+h)$. :::::::{.my-solution-container}$f(x) = 2x -5$$$\begin{align*}f(-3) = -6 -5 = -11 \\f(2) = -1 \\f(-a) = -2a -5 \\-f(a) = -(2a -5) = -2a + 5\\f(a+h) = 2(a+h) - 5 = 2a + 2h - 5\end{align*}$$::::::::::::::{.my-solution}:::{.my-solution-header}29. Evaluate $f$ at the indicated values $f(-3), f(2), f(-a), -f(a), f(a+h)$. :::::::{.my-solution-container}$f(x) = \sqrt{2-x} + 5$$$\begin{align*}f(-3) = \sqrt{2-(-3)} + 5 = \sqrt{5} + 5 \\f(2) = \sqrt{2-2} + 5 = 5 \\f(-a) = \sqrt{2-(-a)} + 5 = \sqrt{2+a} + 5 \\-f(a) = -(\sqrt{2-a} + 5) = -\sqrt{2-a} - 5 \\f(a+h) = \sqrt{2-(a+h)} + 5 = \sqrt{2 - a - h} + 5\end{align*}$$::::::::::::::{.my-solution}:::{.my-solution-header}31. Evaluate $f$ at the indicated values $f(-3), f(2), f(-a), -f(a), f(a+h)$.:::::::{.my-solution-container}$f(x) = \mid x-1 \mid - \mid x+1 \mid$$$\begin{align*}f(-3) = | - 3 - 1 | - | -3 + 1 | = 4 - 2 = 2\\f(2) = | 2 - 1 | - | 2 + 1 | = 1 - 3 = -2 \\f(-a) = |-a -1| - |-a +1| \\-f(a) = -(|a - 1| - |a + 1|) \\f(a+h) = |a + h -1| - |a + h +1|\end{align*}$$::::::::::::::{.my-solution}:::{.my-solution-header}33. Given the function $g(x) = x^2 + 2x$, evaluate $\frac{g(x) - g(a)}{x-a}, x \ne a$.:::::::{.my-solution-container}$$\begin{align*}\frac{g(x) - g(a)}{x-a} = \frac{(x^2 + 2x) - (a^2 + 2a)}{x-a} \\\frac{g(x) - g(a)}{x-a} = \frac{x^2 + 2x - a^2 - 2a}{x-a} \\\frac{g(x) - g(a)}{x-a} = \frac{(x-a)(x+a+2)}{x-a} \\\frac{g(x) - g(a)}{x-a} = x + a + 2\end{align*}$$ {#eq-exercise-1-33}:::::::::::: {.callout-warning}I had no idea how to solve Exercise 33 (@eq-exercise-1-33) . Again I found the explication of the solution at [math.stackexchange](https://math.stackexchange.com/questions/3619578/given-gx-x2-2x-evaluate-frac-gx-gax-a).Decisive for my understanding were three points:1. I had only to substitute for $g(x)$ and $g(a)$. So the denominator $x-a$ remains $x-a$.2. The substitute for $g(a)$ is equivalent to the substitute for $g(x)$. Instead of $g(x) = x^2 + 2x$ I have to use $g(a) = a^2 + 2a$.3. The factorization with $(x-a)$, so that the denominator can be cancelled. I have to confess that I have limited knowledge of [polynomial factorization](https://mathworld.wolfram.com/PolynomialFactorization.html).::::::::{.my-solution}:::{.my-solution-header}35. Given the function $f(x) = 8-3x$:::::::{.my-solution-container}Evaluate $f(-2)$$$\begin{align*}f(-2) = 8 - 3 (-2) \\f(-2) = 14\end{align*}$$Solve $f(x) = -1$$$\begin{align*}-1 = 8 - 3x \\- 1 - 8 = -3x \\\frac{-9}{-3} = x \\3 = x\end{align*}$$::::::::::::::{.my-solution}:::{.my-solution-header}37. Given the function $f(x) = x^2 - 3x$:::::::{.my-solution-container}Evaluate $f(5)$$$\begin{align*}f(5) = 5^2 - 3 \times 5\\f(5) = 10\end{align*}$$ Solve $f(x) = 4$$$\begin{align*}x^2 - 3x = 4\\4 + 3x = x^2 \\\end{align*}$$ {#eq-exercise-1-37}:::::::::::: {.callout-warning}I couldn't solve the second part of the exercise: Solve $f(x) = 4$. I searched on the internet and discovered [Mathepower](https://www.mathepower.com/en/index.php), a program for solving equation. I entered my problem and got the following correct answer with a detailed explanation of every step of calculation.My problem: I do not know how to complete the square.{#fig-mathepower-solution.png fig-alt="Calculation of $x^2 - 3x = 4$, explained step by step" fig-align="center" width="100%"}To generate a soluton I could have used also [WolframAlpha](https://www.wolframalpha.com/).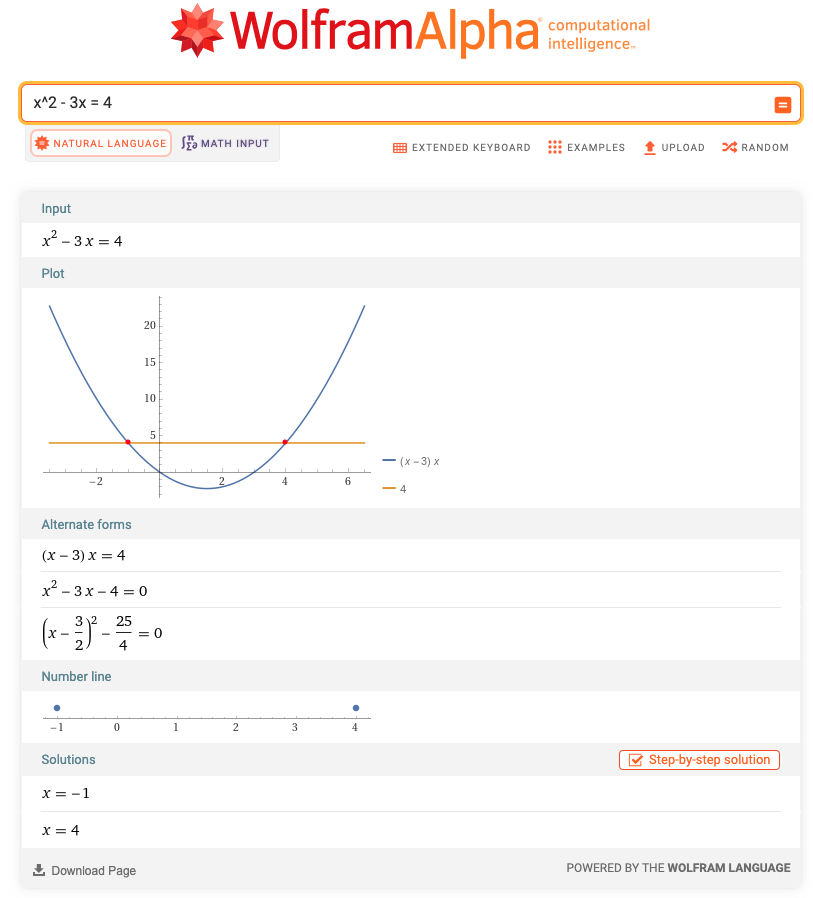{#fig-wolfram-alpha-solutionfig-alt="Displays input ($x^2 - 3x = 4$), plots the graph, shows alternate form of the equation, the numberline with the solution and the algebraic solution set." fig-align="center" width="100%"}:::::: {.callout-caution}I got the impression that I need to refresh my knowledge about factoring `r glossary("polynomials")` and solving of quadratic equations. So I registered with the Khan Academy and finished Unit 13 [Quadratics:Multiplying & Factoring](https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:quadratics-multiplying-factoring) of Algebra 1.At first I thought I would need also need Unit 14 [Quadratic functions & equation](https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:quadratic-functions-equations), but after some exercises I got the impression that these skills already overlap with the tutorials of the Precalculus book, so I stopped my excursion for the time being.:::::: {.callout-warning}Ok, so with that refreshed knowledge I understand now better the factoring solution of Exercise 33 (@eq-exercise-1-33) and solving strategy of Exercise 37 (@eq-exercise-1-37). But still it was not everything completely clear to me.**1. Given the function $g(x) = x^2 + 2x$, evaluate $\frac{g(x) - g(a)}{x-a}, x \ne a$**In @eq-exercise-1-33 I understood that I need to factor out the denominator $x-a$. But whenever I tried it I got a slightly different result $x+a+4$ instead of $x+a+2$. Looking again in the internet I noticed that there is a [YouTube video](https://www.youtube.com/watch?v=xdQj-YWHFhg) by [The Glaser Tutoring Company](https://www.youtube.com/@GlaserTutoring) exactly to the same problem: Evaluate the Given Function: $g(x) = x2 + 2x$!!It turned out that I factored out wrongly:$$\begin{align*}\frac{g(x) - g(a)}{x-a} = \frac{(x^2 + 2x) - (a^2 + 2a)}{x-a}\\= \frac{x(x+2)-(a)(a+2)}{x-a} \\= (x+2)-(a+2) \text{ Cancelation of } x-a \text{ is WRONG!}\\= x-a+4\end{align*}$$The correct way is:$$\begin{align*}\frac{g(x) - g(a)}{x-a} = \frac{(x^2 + 2x) - (a^2 + 2a)}{x-a} \\= \frac{x^2 + 2x - a^2 - 2a}{x-a} \\= \frac{x^2 - a^2 + 2x - 2a}{x-a} \text{ regrouping the nominator!} \\= \frac{(x+a)(x-a) + (2x - 2a)}{x-a} \text{ a term of the form } (a^2-b^2) \text{ is always} (a+b)(a-b)! \\= \frac{(x+a)(x-a) +2(x - a)}{x-a} \text{ factor out 2 in the second term}\\\text{ only now it is save to cancel } (x-a)!\\= (x+a)+2 \text{ = solution!}\end{align*}$$**2. Given the function $f(x) = x^2 - 3x$ solve for $f(x) = 4$**Concerning @eq-exercise-1-37 I learned that I have to set quadratic equations to 0. But I didn't understand why MathePower completed the square by adding $-(\frac{3}{2})^2$. Finally I solved this exercise again with the help of a [YouTube video](https://www.youtube.com/watch?v=5MOD3OoP2nI) by [The Glaser Tutoring Company](https://www.youtube.com/@GlaserTutoring). I knew that I could factor out the equation $0 = x^2 - 3x - 4$ with +1 and -4 but then I forgot that each product has to be set to zero. (Even I learned this one day before!). So - instead of not using the more complex solution with $-(\frac{3}{2})^2$ - I got:$$\begin{align*}x^2 - 3x = 4\\x^2 - 3x - 4 = 0 \\(x - 4)(x + 1) = 0 \text{ now: set each term to zero} \\x - 4 = 0; x = 4 \\x + 1 = 0; x = -1 \\\text{The solution set is } \{4; -1\}\end{align*}$$:::### Graphical### Numeric### Technology### Real-world Applications