Capitolo 6 Analisi statistica multivariata

Seppure aspetti di grande interesse possono già emergere da una corretta analisi di coppie di variabili, l’analisi congiunta di un insieme più ampio delle variabili disponibili (che a volte possono essere anche molto numerose) consente di cogliere relazioni complesse presenti nei dati.

Nel seguito quindi si introdurranno elementi che riguardano l’analisi di un insieme variabili $x_1, x_2, \dots, x_p$ (con $p \geq 3$ ) misurate su $n$ unità. Si parla in tal caso di insieme di dati multivariato e di analisi dei dati multivariata.

Le variabili coinvolte possono essere di diversa natura: quantitative o categoriali. La trattazione fatta precedentemente per l’analisi bivariata distingueva i casi in cui entrambe le variabili erano categoriali, una variabile era quantitativa e una categoriale ed entrambe quantitative. Sono stati illustrati strumenti di analisi e di visualizzazione adatti ai diversi casi che richiedono scelte tecniche adeguate.

Nel caso di un insieme di dati multivariato sarà ancora più frequente trovarsi nella situazione in cui i dati sono di tipo misto (sia quantitative che categoriali) e converrà sempre tenere a mente tale distinzione. Vale sempre, se si utilizza R la regola aurea in di definire come fattore (factor) le variabili categoriali.

Si inizia con l’introduzione di primi semplici strumenti di analisi per i casi in cui tutte le variabili sono della medesima natura. Successivamente, si introdurranno due particolari tematiche tipiche dell’analisi di dati multivariati.

Il primo tema è l’estensione dell’analisi di regressione semplice (che interessava due sole variabili) al caso in cui fra le informazioni disponibili si individua una variabile risposta (output o target) quantitativa e l’obiettivo è quello di spiegare (o prevedere) tale variabile utilizzando un insieme di variabili esplicative (regressori, input) più ampio. Tale analisi è detta di regressione multipla e costituisce uno delle principali tecniche di analisi statistica: essa verrà ripresa in altri corsi, a partire da quelli di machine learning, ma se si vuole approfondire realmente, e in modo serio, tale fondamentale tematica il consiglio vivissimo è di seguire il corso di Modelli Statistici, da inserire come scelta nel piano di studi.

Il secondo tema che verrà introdotto cerca di utilizzare le misure multivariate ottenute sulle diverse unità per cercare pattern nei dati individuando le unità simili tra di loro con riferimento alle variabili osservate. Non c’è quindi in questo caso una variabile risposta e l’obiettivo non è quello di prevedere o spiegare una variabile ma è quello di cercare strutture nei dati multivariati che non sono immediatamente riconoscibili. Si fa riferimento a tali problemi con il termine analisi di raggruppamento o cluster analysis.

I due approcci sono paradigmatici di una serie molto più ampia di tecniche di analisi statistiche oltre che dei due approcci all’apprendimento statistico (o automatico, machine learning) detti apprendimento supervisionato (la regressione ne è l’esempio più semplice e immediato) e apprendimento non supervisionato (per il quale la cluster analysis rappresenta una delle tecniche di maggior rilievo).

6.1 L’analisi di più variabili categoriali

Nel caso di due sole variabili categoriali l’analisi è apparentemente molto semplice. Gli strumenti principali sono la rappresentazione in una tabella di frequenze a doppia entrata, la rappresentazione mediante barplot affiancati e la costruzione di misure di associazione come l’indice $X^2$ o, nel caso di tabelle $2\times2$ , il rapporto dei prodotti incrociati (odds ratio).

Non appena le variabili che vogliamo analizzare congiuntamente sono tre, o anche più di tre, l’analisi diviene più complessa e difficile da gestire. Questo anche perché l’associazione congiunta fra più variabili può essere caratterizzata da aspetti che coinvolgono forme di indipendenza (è il caso, ad esempio, dell’indipendenza condizionale) che non sono semplicemente l’indipendenza mutua completa fra tutte le variabili.

Come già detto lo strumento di base per l’analisi di più variabili categoriali è semplicemente la tabella incrociata a più entrate.

Un’analisi approfondita della tematica relativa alla valutazione delle relazioni fra più variabili categoriali va ben oltre questa trattazione introduttiva. E’ tuttavia di qualche interesse fornire un esempio del concetto di indipendenza condizionale quando a essere coinvolte sono tre variabili categoriali.

6.1.1 L’associazione marginale, l’associazione condizionale e il paradosso di Simpson

Quando si considera la relazione fra una coppia di variabili, categoriali in questo caso, isolatamente, senza cioè tenere conto della presenza di ulteriori altre variabili, si parla di relazione marginale: se quindi c’è indipendenza fra tali due variabili dovremmo più correttamente parlare di indipendenza marginale o se ci fosse associazione di associazione marginale.

Se tuttavia si osservano altre variabili, nel caso in questione ancora categoriali, si potrebbe considerare la relazione fra le due variabili condizionatamente alla terza variabile. La relazione fra le due variabili, quando si tenga conto della terza variabile, può essere diversa da quella osservata a livello marginale.

Potrebbe quindi accadere che una relazione di associazione (o di indipendenza) marginale non sia più presente a livello condizionale o addirittura possa invertirsi (in tali caso si parla di paradosso di Simpson). Vale la pena di ricordare che l’associazione marginale fra due variabili potrebbe essere illusoria e pertanto non bisognerebbe mai trarre conclusioni sulle relazioni fra variabili solo basandosi sull’associazione marginale. In particolare: la presenza di una associazione marginale fra due variabili non implica che vi sia una relazione causale, questo in quanto non si controllano, di solito, tutte le altre variabili in gioco.

6.1.1.1 Un esempio

Per esemplificare quanto detto sopra si considerino i seguenti dati relativi alle ammissioni ai vari dipartimenti all’università di Berkeley nel 1973 contenuti nella tabella a tre entrate:UCBAdmissions (che è di fatto un array a tre dimensioni)

Le variabili coinvolte sono 3:

Ammissione (due modalità: Admitted, Rejected)
Genere (due modalità: Male, Female)
Dipartimento (6 dipartimenti).

I dati sono riportati di seguito:

DIPARTIMENTO A

	Male	Female
Admitted	512	89
Rejected	313	19

DIPARTIMENTO B

	Male	Female
Admitted	353	17
Rejected	207	8

DIPARTIMENTO C

	Male	Female
Admitted	120	202
Rejected	205	391

DIPARTIMENTO D

	Male	Female
Admitted	138	131
Rejected	279	244

DIPARTIMENTO E

	Male	Female
Admitted	53	94
Rejected	138	299

DIPARTIMENTO F

	Male	Female
Admitted	22	24
Rejected	351	317

Si consideri dapprima la tabella a doppia entrata per le prime due variabili (la tabella marginale bivariata) ottenuta sommando rispetto ai diversi Dipartimenti

marg<-margin.table(UCBAdmissions,c(1,2))
kable(marg)

	Male	Female
Admitted	1198	557
Rejected	1493	1278

Per valutare l’associazione fra Ammissione e Genere: ad esempio, calcoliamo il rapporto dei prodotti incrociati OR.

OR<-marg[1,1]*marg[2,2]/(marg[1,2]*marg[2,1])
OR

## [1] 1.84108

come si vede il valore ottenuto è abbastanza lontano da 1 (nel caso fosse vicina a 1 si propenderebbe per l’indipendenza fra i caratteri), e in effetti osservando i dati sembrerebbe che ci sia un bias nell’ammissione per cui la proporzione di ammissione è più alta per gli uomini che per le donne. Si sarebbe tentati di concludere che gli uomini risultino più preparati e vengano ammessi più spesso.

Nelle tabelle, per le due variabili prese condizionatamente al dipartimento (cioè separatamente per ogni dipartimento) la situazione però appare diversa. Ad esempio, nel dipartimento A, si ha la seguente tabella a doppia entrata (distribuzione bivariata fra Ammssione e Genere condizionata al Dipartimento A)

cond<-UCBAdmissions[,,1]
kable(cond)

	Male	Female
Admitted	512	89
Rejected	313	19

Si vede subito che nel dipartimento A non è presente la stessa relazione osservata a livello marginale, infatti sembra che in questo caso la relazione sia opposta. Se calcoliamo anche per questa l’odds-ratio:

ORA<-cond[1,1]*cond[2,2]/(cond[1,2]*cond[2,1])
ORA

## [1] 0.349212

Il rapporto dei prodotti incrociati è di segno opposto rispetto a quello marginale e in questo Dipartimento si verifica un’ammissione preferenziale per le donne.

Potremmo fare lo stesso per tutti i dipartimenti e calcolare i 6 odds-ratio condizionali

nn<-dim(UCBAdmissions)[3]
ordip<-1:nn
for (i in 1:nn) 
{
ordip[i]<-UCBAdmissions[1,1,i]*UCBAdmissions[2,2,i]/(UCBAdmissions[1,1,i]*UCBAdmissions[2,1,i])
ordip
}
ordip

## [1] 0.06070288 0.03864734 1.90731707 0.87455197 2.16666667
## [6] 0.90313390

Come si vede la relazione marginale non è uguale alle relazioni condizionali e in 4 dipartimenti su 6 la relazione è invertita sono le femmine ad essere ammesse più spesso. L’apparente associazione marginale tra ammissione e sesso, a favore dei maschi, è il risultato del fatto che vi è diversa propensione di maschi e femmine a candidarsi all’ammissione ai singoli dipartimenti. Le candidate femmine, in effetti, facevano prevalentemente domanda di ammissione ai dipartimenti con tassi di rifiuto più elevati (che sono il C, E e D) mentre i maschi fanno domanda a Dipartimenti in cui è facile essere ammessi. Quando si sommano i dati per tutti i dipartimenti appare quindi complessivamente che i maschi sono ammessi più spesso ma da questo non possiamo concludere che i maschi siano più bravi o che vi sia una preferenza a ammettere i maschi. Questo è appunto un esempio di quello che è detto paradosso di Simpson.

6.2 L’analisi di piu variabili quantitative

Quando si analizzano più variabili, tutte quantitative, si può sempre partire dall’esame delle relazione fra coppie di variabili. Si può inizialmente guardare a un indice che misuri la forza della relazione lineare fra esse: ovvero la covarianza o il coefficiente di correlazione lineare.

6.2.1 La matrice di varianza-covarianza e la matrice di correlazione

Se sono disponibili $p$ variabili $X_1, X_2, \dots X_p$ è possibile quindi calcolare la covarianza o il coefficiente di correlazione lineare fra ciascuna coppia di variabili ottenendo $\frac{p\times(p-1)}{2}$ covarianze (o correlazioni) distinte. Di solito tali indici vengono organizzati in una matrice di dimensione $p$ .

Nel caso delle covarianze, si definisce la matrice di varianze-covarianze $S$ il cui generico elemento si denota $s(i,j)=cov(X_i,X_j)$ .

Tale matrice risulterà essere simmetrica poichè $s(i,j)=s(j,i)$ . Inoltre sulla diagonale di tale matrice saranno presenti i valori di $cov(X_i,X_i)=\frac{\sum_k^n(X_ik-M(X_i))^2}{n-1}=var(X_i)$ ovvero le varianze delle variabili.

Nel caso dei coefficienti di correlazione lineare, si definisce la matrice di correlazione $R$ il cui generico elemento si denota con $r(i,j)=cor(X_i,X_j)$ . Tale matrice è anch’essa simmetrica essendo $r(i,j)=r(j,i)$ . Inoltre sulla diagonale di tale matrice saranno presenti valori unitari essendo pari a 1 la correlazione fra una variabile e se stessa. La matrice di correlazione è spesso preferibile in prima istanza essendo più agevole avere un’indicazione fra l’intensità del legame lineare fra le coppie di variabili.

Le funzioni cov() e cor(), già introdotte nel caso di due variabili, permettono di ottenere la matrice di covarianze se in input viene fornita una matrice di dati (o un data frame) di variabili numeriche. Ad esempio.

irisnum<- iris[,-5] # elimino l'ultima variabile del dataframe che è un fattore

# Matrice di varianza/covarianza
kable(round(cov(irisnum),2))

	Sepal.Length	Sepal.Width	Petal.Length	Petal.Width
Sepal.Length	0.69	-0.04	1.27	0.52
Sepal.Width	-0.04	0.19	-0.33	-0.12
Petal.Length	1.27	-0.33	3.12	1.30
Petal.Width	0.52	-0.12	1.30	0.58

# Matrice di correlazione
kable(round(cor(irisnum),2))

	Sepal.Length	Sepal.Width	Petal.Length	Petal.Width
Sepal.Length	1.00	-0.12	0.87	0.82
Sepal.Width	-0.12	1.00	-0.43	-0.37
Petal.Length	0.87	-0.43	1.00	0.96
Petal.Width	0.82	-0.37	0.96	1.00

ggplot2 consente di usare alcuni strumenti grafici per visualizzare la matrice di correlazione, ad esempio il package ggcorrplot (che va installato).

library(ggcorrplot)
library(ggplot2)
ggcorrplot(cor(iris[,-5]),type="lower", method="circle", lab=TRUE)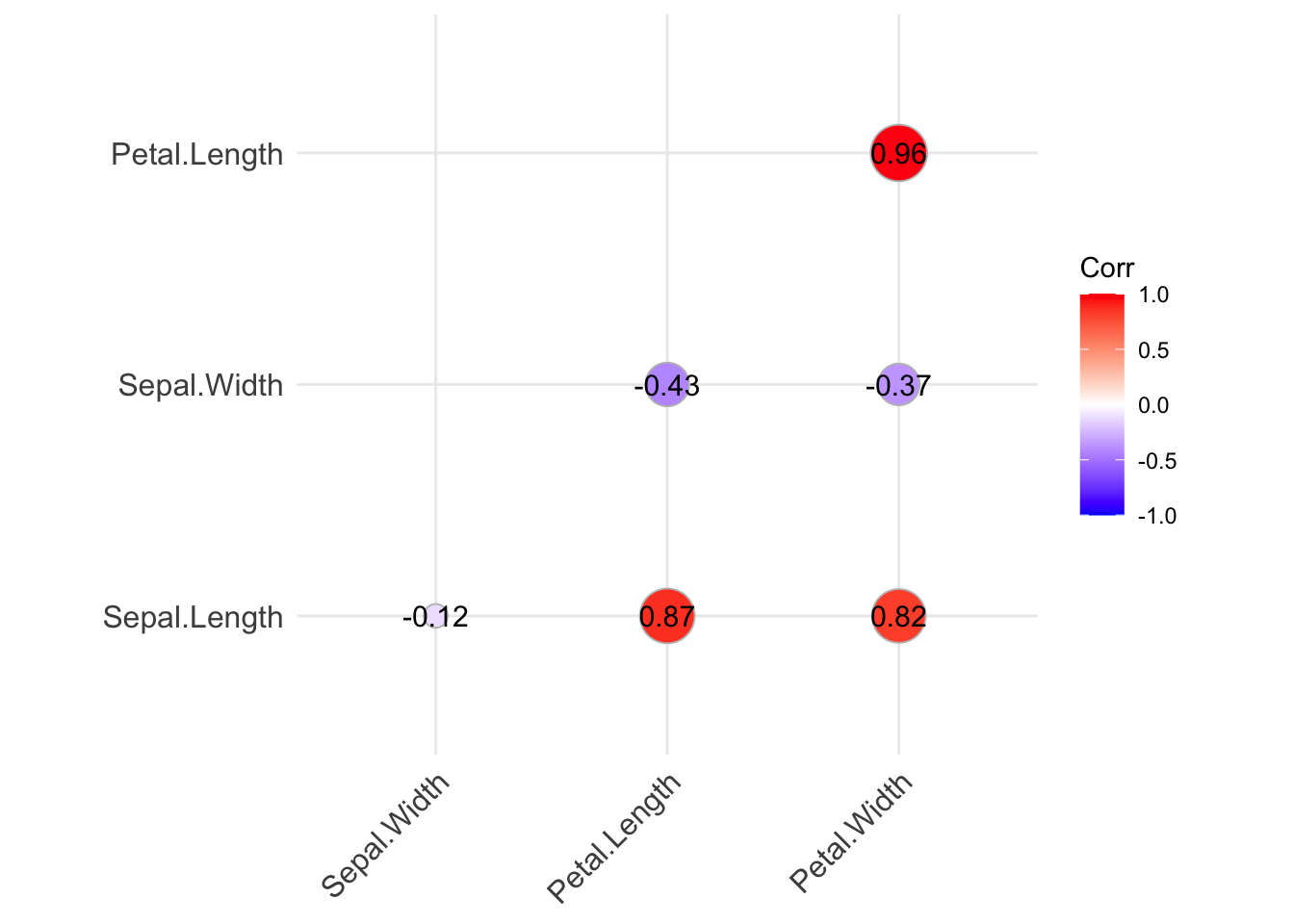

Si noti che la funzione richiede in input una matrice di correlazione. Vi sono vari parametri che permettono di abbellire il grafico. negli esempi che seguono se ne usano alcuni ma si consiglia di guardare i tutorial presenti in rete sull’uso della funzione ggcorrplot.

Un secondo esempio, con il data frame delle auto già usato in precedenza (ii noti il primo comando che sfrutta le potenzialità di dplyr per selezionare solo le variabili numeriche) è fornito di seguito:

library(dplyr)
Cars93num<- Cars93 %>% select_if(is.numeric)
corrcar<-round(cor(Cars93num, use = "complete.obs", method="pearson"),2)
ggcorrplot(corrcar,type="lower")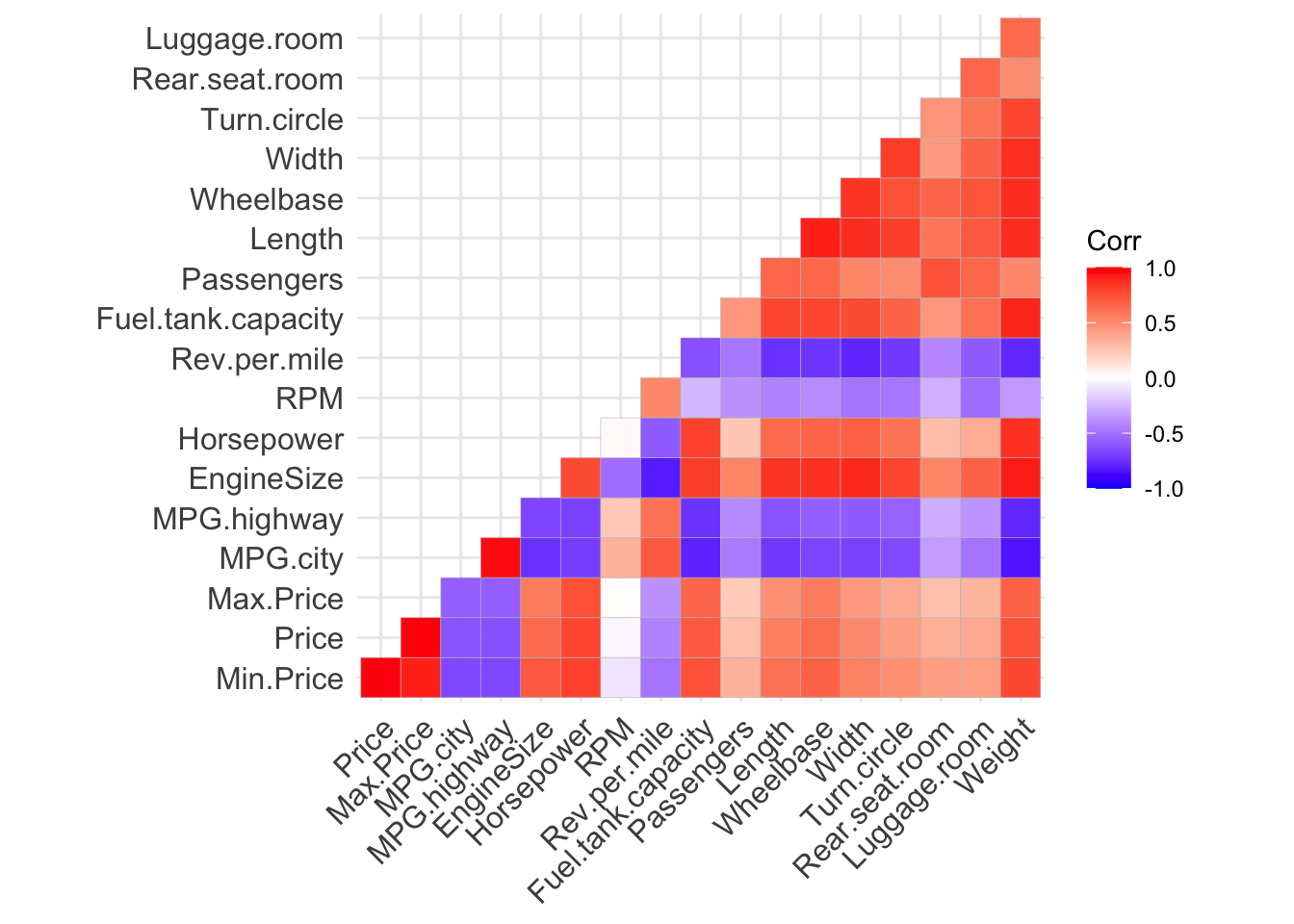

Un altra utile funzione per verificare le relazioni fra tutte le variabili, senza calcolare il coefficiente di correlazione ma rappresentando come in una matrice di correlazione tutti gli scatterplot delle coppie, è la funzione pairs()

pairs(iris[,-5])

Si osservi che pairs funzionerebbe anche se le variabili coinvolte non sono numeriche. Ad ogni modalità del fattore vengono associati livelli numerici e si ottiene un grafico che tuttavia in molti casi risulterà privo di significato o di non facile interpretazione. Si osservi ad esempio cosa accade se utilizziamo pairs per il data frame AutoBi che conteneva sia variabili numeriche che fattori.

data(AutoBi)
pairs(AutoBi)

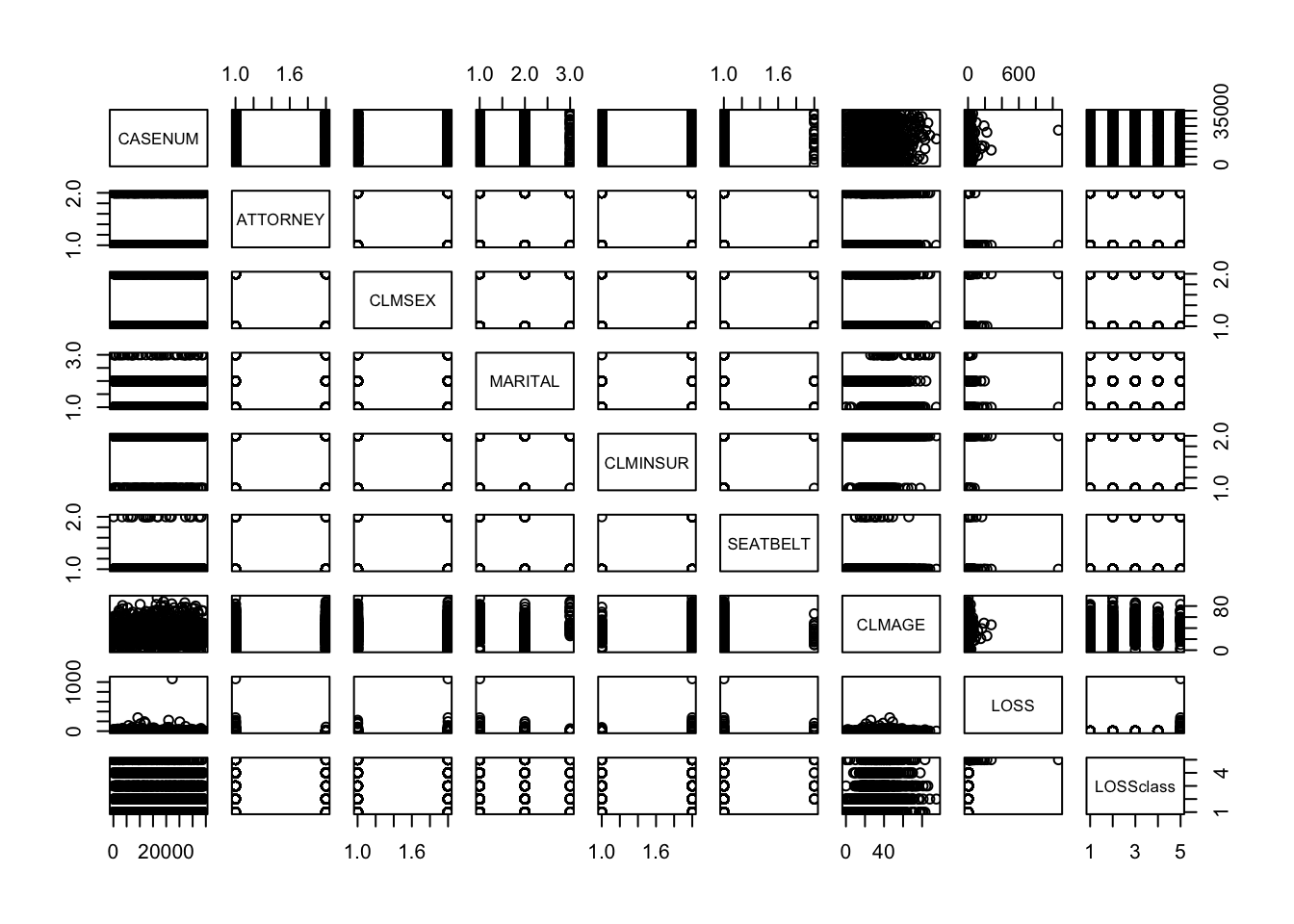
I grafici per alcune coppie sono o poco informativi o non molto sensati.

Tuttavia, se vi sono nel data frame, variabili sia numeriche che fattori esistono altre funzioni molto utili. Si illustra, ad esempio, la funzione ggpairs nel package GGally di ggplot.

library(GGally)
ggpairs(iris)

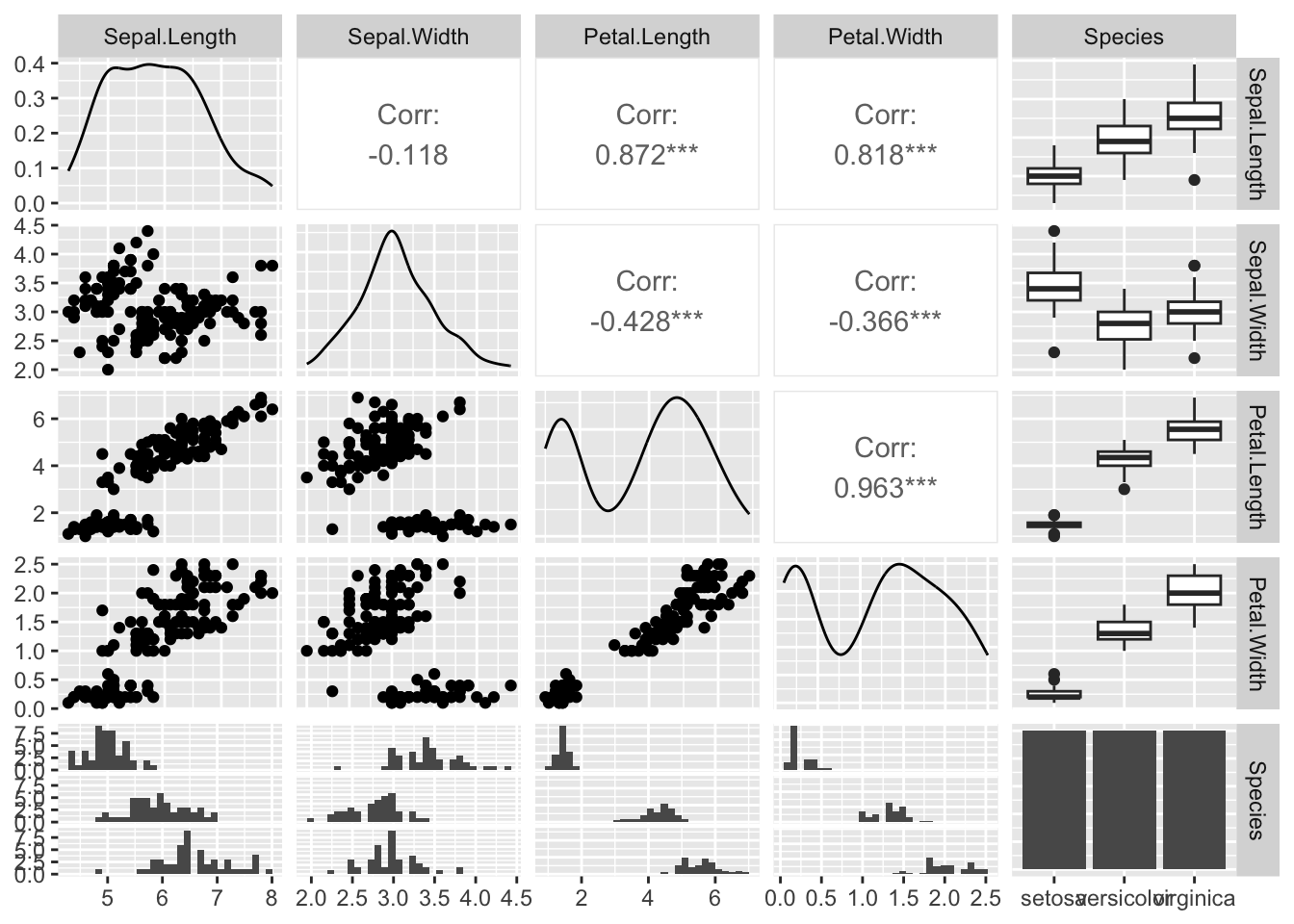
Come si vede in questo caso si adotta la rappresentazione grafica più appropriata data la natura delle variabili.

6.2.2 La correlazione parziale

Nel caso dell’analisi tra due variabile categoriali si era già introdotta l’idea che, se fossero presenti più variabili, non era sufficiente guardare all’associazione marginale fra esse e che poteva esser di intersse guardare all’associazione fra esse condizionatamente a queste ulteriori variabili. In particolare, si voleva mettere in guardia dal non interpretare l’associazione marginale come indicazione di un legame (anche causale fra le due variabili) perchè esso poteva non essere presente quando si tenga conto delle altre variabili.

Una simile attenzione va posta anche nel caso delle variabili quantitative. Quando si calcola il coefficiente di correlazione lineare fra una coppia di variabili, è a volte difficile resistere alla tentazione di interpretare la presenza di un alto livello di correlazione come indicativo di una relazione di “causa-effetto” fra esse. Tuttavia, specie in ambito osservazionale, tale conclusione è all’origine di una fallacia da evitare: occorre ricordare quindi sempre che:

La presenza di un elevato livello di associazione (lineare) (misurata dal coefficiente di correlazione lineare) non può, in genere, essere considerato una prova di un legame causale fra le variabili.

Anche in questo caso, occorre individuare uno strumento che consenta di misurare l’associazione fra le variabili tenendo conto anche delle interazioni con ulteriori variabili osservate.

E’ possibile ottenere misure di correlazione fra coppie di variabili tenendo conto anche di altre variabili introducendo il concetto di correlazione parziale.

Può essere utile considerare un semplice esempio per illustrare sia l’idea di correlazione parziale che le misure che ne derivano.

6.2.2.1 Il consumo di carne causa il cancro?

I dati nel file cancer.csv contengono alcune variabili quantitative relative a dati del 2021 per i paesi delle Americhe.

america<-read.csv("spurious/cancerdata.csv", header=T)
kable(america[,-c(1,6,9)])

country	case	rate	arate	meat	GDP
Argentina	133420	290.0	215.8	115.47999	26300.273
Bahamas	955	238.4	192.7	111.89726	29340.473
Barbados	1120	388.9	205.3	86.37877	15683.885
Belize	409	99.2	114.7	56.61901	11677.461
Bolivia	17579	146.6	143.8	78.36997	9454.198
Brazil	627193	291.2	214.4	98.84000	18075.705
Canada	292098	760.9	345.9	86.85000	55781.700
Chile	59876	311.0	188.7	97.78003	29105.102
Colombia	117620	228.3	177.6	60.94000	17700.060
Costa Rica	13325	257.1	177.7	62.17001	24140.434
Dominican Republic	20171	182.4	167.0	53.52998	21912.260
Ecuador	30888	170.5	152.7	50.91001	13539.711
El Salvador	9799	149.6	127.1	43.85003	10809.714
Guatemala	17801	95.8	121.8	42.08999	11828.330
Guyana	1225	154.3	142.5	72.41991	22865.932
Haiti	13860	118.7	141.1	21.54999	3134.950
Honduras	10815	105.8	128.0	38.75001	6202.981
Jamaica	7500	251.3	199.6	63.40998	9577.164
Mexico	207154	157.5	140.9	75.42000	21031.709
Nicaragua	8409	124.0	133.5	31.52997	7086.623
Panama	8353	187.8	154.9	85.04012	30932.764
Paraguay	13783	188.7	192.2	36.43999	15406.167
Peru	72827	216.2	173.8	54.01001	15282.273
Saint Lucia	448	242.0	166.8	89.60352	19101.166
Suriname	1119	187.5	169.5	60.79010	18458.234
Trinidad and Tobago	3931	279.5	186.7	58.49958	30826.209
United States	2380189	710.9	367.0	126.83000	71318.305
Uruguay	16817	481.0	279.9	62.76991	29441.477

daticanc<-america[,c(3,4,5,7,8)]
corcanc<-round(cor(daticanc),2)
pairs(daticanc)

ggcorrplot(corcanc, type="lower", method="circle", lab=TRUE)

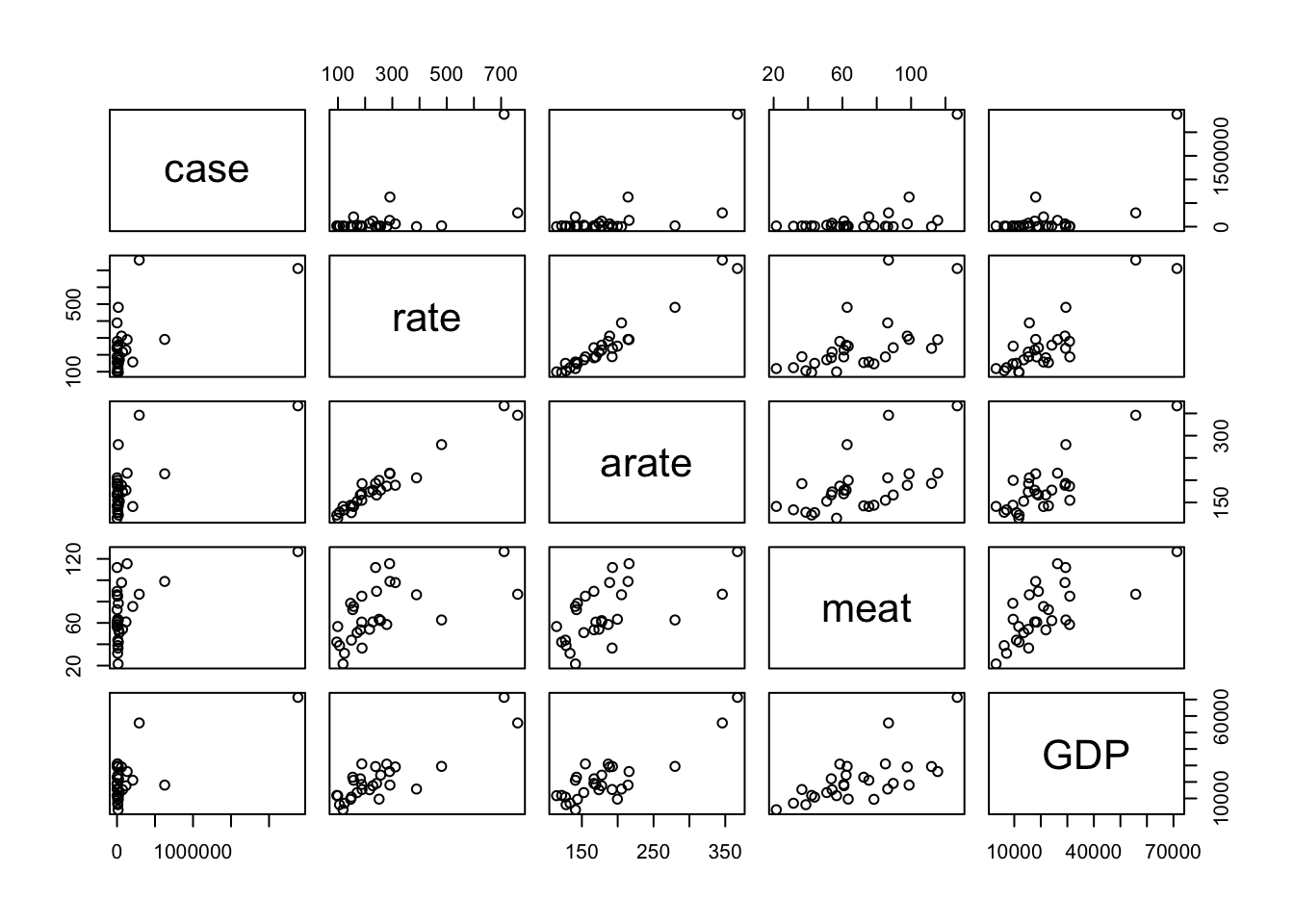
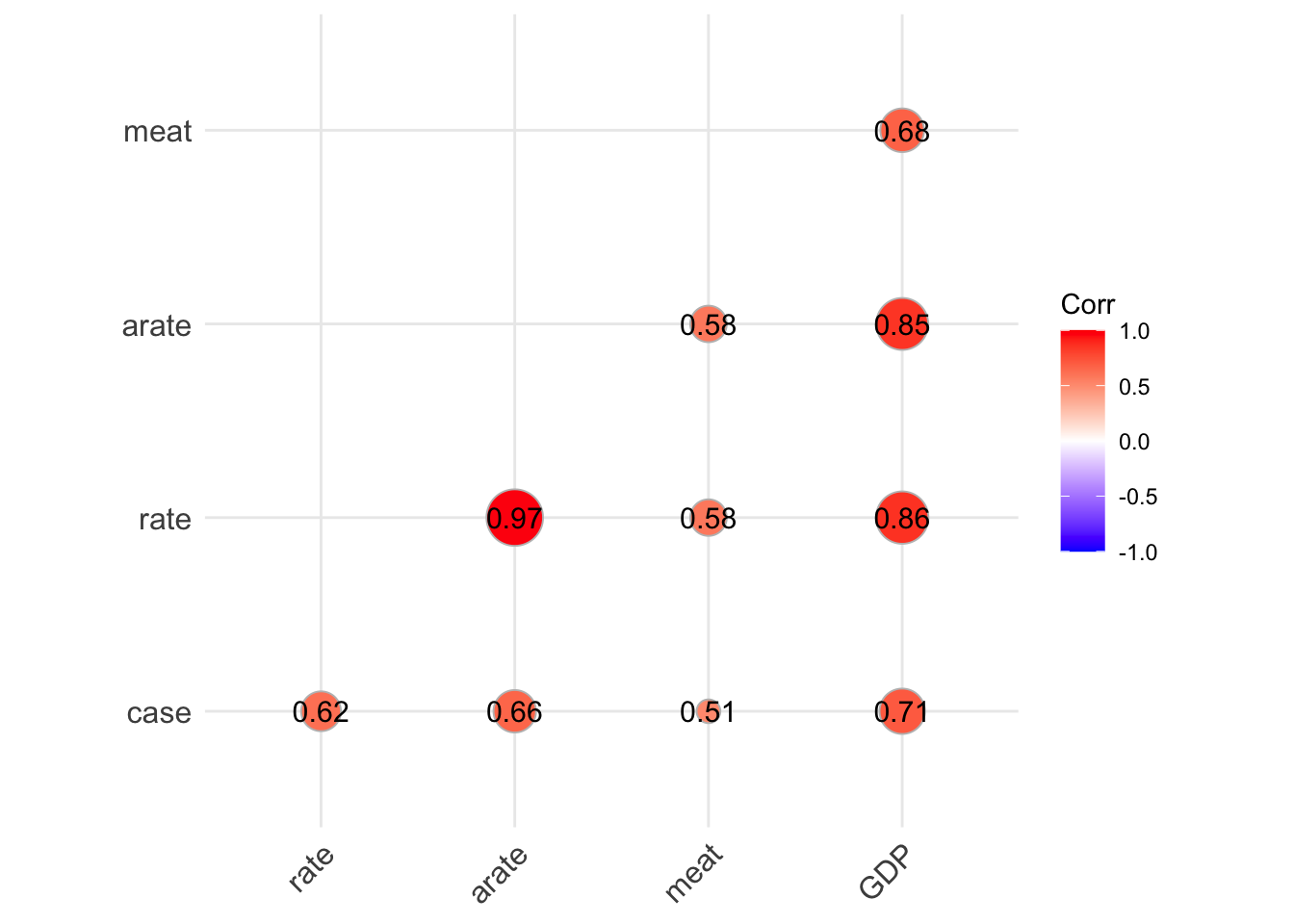Vi sono correlazioni elevate fra le variabili coinvolte. In particolare, si osservi la correlazione fra la variabile meatche è il consumo di carne pro-capite nei diversi paesi e arate che è il tasso di tumori al colon-retto nei diversi paesi (aggiustato per la diversa struttura di età).

Il coefficiente di correlazione lineare è 0.68, elevato e positivo. Vale la pena di osservare anche il diagramma di dispersione più in dettaglio.

ggplot(america, aes(x=meat, y=arate)) +
  geom_point(colour="red", size=2) + # Show dots
  geom_text(
    label=america$Code, color="blue", size=3, 
    nudge_x = 3, nudge_y = 1.75, 
    check_overlap = F
  )

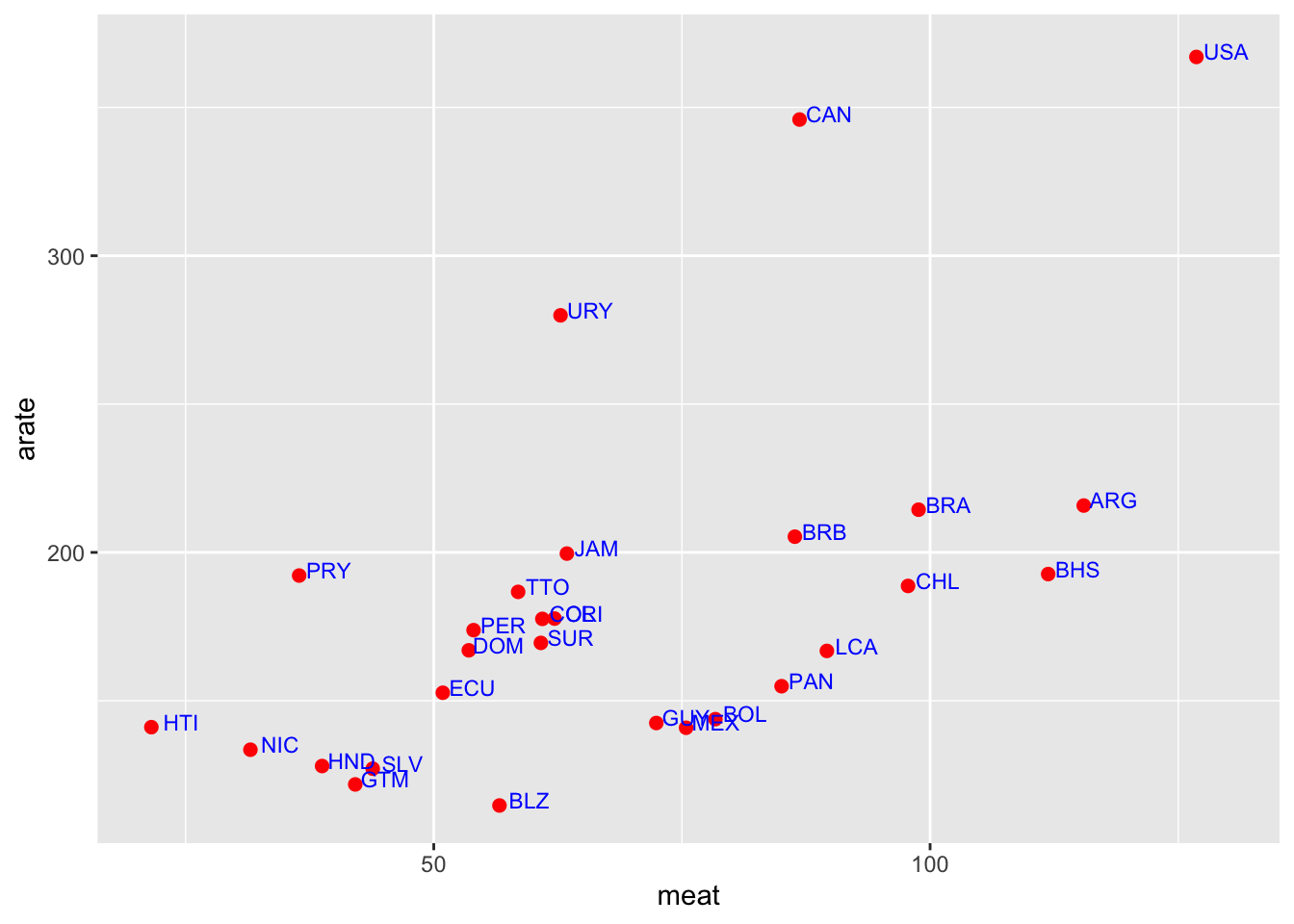
Vi è quindi una associazione fra il consumo di carne e il numero di tumori all’apparato intestinale. Ma è questo un indizio che il consumo di carne possa essere uno dei fattori che causano i tumori al colon-retto? L’evidenza contenuta nei dati sulle due variabili non consetirebbe di trarre tale conclusione: si tratta di dati osservazionali e non sperimentali e quindi l’associazione potrebbe esser dovuta all’effetto di altre variabili.

Ad esempio,in questo caso uno può osservare che entrambe le variabili, meat e arate, sono anche fortemente correlate con la variabile GDP che rappresenta il Prodotto Interno Lordo (PIL in Italia, in inglese GDP, Gross Domestic Product) pro-capite nei diversi paesi.

In effetti, il cancro è una malattia degenerativa e si osserva una maggiore incidenza della malattia in paesi più ricchi nei quali la vità è più lunga e nei quali è meno frequente che si contraggano anche in età giovane malattie che si rilevano fatali come accade in paesi meno ricchi. In alto a destra nel grafico vedete rappresentati i paesi più “ricchi”.

Dovremmo potere quindi misurare la correlazione fra metae arate avendo eliminato l’influenza della terza variabile che è un fattore comune che determina sia alti livelli di casi di tumore che alti livelli di consumo della carne: si tratterebbe di valutare la relazione fra le due variabili al netto della ricchezza, cioè della variabile GDP.

Questo è possibile misurando la correlazione parziale fra due variabili al netto di una terza. L’idea è di calcolare la correlazione fra le variabile avendo prima eliminato l’influenza lineare della terza. Per fare questo possiamo ricorrere a una semplice idea:

si consideri la regressione lineare della variabile meatsu GDP e otteniamo i residui di questa. Si ottiene la variabile consumo di carne meat dalla quale si è eliminata l’influenza lineare del reddito.
si passa poi a fare la stessa cosa con la variabile arate; anche in questo caso si calcolano i residui della regressione del tasso di tumori sul reddito: tali valori non risentiranno più della relazione lineare con il reddito.
si calcola infine la correlazione lineare fra i residui delle due regressioni che rappresentano le due variabili al netto dell’influenza comune del livello di reddito.

resarate<-residuals(lm(arate~GDP,data=america))
resmeat<-residuals(lm(meat~GDP,data=america))
cor(resarate,resmeat)

## [1] 0.004255976

# si noti che il coefficiente è ora quasi pari a zero 
# evidenziando assenza di correlazione lineare

ggplot(america, aes(x=resmeat, y=resarate)) +
  geom_point(colour="red", size=2) + # Show dots
  geom_text(
    label=america$Code, color="blue", size=3, 
    nudge_x = 3, nudge_y = 1.75, 
    check_overlap = F
  )

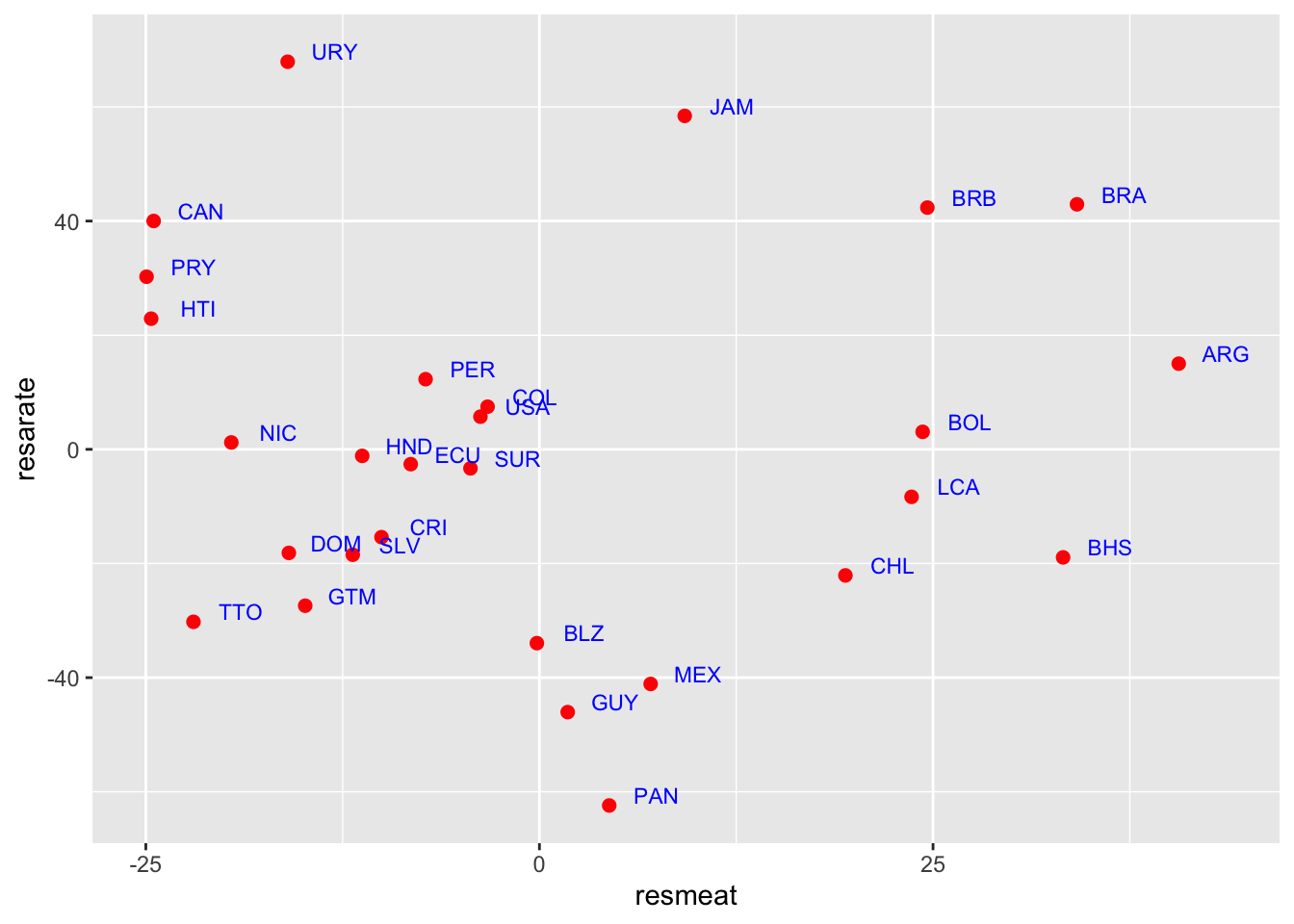
Il coefficente di correlazione appena ottenuto è detto coefficiente di correlazione parziale fra meat e arate al netto di GDP e evidenzia come la correlazione esistente fra le due variabili prese isolatamente potrebbe esser dovuta al fatto che esse condividono una forte relazione lineare con la ricchezza che le determina entrambe: paesi più ricchi hanno sia un alto consumo di carne che un tasso di tumori più elevato (la popolazione è più anziana).

Esistono formule dirette per calcolare i coefficienti di correlazione lineare parziale fra due variabili al netto di una terza in funzione dei coefficienti di correlazione lineare semplice che sono detti anche coefficienti di correlazione totale.

Si usa denotare il coefficiente di correlazione parziale (o netto) fra due variabili $x$ e $y$ al netto di una terza $z$ con $r_{xy.z}$ ed esso può essere calcolato nel modo visto o direttamente, attraverso i coefficienti di correlazione lineare semplici usando la formula: $r_{xy.z}=\frac{r_{xy}-r_{xz}r_{yz}}{\sqrt{1-r^2_{xz}}\sqrt{1-r^2_{yz}}}$

Analogamente si potrebbe definire un coefficiente di correlazione parziale al netto di più variabili, riprenderemo tale concetto in seguito.

6.3 La Regressione lineare multipla

L’analisi di regressione lineare con due variabili (detta regressione semplice) può essere estesa al caso in cui si vogliano inserire fra le variabili esplicative altre variabili.

In particolare quindi, nei modelli di regressione lineare multipla viene definita una variabile risposta (rigorosamente quantitativa), per distinguerla dalle altre variabili la denoteremo con $Y$ e sarà $Y_i$ il valore osservato per l’i-esima unità. Possono essere però inserite molte variabili fra le esplicative (e queste come vedremo possono essere sia qualitative che quantitative). Tali variabili verranno denotate in generale con $X$ , $Z$ , etc., o, meglio con $X_1,X_2, \dots,X_p$ .

L’idea di fondo resta la stessa: vogliamo usare una semplice funzione (di più variabili) per descrivere la media della variabile risposta. Quindi in generale la funzione di regressione multipla ha la forma $M(Y|x_1,x_2,\dots,x_p)=f(x_1,x_2,\dots,x_p)$ ove $f()$ è la funzione sulla quale si trovano le medie condizionate della variabile $Y$ in corrispondenza dei valori delle esplicative.

Nell’analisi di regressione lineare multipla la funzione $f()$ è assunta essere una funzione lineare ovvero una combinazione lineare delle variabili esplicative con coefficienti $\beta$ da determinare secondo qualche criterio avendo a disposizione dati sulle variabili $(Y,x_1,x_2,\dots,x_p)$ quindi si porrà $M(Y|x_1,x_2,\dots,x_p)=f(x_1,x_2,\dots,x_p)=\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_px_p$ Si noti che le variabili $x_k$ che inseriamo possono essere trasformazioni delle variabili: ad esempio, considerando il logaritmo o qualche potenza della variabile originalmente osservata.

Questo implica che nel modello di regressione lineare multipla si può specificare una funzione come: $f(x)=\beta_0+\beta_1x+\beta_2x^2$

Ottenendo così un allontanamento dalla forma lineare della funzione e quindi immaginando che le medie di $Y$ siano collocate lungo una parabola invece che lungo una retta. Si potrebbe pensare anche a una cubica o, più in generale, alla regressione polinomiale. Questo implica che l’analisi di regressione lineare (multipla) è in realtà molto più flessibile di quanto possa apparire a prima vista.

In questa sede vedremo si fornirà una semplice e informale introduzione all’analisi di regressione (multipla) e ai suoi usi. Non verranno approfonditi gli aspetti che richiedono elementi di statistica inferenziale anche se si farà riferimento ad alcuni quantità solo a scopo interpretativo essendo forniti dai principali software. Come già detto, l’analisi di regressione multipla è uno dei principali strumenti della statistica (e non solo) per cui si rinnova il consiglio di seguire un corso ad esso dedicato come quello di Modelli Statistici in cui verranno chiariti gli aspetti formali e inferenziali e verrà approfondito il suo uso.

6.3.1 La funzione di regressione dei minimi quadrati

Data una variabile risposta (target) $Y$ e $p$ predittori $x_1, \ldots, x_p$ , osservati su un campione di $n$ soggetti, la regressione lineare multipla specifica che: $M(Y_i) = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2}+ \ldots +\beta_p x_{ip}$ Le medie condizionate di $Y$ sono supposte come giacenti su un iperpiano nello spazio $p+1$ -dimensionale. L’equazione di regressione sopra contiene i parametri $\beta_0, \beta_1 ,\beta_2 \dots +\beta_p$ ed essi vanno determinati utilizzando i dati a disposizione.

Per determinare l’equazione di regressione si può ricorrere ancora al criterio dei minimi quadrati, per cui si cercano i valori dei parametri $\beta_j$ per cui è minima la funzione $L(\beta_0, \beta_1 ,\beta_2 \dots \beta_p)=\sum_{i=1}^n (Y_i - \beta_0 - \beta_1 x_{i1} - \beta_2 x_{i2}- \ldots +\beta_p x_{ip})^2$ Per ottenere la soluzione di questo problema di minimo conviene ancora ricorrere alla notazione matriciale per cui si può scrivere la somma sopra come $Y-X\beta$ ove In particolare, si ha $\begin{eqnarray*} \left( \begin{array}{c} y_1\\ \vdots\\ y_n \end{array} \right) = \left( \begin{array}{cccc} 1&x_{11}&\cdots& x_{1p-1}\\ \vdots&&&\vdots\\ 1&x_{n1}&\cdots&x_{np-1} \end{array} \right) \left( \begin{array}{c} \beta_0\\ \vdots\\ \beta_{p-1} \end{array} \right) + \left( \begin{array}{c} \epsilon_1\\ \vdots\\ \epsilon_n \end{array} \right), \end{eqnarray*}$ con:

La funzione $L(\beta_0, \beta_1 ,\beta_2 \dots +\beta_p)$ può quindi esser riscritta usando le matrici introdotte come

$L(\boldsymbol{\beta})=(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta})^T(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta})$

per cui se si deriva rispetto a $\boldsymbol{\beta}$ e si uguaglia al vettore $\boldsymbol{0}$ si ottiene

$\frac{\partial L(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}}=(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta})^T(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta})= -\boldsymbol{X}^T\boldsymbol{y}+\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\beta}=\boldsymbol{0}$ da cui risolvendo si ottiene $\hat{\boldsymbol{\beta}}=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}$ Con $\hat{\boldsymbol{\beta}}$ si denotano i valori dei coefficienti di regressione ottenuti come soluzione del sistema di equazioni dei minimi quadrati. Si noti che la soluzione esiste se la matrice quadrata $(\boldsymbol{X}^T\boldsymbol{X})$ è invertibile. Tale condizione si realizza se le variabili (ovvero le colonne) nella matrice $\boldsymbol{X}$ sono linearmente indipendenti così che la matrice quadrata abbia rango pieno.

Problemi potrebbero emergere, ad esempio, se alcune fra le variabili $x_1, x_2,\dots, x_p$ fossero perfettamente correlate. In realtà sarebbe bene evitare anche di inserire fra le varibili esplicative variabili con correlazione molto elevata.

6.3.2 Il controllo della qualità della funzione di regressione

6.3.2.1 La significatività dei singoli coefficienti di regressione multipla

Anche in questo caso una variabile introdotta nel modello è di interesse se il coefficientre $\beta$ ad essa associato ha un valore diverso da 0. Se il coefficiente fosse 0, la variabile non avrebbe rilievo per prevedere la $Y$ e quindi andrebbe omessa. Come sempre a partire dai dati non si otterrà un valore esattamente pari a 0 e si tratta di giudicare se si possa considerare sufficientemente grande da poter escludere che esso sia diverso da zero solo per effetto del caso e dei particolari valori osservati nei nostri dati.

Una risposta rigorosa a tale quesito può essere fornita ricorrendo ai metodi dell’inferenza statistica; essi consentono di ottenere per ogni coefficiente il cosiddetto $p-$ value che può essere interpretato col medesimo criterio introdotto nel caso dell’analisi con due sole variabili: esso, sotto opportune ipotesi relative a un modello probabilistico che generi i dati, consente di valutare la probabilità che, se effettivamente fosse pari a 0 il coefficiente, si osservi un valore ancora più estremo (quindi lontano dallo 0) di quello ottenuto: se tale probabilità e molto piccola allora possiamo ritenere che i dati non forniscono supporto alla congettura che il coefficiente sia pari a zero. La variabile quindi è da ritenersi rilevante (significativa) per prevedere il valore di $Y$ .

Il modello generatore che si adotta per fare inferenza prevede che i valori $Y_i$ osservati derivino da $Y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2}+ \ldots +\beta_p x_{ip}+ \epsilon_i$ dove $\epsilon_i$ sono valori tratti da variabili aleatorie per le quali valgono alcune assunzioni (ad esempio, tali variabili aleatorie hanno valore atteso pari a 0, hanno varianza costante per ogni $i$ , sono incorrelate $\forall i\neq j$ e, talvolta, si assume che siano variabili gaussiane). L’affidabilità delle valutazioni sulla significatività dipende, in genere, da quanto sono realistiche tali assunzioni.

6.3.2.2 Il coefficiente di determinazione lineare $R^2$

Per l’analisi di regressione multipla vale la scomposizione della varianza già introdotta nel caso della regressione con due variabili. Pertanto: $Dev(Y)=DEV(residua)+ DEV(spiegata)=\sum_{i=1}^n(Y_i-\hat{Y}_i)^2+\sum_{i=1}^n(\hat{Y}_i-M((Y)))^2$ e quindi si può ancora proporre l’indice $R^2=\frac{DEV(spiegata)}{Dev(Y)}=1-\frac{DEV(residua)}{Dev(Y)}$ Quanto più $R^2% è vicino a 1 tanto migliore è l’approssimazione della funzione ai dati osservati. Si noti che tale indice aumenterà sempre se si introducono nuove variabili, al più resta costante. Per tale motivo spesso si considera anche $R^2_C$ detto $R^2$ corretto o aggiustato (adjusted). $R^2_C=R^2\mbox{corretto}=1-(1-R^2)*\frac{n-1}{n-p}$ potrebbe anche decrescere se una nuova variabile inserita non è significativa.

$R^2_C$ avrà quindi un valore sempre inferiore o uguale a quello di $R^2$ . A differenza di $R^2$ , l’ $R^2_C$ aumenta solo quando l’aumento di $R^2$ (a seguito dell’inclusione di una nuova variabile esplicativa) è maggiore di quanto ci si aspetterebbe di vedere per caso. Se un insieme di variabili esplicative con una gerarchia di importanza predeterminata venissero introdotte in una regressione una alla volta, calcolando ogni volta l’ $R^2$ aggiustato, il livello al quale $R^2_C$ aggiustato raggiunge un massimo, e poi potrebbe diminuire; quando ciò accade l’analisi di regressione realizza il compromesso ideale fra capacità esplicativa e complessità del modello evitando di aggiungere variabili esplicative superflue.

L’ $R^2_C$ corretto risolve il compromesso (trade off) bias-varianza. Quando consideriamo le prestazioni di un modello, un errore inferiore, misurato in questo caso dalla riduzione della devianza residua, rappresenta una prestazione migliore. Quando il modello diventa più complesso, esso diviene tuttavia più instabile e meno affidabile nel fare previsione per nuovi dati (c’è il cosidetto rischio di sovra adattamento): aumenta cioè la varianza legata al modello.

Un modello più semplice invece sarà spesso più distante dalla realtà, cioè sarà più distorto (biased). L’errore totale, quando si usa il modello per fare previsioni, dipende dalla somma di queste due componenti. Un $R^2$ elevato indica un errore di distorsione inferiore perché il modello può prevedere meglio la variazione per i valori di $Y$ osservato se si usano numerosi predittori. Nel frattempo, il modello tende ad essere più complesso e sarà più difficile che si adatti a nuove situazioni (e prevedere con nuovi dati). Guardare a $R^2_C$ corretto è quindi opportuno perchè di fatto si penalizza la complessità della equazione di regressione se le nuove componenti introdotte non aggiungono molta capacità predittiva.

Inoltre spesso per decidere fra modelli alternativi evitando l’eccessiva complessità, si fa ricorso a degli indici detti criteri di informazione: un esempio è l’AIC. Si tratta di una misura che tiene conto del compromesso tra la bontà dell’adattamento e la complessità del modello (trade-off bias-varainza) ma esso richiede però alcune assunzioni sul modello generatore: più piccolo è l’AIC, migliore è il modello.

6.3.2.3 Selezione (automatica) del modello

Esistono vari metodi per rendere più agevole la scelta del modello quando sono presenti molte potenziali variabili di input. Fra questi ricordiamo quelli basati sull’inserimento o la eliminazione progressiva di regressori nell’equazione. Ad esempio:

regressione backward: inizia con tutti i predittori
1. determina i parametri dell’equazione di regressione
2. se sono presenti coefficienti non significativi, rimuovere il predittore corrispondente con il $p-$ value più alto e tornare al punto 1
regressione forward: inizia con la regressione con la sola intercetta (detto modello nullo)
1. aggiunge un nuovo candidato predittore (scegliendo in prima istanza quello più correlato)
2. determina i parametri dell’equazione di regressione
3. se il coefficiente associato alla variabile è significativo la si mantiene nell’equazione e si prova a introdurre un nuovo predittore.
regressione stepwise: una combinazione delle precedenti. Si inizia come nella regressione forward ma ad ogni nuova inclusione di predittori l’equazione di regressione viene controllata ed eventualmente i predittori non significativi vengono rimossi, come nell’eliminazione backward. Quest’ultima procedura è utile (è presente inoltre un’apposita opzione nei software perl’analisi di regerssione), ma è da usare con cautela.

Esiste inoltre una versione di tali procedure per passi (stepwise appunto) che procede analogamente basandosi però sulla valutazione dell’AIC.

6.3.2.4 L’analisi dei residui

I residui da un’analisi di regressione sono definiti come $\begin{eqnarray*} r_i &=& y_i - (\hat{\beta}_0 + \hat{\beta}_1 x) \\ &=& y_i - \hat{y}_i \quad i=1, \ldots n \end{eqnarray*}$ Essi danno preziose indicazioni su aspetti che potrebbero esser migliorati.

Se l’analisi funziona adeguatamente, essi dovrebbero:

essere vicini a 0
mostrare sia valori positivi che negativi (si ricordi che la loro somma è pari a 0).

Di solito si guarda a uno scatterplot in cui si mettono in ordinata i valori dei residui e in ascissa i valori di $\hat{y}_i$ , cioè $r_i$ contro $\hat{y}_i$ .

In tale grafico i valori dovrebbero:

“ballare” attorno a 0 e distribuirsi in un modo che potremmo definire casuale senza mostrare alcuna regolarità
non mostrare quindi pattern caratteristici (ad esempio, piu piccoli nella parte destra del grafico e più grandi nella parte sinistra, con una forma a imbuto)

Altri grafici dei residui interessanti sono:

$r_i$ contro $x_i$
QQ-plot di $r_i$ contro la gaussiana (qqnorm)
il grafico dei residui standardizzati, delle azioni di leva (leverage) e delle distanze di Cook: si tratta di indici che evidenziano la presenza di valori anomali e/o influenti (ovvero la cui omissione cambierebbe in modo non irrilevante la determinazione dell’equazione di regressione)

6.3.2.5 La natura delle variabili coinvolte e l’interpretazione dei parametri di regressione

La variabile $Y$ , come detto, deve essere una variabile quantitativa perchè l’analisi abbia senso, di tipo continuo (o anche discreta ma con un numero molto elevata di valori distinti)

Le variabili $x_j$ possono invece essere: + quantitative + categoriali (fattori qualitativi)

Se $x_j$ è quantitativa allora il coefficiente $\beta_j$ associato ha la stessa interpretazione che per il modello lineare semplice: rappresenta di quanto in media cambia $Y$ se aumento di una unità la variabile $X_j$ . Si faccia attenzione però che nel modello di regerssione multipla sono coinvolte altre variabili per cui il coefficiente $\beta_j$ misura l’impatto della variabile $x_j$ sulla media di $Y$ immaginando di tenere ferme le altre variabili (al netto delle altre variabili) incluse nel modello. Il coefficiente $\beta_j$ è infatti, per tale motivo, detto coefficiente di regressione parziale: ed esso non sarà lo stesso coefficiente che otterrei in un modello di regressione semplice che includa la sola variabile $x_j$ .

Se invece $x_j$ è categoriale, un fattore con $K$ livelli $l_1, \ldots, l_K$ può essere codificata con $k-1$ variabili indicatrici: $d_{ik} = \left\{\begin{array}{ll} 1 & \mbox{quando } x_{ij} = l_k\\ 0 & \mbox{altrimenti} \\ \end{array}\right.$ for $k= 1, \ldots, K - 1$ .

Se quindi $x_j$ è un fattore categoriale scrivere $\begin{eqnarray*} y_i &=& \beta_0 + \beta_j x_j + \epsilon_i \qquad \mbox{non avrebbe senso, mentre si può scrivere}\\ &=& \beta_0 + \alpha_1 d_{i1} + \ldots + \alpha_{k}d_{ik} + \ldots+ \alpha_{K-1} d_{iK-1} + \epsilon_i \\ &=& \beta_0 + \alpha_{k} + \epsilon_i \mbox{ quando } x_j = l_k \mbox{for }k = 1, \ldots K-1\\ &=& \beta_0 \mbox{ quando } x_j = l_K \mbox{ è assunto come livello di riferimento} \end{eqnarray*}$ Il parametro $\alpha_k$ va interpretato come il cambiamento medio $y$ associato al passaggio di $x_i$ dal livello $l_K$ , assunto come riferimento, al livello $l_k$ .

6.3.3 Un esempio con l’aggiunta di una seconda variabile esplicativa categoriale

Si riconsiderino i dati whiteside. I dati su Gas e temperature sono stati raccolti in due condizioni, prima e dopo l’intervento di isolamento della casa (questa informazione è nella variabile Insul che presenta due modalità “Before” e “After”).

Si riprenda l’analisi di regressione svolta e si calcolino i residui

library(MASS)
data(whiteside)
linm <- lm(Gas~Temp, data=whiteside)
res <- residuals(linm)
yhat <- fitted(linm)
par(mar=c(4,4,2,1))
plot(yhat, res, pch=20, col=4, xlab=expression(hat(y)), ylab = "residui")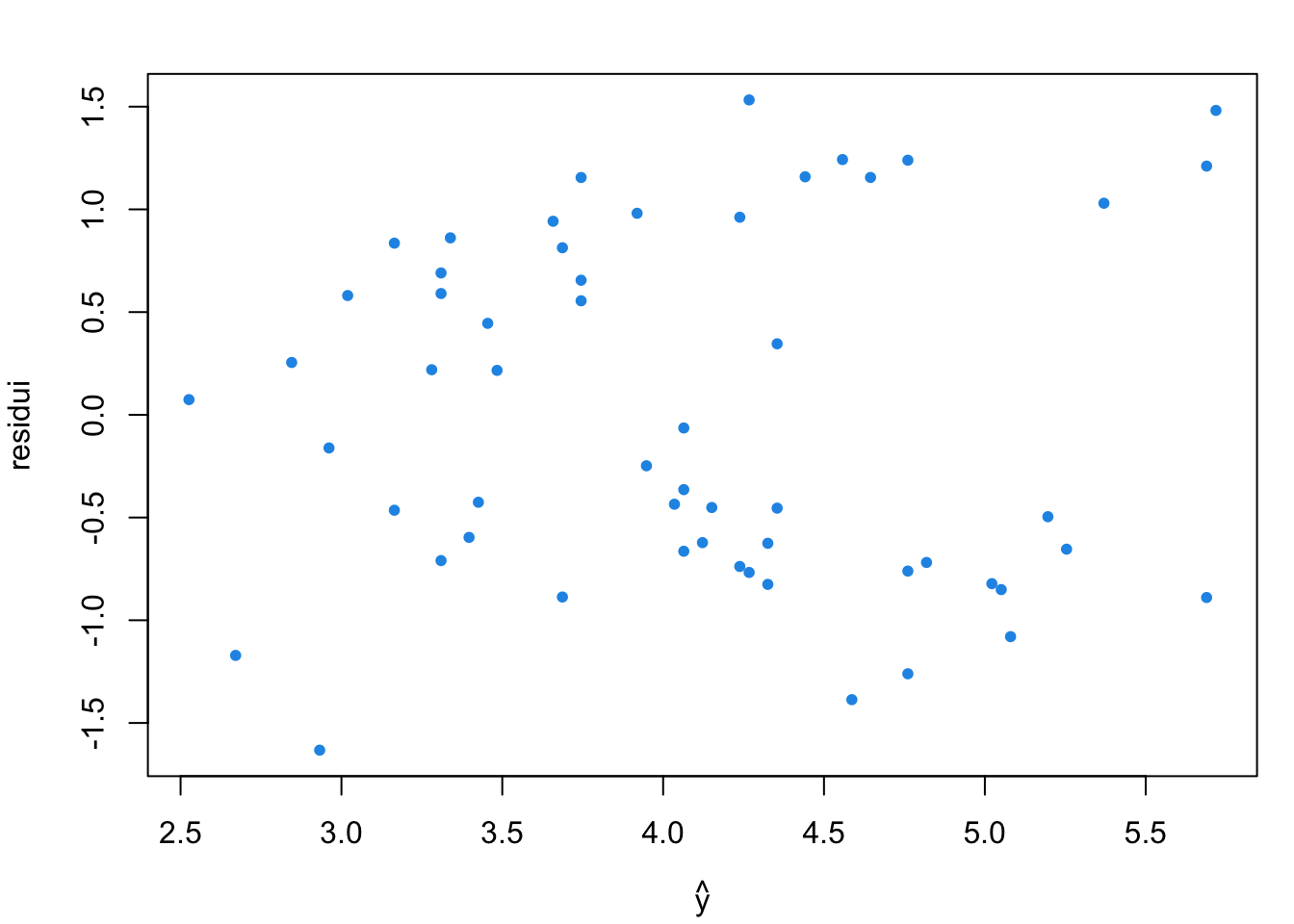

Sebbene non appaiono grosse anomalie, il grafico dei residui suggerisce alcuni problemi

La variabilità dei residui non è costante
Sembra che ci siano due gruppi di residui

I residui positivi aumentano all’aumentare di $\hat{y}$
I residui negativi diminuiscono all’aumentare di $\hat{y}$

Esistono due gruppi di osservazioni nei quali la relazione presente tra consumo di riscaldamento e la temperatura esterna è diversa da quella precedentemente ottenutata (i residui presentano un andamento in cui sono ancora funzione della temperatura tramite $\hat{y}$ ) e non dovrebbero visto che la variabile temperatura è stata già introdotta.

Si è tralasciato qualcosa di rilevante?

Si consideri la terza variabile, quindi si ha:

Gas (la variabile risposta che denoteremo con $Y$ )
Temperature (che denoteremo con $x$ )
Insul (che denoteremo con $z$ )

I dati disponibili sono quindi $(x_1, z_1, y_1), (x_2, z_2, y_2), \ldots, (x_i, z_i, y_i), \ldots, (x_{n}, z_n, y_{n})$ con $z_i =$ “Before” for $i=1, \ldots, 26$ , and $z_i =$ “After” for $i=27, \ldots, 56$ .

È ragionevole aspettarsi che l’intervento di isolamento abbia un impatto sul consumo medio di gas per riscaldamento e che dopo l’intervento il consumo di gas sia inferiore rispetto a prima.

Si crei la variabile $z$ a partire da $Insul$

z <-  whiteside[,1] 
par(mar=c(4,4,2,1))
plot(whiteside$Temp, whiteside$Gas, pch=as.character(z), 
     col=as.numeric(z)+1, xlab="temperatura", ylab="consumo di gas")

Considerando la terza variabile il nuovo modello può essere genericamente specificato come segue: $\begin{eqnarray*} \mbox{Consumo di gas} &= &g(\mbox{temperatura}, \\ & &\hspace{.3cm}\mbox{prima/dopo l'intervento}) \\ \hspace{-1cm}y_{i}&=& g(x_i, z_i; \epsilon_i ) \end{eqnarray*}$

Essendo presenti ora 32 variabili esplicative si è passati a un’analisi di regressione lineare multipla

$M(Gas_i) = \beta_0 + \beta_1 Temp + \beta_2 Insul_i$ Quindi la media condizionata di $Y_i$ è ora una funzione lineare di due variabili.

Tuttavia la variabile aggiuntiva che è stata inserita $Insul$ è qualitativa con modalità “Before” e “After” e il modello scritto come sopra non avrebbe senso in quanto $Insul$ non ha valori numerici. L’approccio standard per superare il problema è quello di introdurre una variabile ausiliaria (indicatrice) definita come: $d_i = \left\{ \begin{array}{ll} 0 & se~~~~ Insul_i = \mbox{"Before"}\\ 1 & se~~~~ Insul_i = \mbox{"After"}\\ \end{array} \right.$ - la precedente equazione di regressione allora diventa: $\begin{eqnarray*}M(Gas_i) &=& \beta_0 + \beta_1 Temp_i + \beta_2 d_i\\ & = & \beta_0 + \beta_1 x_i \quad \mbox{prima dell'intervento}\\ & = & (\beta_0 + \beta_2) + \beta_1 Temp_i + \quad \mbox{dopo l'intervento} \end{eqnarray*}$ In altre parole l’introduzione della variabile fittizia dà origine a due rette parallele, una per ogni valore di $Insul_i$

La determinazione dei parametri del modello tramite i minimi quadrati si estende facilmente al seguente modello di regerssione lineare multipla: $min_{\beta_0, \beta_1, \beta_2} \sum_{i=1}^n \left(Gas_i - (\beta_0 + \beta_1 Temp_i + \beta_2 d_i)\right)^2$

Per ottenere i valori dei minimi quadrati per i tre parametri si può ancora usare la funzione lm(). La sintassi è la stessa e la variabile Insul viene trasformata automaticamente nella variabile ausiliaria vista prima.

whiteside$Insul <- relevel(whiteside$Insul, ref="Before")
# possiamo
mlm <- lm(Gas~Temp+Insul, data=whiteside)
beta0 <- coef(mlm)[1]
beta1 <- coef(mlm)[2]
beta2 <- coef(mlm)[3]

beta0 # l'intercetta

## (Intercept) 
##    6.551329

beta1 # il coefficiente lineare della regressione di Gas su Temp

##      Temp 
## -0.336697

beta2 # misura l'effetto della terza variabile

## InsulAfter 
##  -1.565205

Come interpretare $\beta_2$ ?

options(width=60)
par(mar=c(4,4,2,1))
plot(whiteside$Temp,whiteside$Gas, pch=as.character(z), col=as.numeric(z)+1, 
     xlab="temperatura", ylab="consumo di gas")
abline(beta0, beta1, col=2)
abline(beta0+beta2, beta1, col=3)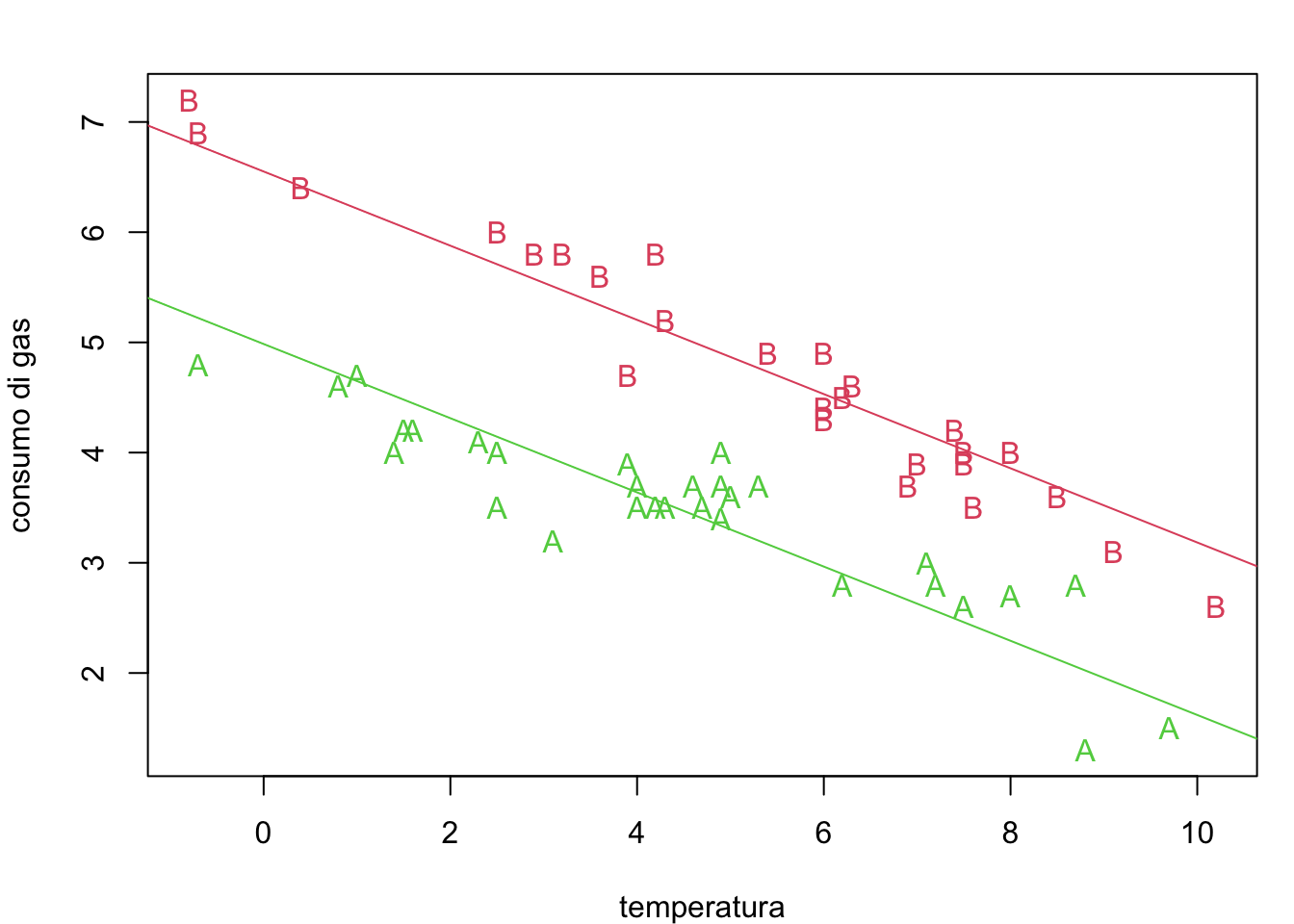

Si consideri, l’interpretazione dei parametri ottenuti con i minimi quadrati (indicati col “cappelletto”): $\hat{\beta}_0$ : Consumo medio di Gas quando tutti predittori sono pari a 0. In questo caso ha un senso interpretarlo perchè $0$ è un valore che fa parte del range dei valori dei predittori. Spesso l’intercetta non ha un’interpretazione: se la temperatura è 0 gradi, e siamo prima dell’isolamento ( $d_i = 0$ ), il consumo medio di gas sarebbe 6.6 metri cubi.

$\hat{\beta}_j$ $(j >1)$ : in generale i valori dei coefficienti associati alla $j-$ ma variabile misurano la variazione media di $y$ quando la $j-$ ma variabile esplicativa è incrementata di 1 unità e tutti le altre variabili predittive sono tenute costanti. Quindi se la temperatura esterna aumenta di un grado, il consumo medio di gas decresce di circa 0.34 metri cubo, indipendentemente dal fatto che si tratti di una misura ottenutra prima o dopo l’isolamento. Infine, se le case vengono isolate ( $d_i$ passa da $0$ , cioe da “Before”, a $1$ , cioè “After”), il consumo medio di gas decresce di circa 1.57 metri cubi indipendentemente dalla temperatura.

Ovviamente, possiamo usare la funzione ottenuta per ottenere una previsione del consumo di Gas per qualsiasi valore delle variabili predittrici (possibilmente limitandosi al range dei valori osservati)
$\hat{Gas}= M(y) =\hat{\beta}_0 + \hat{\beta}_1 Temp + \hat{\beta}_2 d$

Ad esempio, qual è il consumo medio del gas quando la temperature è 5? - se la casa non è isolata $\begin{eqnarray*} \hat{y} &=& 5.486 -0.2902 x \\ &=& 6.551 -0.3367 \cdot 5 = 4.8675\mbox{ metri cubi}\\ \end{eqnarray*}$ - se la casa è isolata: $\begin{eqnarray*} \hat{y} &=& 5.486 -0.2902 x \\ &=& 6.551 -1.565 - 0.3367 \cdot 5 =3.3025 \mbox{ metri cubi}\\ \end{eqnarray*}$

Un ulteriore estensione del modello, sempre limitandoci alle sole due variabili esplicative disponibili, sarebbe quella di introdurre il prodotto fra le variabili Tempe la varabile indicatrice $d$ che è legata all’isolamento.

L’equazione di regressione diviene: $M(Gas_i) = \beta_0 + \beta_1 Temp_i + \beta_2 Insul_i+\beta_3 Insul_i*Temp_i$

Si noti che in questo caso l’equazione ottenuta equivarrebbe alla seguente situazione $\begin{eqnarray*}M(Gas_i) &=& \beta_0 + \beta_1 Insul_i + \beta_2 d_i\\ & = & \beta_0 + \beta_1 x_i \quad \mbox{prima dell'intervento}\\ & = & (\beta_0 + \beta_2) + (\beta_1+\beta_3) Insul_i + \quad \mbox{dopo l'intervento} \end{eqnarray*}$

Ci sono cioè due diversi effetti della temperatura nei due regimi (prima e dopo l’isolamento). Questo può essere specificato in R introducendo l’interazione fra le due variabili Temp e Insul.

mlmint <- lm(Gas~Temp+Insul+Temp*Insul, data=whiteside)
summary(mlmint)

## 
## Call:
## lm(formula = Gas ~ Temp + Insul + Temp * Insul, data = whiteside)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.97802 -0.18011  0.03757  0.20930  0.63803 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      6.85383    0.13596  50.409  < 2e-16 ***
## Temp            -0.39324    0.02249 -17.487  < 2e-16 ***
## InsulAfter      -2.12998    0.18009 -11.827 2.32e-16 ***
## Temp:InsulAfter  0.11530    0.03211   3.591 0.000731 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.323 on 52 degrees of freedom
## Multiple R-squared:  0.9277, Adjusted R-squared:  0.9235 
## F-statistic: 222.3 on 3 and 52 DF,  p-value: < 2.2e-16

beta0 <- coef(mlmint)[1]
beta1 <- coef(mlmint)[2]
beta2 <- coef(mlmint)[3]
beta3 <- coef(mlmint)[4]

beta0 # l'intercetta

## (Intercept) 
##    6.853828

beta1 # il coefficiente lineare della regressione di Gas su Temp

##       Temp 
## -0.3932388

# beta2 e beta3 # misurano le variazioni che l'introduzione
#                della terza variabile comporta nell'inetrecetta e nel
#                coefficiente angolare

Si noti che tale modello migliora le equazioni precedenti (si vedano i coefficienti e la loro significatività). Graficamente equivale a:

options(width=60)
par(mar=c(4,4,2,1))
plot(whiteside$Temp,whiteside$Gas, pch=as.character(z), col=as.numeric(z)+1, 
     xlab="temperatura", ylab="consumo di gas")

abline(beta0, beta1, col=2)
abline(beta0+beta2, beta1+beta3, col=3)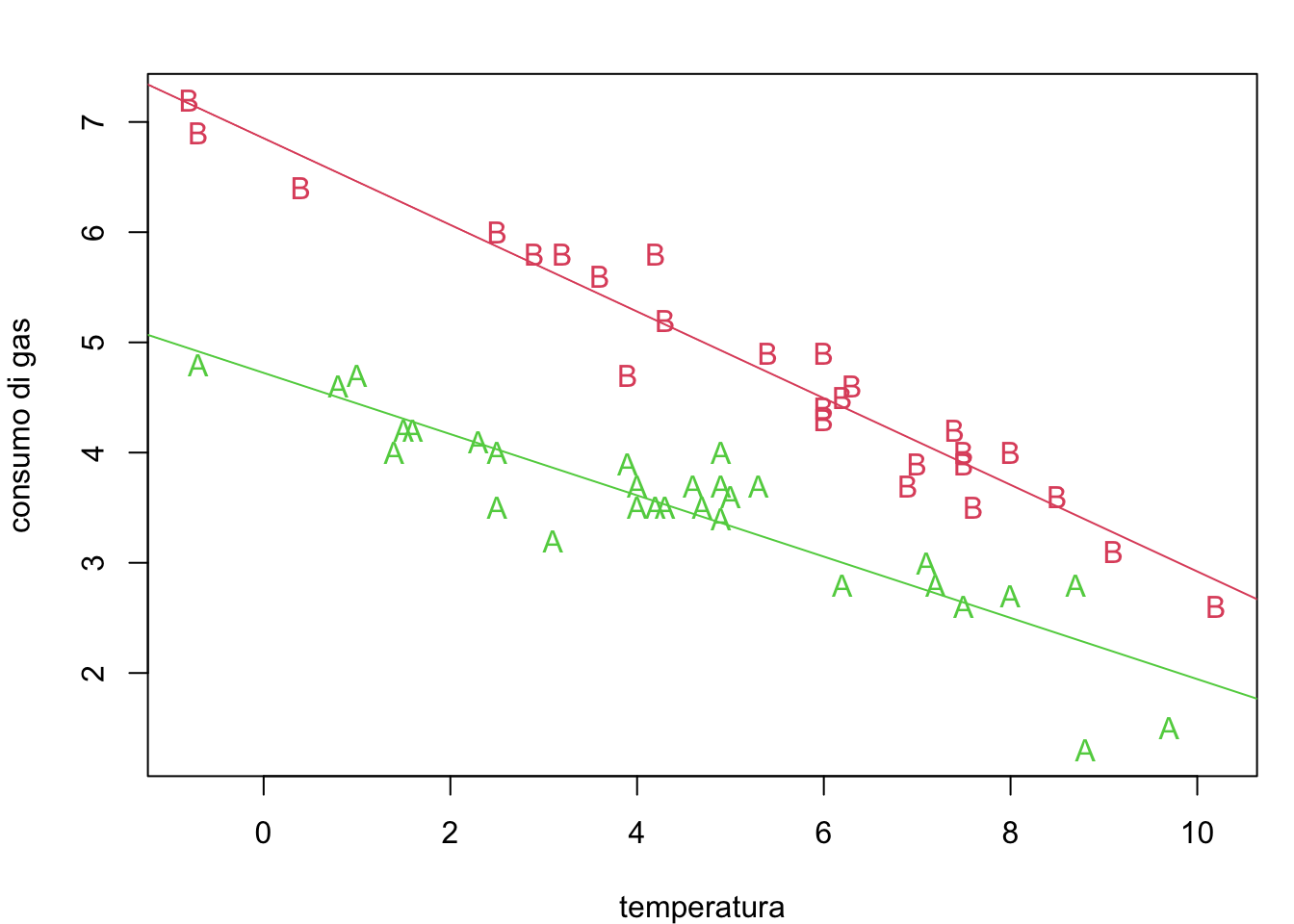

6.3.4 Regressione multipla: un esempio guidato con R

In questo esempio, si esaminano i dati della Survey of Consumer Finances (SCF), indagine condotta in USA su un campione di 275 cittadini che hanno acquistato una polizza vita e per i quali si raccolgono informazioni sul loro reddito e sulle loro caratteristiche demografiche.

i dati sono disponibili su

Obiettivo dell’analisi è determinare quali caratteristiche influenzino la spesa per polizze vita. Per quanto riguarda le polizze temporanee in caso morte (term life insurance), l’ammontare che viene rilevato è FACE, ovvero quanto la compagnia pagherà in caso di morte dell’assicurato.

Le informazioni disponibili sono riassunte nella seguente tabella:

Col seguente comando carichiamo i dati sul workspace di R:

TL <- read.csv("TL.csv", header=TRUE, sep=",", row.names=1)

Consideriamo la struttura dell’oggetto TL.

str(TL)

## 'data.frame':    275 obs. of  6 variables:
##  $ AGE      : int  30 50 39 43 34 29 72 51 58 73 ...
##  $ MARSTAT  : chr  "not single" "not single" "not single" "not single" ...
##  $ EDUCATION: int  16 9 16 17 11 16 17 16 14 12 ...
##  $ NUMHH    : int  3 3 5 4 4 3 2 4 1 2 ...
##  $ INCOME   : int  43000 12000 120000 40000 28000 100000 112000 15000 32000 25000 ...
##  $ FACE     : int  20000 130000 1500000 50000 220000 600000 100000 2500000 250000 50000 ...

# conviene trasformare in fattore la variabile MARSTAT
TL$MARSTAT<-factor(TL$MARSTAT)

La variabile risposta che consideriamo è FACE, e come prima possibile variabile esplicativa usiamo solo INCOME che è ragionevole pensare che sia legata alla prima.

Vediamo la sintesi delle due variabili

summary(TL$FACE)

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
##      800    50000   150000   747581   590000 14000000

summary(TL$INCOME)

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
##      260    38000    65000   208975   120000 10000000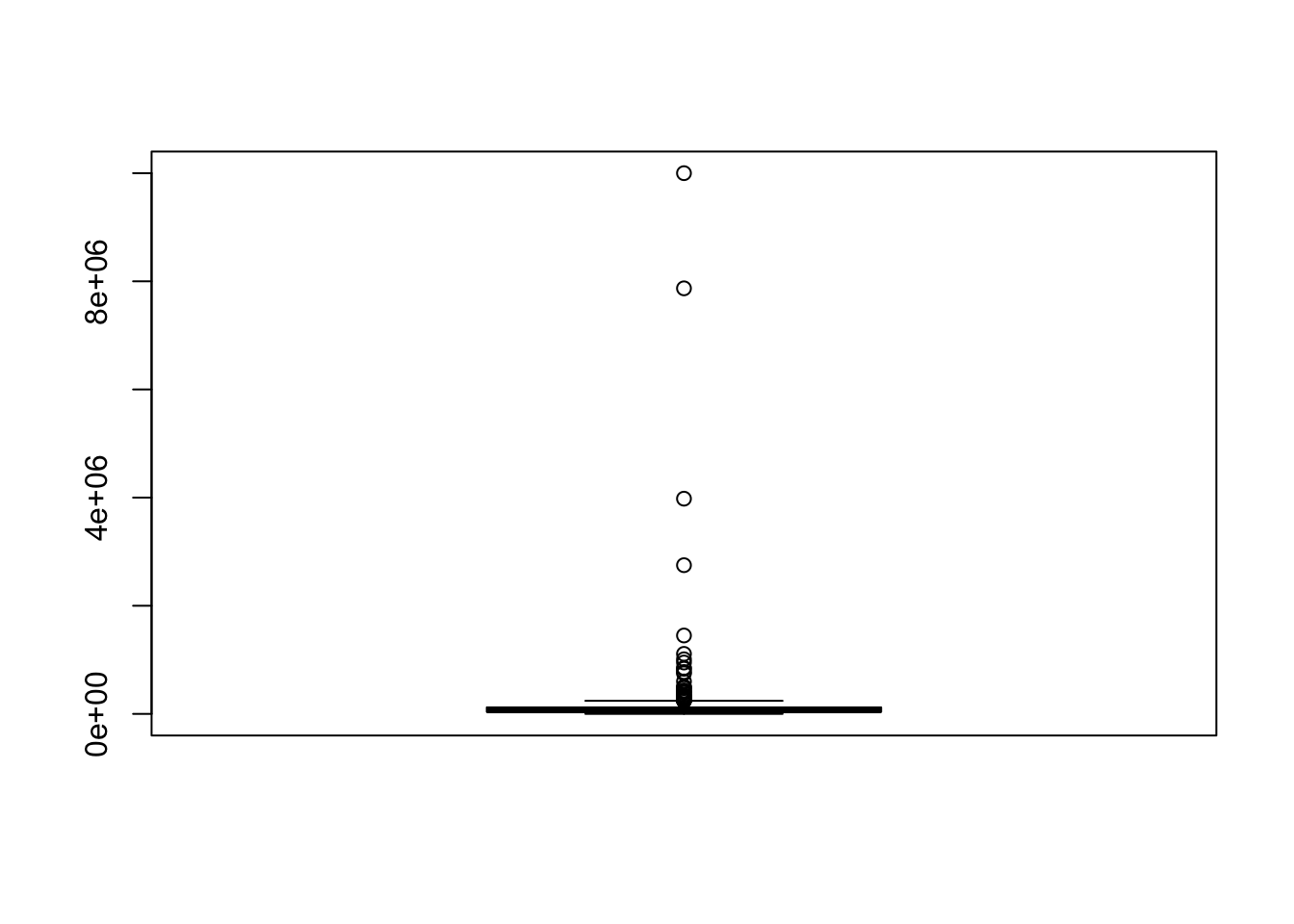

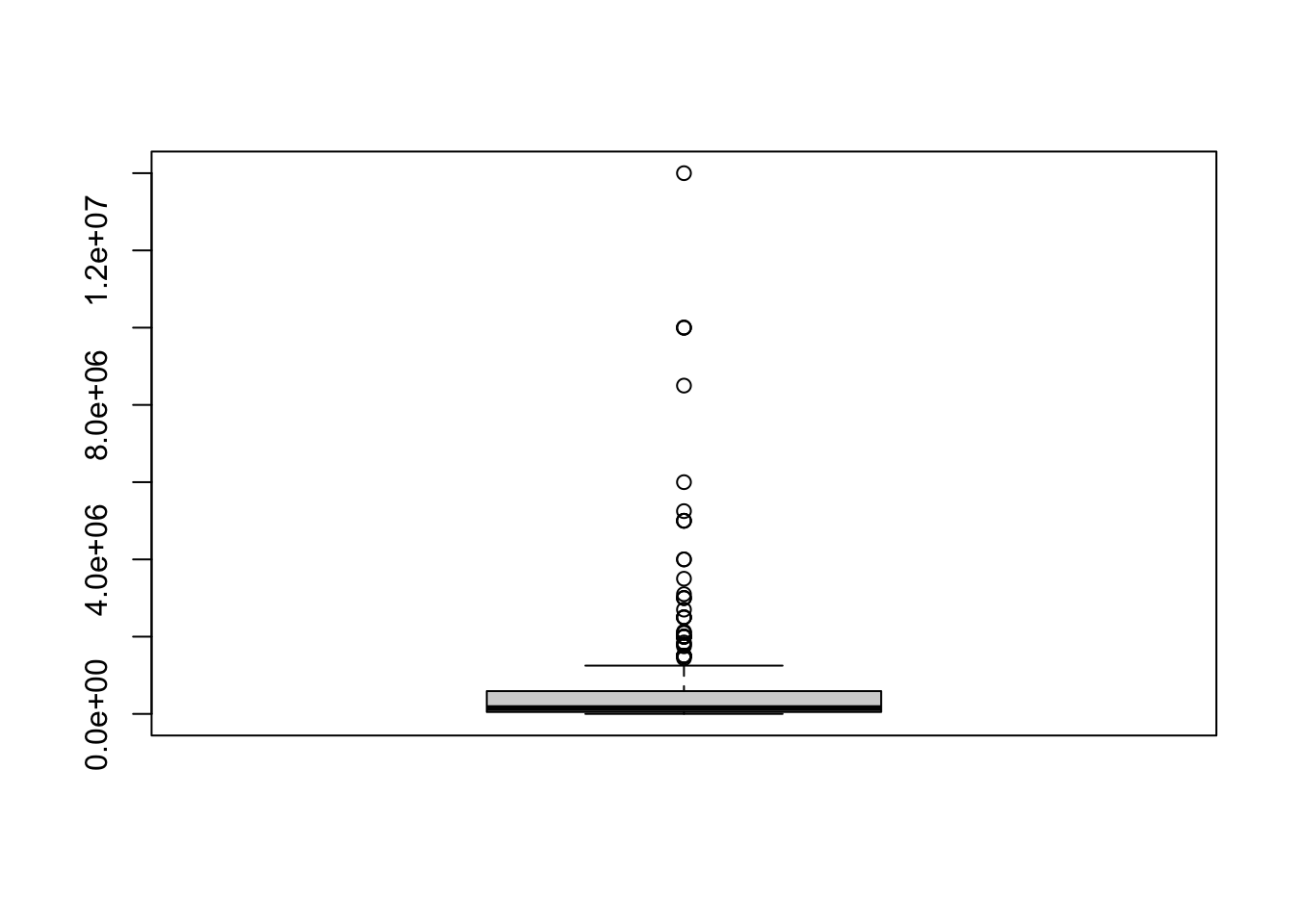
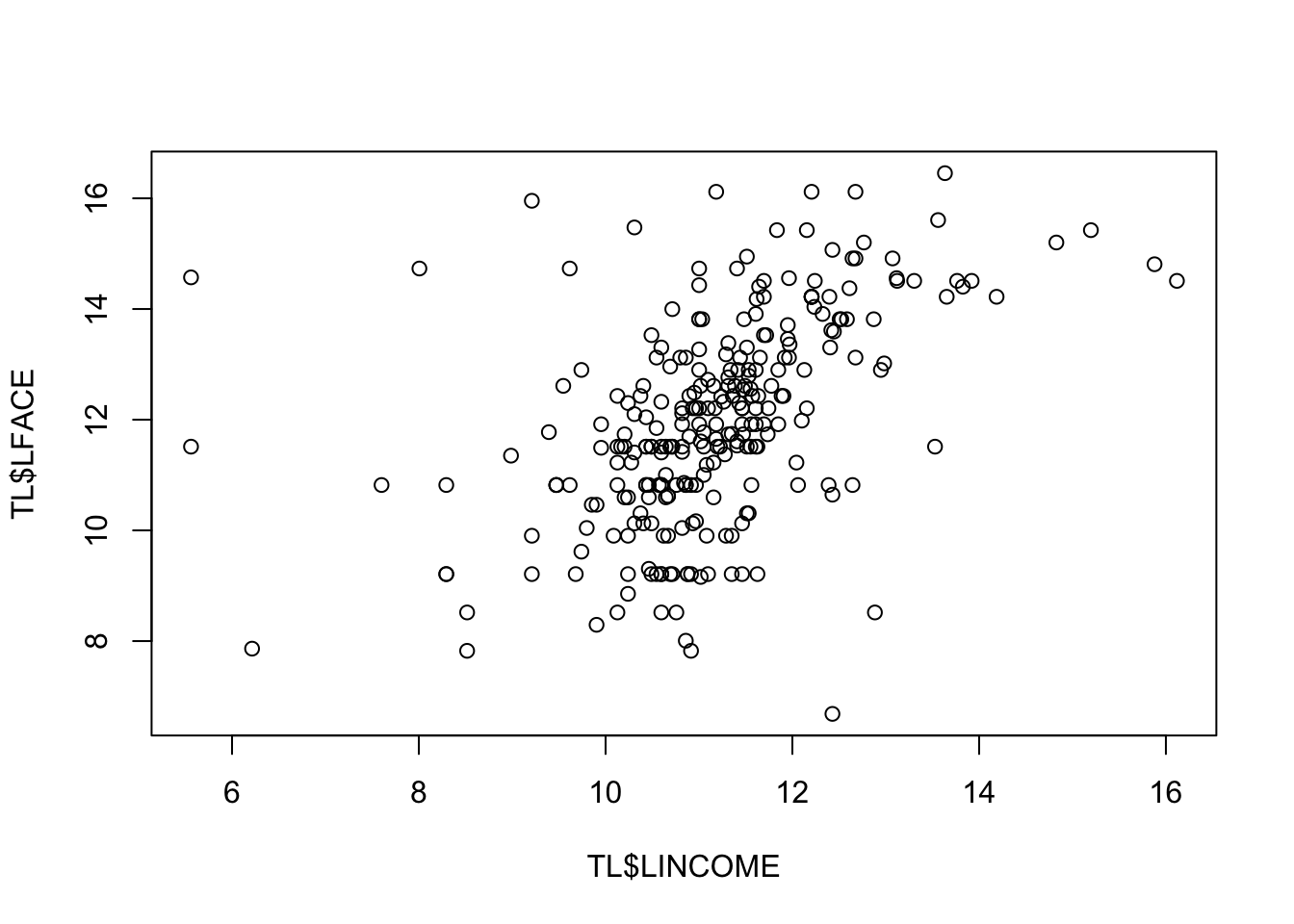
boxplot(TL$INCOME)

boxplot(TL$FACE)

Le due variabili sembrano avere una forte asimmetria positiva (si vedano media e mediana, ove la seconda è di molto minore della prima) e questo appare chiaramente anche dal diagramma di dispersione:

plot(TL$INCOME, TL$FACE)

la grande maggioranza dei valori sono in basso a sinistra mentre solo pochi valori, molto elevati appaiono in alto, `e una conseguenza della forte asimmetria, e questo maschera la relazione fra le variabili.

6.3.5 Costruzione dell’equazione di regressione

Come primo banale esercizio, proviamo la regressione lineare semplice di FACE, vs INCOME, ignorando per ora il problema dell’asimmetria nella distribuzione delle due variabili. L’equazione di regressione ha la forma

$M(FACE_i) = \beta_0 + \beta_1 INCOME_i$

Utilizzare lm()

m0<- lm(TL$FACE~TL$INCOME)

Una sintesi dei risultati della stima dei parametri si può visualizzare con il comando generico summary:

summary(m0)

## 
## Call:
## lm(formula = TL$FACE ~ TL$INCOME)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3069185  -628950  -551689  -167579 12976542 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 6.553e+05  1.019e+05   6.433 5.59e-10 ***
## TL$INCOME   4.414e-01  1.200e-01   3.677 0.000284 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1637000 on 273 degrees of freedom
## Multiple R-squared:  0.04718,    Adjusted R-squared:  0.04369 
## F-statistic: 13.52 on 1 and 273 DF,  p-value: 0.0002843

Innanzitutto si può provare a dare un’interpretazione dei coefficienti ottenuti

La tabella consente di valutare agevolmente se i parametri sono significativamente differenti da zero. Si guardano ad esempio i $p-$ values e si conclude che il parametro è significativamente diverso da 0 se essi sono molto piccoli (sotto 0.01 ad esempio) ovvero è molto bassa la probabilità di ottenere valori ancora più estremi del parametro nell’ipotesi che questo coefficiente sia in realtà pari a 0. In particolare, $\hat{\beta}_1$ è significativo e conferma che il reddito ha un effetto sull’ammontare delle polizze acquistate e non è plausibile pensare che questo sia dovuto al caso.

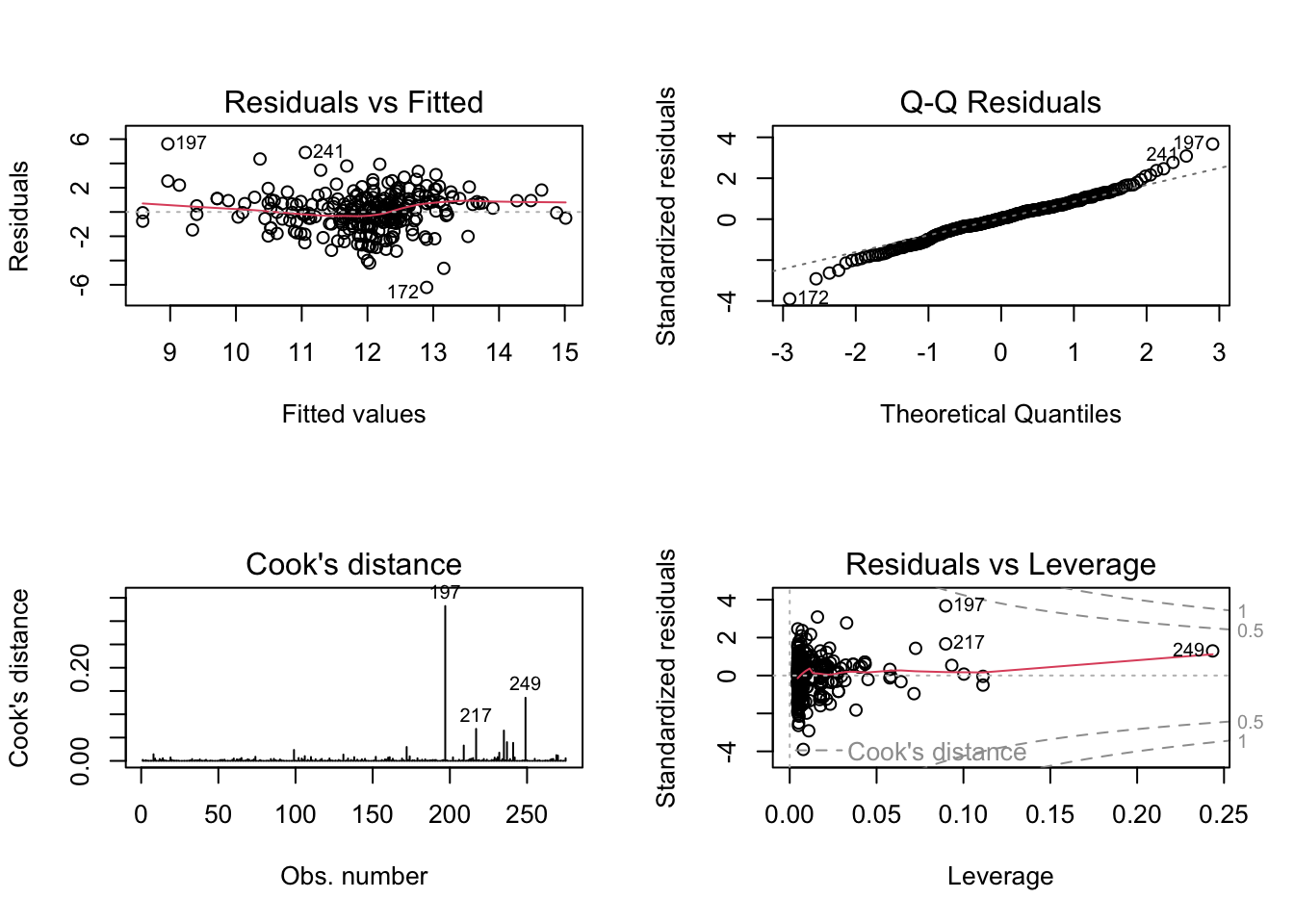
Tuttavia si noti che $R^2$ `e quasi 0. Inoltre, si può guardare ai residui

par(mfrow=c(1,2))
plot(m0, which=1:2)

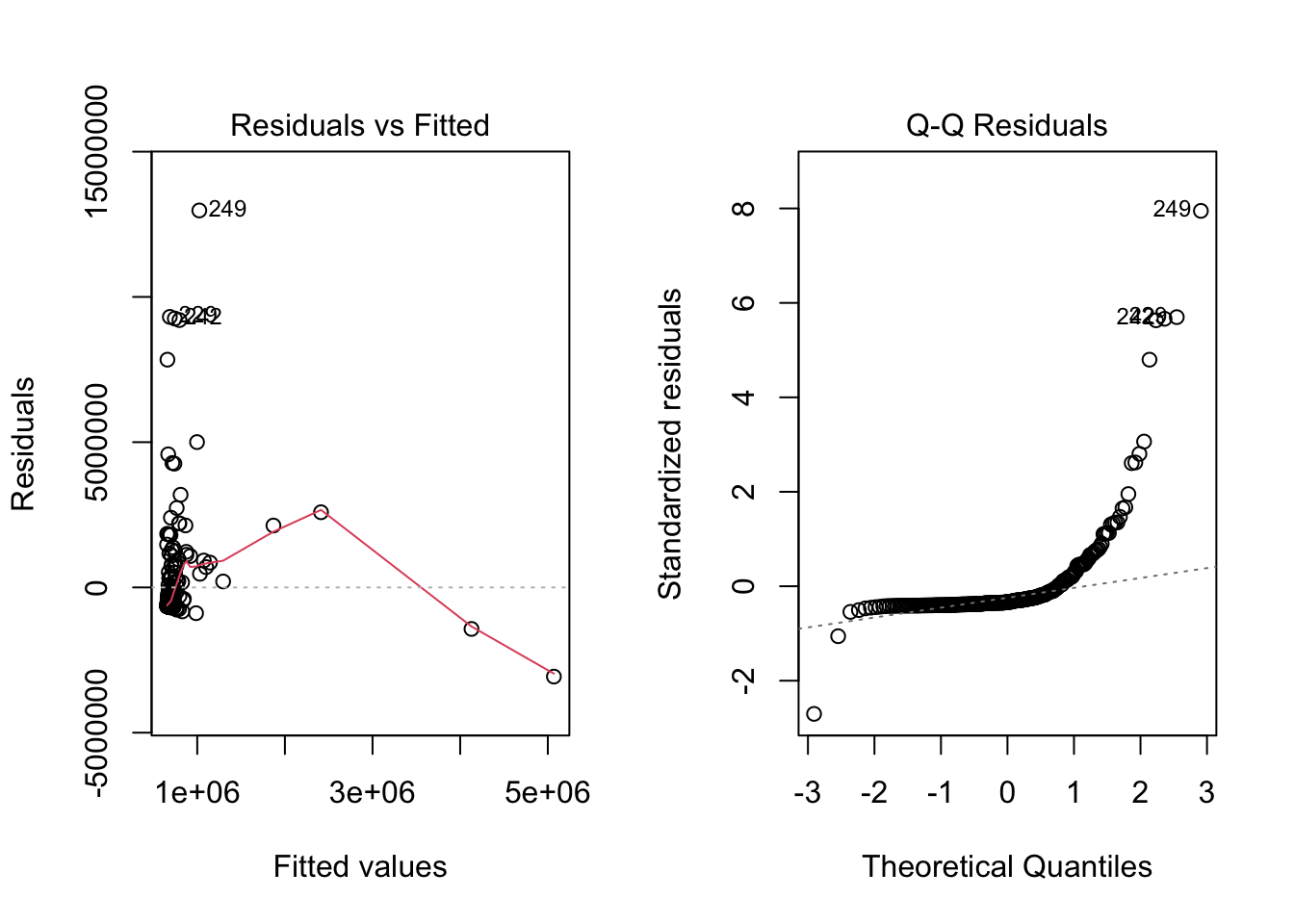
Tali grafici confermano che tale equazione di regressione non è del tutto convincente. I residui non seguono un pattern regolare e non sembrano adattarsi a una gaussiana (primi due grafici).

Una possibile causa del non soddisfacente adattamento è la presenza di variabili fortemente asimmetriche. In questo caso potrebbe rivelarsi più opportuno utilizzare una trasformazione delle variabili che riduca l’asimmetria.

TL$LFACE <- log(TL$FACE)
TL$LINCOME <- log(TL$INCOME)

boxplot(TL$LINCOME)

boxplot(TL$LFACE)

plot(TL$LINCOME, TL$LFACE)

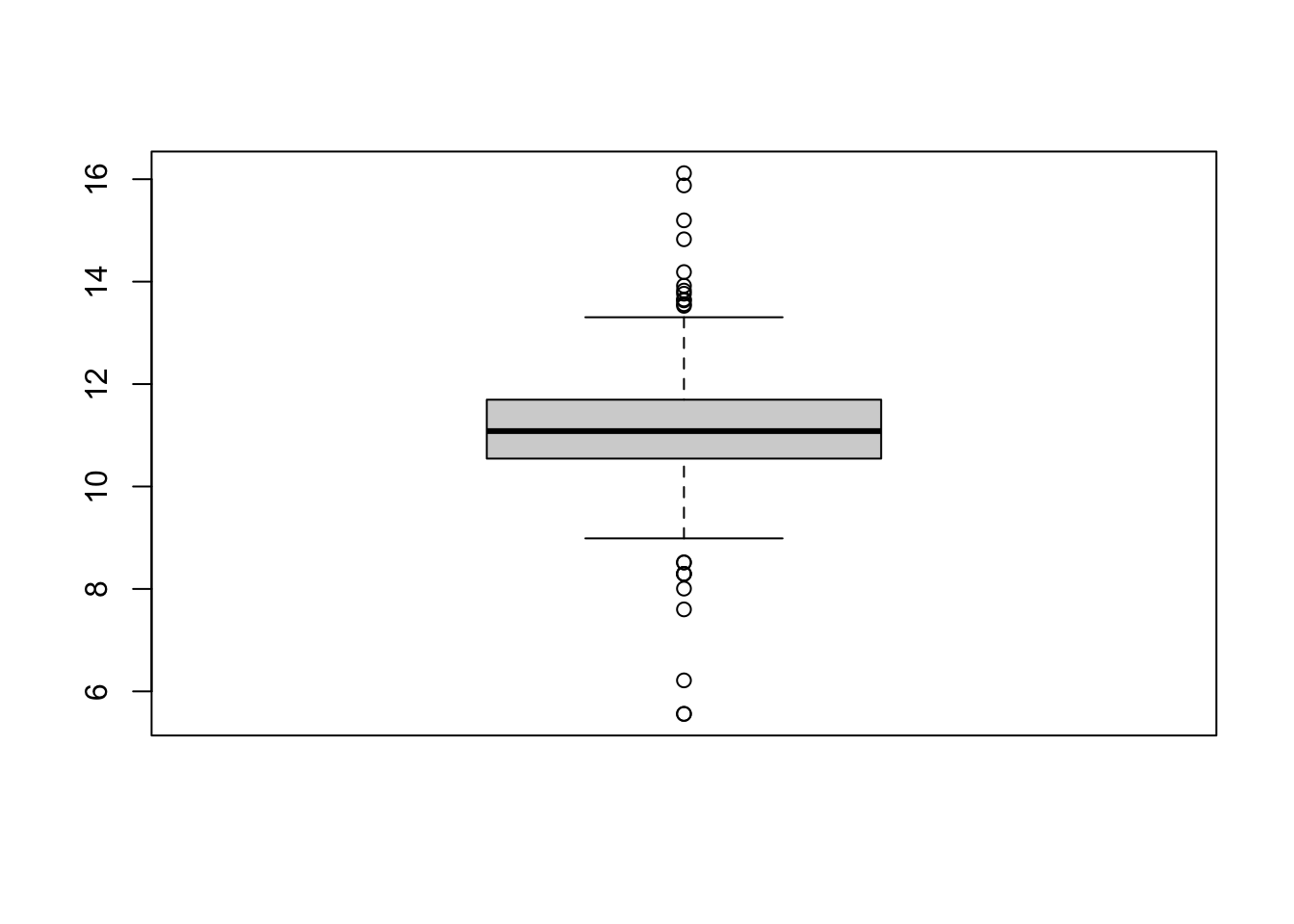
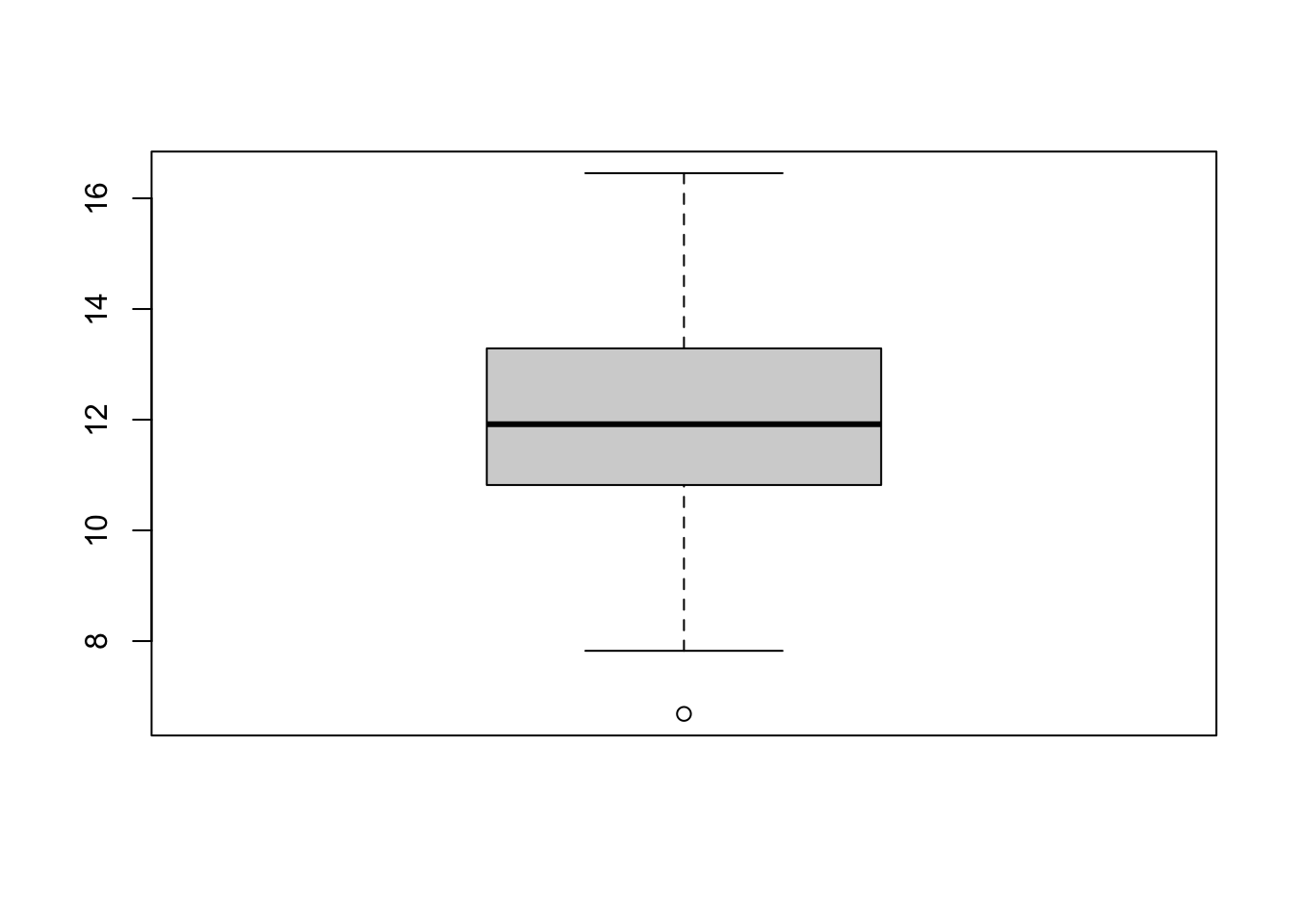
Prima di specificare una nuova analisi di regressione, può essere comodo rimpiazzare nella matrice dei dati (data frame), le variabili trasformate.

Si ottengano i parametri della seguente equazione di regressione lineare semplice dopo avere trasformato le variabili $M(\log(FACE_i)) = \beta_0 + \beta_1 \log(INCOME_i)$

m1 <- lm(LFACE~LINCOME, data=TL)

summary(m1)

## 
## Call:
## lm(formula = LFACE ~ LINCOME, data = TL)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -6.1967 -0.8032 -0.0018  0.8954  6.4711 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.23003    0.85985   4.920  1.5e-06 ***
## LINCOME      0.69604    0.07661   9.086  < 2e-16 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.642 on 273 degrees of freedom
## Multiple R-squared:  0.2322, Adjusted R-squared:  0.2294 
## F-statistic: 82.55 on 1 and 273 DF,  p-value: < 2.2e-16

Nell’interpretazione dei coefficienti è necessario ricordare che le variabili sono ora espresse nei logaritmi

Ancora una volta i parametri ottenuti, e in particolare $\hat{\beta}_1$ sono diversi da zero ( $p-$ values sempre molto piccoli).

exp(11.41)

## [1] 90219.42

Si può sovrapporre la retta con i coefficienti stimati sul grafico come segue:

beta<- coef(m1)
plot(TL$LINCOME, TL$LFACE)
abline(beta[1], beta[2])

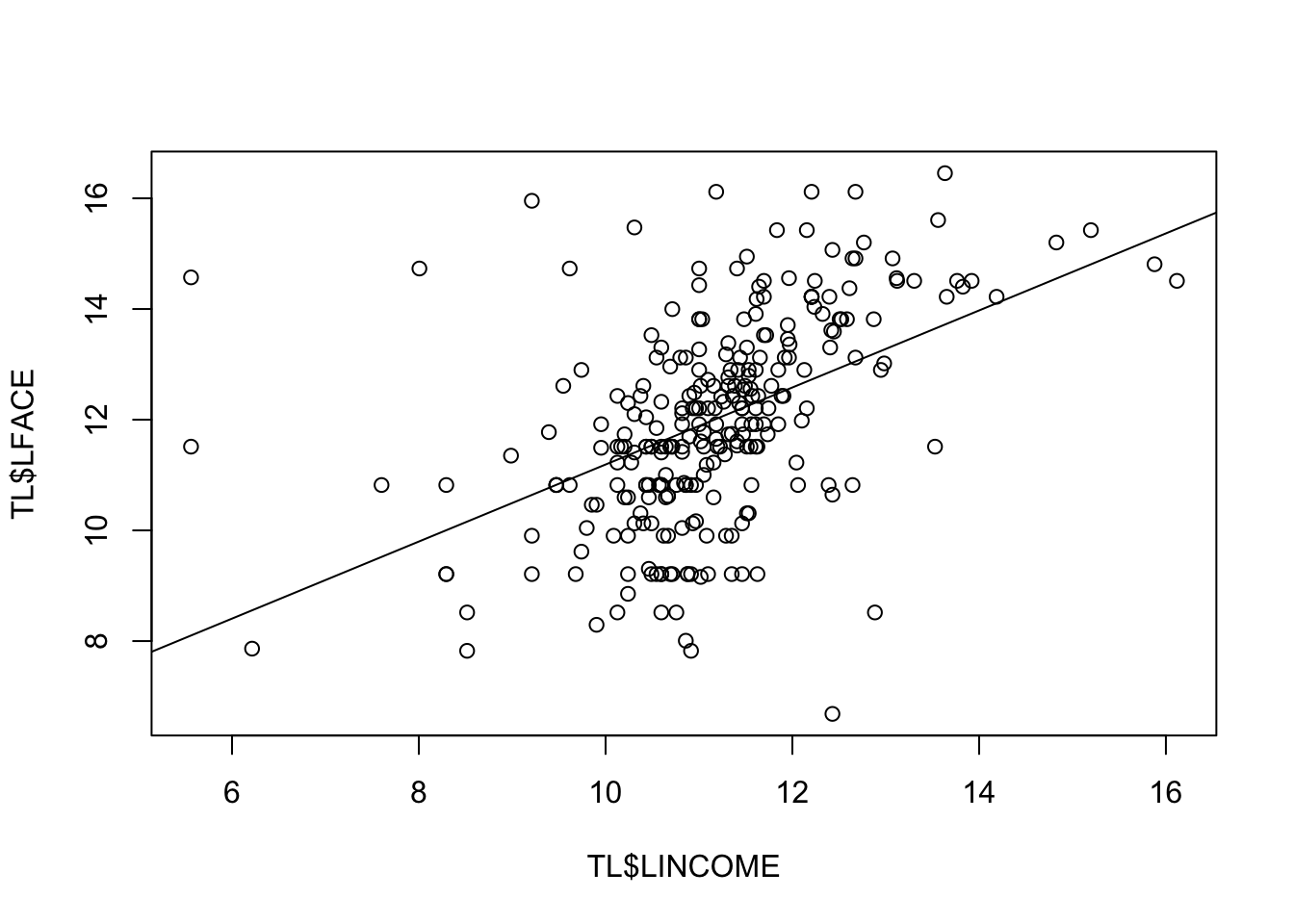
e dare uno sguardo ai residui

par(mfrow=c(2,2))
plot(m1, c(1,2,4,5))

par(mfrow=c(1,1))

I grafici vanno meglio e

$R^2$ è più elevato. Ci sono però ancora margini di miglioramento:

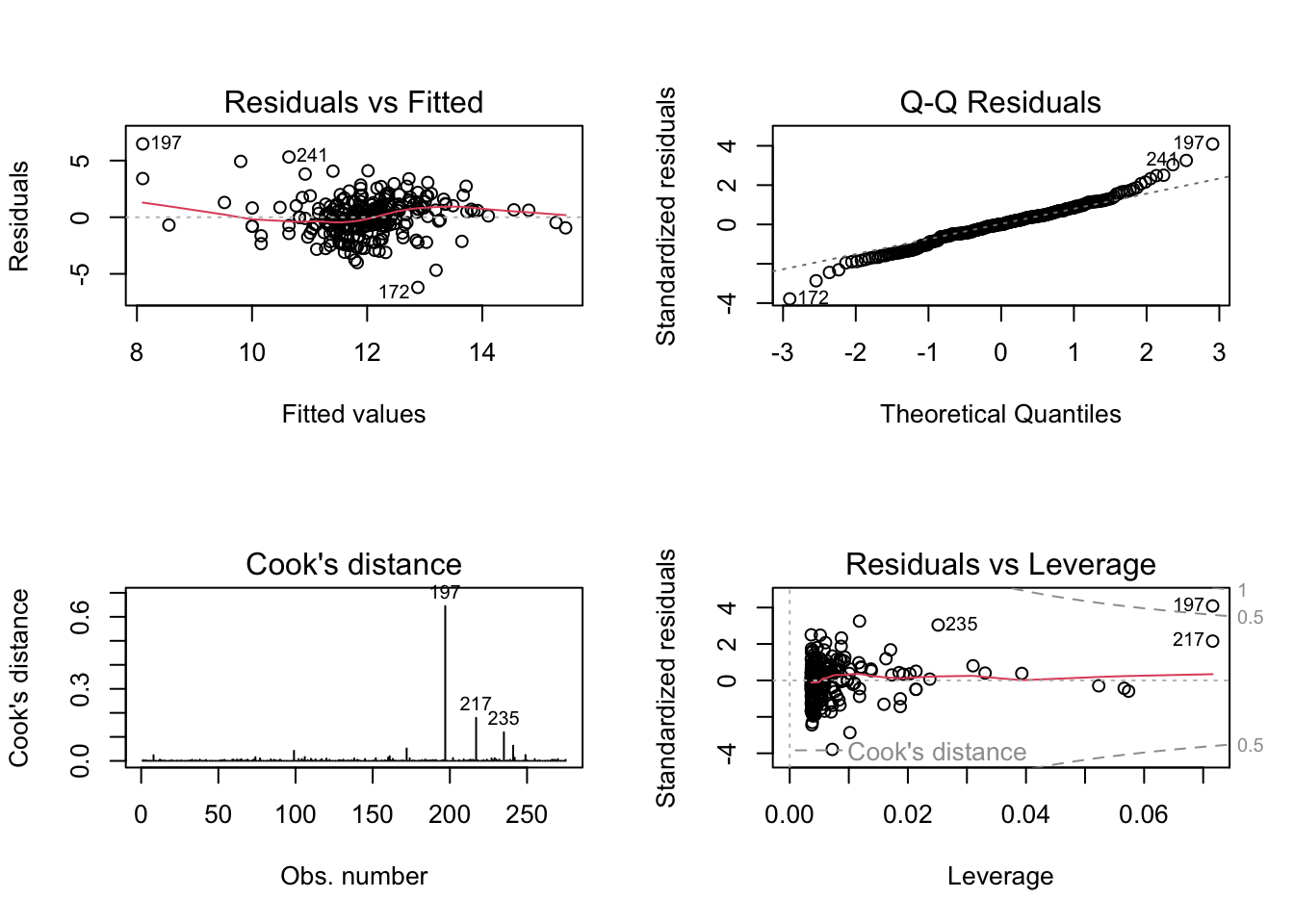
6.3.5.1 L’inserimento di predittori categoriali

Il data frame contiene altre variabili di potenziale valore predittivo. Per esempio, essere sposati o meno potrebbe avere qualche rilievo. la variabile MARSTAT assume solo due valori: single e not single. Si può tracciare lo scatterplot LFACE vs LINCOME e usare simboli diversi per le due categorie della variabile MARSTAT.

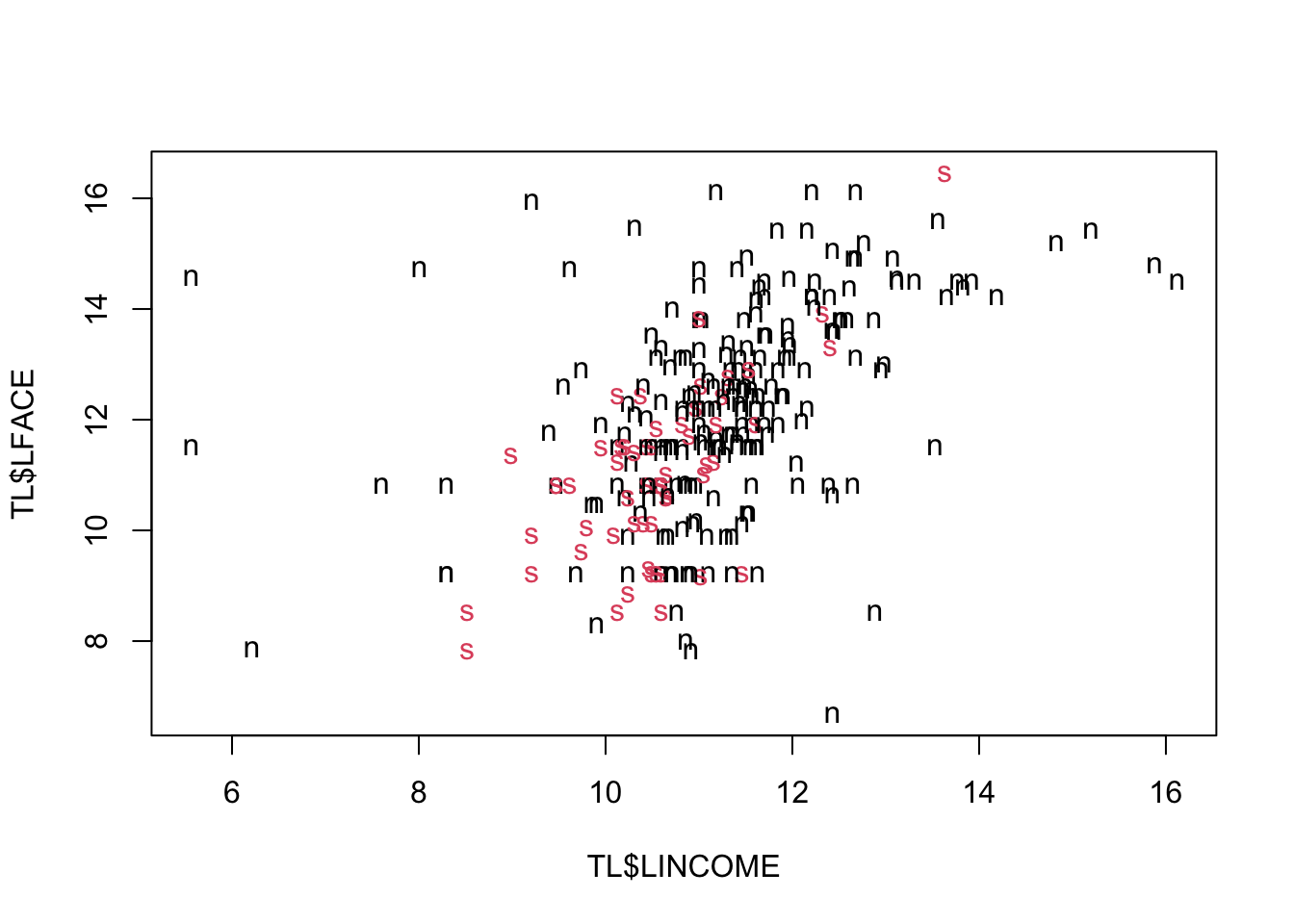
plot(TL$LINCOME, TL$LFACE, pch=as.character(TL$MARSTAT), col=as.numeric(TL$MARSTAT))

Le due nuvole di punti si sovrappongono ma si vede abbastanza bene che i single tendono a avere polizze meno elevate. Si vede anche che la relazione fra reddito e polizza è meno marcata per le coppie cio`e potrebbe esserci un’interazione fra MARSTAT e LINCOME. Si provi allora l’equazione di regressione

$M(\log(FACE_i)) = \beta_0 + \beta_1 \log(INCOME)_i + \beta_2 MARSTAT + \beta_3 \log(INCOME)_i \cdot MARSTAT$

m2 <- lm(LFACE~LINCOME+MARSTAT+LINCOME*MARSTAT, data=TL)
print(summary(m2), digits=3, signif.stars = FALSE)

## 
## Call:
## lm(formula = LFACE ~ LINCOME + MARSTAT + LINCOME * MARSTAT, data = TL)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -6.215 -0.829  0.070  0.931  5.607 
## 
## Coefficients:
##                       Estimate Std. Error t value Pr(>|t|)
## (Intercept)             5.7790     0.9255    6.24  1.6e-09
## LINCOME                 0.5729     0.0812    7.05  1.5e-11
## MARSTATsingle          -7.2921     2.7422   -2.66   0.0083
## LINCOME:MARSTATsingle   0.6124     0.2576    2.38   0.0181
## 
## Residual standard error: 1.6 on 271 degrees of freedom
## Multiple R-squared:  0.276,  Adjusted R-squared:  0.268 
## F-statistic: 34.4 on 3 and 271 DF,  p-value: <2e-16

l’equazione risulta essere: $\begin{eqnarray*} \hat{\log(FACE_i)} &=& \hat{\beta}_0 + \hat{\beta}_1 \log(INCOME)_i + \hat{\beta}_2 MARSTAT + \hat{\beta}_3 \log(INCOME)_i \cdot MARSTAT\\ &=& \hat{\beta}_0 + \hat{\beta}_1 \log(INCOME)_i \qquad \mbox{when } i \mbox{ is not single} \\ &=& 5.7790 + 0.5729 \log(INCOME)_i\\ &=& (\hat{\beta}_0+\hat{\beta}_2) + (\hat{\beta}_1+\hat{\beta}_3) \log(INCOME)_i \qquad \mbox{when } i \mbox{ is single} \\ &=& (5.7790-7.2921) + (0.5729+0.6124) \log(INCOME)_i\\ &=& -1.5131 + 1.1853 \log(INCOME)_i \end{eqnarray*}$ In altre parole, i single comprano meno polizze per i redditi bassi ma se il reddito cresce l’ammontare delle polizze aumenta più che negli sposati e quindi per redditi alti i single comprano in media più polizze.

beta<- coef(m2)
plot(TL$LINCOME, TL$LFACE, pch=as.character(TL$MARSTAT), col=as.numeric(TL$MARSTAT))
abline(beta[1], beta[2])
abline(beta[1]+beta[3], beta[2]+beta[4], col=2)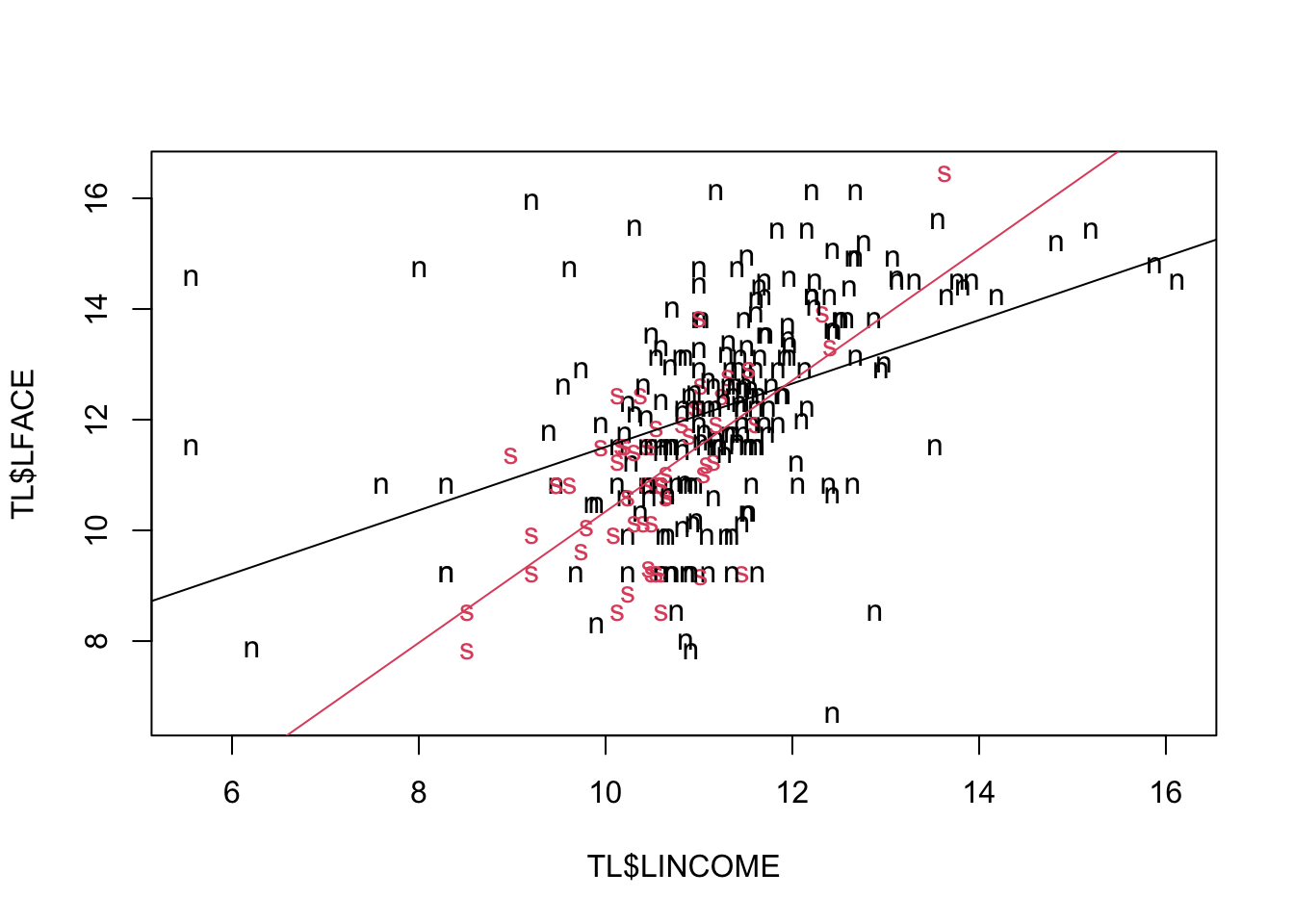

par(mfrow=c(2,2))
plot(m2, c(1,2,4,5))

par(mfrow=c(1,1))

–> –>

E’ possibile a questo punto arricchire l’analisi con le altre variabili disponibili (EDUCATION e NUMHH e AGE) e verificare se si abbia un ulteriore miglioramento della capacità predittiva.

m3 <- lm(LFACE~LINCOME+MARSTAT+LINCOME*MARSTAT+NUMHH+EDUCATION+AGE, data=TL)
print(summary(m3), digits=3, signif.stars = FALSE)

## 
## Call:
## lm(formula = LFACE ~ LINCOME + MARSTAT + LINCOME * MARSTAT + 
##     NUMHH + EDUCATION + AGE, data = TL)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -5.718 -0.790  0.166  0.879  4.619 
## 
## Coefficients:
##                       Estimate Std. Error t value Pr(>|t|)
## (Intercept)            4.09101    1.00424    4.07  6.1e-05
## LINCOME                0.40596    0.08131    4.99  1.1e-06
## MARSTATsingle         -7.27081    2.58856   -2.81  0.00534
## NUMHH                  0.25345    0.07429    3.41  0.00075
## EDUCATION              0.20370    0.03839    5.31  2.3e-07
## AGE                   -0.00464    0.00795   -0.58  0.55996
## LINCOME:MARSTATsingle  0.63895    0.24426    2.62  0.00940
## 
## Residual standard error: 1.5 on 268 degrees of freedom
## Multiple R-squared:  0.369,  Adjusted R-squared:  0.355 
## F-statistic: 26.1 on 6 and 268 DF,  p-value: <2e-16

si noti che l’età non sembra aver un effetto significativo per cui essa può essere esclusa dall’equazione di regressione.

m4 <- lm(LFACE~LINCOME+MARSTAT+LINCOME*MARSTAT+NUMHH+EDUCATION, data=TL)
print(summary(m4), digits=3, signif.stars = FALSE)

## 
## Call:
## lm(formula = LFACE ~ LINCOME + MARSTAT + LINCOME * MARSTAT + 
##     NUMHH + EDUCATION, data = TL)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -5.769 -0.762  0.140  0.919  4.572 
## 
## Coefficients:
##                       Estimate Std. Error t value Pr(>|t|)
## (Intercept)             3.8589     0.9210    4.19  3.8e-05
## LINCOME                 0.4036     0.0811    4.98  1.2e-06
## MARSTATsingle          -7.2195     2.5839   -2.79  0.00558
## NUMHH                   0.2689     0.0694    3.88  0.00013
## EDUCATION               0.2027     0.0383    5.29  2.5e-07
## LINCOME:MARSTATsingle   0.6364     0.2439    2.61  0.00959
## 
## Residual standard error: 1.5 on 269 degrees of freedom
## Multiple R-squared:  0.368,  Adjusted R-squared:  0.356 
## F-statistic: 31.3 on 5 and 269 DF,  p-value: <2e-16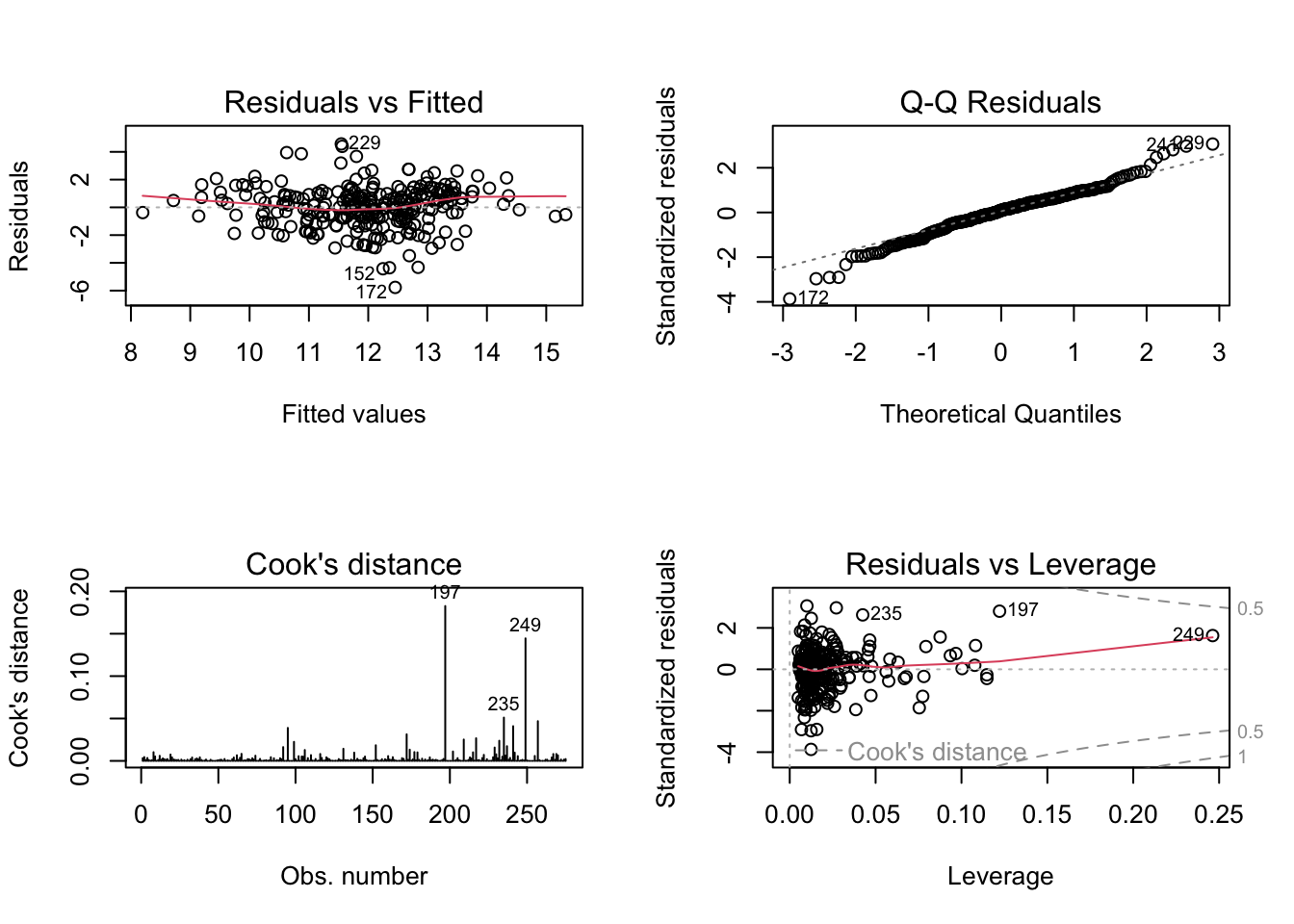

par(mfrow=c(2,2))
plot(m4, c(1,2,4,5))

Il comando permette di ottenere ancora i grafici dei residui. Si vede che ora la situazione e molto migliorata. Tuttavia sono presenti alcuni valori anomali (quelli cui sono associati valori del residuo di Cook elevato e con effetto leva elevato). Anche se il modello potrebbe essere suscettibile di ulteriori ritocchi, esso appare ora accettabile.

L’equazione finale ottenuta `e quindi: $\begin{eqnarray*} \hat{\log(FACE_i)} &=& \hat{\beta}_0 + \hat{\beta}_1 \log(INCOME)_i + \hat{\beta}_2 MARSTAT_i +\\ &&+\hat{\beta}_3 \log(INCOME)_i \cdot MARSTAT_i + \hat{\beta}_4 EDUCATION_i + \hat{\beta}_5 NUMHH_i\\ &=& \hat{\beta}_0 + \hat{\beta}_1 \log(INCOME)_i + \hat{\beta}_4 EDUCATION_i + \hat{\beta}_5 NUMHH_i\\ &=& 3.86 + 0.40 \log(INCOME)_i + 0.20 EDUCATION_i + 0.27 NUMHH_i\\ &&\qquad \mbox{ quando } i \mbox{ non è single} \\ \\ &=& (\hat{\beta}_0+\hat{\beta}_2) + (\hat{\beta}_1+\hat{\beta}_3) \log(INCOME)_i+ \hat{\beta}_4 EDUCATION_i + \hat{\beta}_5 NUMHH_i\\ &=& (3.86-7.21) + (0.40+0.64) \log(INCOME)_i + 0.20 EDUCATION_i + 0.27 NUMHH_i \\ &=& -3.35 + 1.04 \log(INCOME)_i+ 0.20 EDUCATION_i + 0.27 NUMHH_i\\ &&\qquad \mbox{ quando } i \mbox{ è single} \\ \end{eqnarray*}$

6.4 Introduzione all’analisi di raggruppamento

Si consideri un insieme di variabili $x_1, x_2, \dots, x_p$ misurate su $n$ unità. Piuttosto che considerare la relazione fra una variabile risposta e un insieme di esplicative, come, ad esempio, per la regressione multipla, siamo principalmente interessati a scoprire altri aspetti relativi alle variabili osservate.

Uno di questi riguarda l’individuazione di sottogruppi di osservazioni (o talvolta di variabili) che sono ‘omogenee’ secondo un determinato criterio.

Le tecniche di questo tipo appartengono a quelle denominate anche di apprendimento non supervisionato e includono, fra le principali, l’analisi di raggruppamento (cluster analysis) e l’analisi delle componenti principali.

L’analisi di raggruppamento, in particolare, consiste in un’ampia classe di metodi per individuare sottogruppi nei dati non noti a priori. Il problema di base del clustering può essere affermato come segue:

Dato un insieme di dati vogliamo suddividerli in un insieme di gruppi tali che i dati in ciascun gruppo sono il più possibile simili tra loro e i dati di gruppi diversi siano il più possibile diversi tra loro.

I metodi per affrontare tale problema possono condurre a risultati diversi a seconda dell’approccio, per la specifica definizione utilizzata per definire la somiglianza tra due unità, per l’algoritmo usato per derivare i cluster (metodi gerarchici e non gerarchici) e in relazione allo specifico tipo di dati (alcune tecniche sono applicabili solo a dati quantitativi, alcuni altri metodi possono essere utilizzati su dati qualitativi o anche su dati misti).

6.4.1 Un semplice esempio con dati simulati

L’esempio che segue utilizza dati simulati: essi sono costituiti dal numero medio di volte in cui il cibo fuori casa viene acquistato dai ristoranti (mensile) e dalle spese per il cibo consumato a casa (annuale) per un insieme di 100 famiglie. Prima si leggano i dati dal file food_spending.csv, che contiene le colonne FreqAway e Home, e poi si ottenga il grafico di dispersione dei dati:

FoodS<-read.csv("food_spending.csv", header=TRUE)
head(FoodS)

##    FreqAway      Home
## 1  6.951280 10965.524
## 2  7.415451  9854.342
## 3 12.462907  6824.662
## 4 14.136932  8982.304
## 5  5.969204  9276.950
## 6  7.976161 10131.322

dim(FoodS)

## [1] 100   2

plot(FoodS$FreqAway, FoodS$Home, pch=20)

I dati del grafico sembrano raggrupparsi in due gruppi ben separati, il gruppo con basse spese per il cibo a casa e alta frequenza di cibo fuori casa, e il gruppo di famiglie con una grande spesa per il cibo a casa e una bassa media dei pasti fuori casa.

In un problema di raggruppamento si mira ad identificare gruppi (cluster) distinti sulla base delle misurazioni ottenute su un insieme di variabili. I gruppi risultanti sono tali che i membri di uno stesso gruppo sono omogenei rispetto alle variabili coinvolte, mentre le osservazioni in gruppi diversi sono abbastanza diverse l’una dall’altra. Per rendere questo concreto, dobbiamo definire tuttavia cosa significa che due osservazioni qualsiasi siano ‘simili’ o ‘dissimili’, per caratterizzare i diversi gruppi.

6.4.2 Misure di dissomiglianza

In R, la libreria cluster può essere utilizzata per calcolare le dissomiglianze (distanze) a coppie tra le osservazioni nel set di dati tramite la funzione daisy inoltre contiene, come si vedrà, diversi metodi per condurre l’analisi dei cluster.

library(cluster)  # load cluster library

Come primo esempio, si calcoleranno le distanze euclidee tra i record (righe) del set di dati FoodS (opzione di default per l’argomento metric è la distanza euclidea)

dist1<-daisy(FoodS)
?daisy

Data una matrice numerica o un dataframe con $n$ righe e $p$ colonne, le dissomiglianze vengono in questo caso calcolate tra le righe, risultando in una matrice simmetrica $n \times n$ , con valore nella cella $(i,j)$ dato da

$d_{ij}=\sqrt{\sum_{k=1}^{p}(x_{ik}-x_{jk})^2}$

In questo esempio si hanno due variabili ( $p=2$ ) e $n=100$ misurazioni. Le prime righe/colonne della matrice di dissomiglianza per i dati simulati possono essere ottenute come

as.matrix(dist1)[1:5, 1:5]

##          1         2        3         4         5
## 1    0.000 1111.1824 4140.866 1983.2338 1688.5747
## 2 1111.182    0.0000 3029.684  872.0644  577.3939
## 3 4140.866 3029.6844    0.000 2157.6424 2452.2967
## 4 1983.234  872.0644 2157.642    0.0000  294.7596
## 5 1688.575  577.3939 2452.297  294.7596    0.0000

Si noti che la scala di misura in genere influisce in modo determinante sui risultati dell’analisi di raggruppamento. Per questo motivo, in alcuni casi, si consiglia di standardizzare i dati prima di eseguire una procedura di clustering, in modo che tutte le variabili siano su una scala comparabile. Questo può essere fatto, ad esempio, trasformando le variabili in modo che abbiano tutte media zero e deviazione standard uno. Nel caso in cui le variabili siano tutte misurate nelle stesse unità di misura, si potrebbe scegliere di non standardizzarle.

Si noti che la funzione daisy può procedere alla standardizzazione specificando l’argomento stand=TRUE ma viene utilizzata la deviazione media assoluta anziché la deviazione standard:

dist2<-daisy(FoodS, stand=TRUE)

L’oggetto che si ottiene appartiene alla classe “dist”, tuttavia può essere trasformato in una matrice come segue

dist2m<-as.matrix(dist2)
dist2m[1:5, 1:5]

##           1         2        3        4         5
## 1 0.0000000 0.9536446 3.945398 2.891414 1.4663512
## 2 0.9536446 0.0000000 3.053032 2.321756 0.6808883
## 3 3.9453977 3.0530320 0.000000 1.908494 2.9730049
## 4 2.8914145 2.3217564 1.908494 0.000000 2.6862840
## 5 1.4663512 0.6808883 2.973005 2.686284 0.0000000

Una funzione R alternativa per il calcolo della matrice delle distanze è dist(), che usa la metrica specificata dall’argomento method per calcolare le distanze tra le righe di una matrice di dati (si possono scegliere tra metodi “euclideo”, “massimo”, “manhattan”, “canberra”, “binario” o “minkowski”).

La funzione dist() per calcolare la matrice 100X100 della distanza euclidea tra le osservazioni dell’esempio:

D <- as.matrix(dist(FoodS))
D[1:5, 1:5]

##          1         2        3         4         5
## 1    0.000 1111.1824 4140.866 1983.2338 1688.5747
## 2 1111.182    0.0000 3029.684  872.0644  577.3939
## 3 4140.866 3029.6844    0.000 2157.6424 2452.2967
## 4 1983.234  872.0644 2157.642    0.0000  294.7596
## 5 1688.575  577.3939 2452.297  294.7596    0.0000

Per standardizzare le variabili prima di eseguire il calcolo della dissomiglianza con dist(), si può usare la funzione scale() che standardizza però dividendo per lo scarto quadratico medio.

D <- as.matrix(dist(scale(FoodS))) 
D[1:5, 1:5]

##           1         2        3        4         5
## 1 0.0000000 0.7916579 3.369431 2.631689 1.2216515
## 2 0.7916579 0.0000000 2.639903 2.178157 0.6049498
## 3 3.3694312 2.6399030 0.000000 1.598605 2.6515809
## 4 2.6316888 2.1781567 1.598605 0.000000 2.5489766
## 5 1.2216515 0.6049498 2.651581 2.548977 0.0000000

# si noti la differenza da quanto ottenuto con daisy

La gestione di variabili di tipo misto (ad es. dati binari nominali, ordinali e (a)simmetrici) può essere ottenuta utilizzando il coefficiente di Gower, impostando metric = "gower" nella funzione daisy.

Si utilizza ora il set di dati simulati sui reclami che contiene le seguenti variabili:

“litig”: se c’è un contenzioso
“soft_injury”: se la lesione è stata una lesione dei tessuti molli
“emergency_tr”: se c’è stato un trattamento di emergenza
“NumProv”: numero di provider (numerico)
“NumTreat”: numero di cure mediche (numerico)

Le prime tre sono variabili categoriali, assumendo valore zero per “no” e uno per “sì”. Per prima cosa leggiamo i dati e convertiamo le variabili categoriali in fattori

d<-read.csv(file="simclust2.csv", header = TRUE)

d$litig<-as.factor(d$litig)
d$soft_injury<-as.factor(d$soft_injury)
d$emergency_tr<-as.factor(d$emergency_tr)

str(d)

## 'data.frame':    1000 obs. of  6 variables:
##  $ ID          : int  1 1 1 1 1 1 1 1 1 2 ...
##  $ litig       : Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 1 2 ...
##  $ soft_injury : Factor w/ 2 levels "0","1": 2 1 1 1 2 2 1 1 1 2 ...
##  $ emergency_tr: Factor w/ 2 levels "0","1": 1 2 1 1 2 2 2 1 2 2 ...
##  $ NumProv     : int  2 2 0 2 1 0 1 2 2 5 ...
##  $ NumTreat    : int  2 1 2 4 5 3 4 3 1 8 ...

Si può utilizzare la metrica di Gower per calcolare la dissomiglianza tra i ricorrenti sulla base di dati misti. La “distanza” tra due unità è la media ponderata dei contributi di ciascuna variabile, dove

il contributo di una variabile nominale o binaria alla dissomiglianza totale è 0 se entrambi i valori sono uguali, 1 altrimenti
il contributo delle variabili ordinali codificate come ordered factor è la differenza in valore assoluto
il contributo delle altre variabili è la differenza assoluta di entrambi i valori, divisa per l’intervallo totale di quella variabile. Alle variabili ordinali codificate come ordered factor con K livelli, si associa un intero (da 0 a K-1) ad ogni livello secondo l’ordine definito.
nella formula originale di Gower è possibile assegnare un peso per ogni variabile.

La dissomiglianza basata solo su variabili categoriali è calcolata di seguito:

head(d)

##   ID litig soft_injury emergency_tr NumProv NumTreat
## 1  1     0           1            0       2        2
## 2  1     0           0            1       2        1
## 3  1     0           0            0       0        2
## 4  1     0           0            0       2        4
## 5  1     0           1            1       1        5
## 6  1     0           1            1       0        3

d3var<-d[ , c("litig", "soft_injury", "emergency_tr")]
as.matrix(daisy(d3var, metric= "gower"))[1:5, 1:5]

##           1         2         3         4         5
## 1 0.0000000 0.6666667 0.3333333 0.3333333 0.3333333
## 2 0.6666667 0.0000000 0.3333333 0.3333333 0.3333333
## 3 0.3333333 0.3333333 0.0000000 0.0000000 0.6666667
## 4 0.3333333 0.3333333 0.0000000 0.0000000 0.6666667
## 5 0.3333333 0.3333333 0.6666667 0.6666667 0.0000000

Si noti che il peso assegnato a ciascuna variabile è 1 nel nostro esempio. Si calcoli ora la matrice di dissomiglianza sull’intero set di dati (la prima colonna contiene le vere etichette del cluster, quindi è stata scartata).

diss<-as.matrix(daisy(d[, -1], metric= "gower"))
diss[1:5, 1:5]

##           1         2          3          4         5
## 1 0.0000000 0.4142857 0.24000000 0.22857143 0.2628571
## 2 0.4142857 0.0000000 0.25428571 0.24285714 0.2771429
## 3 0.2400000 0.2542857 0.00000000 0.06857143 0.4628571
## 4 0.2285714 0.2428571 0.06857143 0.00000000 0.4342857
## 5 0.2628571 0.2771429 0.46285714 0.43428571 0.0000000

6.4.3 I diversi metodi di raggruppamento

Nell’ultimo esempio, oltre alle caratteristiche utilizzate, è possibile includere nel set di dati altre variabili di interesse (ad esempio un sinistro precedente, contraente di polizza) e quindi utilizzare l’analisi di raggruppamento per identificare gruppi di records simili tra loro.

Esiste un gran numero di metodi di raggruppamento. Se ne introdurranno brevemente alcuni che corrispondono a tre approcci per il clustering più comunemente utilizzati:

tecniche di raggruppamento non gerarchico;
metodi di clustering gerarchico;
clustering basato sulla densità: l’algoritmo DBSCAN.

6.4.4 I metodi di raggruppamento non gerarchico

6.4.4.1 Il metodo delle K-medie (K-means)

La funzione kmeans() esegue il clustering di K-medie in R: richiede in input i dati e il numero di gruppi che si vogliono ottenere (centri).

Si consideri ancora il semplice esempio simulato che utilizza i dati in food_spending.csv, riguardanti le spese per il cibo a domicilio e la media mensile dei pasti fuori casa per 100 famiglie:

x<-read.csv("food_spending.csv", header=TRUE)
head(x)

##    FreqAway      Home
## 1  6.951280 10965.524
## 2  7.415451  9854.342
## 3 12.462907  6824.662
## 4 14.136932  8982.304
## 5  5.969204  9276.950
## 6  7.976161 10131.322

Il metodo di raggruppamento delle K-medie prevede che sia specificato il numero di cluster (si noti che in realtà esso di solito non è noto).

L’algoritmo è piuttosto semplice e procede come segue:

sia K il numero di gruppi prefissato (da cui il nome del metodo K-medie).
Si scelgono in modo casuale K punti (semi) fra i dati osservati con la sola condizione che non siano coincidenti. Questi fungono da centroidi provvisori attorno a cui costruire un’aggregazione dei dati;
si calcola la distanza di ogni dato da ogni centroide e il dato viene viene associato al centroide più vicino. Al termine di questa fase avremo K gruppi costituiti attorno ai centroidi;
per ogni gruppo, si calcola un nuovo centroide come il vettore di medie $M(x_k)=\sum_{\forall i \in C_k} x_i/n_k$ (ove ove $x_i$ è il vettore dei dati per l’i-esima unità e $n_k$ è la numerosità del $k$ -esimo gruppo) tutti i punti del cluster associato a tale centroide;
si itera dal punto 3 fino a quando la soluzione è stabile (nessun dato cambia di classe quando si calcola il nuovo centroide);
la funzione obiettivo da minimizzare è la somma delle distanze al quadrato dai centroidi di ciascun gruppo cui il dato è associato, ovvero
$Dev(entro)=\sum_{k=1}^K\sum_{\forall i \in C_k}\lVert x_i-M(x_k) \rVert$ Si noti che tale quantità decresce al crescere di $K$ .

Si illustra ora il funzionamento dell’algoritmo con i dati simulati sopra.

Prima si standardizzano i dati e quindi si esegue il raggruppamento con le K-medie con $K = 2$ centri (la funzione set.seed() viene utilizzata per garantire che l’output delle K-medie sia completamente riproducibile così che i centroidi scelti casualmente all’inizio siano gli stessi a ogni prova).

x.scalato<-scale(x) # standardiziiamo i dati
set.seed(4)
km.out <- kmeans(x.scalato, centers=2) # scegliamo una soluzione con 2 gruppi
km.out

## K-means clustering with 2 clusters of sizes 43, 57
## 
## Cluster means:
##     FreqAway       Home
## 1 -1.1045122  0.9206786
## 2  0.8332285 -0.6945470
## 
## Clustering vector:
##   [1] 1 1 2 2 1 1 1 1 2 2 1 1 2 2 1 2 2 1 2 1 1 1 2 2 1 2 2
##  [28] 1 2 2 2 2 1 1 2 1 2 2 1 1 1 1 2 1 1 1 2 2 2 1 2 2 2 1
##  [55] 1 1 1 2 2 2 2 1 1 1 2 1 2 1 1 2 2 2 1 2 1 2 2 1 2 2 2
##  [82] 2 2 1 2 2 2 2 2 1 2 2 2 2 1 2 2 1 2 2
## 
## Within cluster sum of squares by cluster:
## [1] 21.96630 20.05714
##  (between_SS / total_SS =  78.8 %)
## 
## Available components:
## 
## [1] "cluster"      "centers"      "totss"       
## [4] "withinss"     "tot.withinss" "betweenss"   
## [7] "size"         "iter"         "ifault"

L’output mostra:

le medie dei cluster ottenuti: una matrice $KXP$ , nella quale per ogni gruppo (riga) sono riportate le medie delle variabili;
il vettore con la attribuzione di gruppo (vettore di clustering): un vettore di interi (da 1 a $K$ ) che indica il cluster a cui è allocato ciascuna unità;
il rapporto tra $\frac{\mbox {somma dei quadrati}}{\mbox{somma totale dei quadrati}}$ (cioè la parte della varianza spiegata attraverso il raggruppamento). Avendo raggruppato i dati si ricorda che è possibile calcolare la devianza tra i gruppi e la devianza entro i gruppi (la loro somma come sappiamo da la devianza totale). Il risultato di un algorimo di raggruppamento è tanto migliore quanto maggiore è la devianza entro i gruppi o, in alternativa, quanto più piccola è la devianza tra i gruppi. Una funzione obiettivo è quindi il rapporto tar devianza tra i gruppi e devianza totale che deve essere quanto più grande possibile.

Il vettore con la attribuzione di ogni unità ai cluster è in km.out$cluster:

str(km.out$cluster)

##  int [1:100] 1 1 2 2 1 1 1 1 2 2 ...

table(km.out$cluster)

## 
##  1  2 
## 43 57

I due cluster ottenuti contengono rispettivamente 56 e 44 osservazioni, le famiglie sono raggruppate in due cluster ben separati.

Poiché, in questo caso, vi sono solo due dimensioni, possiamo ottenere il diagramma di dispersione dei dati, usando colori diversi per i punti in ogni cluster

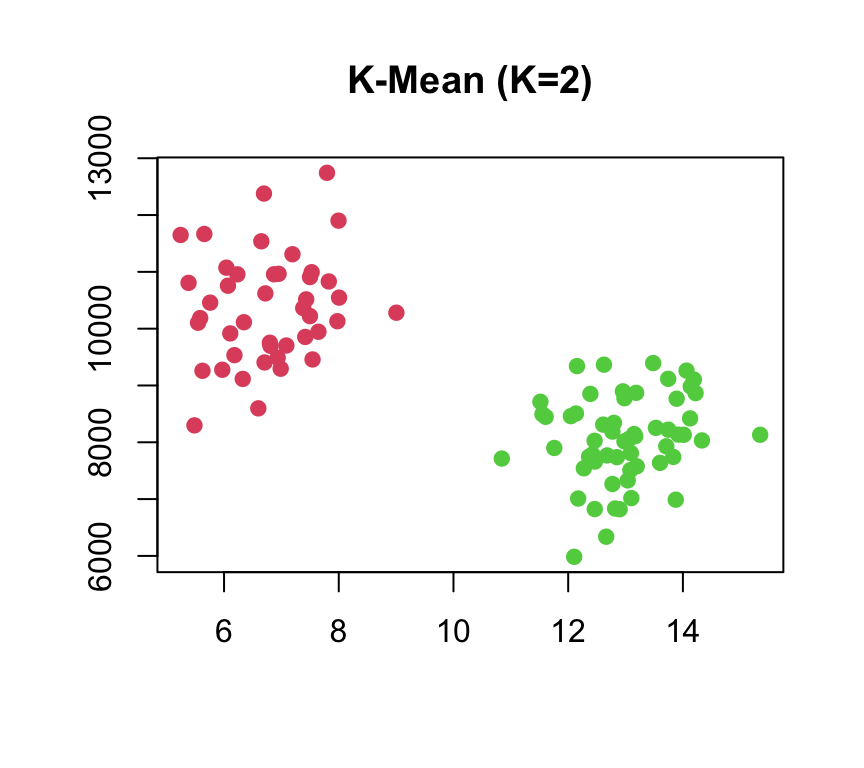
plot(x, col =(km.out$cluster+1),main="K-Mean (K=2)", xlab ="", ylab="",pch=19)

I risultati ottenuti dipenderanno dall’assegnazione iniziale (casuale) del cluster di ciascuna osservazione nel primo passaggio dell’algoritmo. Per questo motivo, una pratica comune consiste nell’eseguire l’algoritmo più volte da diverse centroidi iniziali casuali e scegliere la soluzione per cui la funzione obiettivo (in questo caso la funzione obiettivo è between_SS/total_SS) è più piccola. Per fare ciò, si può semplicemente impostare l’argomento nstart su un valore molto maggiore di uno (es. nstart=10 o nstart=20), in tal caso kmeans() riporterà solo la soluzione migliore.

set.seed(5)
km.out<-kmeans(scale(x), 3)
km.out

## K-means clustering with 3 clusters of sizes 23, 20, 57
## 
## Cluster means:
##     FreqAway       Home
## 1 -1.1065155  0.4232302
## 2 -1.1022083  1.4927443
## 3  0.8332285 -0.6945470
## 
## Clustering vector:
##   [1] 2 1 3 3 1 1 1 1 3 3 2 2 3 3 2 3 3 1 3 1 2 1 3 3 2 3 3
##  [28] 2 3 3 3 3 1 1 3 2 3 3 1 1 2 1 3 2 1 1 3 3 3 2 3 3 3 1
##  [55] 1 1 2 3 3 3 3 2 1 2 3 1 3 2 2 3 3 3 1 3 1 3 3 2 3 3 3
##  [82] 3 3 2 3 3 3 3 3 2 3 3 3 3 1 3 3 2 3 3
## 
## Within cluster sum of squares by cluster:
## [1]  4.671572  5.057885 20.057140
##  (between_SS / total_SS =  85.0 %)
## 
## Available components:
## 
## [1] "cluster"      "centers"      "totss"       
## [4] "withinss"     "tot.withinss" "betweenss"   
## [7] "size"         "iter"         "ifault"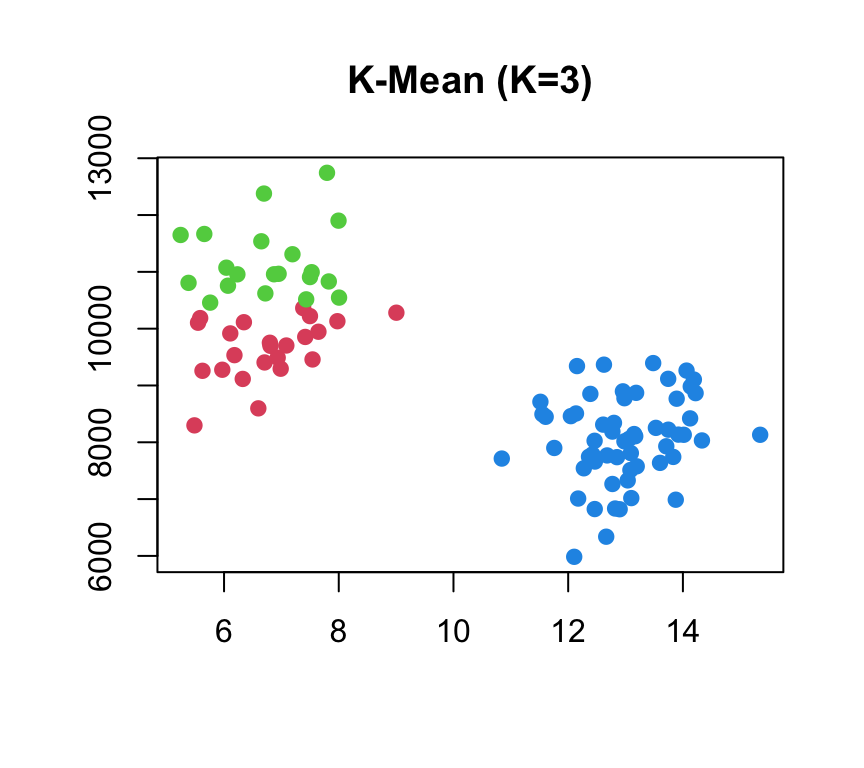

plot(x, col =(km.out$cluster+1), main="K-Mean (K=3)", xlab ="", ylab="", pch=19)

Qui si confrontano le soluzioni usando nstart=1e nstart=20 in termini di somma totale di quadrati delle distanze dai centroidi all’interno del cluster, che cerchiamo di ridurre al minimo eseguendo il clustering di K-medie

set.seed(6)
km.out<-kmeans(x, 3, nstart=1)
km.out$tot.withinss

## [1] 31535467

km.out<-kmeans(x, 3, nstart=20)
km.out$tot.withinss

## [1] 31385541

In questo esempio con dati simulati era noto che erano presenti due cluster. Tuttavia, per i dati reali non è noto il numero reale di cluster. Si sarebbe invece potuto eseguire il clustering K-medie con $K$ variabile da 2 a 10 e confrontare i risultati in termini del rapporto fra devianza tra i gruppi e devianza totale o del valore della devianza entro i gruppi.

Si consideri ora un altro esempio riprendendo i dati iris. Anche qui conosciamo il numero dei gruppi, corrispondente alle 3 specie: versicolor, virginica, setosa.

Vediamo se è possibile riconoscerli a partire dalle 4 variabili e, successivamente, calcolare soluzioni con K che va da 2 a 10.

set.seed(7)
irisgroup<-kmeans(iris[,-5], 3, nstart=10)
plot(iris$Sepal.Length, iris$Petal.Length, col =(irisgroup$cluster+1), 
     main="K-Mean (K=3)", xlab ="", ylab="", pch=19)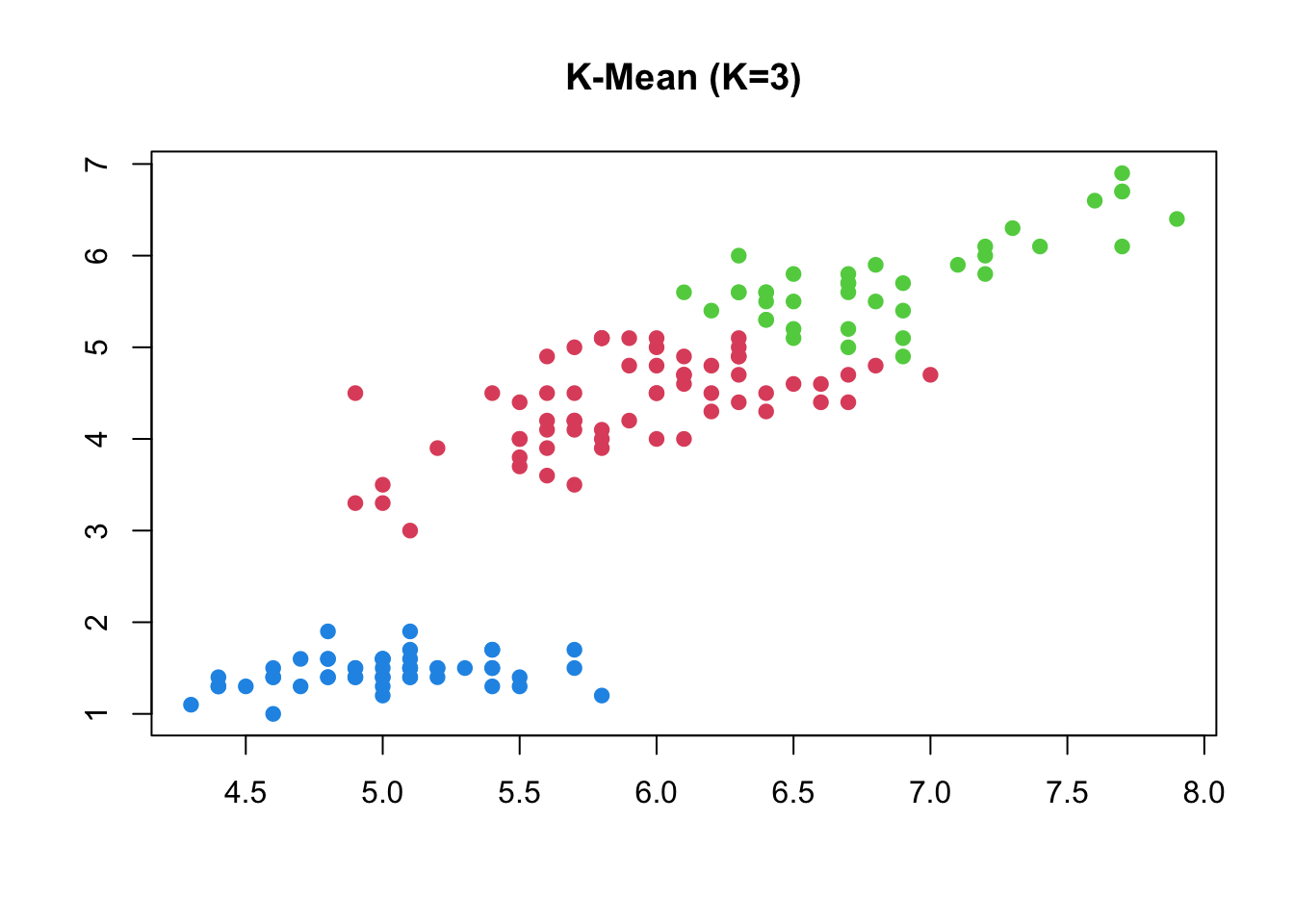

table(irisgroup$cluster,iris$Species)

##    
##     setosa versicolor virginica
##   1      0         48        14
##   2      0          2        36
##   3     50          0         0

crit<-0
for (i in 2:10) {
set.seed(7)
irisgroup<-kmeans(iris[,-5], i, nstart=10)
crit[i-1]<-irisgroup$tot.withinss
}
plot(2:10, crit)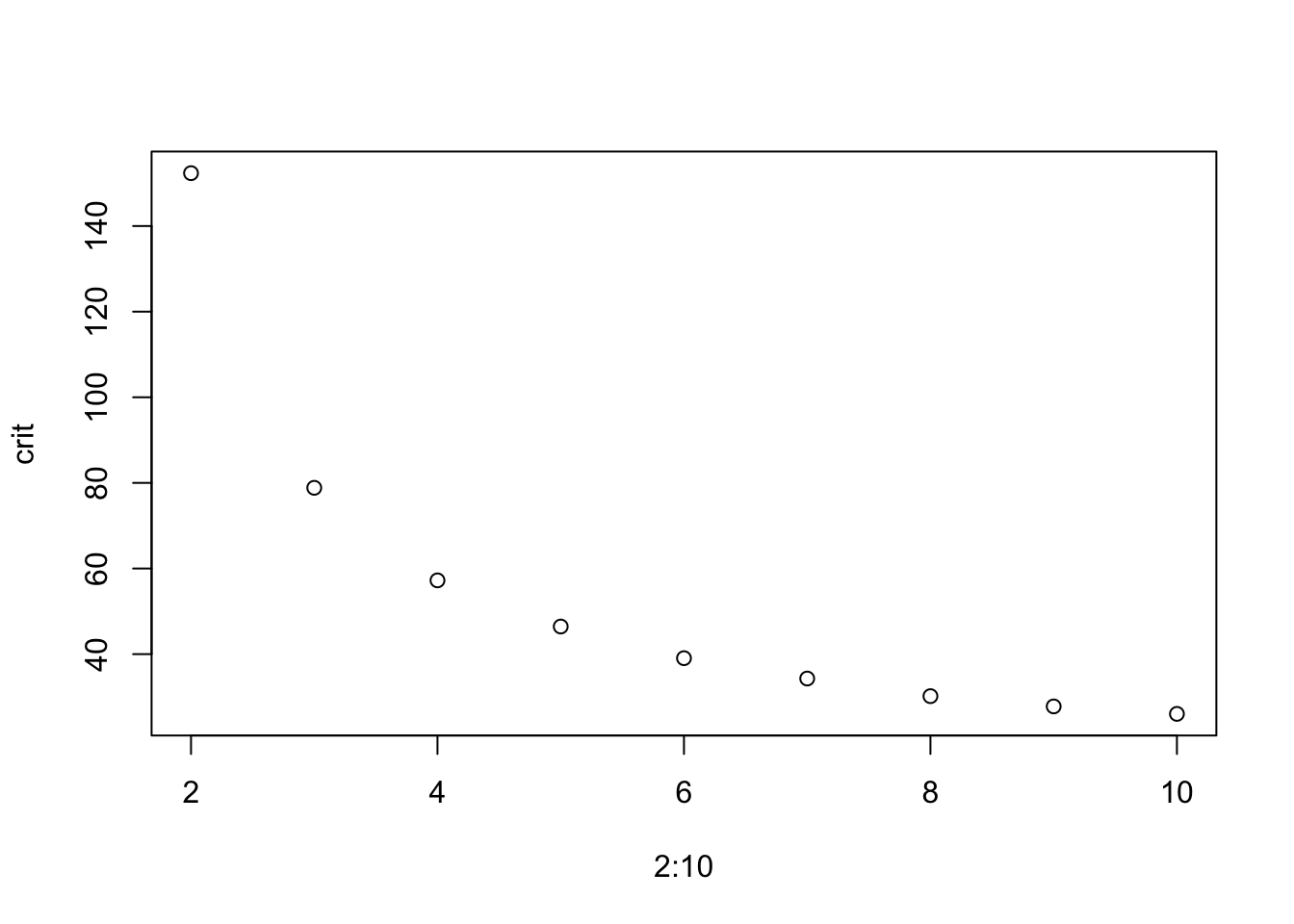

6.4.4.2 Partizionamento intorno ai Medoidi (PAM)

Sempre per l’esempio precedente, si introduce un altro metodo non gerarchico basato su medoidi. Si tratta di una versione più robusta di $K$ -means e restituisce i $K$ oggetti rappresentativi, uno per ogni cluster.

L’algoritmo di clustering è il seguente:

si inizia con una selezione di k punti, detti medoidi, con un criterio tale da minimizzare una funzione obiettivo (ad esempio, la somma delle distanze entro i gruppi) e si associa ogni dato al medoide più simile;
la similarità fra i punti è definita usando distanze come la distanza euclidea, la distanza di Manhattan o la distanza di Minkowski, ma si possono anche usare misure di dissimilarità più generali;
si selezionano in modo casuale nuovi candidati come medoidi $O^{'}$ ;
si calcola il costo totale $S_i$ come la somma delle distanze dei singoli elementi dai corrispondenti medoidi iniziali e il costo totale $S_f$ nel caso dei nuovi medoidi $O^{'}$ e se ne calcola la differenza $S=S_f-S_i$ ;
se $S<0$ allora si scambia il medoide iniziale con il nuovo (se $S<0$ ci sarà quindi un nuovo insieme di medoidi);
si ripetono i passi dal 2 al 5 sino a quando si hanno cambiamenti nell’insieme dei medoidi.

A differenza delle K-medie i medoidi sono sempre punti che corrispondono a dati osservati. Inoltre si possono usare i diversi tipi di distanze. Non c’è infine bisogno di iterare con diverse scelte dei semi iniziali.

La funzione pam nel pacchetto cluster può essere usata per eseguire il partizionamento attorno ai medoidi. Si noti che questa funzione opera la standardizzazione preliminare delle variabili (ogni colonna del database viene trasformata sottraendo la media e dividendo per lo scarto medio assoluto) se tra gli argomenti è specificato stand = TRUE (il default è FALSE). La metrica utilizzata per calcolare le dissomiglianze tra le osservazioni è euclidea (predefinita), l’alternativa è la distanza di Manhattan:

pam.out<-pam(x, 2, metric="euclidean", stand=TRUE)
pam.out

## Medoids:
##      ID  FreqAway      Home
## [1,] 42  7.380646 10362.114
## [2,] 53 13.059628  8058.363
## Clustering vector:
##   [1] 1 1 2 2 1 1 1 1 2 2 1 1 2 2 1 2 2 1 2 1 1 1 2 2 1 2 2
##  [28] 1 2 2 2 2 1 1 2 1 2 2 1 1 1 1 2 1 1 1 2 2 2 1 2 2 2 1
##  [55] 1 1 1 2 2 2 2 1 1 1 2 1 2 1 1 2 2 2 1 2 1 2 2 1 2 2 2
##  [82] 2 2 1 2 2 2 2 2 1 2 2 2 2 1 2 2 1 2 2
## Objective function:
##     build      swap 
## 0.8438882 0.6608854 
## 
## Available components:
##  [1] "medoids"    "id.med"     "clustering" "objective" 
##  [5] "isolation"  "clusinfo"   "silinfo"    "diss"      
##  [9] "call"       "data"

La funzione pam() restituisce un oggetto i cui componenti includono i medoidi (oggetti che rappresentano i cluster) e il vettore di clustering. È possibile accedere a questi componenti come segue:

pam.out$medoids

##       FreqAway      Home
## [1,]  7.380646 10362.114
## [2,] 13.059628  8058.363

head(pam.out$clustering)

## [1] 1 1 2 2 1 1

Il risultato del clustering può essere visualizzato sul data scatter plot, vengono visualizzati anche i medoidi:

plot(x, col =(pam.out$cluster+1), main="PAM (K=2)", xlab ="", ylab="", pch=19)
points(pam.out$medoids, pch=as.character(pam.out$cluster[pam.out$id.med]))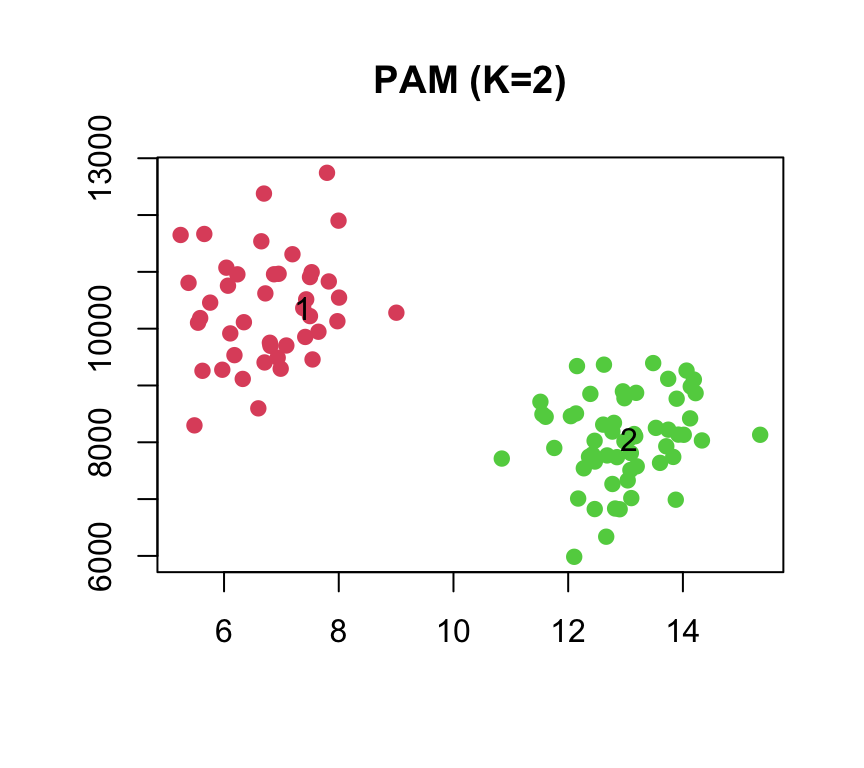

6.4.4.3 Valutare la qualità del raggruppamento: il grafico della silhouette

La statistica silhouette misura la somiglianza $s_i$ dei membri all’interno di un cluster rispetto aquelli degli altri cluster (ovvero, il cluster successivo più vicino nel caso di più di due cluster). Il grafico delle silhouette è un grafico a barre delle sagome dei punti per ciascun cluster, ordinate per gruppo in ordine decrescente. Da questa trama, è facile identificare osservazioni problematiche. esso può esser calcolato nel caso si misurino le distanze con metriche come quella euclidea o quella di Manhattan.

Il codice seguente produce il grafico della silhouette per i risultati dell’algoritmo PAM:

plot(pam.out, which=2, main="") #silhouette plot

Le osservazioni con un $s_i$ grande (quasi 1) sono molto ben raggruppate, un piccolo $s_i$ (vicino a 0) significa che l’osservazione si trova in mezzo due cluster e le osservazioni con $s_i$ negativo sono probabilmente posizionato nel cluster sbagliato.

Le informazioni sulla larghezza media della silhouette totale in base alle singole larghezze della silhouette possono fornire indicazioni utili per la convalida del clustering.

Nota Per set di dati di grandi dimensioni, pam può essere impegnativo dal punto di vista computazionale. Quindi clara() è preferibile, vedere la documentazione online se necessario.

Si noti che l’idea della silhouette è generale e può essere usata anche per valutare i raggruppamenti ottenuti con altri metodi.

6.4.4.4 PAM con matrice di dissomiglianza arbitraria

La funzione pam permette all’utente di fornire una matrice di dissomiglianza arbitraria, impostando diss=TRUE.

Ad esempio, si supponga di voler identificare i gruppi per i dati simulati nel file “simclust2.csv”, che contiene informazioni sulle caratteristiche di 1000 reclami. In particolare, questo set di dati contiene tre variabili binarie (contenzioso, lesione dei tessuti molli, trattamento di emergenza) e due variabili numeriche (numero di fornitori e numero di trattamenti).

Prima si leggono i dati

d<-read.csv(file="simclust2.csv", header = TRUE)
head(d)

##   ID litig soft_injury emergency_tr NumProv NumTreat
## 1  1     0           1            0       2        2
## 2  1     0           0            1       2        1
## 3  1     0           0            0       0        2
## 4  1     0           0            0       2        4
## 5  1     0           1            1       1        5
## 6  1     0           1            1       0        3

Successivamente, come già in precedenza, si definiscano come fattori le variabili categoriali e si crei un nuovo frame di dati per l’analisi dei cluster:

d$litig<-as.factor(d$litig)
d$soft_injury<-as.factor(d$soft_injury)
d$emergency_tr<-as.factor(d$emergency_tr)

ClusterDat<-d[ , -1]
str(ClusterDat)

## 'data.frame':    1000 obs. of  5 variables:
##  $ litig       : Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 1 2 ...
##  $ soft_injury : Factor w/ 2 levels "0","1": 2 1 1 1 2 2 1 1 1 2 ...
##  $ emergency_tr: Factor w/ 2 levels "0","1": 1 2 1 1 2 2 2 1 2 2 ...
##  $ NumProv     : int  2 2 0 2 1 0 1 2 2 5 ...
##  $ NumTreat    : int  2 1 2 4 5 3 4 3 1 8 ...

La metrica di Gower viene quindi utilizzata per derivare la matrice di dissomiglianza

dclaims<-as.matrix(daisy(ClusterDat, metric= "gower"))

Infine, si esegua l’algoritmo PAM, usando $K=2$ :

pam.claims<-pam(dclaims, 2, diss=TRUE)

Di seguito si possono ottenere informazioni numeriche per ciascun cluster: la cardinalità, la massima e media dissomiglianza tra le osservazioni nel cluster e il medoide del cluster, la massima dissomiglianza tra due osservazioni del cluster (diametro), la minima dissomiglianza tra un’osservazione del cluster e un’osservazione di un altro gruppo (separazione), la larghezza media della silhouette

pam.claims$clusinfo

##      size  max_diss   av_diss  diameter separation
## [1,]  635 0.3885714 0.1601935 0.6571429        0.2
## [2,]  365 0.3771429 0.1744736 0.7085714        0.2

pam.claims$silinfo$clus.avg.widths

## [1] 0.5307724 0.4396967

Il grafico della silhouette viene visualizzato per un sottoinsieme delle osservazioni

# silhouette di 100 os. dei dati sui sinistri
plot(silhouette(pam.claims$clustering[1:100],
                as.matrix(dclaims)[1:100, 1:100]), main="")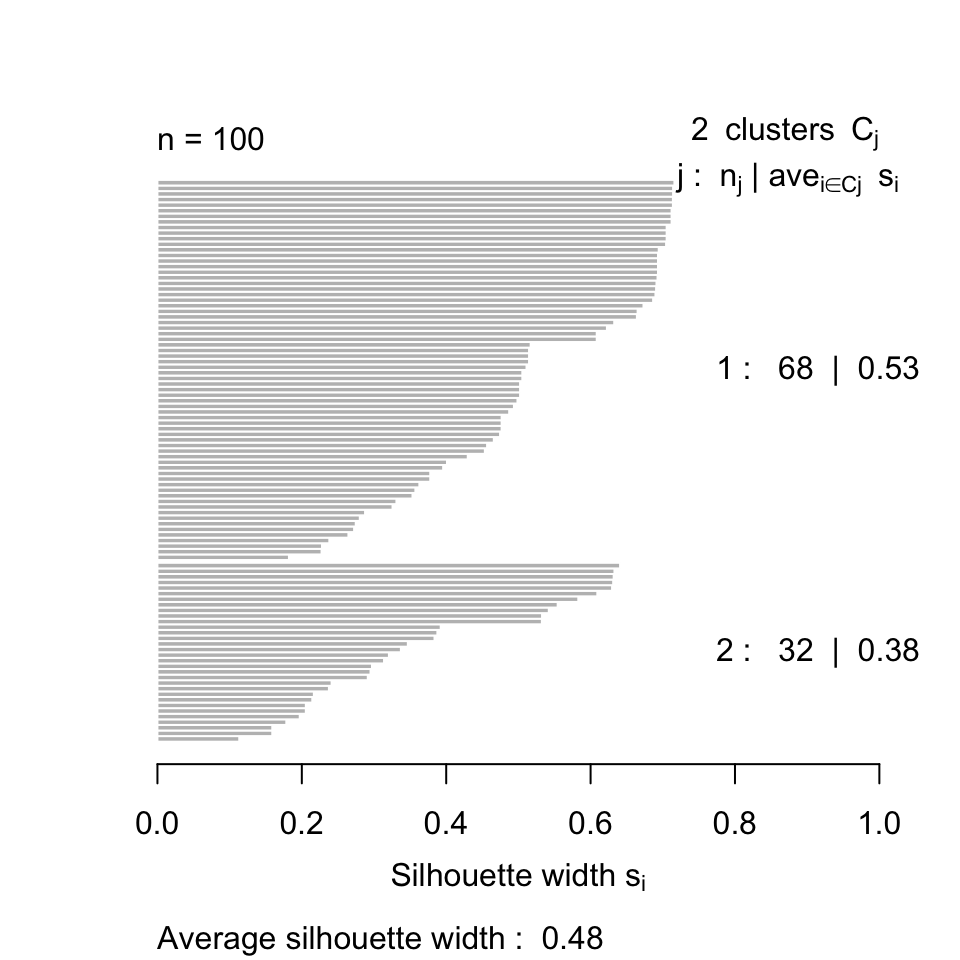

Per confrontare i risultati del clustering con i gruppi effettivi si può usare la funzione table()

attuale<-d$ID
pred<-pam.claims$clustering
table(attuale, pred)

##        pred
## attuale   1   2
##       1 608  98
##       2  27 267

Si può notare che i cluster ottenuti utilizzando l’algoritmo PAM sono leggermente diversi dalle partizioni vere, dove la procedura alloca correttamente $91\%$ del cluster più piccolo e $86\%$ di quello più grande.

Per aggiungere le classificazioni dei punti ai dati originali, si puo utilizzare:

dd <- cbind(ClusterDat, pam.cluster=pam.claims$clustering)
head(dd, n = 3)

##   litig soft_injury emergency_tr NumProv NumTreat
## 1     0           1            0       2        2
## 2     0           0            1       2        1
## 3     0           0            0       0        2
##   pam.cluster
## 1           1
## 2           1
## 3           1

Infine, si può esaminare il riepilogo di ciascun cluster

pam_results <- split(dd, dd$pam.cluster)

summary(pam_results[[1]]) #gruppo 1

##  litig   soft_injury emergency_tr    NumProv     
##  0:612   0:543       0:374        Min.   :0.000  
##  1: 23   1: 92       1:261        1st Qu.:1.000  
##                                   Median :2.000  
##                                   Mean   :2.107  
##                                   3rd Qu.:3.000  
##                                   Max.   :8.000  
##     NumTreat       pam.cluster
##  Min.   : 0.000   Min.   :1   
##  1st Qu.: 2.000   1st Qu.:1   
##  Median : 3.000   Median :1   
##  Mean   : 3.074   Mean   :1   
##  3rd Qu.: 4.000   3rd Qu.:1   
##  Max.   :12.000   Max.   :1

summary(pam_results[[2]]) #gruppo 2

##  litig   soft_injury emergency_tr    NumProv      
##  0:120   0: 45       0: 34        Min.   : 0.000  
##  1:245   1:320       1:331        1st Qu.: 2.000  
##                                   Median : 3.000  
##                                   Mean   : 3.551  
##                                   3rd Qu.: 5.000  
##                                   Max.   :10.000  
##     NumTreat       pam.cluster
##  Min.   : 0.000   Min.   :2   
##  1st Qu.: 3.000   1st Qu.:2   
##  Median : 5.000   Median :2   
##  Mean   : 5.356   Mean   :2   
##  3rd Qu.: 7.000   3rd Qu.:2   
##  Max.   :14.000   Max.   :2

Si noti che esistono molti altri algoritmi per gestire dati di tipo variabile misto e relativi pacchetti R (si veda, ad esempio, il pacchetto clustMixType per eseguire il clustering di partizionamento $k$ -prototipi di Huang, 1998).

6.4.5 Raggruppamento gerarchico

Ci sono diverse funzioni disponibili in R per il clustering gerarchico:

Approccio agglomerativo (dal basso): hclust() (nel package stats), agnes() (pacchetto cluster).
Approccio divisivo (top-down): diana() (sempre in cluster )

Il clustering gerarchico è particolarmente noto nella sua versione agglomerativa, che unisce cluster “simili”, fino a quando tutte le unità sono raggruppate in un unico cluster. Come vedremo, il processo crea una gerarchia di cluster, rappresentata dal cosiddetto dendrogramma.

Le funzioni hclust() e agnes() sono abbastanza simili; tuttavia, con la funzione agnes si può anche ottenere il coefficiente agglomerativo, che misura la qualità della struttura di raggruppamento trovata (valori più vicini a 1 suggeriscono una struttura di raggruppamento forte).

Per iniziare con un semplice esempio, considereremo il dataset di eurodist R, contenente le distanze geografiche tra le città europee:

data(eurodist)

# poche righe e colonne
as.matrix(eurodist)[1:8, 1:8]

##            Athens Barcelona Brussels Calais Cherbourg
## Athens          0      3313     2963   3175      3339
## Barcelona    3313         0     1318   1326      1294
## Brussels     2963      1318        0    204       583
## Calais       3175      1326      204      0       460
## Cherbourg    3339      1294      583    460         0
## Cologne      2762      1498      206    409       785
## Copenhagen   3276      2218      966   1136      1545
## Geneva       2610       803      677    747       853
##            Cologne Copenhagen Geneva
## Athens        2762       3276   2610
## Barcelona     1498       2218    803
## Brussels       206        966    677
## Calais         409       1136    747
## Cherbourg      785       1545    853
## Cologne          0        760   1662
## Copenhagen     760          0   1418
## Geneva        1662       1418      0

6.4.5.1 I metodi agglomerativi

Il clustering gerarchico agglomerativo prevede che si parta dai singoli punti e si proceda aggregando questi in gruppi sempre più ampi fino ad avere tutti i punti in un unico gruppo.

Si parte quindi da una matrice di dissimilarità (ad esempio generata con daisy() o dist()) e si cerca in essa quei due punti che sono meno dissimili (ovvero con dissimilarità più bassa).
Si uniscono quindi tali due punti ch formano un primo gruppo e si ricalcola la distanza di questo dagli altri punti.
La distanza del nuovo gruppo da un altro punto (o da un altro gruppo) si può calcolare in diversi metodi (legami) usando una misura di dissimilarità $d(i,j)$ adeguata. Ne citiamo alcuni fra i più comuni (detti $A$ e $B$ gli insiemi dei punti di due cluster):

legame singolo: la minima distanza fra gli elementi di ciascun cluster (single linkage) $min[d(i,j): i \in A e j\in B)]$
legame completo: la massima distanza fra gli elementi di ciascun cluster (complete linkage) $max[d(i,j): i \in A e j\in B)]$
legame medio: la ditanza media fra tutti gli elementi di ciascun cluster (average linkage)
Ward: l’aumento in termini di varianza per il cluster che viene unito.

Eseguiamo il clustering gerarchico agglomerativi usando agnes() (all’interno del pacchetto cluster) sulle distanze eurodist, usando method=single per il collegamento singolo (se passiamo un oggetto dist come primo argomento allora non c’è bisogno di specificare altro)

#collegamento unico
agnes.single<-agnes(eurodist, method="single")
# coefficiente agglomerato
agnes.single$ac

## [1] 0.5115696

Per visualizzare il dendrogramma, si utilizza la funzione pltree()

# Metti le etichette alla stessa altezza: hang = -1
pltree(agnes.single, cex=0.8, hang = -1, main = "agnes (single)", xlab="", sub ="")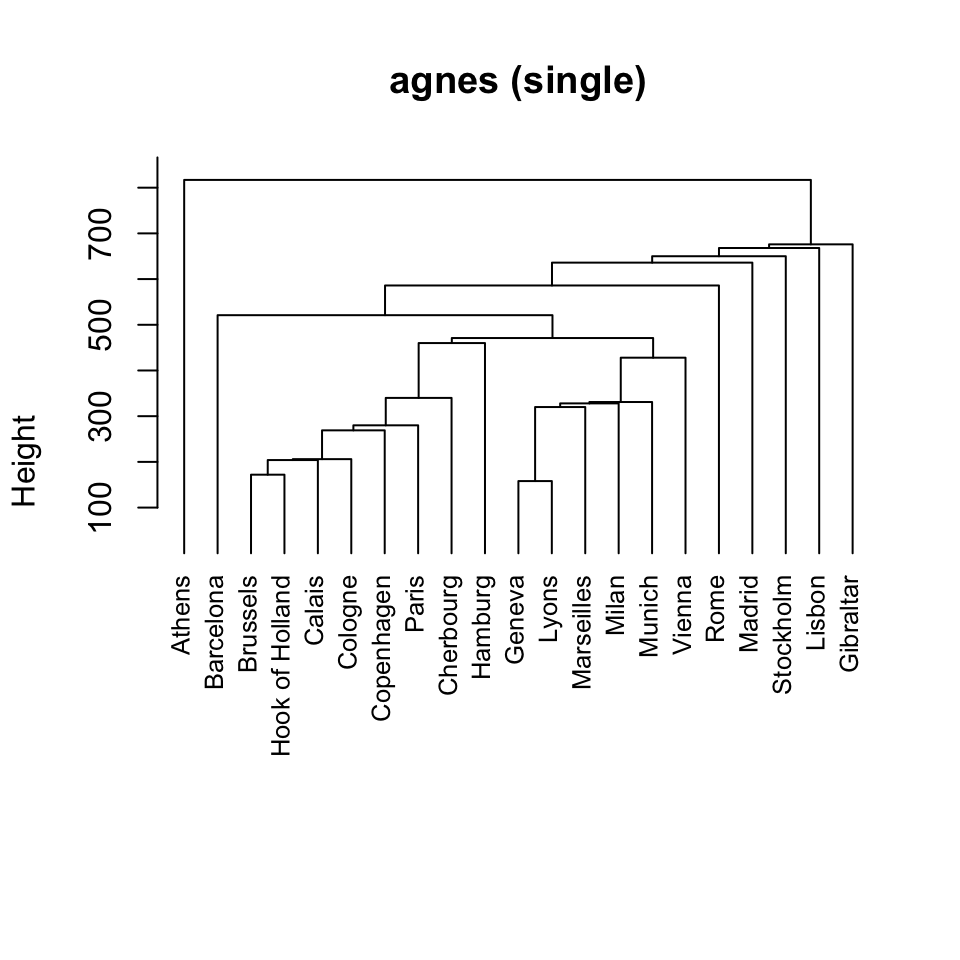

La funzione agnes fornisce una visualizzazione alternativa dell’aggregazione dei cluster:

plot(agnes.single, which=1, col=c(8,1), main="")

Se sono necessari grafici più flessibili, una soluzione alternativa è chiamare la funzione plot(), dopo la coercizione alla classe “hclust” e “dendrogram”, come nel codice seguente

# Converti in un dendrogramma e traccia
eurocity.dend<-as.dendrogram(as.hclust(agnes.single))

# trama(eurocity.dend)

L’output del legame singolo spesso non da risultati molto soddisfacenti, a causa di un effetto catena. Si possono replicare i passaggi precedenti utilizzando gli altri legami, che porteranno a risultati diversi

#legame completo
agnes.comp<-agnes(eurodist,method="complete")
agnes.comp$ac

## [1] 0.8979532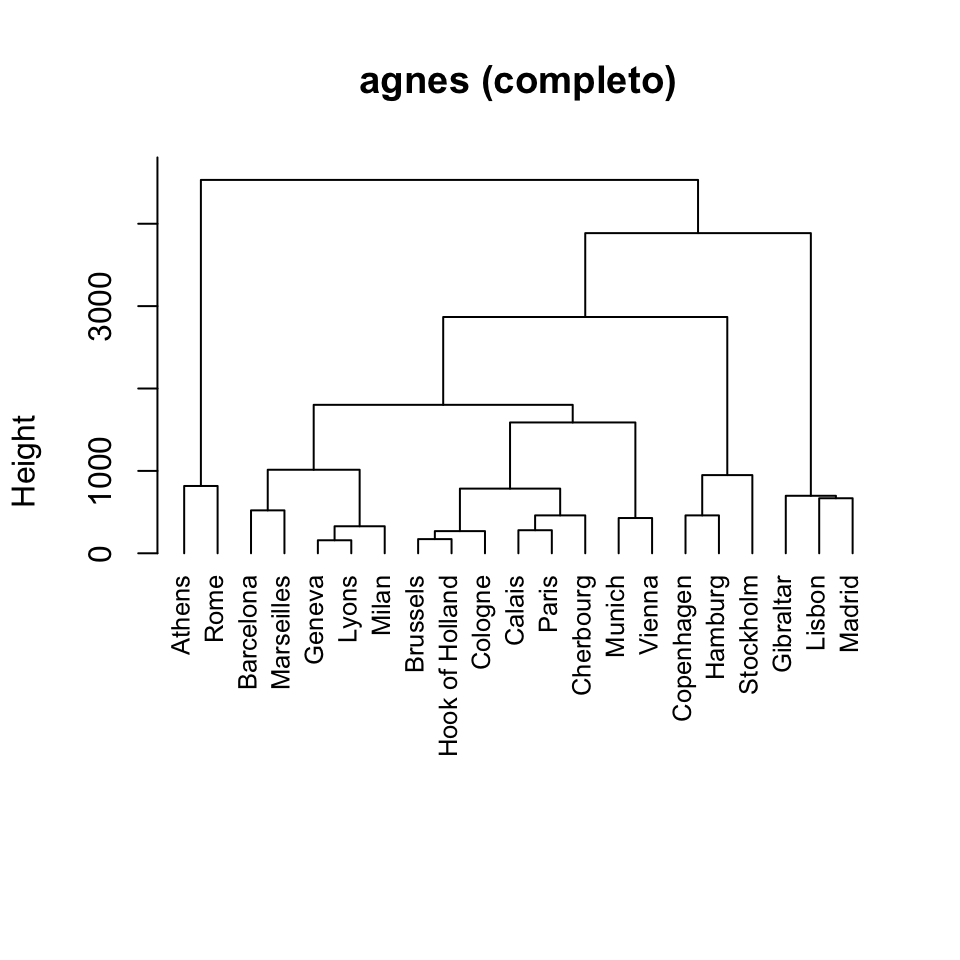

pltree(agnes.comp, cex = 0.8, hang = -1, main = "agnes (completo)", xlab="", sub ="")

Il collegamento completo identifica bene i gruppi “estremi”, che corrispondono al sud (Roma, Atene), alla penisola iberica (Madrid, Gibilterra e Lisbona) e a un gruppo di città del nord Europa (Amburgo, Copenaghen e Stoccolma).

#average linkage
agnes.ave<-agnes(eurodist,method="average")
agnes.ave$ac

## [1] 0.8063934

pltree(agnes.ave, cex = 0.8, hang = -1, main = "agnes (average)", xlab="", sub ="")

# Ward's method
agnes.Ward<-agnes(eurodist,method="ward")
agnes.Ward$ac

## [1] 0.905946

pltree(agnes.Ward, cex = 0.8, hang = -1, main = "agnes (Ward)", xlab="", sub ="")

Il legame medio e il metodo di Ward producono risultati simili: sono ancora identificati il cluster meridionale, la penisola iberica e una regione nord-orientale. Inoltre, possiamo identificare

una regione centro-settentrionale continentale (Bruxelles, Hoek van Holland, Colonia)
una regione del Centro (Ginevra, Lione, Marsiglia, Milano, Monaco e Vienna)
il cluster della Francia settentrionale (Calais, Parigi, Cherbourg)

Per determinare le etichette dei cluster per ogni osservazione associata a un dato taglio del dendrogramma, si può usare la funzione cutree():

hc<-cutree(agnes.ave, 4)
# hc4 <- cutree(as.hclust(agnes.ave), h = 1000)

cnames<-row.names(as.matrix(eurodist))
cnames[hc==1]

## [1] "Athens" "Rome"

cnames[hc==2]

## [1] "Barcelona" "Gibraltar" "Lisbon"    "Madrid"

cnames[hc==3]

##  [1] "Brussels"        "Calais"          "Cherbourg"      
##  [4] "Cologne"         "Geneva"          "Hook of Holland"
##  [7] "Lyons"           "Marseilles"      "Milan"          
## [10] "Munich"          "Paris"           "Vienna"

cnames[hc==4]

## [1] "Copenhagen" "Hamburg"    "Stockholm"

La funzione abline() disegna una linea retta sopra ogni tracciato esistente in R. Il codice seguente traccia una linea orizzontale ad altezza 1000 sul dendrogramma, producendo i quattro cluster ottenuti sopra. È possibile anche visualizzare i cluster all’interno del dendogramma stesso inserendo i bordi come mostrato di seguito

pltree(agnes.ave, hang=-1, cex = 0.7, main="")
abline(h=1000)
rect.hclust(agnes.ave, k = 4, border = 3:7)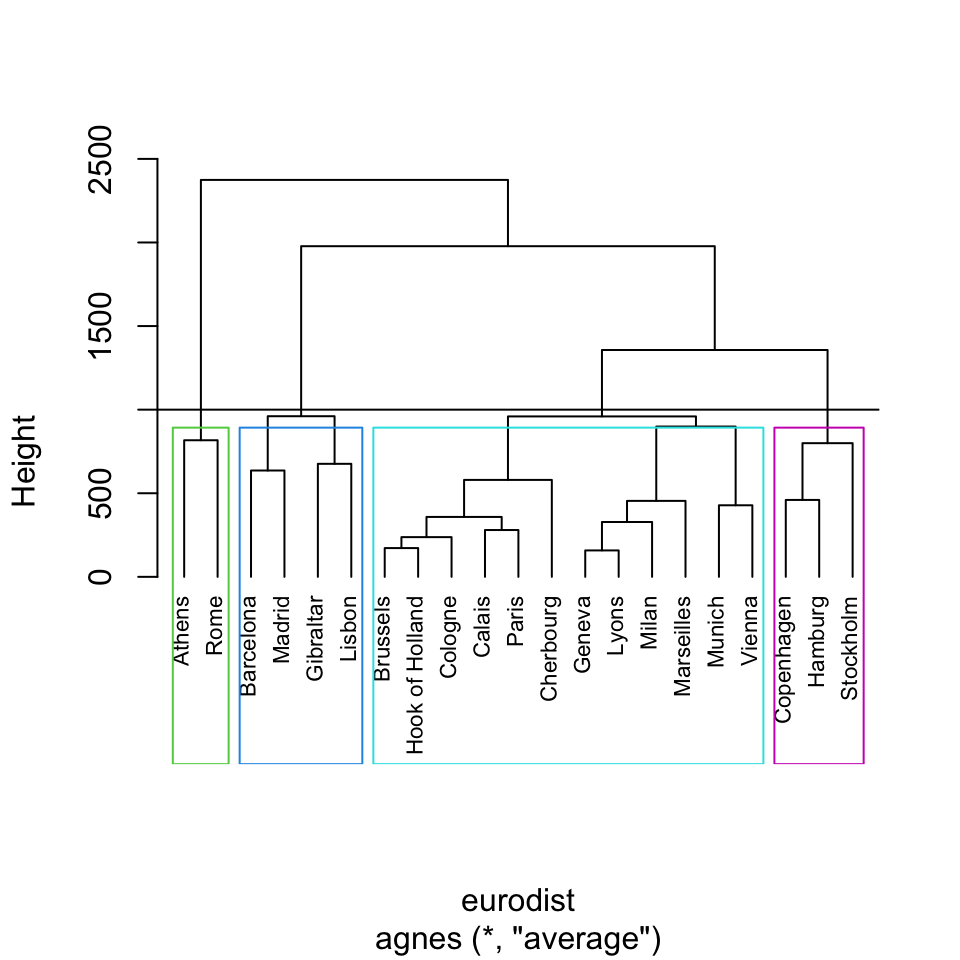

Si proceda ora a raggruppare gerarchicamente le capitali del mondo, utilizzando il database delle città del mondo nel pacchetto mappe, con l’obiettivo di visualizzare gruppi di città sulla base di informazioni geografiche.

library(maps)
data(world.cities)
str(world.cities) #vedi i componenti del set di dati

## 'data.frame':    43645 obs. of  6 variables:
##  $ name       : chr  "'Abasan al-Jadidah" "'Abasan al-Kabirah" "'Abdul Hakim" "'Abdullah-as-Salam" ...
##  $ country.etc: chr  "Palestine" "Palestine" "Pakistan" "Kuwait" ...
##  $ pop        : int  5629 18999 47788 21817 2456 3434 9198 5492 22706 41731 ...
##  $ lat        : num  31.3 31.3 30.6 29.4 32 ...
##  $ long       : num  34.3 34.4 72.1 48 35.1 ...
##  $ capital    : int  0 0 0 0 0 0 0 0 0 0 ...

Per selezionare le maiuscole, si considera il sottoinsieme di righe per cui capital==1

d1<-subset(world.cities,capital==1)

# seleziona colonne con latitudini e longitudini
d2<-d1[ ,c(4,5)]
head(d2)

##        lat    long
## 26   31.95   35.93
## 265  24.48   54.37
## 280   9.18    7.17
## 308   5.56   -0.20
## 366 -25.05 -130.10
## 382   9.03   38.74

Dato il numero di città coinvolte, si possono rappresentare i raggruppamenti disegnando le città su una mappa utilizzando colori e simboli diversi per i diversi gruppi, anziché il dendrogramma. Di seguito si esegue il clustering agglomerativo e si confrontano le soluzioni per $k=5$ e $k=8$ :

ris.agnes<-agnes(d2, method="average")

gruppi_5<-cutree(ris.agnes,k=5)
table(gruppi_5)

## gruppi_5
##   1   2   3   4   5 
## 136   9  22  51  12

gruppi_8<-cutree(ris.agnes,k=8)
table(gruppi_8)

## gruppi_8
##  1  2  3  4  5  6  7  8 
## 30 52  9 22 54  8 12 43

# plot on map with 5 clusters
par(mar=c(0,0,0,0))
map("world",interior=FALSE)
points(d2[,2],d2[,1],col=gruppi_5,pch=gruppi_5)

# plot on map with 8 clusters
par(mar=c(0,0,0,0))
map("world",interior=FALSE)
points(d2[,2],d2[,1],col=gruppi_8,pch=gruppi_8)

Infine, è semplice ottenere le silhouette da raggruppamenti gerarchici usando la funzione silhouette con cutree() e la distanza come input:

# Silhouette per un clustering gerarchico:
labels<-d1$name
sil<- data.frame(Name=labels, silhouette(gruppi_5, daisy(d2))[, 1:3])
head(sil)

##          Name cluster neighbor sil_width
## 1      'Amman       1        3 0.5763558
## 2   Abu Dhabi       1        3 0.3039018
## 3       Abuja       1        4 0.5128536
## 4       Accra       1        4 0.4079634
## 5   Adamstown       2        4 0.4662954
## 6 Addis Abeba       1        3 0.4906205

6.4.5.2 Clustering basato sulla correlazione

Finora, si è usata la distanza euclidea come misura di dissomiglianza. Questa è la radice quadrata della somma delle differenze quadrate. In alcune circostanze, potrebbero essere preferite altre misure di dissomiglianza.

Ad esempio, una distanza basata sulla correlazione viene utilizzata per concentrarsi sulle forme dei profili di osservazione piuttosto che sulle loro grandezze. Si presume che due righe della matrice di dati siano simili se le loro caratteristiche sono altamente correlate, producendo così una distanza uguale a zero quando sono perfettamente correlate:

$d(x,y)=1-r_{xy}$ dove $r_{xy}$ è il coefficiente di correlazione di Pearson. La matrice di distanza risultante può essere utilizzata come input per il clustering gerarchico. La correlazione di Spearman può essere utilizzata al posto della correlazione di Pearson, che corrisponde al calcolo di $r_{xy}$ sui ranghi.

Esempi: La correlazione funziona bene per l’espressione genica nel raggruppamento di campioni e geni. Un altro esempio è il seguente.

Si consideri una matrice in cui le righe sono acquirenti e le colonne sono gli articoli disponibili per l’acquisto; gli elementi di matrice rappresentano il numero di volte in cui un determinato acquirente ha acquistato un determinato articolo. La distanza basata sulla correlazione viene utilizzata per identificare gli acquirenti con preferenze simili (ad es. acquirenti che hanno acquistato articoli A e B ma mai articoli C o D), indipendentemente dalle differenze di volume.

x<-c(2,4,6,2,1,4,3,4,6,1)
y<-c(2,3,2,3,2,2,2,5,3,5)
z<-c(10,12,14,10,9,12,11,12,13,11)

d<-rbind(x, y, z) # data matrix

par(mfrow=c(1,2))
plot(1:10, z, type="l", col="red", ylim=c(0,18), xlab="items index",
     ylab="n.items purchased")
points(x, type="l", col="green")
points(y, type="l", col="blue")

# compute Pearson correlation between rows
r<-cor(t(d))
# distance
cor.d<-as.dist(1-r)
#dendrogram
pltree(agnes(cor.d, method ="complete"), main="Correlation-based HAC")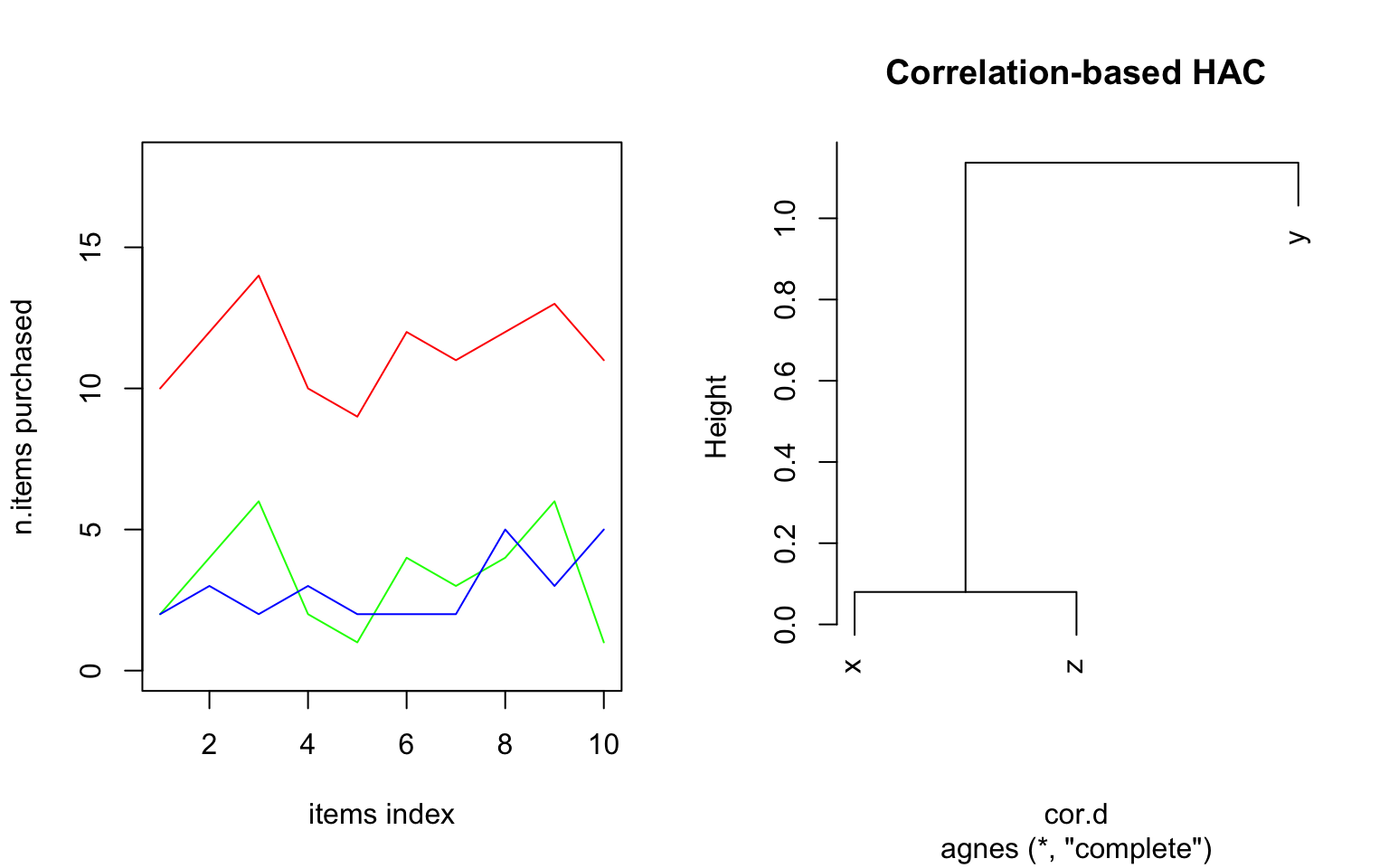

I clienti “x” e “z” hanno valori abbastanza diversi per ciascuna variabile, ma sono altamente correlati, quindi c’è una piccola distanza basata sulla correlazione tra loro, quindi sono raggruppati insieme.

Nota: il clustering basato sulla correlazione viene utilizzato anche nelle applicazioni dei mercati finanziari, dove è opportuno determinare gruppi di titoli che si muovono insieme nel tempo. In tale contesto, i coefficienti di correlazione $r_{ij}$ vengono convertiti in distanze, ad esempio utilizzando $d_{ij}=\sqrt{(2(1-r_{ij}))}$ . Approcci alternativi utilizzano misure di associazione/concordanza come la correlazione di Kendall e Spearman, nonché varie misure di dipendenza dalla coda.

6.4.6 Metodi di raggruppamento basati sulla densità

6.4.6.1 Il metodo DBSCAN

L’obiettivo dell’algoritmo DBSCAN è identificare i cluster come regioni dense, che possono essere misurate dal numero di oggetti “vicini” a un dato punto.

La funzione R per implementare il metodo DBSCAN è la funzione dbscan nel pacchetto dbscan. Per illustrare come funziona l’algoritmo, simuleremo prima tre cluster nello spazio bidimensionale con 100 punti ciascuno:

set.seed(2)
n <- 300
d <- cbind(x = runif(3, 0, 1) + rnorm(n, sd = 0.1),
           y = runif(3, 0, 1) + rnorm(n, sd = 0.1))
head(d)

##               x          y
## [1,] 0.08869306 0.03626618
## [2,] 0.86083718 0.88495681
## [3,] 0.67011472 0.22061473
## [4,] 0.19744429 0.24429363
## [5,] 0.63138780 0.90385668
## [6,] 0.48210192 0.26570588

true_cl <- rep(1:3, 100)
plot(d, col = true_cl, pch = true_cl)

Per DBSCAN sono necessari due parametri importanti:

il parametro eps definisce il raggio dell’intorno attorno ad un punto x.
Il parametro MinPts, il numero minimo di punti entro la distanza eps, necessario per produrre un nuovo cluster

Il valore predefinito per MinPts nella funzione dbscan è 5 (usa almeno il numero di dimensioni del set di dati più uno). Per eps, possiamo trovare un valore adatto esplorando un diagramma K-NN dei punti (cioè il diagramma delle distanze al k-esimo vicino più vicino in ordine decrescente) e cercare un angolo acuto nel diagramma:

library(dbscan) # carica la libreria

# trova il parametro eps adatto usando un diagramma k-NN
kNNdistplot(d, k = 3)
abline(h=.05, col = "red", lty=2)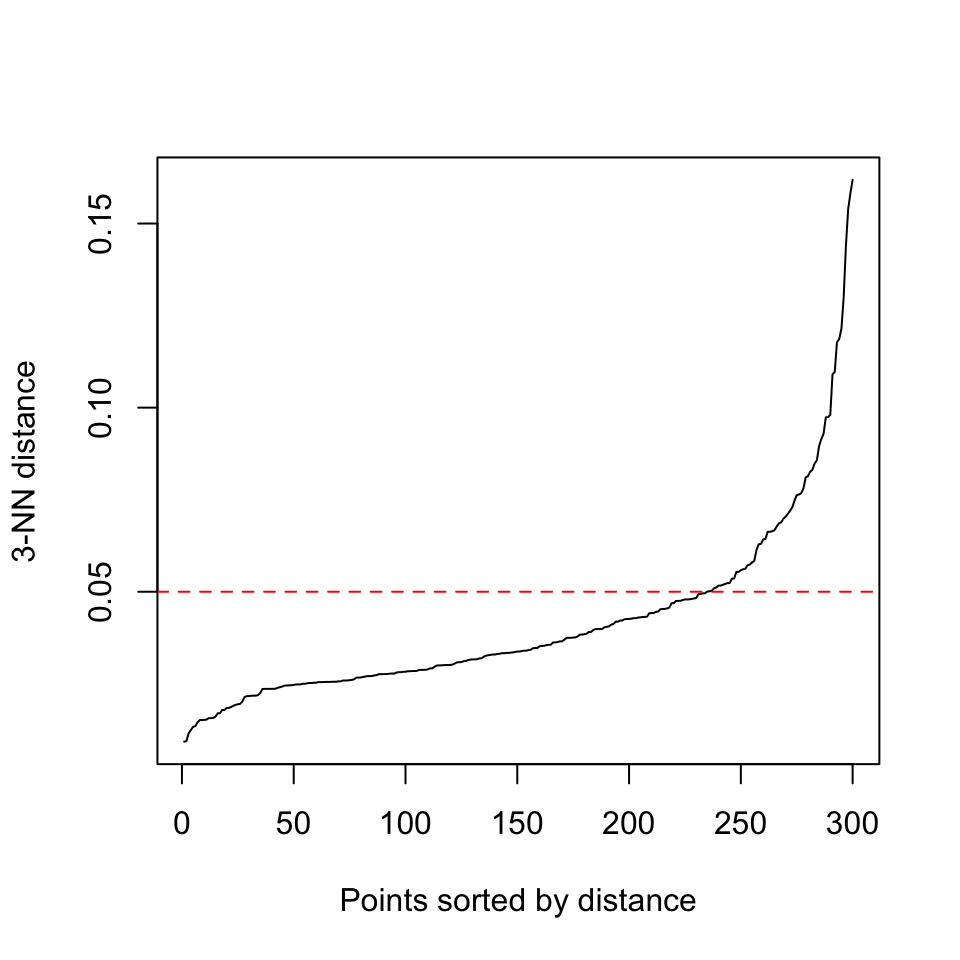

Un gomito” può essere identificato a una distanza di circa 3-NN di 0.05. Successivamente, possiamo eseguire il clustering con i parametri scelti:

db.out <- dbscan(d, eps = 0.05, minPts = 3)
db.out

## DBSCAN clustering for 300 objects.
## Parameters: eps = 0.05, minPts = 3
## Using euclidean distances and borderpoints = TRUE
## The clustering contains 5 cluster(s) and 30 noise points.
## 
##  0  1  2  3  4  5 
## 30 90 89 81  4  6 
## 
## Available fields: cluster, eps, minPts, metric,
##                   borderPoints

Vengono identificati i tre cluster più grandi, insieme a due piccoli gruppi di 4 e 6 punti.

Per confrontare i cluster identificati con i gruppi effettivimante esistenti possiamo utilizzare il cosiddetto Adjusted Rand Index (ARI), che è un indice esterno per la valutazione del clustering, misurando la somiglianza tra due classificazioni degli stessi oggetti dal proporzioni degli accordi tra le due partizioni. La funzione adj.rand.index() nel pacchetto pdfCluster può essere utilizzata per questo compito:

library(pdfCluster)
adj.rand.index(true_cl, db.out$cluster)

## [1] 0.7692038

Come altri indici di validità del cluster, l’ARI assume un valore compreso tra 0 e 1 e maggiore è il valore dell’indice, migliore è la qualità del clustering se comparata con la vera classificazione (che però di solito non è nota come in questo caso in cui avevamo una simulazione).

Infine, le informazioni sull’assegnazione dei cluster possono essere utilizzate per tracciare i dati con i cluster identificati da etichette e colori diversi

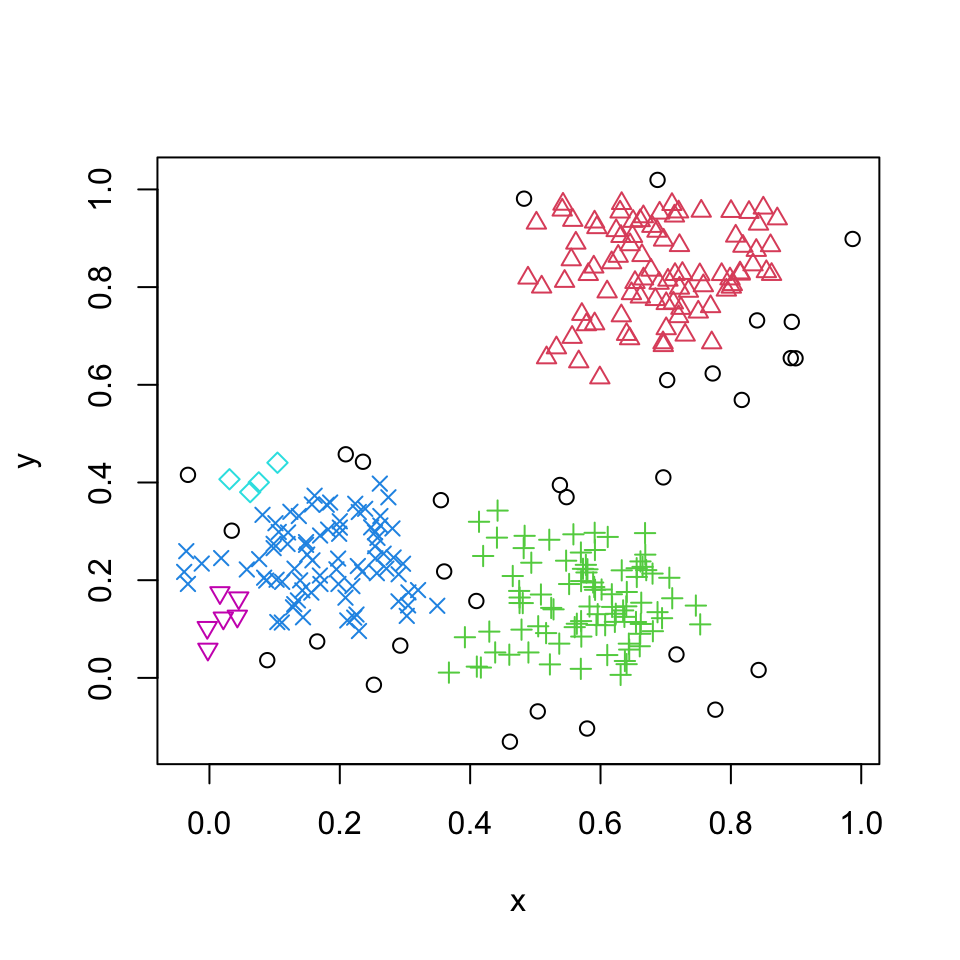
plot(d, col = db.out$cluster + 1, pch = db.out$cluster + 1)

La funzione predict può essere utilizzata per prevedere le appartenenze ai cluster per nuovi punti dati.

6.4.6.2 Raggruppamento basato sulla ricerca di mode: `pdfCluster`.

Un altro metodo per ottenere cluster basati sulla densità è disponibile con la funzione pdfCluster. Esso è basato su una stima non parametrica della funzione di densità immaginando che la distribuzione abbia più regioni a alta densità che sono identificabili come mode. È quindi basato sulla ricerca di mode nella distribuzione dei dati (che si immagina siano quantitativi).