Chapter 5 Lab 3 - 08/11/2021

In questa lezione impareremo poi a calcolare i rendimenti e a studiarne la distribuzione utilizzano boxplot, istogramma e stima kernel della densità.

Per questa lezione useremo il file denominato prices.csv. Procediamo quindi con l’importazione dei dati come descritto nella sezione 4.1 utilizzando l’opzione Import dataset di RStudio (pannello in alto a destra). L’oggetto prices verrà di fatto creato quando si lancia il seguente codice:

prices <- read.csv("./data/prices.csv")

E’ buona pratica controllare di che tipo di oggetto si tratta

class(prices)

## [1] "data.frame"

la parte iniziale e finale del data frame (per verificare l’ordinamento dai dati più vecchi a quelli più recenti)

head(prices)

##       Date   A2Aadj   ISPajd  JUVEadj
## 1 10/01/17 0.982659 1.597666 0.288256
## 2 11/01/17 0.999368 1.595077 0.289546
## 3 12/01/17 1.012895 1.573067 0.288164
## 4 13/01/17 1.030400 1.596372 0.289546
## 5 16/01/17 1.021647 1.566594 0.284573
## 6 17/01/17 1.022443 1.566594 0.288256

tail(prices)

##          Date A2Aadj   ISPajd JUVEadj
## 1208 13/10/21 1.8385 2.398494  0.7120
## 1209 14/10/21 1.8535 2.425892  0.7265
## 1210 15/10/21 1.8450 2.475400  0.7195
## 1211 18/10/21 1.8265 2.491500  0.7245
## 1212 19/10/21 1.8470 2.451000  0.7230
## 1213 20/10/21 1.8790 2.467000  0.7275

e la struttura del data frame (con le variabili quantitative num per i prezzi)

str(prices)

## 'data.frame':    1213 obs. of  4 variables:
##  $ Date   : Factor w/ 1213 levels "01/02/17","01/02/18",..: 356 396 437 479 599 640 680 721 762 884 ...
##  $ A2Aadj : num  0.983 0.999 1.013 1.03 1.022 ...
##  $ ISPajd : num  1.6 1.6 1.57 1.6 1.57 ...
##  $ JUVEadj: num  0.288 0.29 0.288 0.29 0.285 ...

5.1 Calcolo dei rendimenti

5.1.1 Per un singolo titolo

Come già visto nella Sezione 4.5 è utile iniziare con il calcolo dei rendimenti logaritmi utilizzando le funzioni log e diff. Calcoliamo quindi i log-rendimenti per il titolo A2A con il codice che segue:

A2Alogret = diff(log(prices$A2Aadj))
class(A2Alogret) #vettore!

## [1] "numeric"

Si noti che l’oggetto A2Alogre è un vettore. E’ possibile rappresentare graficamente la serie di log-rendimenti come segue, includendo anche nel grafico una linea orizzontale in corrispondenza di 0 che è il valore di riferimento:

plot(A2Alogret, type="l")
abline(h = 0, col="red")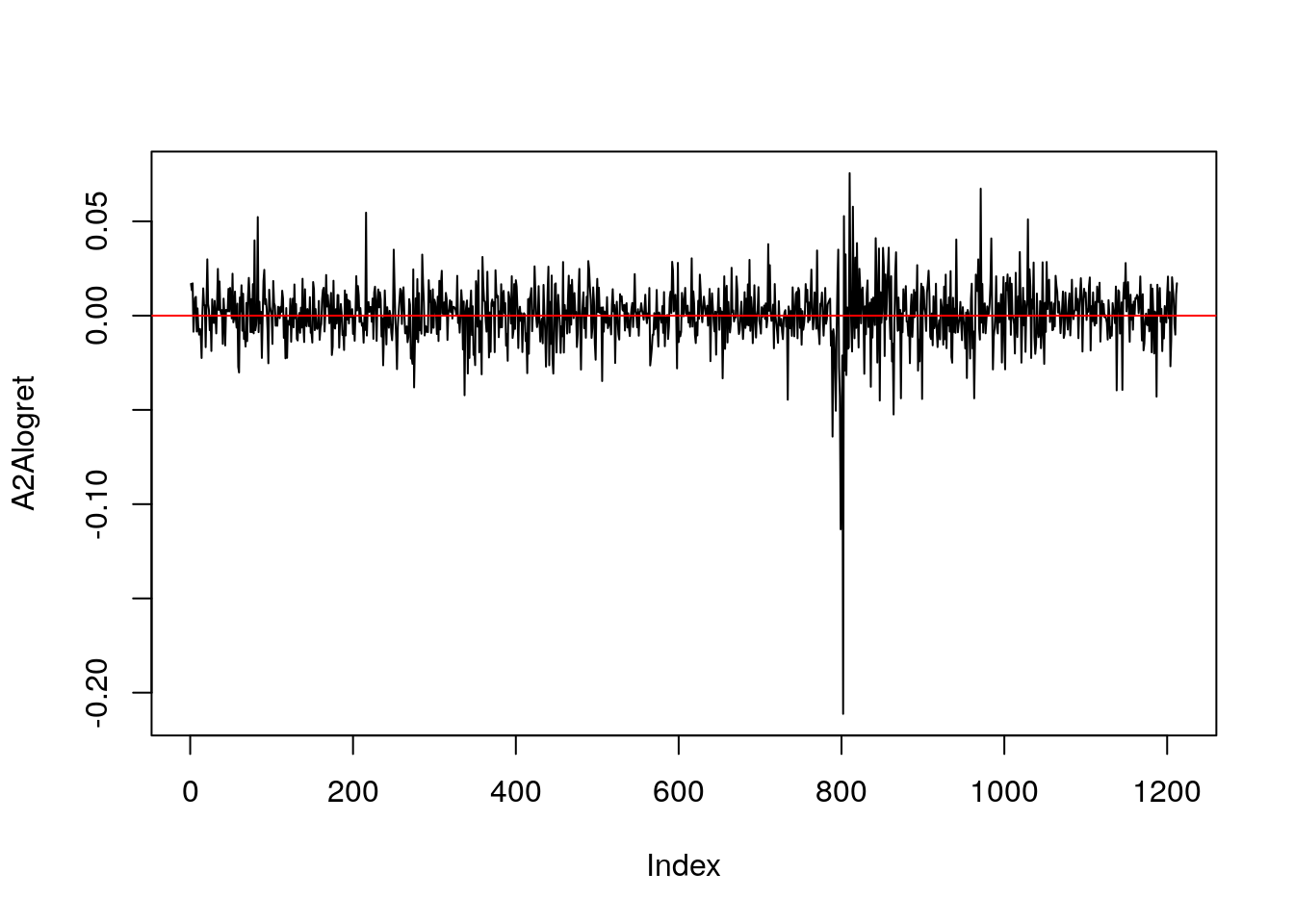

Dati i log-rendimenti \(r_t\) è possibile calcolare i rendimenti lordi e poi quelli netti utilizzando le seguenti formule: \[ R_t + 1= \exp(r_t) \]

\[ R_t = \frac{P_t}{P_{t-1}}-1 \]

Qui di seguito il codice di R per il calcolo dei rendimenti lordi e netti:

A2Agrossret = exp(A2Alogret)
A2Anetret = A2Agrossret - 1

Le tre serie storiche di rendimenti posso essere rappresentate graficamente come descritto nella Sezione 4.4:

plot(A2Alogret, type="l",
     ylim=c(-0.5, 1.5), ylab="Returns")
lines(A2Agrossret, col="blue")
lines(A2Anetret, col="red")
abline(h = 1, col="red")
abline(h = 0, col="green")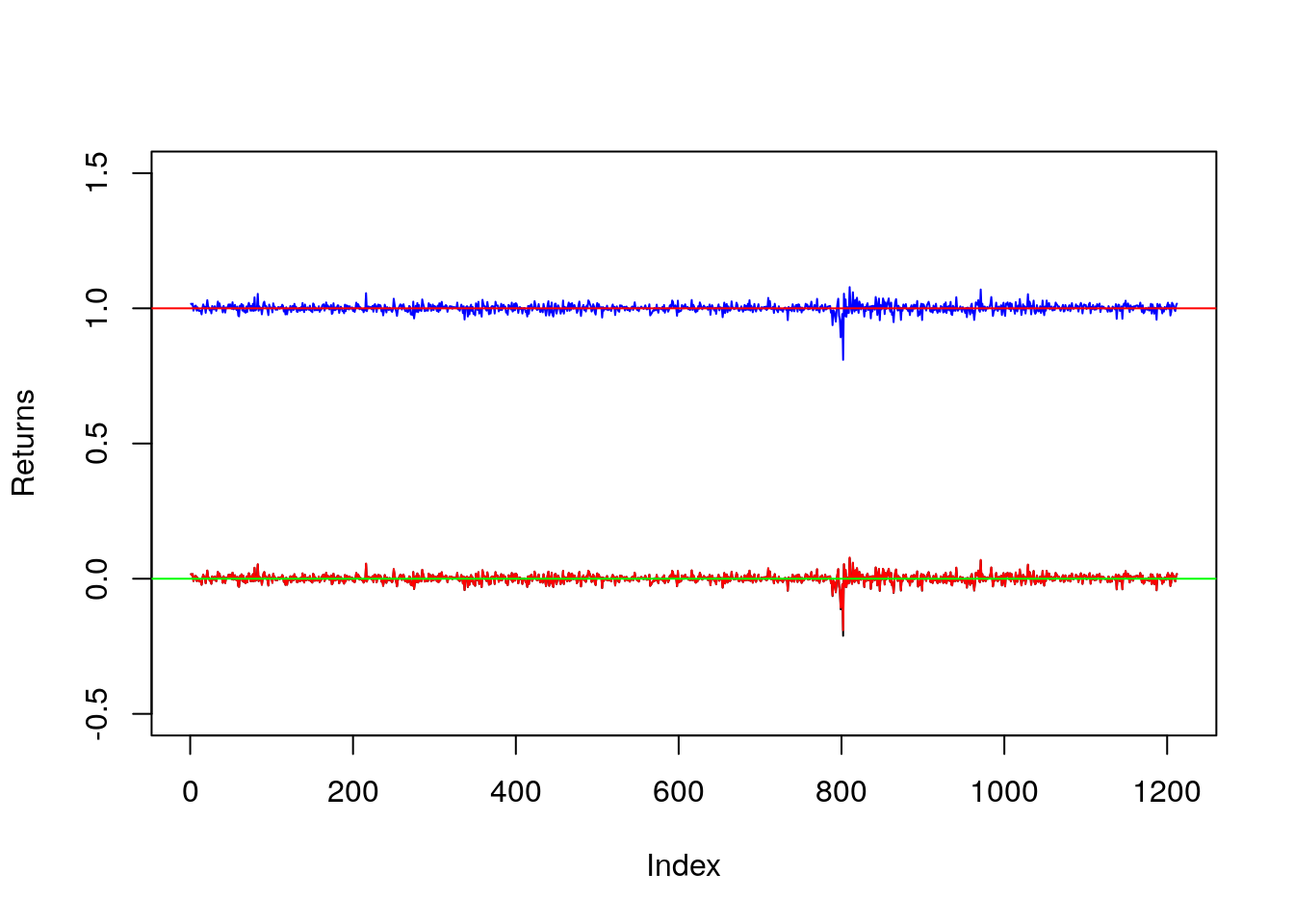

Si noti che la serie storica rossa di rendimenti logaritmici copre quasi interamente la serie storica nera dei rendimenti netti; questo è dovuto alle proprietà teoriche dei rendimenti e al fatto che \(r_t\simeq R_t\) per valori piccoli di \(R_t\).

La funzione abline aggiunge una linea costante orizzontale al grafico per \(y=1\) e \(y=0\) che rappresentano il valore di riferimento per i rendimenti lordi e netti/logaritmici (indicano nessun cambiamento nel prezzo).

5.1.2 Per tutti i titoli congiuntamente

Utilizzando la funzione apply (si veda Sezione 4.3) è possibile calcolare i rendimenti logaritmici per tutti i titoli congiuntamente (questo è utile quando si ha un numero elevato di colonne e si vuole evitare di ripetere molte volte copia-incolla).

Si procede quindi in due passi: 1) si calcolano i log prezzi usando la funzione log; 2) si calcolano le differenze dei log prezzi usando la funzione diff:

# 1) calcolo i log prezzi
logprezzi = apply(prices[,-1], 2, log)
head(logprezzi)

##             A2Aadj    ISPajd   JUVEadj
## [1,] -0.0174931163 0.4685438 -1.243906
## [2,] -0.0006321998 0.4669220 -1.239441
## [3,]  0.0128125674 0.4530272 -1.244226
## [4,]  0.0299470764 0.4677336 -1.239441
## [5,]  0.0214160309 0.4489038 -1.256765
## [6,]  0.0221948617 0.4489038 -1.243906

# 2) calcolo i log rendimenti
logret = data.frame(apply(logprezzi, 2, diff))
head(logret)

##          A2Aadj       ISPajd      JUVEadj
## 1  0.0168609165 -0.001621803  0.004465205
## 2  0.0134447672 -0.013894794 -0.004784417
## 3  0.0171345090  0.014706338  0.004784417
## 4 -0.0085310454 -0.018829719 -0.017324368
## 5  0.0007788307  0.000000000  0.012859163
## 6  0.0092950844 -0.002482982  0.000000000

class(logret)

## [1] "data.frame"

dim(logret)

## [1] 1212    3

Si noti che per il calcolo di logret si utilizza la funzione data.frame che permette di ottenere un oggetto di tipo data frame (mentre di default la funzione apply restituisce un oggetto di tipo matrix).

E’ possibile rappresentare graficamente le tre serie storiche dei log-rendimenti come segue:

plot(logret$A2Aadj, type = "l",
     ylim = c(min(logret), max(logret)))
lines(logret$ISPajd, col = "red")
lines(logret$JUVEadj, col = "blue")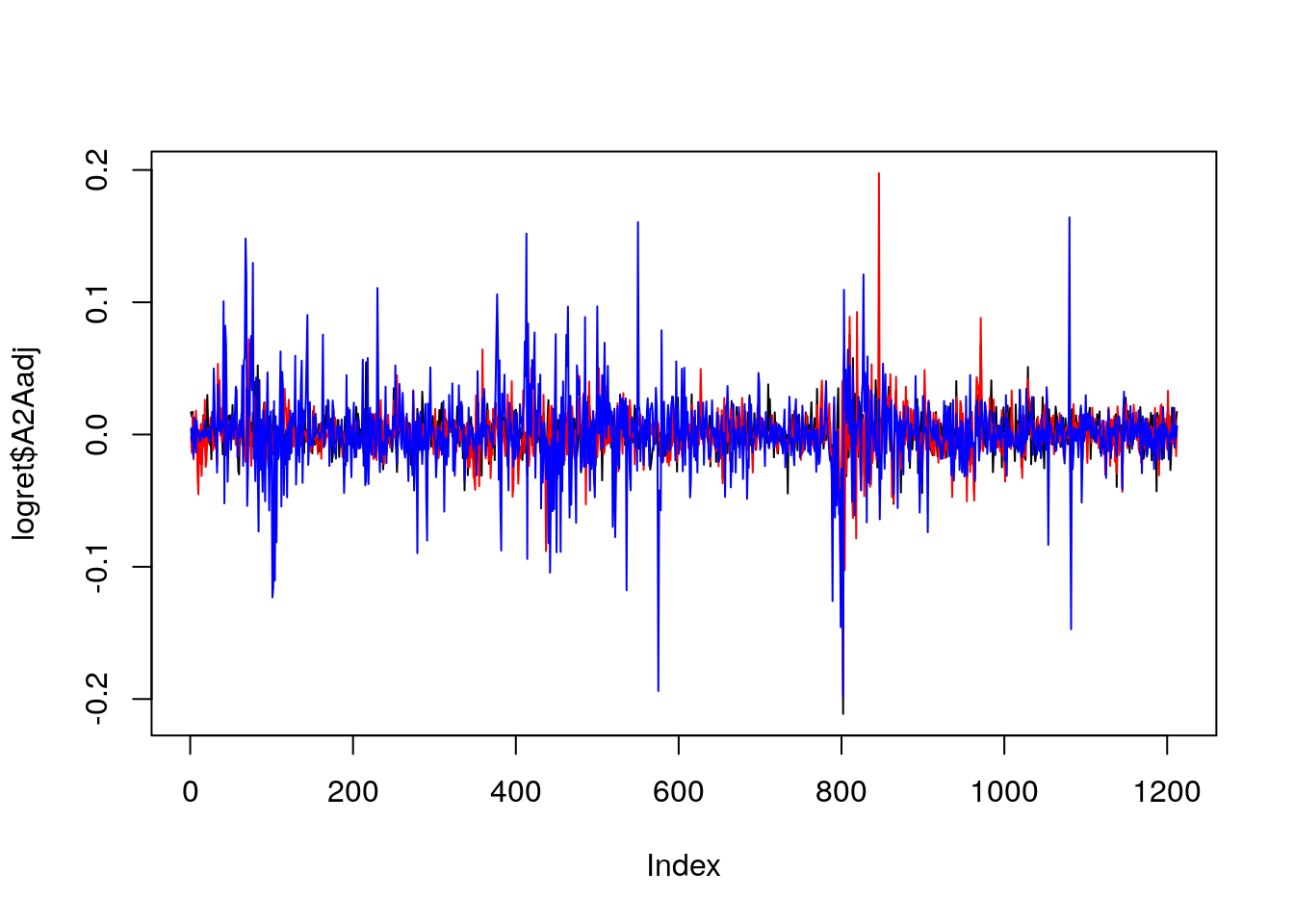

Si osserva la maggior variabilità per il titolo JUVE (maggiori e più ampie fluttuazioni).

Qualche statistica descrittiva può essere ottenuta con il seguente codice:

apply(logret, 2, summary)

##                A2Aadj        ISPajd       JUVEadj
## Min.    -0.2112382259 -0.1958118062 -0.1980985831
## 1st Qu. -0.0076642320 -0.0082247367 -0.0115276387
## Median   0.0012597454  0.0002748674  0.0006788867
## Mean     0.0005348456  0.0003584645  0.0007638325
## 3rd Qu.  0.0090198024  0.0087726624  0.0130212164
## Max.     0.0755707142  0.1976145212  0.1642638487

# CV
apply(logret, 2, sd) / apply(logret, 2, mean)

##   A2Aadj   ISPajd  JUVEadj 
## 29.88187 53.32222 39.54724

5.2 Boxplot

Il boxplot è un utile strumento grafico per lo studio di una distribuzione e per il confronto tra distribuzioni diverse.

Utilizzando una singola variabile si procede come segue:

boxplot(logret$A2Aadj)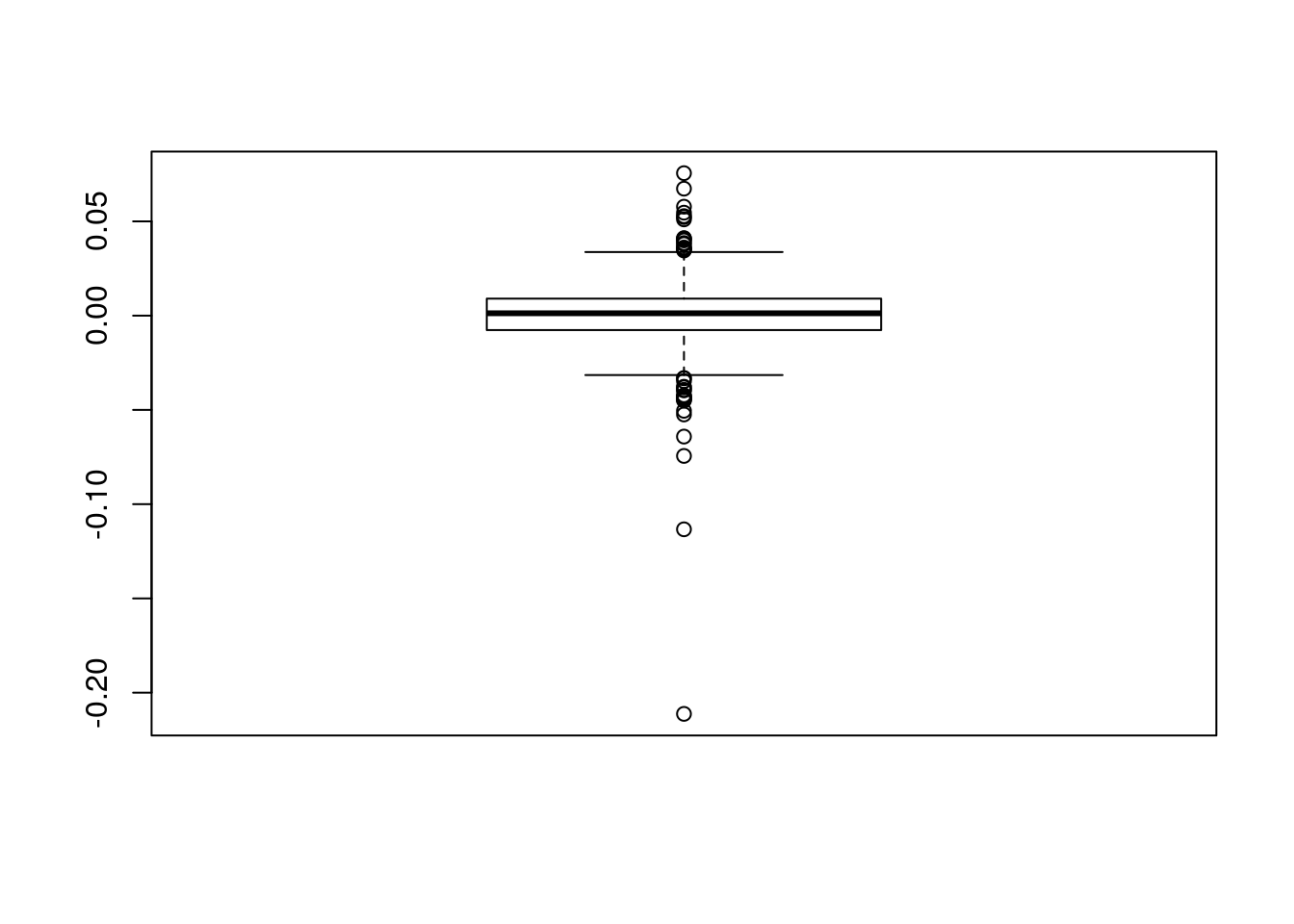

Si ricorda che i baffi del boxplot sono posizionati in corrispondenza del terzo quartile + 1.5\(*\)differenza intequartile (baffo superiore) e del primo quartile - 1.5\(*\)differenza interquartile. I punti rappresentano quindi osservazioni estreme (o outliers). In alternativa è possibile posizionare i baffi del boxplot in corrispondenza del valore minimo e massimo della distribuzione utilizzando l’opzione range:

boxplot(logret$A2Aadj, range = 0)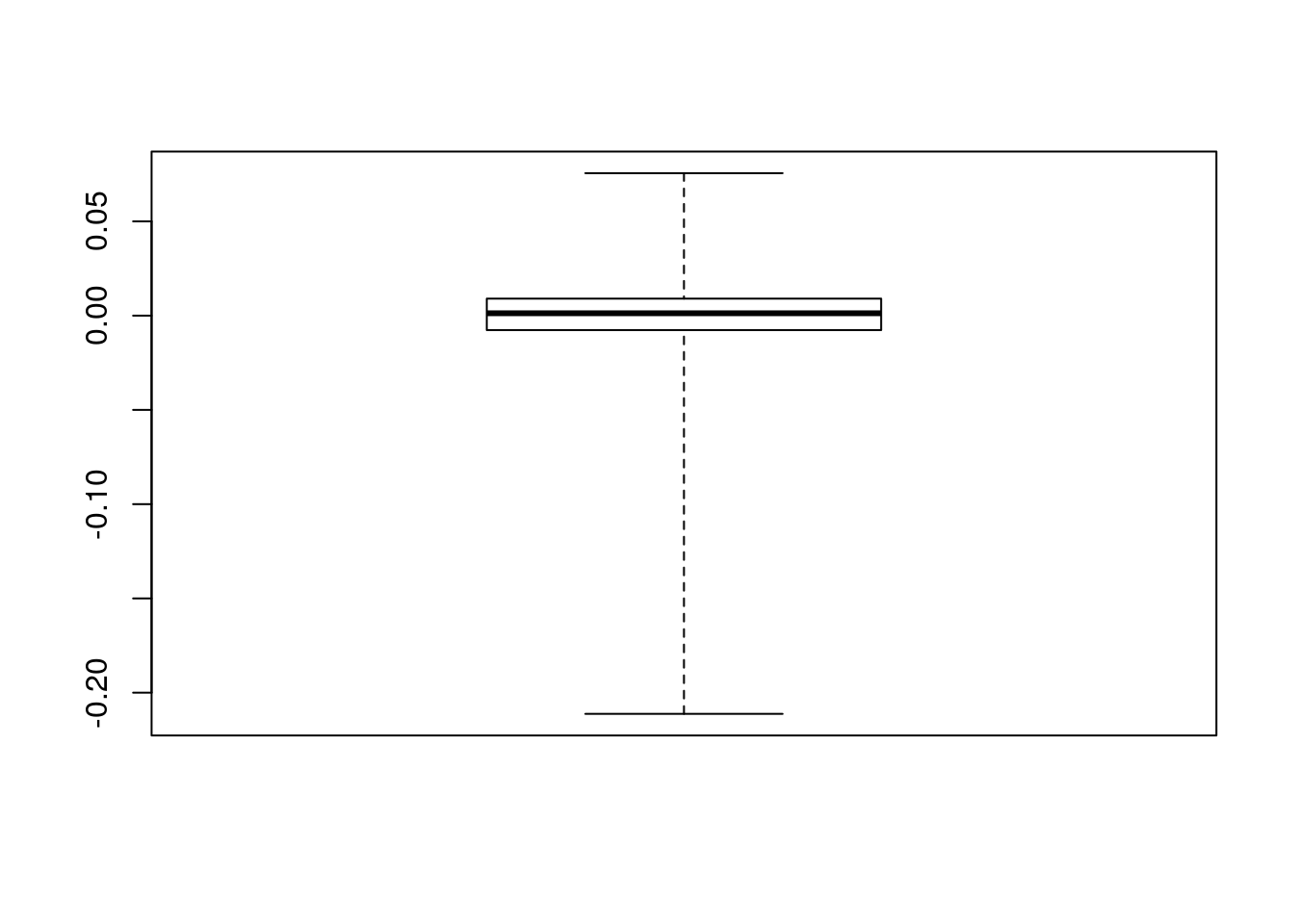

E’ anche possibile confrontare le diverse distribuzioni di rendimenti logaritmici applicando la funzione boxplot all’interno data frame:

boxplot(logret,
        col = rainbow(3))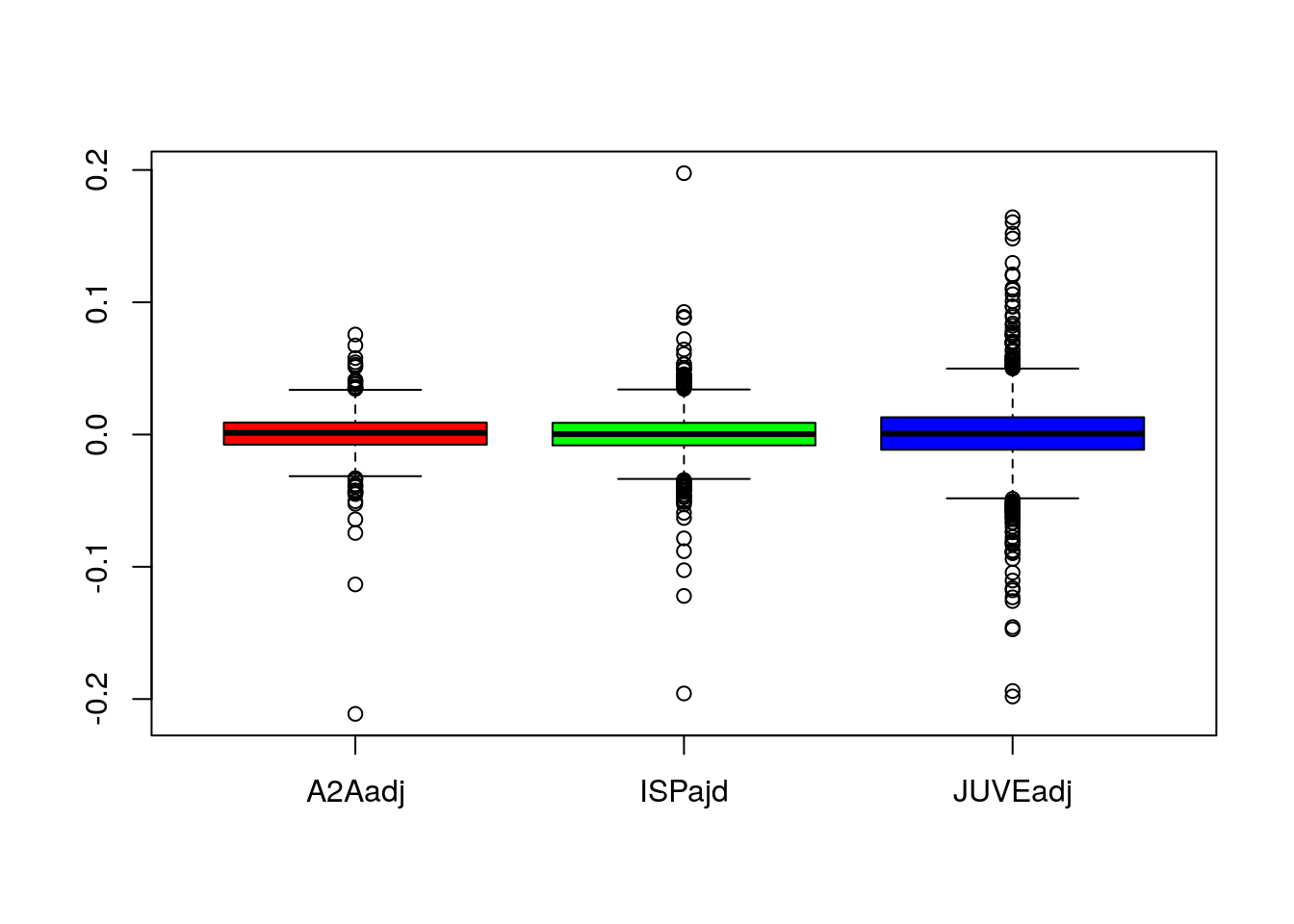

L’opzione rainbow(3) permette di scegliere 3 colori da una palette di colori denominata rainbow.

Si nota che i rendimenti di JUVE presentano una maggiore variabilità rispetto agli altri titoli. La distribuzione risulta inoltre caratterizzata da un numero più elevato di valori estremi (positivi e negativi). Per tutti i titoli la mediana è vicino a zero e i baffi risultano simmetrici rispetto alla scatola.

5.3 Istogramma

L’asimmetria è evidente anche dalla rappresentazione grafica della distribuzione tramite istogramma:

hist(logret$A2Aadj)
abline(v=mean(logret$A2Aadj),col="blue")
abline(v=median(logret$A2Aadj),col="red")
abline(v=quantile(logret$A2Aadj, 0.9),col="violet")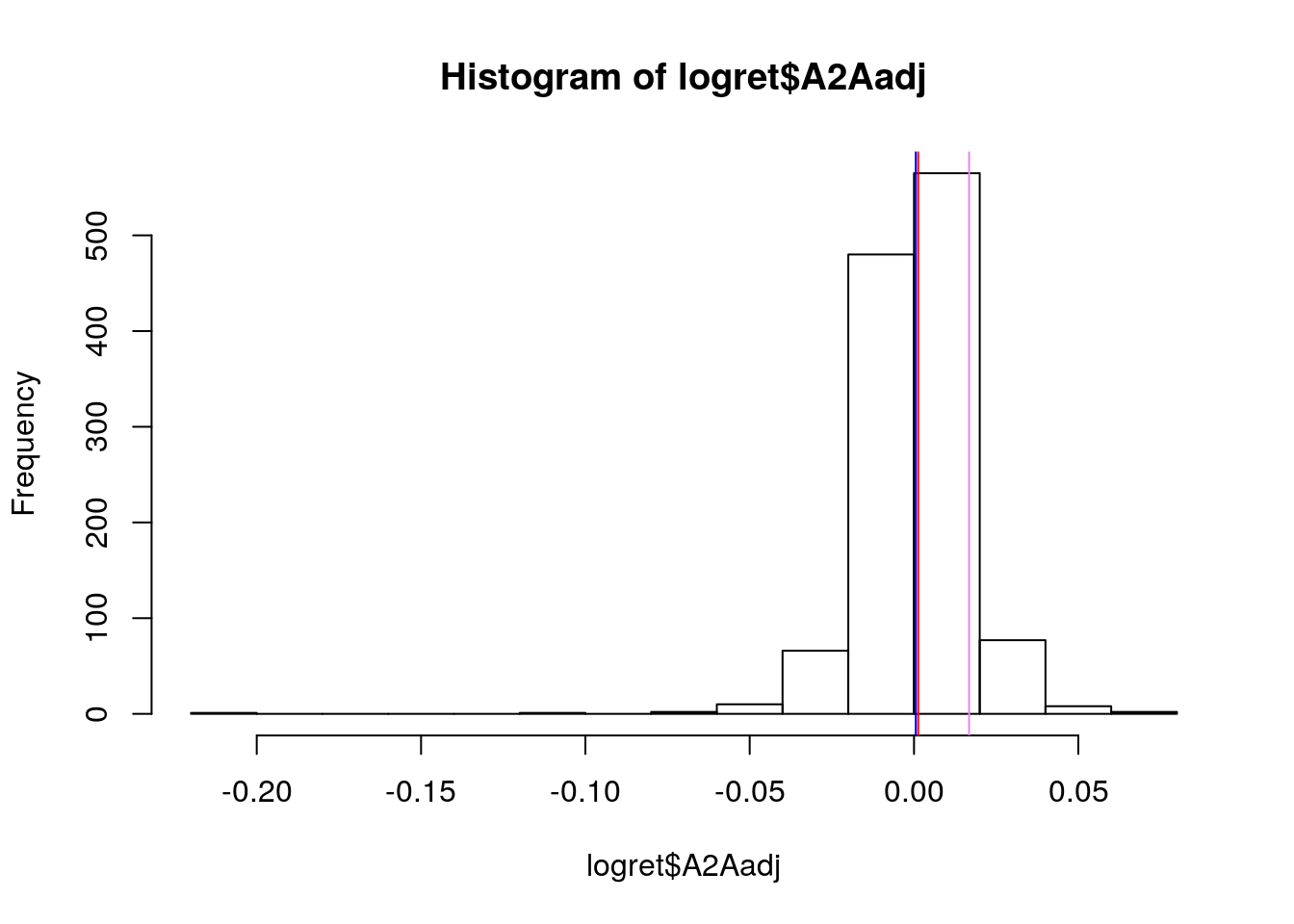

L’istogramma riporta sull’asse delle x i valori dei rendimenti in classi e sull’asse delle y le corrispondente frequenze (i.e. numero di giorni). La funzione abline è utilizzata qui per aggiungere 3 linee verticali costanti in corrispondenza della media, della mediana e del novantesimo quantile della distribuzione. In particolare,

quantile(logret$A2Aadj, 0.9)

##        90% 
## 0.01675133

rappresenta il valore dei rendimenti logaritmici che divide in due la distribuzione, con 90% dei dati a sinistra e 10% a destra.

Per ottenere i valori con cui è costruito l’istogramma (estremi delle classi e relative frequenze) si può usare:

hist(logret$A2Aadj, plot = FALSE)

## $breaks
##  [1] -0.22 -0.20 -0.18 -0.16 -0.14 -0.12 -0.10 -0.08 -0.06 -0.04 -0.02  0.00
## [13]  0.02  0.04  0.06  0.08
## 
## $counts
##  [1]   1   0   0   0   0   1   0   2  10  66 480 565  77   8   2
## 
## $density
##  [1]  0.04125413  0.00000000  0.00000000  0.00000000  0.00000000  0.04125413
##  [7]  0.00000000  0.08250825  0.41254125  2.72277228 19.80198020 23.30858086
## [13]  3.17656766  0.33003300  0.08250825
## 
## $mids
##  [1] -0.21 -0.19 -0.17 -0.15 -0.13 -0.11 -0.09 -0.07 -0.05 -0.03 -0.01  0.01
## [13]  0.03  0.05  0.07
## 
## $xname
## [1] "logret$A2Aadj"
## 
## $equidist
## [1] TRUE
## 
## attr(,"class")
## [1] "histogram"

E’ anche possibile cambiare il numero di classi attraverso l’opzione breaks. Si può in particolare specificare un numero diverso di classi della stessa ampiezza (ad esempio 3):

hist(logret$A2Aadj, breaks = 3)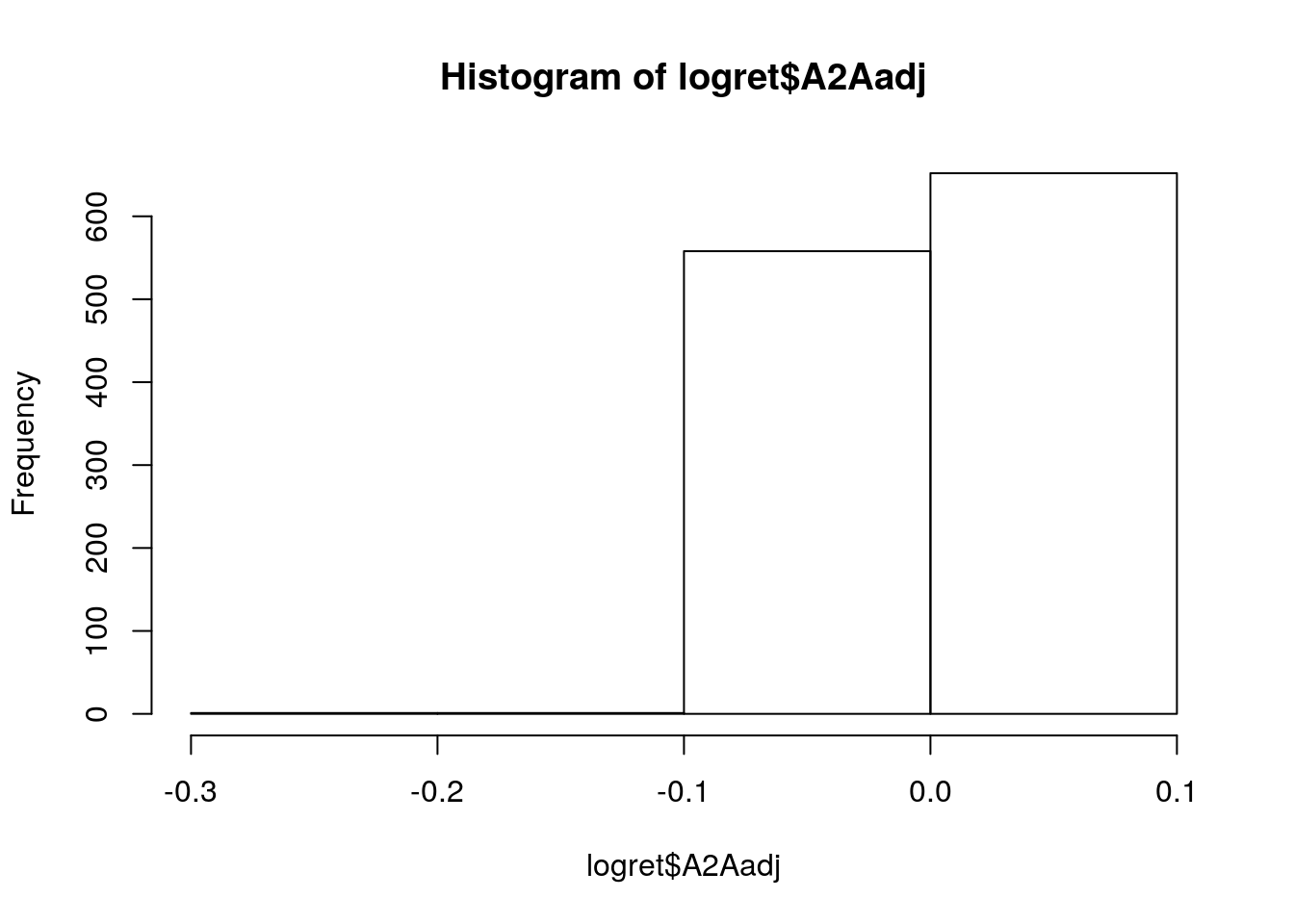

In particolare, specificando un numero intero positivo la funzione hist calcolerà poi il numero ottimale di classi più vicino a quanto specificato (per questo motivo può succedere che il numero di classi nel grafico sia leggermento diverso rispetto a quanto specificato).

In alternativa è possibile specificare a mano gli estremi delle classi prescelte (ad esempio \([-0.25,0.05]\), \((0.05,0]\), \((0, 0.03]\). \((0.03, max]\)):

hist(logret$A2Aadj,
     breaks = c(-0.25, 0.05, 0, 0.03, max(logret$A2Aadj)))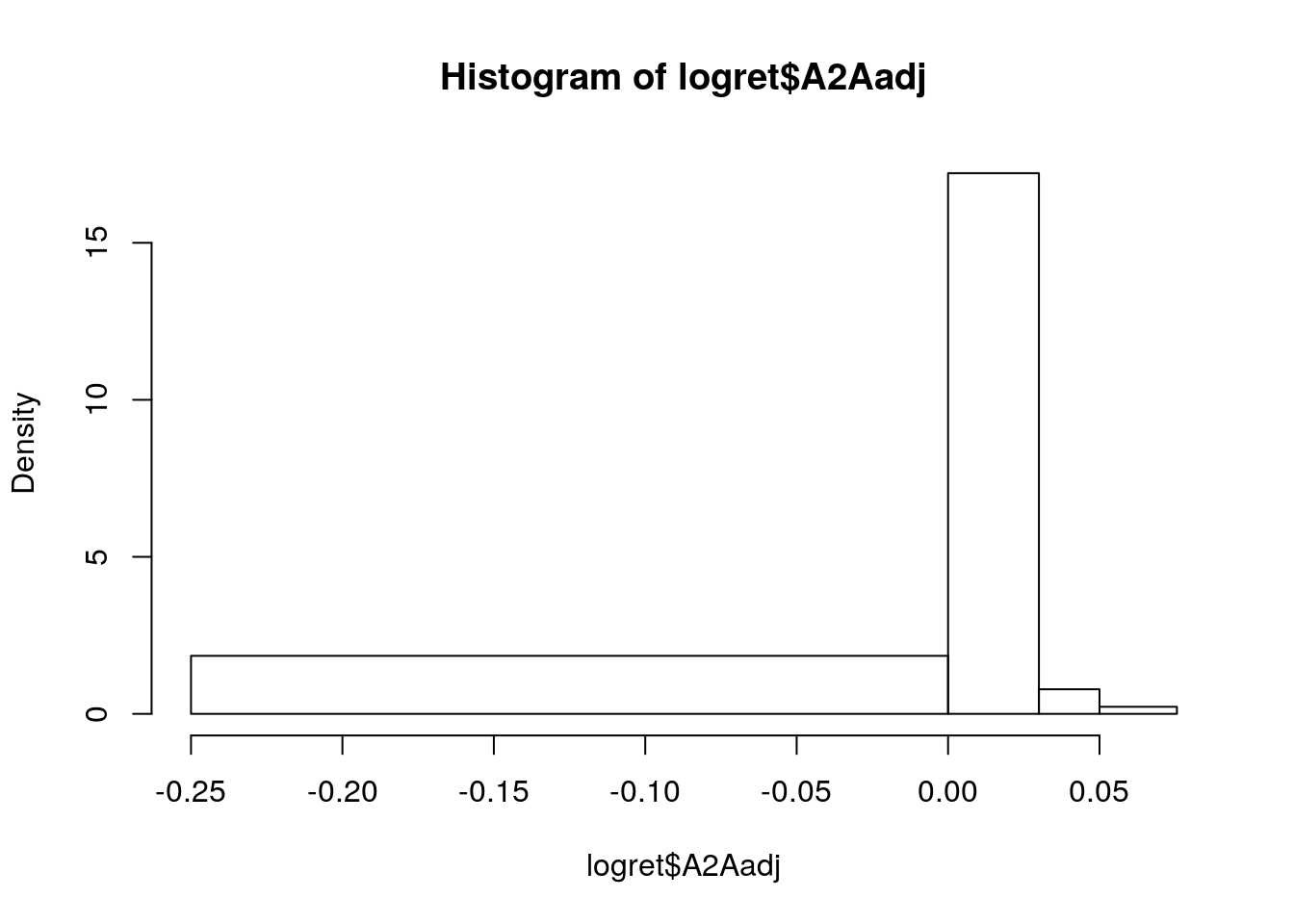

In questo caso sull’asse delle y è riportata la Density (invece della Frequency) data dal rapporto tra la frequenza relativa (Frequency/1212) e l’ampiezza di ogni classe. In questo caso l’altezza delle barre tiene conto dell’ampiezza di classe; inoltre l’area di tutte le barre è pari a 1.

5.4 KDE

Il grafico della stima kernel della densità (KDE) si può ottenere usando le funzioni plot e density:

plot(density(logret$A2Aadj))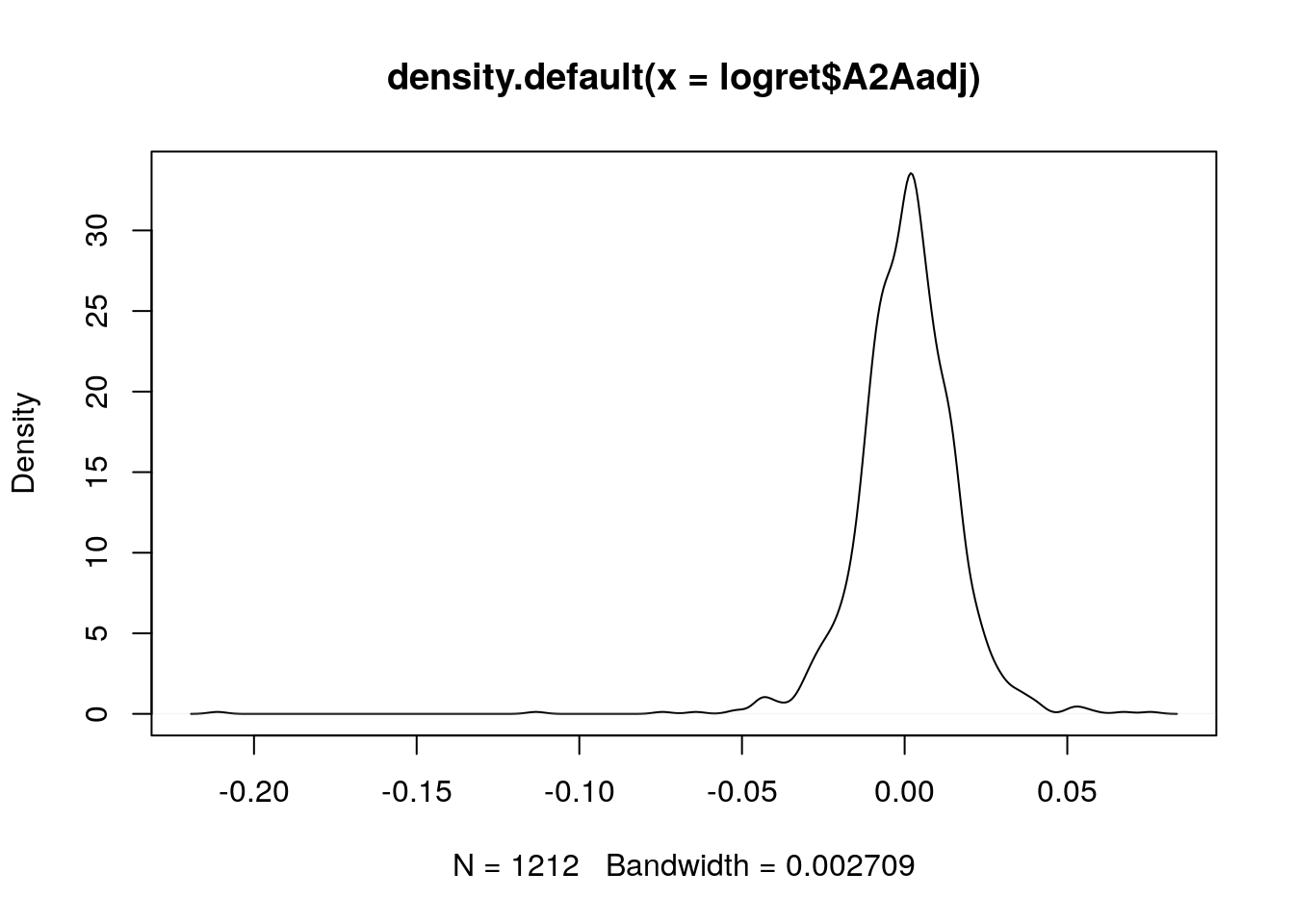

Anche in questo caso, come già emerso dall’istogramma, si nota una coda lunga a sinistra.

Si noti che R di default sceglie il miglior valore per l’ampiezza di banda (bandwidth, riportato in basso nel grafico). Con l’obiettivo di studiare l’effetto dell’ampiezza di banda sul grafico finale della KDE, possiamo ad esempio raddopiarne il valore utilizzando l’opzione adjust:

# Raddoppio il parametro di bandwidth
plot(density(logret$A2Aadj,adjust = 2))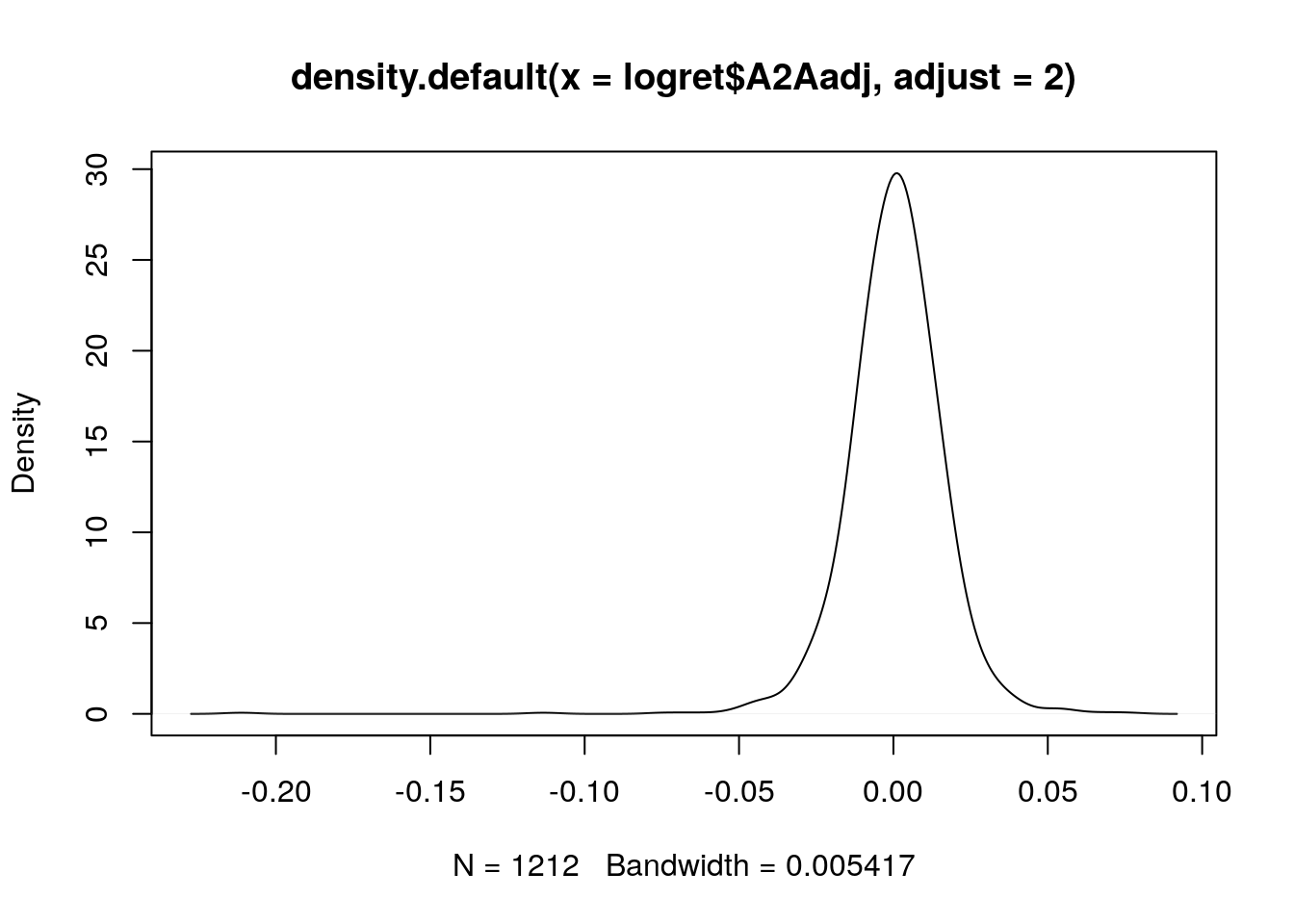

La costante moltiplicativa definita con adjust viene applicata al valore dell’ampiezza di banda scelta automaticamente da R. Quando l’ampiezza di banda raddoppia la curva è più liscia. Se invece l’ampiezza viene dimezzata

plot(density(logret$A2Aadj,adjust=0.5))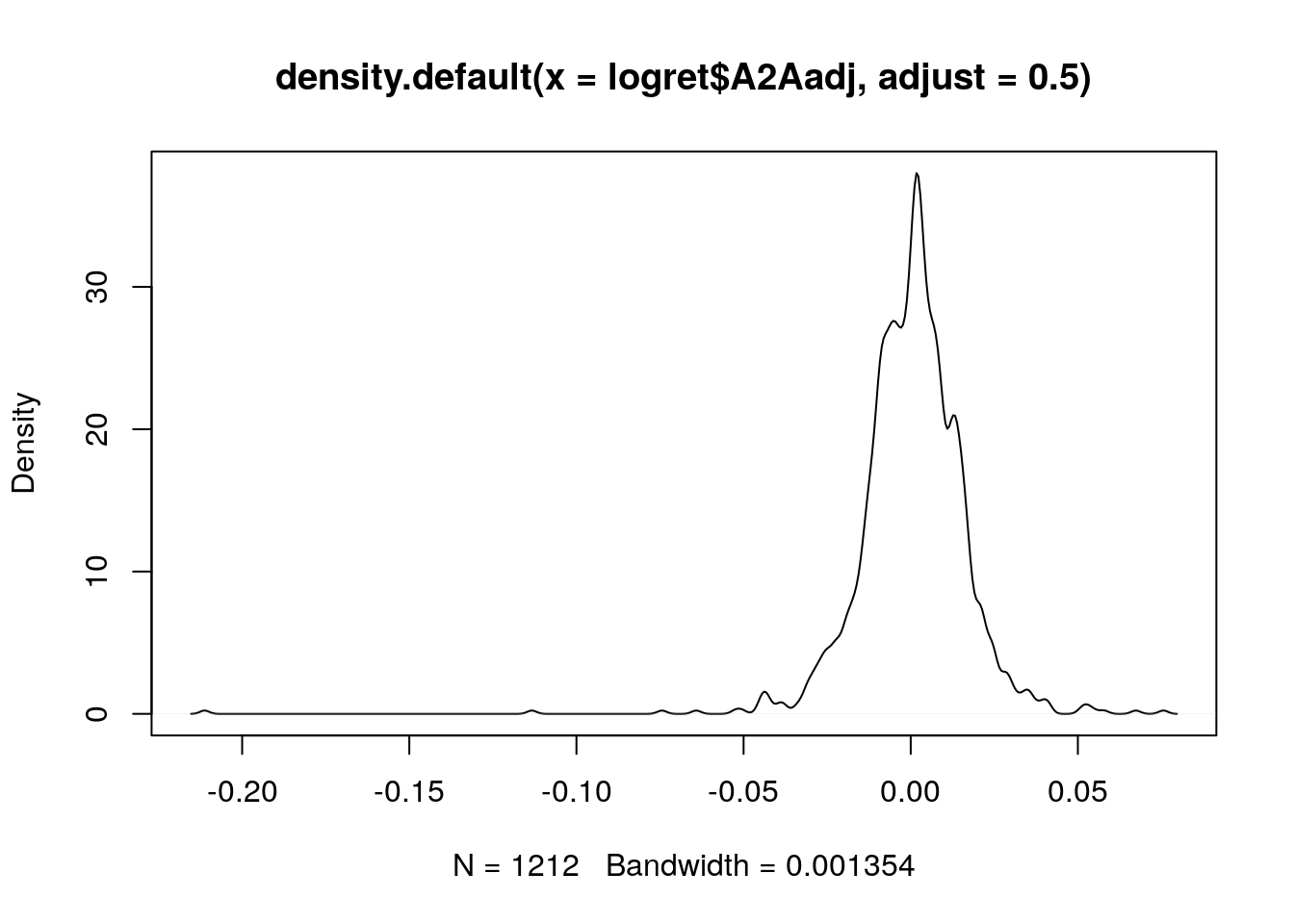

la KDE finale mostra più dettagli ed è meno liscia (più variabile).

E’ anche possibile mostrare insieme l’istogramma e la linea della KDE:

hist(logret$A2Aadj,
     freq = F, ylim = c(0,35))
lines(density(logret$A2Aadj))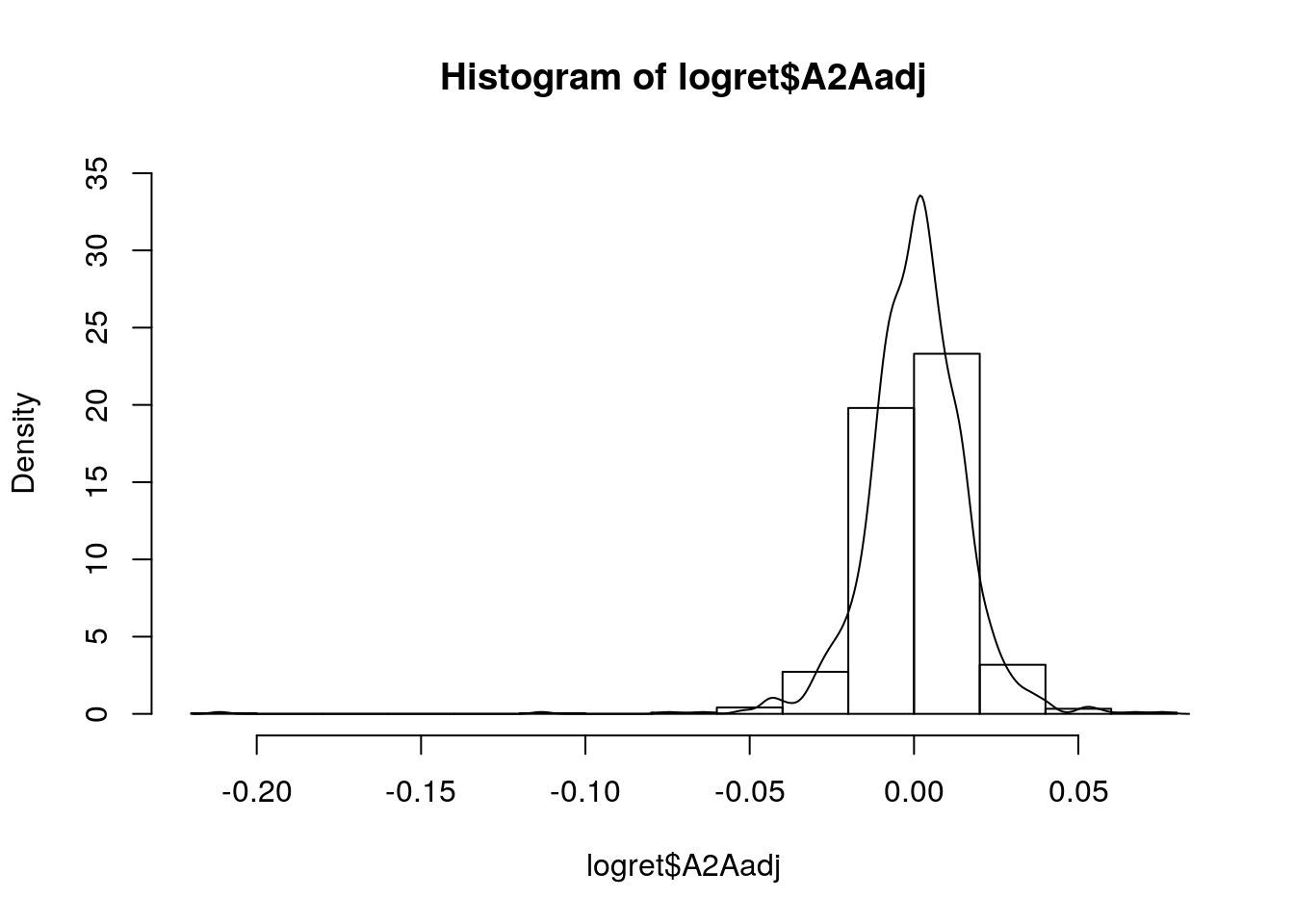

L’argomento freq=F serve per poter rappresentare sull’asse delle y le densità di frequenza invece delle frequenze assolute. In questo modo l’istogramma e la KDE sono comparabili e possono essere rappresentati insieme sullo stesso grafico.

5.5 Indice campionario di asimmetria e curtosi

La formula per il calcolo dell’indice di asimmetria (skewness) è data da \[ sk = \frac{\frac{\sum_{i=1}^n (x_i-\bar x)^3}{n}}{\sigma^3} \] dove \(\bar x\) rappresenta la media aritmetica e \(\sigma\) la standard deviation (scarto quadratico medio) dei dati. In R l’indice può essere calcolato come segue:

mean((logret$A2Aadj  - mean(logret$A2Aadj ))^3) / sd(logret$A2Aadj )^3

## [1] -2.206542

Essendo l’indice negativo, si può quindi concludere che la distribuzione dei rendimenti logaritmici è caratterizzata da asimmetria negativa (coda lunga a sinistra).

La curtosi campionaria può essere calcolata usando la seguente formula: \[ kur = \frac{\frac{\sum_{i=1}^n (x_i-\bar x)^4}{n}}{\sigma^4} \]

mean((logret$A2Aadj - mean(logret$A2Aadj))^4) / sd(logret$A2Aadj)^4

## [1] 31.29707

Essendo l’indice superiore a 3 si è in presenza di una distribuzione con code più pesanti rispetto alla normale e con picco più pronunciato.

5.6 Esercizi Lab 3

5.6.1 Esercizio 1

Il file AdjclosepricesLab3.csv contiene i prezzi giornalieri aggiustati per il periodo dal 01-09-2016 al 27-08-2020 per i seguenti indici: NASDAQ Composite (IXIC), Dow Jones Industrial Average (DJI), Gold (Gold) e CBOE Volatility Index (VIX). Fonte: Yahoo Finance.

Importare i dati in R e verificare la struttura dei dati.
Calcolare, usando il minor numero possibile di righe di codice, i rendimenti lordi per tutti le variabili. Creare un nuovo data frame che contiene i rendimenti lordi. Calcolare il rendimento lordo medio per ogni variabile.
Rappresentare graficamente le serie storiche dei rendimenti lordi. Commentare il grafico.
Rappresentare graficamente la distribuzione marginale dei dati utilizzando i boxplot (in una singola finestra). Commentare il grafico.
Rifare il grafico del punto precedente dopo aver eliminato i dati relativi a VIX. Cosa si osserva?
Rappresentare nello stesso grafico la KDE e l’istogramma per i rendimenti di IXIC. Commentare il grafico.
Rappresentare nelo stesso grafico le 4 KDE. Commentare il grafico.
Calcolare per tutte le variabili l’indice di skewness e curtosi. Commentare i valori.