7.1 Guiding Principles in the Search for Interactions
First, expert knowledge of the system under study is critical for guiding the process of selecting interaction terms. Neter et al. (1996) recognize the importance of expert knowledge and recommend:
“It is therefore desirable to identify in advance, whenever possible, those interactions that are most likely to influence the response variable in important ways.”
Therefore, expert-selected interactions should be the first to be explored. In many situations, though, expert guidance may not be accessible or the area of research may be so new that there is no a priori knowledge to shepherd interaction term selection. When placed in a situation like this, sound guiding principles are needed that will lead to a reasonable selection of interactions.
One field that has tackled this problem is statistical experimental design. Experimental design employs principles of control, randomization, and replication to construct a framework for gathering evidence to establish causal relationships between independent factors (i.e., predictors) and a dependent response. The process begins by determining the population (or units) of interest, the factors that will be systematically changed, and the specific ranges of the factors to be studied. Specific types of experimental designs, called screening designs, generate information in a structured way so that enough data are collected to identify the important factors and interactions among two or more factors. Figure 7.4 conceptually illustrates an experiment with three factors.
While data from an experiment has the ability to estimate all possible interactions among factors, it is unlikely that each of the interactions explain a significant amount of the variation in the measured response. That is, many of these terms are not predictive of the response. It is more likely, however, that only a few of the interactions, if any, are plausible or capture significant amounts of response variation. The challenge in this setting is figuring out which of the many possible interactions are truly important. Wu and Hamada (2011) provide a framework for addressing the challenge of identifying significant interactions. This framework is built on concepts of interaction hierarchy, effect sparsity, and effect heredity. These concepts have been shown to work effectively at identifying the most relevant effects for data generated by an experimental design. Furthermore, this framework can be extended to the predictive modeling framework.
The interaction hierarchy principle states that the higher degree of the interaction, the less likely the interaction will explain variation in the response. Therefore, pairwise interactions should be the first set of interactions to search for a relationship with the response, then three-way interactions, then four-way interactions, and so on. A pictorial diagram of the effect hierarchy can be seen in Figure 7.4 for data that has three factors where the size of the nodes represents the likelihood that a term is predictive of the response. Neter et al. (1996) advises caution for including three-way interactions and beyond since these higher-order terms rarely, if ever, capture a significant amount of response variation and are almost impossible to interpret.
The second principle, effect sparsity, contends that only a fraction of the possible effects truly explain a significant amount of response variation (Figure 7.4). Therefore, the approach could greatly pare down the possible main effects and interactions terms when searching for terms that optimize the predictive ability of a model.
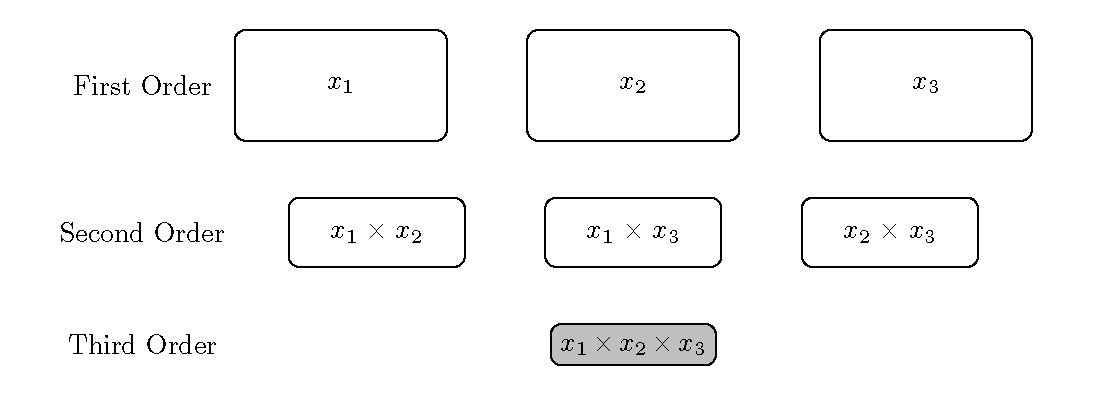
Figure 7.4: An illustration of a set of first-, second-, and third-order terms from a full factorial experiment. The terms are sized based on the interaction hierarchy principle. The three-way interaction term is greyed out due to the effect sparsity principle.
The effect heredity principle is based on principles of genetic heredity and asserts that interaction terms may only be considered if the ordered terms preceding the interaction are effective at explaining response variation. This principle has at least two possible implementations: strong heredity and weak heredity. The strong heredity implementation requires that for an interaction to be considered in a model, all lower-level preceding terms must explain a significant amount of response variation. That is, only the \(x_1 \times x_2\) interaction would be considered if the main effect of \(x_1\) and the main effect of \(x_2\) each explain a significant amount of response variation66. But if only one of the factors is significant, then the interaction will not be considered. Weak heredity relaxes this requirement and would consider any possible interaction with the significant factor. Figure 7.5 illustrates the difference between strong heredity and weak heredity for a three-factor experiment. For this example, the \(x_1\) main effect was found to be predictive of the response. The weak heredity principle would explore the \(x_1 x_2\) and \(x_1 x_3\) interaction terms. However, the \(x_2 x_3\) interaction term would be excluded from investigation. The strong heredity principle would not consider any second-order terms in this example since only one main effect was found to be significant.
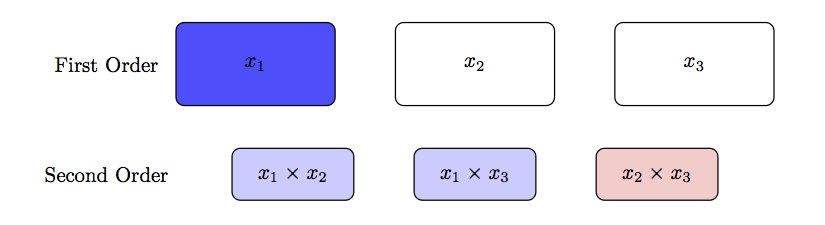
Figure 7.5: An illustration of the effect heredity principle for an example data set with three factors.
While these principles have been shown to be effective in the search for relevant and predictive terms to be included in a model, they are not always applicable. For example, complex higher-order interactions have been shown to occur in nature. Bairey, Kelsic, and Kishony (2016) showed that high-order interactions among species can impact ecosystem diversity. The human body is also a haven of complex chemical and biological interactions where multiple systems work together simultaneously to combat pathogens and to sustain life. These examples strengthen our point that the optimal approach to identifying important interaction terms will come from a combination of expert knowledge about the system being modeled as well as carefully thought-out search routines based on sound statistical principles.