5 ANÁLISIS MULTIVARIADO
Juan Manuel Solís
5.0.1 Análisis multivariado
5.0.1.1 Análisis de Componentes Principales
Intuición
Considere el siguiente modelo:
\[y = \alpha+\beta x\] ¿Qué representa la ecuación anterior? ¿Cuántas variables (dimensiones) están involucradas?
Ahora considere el siguiente modelo:
\[y = \alpha+\beta x+\epsilon\]
¿qué representa ahora la ecuación, habiendo añadido \(\epsilon\)? Comente en términos de rotación de ejes.
Considere el siguiente modelo:
\[z = \alpha+\beta x+\gamma y+\epsilon\]
¿qué representa ahora la ecuación, habiendo añadido una nueva dimensión? Comente en términos de rotación de ejes.
Finalmente, incorpore la última dimensión dentro de las variables predictoras (junto con su respectivo coeficiente). Todas juntas serán predictoras de una nueva variable sintética llamada componente principal (CP), que no es otra cosa que un eje rotado de forma tal que se ha maximizado la varianza de las proyecciones de cada valor en el CP.
El objetivo del método consiste en reducir la dimensionalidad original de un set de datos preservando las relaciones entre las variables incluidas. Éste método se utiliza con fines exploratorios, para observar posibles relaciones de proximidad entre dichas variables.
Ejemplo
El set de datos “datos2.csv” contiene los valores simulados de variables físico-químicas de 8 ambientes: 4 sitios muestreados en dos momentos cada uno. Importe el set de datos y luego realice un ACP analítico y gráfico, utilizando la librería FactoMiner.
- Importación de datos
- Dado que el ACP se debe realiza únicamente con variables numéricas, seleccionaremos únicamente las columnas numéricas. Es posible nombrar las filas con el nombre de los sitios, a fin de identificarlas. Finalmente, dado que las variables tienen diferentes unidades de medida, se realiza una estandarización de las mismas.
# De-seleccionamos la primer columna de datos2
datos2.num = datos2[,-1]
# Renombrar filas con el nombre de sitios (opcional)
rownames(datos2.num) = datos2$Sitio
# Estandarización
datos2.num.st = scale(datos2.num)- ACP (previa instalación del paquete “FactoMiner”) y gráfico (previa instalación de “factoextra”)
##
## Call:
## PCA(X = datos2.num.st, ncp = 2, graph = FALSE)
##
##
## Eigenvalues
## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7
## Variance 3.512 2.348 0.769 0.321 0.049 0.002 0.000
## % of var. 50.175 33.541 10.983 4.585 0.694 0.021 0.000
## Cumulative % of var. 50.175 83.716 94.700 99.285 99.979 100.000 100.000
##
## Individuals
## Dist Dim.1 ctr cos2 Dim.2 ctr cos2
## R1S | 2.015 | -0.251 0.225 0.016 | 1.835 17.937 0.830 |
## R1L | 3.580 | -3.001 32.056 0.703 | -1.697 15.336 0.225 |
## R2S | 2.073 | -1.150 4.705 0.308 | 1.621 13.995 0.612 |
## R2L | 2.596 | -1.810 11.657 0.486 | 1.478 11.634 0.324 |
## R3S | 2.691 | 1.877 12.543 0.487 | -0.434 1.001 0.026 |
## R3L | 1.993 | 0.449 0.718 0.051 | -1.920 19.631 0.928 |
## R4S | 3.533 | 3.199 36.418 0.820 | 0.872 4.049 0.061 |
## R4L | 2.096 | 0.687 1.679 0.107 | -1.756 16.417 0.702 |
##
## Variables
## Dim.1 ctr cos2 Dim.2 ctr cos2
## T | 0.606 10.462 0.367 | 0.658 18.459 0.433 |
## pH | 0.816 18.977 0.667 | 0.362 5.587 0.131 |
## NaCl | -0.846 20.364 0.715 | 0.516 11.338 0.266 |
## SDT | -0.662 12.471 0.438 | 0.720 22.059 0.518 |
## CE | -0.855 20.803 0.731 | 0.498 10.548 0.248 |
## O2 | 0.581 9.608 0.337 | 0.783 26.136 0.614 |
## caudal | 0.507 7.315 0.257 | 0.371 5.873 0.138 |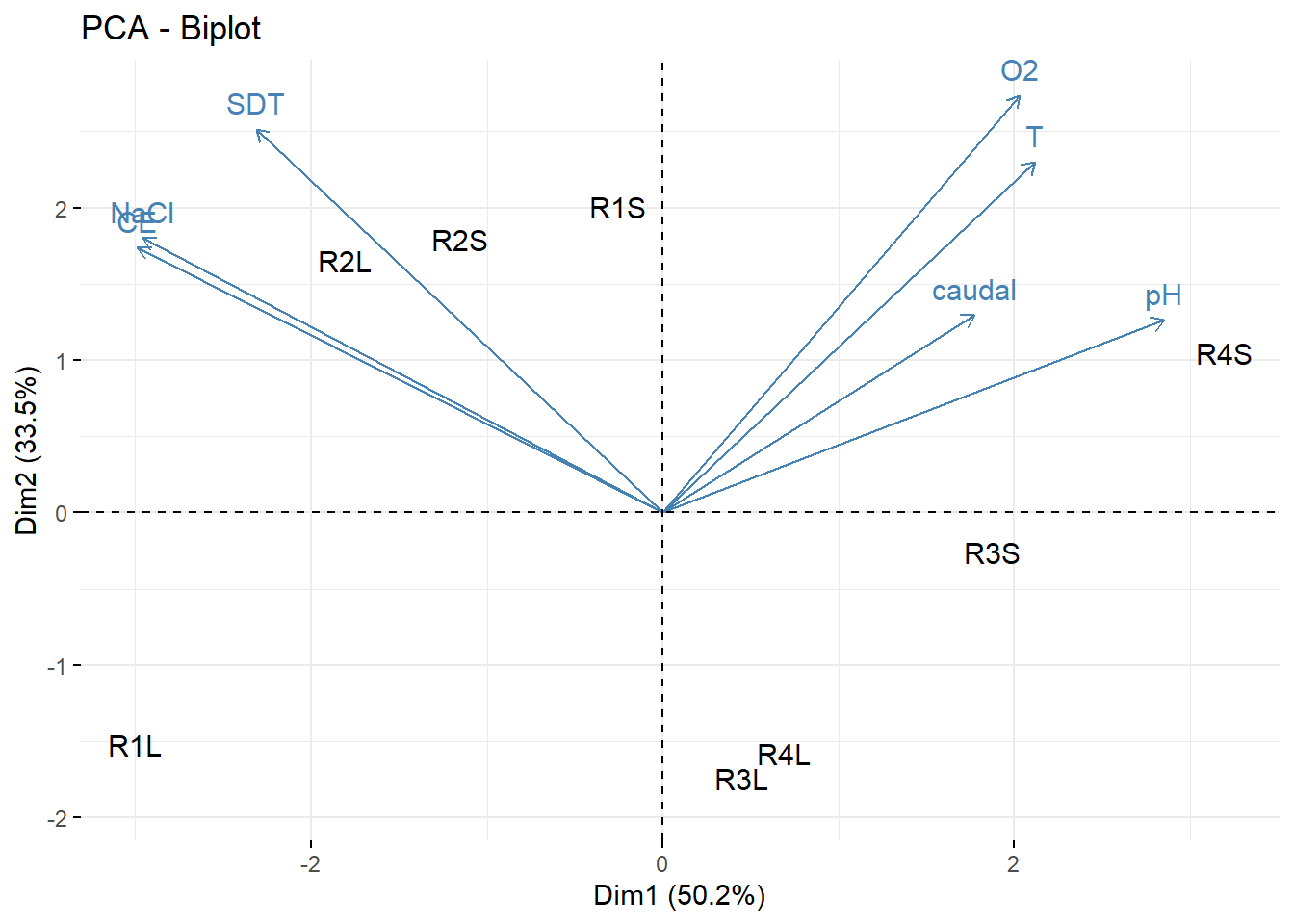
¿Qué representan los vectores azules? ¿Qué implica que el conjunto de variables NaCl, CE, SDT forme un “ángulo recto” con respecto al conjunto a las variables O2, T, caudal y pH?
5.0.2 ASPT (average score per taxon)
Se define ASPT como el promedio de las puntuaciones de tolerancia (BMWP) de todas las familias de macroinvertebrados encontradas y oscila entre 0 y 10.
library(MacroZooBenthosWaterA)
Site = c("S1", "S2", "S2")
Family = c("Capniidae", "Aeshnidae", "Chloroperlidae")
test = data.frame(Family, Site)
calculate_ASPT(test, Site = "Site")
library(metrix)
data("example_data")
View(example_data)
bmwp_ind(example_data)
## Puntuaciones asignadas a los diferentes taxones de macroinvertebrados acuáticos para la obtención del índice BMWP (modificado de Alba-Tercedor y Sánchez-Ortega, 1988; Domínguez y Fernández, 1998). Actualizados con datos 2019.
puntuaciones = data.frame(
TAXON = c(
"Leptophlebilidae",
"Peridae",
"Gripopterygidae",
"Corydalidae",
"Libelluilidae",
"Leptoceridae",
"Psephenidae",
"Crambidae",
"Leptohyphidae",
"Glossosomatidae",
"Odontoceridae",
"Philopotamidae",
"Chironomidae.Podonominae",
"Chironomidae.Orthocladinae",
"Odonata",
"Rhyacophilidae",
"Limnephilidae",
"Hidroptylidae",
"Unionidae",
"Lymnaeidae",
"Oligoneuriidae",
"Caenidae",
"Elmidae",
"Staphylinidae",
"Hydropsychidae",
"Tipulidae",
"Simulidae",
"Mycetopodidae",
"Baetidae",
"Haliplidae",
"Tabanidae",
"Dixidae",
"Stratiomyridae",
"Empididae",
"Dolichopodidae",
"Ceratopogonidae",
"Psychodidae",
"Palaemonidae",
"Aeglidae",
"Hydracarina",
"Dytiscidae",
"Hydrophilidae",
"Physidae",
"Planorbidae",
"Ancylinae",
"Trichodactylidae",
"Ostracoda",
"Copepoda",
"Hemiptera",
"Hirudinea",
"Culicidae",
"Ephydridae",
"Ampullariidae",
"Oligochaeta",
"Chironomidae"
),
PUNTAJE = c(
rep(10, 7),
9,
rep(8,7),
rep(7,2),
rep(6,3),
rep(5,8),
rep(4,12),
rep(3,10),
rep(2,3),
rep(1,2)
)
)
#datos3 = read.csv2(file.choose(),header = TRUE)
# ASPT POR SITIO: EJEMPLO PARA SITIO 1
n.sitios = ncol(datos3)
BMWP.1 = sum(puntuaciones$PUNTAJE[match(puntuaciones$TAXON,datos3[[1]])],na.rm = TRUE)
n.taxa.1 = length(unique(datos3$S1))
(ASPT.1 = BMWP.1 / n.taxa.1)
# ASPT PARA TODOS LOS SITIOS
(BMWP = sapply(c(1:ncol(datos3)),function(i){
sum(puntuaciones$PUNTAJE[match(puntuaciones$TAXON,datos3[[i]])],na.rm = TRUE)
}))
(n.taxa = sapply(c(1:ncol(datos3)), function(i){
length(unique(datos3[[i]]))
}))
(ASPT = BMWP / n.taxa)