Bab 4 Pemodelan

library(forecast)
library(TSA)

4.1 Analisis intervensi untuk data mingguan

4.1.1 COVID

Secara umum metode pemulusan cukup buruk dalam meramal harga minyak saat COVID dan perang Rusia-Ukraina. Oleh karena itu, coba ambil data saat COVID terlebih dahulu. Jika dilihat dari tabel di bawah, harga minyak mulai turun pada minggu kesembilan 2020 (28 Februari 2020), dan tetap turun. Oleh karena itu, ambil dua titik data awal dari penurunan tersebut (28 Februari dan 06 Februari) untuk menandakan intervensi tersebut, lalu coba ramal titik-titik selanjutnya.

knitr::kable(weeklyCrude[160:170])

Week	Date	Close	Dist	6DW	8DW	2017 - Siklik	Awal 2018 - harga naik	Akhir 2018 - harga turun	Pra-COVID	COVID	Pemulihan	Vaksin, Varian	2022
2020-W04	2020-01-24	54.19	7 days	0	0	FALSE	FALSE	FALSE	TRUE	FALSE	FALSE	Lainnya	Lainnya
2020-W05	2020-01-31	51.56	7 days	0	0	FALSE	FALSE	FALSE	TRUE	FALSE	FALSE	Lainnya	Lainnya
2020-W06	2020-02-07	50.32	7 days	0	0	FALSE	FALSE	FALSE	FALSE	TRUE	FALSE	Lainnya	Lainnya
2020-W07	2020-02-14	52.05	7 days	0	0	FALSE	FALSE	FALSE	FALSE	TRUE	FALSE	Lainnya	Lainnya
2020-W08	2020-02-21	53.38	7 days	0	0	FALSE	FALSE	FALSE	FALSE	TRUE	FALSE	Lainnya	Lainnya
2020-W09	2020-02-28	44.76	7 days	0	0	FALSE	FALSE	FALSE	FALSE	TRUE	FALSE	Lainnya	Lainnya
2020-W10	2020-03-06	41.28	7 days	0	0	FALSE	FALSE	FALSE	FALSE	TRUE	FALSE	Lainnya	Lainnya
2020-W11	2020-03-13	31.73	7 days	0	0	FALSE	FALSE	FALSE	FALSE	TRUE	FALSE	Lainnya	Lainnya
2020-W12	2020-03-20	22.43	7 days	0	0	FALSE	FALSE	FALSE	FALSE	TRUE	FALSE	Lainnya	Lainnya
2020-W13	2020-03-27	21.51	7 days	0	0	FALSE	FALSE	FALSE	FALSE	TRUE	FALSE	Lainnya	Lainnya
2020-W14	2020-04-03	28.34	7 days	0	0	FALSE	FALSE	FALSE	FALSE	TRUE	FALSE	Lainnya	Lainnya

Ambil semua data sampai 6 Maret 2020 (observasi ke-166) sebagai data latih. Titik intervensi COVID yang diambil adalah 28 Februari (observasi ke-166)

wcrude.covid<-subset(weeklyCrude, Date<=as.Date("2020-04-13"))
wcrude.train<-subset(wcrude.covid, Date<=as.Date("2020-03-06"))

Model Arima terbaik adalah $ARIMA(1,1,1)$ - note, ini cari sendiri aja

covArima<-Arima(wcrude.train$Close,
                order=c(1,1,1),
                method="ML")

Diagnostik model sebenarnya cukup oke:

checkresiduals(covArima)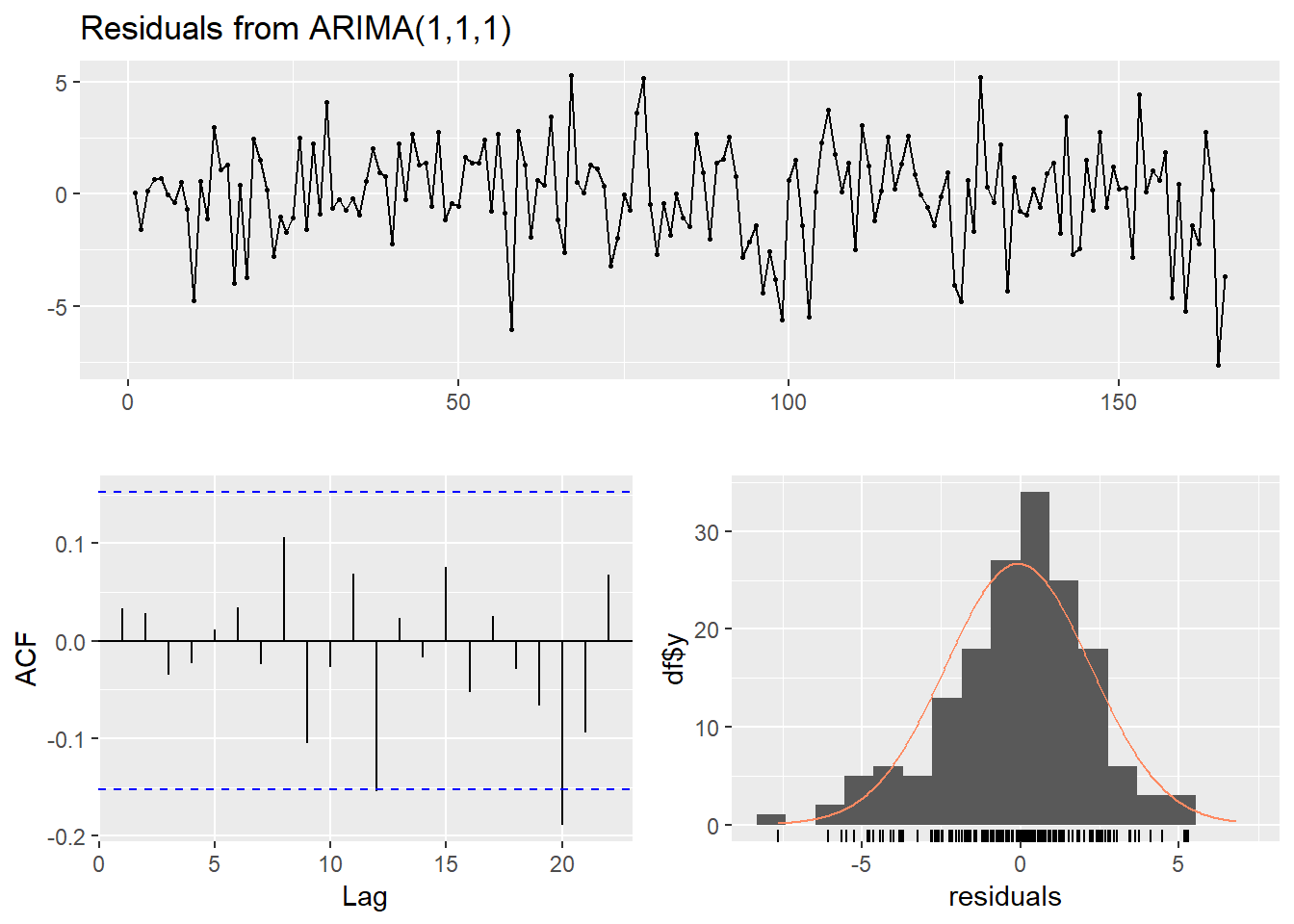

## 
##  Ljung-Box test
## 
## data:  Residuals from ARIMA(1,1,1)
## Q* = 5.0142, df = 8, p-value = 0.7561
## 
## Model df: 2.   Total lags used: 10

Tapi prediksi model tidak sesuai dengan apa yang akan terjadi. Bandingkan prediksi untuk 2 minggu saja:

forcdef<-forecast(covArima,5)


wcrude.covid[,`:=`("fitted.def"=c(forcdef$fitted,rep(NA,5)),  
                  "predicted.def"=c(rep(NA,166),forcdef$mean))]


ggplot(aes(x=Date,y=Close),data=wcrude.covid[150:168])+
  geom_point(size=3, alpha=0.3, color="gray")+
  geom_line(aes(y=fitted.def,color="Fitted"))+
  geom_line(aes(y=predicted.def,color="Prediksi"))+
  geom_point(aes(y=predicted.def,color="Prediksi"), size=3,alpha=0.3)+
  scale_color_manual(name='Prediksi ARIMA',
                     breaks=c('Fitted', 'Prediksi'),
                     values=c('Fitted'='black', 'Prediksi'='#DB0000'))+
    theme_minimal()

## Warning: Removed 2 row(s) containing missing values (geom_path).

## Warning: Removed 17 row(s) containing missing values (geom_path).

## Warning: Removed 17 rows containing missing values (geom_point).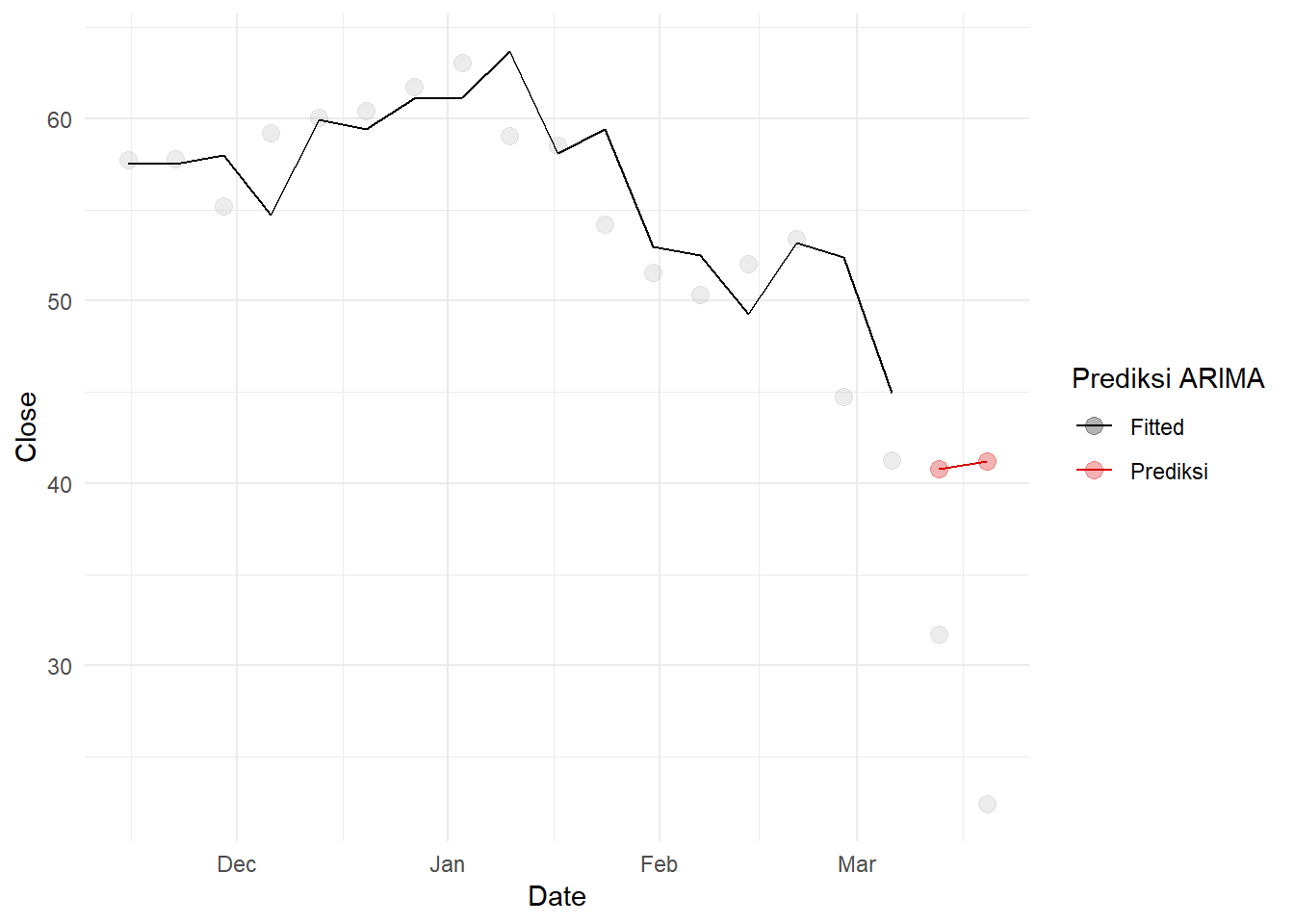

Tentu prediksi tersebut cukup buruk. Lakukan pemodelan ARIMAX dengan sebuah fungsi transfer. Pada dasarnya kita akan membuat suatu peubah dummy pada 28 Februari 2020 untuk menandakan reaksi pasar terhadap COVID. Lalu akan dimodelkan dengan suatu fungsi:

$$m_t=\frac{(\theta_0+\theta_1B+...+\theta_{q-1}B^{q-1})}{(1-\phi_1 B -...-\phi_p B^p)} P_t$$

Dengan: $$\begin{aligned} m_t&=\text{ Pengaruh intervensi (COVID) di waktu ke-t}\\ Z_t&=\begin{cases} 1, & t=165 \text{ (28 Februari 2020, mulai COVID)}\\ 0, &\text{lainnya}\\ \end{cases}\\ \end{aligned}$$

Salah satu model paling sederhana adalah dengan $AR(1)$ - pada dasarnya model intervensi akan menjadi:

$$\begin{aligned} m_t&=\frac{\theta_0}{(1-\phi_1 B)} P_t\\ (1-\phi_1B)m_t&=\theta_0P_t\\ m_t-\phi_1m_{t-1}&=\theta_0P_t\\ m_t&=\theta_0P_t+\phi_1m_{t-1} \end{aligned}$$

Saat $P_{t}=1$, tentu $P_{t-1}=0$, $m_{t-2}=0$ (intervensi belum memiliki efek). Oleh karena itu dapat dilihat bahwa di waktu intervensi ke-r:

$$\begin{aligned} m_r&=\theta_0\\ m_{r+1}&=\theta_0\cdot0+\phi_1m_{r}=\phi_1\theta_0\\ m_{r+2}&=\theta_0\cdot0+\phi_1m_{r+1}=\phi_1^2\theta_0\\ \end{aligned}$$

Dan seterusnya. Saat $\phi_1<0$, fungsi ini menandakan suatu efek yang lama-kelamaan mengalami decay. Coba modelkan fungsi yang ada dengan metode tersebut:

intvmod<-arimax(wcrude.train$Close, order=c(1,1,1),
       xtransf=data.frame(COVID=1*(seq(nrow(wcrude.train))==165)),
       transfer=list(c(1,0)))
intvmod

## 
## Call:
## arimax(x = wcrude.train$Close, order = c(1, 1, 1), xtransf = data.frame(COVID = 1 * 
##     (seq(nrow(wcrude.train)) == 165)), transfer = list(c(1, 0)))
## 
## Coefficients:
##           ar1     ma1  COVID-AR1  COVID-MA0
##       -0.8990  0.9625     1.5199    -7.9141
## s.e.   0.0594  0.0388     0.3160     2.2452
## 
## sigma^2 estimated as 4.819:  log likelihood = -363.99,  aic = 735.98

Terlihat bahwa AIC model dengan intervensi lebih baik

knitr::kable(
  cbind(c("Tanpa Intervensi","Intervensi"),
        c(covArima$aic,intvmod$aic)),
  col.names=c("Model","AIC")
)

Model	AIC
Tanpa Intervensi	748.606798472797
Intervensi	735.979604802578

Begitu juga akurasinya:

compAcc<-rbind(accuracy(covArima),accuracy(intvmod))
rownames(compAcc)<-c("Tanpa Intervensi","Intervensi")

knitr::kable(
        compAcc,
  row.names=T,
  digits =4
)

	ME	RMSE	MAE	MPE	MAPE	MASE	ACF1
Tanpa Intervensi	-0.0744	2.2868	1.7466	-0.2395	3.1249	0.9709	0.0328
Intervensi	-0.0054	2.1886	1.6826	-0.0829	2.9732	0.9354	0.0287

Diagnostik residual juga oke:

checkresiduals(intvmod)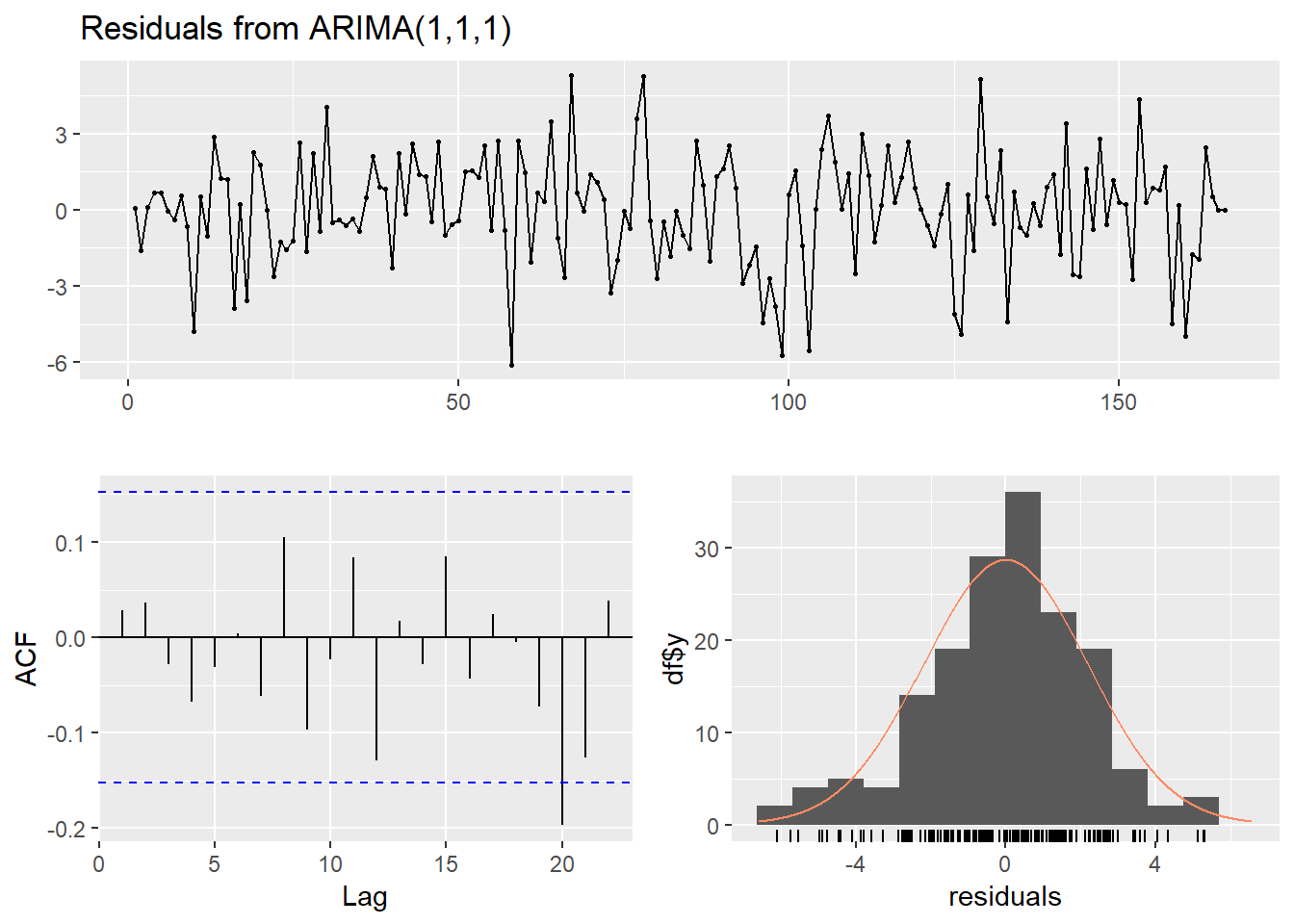

## 
##  Ljung-Box test
## 
## data:  Residuals from ARIMA(1,1,1)
## Q* = 5.8303, df = 6, p-value = 0.4425
## 
## Model df: 4.   Total lags used: 10

Nampaknya di term intervensi $AR(1)$ merupakan model terbaik:

arimax(wcrude.train$Close, order=c(1,1,1),
       xtransf=data.frame(COVID=1*(seq(nrow(wcrude.train))==165)),
       transfer=list(c(0,0)))

## 
## Call:
## arimax(x = wcrude.train$Close, order = c(1, 1, 1), xtransf = data.frame(COVID = 1 * 
##     (seq(nrow(wcrude.train)) == 165)), transfer = list(c(0, 0)))
## 
## Coefficients:
##           ar1     ma1  COVID-MA0
##       -0.4994  0.6033    -2.5717
## s.e.   0.5154  0.4752     1.5625
## 
## sigma^2 estimated as 5.273:  log likelihood = -371.3,  aic = 748.6

AIC model intervensi $MA(0)$ lebih tinggi. Model intervensi lain tidak dapat diduga dengan informasi yang ada:

arimax(wcrude.train$Close, order=c(1,1,1),
       xtransf=data.frame(COVID=1*(seq(nrow(wcrude.train))==165)),
       transfer=list(c(0,1)))

## Error in optim(init[mask], armaCSS, method = "BFGS", hessian = FALSE, : initial value in 'vmmin' is not finite

arimax(wcrude.train$Close, order=c(1,1,1),
       xtransf=data.frame(COVID=1*(seq(nrow(wcrude.train))==165)),
       transfer=list(c(1,1)))

## Error in optim(init[mask], armaCSS, method = "BFGS", hessian = FALSE, : initial value in 'vmmin' is not finite

Forecasting model intervensi ini cukup kompleks. Dapat digunakan fungsi filter di R untuk menduga efek dari intervensi tersebut:

m.earlyCOV<-stats::filter(1*(seq(nrow(wcrude.train)+5)==165),
              filter=1.5199, "recursive")* -7.914

Ini dapat diverifikasi dengan manual:

$$\begin{aligned} m_r&=-7.9141\\ m_{r+1}&=\phi_1\theta_0=1.5199\cdot -7.9141=-12.02864059\\ m_{r+2}&=\phi_1^2\theta_0=1.5199^{2}\cdot7.9141=-18.28233083\\ m_{r+3}&=\phi_1^3\theta_0=1.5199^{3}\cdot7.9141=-27.78731\\ \end{aligned}$$

Lalu, hasil dari filter akan dimasukkan sebagai regressor di fungsi Arima yang dimiliki package forecast

intv.mod<-Arima(wcrude.train$Close, order=c(1,1,1),
      xreg=m.earlyCOV[1:166])
intv.mod

## Series: wcrude.train$Close 
## Regression with ARIMA(1,1,1) errors 
## 
## Coefficients:
##           ar1     ma1    xreg
##       -0.8992  0.9626  1.0000
## s.e.   0.0592  0.0385  0.2538
## 
## sigma^2 = 4.908:  log likelihood = -363.99
## AIC=735.98   AICc=736.23   BIC=748.4

Terlihat bahwa koefisien COVID sama dengan satu, sehingga sebenarnya akan diregresikan nilai-nilai $m_{t}$ yang telah ditemukan saja. Lakukan pendugaan:

forcinv<-forecast(intv.mod,5,xreg=m.earlyCOV[167:171])

Dan plot. Awalnya, duga sebanyak 2 periode saja:

wcrude.covid[,`:=`("fitted.intv"=c(forcinv$fitted,rep(NA,5)),  
                  "predicted.intv"=c(rep(NA,166),forcinv$mean))]

ggplot(aes(x=Date,y=Close),data=wcrude.covid[150:168])+
  geom_point(size=3, alpha=0.3, color="gray")+
  geom_line(aes(y=fitted.intv,color="Fitted"))+
  geom_line(aes(y=predicted.intv,color="Prediksi"))+
  geom_point(aes(y=predicted.intv,color="Prediksi"),size=3,alpha=0.3)+
    scale_color_manual(name='Prediksi ARIMA',
                     breaks=c('Fitted', 'Prediksi'),
                     values=c('Fitted'='black', 'Prediksi'='#DB0000'))+
    theme_minimal()

## Warning: Removed 2 row(s) containing missing values (geom_path).

## Warning: Removed 17 row(s) containing missing values (geom_path).

## Warning: Removed 17 rows containing missing values (geom_point).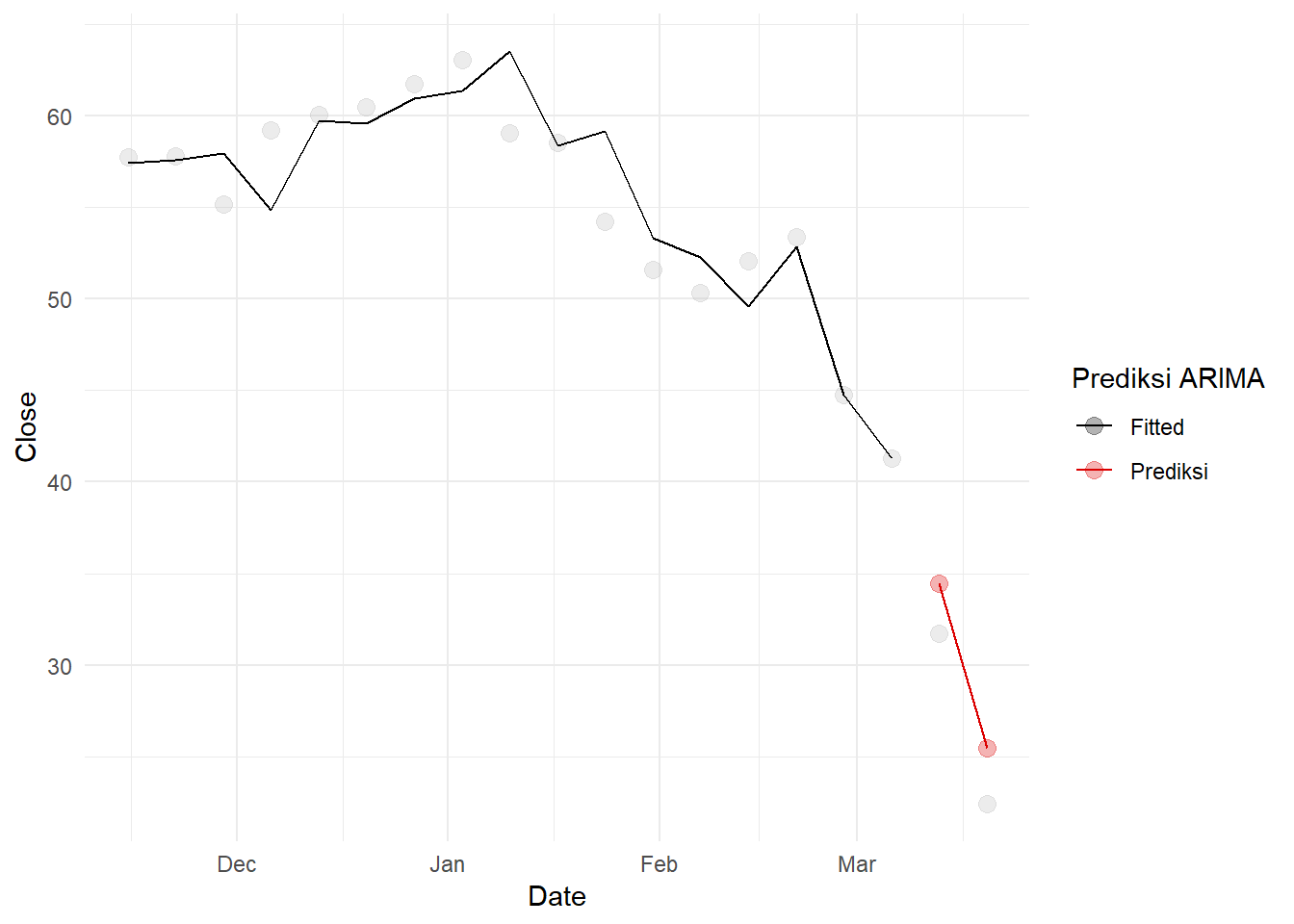

Namun, model ini tidak cocok untuk peramalan jangka panjang. Jika dilakukan peramalan dengan durasi sebulan (4 minggu), dugaan akan sangat jauh dari aktual. Fakta ini dapat dilihat dari plot:

ggplot(aes(x=Date,y=Close),data=wcrude.covid[150:170])+
  geom_point(size=3, alpha=0.3, color="gray")+
  geom_line(aes(y=fitted.intv,color="Fitted"))+
  geom_line(aes(y=predicted.intv,color="Prediksi"))+
  geom_point(aes(y=predicted.intv,color="Prediksi"),size=3,alpha=0.3)+
    scale_color_manual(name='Prediksi ARIMA',
                     breaks=c('Fitted', 'Prediksi'),
                     values=c('Fitted'='black', 'Prediksi'='#DB0000'))+
    theme_minimal()

## Warning: Removed 4 row(s) containing missing values (geom_path).

## Warning: Removed 17 row(s) containing missing values (geom_path).

## Warning: Removed 17 rows containing missing values (geom_point).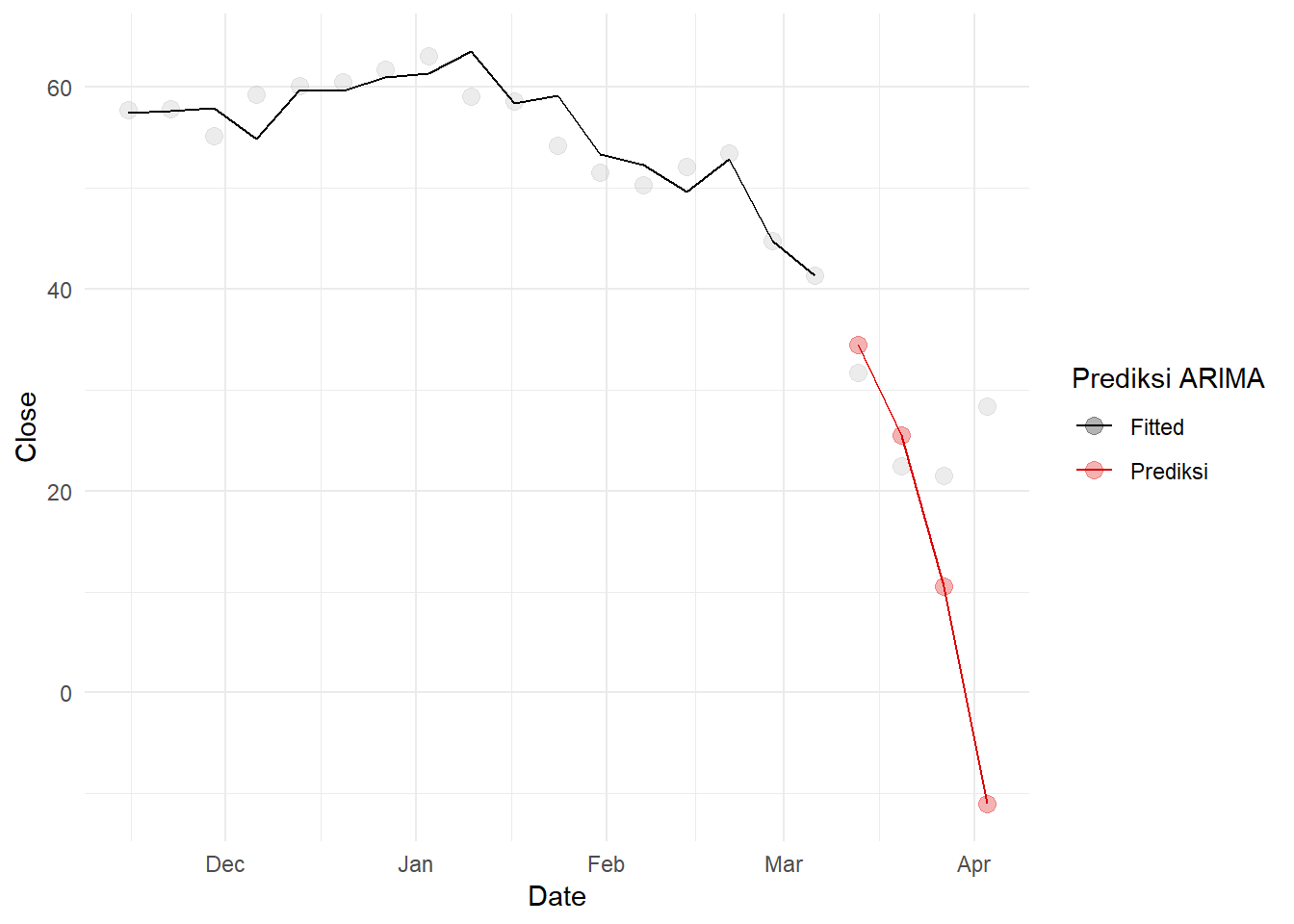

Ini terjadi karena kita tidak mengetahui cerita dari intervensi tersebut secara sepenuhnya. Terakhir, bandingkan error testing, pertama untuk prediksi dua periode ke depan:

compAcc<-rbind(accuracy(wcrude.covid$Close[1:168],
                        wcrude.covid$predicted.def[1:168]),
               accuracy(wcrude.covid$Close[1:168],
                        wcrude.covid$predicted.intv[1:168]))
rownames(compAcc)<-c("Tanpa Intervensi","Intervensi")

knitr::kable(
        compAcc,
  row.names=T,
  digits =4
)

	ME	RMSE	MAE	MPE	MAPE
Tanpa Intervensi	13.9157	14.7441	13.9157	33.8807	33.8807
Intervensi	2.8801	2.8843	2.8801	9.9138	9.9138

Dan untuk lima periode ke depan:

compAcc<-rbind(accuracy(wcrude.covid$Close,
                        wcrude.covid$predicted.def),
               accuracy(wcrude.covid$Close,
                        wcrude.covid$predicted.intv))
rownames(compAcc)<-c("Tanpa Intervensi","Intervensi")

knitr::kable(
        compAcc,
  row.names=T,
  digits =4
)

	ME	RMSE	MAE	MPE	MAPE
Tanpa Intervensi	15.6177	16.1276	15.6177	38.1101	38.1101
Intervensi	-22.4012	35.3207	24.7053	84.9935	126.4934

Jelas bahwa secara jangka pendek (dua minggu), model dengan intervensi lebih baik daripada model tanpa intervensi.

4.1.2 COVID rebuilding

Analisis intervensi juga berguna untuk pemodelan data setelah efek intervensi habis, misal saat harga minyak naik kembali setelah COVID. Ambil data sampai akhir 2020:

wcrude.rebuild1<-subset(weeklyCrude,Date<=as.Date("2020-12-31"))

Plot data tersebut:

ggplot(aes(x=Date,y=Close),data=wcrude.rebuild1[160:209,])+
  geom_point(size=3, alpha=0.6, color="gray")+theme_minimal()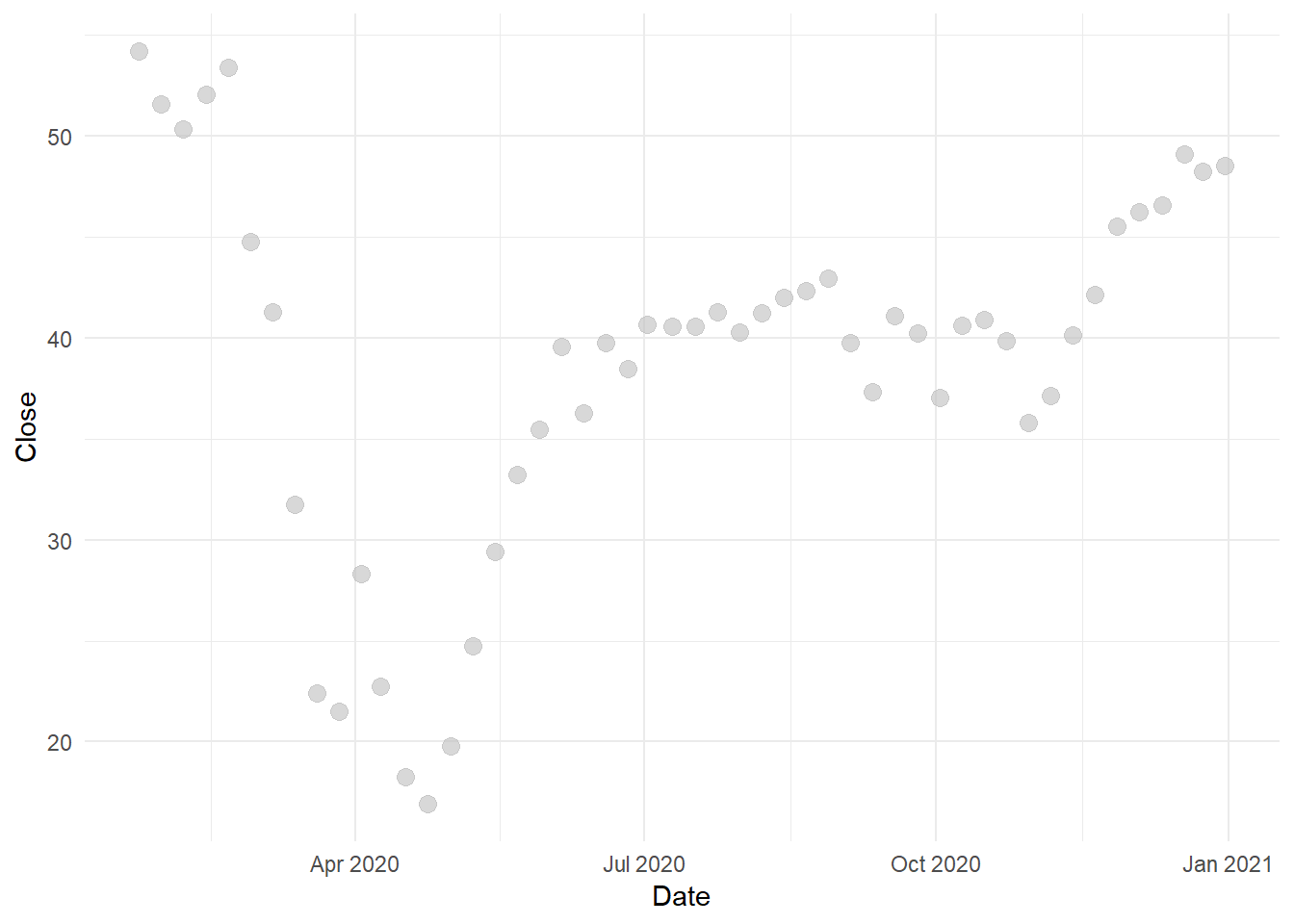

Ambil data sapai Juni 2020 sebagai data latih. Secara umum, rebuilding terjadi setelah harga sangat rendah di sekitar Mei 2020, sehingga saat Juni 2020 sudah terjadi sedikit kenaikan harga minyak:

wcrude.train2<-subset(weeklyCrude,Date<=as.Date("2020-05-21"))

(Inset model step here) menunjukkan bahwa Arima(0,1,1) model terbaik:

diff2<-diff(wcrude.train2$Close,1)
acf(diff2)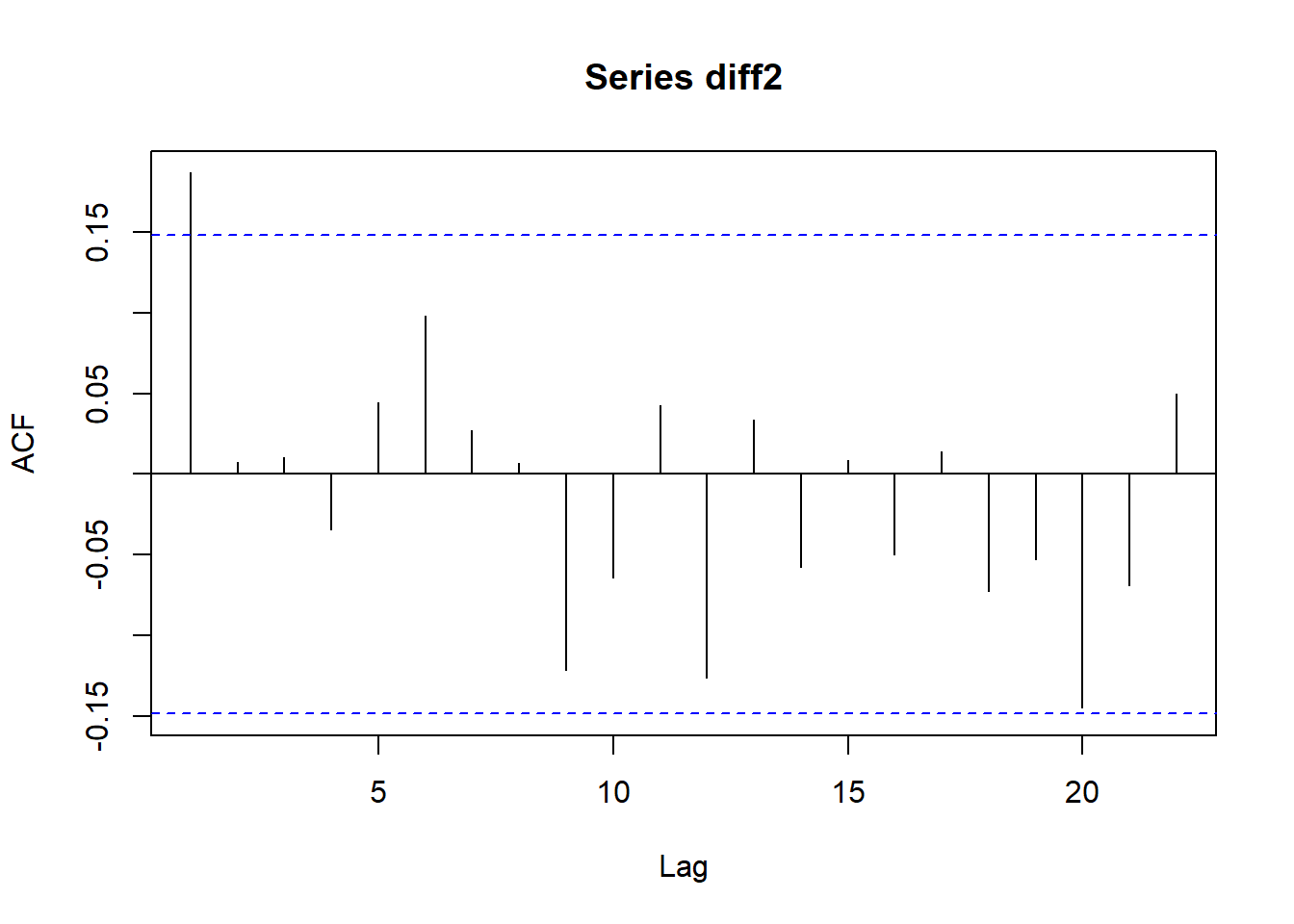

pacf(diff2)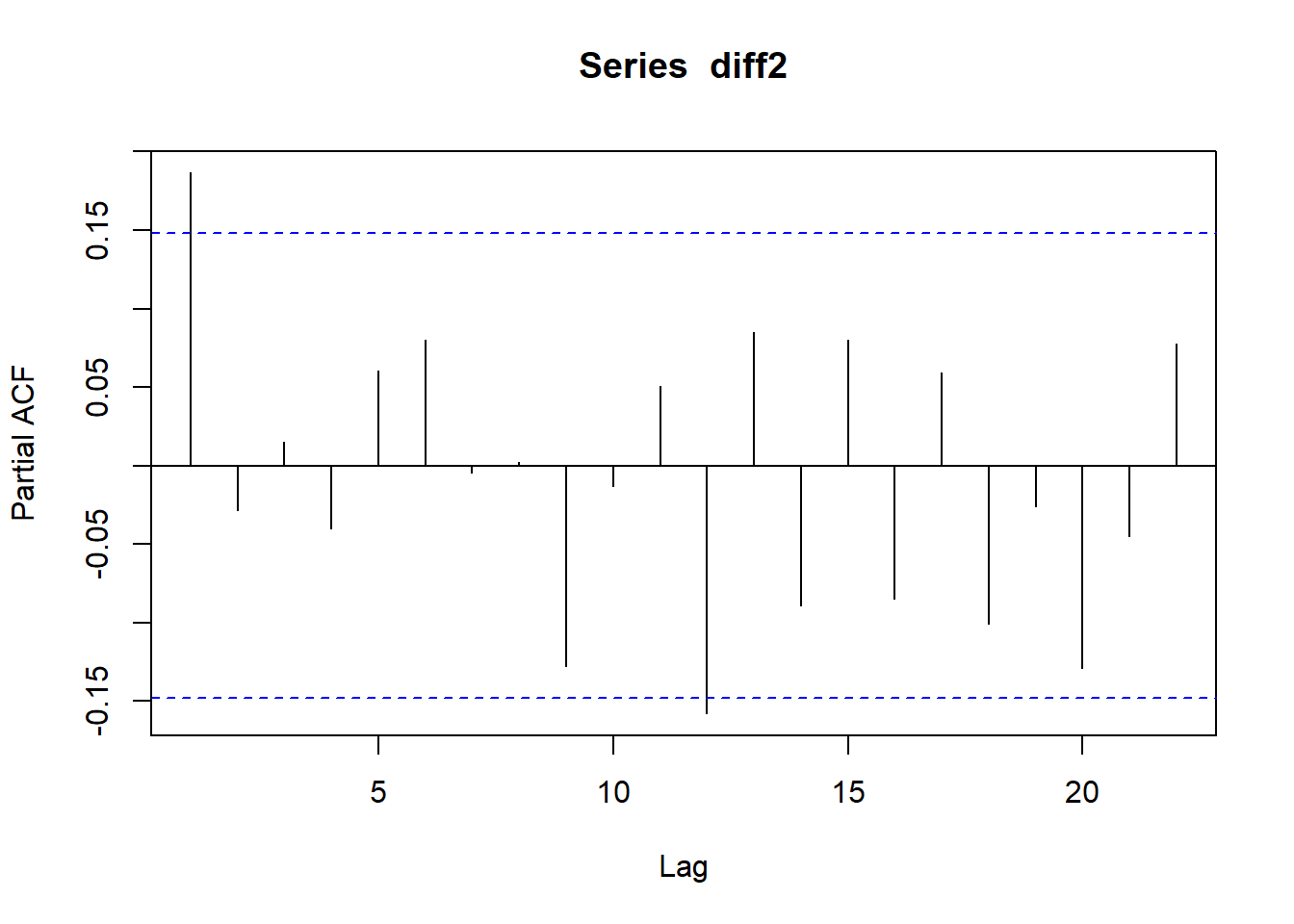

eacf(diff2)

## AR/MA
##   0 1 2 3 4 5 6 7 8 9 10 11 12 13
## 0 x o o o o o o o o o o  o  o  o 
## 1 o o o o o o o o o o o  o  o  o 
## 2 x o o o o o o o o o o  o  o  o 
## 3 x x o o o o o o o o o  o  o  o 
## 4 x o x x o o o o o o o  o  o  o 
## 5 x x x x x o o o o o o  o  o  o 
## 6 o o x x x o o o o o o  o  o  o 
## 7 x o x x o x o o o o o  o  o  o

Intinya setelah dicoba $ARIMA(0,1,1)$ oke:

rebuildMod<-Arima(wcrude.train2$Close,order=c(0,1,1))
rebuildMod

## Series: wcrude.train2$Close 
## ARIMA(0,1,1) 
## 
## Coefficients:
##          ma1
##       0.1961
## s.e.  0.0746
## 
## sigma^2 = 6.799:  log likelihood = -415.55
## AIC=835.11   AICc=835.18   BIC=841.44

Tren naik kembali tidak dapat diprediksi.

forcdef.reb<-forecast(rebuildMod,33)

wcrude.rebuild1[,`:=`("fitted.def"=c(forcdef.reb$fitted,rep(NA,33)),  
                  "predicted.def"=c(rep(NA,176),forcdef.reb$mean))]


ggplot(aes(x=Date,y=Close),data=wcrude.rebuild1[150:185])+
  geom_point(size=3, alpha=0.3, color="gray")+
  geom_line(aes(y=fitted.def,color="Fitted"))+
  geom_line(aes(y=predicted.def,color="Prediksi"))+
  geom_point(aes(y=predicted.def,color="Prediksi"), size=3, alpha=.3)+
    scale_color_manual(name='Prediksi ARIMA',
                     breaks=c('Fitted', 'Prediksi'),
                     values=c('Fitted'='black', 'Prediksi'='#DB0000'))+
    theme_minimal()

## Warning: Removed 9 row(s) containing missing values (geom_path).

## Warning: Removed 27 row(s) containing missing values (geom_path).

## Warning: Removed 27 rows containing missing values (geom_point).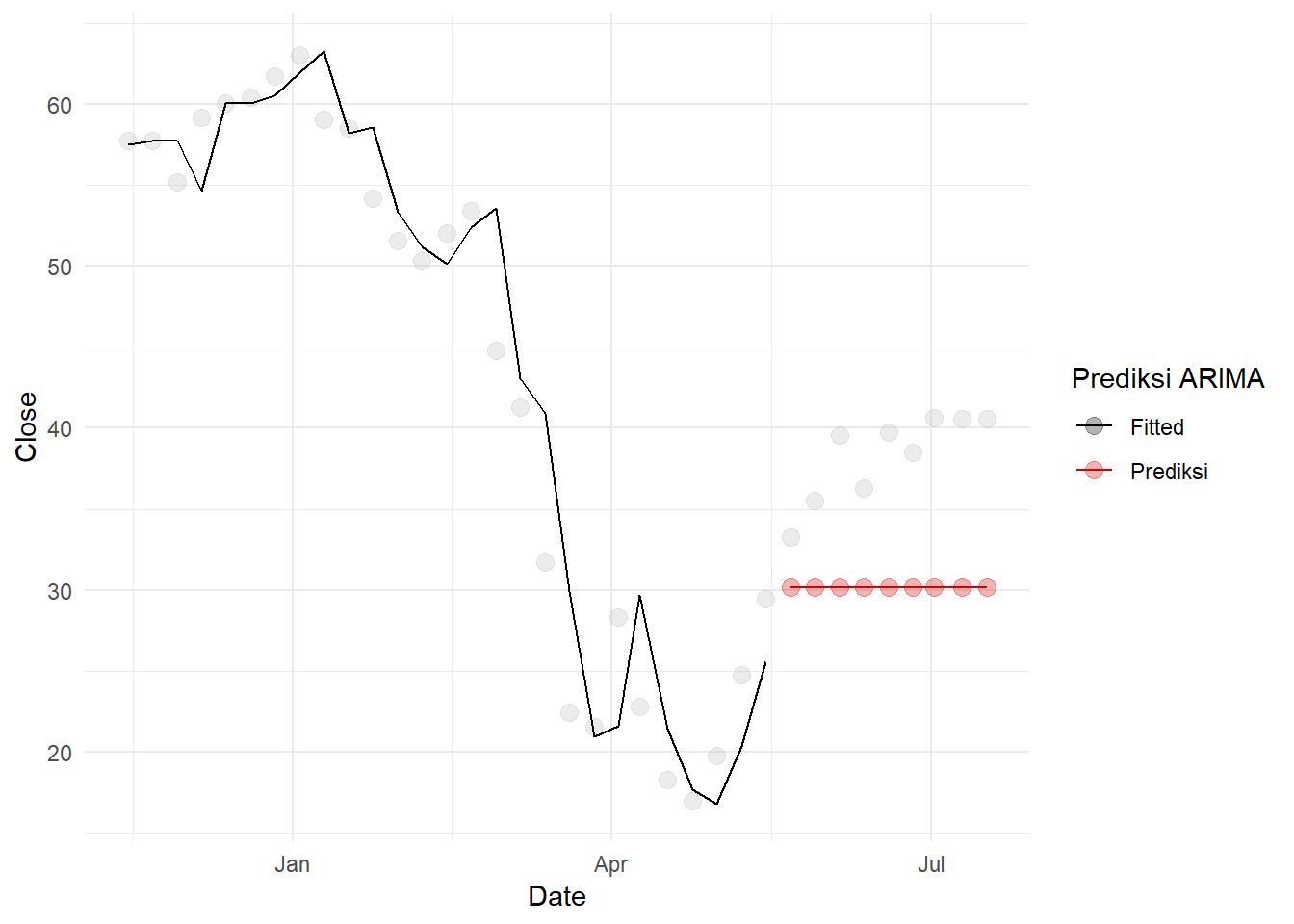

Dapat dicoba berbagai spesifikasi model arimax. Pertama akan dicobakan spesifikasi arimax sebelumnya, yaitu AR saja. Koefisien MA lalu ditingkatkan sampai 3, lalu dicobakan cara (Cryer dan Chan 2008), yaitu membuat dua peubah untuk memisahkan efek langsung dari COVID dan efek yang secara eksponen turun. Efek langsung dimodelkan dengan MA dan efek turun dimodelkan dengan AR.

arimaxdef<-arimax(wcrude.train2$Close,order=c(1,1,0),
       xtransf=data.frame(COVID=1*(seq(nrow(wcrude.train2))==165)),
       transfer=list(c(1,0)))
arimaxmad1<-arimax(wcrude.train2$Close,order=c(1,1,0),
       xtransf=data.frame(COVID=1*(seq(nrow(wcrude.train2))==165)),
       transfer=list(c(1,1)))
arimaxmad2<-arimax(wcrude.train2$Close,order=c(1,1,0),
       xtransf=data.frame(COVID=1*(seq(nrow(wcrude.train2))==165)),
       transfer=list(c(1,2)))
arimaxmad3<-arimax(wcrude.train2$Close,order=c(1,1,0),
       xtransf=data.frame(COVID=1*(seq(nrow(wcrude.train2))==165)),
       transfer=list(c(1,3)))
arimaxd1<-arimax(wcrude.train2$Close,order=c(1,1,0),
       xtransf=data.frame(COVID=1*(seq(nrow(wcrude.train2))==165),
                          COVIDb=1*(seq(nrow(wcrude.train2))==165)),
       transfer=list(c(0,1),c(1,0)))
arimaxd2<-arimax(wcrude.train2$Close,order=c(1,1,0),
       xtransf=data.frame(COVID=1*(seq(nrow(wcrude.train2))==165),
                          COVIDb=1*(seq(nrow(wcrude.train2))==165)),
       transfer=list(c(0,2),c(1,0)))

Bandingkan AIC tiap spesifikasi model tersebut:

knitr::kables(list(
  knitr::kable(arimaxdef$aic,col.names="Intervensi AR(1)"),
  knitr::kable(cbind(arimaxmad1$aic,arimaxmad2$aic,arimaxmad3$aic),
               col.names=c("ARMA(1,1)","ARMA(1,2)","MA(1,3)")),
  knitr::kable(cbind(arimaxd1$aic,arimaxd2$aic),col.names=c("MA(1)+AR(1)","MA(2)+AR(1)"))
  )
)

Intervensi AR(1) 832.4362

ARMA(1,1) ARMA(1,2) MA(1,3) 829.9415 827.1838 794.4952

MA(1)+AR(1) MA(2)+AR(1) 816.3303 798.1868

Sehingga model terbaik adalah:

arimaxmad3

## 
## Call:
## arimax(x = wcrude.train2$Close, order = c(1, 1, 0), xtransf = data.frame(COVID = 1 * 
##     (seq(nrow(wcrude.train2)) == 165)), transfer = list(c(1, 3)))
## 
## Coefficients:
##          ar1  COVID-AR1  COVID-MA0  COVID-MA1  COVID-MA2  COVID-MA3
##       0.0857     0.9605    -8.4711    -4.4471   -10.6113   -10.6437
## s.e.  0.0767     0.0243     2.3488     2.3693     2.3759     2.3828
## 
## sigma^2 estimated as 5.537:  log likelihood = -391.25,  aic = 794.5

Terlihat bahwa semua koefisien lebih besar dari galat baku, sehingga kemungkinan signifikan. Residual kedua model tampak oke:

checkresiduals(rebuildMod)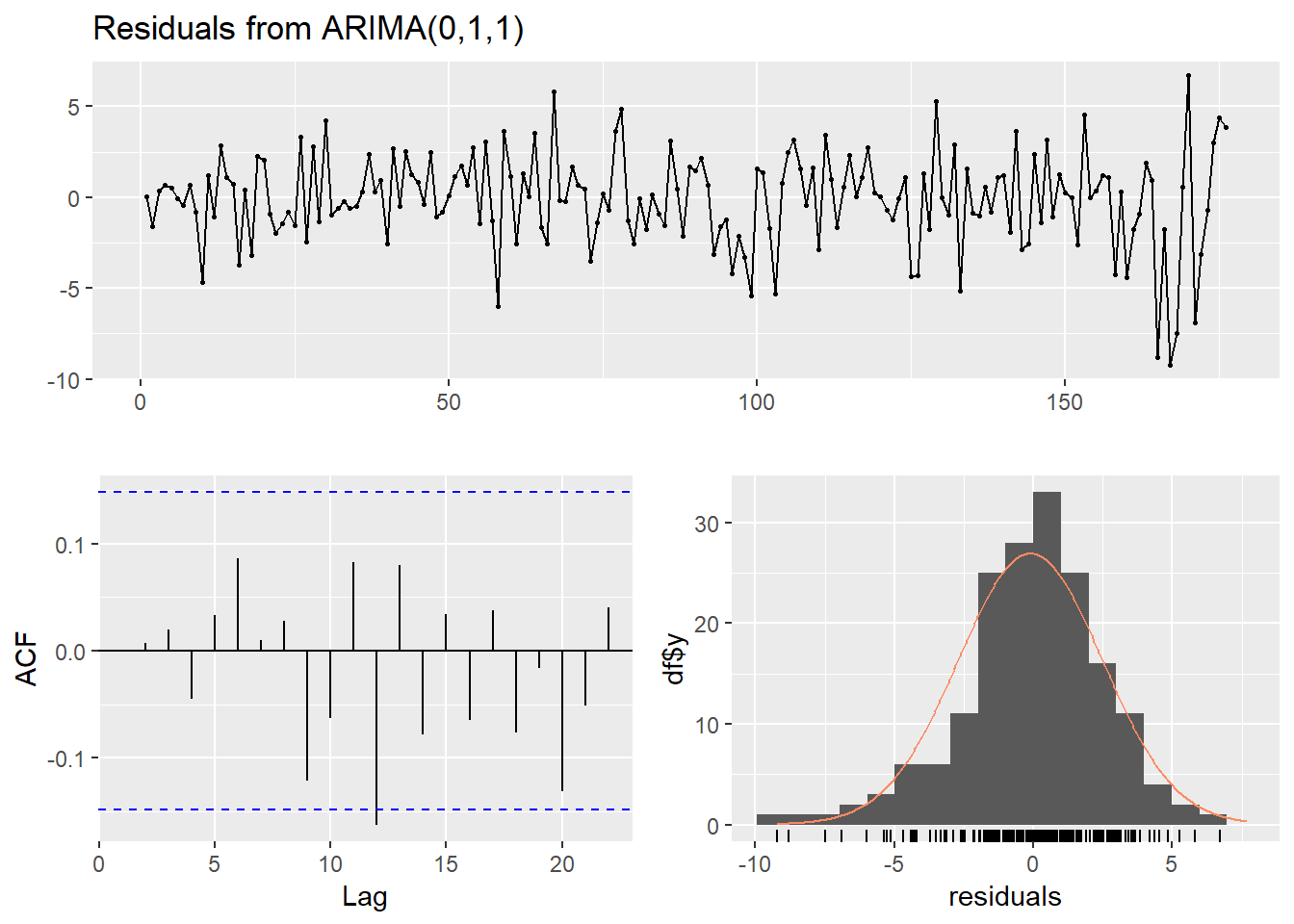

## 
##  Ljung-Box test
## 
## data:  Residuals from ARIMA(0,1,1)
## Q* = 5.6654, df = 9, p-value = 0.7729
## 
## Model df: 1.   Total lags used: 10

checkresiduals(arimaxmad3)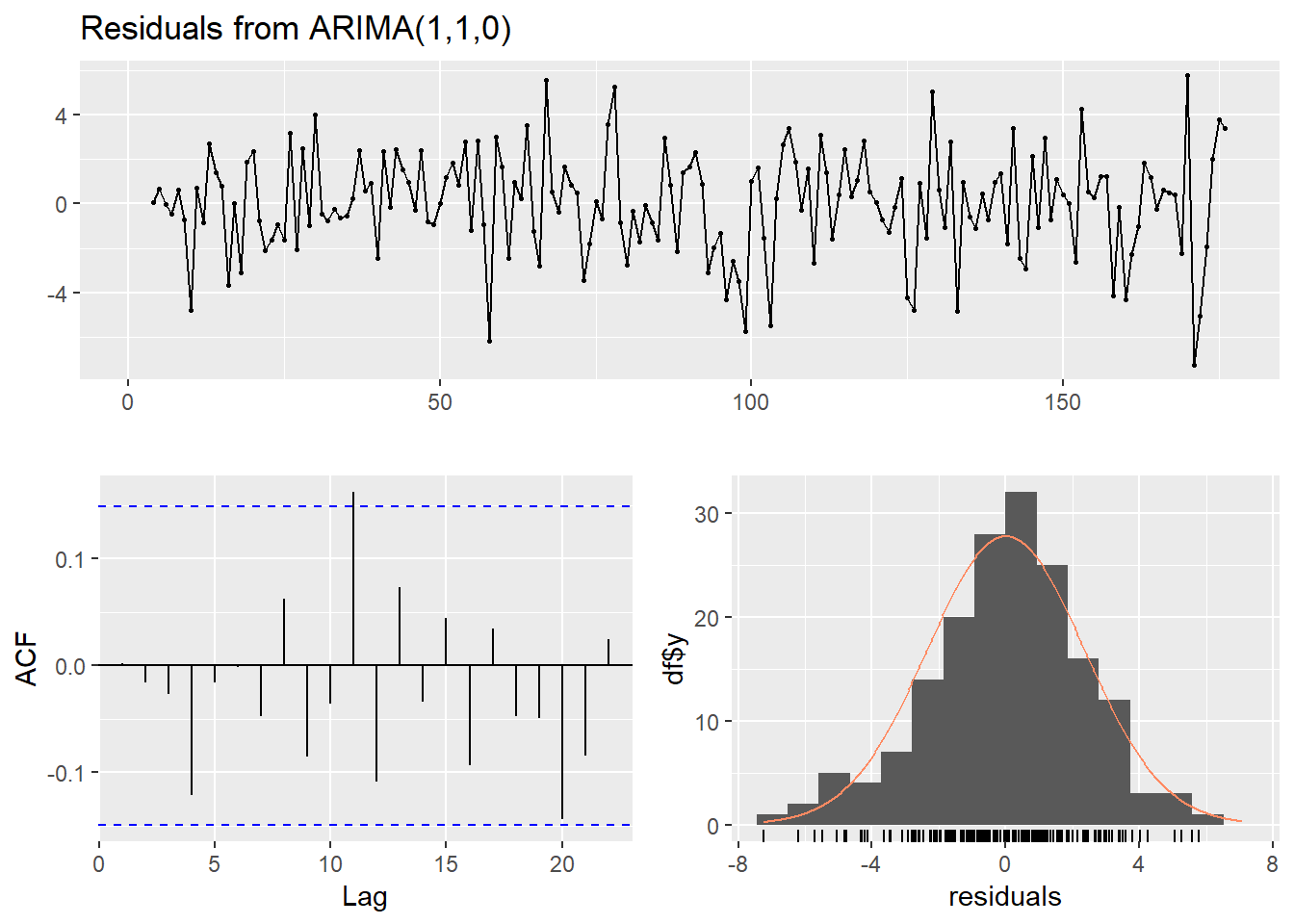

## 
##  Ljung-Box test
## 
## data:  Residuals from ARIMA(1,1,0)
## Q* = 5.5843, df = 4, p-value = 0.2324
## 
## Model df: 6.   Total lags used: 10

Perhatikan spesifikasi model tersebut secara matematis:

$$\begin{aligned} m_t&=\frac{(\theta_0+\theta_1B+\theta_2B^2+\theta_3B^3)}{(1-\phi_1 B)} P_t\\ (1-\phi_1B)m_t&=\theta_0P_t+\theta_1P_{t-1}+\theta_2P_{t-2}+\theta_3P_{t-3}\\ m_t-\phi_1m_{t-1}&=\theta_0P_t+\theta_1P_{t-1}+\theta_2P_{t-2}+\theta_3P_{t-3}\\ m_t&=\theta_0P_t+\theta_1P_{t-1}+\theta_2P_{t-2}+\theta_3P_{t-3}+\phi_1m_{t-1}\\ \end{aligned}$$

Sama seperti sebelumnya, untuk forecasting nilai tersebut dapat dicari dengan fungsi filter:

COVID=1*(seq(nrow(wcrude.rebuild1))==165)

tss<-stats::filter(COVID,c(-8.4711,    -4.4471,   -10.6113,   -10.6437),"convolution",sides=1)
tss[is.na(tss)]<-0

m<-stats::filter(tss,0.9605,"recursive",sides=1)
m[165:209]

##  [1]  -8.471100 -12.583592 -22.697840 -32.444975 -31.163399 -29.932444 -28.750113 -27.614483 -26.523711 -25.476025 -24.469722
## [12] -23.503168 -22.574792 -21.683088 -20.826606 -20.003955 -19.213799 -18.454854 -17.725887 -17.025715 -16.353199 -15.707248
## [23] -15.086811 -14.490882 -13.918492 -13.368712 -12.840648 -12.333442 -11.846271 -11.378344 -10.928899 -10.497207 -10.082568
## [34]  -9.684306  -9.301776  -8.934356  -8.581449  -8.242482  -7.916904  -7.604186  -7.303821  -7.015320  -6.738215  -6.472055
## [45]  -6.216409

Empat hasil hitungan pertama mirip dengan hitungan manual. Selanjutnya dapat dengan mudah diverifikasi dengan mengalikan dengan pangkat dari $\phi_1$.

$$\begin{aligned} m_{r}&=\theta_0&&=-8.4711 \\ m_{r+1}&=\theta_1+\phi_1\theta_0&=-4.4471+0.9605 \cdot -8.4711&=−12.5835\\ m_{r+2}&=\theta_2+\phi_1m_{r+1}=\theta_2+\phi_1\theta_1+\phi_1^2\theta_0&=-10.6113+0.9605\cdot−12.5835&=−22.69775175\\ m_{r+3}&=\theta_3+\phi_1m_{r+2}=\theta_3+\phi_1\theta_2+\phi_1^2\theta_1+\phi_1^3\theta_0&=-10.6437+0.9605\cdot−22.69775175&=−32.44489057\\ m_{r+k}&=\phi_1^{k-3}m_{r+k-1}=\phi_1^{k-3}\theta_3+\phi_1^{k-2}\theta_2+\phi_1^{k-1}\theta_1+\phi_1^k\theta_0\\ \end{aligned}$$

(0.9605^(1:20))*-32.44489057

##  [1] -31.16332 -29.93237 -28.75004 -27.61441 -26.52364 -25.47596 -24.46966 -23.50311 -22.57473 -21.68303 -20.82655 -20.00390
## [13] -19.21375 -18.45481 -17.72584 -17.02567 -16.35316 -15.70721 -15.08677 -14.49084

Gunakan fungsi Arima lalu prediksi:

rebuildModfin<-Arima(wcrude.train2$Close,order=c(1,1,0),
                     xreg=m[1:176])
rebuildModfin

## Series: wcrude.train2$Close 
## Regression with ARIMA(1,1,0) errors 
## 
## Coefficients:
##          ar1    xreg
##       0.0850  0.9505
## s.e.  0.0758  0.1424
## 
## sigma^2 = 5.519:  log likelihood = -396.78
## AIC=799.57   AICc=799.71   BIC=809.06

forc.inv.reb<-forecast(rebuildModfin,33,xreg=m[177:209])

Dalam periode sama, dapat dilihat bahwa prediksi model ARIMAX lebih baik:

wcrude.rebuild1[,`:=`("fitted.intv"=c(forc.inv.reb$fitted,rep(NA,33)),  
                  "predicted.intv"=c(rep(NA,176),forc.inv.reb$mean))]


ggplot(aes(x=Date,y=Close),data=wcrude.rebuild1[150:185])+
  geom_point(size=3, alpha=0.3, color="gray")+
  geom_line(aes(y=fitted.intv,color="Fitted"))+
  geom_line(aes(y=predicted.intv,color="Prediksi"))+
  geom_point(aes(y=predicted.intv,color="Prediksi"),size=3, alpha=0.3)+
  scale_color_manual(name='Prediksi ARIMA',
                     breaks=c('Fitted', 'Prediksi'),
                     values=c('Fitted'='black', 'Prediksi'='#DB0000'))+
    theme_minimal()

## Warning: Removed 9 row(s) containing missing values (geom_path).

## Warning: Removed 27 row(s) containing missing values (geom_path).

## Warning: Removed 27 rows containing missing values (geom_point).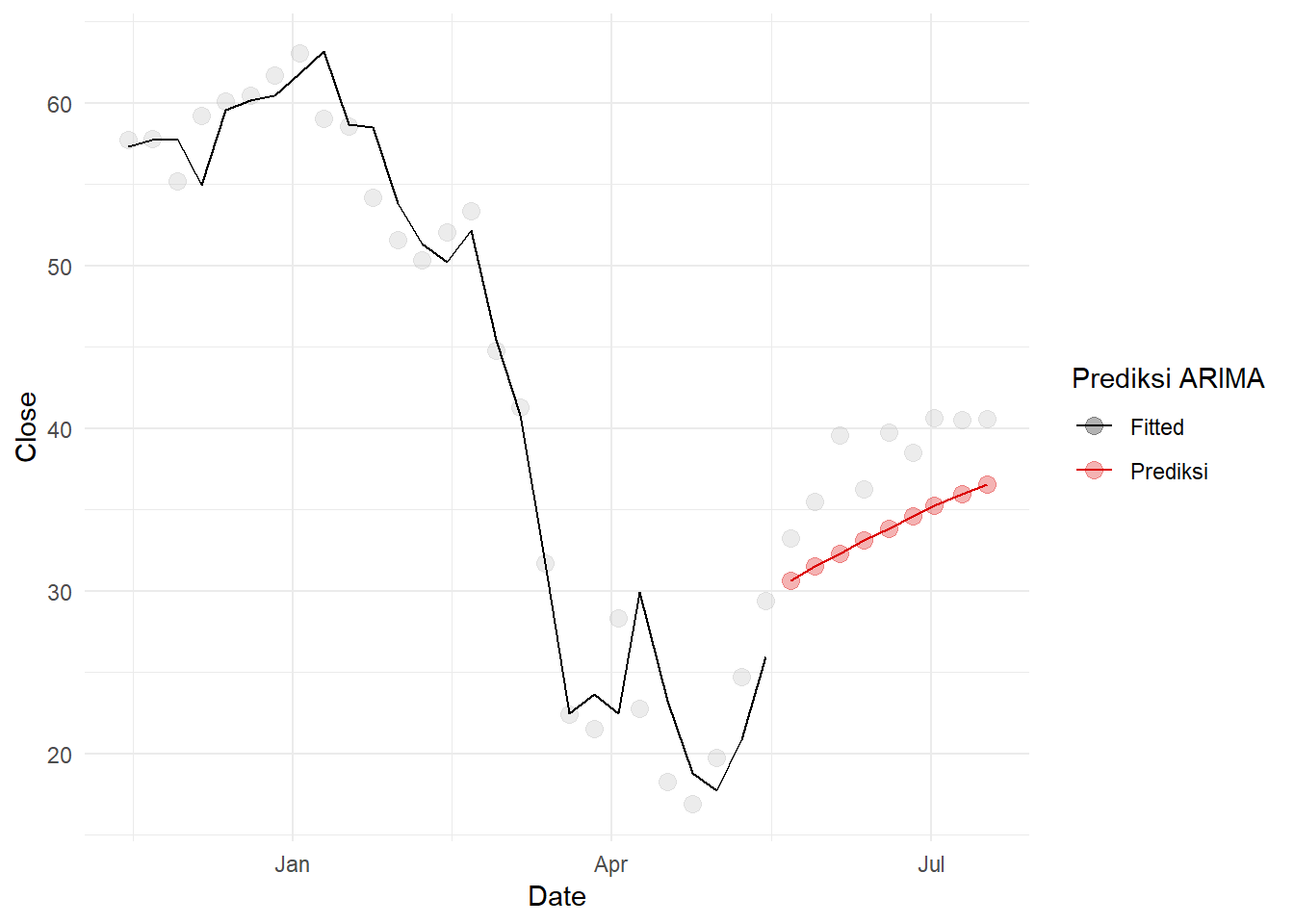

Bahkan, jika diekspansi sampai akhir 2020, prediksi masih baik.

ggplot(aes(x=Date,y=Close),data=wcrude.rebuild1[150:209 ])+
  geom_point(size=3, alpha=0.3, color="gray")+
  geom_line(aes(y=fitted.intv,color="Fitted"))+
  geom_line(aes(y=predicted.intv,color="Prediksi"))+
    geom_point(aes(y=predicted.intv,color="Prediksi"),size=3, alpha=0.3)+
  scale_color_manual(name='Prediksi ARIMA',
                     breaks=c('Fitted', 'Prediksi'),
                     values=c('Fitted'='black', 'Prediksi'='#DB0000'))+
    theme_minimal()

## Warning: Removed 33 row(s) containing missing values (geom_path).

## Warning: Removed 27 row(s) containing missing values (geom_path).

## Warning: Removed 27 rows containing missing values (geom_point).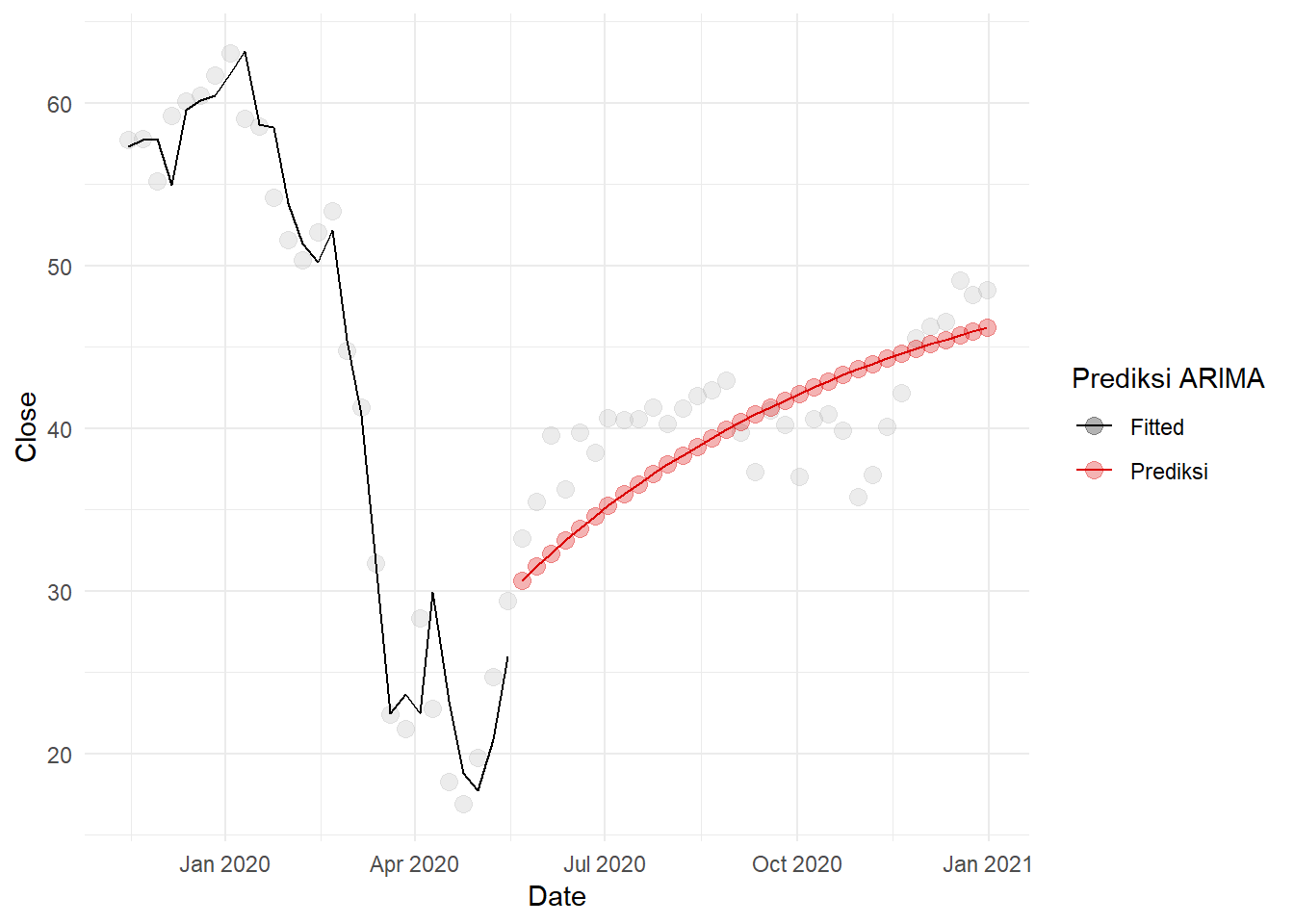

Dapat dibandingkan akurasi di training, peramalan 9 periode, dan peramalan 33 periode:

compAcc<-rbind(accuracy(rebuildMod),accuracy(arimaxmad3))
rownames(compAcc)<-c("Tanpa Intervensi","Intervensi")

compAcc.1<-rbind(accuracy(wcrude.rebuild1$Close[1:185],
                          wcrude.rebuild1$predicted.def[1:185]),
                 accuracy(wcrude.rebuild1$Close[1:185],
                          wcrude.rebuild1$predicted.intv[1:185]))
rownames(compAcc.1)<-c("Tanpa Intervensi","Intervensi")

compAcc.2<-rbind(accuracy(wcrude.rebuild1$Close[1:209],
                          wcrude.rebuild1$predicted.def[1:209]),
                 accuracy(wcrude.rebuild1$Close[1:209],
                          wcrude.rebuild1$predicted.intv[1:209]))
rownames(compAcc.2)<-c("Tanpa Intervensi","Intervensi")


knitr::kables(list(knitr::kable(compAcc,
                                row.names=T,
                                digits =4),
                   knitr::kable(compAcc.1,
                                row.names=T,
                                digits =4),
                   knitr::kable(compAcc.2,
                                row.names=T,
                                digits =4)),
              )

ME RMSE MAE MPE MAPE MASE ACF1 Tanpa Intervensi -0.1127 2.5927 1.9500 -0.4368 4.0818 0.9826 -0.0009 Intervensi 0.0008 2.3463 1.8217 -0.1753 3.7110 0.9179 0.0016

ME RMSE MAE MPE MAPE Tanpa Intervensi -8.1052 8.4875 8.1052 -26.8550 26.8550 Intervensi -4.5318 4.7281 4.5318 -13.4257 13.4257

ME RMSE MAE MPE MAPE Tanpa Intervensi -10.7561 11.3870 10.7561 -35.6383 35.6383 Intervensi -0.9257 3.8008 3.3252 -3.0531 8.6213

Model dengan intervensi umumnya lebih baik.

References

Cryer JD, Chan KS. 2008. Time Series Analysis: With Applications in R. Springer New York. (Springer Texts in Statistics).