Business Intelligence II, forår 2023: Anvendt Machine Learning
2023-01-02
Modul 1: Introduktion - EKSEMPEL
Første modul omhandler en generel introduktion til softwareprogrammet R (https://www.r-project.org/). Her gengives en række eksempler på R-kode samt det tilhørende R-output for at illustrere forskellige grundlæggende funktionaliteter i programmet.
Programmet R tager koder som input, så hver gang man skal have udført noget, skal man skrive de(n) relevante kode(r), som herefter eksekveres af programmet og giver det efterspurgte output.
R introduktion
Almindelige regnearter
Man kan bruge de almindelige regnearter plus (+), minus (-), multiplikation (*) og division (/) på helt normal vis. For at sikre overskuelighed er det altid en god idé at tilføje korte, forklarende kommentarer til sin kode (kommentarlinjer starter med #).
# beregn antal minutter per dag
60*24
## [1] 1440Hvis man vil gemme et resultat i en variabel, sker det ved hjælp af <- symbolet.
# gem antal minutter per dag i variablen Minutter.per.dag"
Minutter.per.dag <- 24*7Man kan herefter se variablens værdi ved at skrive variablens navn.
Minutter.per.dag
## [1] 168Man kan udskrive tekst og tal ved hjælp af cat.
cat("Antal minutter på en dag:", Minutter.per.dag)
## Antal minutter på en dag: 168Datastrukturer
Der findes en række forskellige måder at gemme data på. Den mest almindelige er at gemme data i én lang række; i en såkaldt vektor.
# lav vektor med antal dage per måned
Dage.per.måned <- c(31,28,31,30,31,30,31,31,30,31,30,31)Hvis man vil lave en vektor med alle tal fra én værdi til en anden værdi, kan det gøres uden at skulle skrive alle tallene selv.
# lav en vektor fra 1 til 12
Et.til.tolv <- 1:12En vektor kan både indeholde tal og tekst.
# lav vektor med månedsnavne
Månedsnavne <-
c("Januar", "Februar", "Marts", "April", "Maj", "Juni",
"Juli", "August", "September", "Oktober", "November", "December")Længden af en vektor findes med length.
# beregn længden af vektoren med månedsnavne
length(Månedsnavne)
## [1] 12Man kan finde det i’te element i en vektor ved at skrive [i] efter vektornavnet.
# udskriv navnet på årets 5'te måned
Månedsnavne[5]
## [1] "Maj"I en vektor ligger alle værdier i én lang række. Ofte har man behov for en mere fleksibel måde at gemme data på. Et eksempel på en mere generel datastruktur er en såkaldt liste.
# gem månedsnavne og antal dage i en liste
Måned.dato.som.liste <- list("Måned" = Månedsnavne, "Dage" = Dage.per.måned)Fordelen ved en liste er blandt andet, at man kan gemme mange forskellige slags data og datastrukturer i én og samme liste (det skal nok siden hen blive klart, hvorfor det kan være bekvemt). Man kan referere til en variabel i en liste ved hjælp af $.
# udskriv indholdet af liste
Måned.dato.som.liste
## $Måned
## [1] "Januar" "Februar" "Marts" "April" "Maj" "Juni" "Juli" "August"
## [9] "September" "Oktober" "November" "December"
##
## $Dage
## [1] 31 28 31 30 31 30 31 31 30 31 30 31
Måned.dato.som.liste$Måned
## [1] "Januar" "Februar" "Marts" "April" "Maj" "Juni" "Juli" "August"
## [9] "September" "Oktober" "November" "December"
Måned.dato.som.liste$Dage
## [1] 31 28 31 30 31 30 31 31 30 31 30 31Man kan finde mere information om lister i R’s indbyggede hjælpefunktion, der kaldes med enten ?eller help(...).
# udskriv hjælpe-information om funktionen "list" (på 2 forskellige måder)
?list
help("list")En tredje datastruktur, som er den vi ofte vil bruge til at gemme data i, er en såkaldt data frame. Man kan tænke på en data frame som et stort skema med rækker og søjler. Hver søjle vil svare til én variabel i datasættet, og hver række vil svare til én observation (af alle datasættets variable).
# gem månedsnavne og antal dage i en data frame
Måned.dato <- data.frame("Måned" = Månedsnavne, "Dage" = Dage.per.måned)Man kan referere til en søjle i en data frame ved hjælp af $.
# udskriv indholdet af Måned.dato
Måned.dato
## Måned Dage
## 1 Januar 31
## 2 Februar 28
## 3 Marts 31
## 4 April 30
## 5 Maj 31
## 6 Juni 30
## 7 Juli 31
## 8 August 31
## 9 September 30
## 10 Oktober 31
## 11 November 30
## 12 December 31
Måned.dato$Måned
## [1] "Januar" "Februar" "Marts" "April" "Maj" "Juni" "Juli" "August"
## [9] "September" "Oktober" "November" "December"
Måned.dato$Dage
## [1] 31 28 31 30 31 30 31 31 30 31 30 31Man kan nemt tilføje nye variable til en eksisterende data frame ved hjælp af <-.
# tilføj variabel med antal minutter per måned til Måned.dato
Måned.dato$Minutter <- Måned.dato$Dage * Minutter.per.dagMan kan vise indholdet af et udsnit af rækkerne i en data frame ved at angive hvilke rækker, man gerne vil se.
# udskriv indholdet af Måned.dato for 2. kvartal (= række 4-6)
Måned.dato[4:6,]
## Måned Dage Minutter
## 4 April 30 5040
## 5 Maj 31 5208
## 6 Juni 30 5040# udskriv indholdet af Måned.dato for 2. og 4. kvartal (= række 4-6, 10-12)
Måned.dato[c(4:6,10:12),]
## Måned Dage Minutter
## 4 April 30 5040
## 5 Maj 31 5208
## 6 Juni 30 5040
## 10 Oktober 31 5208
## 11 November 30 5040
## 12 December 31 5208Man kan på samme måde vise indholdet af et udsnit af søjlerne i en data frame ved at angive navnene på de søjler/variable, man gerne vil se.
# udskriv "Måned" og "Minutter" af Måned.dato (1. og 3. søjle)
Måned.dato[,c("Måned","Minutter")]
## Måned Minutter
## 1 Januar 5208
## 2 Februar 4704
## 3 Marts 5208
## 4 April 5040
## 5 Maj 5208
## 6 Juni 5040
## 7 Juli 5208
## 8 August 5208
## 9 September 5040
## 10 Oktober 5208
## 11 November 5040
## 12 December 5208Man kan også i stedet angive numrene på de søjler, man gerne vil se.
Måned.dato[,c(1,3)]
## Måned Minutter
## 1 Januar 5208
## 2 Februar 4704
## 3 Marts 5208
## 4 April 5040
## 5 Maj 5208
## 6 Juni 5040
## 7 Juli 5208
## 8 August 5208
## 9 September 5040
## 10 Oktober 5208
## 11 November 5040
## 12 December 5208Man kan også angive numrene på de søjler, man ikke vil se ved at angive et minus (-) foran numrene.
# udskriv Måned.dato UDEN antal minutter per måned (3. søjle)
Måned.dato[,-c(3)]
## Måned Dage
## 1 Januar 31
## 2 Februar 28
## 3 Marts 31
## 4 April 30
## 5 Maj 31
## 6 Juni 30
## 7 Juli 31
## 8 August 31
## 9 September 30
## 10 Oktober 31
## 11 November 30
## 12 December 31Funktioner
Hvis man har behov for at lave den samme ting flere gange, kan det være bekvemt at lave en særskilt funktion, der laver det ønskede, og som man så kan kalde efter behov. Funktioner defineres med function.
# lav en funktion der udskriver antal dage og antal minutter i måned nr. x
find_måned <- function(x)
{
output <- Måned.dato[x,]
print(output)
}
find_måned(4)
## Måned Dage Minutter
## 4 April 30 5040Herefter kan den definerede funktion kaldes ved at angive dens navn. I eksemplet her kaldes den 12 gange, én gang for hver af værdierne 1, 2, 3, ….
# udskriv antal dage og minutter for alle måneder
for(i in 1:12)
{
find_måned(i)
}
## Måned Dage Minutter
## 1 Januar 31 5208
## Måned Dage Minutter
## 2 Februar 28 4704
## Måned Dage Minutter
## 3 Marts 31 5208
## Måned Dage Minutter
## 4 April 30 5040
## Måned Dage Minutter
## 5 Maj 31 5208
## Måned Dage Minutter
## 6 Juni 30 5040
## Måned Dage Minutter
## 7 Juli 31 5208
## Måned Dage Minutter
## 8 August 31 5208
## Måned Dage Minutter
## 9 September 30 5040
## Måned Dage Minutter
## 10 Oktober 31 5208
## Måned Dage Minutter
## 11 November 30 5040
## Måned Dage Minutter
## 12 December 31 5208En nyttig indbygget R-funktion er if, der kan bruges til at opstille betingelser for, hvornår en given kode udføres. Den kan f.eks. kombineres med %in% til at afgøre om et element findes i en vektor eller ej.
# udskriv antal dage og minutter for alle sommermåneder (måned 6,7,8)
for(i in 1:12){
if(i %in% c(6,7,8)){
find_måned(i)
}
}
## Måned Dage Minutter
## 6 Juni 30 5040
## Måned Dage Minutter
## 7 Juli 31 5208
## Måned Dage Minutter
## 8 August 31 5208# udskriv hjælpe-information om funktionen "%in%"
help("%in%")Et andet eksempel på brug af if er sammen med %%, der angiver den såkaldte “rest efter division”.
# udskriv antal dage og minutter for alle lige måneder
for(i in 1:12){
if(i %% 2==0){
find_måned(i)
}
}
## Måned Dage Minutter
## 2 Februar 28 4704
## Måned Dage Minutter
## 4 April 30 5040
## Måned Dage Minutter
## 6 Juni 30 5040
## Måned Dage Minutter
## 8 August 31 5208
## Måned Dage Minutter
## 10 Oktober 31 5208
## Måned Dage Minutter
## 12 December 31 5208# udskriv hjælpe-information om funktionen "%%"
help("%%")Udvælge stikprøve
En klassisk teknik til at sikre robusthed af statistiske anallyser er, at man kun laver sin analyse på en delmængde (stikprøve) af det fulde datasæt. Til gengæld gentager man så analysen for en række forskellige stikprøver af datasættet og ser så på, om de forskellige analyser leder til samme eller forskellige konklusioner.
For at kunne bruge denne teknik har vi behov for at kunne udtage en stikprøve af et datasæt. Det kan gøres ved hjælp af sample.
# tag en stikprøve på 3 måneder
sample(Et.til.tolv, 3)
## [1] 3 9 10sample udvælger tilfældigt en stikprøve af en given størrelse. Hvis man bruger funktionen til at udtage en stikprøve flere gange efter hinanden, får man derfor en ny stikprøve for hver gang.
# tag en stikprøve mere (bemærk den er anderledes)
sample(Et.til.tolv, 3)
## [1] 12 7 6Når et softwareprogram trækker “tilfældige” tal, er det i virkeligheden aldrig rigtig tilfældigt. I praksis foregår det ved hjælp af en sofistikeret deterministisk algoritme, der får ting til at se tilfældige ud.
Ved at angive hvad denne deterministiske algoritme skal bruge som udgangspunkt (ved hjælp af set.seed) for at udvælge de tilfældige tal, kan man “styre” tilfældigheden og dermed er det muligt at gendanne “tilfældige” eksperimenter. Det kan i mange sammenhænge være bekvemt (f.eks. i forbindelse med kontrol af beregninger o.lign.)
# sæt et random seed og gentag
udtræk_måneder <- function(n){
set.seed(100)
sample(Et.til.tolv, n)
}
udtræk_måneder(3)
## [1] 10 7 6
udtræk_måneder(3) # Bemærk: Vi får den samme stikprøve, fordi vi bruger samme seed (= 100)
## [1] 10 7 6Opsætning
Når man arbejder med et konkret datamateriale ender man ofte med at køre de samme koder gentagne gange, f.eks. fordi man undervejs retter i sin kode, i takt med at man tilpasser sin analyse. Det kan derfor være bekvemt at kunne slette alt gammelt indhold (variable, data, funktioner etc.), og det kan gøres med nedenstående kommando.
# slet eventuelt gammelt indhold
rm(list = ls())På samme måde kan det være bekvemt at slette al output fra skærmen.
# slet skærmindhold
cat("\014")Der findes et meget stort antal forprogrammerede funktioner til R. Funktioner der kan bruges til at lave alskens forskellige ting (grafer, analyser, datahåndtering osv.). Langt de fleste af disse funktioner er organiseret i såkaldte biblioteker (“libraries”). Man kan bruge R’s indbyggede hjælpe-funktion til at søge efter funktioner og her få at vide hvilke(t) bibliotek(er), der indeholder de(n) funktion(er), man søger efter.
For at få adgang til de funktioner, der ligger i et givet bibliotek, skal man først installere og dernæst indlæse det bibliotek, man ønsker at anvende. Installation sker ved hjælp af install.packages-funktionen, mens indlæsning sker ved hjælp af library. NB: Man skal KUN installere biblioteket FØRSTE GANG, man skal bruge det.
# indlæs funktionsbiblioteker [NB: Før et bibliotek kan indlæses FØRSTE gang skal det installeres v.hj.a. install.packages("...")]
library(dplyr) # bibliotek til manipulation af data
library(DescTools) # bibliotek til deskriptiv statistik
library(ggplot2) # bibliotek til tegning af grafer
library(openxlsx) # bibliotek til håndtering af Excel-filerNår man arbejder med datasæt er det ofte bekvemt at kunne styre, hvor data læses fra og skrives til. Det gøres ved at angive filstien på den mappe, man ønsker at bruge som sit arbejdskatalog (“working directory”) ved hjælp af setwd.
# vælg filsti til datafil m.m.
setwd(r"(C:\Users\msn.fi\OneDrive - CBS - Copenhagen Business School\Desktop\CBS\HD Business Intelligence II (forår 2023)\Noter)")En Excel-datafil placeret i sit arbejdskatalog kan indlæses ved hjælp af read.xlsx. Funktionen er tilgængelig, fordi vi ovenfor har indlæst biblioteket “openxlsx”, der indeholder denne funktion. Det er nødvendigt først at indlæse “openxlsx” biblioteket, for at vi kan få adgang til read.xlsx.
I eksemplet her i modul 1 anvender vi data i Excel-filen “Boligsiden.xlsx”.
# indlæs data
bolig <- read.xlsx("Boligsiden.xlsx", colNames = TRUE, detectDates = TRUE)Indledende analyse
Overblik over data
Når man skal analysere et datasæt, er det altid en god idé først at skabe sig et overblik over datasættet. Et sted at starte er ved at bruge ``str’’-funktionen til at vise strukturen (“structure”), dvs. variabeltyperne, i datasættet.
# vis strukturen ("structure) af data
str(bolig)
## 'data.frame': 9162 obs. of 10 variables:
## $ Postnummer : num 2800 2800 2800 2800 2800 2800 2800 2800 2800 2800 ...
## $ Vejnavn : chr "Vinagervej" "Vinagervej" "Vinagervej" "Vinagervej" ...
## $ Husnummer : chr "15" "15" "21" "23" ...
## $ Salgspris : num 4700000 4000000 2800000 3400000 4900000 ...
## $ Salgsdato : Date, format: "2016-08-16" "2006-12-28" "2014-02-27" ...
## $ Opførselsår : num 1954 1954 1951 1955 1959 ...
## $ Antal.værelser : num 5 5 5 7 8 6 6 6 7 5 ...
## $ Grundareal : num 1149 1149 1568 1764 2146 ...
## $ Boligareal : num 120 120 211 190 181 206 206 156 176 105 ...
## $ Tidligere.solgt: chr "Nej" "Nej" "Nej" "Ja" ...Navnene på variablene i datasættet kan fås frem ved hjælp af names.
# vis navnene på variablene i datasættet
names(bolig)
## [1] "Postnummer" "Vejnavn" "Husnummer" "Salgspris" "Salgsdato"
## [6] "Opførselsår" "Antal.værelser" "Grundareal" "Boligareal" "Tidligere.solgt"Antallet af observationer, dvs. antallet af rækker i datasættet, fås frem med ``nrow’’ (“number of rows”).
# vis antal rækker i datasættet
nrow(bolig)
## [1] 9162Antallet af variable, dvs. antallet af søjler i datasættet, fås frem med ncol (“number of cols”).
# vis antal søjler i datasættet
ncol(bolig)
## [1] 10Man kan se de første n observationer (rækker) i datasættet med head(n).
# vis første 10 observationer af Salgspris
head(bolig$Salgspris, 10)
## [1] 4700000 4000000 2800000 3400000 4900000 4150000 5175000 3450000 3325000 2900000På tilsvarende vis kan man se sidste n observationer i datasættet med tail(n).
# vis sidste 10 observationer af Salgspris
tail(bolig$Salgspris, 10)
## [1] 1350000 720000 1400000 800000 870000 1000000 1585000 1100000 1900000 1900000Ved at formulere “logiske betingelser” og summere over dem (med sum) kan man beregne, for hvor mange observationer en given betingelse er opfyldt.
# find antal boliger med Salgspris på mindst 5 mio. kr.
sum(bolig$Salgspris >= 5000000)
## [1] 3389Ofte har man behov for at lave deldatasæt af det oprindelige datasæt, bestemt ved at deldatasættet opfylder en eller flere logiske betingelser. Et deldatasæt kan konstrueres ved at “filtrere” det opfindelige datasættet ud fra den eller de opstillede betingelser (med filter).
# lav deldatasæt af boliger med Salgspris på mindst 5 mio. kr.
bolig.5mio <- filter(bolig, "Salgspris" >= 5000000)# vis første 5 boliger med Salgspris på mindst 5 mio. kr.
head(bolig.5mio, 5)
## Postnummer Vejnavn Husnummer Salgspris Salgsdato Opførselsår Antal.værelser Grundareal Boligareal
## 1 2800 Vinagervej 15 4700000 2016-08-16 1954 5 1149 120
## 2 2800 Vinagervej 15 4000000 2006-12-28 1954 5 1149 120
## 3 2800 Vinagervej 21 2800000 2014-02-27 1951 5 1568 211
## 4 2800 Vinagervej 23 3400000 2014-03-23 1955 7 1764 190
## 5 2800 Vinagervej 25 4900000 2009-12-18 1959 8 2146 181
## Tidligere.solgt
## 1 Nej
## 2 Nej
## 3 Nej
## 4 Ja
## 5 JaDet kan ofte være bekvemt at få udskrevet et datasæt på en “pæn” måde (i et separat output-vindue) ved at bruge View.
# vis boliger med Salgspris på mindst 5 mio. kr. i output-vindue
View(bolig.5mio)Numerisk variabel
En god måde at danne sig et overblik over numeriske variable i et datasæt er ved at beregne forskellige summariske størrelser med summary.
# beregn summariske tal for alle variable
summary(bolig)
## Postnummer Vejnavn Husnummer Salgspris Salgsdato Opførselsår
## Min. :2800 Length:9162 Length:9162 Min. : 85000 Min. :2006-01-02 Min. :1541
## 1st Qu.:2900 Class :character Class :character 1st Qu.: 826750 1st Qu.:2008-04-28 1st Qu.:1926
## Median :2920 Mode :character Mode :character Median : 3600000 Median :2011-03-07 Median :1939
## Mean :4350 Mean : 4193338 Mean :2011-04-27 Mean :1939
## 3rd Qu.:6270 3rd Qu.: 6291250 3rd Qu.:2014-04-08 3rd Qu.:1965
## Max. :6792 Max. :75000000 Max. :2016-12-31 Max. :2017
## Antal.værelser Grundareal Boligareal Tidligere.solgt
## Min. : 1.000 Min. : 33 Min. : 38.0 Length:9162
## 1st Qu.: 4.000 1st Qu.: 663 1st Qu.: 123.0 Class :character
## Median : 5.000 Median : 830 Median : 154.0 Mode :character
## Mean : 5.351 Mean : 2084 Mean : 165.6
## 3rd Qu.: 6.000 3rd Qu.: 1066 3rd Qu.: 195.0
## Max. :20.000 Max. :1470512 Max. :1205.0Én af de ting der kan have allerstørste betydning for resultatet af de analyser man laver af et givet datasæt er, hvis datasættet indeholder enkelte observationer af numeriske variable, som skiller sig ud fra resten ved enten at være meget små eller meget store (såkaldte “outliers”). Med Outlier-funktionen (fra biblioteket “DescTools” indlæst ovenfor) kan man få hjælp til at finde mulige outliers i datasættet.
Betingelsen na.rm=TRUE betyder, at beregningen ser bort fra eventuelt manglende observationer (NA = Not Available). Uden denne betingelse vil man ikke få returneret nogen brugbar værdi, såfremt datasættet indeholder observationer med manglende værdier.
# find mulige outlier observationer af Salgspris
Outlier(bolig$Salgspris, na.rm=TRUE)
## [1] 15000000 18500000 18250000 15800000 18500000 16950000 19260000 16000000 19995000 17000000 18000000
## [12] 17000000 28000000 19000000 15000000 35900000 15500000 17000000 18000000 15000000 16150000 15000000
## [23] 34000000 34600000 17500000 34000000 27000000 22100000 65000000 50000000 75000000 26500000 19300000
## [34] 19000000 19000000 15000000 20500000 14500000 15100000 18000000 15900000 15700000 15750000 18500000
## [45] 17500000 14500000 15350000 15000000 23000000 23000000 16200000 30000000 15500000 16300000 16500000
## [56] 20700000 15000000 17000000 65500000 37000000 23500000 20000000 17000000 30350000 20000000 28500000
## [67] 55000000 27500000 15500000 20500000 16000000 21500000 15700000 15000000 16445000 20000000 14600000
## [78] 15750000 28000000 19700000 23250000 15700000 14942500 21000000 16650000 23000000 15500000 17500000
## [89] 23441651 23000000 19250000 15000000 14600000 17500000 17500000 17500000 17500000 17500000 17500000
## [100] 16800000 15500000 29000000 18000000 19000000 16300000 19700000 15500000 19500000 22000000 16000000
## [111] 15900000 24000000 18750000 22250000 15500000 17000000 17000000 18000000 15000000 16400000 14900000
## [122] 14500000 16500000 15500000 17200000 24100000 35000000 18000000 16300000 23750000 16750000 16500000
## [133] 16500000 15750000 18000000 14500000 20650000 21700000 19500000 17500000 15600000 15000000 16500000
## [144] 17000000 17000000 17100000 16250000 19125000 34500000 16400000 15600000 24700000 16500000 19500000
## [155] 15091000 14500000 16000000 15000000 26500000 16350000 17750000 16300000 16500000 20000000 24000000
## [166] 14525000 28000000 32500000 16900000 15500000 18250000 22319597 33000000 27150000 34500000
sort(Outlier(bolig$Salgspris, na.rm=TRUE))
## [1] 14500000 14500000 14500000 14500000 14500000 14525000 14600000 14600000 14900000 14942500 15000000
## [12] 15000000 15000000 15000000 15000000 15000000 15000000 15000000 15000000 15000000 15000000 15000000
## [23] 15091000 15100000 15350000 15500000 15500000 15500000 15500000 15500000 15500000 15500000 15500000
## [34] 15500000 15600000 15600000 15700000 15700000 15700000 15750000 15750000 15750000 15800000 15900000
## [45] 15900000 16000000 16000000 16000000 16000000 16150000 16200000 16250000 16300000 16300000 16300000
## [56] 16300000 16350000 16400000 16400000 16445000 16500000 16500000 16500000 16500000 16500000 16500000
## [67] 16500000 16650000 16750000 16800000 16900000 16950000 17000000 17000000 17000000 17000000 17000000
## [78] 17000000 17000000 17000000 17000000 17100000 17200000 17500000 17500000 17500000 17500000 17500000
## [89] 17500000 17500000 17500000 17500000 17500000 17750000 18000000 18000000 18000000 18000000 18000000
## [100] 18000000 18000000 18250000 18250000 18500000 18500000 18500000 18750000 19000000 19000000 19000000
## [111] 19000000 19125000 19250000 19260000 19300000 19500000 19500000 19500000 19700000 19700000 19995000
## [122] 20000000 20000000 20000000 20000000 20500000 20500000 20650000 20700000 21000000 21500000 21700000
## [133] 22000000 22100000 22250000 22319597 23000000 23000000 23000000 23000000 23250000 23441651 23500000
## [144] 23750000 24000000 24000000 24100000 24700000 26500000 26500000 27000000 27150000 27500000 28000000
## [155] 28000000 28000000 28500000 29000000 30000000 30350000 32500000 33000000 34000000 34000000 34500000
## [166] 34500000 34600000 35000000 35900000 37000000 50000000 55000000 65000000 65500000 75000000De mest almindelige nøgletal af beregne - for at få overblik over en variabel i et datasæt - er middelværdi og standardafvigelse (“standard deviation”).
# beregn middelværdi af Salgspris
mean(bolig$Salgspris, na.rm=TRUE)
## [1] 4193338
# beregn standardafvigelse ("standard deviation") af Salgspris
sd(bolig$Salgspris, na.rm=TRUE)
## [1] 4158338For en numerisk variabel er det - udover nøgletal - også en god idé også at tegne et histogram over variablens fordeling. Man kan vælge bredden af søjlerne i histogrammet med breaks.
# tegn histogram af fordelingen af Salgspris
hist(bolig$Salgspris)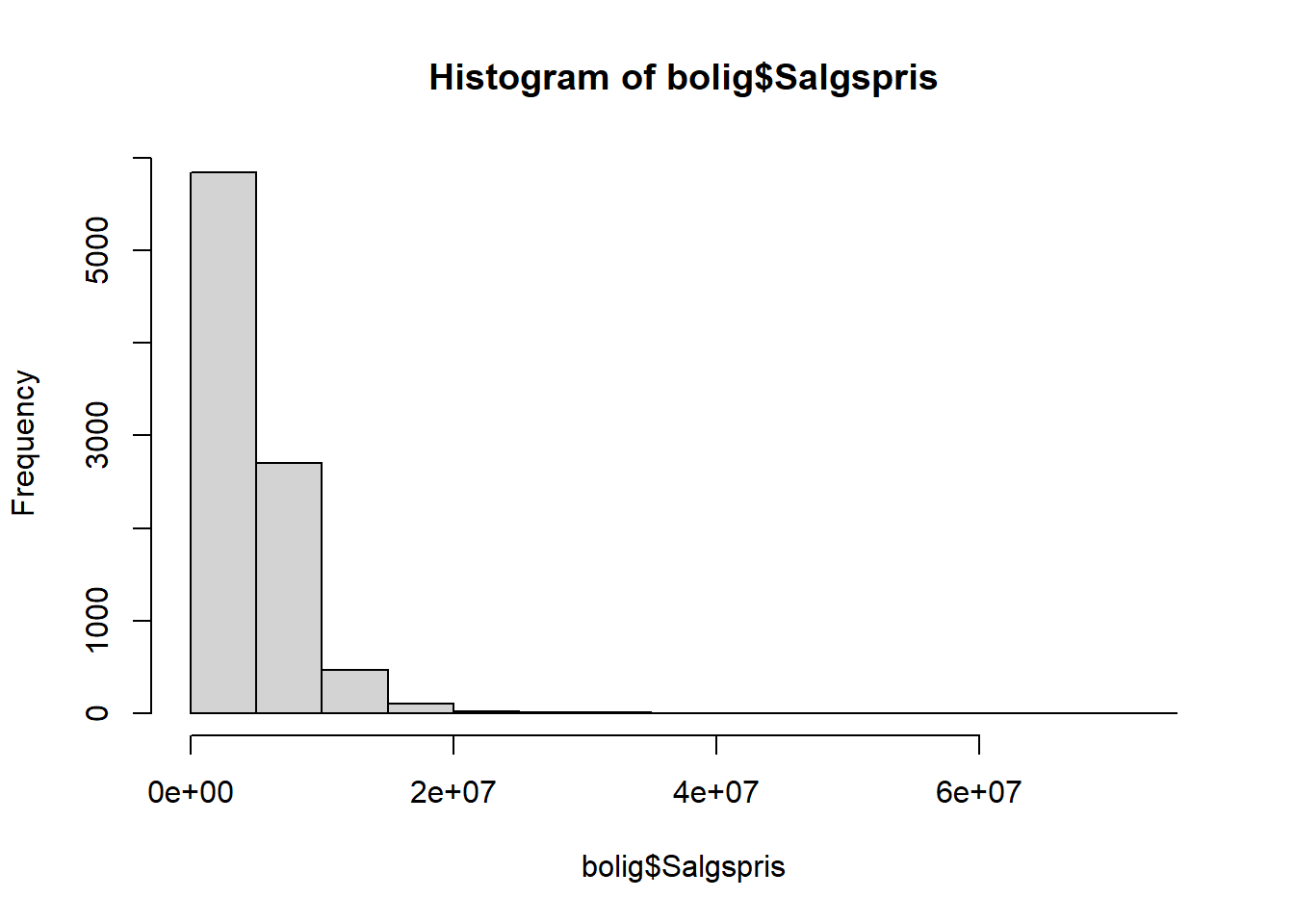
# tegn histogram med finere granularitet
hist(bolig$Salgspris, breaks = 100)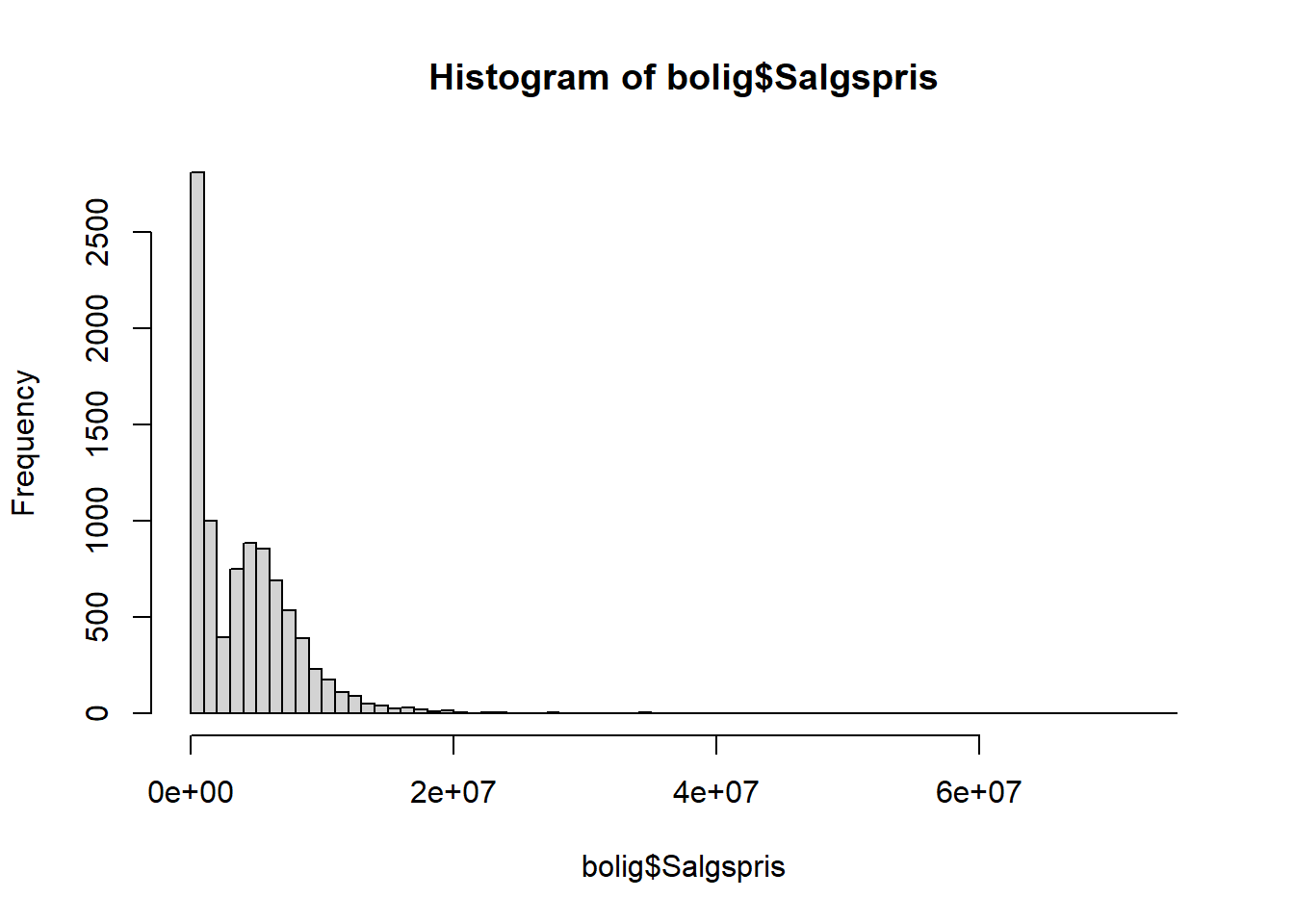
Udover middelværdi og standardafvigelse er det også godt at kende henholdsvis største og mindste værdi.
# vis mindste observation af Salgspris
min(bolig$Salgspris, na.rm=TRUE)
## [1] 85000
# vis største observation af Salgspris
max(bolig$Salgspris, na.rm=TRUE)
## [1] 7.5e+07ligesom det ofte også er bekvemt at kunne beregne udvalgte fraktiler i variablens fordeling
# beregn 10% og 80%-fraktilen af Salgspris
quantile(bolig$Salgspris, probs = c(0.05, 0.80), na.rm=TRUE)
## 5% 80%
## 350000 6995000En måde at imødegå outliers i et datasæt på er ved at “winsorize” data, dvs. sætte et minimum henholdsvis maksimum for variablens værdier og på den måde sikre, at outliers ikke får urimeligt stor indflydelse på eksempelvis nøgletal som middelværdi og standardafvigelse.
I praksis foregår det ved at sætte alle observationer under et valgt mindsteniveau (i eksemplet nedenfor 5%-fraktilen) lig mindsteniveau og på den måde “fjerne” betydningen af de allermindste observationer. Tilsvarende sættes også alle observationer over et valgt størsteniveau (i eksemplet nedenfor 95%-fraktilen) lig størsteniveauet, og på den måde “fjerne” betydningen af de allerstørste observationer.
# winsorize Salgspris på 5%- og 95%-niveau
bolig$Salgspris <- Winsorize(bolig$Salgspris, probs = c(0.05, 0.95))# Se på max/min igen
min(bolig$Salgspris, na.rm=TRUE)
## [1] 350000
max(bolig$Salgspris, na.rm=TRUE)
## [1] 1.1e+07Kategorisk variabel
For en kategorisk variabel giver det ikke mening at beregne nøgletal som middelværdi, standardafvigelse eller andet. I stedet kan man f.eks. se på, hvilke mulige værdier en kategorisk variabel har ved at bruge ``
# vis de mulige værdier af Postnummer
unique(bolig$Postnummer)
## [1] 2800 2820 2870 2900 2920 2930 6240 6261 6270 6280 6520 6534 6535 6541 6780 6792Indledende grafisk analyse
Numerisk variabel
Til at supplerende det indledende overblik over datasættets variable ved hjælp af numeriske beregninger, er det altid en god idé også at lave en række forskellige figurer. Vi har allerede ovenfor set, hvordan vi kan tegne et histogram med hist-funktionen.
Mere generelt, så kan man bruge funktionerne i ““ggplot2”-biblioteket (indlæst ovenfor) til at tegne en masse forskellige grafer med. Biblioteket tillader en stor grad af fleksibilitet i forhold til hvordan man ønsker sine grafer tegnet og har samtidig den fordel, at det - med stort set samme syntaks (= kode) - kan bruges til at tegne mange forskellige typer af grafer med. Bibliteket bruger funktionen aes (“AESthetic mapping” = æstetiske figurer) til at angive hvilke variable, man ønsker i sin figur.
Man kan eksempelvis tegne et histogram på følgende måde (hvor binwidth angiver bredden af søjlerne i histogrammet):
# histogram af fordelingen af Salgspris
ggplot(bolig, aes(x = Salgspris)) +
geom_histogram(binwidth = 500000)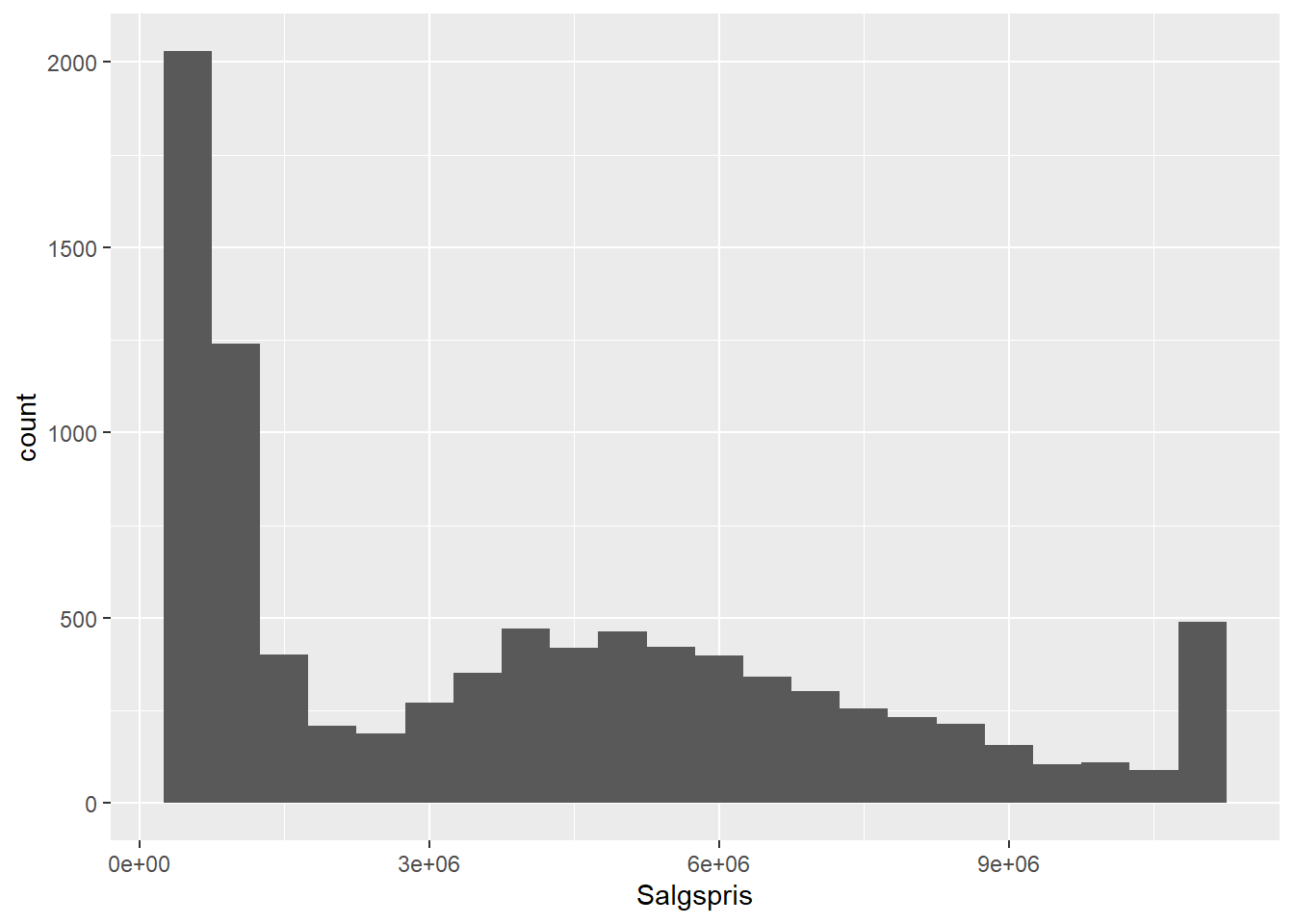
På samme måde kan man tegne et scatterplot af punkter (POINT i geom_pointindikerer, at der tegnes punkter) af to variable mod hinanden.
# scatterplot af Salgspris mod numerisk variabel Boligareal
ggplot(bolig, aes(x = Boligareal, y = Salgspris)) +
geom_point()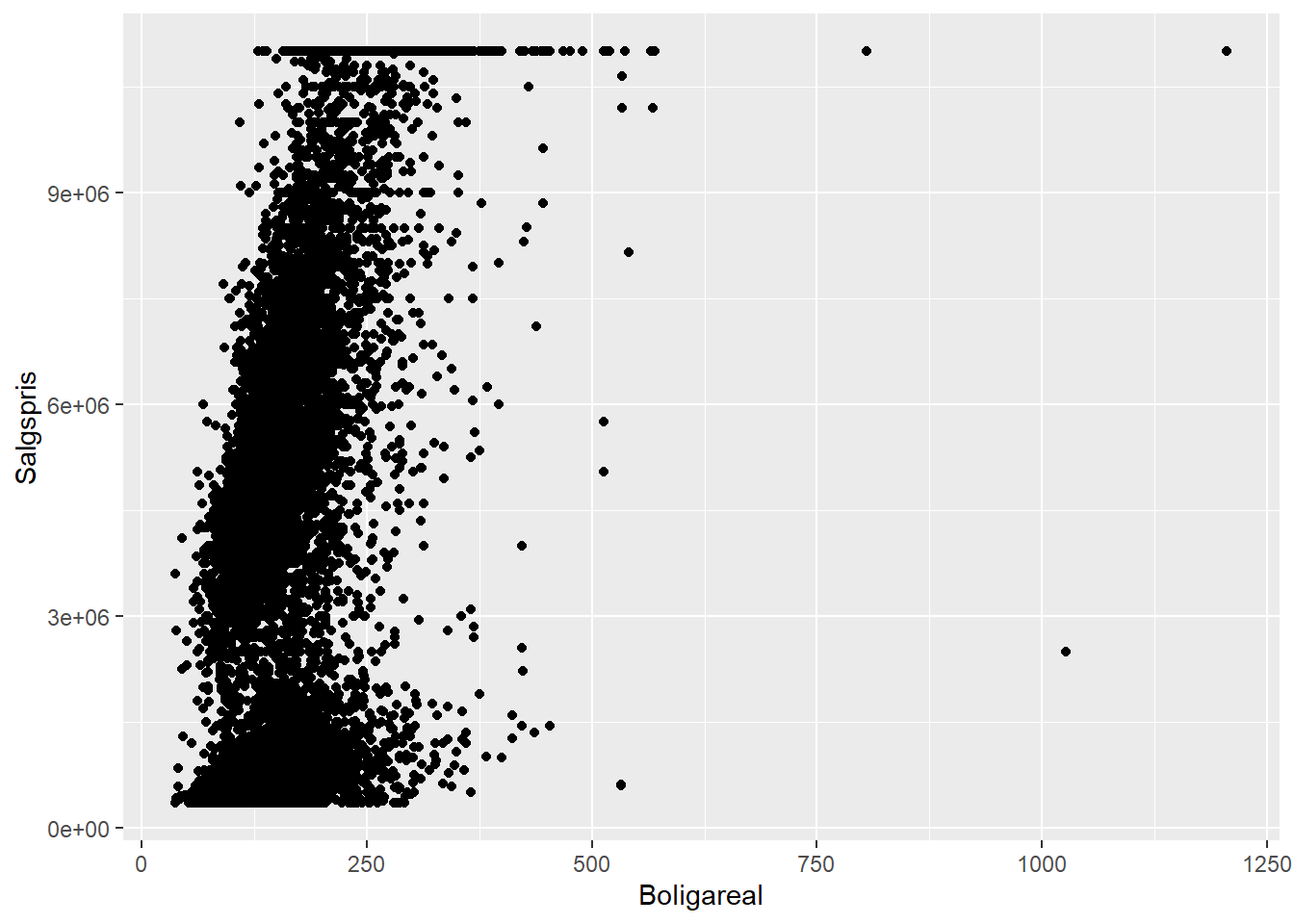
Der findes som nævnt mange måder at tilpasse “ggplot”-figurer på, f.eks. ved at ændre på størrelsen og formen af punkterne i et scatterplot eller ændre på længden af x- eller y-aksen.
# scatterplot med diverse justeringer af figuren
ggplot(bolig, aes(x = Boligareal, y = Salgspris)) +
geom_point(size = 2, shape = 23) +
xlim(0, 1000) +
ylim(0, 6000000)
## Warning: Removed 2476 rows containing missing values (`geom_point()`).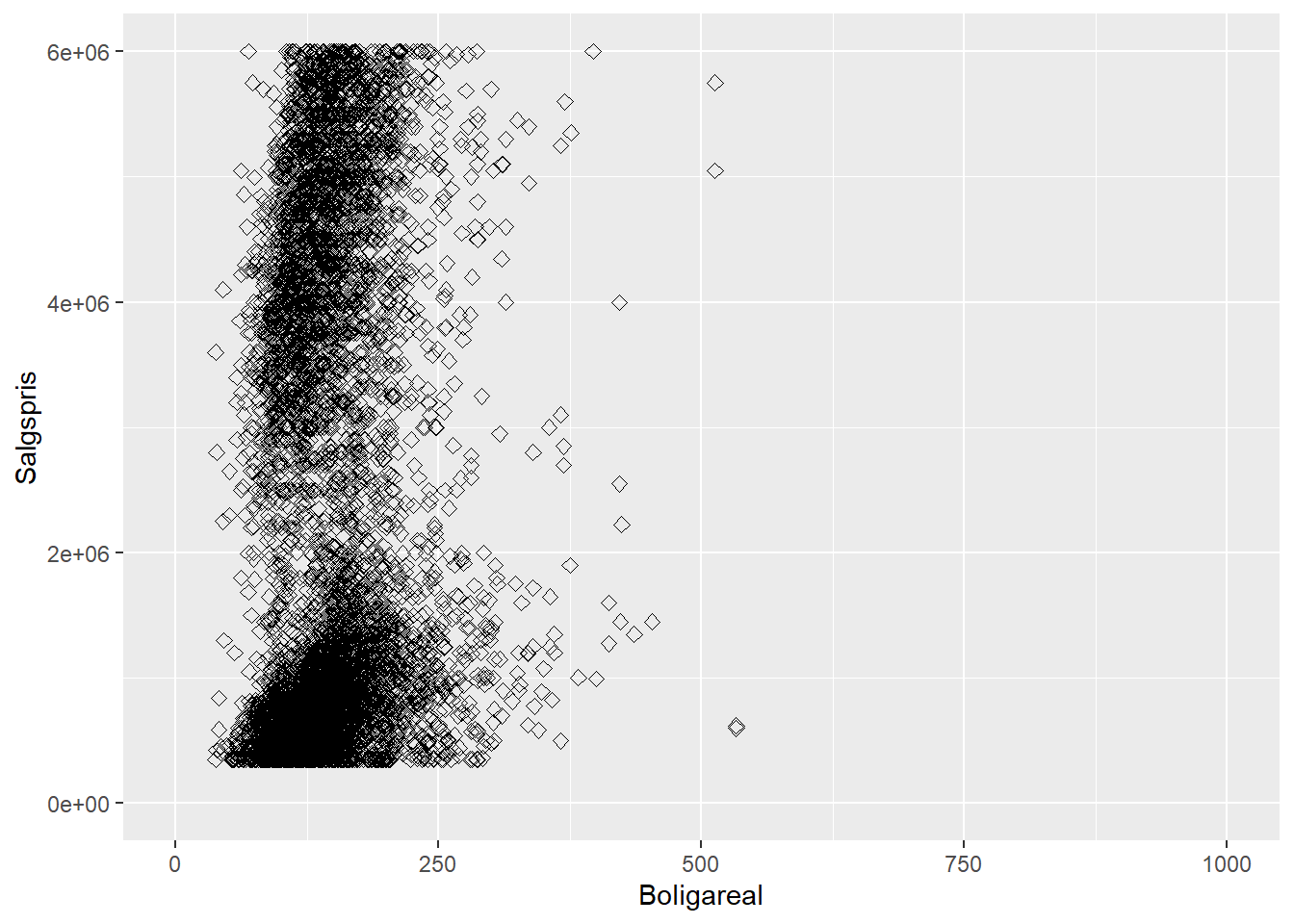
Et scatterplot giver kun mening hvis man ser på to variable, der begge er numeriske. Hvis man i stedet har to variable, hvor den ene er kategorisk og den anden numerisk, så kan man f.eks. i stedet tegne et boxplot af fordelingen af den numeriske variabl opdelt efter værdien af den kategoriske variabel.
# boxplot af Salgspris for hver værdi af kategorisk variabel Tidligere.solgt
ggplot(bolig, aes(x = Tidligere.solgt, y = Salgspris)) +
geom_boxplot()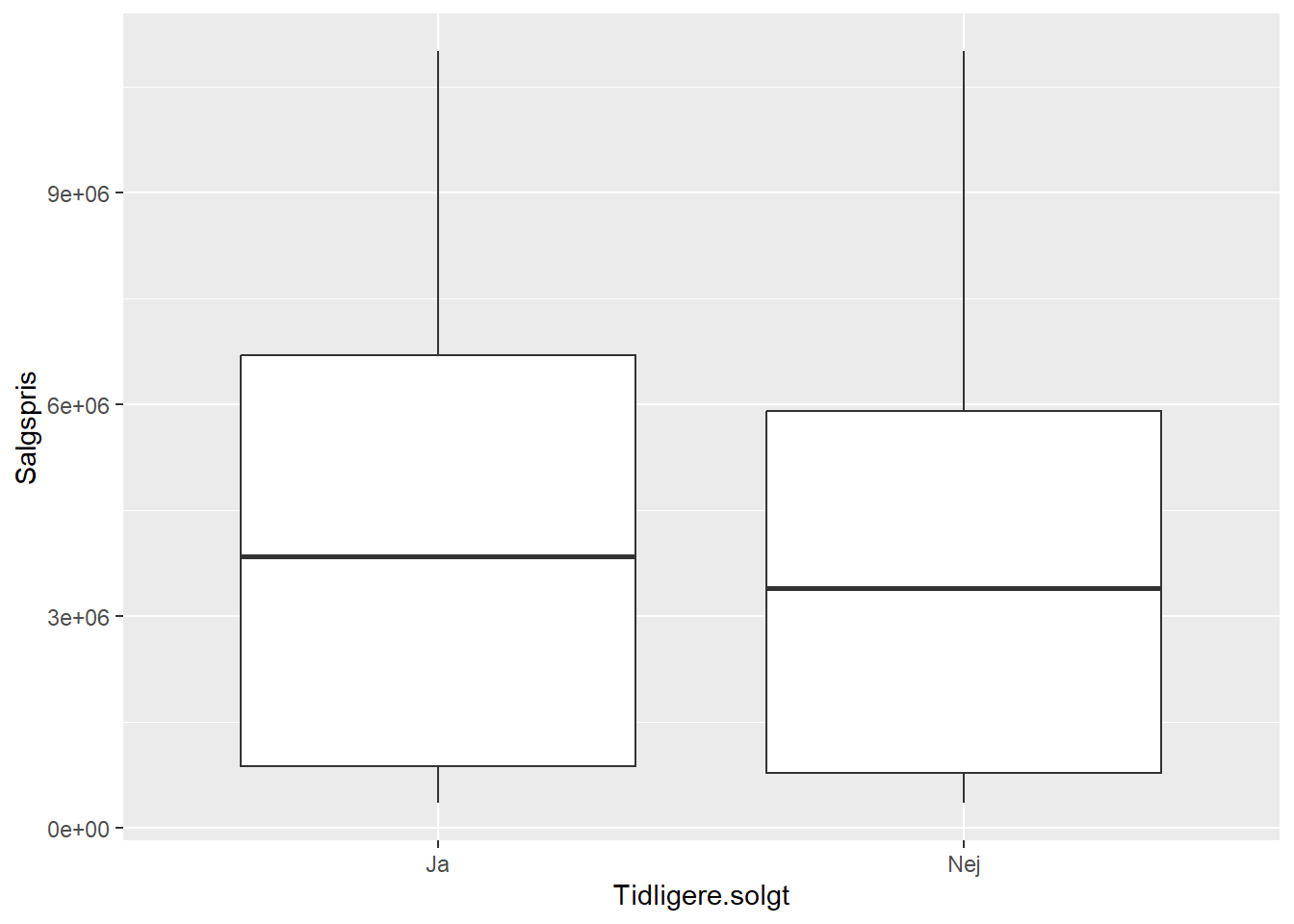
Kategorisk variabel
For kategoriske variable giver det ikke mening at tegne hverken histogrammer eller boxplot. I stedet kan man lave et bar chart af fordelingen af variablen.
# tegn fordelingen af Postnummer
ggplot(bolig, aes(x = factor(Postnummer))) +
geom_bar() +
theme(axis.text.x = element_text(angle = 45, hjust=1))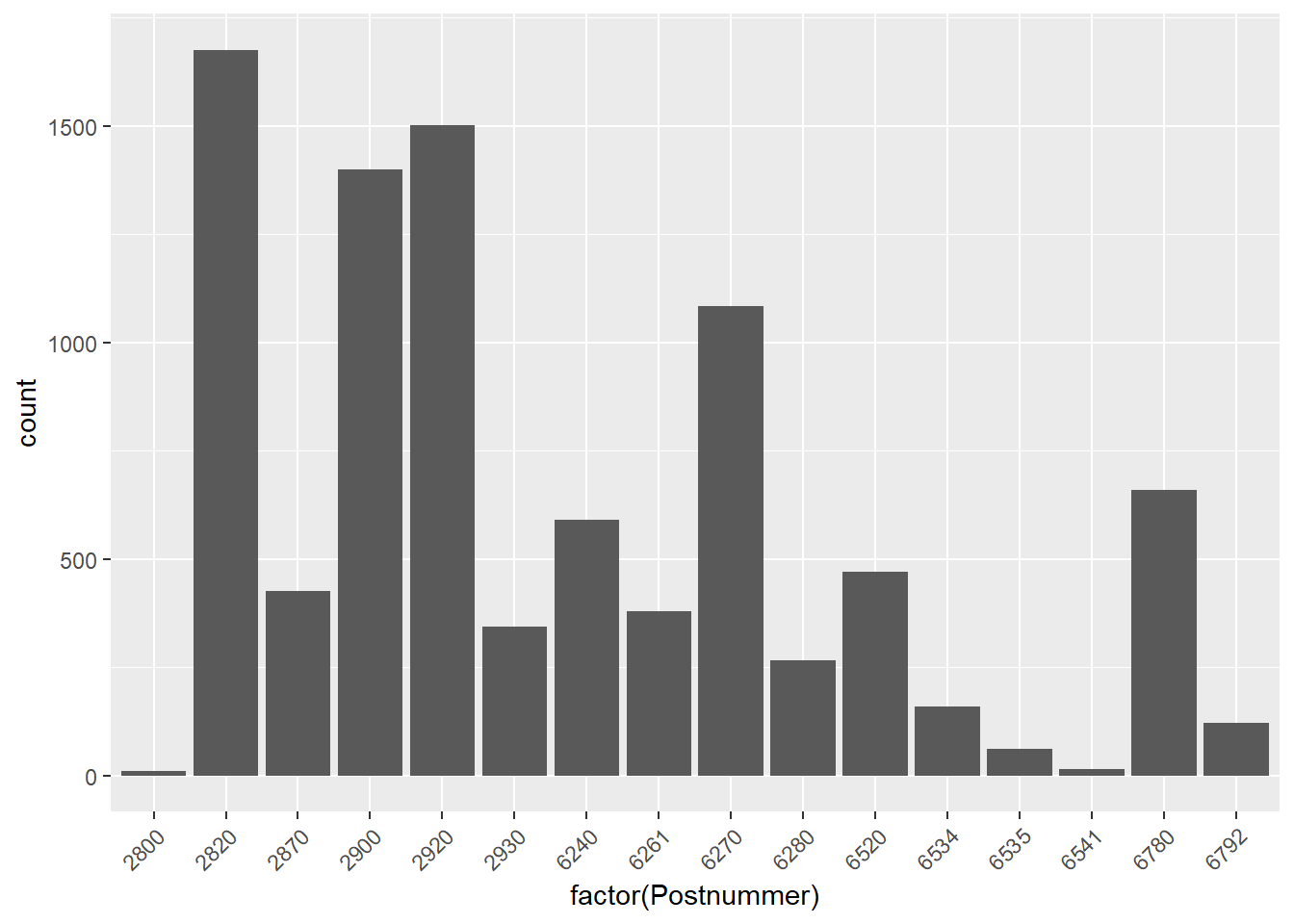
Lineær regressionsanalyse
Efter at have lave en indledende numerisk og grafisk analyse af variablene i sit datasæt er man klar til at gå i gang med mere avancerede metoder med henblik på at opnå større indsigt i de sammenhænge, datasættet rummer. Den naturlige første analyse at se på er den lineære regressionsanalyse (forudsat den giver mening for det datasæt, man kigger på).
Til at illustrere hvordan man laver en lineær regressionsanalyse udvælger vi først et deldatasæt af vores store datasæt. Vi er her interesseret i at undersøge, hvorledes en boligs salgspris (Salgspris) afhænger af boligens opførelsesår, antal værelser i boligen, arealet af den grund boligen ligger på (i \(m^2\)) og arealet af selve boligen (i \(m^2\)).
# nyt deldatasæt med variablene Salgspris, Opførselsår, Antal.værelser, Grundareal, Boligareal
bolig0 <-
select(bolig,
c(
Salgspris,
Opførselsår,
Antal.værelser,
Grundareal,
Boligareal
))Grafisk analyse
Inden vi estimerer den lineære regressionsmodel er det en god idé at tegne scatterplots af alle datasættets variable mod hinanden (to ad gangen) for at se, om der umiddelbart er tegn på indbyrdes sammenhænge mellem variablene. Man kan tegne alle scatterplots på én gang med PlotPairs-funktionen fra “DescTools”-biblioteket.
# indbyrdes scatterplots af deldatasættets variable
PlotPairs(bolig0)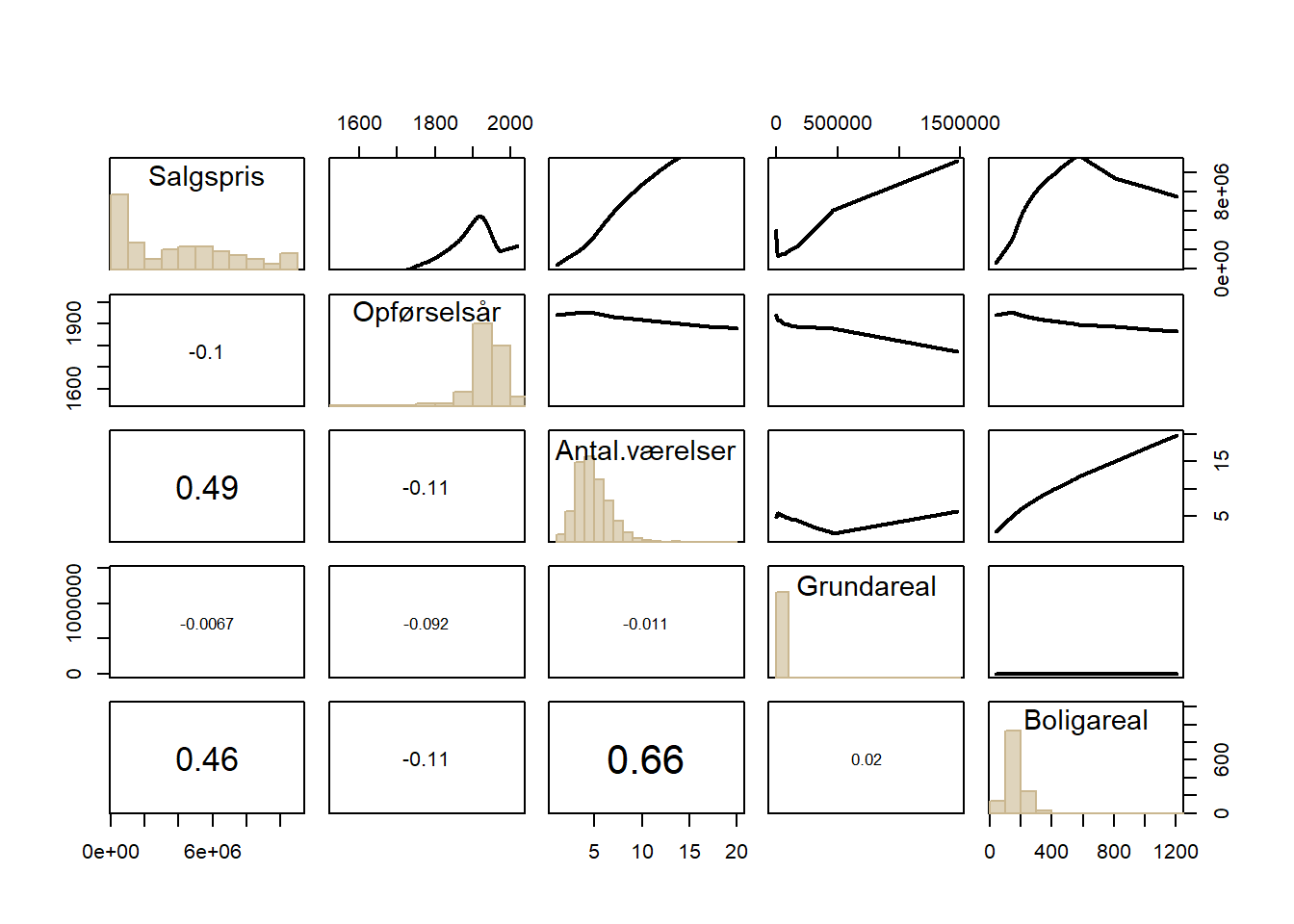
Estimation
Vi er nu klar til at estimere en lineær regressionsmodel (lm = Linear Model). Ved at angive . i formlen nedenfor indikerer vi, at vi ønsker at bruge alle datasættets variable (bortset fra responsvariablen Salgspris) som forklarende variable.
# opstil multipel lineær regression med responsvariabel Salgspris
bolig0.mlr <- lm(Salgspris ~ ., data = bolig0)
# Samme som:
# bolig0.mlr <- lm(Salgspris ~ Opførselsår + Antal.værelser + Grundareal + Boligareal, data = bolig0)Der findes mange måder at gengive resultatet af den estimerede model på. Én måde er ved at se på en kort opsummering af estimationen.
# Vis regressionsmodel
summary(bolig0.mlr)
##
## Call:
## lm(formula = Salgspris ~ ., data = bolig0)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13882648 -2097543 -86124 2072493 8772984
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.096e+06 1.364e+06 3.735 0.000189 ***
## Opførselsår -3.281e+03 6.961e+02 -4.713 2.48e-06 ***
## Antal.værelser 6.042e+05 2.221e+04 27.204 < 2e-16 ***
## Grundareal -2.006e+00 1.500e+00 -1.337 0.181180
## Boligareal 1.213e+04 5.836e+02 20.784 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2794000 on 9157 degrees of freedom
## Multiple R-squared: 0.2747, Adjusted R-squared: 0.2744
## F-statistic: 867 on 4 and 9157 DF, p-value: < 2.2e-16I nogle sammenhænge er vi meget interesserede i at se på, hvor signifikant hver af modellens forklarende variable er i forhold til at forklare værdien af responsvariablen Salgspris. I Machine Learning er der imidlertid ofte et lidt andet fokus. Her handler det først og fremmest om at finde modeller, der giver så god en beskrivelse af responsvariablen som muligt, mens vi ofte er mindre interesserede i, hvilke variable der bidrager med hvor meget til forklaringen. Sidstnævnte skyldes, at de modeller vi skal se på, enten ikke muliggør at se på, hvilke variable der forklarer hvor meget, eller også at modellerne indeholder så mange variable, at det i praksis er tæt på umuligt at lave en sådan analyse.
I stedet for at se på signifikans af forklarende variable, er vi i stedet interesseret i at se på, hvor godt modellen er i stand til at beskrive responsvariablens værdier. Vi beregner derfor først modellens “fittede” værdier, dvs. de modeller modellen forudsiger for responsvariablen Salgspris.
# beregn estimerede værdier af responsvariabel
bolig0.fit <- fitted(bolig0.mlr)For at kunne vurdere om vi har en god eller en dårlig model, sammenligner vi de “fittede” værdier med de faktisk observerede værdier ved at trække de to tal fra hinanden, så vi på den måde får modellens residualer. \[\textrm{residual}=\textrm{faktisk værdi} - \textrm{fittet værdi}\].
# beregn residualer
bolig0.residual <- residuals(bolig0.mlr)Vi kan udskrive de fittede (estimerede) værdier, de faktiske værdier og de deraffølgende residualer for bedre at forstå, hvordan residualerne er beregnet.
# vis estimeret værdi, faktisk værdi og residual for første 10 observationer
bolig0.faktisk_vs_fit <- data.frame(bolig0$Salgspris, bolig0.fit, bolig0.residual)
head(bolig0.faktisk_vs_fit, 10)
## bolig0.Salgspris bolig0.fit bolig0.residual
## 1 4700000 3159914 1540085.90
## 2 4000000 3159914 840085.90
## 3 2800000 4272683 -1472683.10
## 4 3400000 5212854 -1812853.83
## 5 4900000 5694002 -794002.35
## 6 4150000 4833954 -683954.14
## 7 5175000 4833954 341045.86
## 8 3450000 4228022 -778021.90
## 9 3325000 5060909 -1735908.56
## 10 2900000 2984618 -84617.74Evaluering af model fit
Til at vurdere præcis hvor god en given model er, har vi forskellige talstørrelser, der alle har til formål at se på afstanden mellem model og data. I praksis sker det ved at se på hvor store de ovenfor beregnede residualer er.
De tre mål vi vil se på er…
- “mean squared error”
- “root mean squared error”
- “mean absolute error”
Alle tre størrelser måler afstanden mellem model og data, og jo større værdi desto dårligere en sammenhæng er der mellem model og data.
# beregn mean squared error (mse)
bolig0.mse <- MSE(bolig0.fit, bolig0$Salgspris)
bolig0.mse
## [1] 7.803015e+12# beregn root mean squared error (rmse)
bolig0.rmse <- RMSE(bolig0.fit, bolig0$Salgspris)
bolig0.rmse
## [1] 2793388# beregn mean absolute error (mae)
bolig0.mae <- MAE(bolig0.fit, bolig0$Salgspris)
bolig0.mae
## [1] 2346914