2  激斗？“机人” vs “袋人”!

你们可能要熟悉一下我的这种标题党的风格，毕竟这些题目是我花了很久的时间想的。社会心理学的研究者，最擅长的就应该是起这种看上去很有趣的陷阱题目，等你开始读就会发现上当了。

心理统计的真正起点，其实就在两组数据的比较上，从这里开始，就是真正会在发表出来的文章中大量使用的统计方法了。对于心理学这门学科来说，这一点也不奇怪，毕竟我们是一门自诩为科学的学科。那么最自然的，验证因果关系的研究设计，就是一个实验组和一个控制组，通过操纵自变量的水平，探究其对因变量的影响。下面我们就开始回忆一下对这样数据的分析。

首先，我们得有一个数据。由于我是一个很懒的人，不想另外去找一个数据，还要单独提供下载方式，我们直接用下面的代码生成一个“假”数据。因为这不是一本工具书，所以不可能展开讲每段代码具体做了什么，感兴趣的读者可以复制代码后问AI这段代码在做什么，我也尽量写了简单的注释在每段代码上。

## 设定随机种子，保证你能用这段代码得到跟我一样的结果
set.seed(233)
## 生成被试ID
ID <- c(1:100)
## 分类变量（预测变量）
iden <- as.factor(c(rep("武装直升机",50),rep("某品牌塑料袋",50)))
## 连续变量（结果变量）
magic_score <- c(rnorm(n = 50, mean = 80, sd = 10),
                 rnorm(n = 50, mean = 95, sd = 10))
## 生成数据框，不准确的说，就是我们储存上述数据的一个表格
df1.1 <- data.frame(ID,iden,magic_score)
## 看看数据框长啥样
head (df1.1)

  ID       iden magic_score
1  1 武装直升机    88.96133
2  2 武装直升机    87.32445
3  3 武装直升机    76.91846
4  4 武装直升机    70.48573
5  5 武装直升机    76.43755
6  6 武装直升机    93.16133

tail (df1.1)

     ID         iden magic_score
95   95 某品牌塑料袋    99.56399
96   96 某品牌塑料袋    91.93178
97   97 某品牌塑料袋   102.76563
98   98 某品牌塑料袋    91.71003
99   99 某品牌塑料袋   110.25008
100 100 某品牌塑料袋    88.94833

这就是一个我们在学习心理统计时最开始会看到的数据形式了。为了方便大家理解，一个具有现实意义的两水平分类变量当然使用性别最为直观。但是我又不想使用男女这两个现实里纷争不断的性别，以避免无形中再次强化读者们的性别意识。所以使用了“武装直升机”和“XXX塑料袋”这两个网上常见的梗，由于不想在书里为任何品牌宣传，所以又把品牌名字隐去，变成了“某品牌塑料袋”。由此可见我是一个性格上相当谨慎的人了。出于这份谨慎，我还想强调一下使用这两个性别认同只是善意的开个多元性别的玩笑，我本人并不反对lgbtq+运动。

故事的设定是这样，在很近很近的时间点上，也许是平行宇宙，有一个不为你知的世外桃源，上面生活这这样两群人，一群人的自我性别认同是武装直升机，另一群人的自我认同是某品牌塑料袋。由于这两个认同名称实在有点长，后文中我们分别简称他们为“机人”和“袋人”。

好！所以现在我们有了我们的自变量性别认同，在数据里它叫做 iden 。¹ 那么因变量是什么呢，因为我不想用各种成绩或者智商之类的变量，所以把因变量称呼为魔法天赋分数，在数据里它叫做 magic_score。你可以理解成魔法天赋分数越高的人，越有可能有猫头鹰带着录取信敲你窗户。作为一个会闲着没事看睡前统计读物的人，我们当然很关心一个人的魔法天赋是否会受到性别认同的影响。显而易见的，自我认同为武装直升机的机人有着更强的机械亲和，而应该在魔法天赋上逊于自我认同为某品牌塑料袋的袋人。这就是我们的研究假设，机人与袋人的魔法天赋水平有差异。²

2.1 谁的天赋高？回答我！³

首先我们来看一下上面生成的数据的描述统计：

在上面的图里，呈现了袋人和机人魔法天赋分数的情况。我把四种不同的图例叠在了一起。红色的三角形标示的是两组数据的平均数。里面像鱼籽一样的小泡泡，是两组人魔法天赋的散点图，也就是每个点代表一个人的魔法天赋分数。如果你学过心理统计，就会知道什么是箱线图，如果你没学过，看箱线图这么个名字，也能猜出有箱子有线的图是哪个。至于它怎么表示数据的，随便搜一搜或者找AI问问就行，简单来说它就是使用了最大值、最小值、四分位数和中位数标示数据分布情况的图例。最后一种没讲的就是我赶时髦画的小提琴图了，它能直观的反映数据的分布情况，具体怎么理解还是你们自己上网找答案吧。

我们设想一下，如果我们生成的这组数据，就是这个世外桃源里的所有机人和袋人的魔法天赋情况。这时候，我如果问你，这个世外桃源里的机人与袋人的魔法天赋水平有没有差异，你会怎么回答？

你大概会指着图跟我说，有。然后我追问，你怎么看出他们有差异的。你大概会说，你看啊，机人的魔法天赋分数比袋人的低。我说，怎么算低呢，你看这里面有的机人的点比有的袋人的点还高呢。你说，你要看平均数啊，机人的魔法天赋数据平均就是比袋人低呢，你瞎了吗，那两个三角形。

读者们可能看出来了，我就是那种上课喜欢追着学生问大家都知道答案的问题的那种怪老师。

上面的问答，其实就揭示了我们最朴素的统计过程。在比较两组数据时，我们天然的喜欢使用平均数这样的指标帮助我们理解数据是个“什么情况”。比如，如果你有幸当过班干部或者课代表，老师让你“统计”一下两个班同学的期末考情况你会怎么回答呢？

“报告老师！1班里这次英语成绩比2班好，平均分高了5分。“

这就是统计的过程，平均数就是一个最典型的对于数据集中趋势的描述。通过比较平均数，我们就回答了我们的研究问题，机人与袋人的魔法天赋水平有差异。

这时候肯定有读者不理解了，“那我问你，那我问你，你跟我说你要讲统计，结果讲了半天就让我比较平均数谁大谁小就能检验假设了。你当我没上过心理统计吗？我那么大一个统计检验去哪了？这数据不是傻子都知道要做独立样本t检验吗？”⁴

我知道你很急，但你先别急。我们接下来就讲独立样本t检验。

2.2 梦开始的地方：推论统计、抽样分布与独立样本t检验

2.2.1 样本与推论统计

就如上面那节里的暴躁老哥所说，这样的数据，拿去问心理统计课程最终及格的本科同学应该使用什么统计分析，想必他们都会不假思索地回答独立样本t检验（One-Sample T test）。没错，我们可以针对这组数据做独立样本t检验。但是，为什么是选择独立样本t检验呢？

现在，给你几分钟的时间，回想整理一下之前在心理统计课程学独立样本t检验的前前后后，找到一个属于你的答案。如果你没上过心理统计，或者脑子里现在一片空白，别担心，我目前还没有抛弃你的打算，往下看。

首先，我们需要确认的是，直接比较平均数验证假设的前提是什么。有一个关键的前提：

如果我们生成的这组数据，就是这个世外桃源里的所有机人和袋人的魔法天赋情况。

换言之，我们的数据本身就是总体，对他们的描述统计就足以检验假设了。那什么时候我们不能只依靠描述统计呢？显然就是我们的数据本身不是总体的情况了。

设想一下，如果这个世外桃源里，生活着大概两三万的机人和袋人。而你是一个贫穷的社科工作者，这时候你要怎么比较机人和袋人的魔法天赋呢？看起来你没钱把这几万人都调查一遍了。答案很简单，除了自己坐在房间里编造一个结果，你只能调查一部分的机人和袋人，通过比较这一部分的结果，“推断”世外桃源里的机人和袋人的真实情况。这个办法，也是一个近乎直觉的选择。

aggregate(magic_score ~ iden, data = df1.1, FUN = mean, na.rm = TRUE)

          iden magic_score
1 某品牌塑料袋    95.29439
2   武装直升机    81.23953

比如你各抽取了50个机人和袋人，假设这就是我们上面使用的数据。平均数算出来分别是81.24和95.29。这时候你说，好，根据我调查的这100人的结果，我宣布假设成立，世外桃源里的袋人比机人魔法天赋高。像我这样的杠精就会跳出来，“异议！总共有几万人呢，你就靠这50个人凭什么说明袋人比机人会魔法？万一你刚好抽到袋人里魔法天赋高的，机人里魔法天赋低的呢？“

聪明的读者一定已经理解了我的意思，凡是随机抽取的样本，都必然会有取样误差。如何做到准确的抽样是研究方法课程的内容，但即使你做到了，比如，严谨的随机抽样，也不能排除抽样带来的干扰。就像我说的，万一你刚好抽到了一个偏离总体情况很多的样本呢？随机的意思就是能给你带来一些惊喜，就像开盲盒一样，哪怕商家不作弊，100款盲盒里有99款你想要的，你也不能保证你一定不手黑抽到唯一一款你不想要的不是么？

2.2.2 零假设显著性检验

所以这时候就需要一个统计工具来告诉你，我们现在的两个样本平均数的差异，多大程度上可以反应两个样本对应的总体确实存在平均数差异，而不是由抽样的随机性带来的差异。这个统计工具，就是我们聪明的统计学家发明的推论统计。我们接下来要介绍的零假设显著性检验（Null hypothesis significance testing, NHST）就是其中的一种形式，也许也是最广泛使用的推论统计方法。⁵

好的，首先我们要再确认一遍我们的研究假设：机人与袋人的魔法天赋水平有差异。

就如上面所说，我们实际会使用的是关于两个群体魔法天赋分数的平均数来比较。机人的魔法天赋平均分我们用${\mu }_{\mathrm{机}\mathrm{人}}$来表示，那么袋人的魔法天赋平均分类似地就是${\mu }_{\mathrm{袋}\mathrm{人}}$。这里的平均数我们使用$\mu$ 而不是M，因为这个平均数代表的是总体而不是样本。一般我们使用希腊字母代表总体的参数，拉丁字母代表样本的参数。注意，我们的研究假设一般是关于总体，也就是现实中的这两个群体做出的，而不是对于我们抽取的样本做的。

那么，转换成数学的形式我们会怎么表述我们的假设呢？

$${\mu }_{\mathrm{机}\mathrm{人}}\ne {\mu }_{\mathrm{袋}\mathrm{人}}$$

是不是显得很简洁明快？我们再使用一下九年义务制教育给我们装备的基础数学能力，移个项，这个式子就可以写作：

$${\mu }_{\mathrm{袋}\mathrm{人}}-{\mu }_{\mathrm{机}\mathrm{人}}\ne 0$$

换句话说，如果机人和袋人的魔法天赋平均分之差不等于0,就说明这两个群体的魔法天赋水平有差异，没毛病吧？

可能有读者开始着急了，这跟推论统计有什么关系呢？咱们想想，我们现在手里没有总体的数据，所以我们需要用的是样本去“推论”总体。实际上就是用样本的两个群体的平均数之差$M_{\mathrm{袋}\mathrm{人}}-M_{\mathrm{机}\mathrm{人}}$之差，来判断总体水平上${\mu }_{\mathrm{袋}\mathrm{人}}-{\mu }_{\mathrm{机}\mathrm{人}}$是否不等于零。

但是，在统计上似乎直接去证明平均数之差不等于零这件事挺困难的，就像俗话说的，证明你做过一件事很容易，证明你没有做过一件事很难一样。所以统计学家们在NHST上使用了一款著名日式法庭推理游戏的经典桥段，把思路“逆转”了一下。既然证明两个平均数之差不等于零很难，那它的“否命题”，两个平均数之差等于零呢？只要我能说，这两个平均数之差等于零是“错”的，不就证明这个差不等于零是“对”的了吗？

所以，关注点转向了这个假设：机人与袋人的魔法天赋水平没有差异。其数学形式是：

$${\mu }_{\mathrm{袋}\mathrm{人}}-{\mu }_{\mathrm{机}\mathrm{人}}=0$$

这个假设叫做零假设或者虚无假设（Null hypothesis；所以你知道NHST指的是什么了吧）。那么统计学家会怎么通过对它的检验达到目的呢？这个过程使用到了抽样分布的概念。

2.2.3 抽样分布

我们前面提到了，抽样会有各种随机因素的干扰，因此我们不能确定我们抽到的样本能不能准确的反映总体。那么一个办法就是，我多抽几次不就行了。抽一次可能会抽偏了，我抽一万次总不能次次都跑偏吧？总归这一万次里，大部分的样本平均数得跟总体差不多吧。那么我把这一万个样本的平均数再算一个平均数，那它肯定得跟总体的平均数接近啊。这个想法其实就描述了统计中中心极限定理的一部分奥义。完整地来说，中心极限定理比较通俗⁶的表述是，反复地从总体里抽n个个体作为样本，一个独立且分布一样的随机变量在这些样本的均值分布会趋近于正态分布，这个正态分布以总体的均值$\mu$为均值，总体的方差${\sigma }^2/n$为方差，$\sigma$是总体的标准差。这个正态分布，就是所谓的抽样分布。

高尔顿板：中心极限定理示意图

上面的高尔顿板就是一个中心极限定理与抽样分布的现实示例。一群小球在下落的旅途里，会遇到一系列的分叉路；每个分叉路，对小球来说往左走或者往右走的概率都是50%⁷。在这样的过程里，小球每经过一次分叉口，其实都相当于一次抽样，我们可以把它看作在概率论里最经典的抽样——抛一次硬币看正反面。所以高尔顿板最后呈现出来的这个结果，实际可以看作一个样本量为分叉次数（每个样本抛了几次硬币为一组），抽样次数（一共抛了多少组）为小球数量的频数分布（硬币为正面的次数作为横坐标）。显然，抛硬币是一个独立且分布一样（二项分布）的随机变量，高尔顿板展示了一个这样的随机变量，在经过了多次抽样后，其均值分布符合我们定义的正态分布。

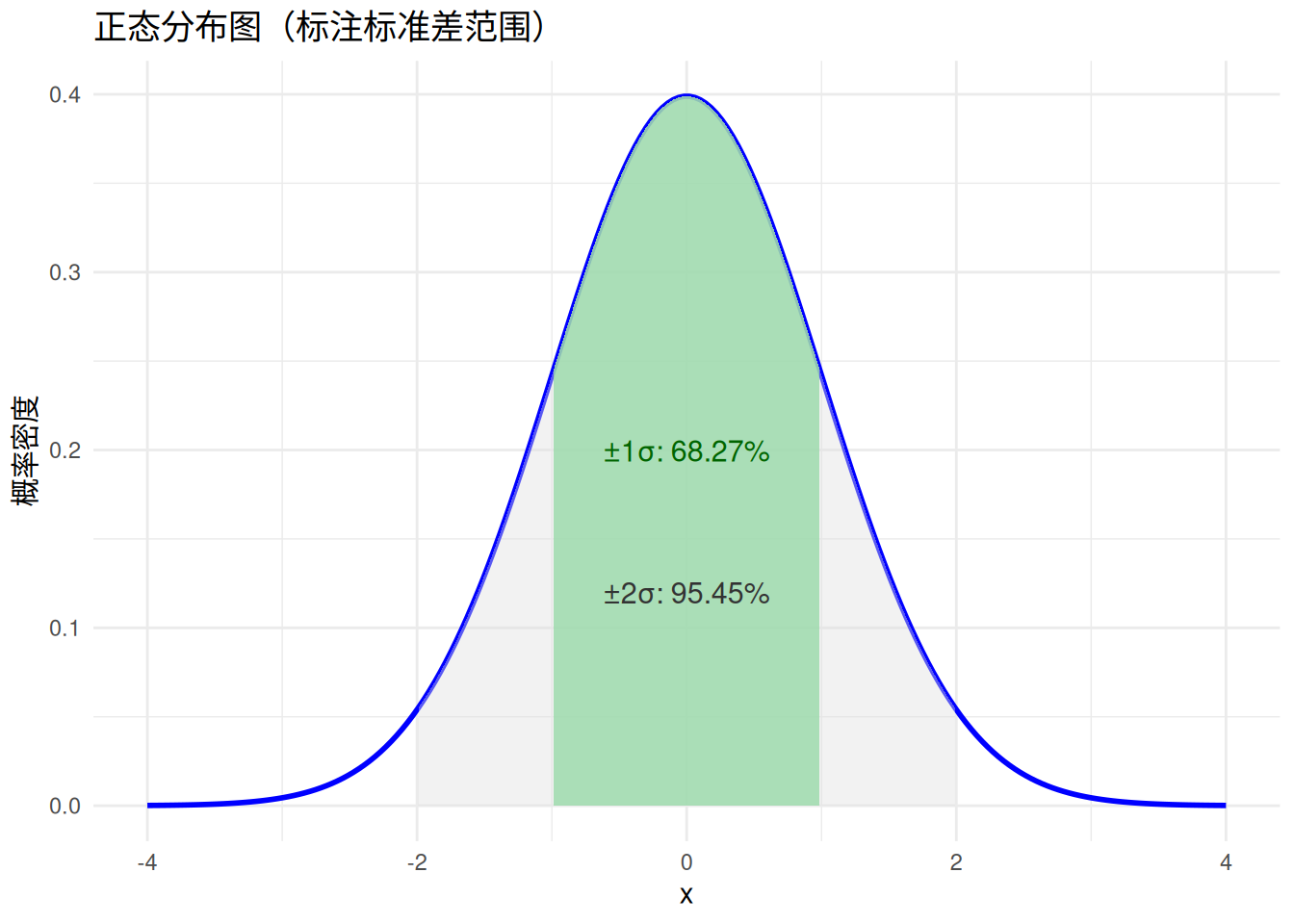
如果你知道正态分布的英文，Normal Distribution，翻译过来就是正常的分布，就大致可以知道这个分布在现实中有多常见，以至于不服从这个分布就“不正常”了（笑）。由于这个这个分布太过正常，所以统计学家们对于它的性质和特点非常非常熟悉。比如，在一个正态分布内，平均数附近一个标准差范围内的数据大致占所有数据的68%，两个标准差范围内的数据则占95%左右。只要知道了一组服从正态分布数据的平均数和标准差，我们就能画出它的分布形态。为了方便起见，统计学家还找到了一个特殊的正态分布，这种分布的平均数为0,标准差为1,我们叫它标准正态分布。而任何服从正态分布的数据，只要把原始分数减去它们的平均数，再除以它们的标准差，就能得到它们的标准正态分数，也就是Z分数。

如果你喜欢看公式，那么$Z=\frac{X-\overline{X}}{s}$,$X$是原始分数，$\overline{X}$ 是原始分数的平均数， $s$ 是原始分数的标准差。

抽样分布服从正态分布意味着什么呢？比如我们有一个均匀的硬币，也就是扔出来是正面和反面的概率都是50%。那么我们反复进行1000组的扔硬币锻炼，每组锻炼扔100次硬币，这100次中硬币正面朝上的个数分布就服从正态分布。那么从概率的角度上说，如果你再自己扔一组100次的硬币锻炼，抽样分布中出现次数越多的正面朝上个数就越可能发生。所以，抽样分布不仅是一个反映了频数，也反映了一个样本出现的可能性。以正态分布的形态来说，越接近中央的地区，出现的概率越大。比如我们上面提到的，两个标准差范围内的数据大致占据了95%的总量，也可以理解为，在进行很多次抽样后，95%的样本的随机变量数据会落在距离平均数两个标准差距离之内。

2.2.4 t分布

那么折腾这么多的意义是什么呢？还记得我们在干嘛吗？我们想要检验我们的虚无假设${\mu }_{\mathrm{袋}\mathrm{人}}-{\mu }_{\mathrm{机}\mathrm{人}}=0$。如果我们的虚无假设式子左边的部分是一个随机变量，就像上面Z分数公式里的X,那么是不是意味着，我们就可以构造出如果这个虚无假设成立的话，它的抽样分布呢？让我们回忆一下，抽样分布的特征是什么，对于一个随机变量X来说，是一个以总体的均值$\mu$为均值，总体的方差${\sigma }^2/n$为方差的正态分布。那么，总体的均值也就是平均数是多少呢？我们的虚无假设式子的右边写着呢，等于0啊。

那么方差是多少呢？显然这一点没在虚无假设中体现。聪明的统计学家找到了一个办法，虽然我们不知道总体的方差，但是我们有样本呀，样本中不就有总体的信息吗。我们可以用样本的方差和容量去估计这个随机变量的抽样分布方差。这个时候，${\mu }_{\mathrm{袋}\mathrm{人}}-{\mu }_{\mathrm{机}\mathrm{人}}$的抽样分布就不是服从正态分布而是一个长得很像但 如果机人和袋人的总体方差是相等的，那么${\mu }_{\mathrm{袋}\mathrm{人}}-{\mu }_{\mathrm{机}\mathrm{人}}$作为一个随机变量的抽样分布服从的就不是正态分布，而是t分布⁸。而要求两组对应的总体方差相等，就是著名的方差齐性假设。

好了，这时候我们就找到了如果我们的虚无假设成立的时候，两个总体均值之差（${\mu }_{\mathrm{袋}\mathrm{人}}-{\mu }_{\mathrm{机}\mathrm{人}}$）的抽样分布。就像正态分布一样，我们一样可以知道，在一个t分布中，有多大比例的数据会分布在均值附近，也就是知道了样本均值在总体均值附近的概率。我们知道样本均值吗，知道呀，机人和袋人的两个样本均值我们都知道，它们的差很容易算。

就像数据可以转换成z分数一样，我们也可以把数据转化成t分数，这样去观察均值差在抽样分布中的位置。

$$\begin{array}{}\text{(2.1)}& t=\frac{{\overline{X}}_1-{\overline{X}}_2}{\sqrt{s_p^2(\frac{1}{n_1}+\frac{1}{n_2})}}\end{array}$$

其中

$$s_p^2=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}$$

敏锐的读者应该已经发现了，其实t分数和z分数的形式很类似，都是均值除以标准差。不过在有两个样本的情况下，我们需要融合两个样本的方差形成一个对两样本方差的总体描述，这就是$s_p^2$。 而推导出$s_p^2$这个公式的前提是两样本的方差相等，也就是我们之前说要求方差齐性的由来。

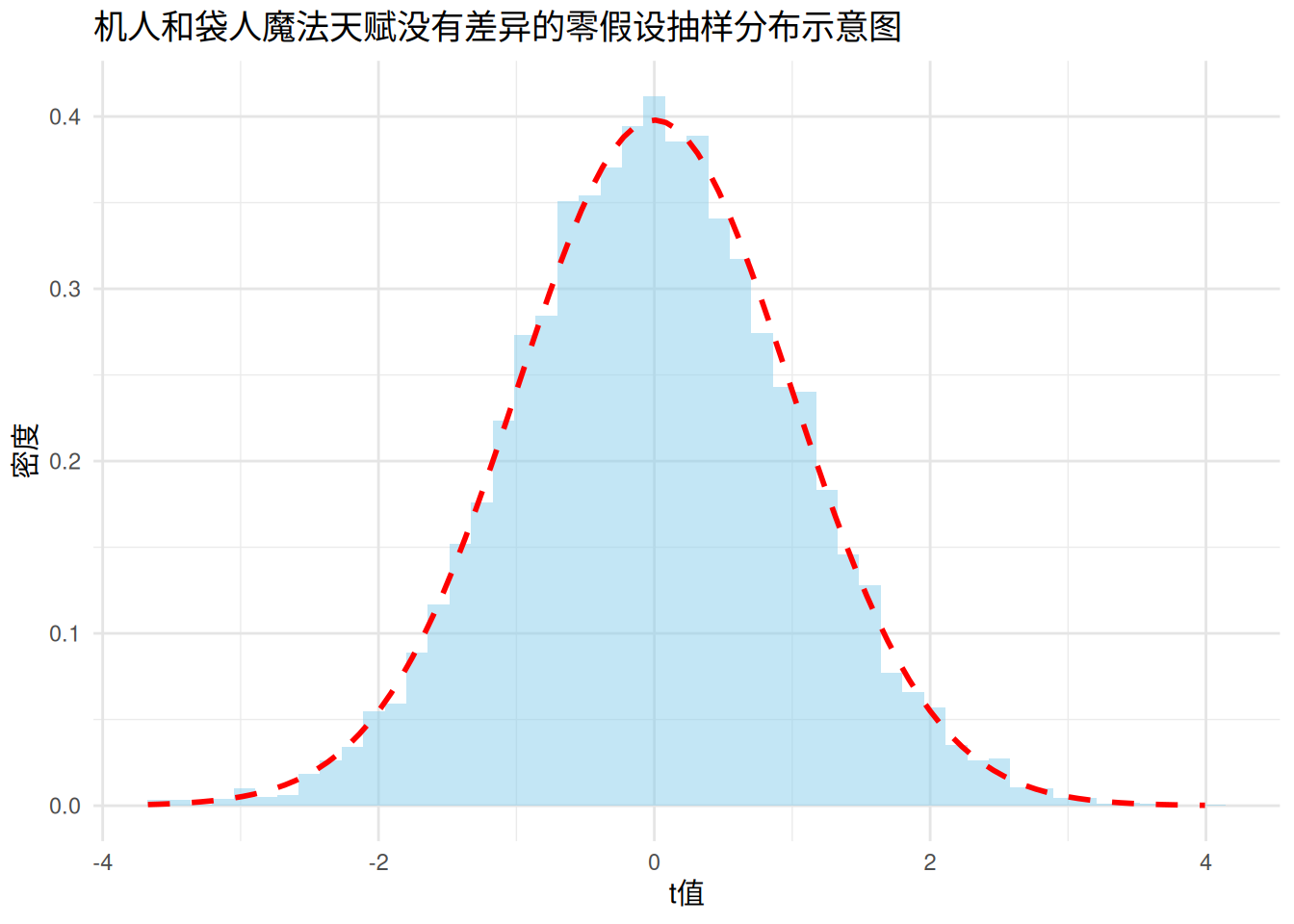
上面的图就是当机人和袋人魔法天赋一样这个零假设成立时，t值的抽样分布了。换句话说，就是如果机人和袋人真的魔法天赋一样，那我们反复地各抽五十个人作为样本计算他们的均值之差，并计算他们的频次，只要抽的次数足够多，就会形成上面的图（上面图里的蓝色直方图就是我们抽了一万次的结果）。在这个图里，t值对应的密度，也就是红色虚线的纵坐标越大，意味着这个t值在抽样中出现的概率越高。所以我们可以看出，集中在均值，也就是t=0（对应${\mu }_{\mathrm{袋}\mathrm{人}}-{\mu }_{\mathrm{机}\mathrm{人}}=0$）极其附近的区域在多次抽样后的发生概率最高。

而根据 Equation 2.1 计算，我们的样本t值是：

## 计算两个样本的均值
X1 <- mean(df1.1[df1.1$iden=="某品牌塑料袋",c("magic_score")])
X2 <- mean(df1.1[df1.1$iden=="武装直升机",c("magic_score")])

## 两个样本的大小均为50人
n1 <- n2 <- 50

## 计算两个样本的方差
s12 <- var(df1.1[df1.1$iden=="某品牌塑料袋",c("magic_score")])
s22 <- var(df1.1[df1.1$iden=="武装直升机",c("magic_score")])

## 计算s^2_p
sp2 <- ((n1-1)*s12 + (n2-1)*s22)/(n1+n2-2)

## 代入公式计算t值
t <- (X1-X2)/sqrt(sp2*(1/n1+1/n2))
t

[1] 7.636829

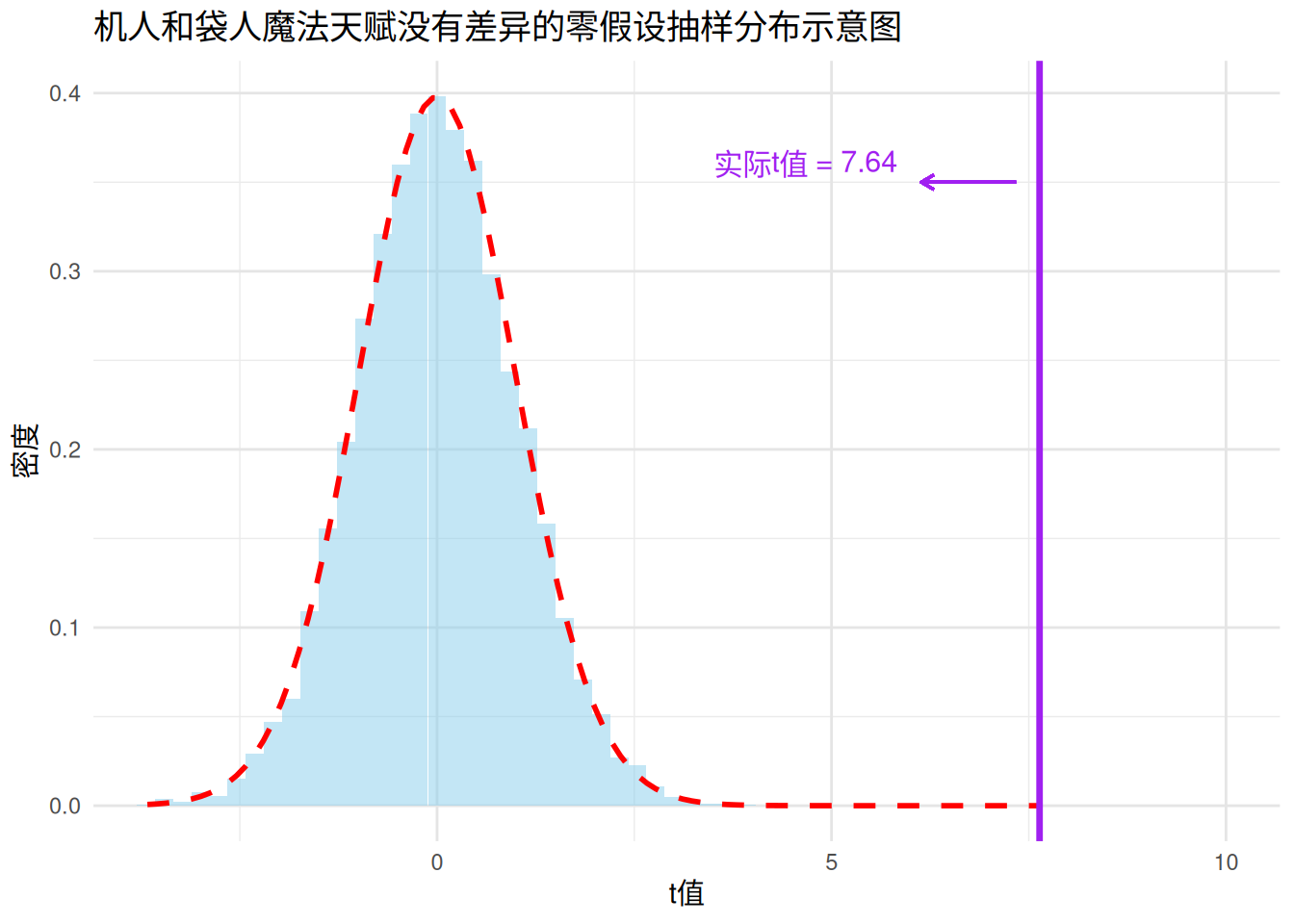
这个t值在上面零假设成立的分布里的位置，我们加进去，画成紫色的竖线。

看看紫色对应的t值在t分布中的位置！显然它距离均值已经非常遥远，对应的红色虚线纵坐标也非常接近于0。换句话说，如果机人和袋人真的魔法天赋一样的话，我们进行一次抽样，结果是这个t值的可能性非常接近于0。

如果一个事件发生的可能性非常低的话，我们运用常识，就会推断它基本不可能发生。那么它的发生要么是我们承认一个发生概率小于0.0000000001的事件发生了，要么我们只能认为这一切的前提不对。前提是什么呢？我们的零假设。

看！这就是我们通过抽样分布拒绝零假设的方式！啰嗦了这么多，我们终于走到了NHST的目的地。通过构造零假设，找到它的抽样分布，在把我们现有的样本情况带入这个抽样分布。来看零假设成立的前提下，我们现有的样本发生概率有多少。如果这个发生概率低到一定程度，我们就可以认为它不太可能是一个巧合，而是零假设本身有问题。那么我们就可以拒绝这个零假设。

拒绝零假设意味着什么呢？意味着我们终于可以接受我们的备择假设了！机人和袋人的魔法天赋不一样！用我们常用的话说，机人和袋人的魔法天赋分数的差异显著了！

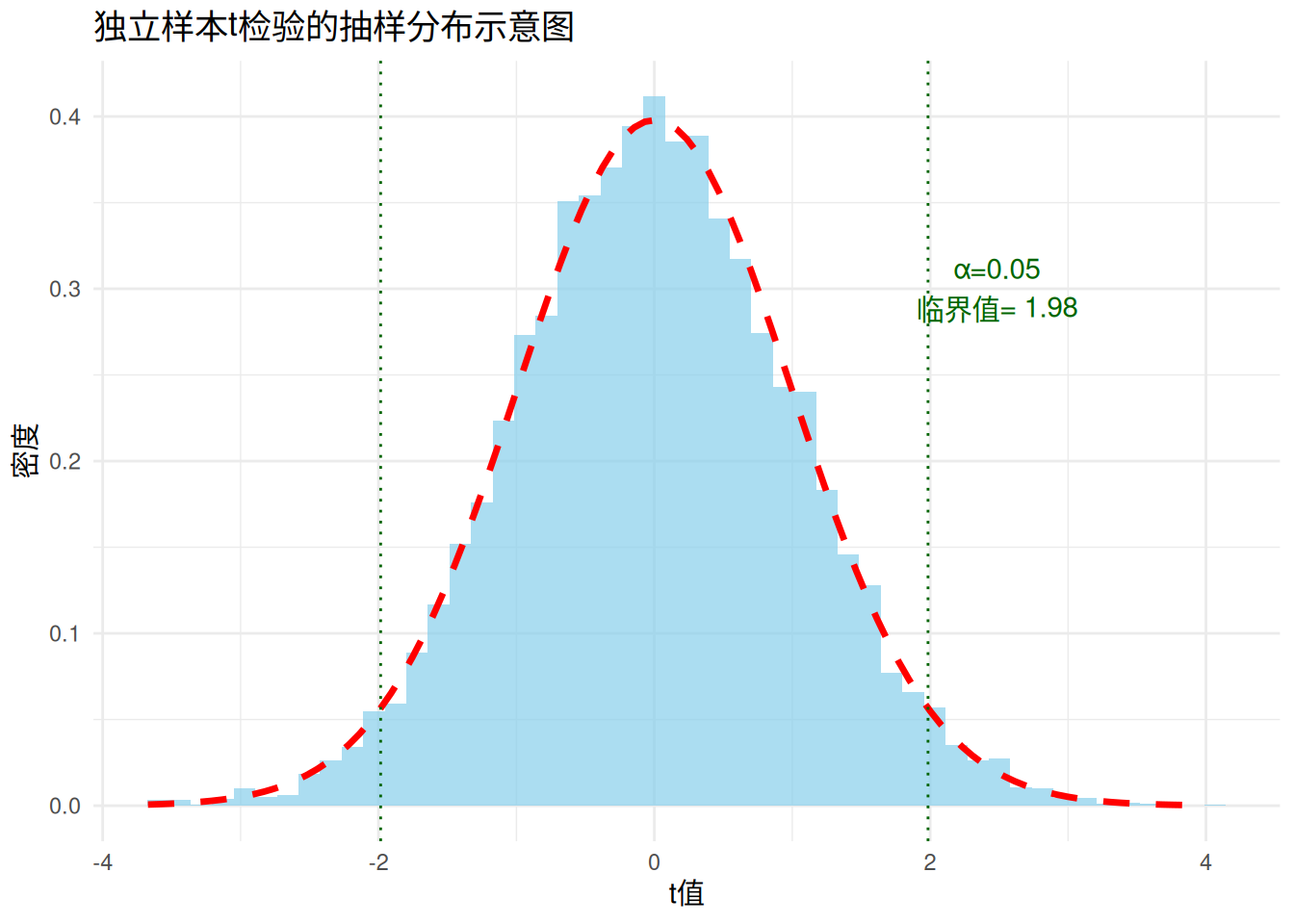
和我一样的杠精朋友可能已经注意到了，上面的这一套论述里，有一个小问题。那就是我们拒绝零假设要样本在零假设的抽样分布里发生的概率低到一定程度。那么这个“低到一定程度”的标准是什么呢？这个问题其实就是NHST被人诟病的一个地方。我们通常在实证研究中使用的标准是5%，换句话说，我们认为，如果这个样本在零假设成立的前提下发生的概率小于5%，那么这就达到了够低的标准，我们可以拒绝零假设了。我们把这个标准叫做一个假设检验的alpha水平，它对应的就是我们允许一类错误的发生概率。一类错误即我们错误地拒绝零假设的情况。这个概念及与之相关的二类错误，及结合效应量衍生的功效分析，读者们可以跳转 番外一 阅读。

所以，如上图，当我们的样本容量是50人时，对应的抽样分布在alpha 水平为0.05时，当t的绝对值大于1.98时，我们就可以拒绝零假设了。

注意

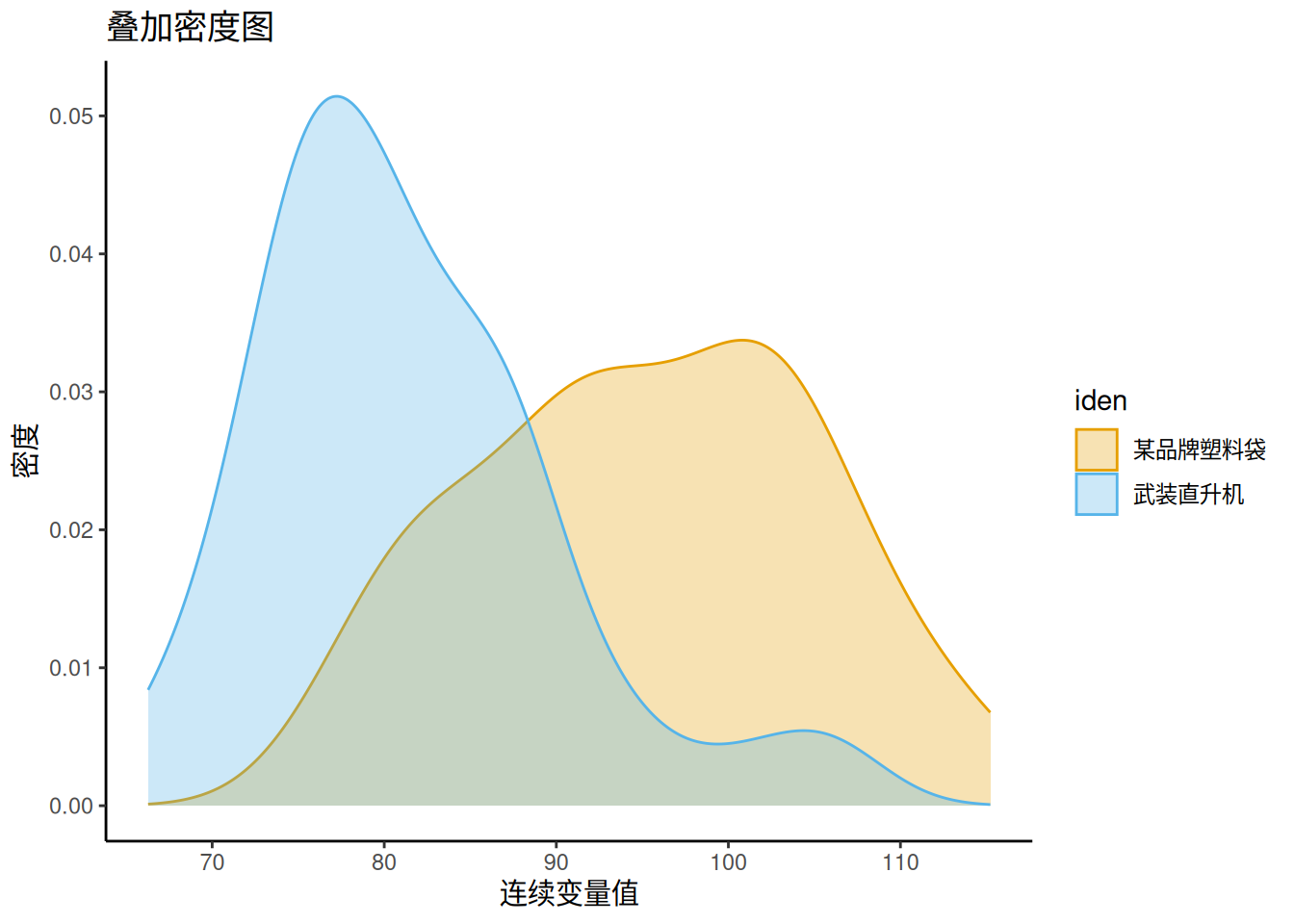
需要注意的是，我们上面使用的是抽样分布，这个分布是基于零假设成立的情况下，假设出来的。这个分布实际上并不是真的在现实中我们真的进行了多次抽样得出的。一个经常搞混的分布是样本的实际数据分布，这个分布是基于我们实际样本得到的数据频次进行统计画出的。以我们的现有数据，它应该长这样。

实际上，两个样本的信息在我们一开始对数据描述使用的小提琴图中已经体现了。大家可以对比一下。

思考：如果不用平均数呢？

在描述统计中，我们用于描述数据“集中”趋势的统计量不仅仅只有平均数。还有中位数（就像箱线图里箱子里的那根线那样）和众数。依据同样的逻辑，你是否可以尝试开发一套基于中位数的“t检验”，在创造这套“t检验”的过程中，你认为相比基于平均数的t检验，存在哪些问题需要解决？

2.2.5 t检验实战

实际上在写作这本书之前，我预设的是你已经知道了上面描述的抽样分布的所有知识。但是，我也知道很多即使学习了心理统计的同学，对上面的NHST逻辑也会有所淡忘。但我上面的描述可能也不够生动形象，没关系，你可以再找找其他教科书和材料复习一遍又一遍。

下面我会呈现，一个训练有素的心理学研究者，会如何快速检验我们的机人和袋人的魔法天赋差异是否显著。无他，唯手熟尔。

首先，在独立样本t检验中，我们一般需要检验方差齐性假设。

## 方差齐性检验
var.test(df1.1[df1.1$iden=="武装直升机",c("magic_score")],
         df1.1[df1.1$iden=="某品牌塑料袋",c("magic_score")])

    F test to compare two variances

data:  df1.1[df1.1$iden == "武装直升机", c("magic_score")] and df1.1[df1.1$iden == "某品牌塑料袋", c("magic_score")]
F = 0.74977, num df = 49, denom df = 49, p-value = 0.3168
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.4254777 1.3212395
sample estimates:
ratio of variances 
         0.7497719 

可以看到，针对方差齐性的检验显示 F = 0.74977, num df = 49, denom df = 49, p-value = 0.3168。检验结果不显著，说明无法拒绝方差齐性的假设，我们就默认它成立了。⁹ 因此，我们接着进行传统的独立样本t检验。

## 独立样本t检验，假设方差齐性
## 下面的代码的意思大致是，魔法分数（magic_score）作为因变量，
## 自我认同（iden）作为自变量进行t检验。
## df1.1是两个变量所属的数据框。
## var.equal = TRUE 即假设方差齐性满足进行检验。
t.test(magic_score~iden, df1.1, var.equal = TRUE)

    Two Sample t-test

data:  magic_score by iden
t = 7.6368, df = 98, p-value = 1.498e-11
alternative hypothesis: true difference in means between group 某品牌塑料袋 and group 武装直升机 is not equal to 0
95 percent confidence interval:
 10.40264 17.70709
sample estimates:
mean in group 某品牌塑料袋   mean in group 武装直升机 
                  95.29439                   81.23953 

可以看到，t检验的结果是 t = 7.6368, df = 98, p-value = 0.00000000001498。作为一个熟练的心理学p值检验机器，想比大家第一时间就已经把目光对准了0.00000000001498这个数，并在脑中自动化生成了“显著”这样一个金灿灿的结果。由于是我们创造的“假数据”，这个结果并不让人意外。

思考：另一个需要满足的统计假设

由于我们这本书的定位并不是一本严谨的教科书，所以实际上我们并不会详细地讨论每个检验必须要满足什么统计假设。而且实际在实证论文的发表中，报告对所有检验的统计假设满足情况的少之又少（笑）。原因有很多，比如很多检验的假设不满足其实也能给出相对稳健的结果 ，比如方差分析如果每组的容量大致平衡，实际上不满足方差齐性假设也能给出足够稳健的结果。还有呢，在现实中很多数据其实并不满足正态分布，这就违反了另一个我们这本书中大部分检验需要满足的假设——因变量（在每一组下）要服从正态分布。

聪明的读者应该注意到了，中心极限定理并没有对那个随机变量，也就是t检验中的因变量的分布做要求啊？比如抛硬币，服从的是二项分布，它的抽样分布在经过足够多次之后一样也服从正态分布。那么为什么t检验会要求因变量在两组被试中均满足正态分布呢？

不同于上一个思考，这个问题会在我们后面的章节中得到一定程度的解答，不过你可以先想一下。

---

1. 准确一点来说，应该叫预测变量，因为性别认同并不能改变；但本书为了方便起见，有时会把预测变量和结果变量叫成自变量和因变量。

2. 严格意义上来说，我们的研究假设可以是机人的魔法天赋水平低于袋人。也就是一个单尾的检验。这里我们为了方便后续的呈现，使用双尾检验。事实上，实践中也有些专家并不喜欢单尾检验，认为双尾检验更加“保守”，毕竟数值上p值翻了倍，会要求将单尾检验改为双尾。

3. 很担心等真的有人看这本书的时候，这个梗已经过时了。

4. 如果真的有读者不知道独立样本t检验，请不要觉得我在攻击你。话不是我说的，是我假设出来的一个读者说的。如果你非要说假设出来的这个读者就是我的一个人格，那么我只能反问：如果我不认同我分裂出来的人格说的话，而我分裂出来的人格也拒绝承认他是我，我们是否可以把这种情况视为平行宇宙的意外重叠？那么基于平行宇宙很大程度上是为了解决波函数坍缩带来的薛定谔的猫的问题，如果是你亲手把薛定谔的猫放进黑箱里的。那么它处于叠加态时，你是否要为此负法律责任呢？如果你都不想负法律责任，那么这个问题的答案还是钝角吗？

5. 前几年有段时间，学界有一股非常强劲的用贝叶斯统计替换NHST的风。贝叶斯统计在逻辑上其实相对来说更好理解，但是在工具的便利性上不如NHST。从我不专业的角度来看，贝叶斯统计和NHST并不存在本质的差别，研究者对NHST能误用，对贝叶斯统计一样能误用。这种误用不仅仅是由实证研究者统计知识不扎实带来的，而是整个科学界对于研究成果评估标准（发表看显著性、期刊看等级等等）带来的系统性问题。而系统性问题并不能通过统计方法的改变解决。

6. 即加上我自己的主观理解但因此会出现偏差的表述

7. 我们在这里没有考虑小球彼此间互相碰撞影响的问题，不过对于结果并没有影响。感兴趣的同学可以自己推导。哪怕一次放一颗球，放一千个小球，最后的结果仍然一样。

8. 准确地说，t分布是一组分布，它的形态会随着自由度变化而变化，我暂时不打算介绍自由度的含义，而这里t分布的自由度是$n_0+n_1-2$。所以你也可以理解为t分布的形态会随样本容量变化。通常样本容量越大，t分布就越接近标准正态分布。相比正态分布来说，t分布更加扁平一些。所以你要小心，不要当着t分布的面问正态分布为什么你的头尖尖的。

9. 其实这种做法有些争议。如果你还记得上面我们的假设检验的逻辑的话，其实我们不能单独从不显著的结果中得出结论。对于NHST的逻辑，我们只能拒绝零假设，而不能验证零假设成立。这也是大多数针对统计假设的检验手段存在的问题。有些观点认为，我们应该默认一些统计假设无法满足，而直接使用稳健性估计处理。