3 Deskriptive Statistik
3.1 Messen von Variablen
3.1.1 Was sind Daten?
``Data are what we hear, see, smell, taste, touch, and more. Data can even be what we sense. Data can represent anything and everything that we can discriminate well enough to distinguish from something else. In short, if it can be perceived, it can be coded and used as data.’’
Sprich, wir meinen damit alles, was uns hilft, zwischen den Einheiten zu unterscheiden bzw. diese gleichzusetzen.
3.1.2 Warum benötigen Daten einen Kontext?
Ein Datenpunkt benötigt eine Referenz, um etwas zu bedeuten. Wir verstehen den Inhalt von Daten nur, wenn wir den Kontext verstehen. So können wir zB die Protestaktivität im Sudan besser beurteilen, wenn wir die Protestaktivität in anderen afrikanischen Staaten kennen. Der Kontext ist wichtig, um Daten interpretieren zu können.
3.1.3 Was können wir messen?
``If you can perceive it, you can measure it. A measurement is an assigned value for a single characteristic. The way a characteristic is captured and, therefore, the way its data should be interpreted determine the measure being used to address the question at hand.’’
Wir müssen uns überlegen, welche Ausprägungen unsere Messung annehmen kann.
Hier ein Beispiel:
- Teilnehmer_innenanzahl: 0-…
- Ort: Seoul, Changwon, Dagjin, Gimje, …
- Thema: Arbeitsstandards, Umweltaspekte, Migration, Investionen, …
- Datum: 1985-01-01, … 2018-11-18, 2018-11-19, …, 2019-03-06
- Alter: 0-130
- Gender: m,f
- Mitglied in Gewerkschaft: ja,nein
Die Ausprägungen geben Aufschluss über die Struktur der Daten. Strukturen bestimmen, wie etwas verwendet werden darf. Man bewegt sich zum Beispiel bei der Stiege anders fort als auf der Achterbahn. Um die Streckenmitte auf der Stiege zu bestimmen, benötigt man eine andere Methode (zählen von Treppen) als beim Bestimmen der Streckenmitte auf der Achterbahn (zählt man die mm). Dies ist dasselbe beim Messen von Daten.
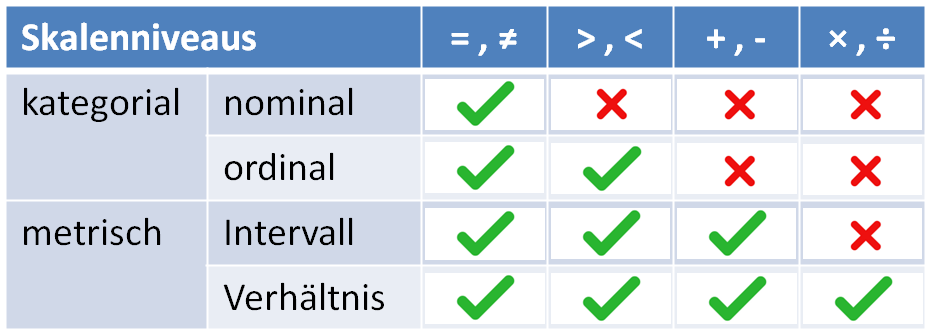
Man nennt diese unterschiedlichen Strukturen der Daten Skalenniveaus. Das Skalenniveau bestimmt auch, was wir mit den Daten machen können.

3.1.4 Worauf muss beim Messen noch geachtet werden?
- Wir sollten Messfehler vermeiden.
[MESSFEHLER] ist der Unterschied zwischen dem tatsächlichen und dem gemessenen Wert.
Beispiel: Das Alter in Korea wird anders gemessen als in Europa. In Korea wird jeder am Neujahrstag nach dem Mondkalendar 1 Jahr älter. So kann es vorkommen, dass man sogar 2 Jahre älter als das echte Alter ist.
Hier ein Beispiel: Wird ein Kind an Silvester (31.12.) geboren, ist es 1 Jahr alt. Zu Neujahr wird in Korea jeder ein Jahr älter, also ist das an Silvester geborene Kind am 1. Januar schon 2 Jahre alt, obwohl es in Wirklichkeit nur 2 Tage alt ist.
Grundsätzlich ist unser Ziel, sowohl die Validität als auch die Reliabilität zu maximieren.
[VALIDITÄT] sagt, ob eine Messung das misst, was es sagt, dass es misst.
[RELIABILITÄT] sagt, ob bei einer wiederholten Messung dasselbe rauskommt.
3.2 Deskriptive Statistik: Was ist das?
Datensätze können sehr unübersichtlich sein. Die deskriptive („beschreibende“) Statistik stellt ein Bündel an Verfahren, Grafiken und Parametern bereit, welche es ermöglichen, die Informationen soweit zu verdichten, dass man sich schnell einen Eindruck über die Daten verschaffen kann. Eine deskriptive Auswertung sollte am Anfang jeder statistischen Analyse stehen. Sie vermittelt dem/der Forscher/-in ein Gefühl für die Daten und hilft ggf., vorhandene Fehler und unplausible Werte (z.B. Ausreißer/ Outlier) zu entdecken. Wichtig hierfür ist die Kenntnis über das Skalenniveau der Daten, die untersucht werden sollen, da die Wahl des Mittels zur Beschreibung eines Datensatzes von diesem abhängt.
Beginnt man mit der Auswertung einer empirischen Studie, so ist es sinnvoll, sich zuerst einen Überblick über den vorliegenden Datensatz zu verschaffen, bevor die angestrebten Auswertungsmethoden angewandt werden. Hierbei geben Lage- und Skalenparameter erste Informationen zu dem Datensatz. Die Visualisierung der Daten ist für das bessere Verständnis des Datensatzes erforderlich. Durch diese kann ein Eindruck von der Verteilung der Merkmale oder dem Zusammenhang zwischen unterschiedlichen Merkmalen gewonnen werden.
DESKRIPTIVE STATISTIK…
- …ordnet Daten
- …vereinfacht Daten
- …beschreibt Daten
- …hilft, Daten zu verstehen
- …hilft, Fehler in den Daten zu erkennen
- …hilft, Muster zu erkennen
3.3 Häufigkeitstabellen
Häufigkeitstabellen sind die erste Variante, welche wir uns ansehen, um Daten darzustellen. Dies ist ein sehr einfacher und schneller Weg, einen Überblick über die Daten zu erlangen.
Nehmen wir das Beispiel des Paris Abkommens. Dies galt als eines der erfolgreichsten Internationalen Treffen im Bezug auf Umweltschutz. 195 Staaten unterschrieben das Abkommen im Dezember 2015. Staaten konnten zwar Ihre individuellen Ziele festlegen, aber diese waren bindend. Ein wichtiger Datenpunkt ist daher, wie hoch diese Zugeständnisse der Staaten waren. Hier hat man die Dokumente, welche die Staaten geschickt haben, analysiert und herausgelesen, welche Ziele diese sich selbst setzten. Das reichte von vollkommen unzureichend zum Vorbild. Die Erderwärmung auf 1.5 Grad zu reduzieren ist das in Paris als erstrebenswert vorgeschlagene Ziel.
Wir müssen zunächst die Daten sortieren. Hier das Resultat. Dann müssen wir zählen. Wieviel Länder haben welches Ziel hineingeschrieben? Und dann haben wir auch schon unsere erste Häufigkeitstabelle. Dies umfasst die absolute Häufigkeit. Das gibt uns ein erstes Gefühl, aber besser ist es, wenn wir dies relativ zu den anderen Beobachtungen sagen können. Hierzu benötigen wir die relativen Häufigkeiten. Dazu dividieren wir die absoluten Häufigkeiten durch die totale Anzahl der Beobachtungen. Relative Häufigkeiten, die wir \(f_i\) nennen, sind die Anteile, die auf jede Ausprägung entfallen.
Dann gibt es noch die kumulierte Häufigkeite. In ihr werden die relativen Häufigkeiten aufsummiert. Die kumulierte Häufigkeitstabelle wird meist nur mit relativen Häufigkeiten gebildet—mit absoluten Häufigkeiten findet sie eigentlich nirgends Verwendung. Die kumulierte Häufigkeit ist sehr praktisch, da man auf einem Blick sagen kann, ab wann eine bestimmte Grenze überschritten wird.
Bei nominalen und ordinalen Variablen sind die Kategorien bereits natürlich definiert. Bei intervall- und verhälntiss-skalierten Daten müssen die Kategorien definiert werden. Dazu werden Intervallbreiten berechnet und die Variable dann in Kategorien geteilt.
\(\text{Invervallbreite} = \frac{\text{Höchster Wert-Niedrigster Wert}}{\text{Anzahl der gewünschten Intervalle}}\)
Was ist, wenn wir aber keine Kategorien bilden wollen? Dann können wir auf eine sogenannte Dichtefunktion zurückgreifen. Eine Dichtefunktion sagt uns die Wahrscheinlicheit für einen bestimmten Wert, wenn wir die Variable nicht in Kategorien einteilen. Wenn wir nämlich keine Kategorien haben, ist es sehr schwierig, jeden Prozentsatz zu berechnen.
Bei kontinuierlichen Variablen ist der Modus da, wo die Dichtefunktion das Maximum hat.
3.4 Statistisches Modell
Ein statistisches Modell dient dazu, Daten vorhersagen zu können. Manche Modelle sind besser und manche schlechter. Wir lernen Qualitäten von statistischen Modellen abzuschätzen. Im Grunde hat ein statistisches Modell aber immer dieselbe Struktur:
\(\text{Ergebnis}_i = \beta_0 + \text{Fehlerterm}_i\)
\(\text{Ergebnis}_i = \beta_0 + \beta_1 X_i + \text{Fehlerterm}_i\)
Es umfasst das Ergebnis auf der linken Seite der Gleichung und Modellterme (wie zB \(\beta_0\) oder \(\beta_1\)) als auch den Fehlerterm auf der rechten Seite. Den Fehlerterm können wir auch so berechnen, dass wir die Modellterme vom Ergebnis substrahieren. Je größer der Fehlerterm, desto ungenauer ist unser statistisches Modell.
3.4.1 Zentrale Tendenz
Bekannte und sehr einfache statische Modelle sind zentrale Tendenzen. Hier unterscheiden wir insbesondere drei Maße: 1) Modus, 2) Median, 3) Arithmetisches Mittel.
Der MODUS, auch Modalwert genannt, ist ein Lageparameter in der deskriptiven Statistik. Er ist definiert als der häufigste Wert, der in der Stichprobe vorkommt. Und was ist, wenn wir zwei Kategorien mit der gleichen Anzahl an Beobachtungen haben? Dann haben wir zwei Modalwerte.
Der MEDIAN, oder auch Zentralwert genannt, ist derjenige Messwert, der genau in der Mitte steht, wenn man die Messwerte der Größe nach sortiert. Im ersten Schritt müssen wir die Daten ordnen. Danach den Wert, welcher in der Mitte steht, auswählen. Bei 31 Beobachtungen ist die Mitte 31+1/2 = 16. Der Median ist besonders für ordinale und metrische Variablen nützlich.
Das ARITHMETISCHE MITTEL, auch arithmetischer Mittelwert genannt, berechnet sich wie folgt: Summe der betrachteten Zahlen geteilt durch ihre Anzahl. Dieses Maß ist sehr nützlich für metrische Variablen. Wir haben eine leicht unterschiedliche Notation wenn wir den Mittelwert von einer Stichprobe bzw. von der Grundgesamtheit berechnen.
Mittelwert der Grundpopulation:
\(\mu = \frac{\sum^n_{i=1}x_i}{N}\)
Mittelwert der Stichprobe:
\(\bar{X} = \frac{\sum^n_{i=1}x_i}{n}\)
Da wir meist Mittelwerte für Stichproben berechnen, ist besonders die zweite Notation für Sie relevant.
3.4.2 Modellqualität
Worin unterscheiden sich die verschiedenen Maße nun?
- Nicht alle Maße sind für alle Datentypen geeignet.
- Ausreißer haben unterschiedlichen Einfluss auf das Ergebnis. Beim Mittelwert haben Außreiser einen viel größeren Einfluss als beim Median und Modus. Ist jetzt der Median besser als der Mittelwert? Nicht unbedingt, da der Mittelwert repräsentativer ist als der Median (er inkludiert alle Datenpunkte).
Die nächsten Frage, die sich stellt, ist, wie gut ein statistischen Modell denn jetzt ist. Wie gut kann die Schätzung, die wir gerade gemacht haben, die einzelnen Datenpunkte repräsentieren?
Wie oben bereits erwähnt, kann uns der Fehlerterm bzw. das Aggregat davon Aufschluss geben.
\(\text{Fehler-Quadratsumme}=\sum_{i=1}^n (x_i-Vorhersage_i)^2\)
, wobei \(x_i\) jeden Beobachtungswert darstellt und die Vorhersage die Modellvorhersage meint. Wir nehmen das Ganze zum Quadrat, um zu vermeiden, dass sich negative und positive Fehlerterme aufheben.
Wenn wir als statistisches Modell den Mittelwert verwenden, würde dies für die Grundpopulation wie folgt aussehen:
\(\text{Fehler-Quadratsumme (SSE)}=\sum_{i=1}^n (x_i-\mu)^2\)
Ausgehend von der Summe können wir nun auch die mittlere Fehler-Quadratsumme berechnen.
\(\text{Mittlere Fehler-Quadratsumme}=\frac{SSE}{N}=\frac{\sum_{i=1}^n (x_i-Vorhersage_i)^2}{N}\)
Wenn das Modell der Mittelwert ist, dann hat dies einen speziellen Namen, nämlich Varianz.
\(\text{Varianz}(\delta^2)=\frac{SSE}{N}=\frac{\sum_{i=1}^n (x_i-\mu)^2}{N}\)
Aber wie wir wissen, repräsentiert mu die Grundpopulation. Hier ist es wichtig, einen Unterschied zwischen Grundpopulation und Stichprobe zu machen. Jetzt wird es kurz etwas komplizierter.
Der Grund ist, dass wir, wenn wir die Varianz für die Grundpopulation anhand von einer Stichprobe vorhersagen, die Varianz unterschätzen. Um diese Unterschätzung zu vermeiden, ziehen wir von der Anzahl der Objekte (\(n\)) 1 ab. Man nennt diese Zahl auch Freiheitsgrade (\(n-1\)).
\(\text{Mittlere Fehler-Quadratsumme}=\frac{SSE}{n-1}=\frac{\sum_{i=1}^n (x_i-Vorhersage_i)^2}{n-1}\)
Auch die Formel der Varianz für die Stichprobe beachtet dies:
\(\text{Varianz}(\delta^2)=\frac{SSE}{n-1}=\frac{\sum_{i=1}^n (x_i-\bar{X})^2}{n-1}\)
Ein Problem haben wir noch mit der Varianz. Nämlich, dass die Relation nicht klar ist: Was bedeutet diese Zahl? Das Verhältnis ist schwer herzustellen, da die Zahl quadriert ist. Deshalb müssen wir die Wurzel ziehen und das nennen wir dann Standardabweichung:
Grundpopulation: \(\text{Standardabweichung}= \sqrt{\delta^2}=\sqrt{\frac{SSE}{N}=\frac{\sum_{i=1}^n (x_i-\mu)^2}{N}}\)
Stichprobe: \(\text{Standardabweichung}=\sqrt{s^2}=\sqrt{\frac{SSE}{n-1}=\frac{\sum_{i=1}^n (x_i-\bar{X})^2}{n-1}}\)
Es gibt aber auch viel einfachere Maßzahlen, beispielsweise die Spannweite. Allerdings beeinflussen Ausreißer dieses Ergebnis dramatisch. Daher ist es besser, wir betrachten den Interquartilsabstand.
Beim Interquartilsabstand müssen wir das 1. Quartil vom 3. Quartil abziehen.
Hier die Berechnung für die Stichprobe 1. Hier erhalten wir einen Interquartilsabstand von 50. Bei Stichprobe 2 haben wir einen Interquartilsabstand von 64.24.
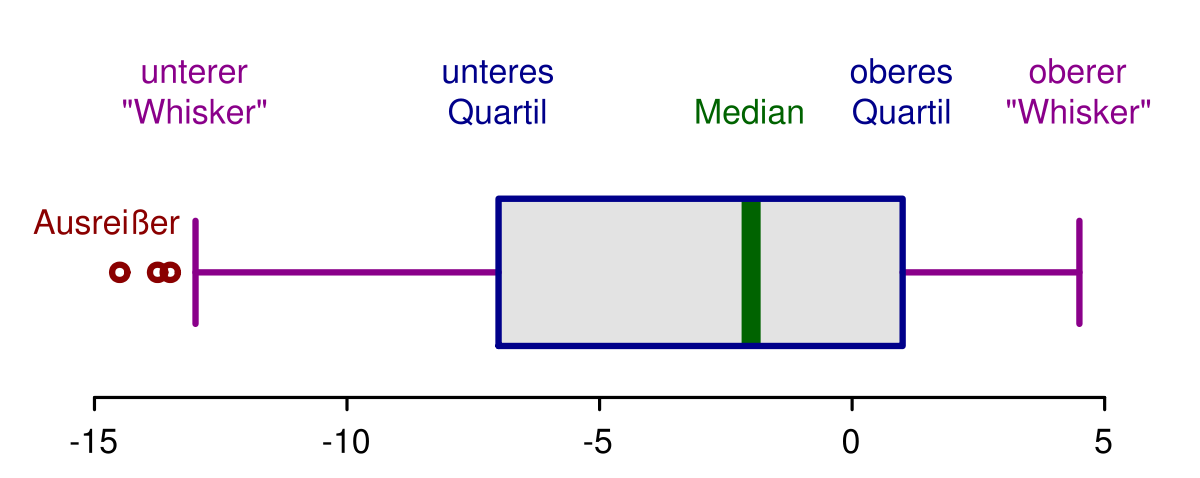
Das Ganze lässt sich auch sehr gut in einem Boxplot abbilden.
Was sehen wir in einem Boxplot:
- Median
- Oberes Quartil (1. Quartil) und unteres Quartil (3. Quartil) grenzen die mittleren 50 Prozent ein.
- Whiskers:
- top 25 Prozent ohne extreme Werte (die extremen Werte sind Werte, die größer sind als das obere Quartil plus 1.5 mal die Spannweite)
- untere 25 Prozent ohne extreme Werte (die extremen Werte sind Werte, die kleiner sind als das untere Quartil minus 1.5 mal die Spannweite)
- Ausreißer/extreme Werte