2 Cônicas
All chapters start with a first-level heading followed by your chapter title, like the line above. There should be only one first-level heading (#) per .Rmd file.
2.1 Parábola
2.1.1 Contexto Histórico
Antes mesmo de introduzirmos o conteúdo de superfícies quadricas é necessário compreender as cônicas que servem de base para esse estudo. Sendo assim, daremos início a parábola e uma breve contextualização histórica. Apolônio de Pergamo foi um matemático e astrônomo grego que viveu por volta de (262 a.c - 190 a.c), ele também era conhecido como o grande Geometra. Além disso, produziu muitas obras, porém muitas delas foram perdidas.
Segundo Bezerra (2010, p. 40), “foi Apolônio quem mostrou que bastaria um cone circular reto de duas folhas qualquer para se obter as três (seções) cônicas; o que deveria variar era o ângulo de interseção do plano com uma das duas geratrizes”.
As cônicas se origina após a intersecção de um plano sobre um cone duplo. Ou seja, dependendo da forma que o plano corte o cone obtemos uma parábola, elipse ou hipérbole.
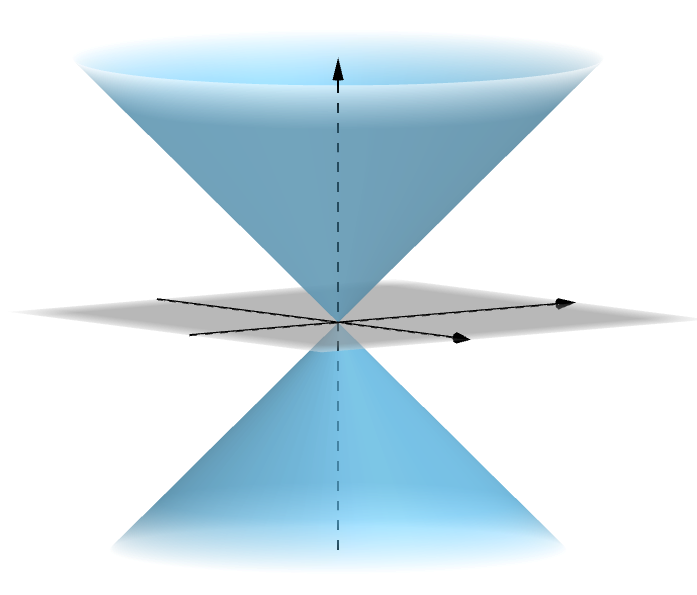
Figure 2.1: Cone de duas folhas
2.1.2 Definição
Definição 2.1 (Parábola). Dado um plano \(\alpha\), uma reta \(d\) e um ponto \(F\), tal que \(F \notin d\). Parábola é o conjunto de todos os pontos pertencentes ao plano \(\alpha\) que são equidistantes a \(F\) e \(d\).
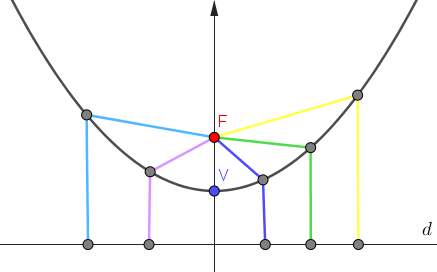
Figure 2.2: Gráfico dos pontos equidistantes.
Note que no gráfico existe vários segmentos de reta a qual as cores iguais representam os segmentos de retas que possuem o mesmo comprimento. Além disso, podemos destacar que os segmentos de reta que tocam a reta diretiz são perpendiculares a ela. O objetivo desse gráfico é mostrar graficamente a definição da parábola a qual \[d(F,P)=d(P,D),\] em que \(P\) é um ponto pertencente a parábola e \(D \in d\). Podemos deixar isso mais claro com um simples exemplo. Considere a parábola \(x^2=2y-1\) que pode ser vista como \(y=\dfrac{1}{2}x^2+\dfrac{1}{2}\).
Através de nossa lei de formação da parábola é possível encontrar todos os seus elementos. Deste modo, ao atribuir \(x=0\) determinamos o valor do vértice da parábola \(V\left(0,\dfrac{1}{2}\right)\) sendo um ponto muito importante, já que ele se encontra no eixo de simetria da parábola e é ponto médio entre o Foco e o ponto \(D\), onde \(D \in d\) e ao eixo de simetria simultaneamente. Ou seja, com essa informação é possível determinar o Foco \(F\) e a reta diretriz \(d\). Então
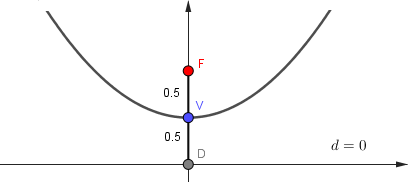
Figure 2.3: Gráfico provisório da parábola.
É fácil ver o Foco \(F(0,1)\) e a reta diretiz \(d = 0\). A partir disso vamos atribuir valores a \(x\) e verificar a definição da parábola. Portanto, vamos tomar o ponto \(D_1 (2,0)\), quando \(x=2\), temos que \(y=\dfrac{5}{2}\), logo \(P_1 (2,\dfrac{5}{2})\). Agora vamos verificar a definição da parábola a qual \(d(F, P_1) = d(P_1 , D_1)\). Dessa forma,
\[\begin{eqnarray*} d(F, P_1) &=& \sqrt{(0 - 2)^2 + \left(1 - \frac{5}{2} \right)^2} = \sqrt{4 + \frac{9}{4}} = \sqrt{\frac{25}{4}} = \frac{5}{2} \\ d(P_1, D_1) &=& \sqrt{(2 - 2)^2 + \left( \frac{5}{2} - 0 \right)^2} = \sqrt{\frac{25}{4}} = \frac{5}{2}. \end{eqnarray*}\]
De fato, isso é válido para toda a parábola, veja o gráfico abaixo.
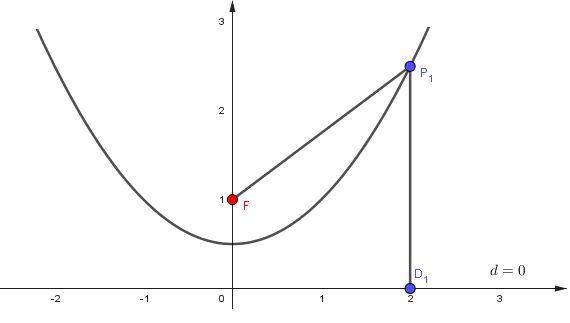
Figure 2.4: Parábola centrada na origem.
2.2 Elipse
2.2.2 Definição
Uma elipse com focos \(F_1\) e \(F_2\), com eixo maior medindo \(2a > d(F_1,F_2)\), é o lugar geométrico formado pelos pontos pertencentes ao plano \(\alpha\), cuja soma das distâncias a dois pontos fixos \(F_1\) e \(F_2\) é igual a \(2a\). Ou seja, se tivermos \(F_1\) e \(F_2\), com \(d(F_1,F_2) = 2c\), e um número \(a>c\), podemos dizer que \(P\) é um ponto dessa elipe se \[\begin{align} d(P, F_1)+d(P,F_2)=2a, \end{align}\] e definimos a elipse como \[Elipse= \{ P \in \alpha \, \lvert \, \, d(P,F_1)+d(P,F_2)=2a\}.\]
Geometricamente, temos que a soma das distâncias \(d_1\) com \(d_2\) é igual a \(2a\), ver Figura 2.1.
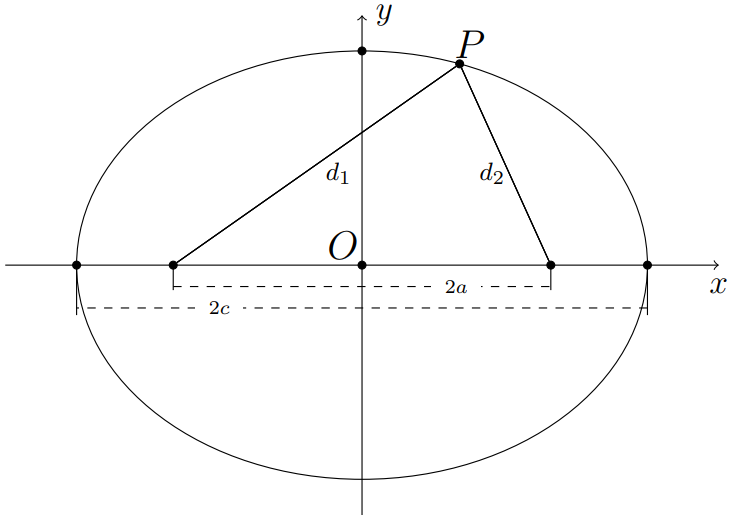
Figure 2.5: Construção do sistema de coordenadas
2.2.3 Elementos da Elipse
Na Figura 2.2 temos os principais elementos da elipse com suas respectivas definições.

Figure 2.6: Construção do sistema de coordenadas
Algumas denominações:
- Chamamos \(F_1\) e \(F_2\) de focos da elipse;
- \(d(F_1,F_2) =\) distância focal da elipse;
- \(O\) é o centro;
- O segmento \(\overline{A_1A_2}\) é chamado de eixo focal da elipse, conhecido também como eixo maior da elipse;
- O segmento \(\overline{B_1B_2}\) é conhecido como eixo menor da elipse;
- A amplitude focal é o comprimento de uma corda que contenha um dos focos da elipse e é perpendicular ao eixo focal desta;
- A menor região retangular que contém a elipse é chamada de retângulo fundamental da elipse.
2.2.4 Equação da Elipse
Para encontrarmos a equação da elipse, vamos primeiro definir um sistema de coordenadas. Vamos considerar o eixo \(x\) como a reta que passa pelos focos \(F_1\) e \(F_2\), com origem em \(O\) situada no ponto médio do segmento \(\overline{F_1F_2}\), e \(y\) sendo a reta perpendicular a esse segmento, que passa por \(O\). A Figura 2.3 ilustra esse sistema de coordenadas.

Figure 2.7: Construção do sistema de coordenadas
Nesse sistema de coordenadas, vamos assumir que os focos \(F_1\) e \(F_2\) possuem coordenadas \((-c,0)\) e \((c,0)\), respectivamente, em que \(c\) é um número real positivo. Se tomarmos um ponto genérico \(P=(x,y)\), teremos que a equação (1) ficará da seguinte forma:
\[\begin{align} d\left(P,F_1\right)+d\left(P,F_2\right)&=2a \\ d\left((x,y),(-c,0)\right)+d\left((x,y),(c,0)\right)&=2a \\ \sqrt{(x-(-c))^2+(y-0)^2}+\sqrt{(x-c)^2+(y-0)^2}&=2a \\ \sqrt{(x+c)^2+(y)^2}+\sqrt{(x-c)^2+(y)^2}&=2a \\ \sqrt{(x+c)^2+y^2}&=2a-\sqrt{(x-c)^2+y^2} \end{align}\]
Ao elevar ambos os membros de (6) ao quadrado, teremos:
\[\begin{align} \left(\sqrt{(x+c)^2+y^2}\right)^2&=\left(2a-\sqrt{(x-c)^2+y^2}\right)^2 \\ (x+c)^2+y^2&=4a^2-4a\sqrt{(x-c)^2+y^2}+(x-c)^2+y^2 \end{align}\] Desenvolvendo os quadrados de (8), teremos:
\[\begin{align} x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{x^2-2cx+c^2+y^2}+x^2-2cx+c^2+y^2 \end{align}\] Simplificando as parcelas iguais: \[\begin{align} 2cx&=4a^2-4a\sqrt{x^2-2cx+c^2+y^2}-2cx \\ 2cx+2cx-4a^2&=-4a\sqrt{x^2-2cx+c^2+y^2} \\ 4cx-4a^2&=-4a\sqrt{x^2-2cx+c^2+y^2} \\ 4(cx-a^2)&=-4a\sqrt{x^2-2cx+c^2+y^2} \\ cx-a^2&=-a\sqrt{x^2-2cx+c^2+y^2} \end{align}\] Eleva ambos os membros de (14) ao quadrado:
\[\begin{align} (cx-a^2)^2&=\left(-a\sqrt{x^2-2cx+c^2+y^2}\right)^2 \\ c^2x^2-2cxa^2+a^4&=a^2(x^2-2cx+c^2+y^2) \\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2 \\ c^2x^2+a^4&=a^2x^2+a^2c^2+a^2y^2 \end{align}\] Soma \(-c^2x^2-a^2c^2\) a ambos os membros de (18):
\[\begin{align} c^2x^2+a^4-c^2x^2-a^2c^2&=a^2x^2+a^2c^2+a^2y^2-c^2x^2-a^2c^2 \\ a^4-a^2c^2&=a^2x^2+a^2y^2-c^2x^2 \\ a^2(a^2-c^2)&=x^2(a^2-c^2)+a^2y^2 \end{align}\] Substituindo \(b^2=a^2-c^2\), temos: \[\begin{align} a^2b^2=x^2b^2+a^2y^2. \end{align}\] Ao dividir (22) por \(a^2b^2\), sendo \(a^2b^2\neq 0\), chegaremos a seguinte expressão
\[\begin{align} \dfrac{1}{a^2b^2}(x^2b^2+a^2y^2)&=\dfrac{1}{a^2b^2}(a^2b^2) \\ \dfrac{x^2b^2}{a^2b^2}+\dfrac{a^2y^2}{a^2b^2}&=1 \\ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}&=1. \end{align}\]
Assim, temos a seguinte proposição:
- For a right triangle, if $c$ denotes the *length* of the hypotenuse
and $a$ and $b$ denote the lengths of the **other** two sides, we have
$$a^2 + b^2 = c^2$$2.3 Hipérbole
A Hipérbole é o lugar geométrico dos pontos de um plano cuja diferença das distâncias, em valor absoluto, a dois pontos fixos desse plano, também denominados de focos, é constante. Tendo a seguinte definição:
2.3.1 Definição
Dados dois pontos fixos \(F_1\) e \(F_2\) e um número real positivo \(a\), definimos uma hipérbole com focos \(F_1\) e \(F_2\), como o conjunto de todos os pontos \(P\) do plano, tais que o módulo da diferença de suas distâncias a esses dois pontos é constante e igual a \(2a\).
Sendo assim, se considerarmos dois pontos distintos \(F_1\) e \(F_2\), em um plano, tal que a distância entre esses dois pontos \(d(F_1,F_2)=2c\), seja um número real \(a\) onde o dobro de \(a\) é menor que a distância entre \(F_1\) e \(F_2\), ou seja, \(2a<2c\).
Ao conjunto de todos os pontos \(P\) de um plano, tal que \[\lvert d(P, F_1) - d(P,F_2)\rvert=2a. \tag{1}\]
Por exemplo, sejam \(P,Q,R,S,F_1\) e \(F_2\), pontos pertencentes a um mesmo plano e \(F_1F_2=2c\), temos:
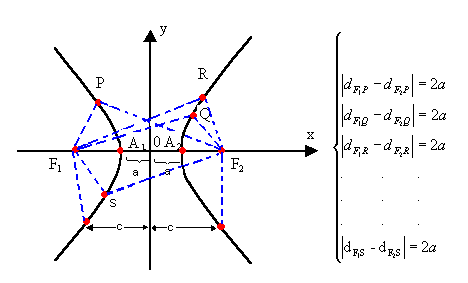
Figure 2.8: Hipérbole
Como se pode observar na Figura 1 e pela equação (1), a hipérbole é uma curva formada por dois ramos, onde se tomarmos um ponto qualquer, este ponto está na hipérbole, se e somente se: \[d(P,F_1) - d(P,F_2) = \pm 2a.\]
Quando o ponto analisado estiver no ramo da direita, a diferença será de \(+2a\), caso esteja no ramo da esquerda será \(-2a\).