3 Smart Case Weighting
What makes case weighting “smart”? Traditional case weighting is extremely laborsome, mainly becuase of the work required to establish and agree upon exact case weights. The idea behind smart case weighting is to let the use of computer algorithms reduce the work associated with case weighting. Smart case weighting differs from traditional case weighting in several ways, though (see table 3.1).
First of all, in traditional case weighting weights are defined by exact (fixed) numbers, like 10 for case type A and 1 for case type B. In contrast, with smart case weighting we consider weights not as fixed, but either as ranges (e.g. the weight for case type A is somewhere between 8 and 12) or as relatives (the weight for case type A is higher than the weight for case type B). The technical term for these assumptions about weights is “weight restrictions.”5. Figure 3.1 illustrates this crucial difference between traditional and smart case weighting.
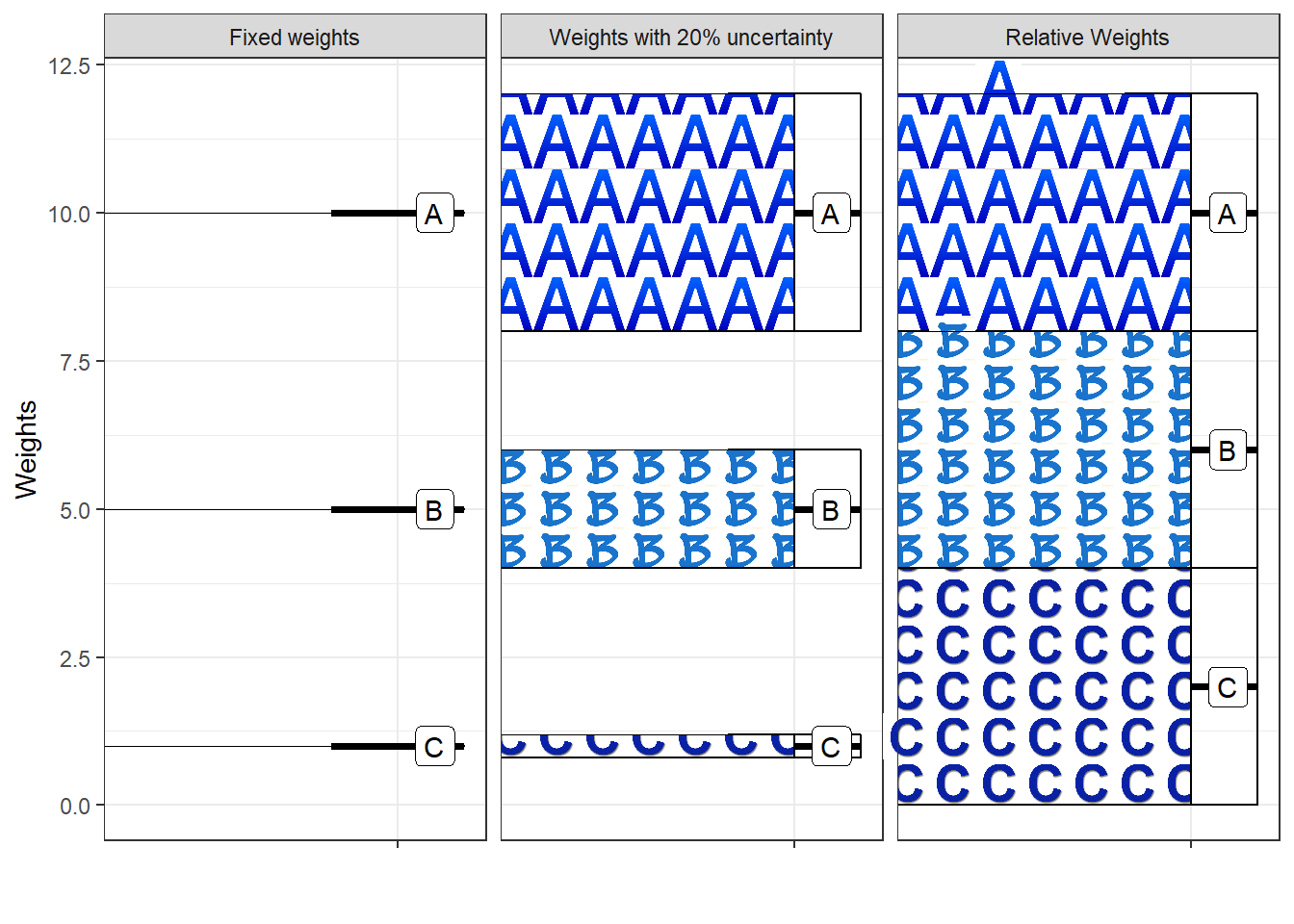
Figure 3.1: Different case weighting assumptions
Given that weights are not considered to be exact/fixed, smart case weighting requires us to consider not just one set of weights, but all possible combinations of weights given the assumptions we have about the weights (the weight restrictions). For this purpose, an algorithm is constructed.
The algorithm is designed to consider all possible combinations of weights and for each court to find the specific combination of weights which puts the court in the best possible light, that is, gives it the highest possible workload estimate compared to the other courts. For example, if a court has particular many case type B cases, it may receive a better estimate if we assign a high weight to case type B. However, if we have prior to this exercise made the basic assumption (weight restriction) that the weight for case type B is lower than the weight for case type A, then assigning a high weight for case type B implies we should assign an even higher weight for case type A. Because of this it may in fact turn out it is not advantageous for the court to set a high weight for case type B. The algorithm is designed to test this by going through all possible weight combinations.
The algorithm seeks for court k to maximize the calculated workload per judge, \(e_k\) of court k in relation to the calculated workload per judge of the other courts. In mathematical terms this can be written as \[e_k = \displaystyle \max_{W_1,…,W_m} \displaystyle \frac{\displaystyle \frac{\sum_{i=1}^m W_iC_{i,k}}{J_k}} {\displaystyle \max_j \displaystyle \frac {\sum_{i=1}^m W_iC_{i,j}} {J_j}} \]
subject to \(W_1,…,W_m\) satisfy our weight restrictions
That is, we find the set of weights among all the feasible weights - given our restrictions - which provides court j with the highest possible (relative) calculated workload per judge and therefore the highest possible indication of staff need6 .
By applying this algorithm together with an appropriate set of weight restrictions, we will end up finding a number of courts which - given a certain combination of weights - appear to have a workload per judge which is higher than or equal to that of all other courts. In addition, however, we will likely find a set of courts which - no matter what combination of weights we apply – will have a lower workload per judge than one or more other courts. The implication is then we can be absolutely certain we – in order to improve the balance of workload – need to move judges away from the set of courts with a lower workload and to the set of courts with a higher workload.
| Smart case weighting | Traditional case weighting |
|---|---|
| Weights are either given by intervals or assumptions about relative weights (e.g. weight for case type A is higher than weight for case type B) | Weights are defined by exact (fixed) numbers. Weights need to be very precise. Otherwise the recommended allocation may be unfair. |
| Easier to establish. But more complicated ex-post-analysis. | Extremely laborsome to establish. Simple to analyse. |
| Advanced math | Simple math |
| Conservative bias: Changes to the allocation are only recommended when we have strong evidence to support these changes. Assessments will tend to vary less from one year to another. | Risk of volatilty: Changes in the composition of cases from one year to another, may lead to large fluctuations in assessment of needs. |
| Easier to update, and udates are required less frequently. | Requires frequent updating. |
In other words, when we have tried for a given court to put it in the best possible light and find it – even with the most optimal set of weights – still has a lower workload per judge than another court, we can be certain it is justified to transfer a judge from the court to this other court. Smart case weighting in this way identifies all the transfers needed to establish a balanced workload among the courts.
Seen in this way, traditional case weighting may be perceived as a special case of smart case weighting (with extremely tight weight restrictions).↩
In technical terms we are applying what is known as Data Envelopment Analysis with weight restrictions. For details about DEA, see e.g. Bogetoft, P., & Otto, L. (2011). Benchmarking with DEA, SFA, and R. New York, NY: Springer↩