4 Pruebas a los modelos

En esta sección, probaremos tres modelos diferentes contra los datos para ver cuál se ajusta mejor.

Antes de hacerlo, tendremos que hacer un ajuste. Dado que todos los modelos suponen que $k$ está en constante crecimiento, modelaremos $k$ en función del tiempo para obtener una función monotónicamente creciente, lo llamaremos $\hat{k}$ . $$k=\beta_0+\beta_1t+\mu$$

Desafortunadamente, usar esta técnica para hacer de $k$ una función creciente solo funciona después del año 1975. Si usáramos toda la serie, la regresión conduciría a un intercepto negativo (y el capital no puede ser negativo). Establecer el intercepto para que sea igual al capital inicial conduce a una regresión que es solo una línea recta.

# Select years after 1975
data <- data%>%
  filter(year>1975)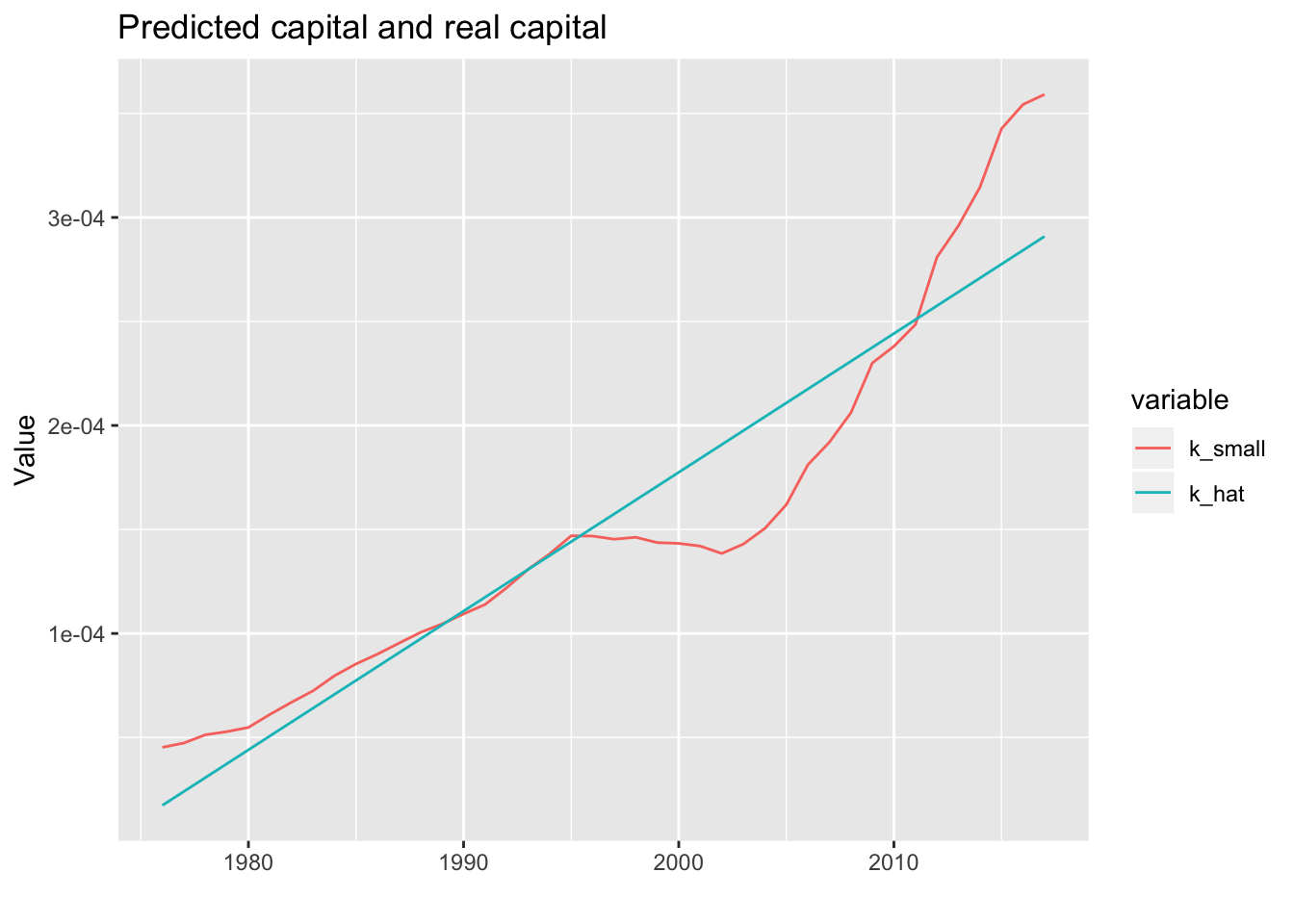

Ahora podemos comenzar a probar los modelos con esta nueva $k$.

4.1 Modelo de Solow

El modelo de solow no es de crecimiento endógeno, pero es un primer test para demostrar que los modelos de crecimiento exogeno no se ajustan bien a los datos.

Suponemos una función de producción de la forma $$y=Ak^{\alpha}$$ Ya tenemos $k$, ahora debemos estimar $A$ y $\alpha$. Para esto estimamos la siguiente funcion: $$log(y)=\beta_0 + \beta_1 log(k) + \mu$$

Donde $\beta_0 = log(A)$ y $\beta_1 = \alpha$

## [1] "A_hat=0.002"

## [1] "Alpha_hat=0.473"

Ahora estimamos $y$ con los parametros encontrandos. La siguiente grafica presenta los valores de $y$ reales y estimados

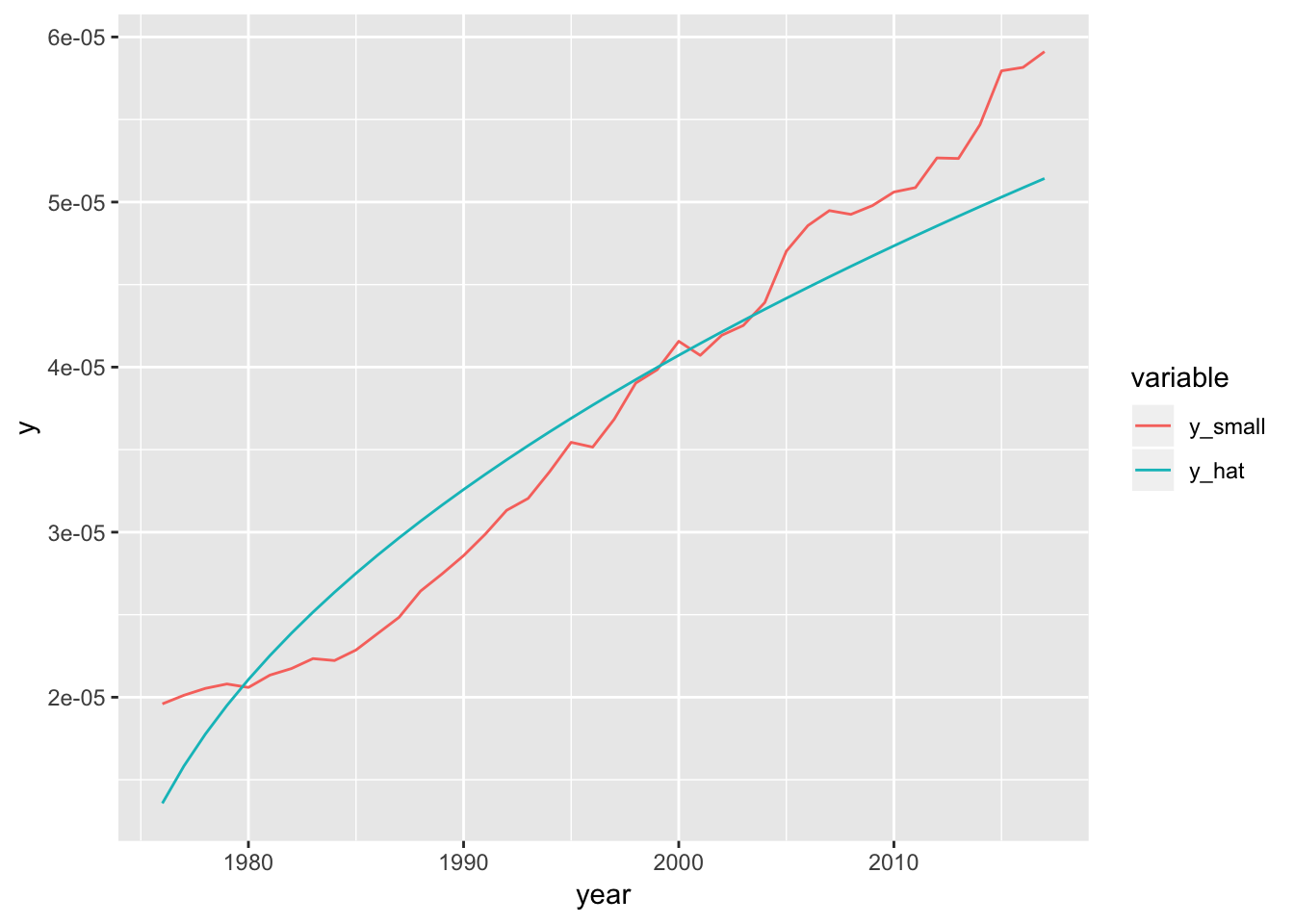
El Modelo de Solow tiene un Error Cuadrático Medio de: 1.349363710^{-11}

4.2 Modelo Ak

Tenemos un modelo de producción de la forma $$y=Ak$$

Con lo que estimamos el modelo sin intercepto $$y=\beta_1 k + \mu$$

## [1] "A_hat = 0.154"

Nuevamente, estimamos $y$ a partir del parámetro encontrado.

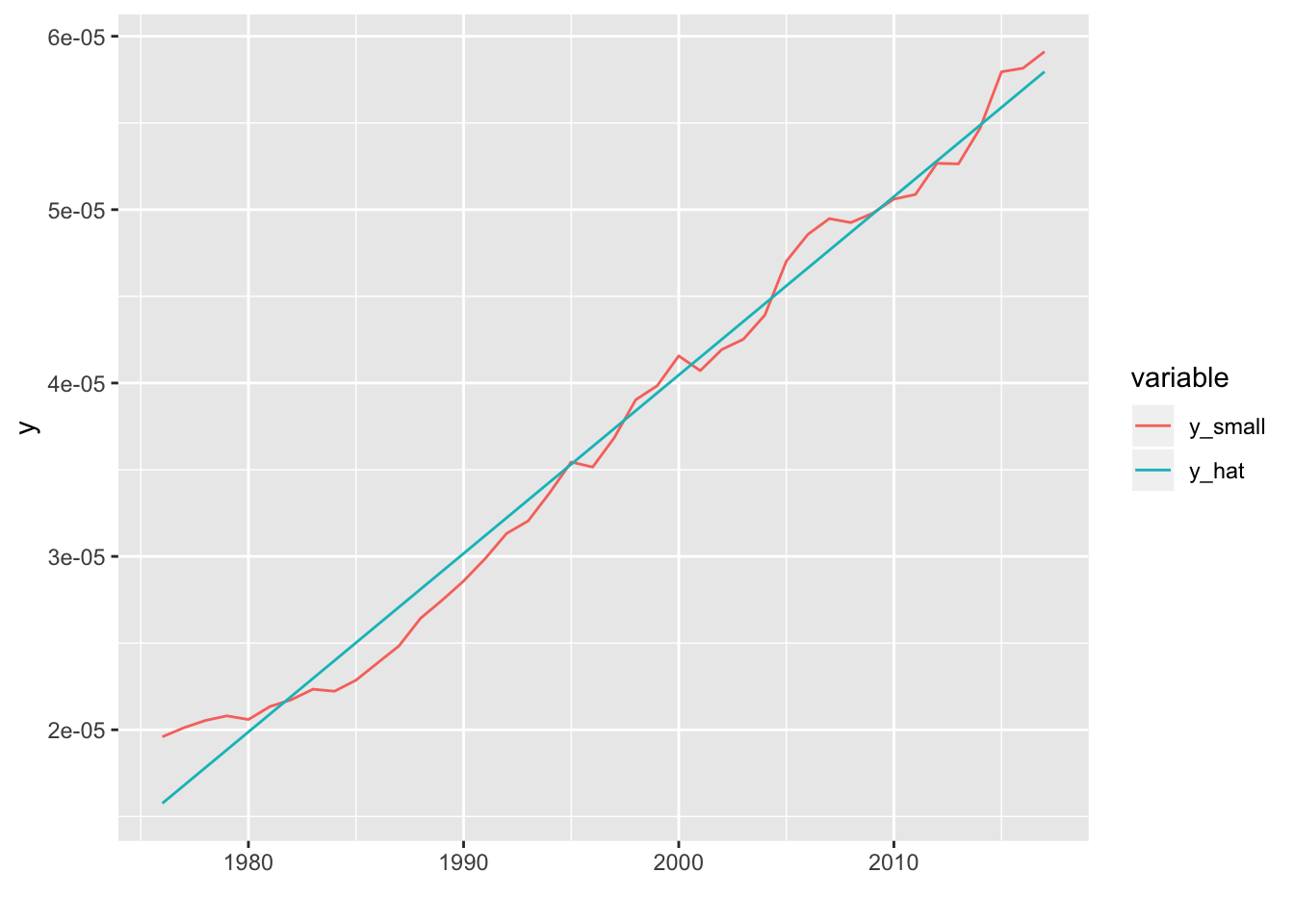
El Modelo Ak tiene un Error Cuadrático Medio de: 2.21595110^{-12}

4.3 Modelo de Lucas

En el modelo de Lucas, la funcion de producción per capita es especificada como: $$y=k^{\alpha}h^{(1-\alpha)}$$ Como no tenemos buenas mediciones del capital humano y debido a que estimamos un modelo con intercepto para acomodar los datos a la realidad, los coeficientes no suman 1.

Estimamos el modelo

$$log(y)=\beta_0 + \beta_1 log(\hat{k}) + \beta_2 log(h) + \mu$$ ,

donde $\beta_0$ es el capital incial, $\beta_1 = \alpha$ y $\beta_2 = \beta$

## [1] "alpha_hat = -0.069"

## [1] "beta_hat = 6.385"

Notemos que $\alpha$ es negativo, lo cual no tiene sentido.

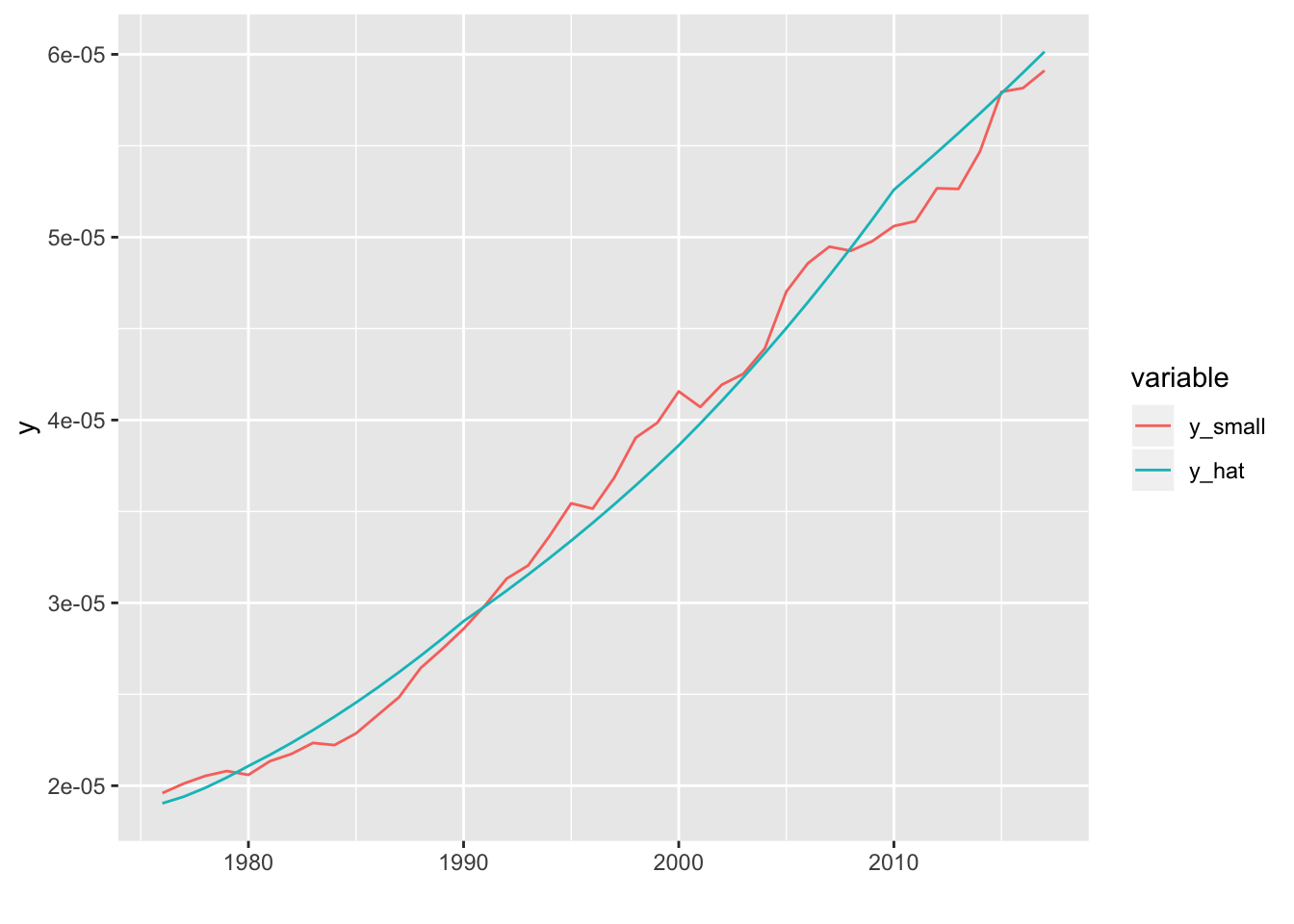
El Modelo de Lucas tiene un Error Cuadrático Medio de: 2.091023910^{-12}

4.3.1 Otra observación

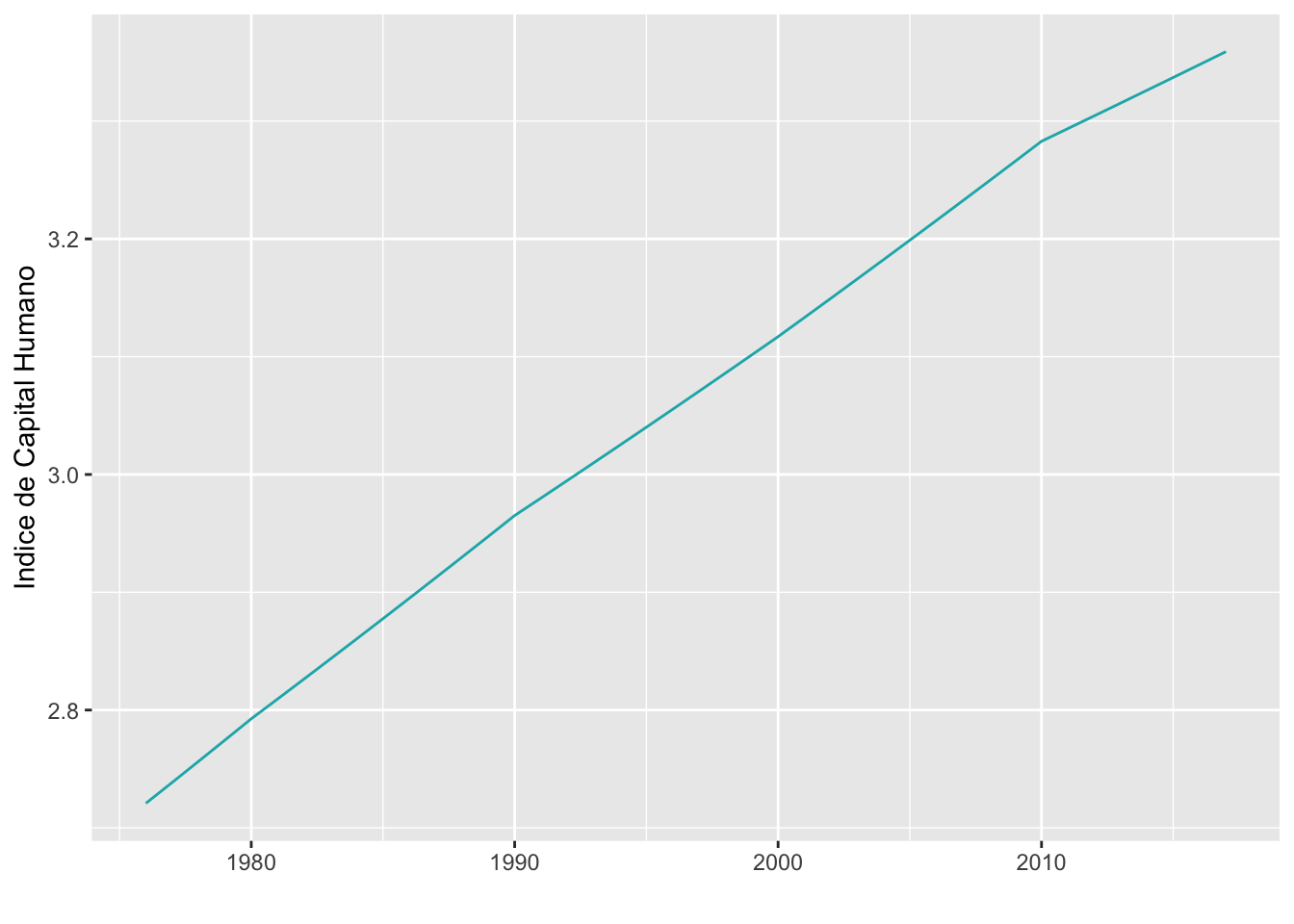
Una característica más que sería importante testear es que según el modelo de Lucas, el capital humano es formado siguiendo: $$\dot{h}=(1-n)h$$

De donde el crecimiento de $h$ con respecto al tiempo debería seguir una forma exponencial

$$h=Ae^{(1-n)t}$$

Observemos que en la realidad el capital humano no crece de forma exponencial.