Preface

This book is still a work in progress

If you encounter any errors/issues, you can reach me here.

This booklet offers an introduction to Bayesian inference. We look at how different models make different claims about a parameter, how they learn from observed data, and how we can compare these models to each other. We illustrate these ideas through an informal beer-tasting experiment conducted at the University of Amsterdam.1 A key concept in Bayesian inference is predictive quality: how well did a model, or parameter value, predict the observed data? We use this predictive quality to update our knowledge about the world, and then use the updated knowledge to make predictions about tomorrow’s world. This learning cycle is visualized below, and will be revisited throughout the booklet.

In the first chapters, the basic Bayesian ingredients (models, prior, posterior, Bayes factor) will be disucssed. In the chapters that follow, these ingredients are used to cook up results for the beer-tasting experiment. Specifically, the Bayesian binomial test, correlation test, and \(t\)-test will be demonstrated.

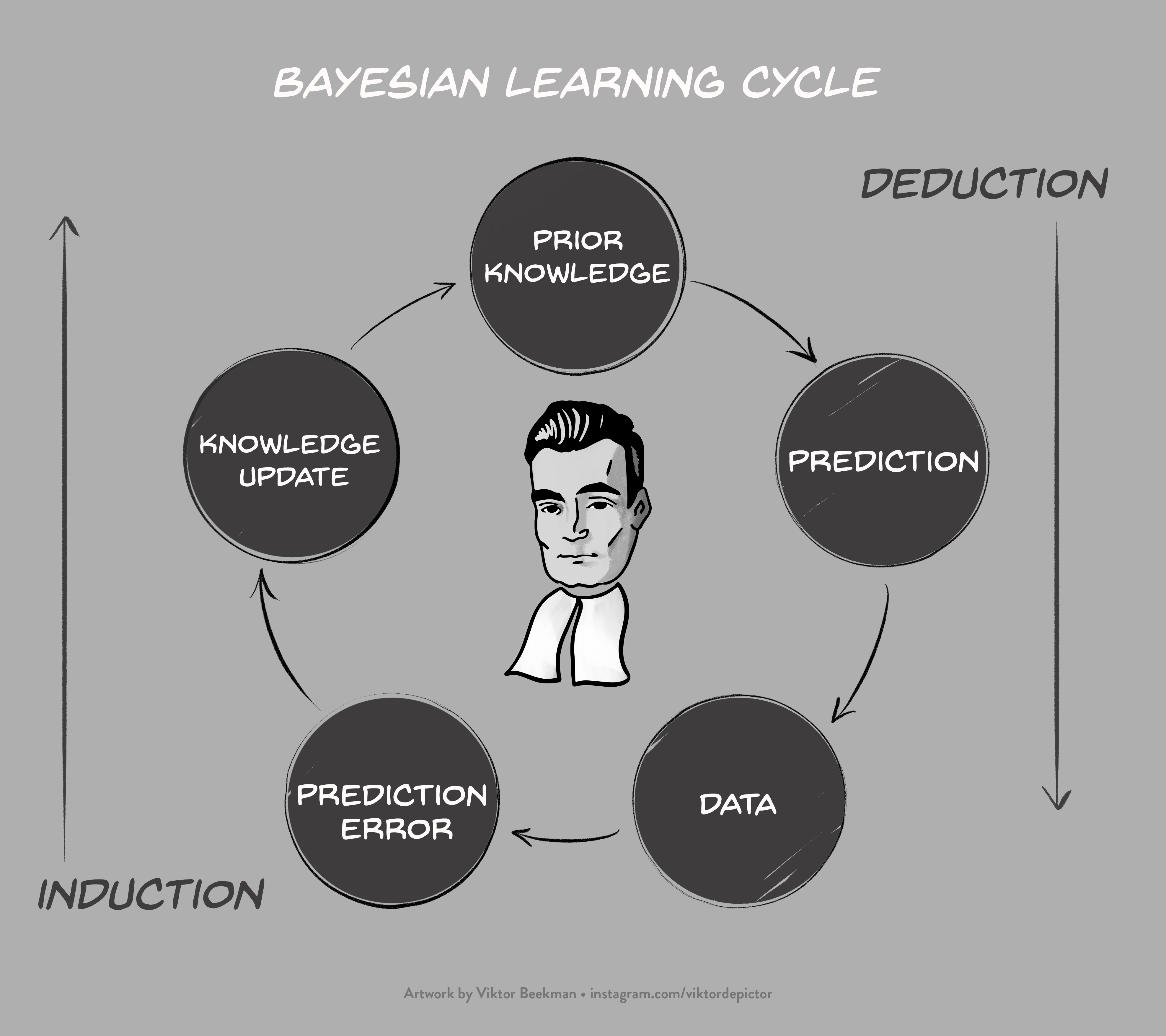
Bayesian learning cycle.

Figure 0.1: Bayesian learning cycle.

References

Doorn, Johnny van, Dora Matzke, and Eric-Jan Wagenmakers. 2020. “An in-Class Demonstration of Bayesian Inference.” Psychology Learning & Teaching 19: 36–45.

  1. In fact, this text is an elaborated version of an article we published on the experiment, see van Doorn, Matzke, and Wagenmakers (2020)↩︎