Big Data Analytics
Lecturer: Cor Beyers
Topic: Basic statistical data analytics

Voorbereiding college
Bekijk deze video’s
Dr. Nic; meetniveau’s; 6 min.
Dr. Nic; samenvattende statistieken centrale tendentie; 5 min.
Tecmath; grafiek van een lineaire functie; 7 min
Simple learning pro; boxplots; 6 min

Literatuur
College handout

Aanbevolen literatuur
Rumsey D. J. (2010). Statistical Essentials for Dummies. Hoboken: Wiley Publishing.

Aanbevolen video’s
Nystrom; uitgebreide uitleg over betekenis standaarddeviatie; 17 min.
Nystrom; verschil populatie en steekproef standaarddeviatie; 12 min.
Principes significantietoets ; 11 min.
Betekenis p-value bij significantietoets (5 min).

1 Data-analyse: eerste verkenning

Bij data-analyse gaat het om het beantwoorden van onderzoeksvragen met behulp van data-analyse. Dit kan een gesloten vraag zijn zoals “is het gemiddelde inkomen in de Publieke sector in 2019 hoger dan in 2018?”, maar – zeker als het gaat om big data-analyse – ook een heel open vraag als “zijn er bepaalde structuren in het koopgedrag van klanten van grote supermarkten te vinden?”.
Het is van belang – zoals bij elk onderzoek – elke stap en/of keuze die gemaakt wordt vanaf de eerste stap goed vast te leggen, voor de onderzoeker zelf en in het kader van reproduceerbaarheid van het onderzoek.

1.1 Data verzamelen

Uitganspunt: wat is de (onderzoeks)vraag?
Vervolgvragen/ stappen:

meetbaar/toetsbaar maken van de vraag door formuleren van deelvragen die aan de hand van te verzamelen data te beantwoorden zijn, m.a.w. operationaliseren;
inventariseren/afbakenen benodigde data; definiëren van populatie en variabelen (kenmerken);
ruwe data verzamelen (N.B. data verzamelen is arbeidsintensief);
bepalen hoe data te verkrijgen zijn (betrouwbaarheid bron?);
enkele betrouwbare Nederlandse bronnen:
– http://opendata.cbs.nl;
– https://data.overheid.nl;
– zie ook de databases die te raadplegen zijn via de bibliotheeksite van De HHS.

Voorbeelden onderzoek/vragen die data-analyse vereisen

vinden van verbanden tussen studieresultaten en kenmerken van studenten;
vinden verbanden tussen bedrag dat consument besteedt en kenmerken van consument;
verband tussen wel/niet overstappen van ziektekostenverzekering en eigenschappen verzekerde;
verbanden tussen artikelen die consumenten bij bezoek aan supermarkt kopen;
verbanden tussen artikelen die bij bezoek aan website bekeken worden;
forensisch onderzoek naar fraude bij een organisatie;
onderzoek naar trending topics op social media;
email berichten herkennen als spam of indelen in ‘Focused’ en ‘Other’.

Zie ook:

1.2 Data cleaning

Ordenen data in datamatrix
Beslissen hoe om te gaan met ontbrekende gegevens
Uitschieter analyse; achterliggende oorzaken; wel/niet meenemen in analyse?

2 Data-analyse: eerste analyse met grafieken en statistieken

Ruwe data dient omgezet te worden in bruikbare informatie.
Eerste stap: grafische data-analyse. Keuze voor grafiek hangt af van schaaltype van de variabele.

2.1 Schaaltypen

Kwalitatief schaaltype, categoriale variabelen

Nominaal;
Ordinaal.

Kwantitatief schaaltype, numerieke variabelen

Interval;
Ratio.

Voorbeelden grafieken http://www.nu.nl/weekend/4339388/facebook-privacydilemma-in-zeven-grafieken.html.

Ruwweg bestaan er twee soorten grafieken:

grafieken om data te analyseren, patronen op te sporen; ‘exploratory graphs’;
grafieken om conclusies in een rapport te verduidelijken/illustreren; ‘explanatory graphs’.

2.2 Univariate, bivariate en multivariate analyses

Als de waarden van één variabele worden geanalyseerd is sprake van univariate statistische analyse, als twee variabelen en de onderlinge samenhang onderwerp van studie is, is sprake van bivariate analyse. Bij een multivariate analyse zijn meer dan twee variabelen in de analyse betrokken.

2.2.1 Veel gebruikte grafieken

Soort analyse en schaaltype(n) van de variabele(n) bepalen welke grafiektypen zinvol zijn. Hieronder een overzicht van veel gebruikte grafieken.

Tabel 1
Soort analyse, schaaltypen en standaardgrafiektypen

Soort analyse	Schaaltype	Standaard grafieken
univariaat	categoriaal	barplots
univariaat	numeriek	histogram; boxplot
univariaat, tijdreeks	numeriek	lijndiagram
bivariaat	categoriaal - categoriaal	stacked barplot; side-by-side barplot; heatmap
bivariaat	categoriaal - numeriek	side-by-side histogram; boxplot
bivariaat	numerieke - numeriek	scatterplots

2.2.1.1 Barplots

studs1 <- read_csv("input/hbostuds.csv")

barplot_basis <-
  studs1 %>% 
    filter(JAAR == 2018) %>%
    group_by(SECTOR, GESLACHT) %>% 
    summarize(TOTAAL = sum(AANTAL)) %>% 
    ggplot(aes(x = reorder(SECTOR, -TOTAAL), y = TOTAAL)) +
    theme_minimal() +
    theme(axis.text.x = element_text(angle=45, hjust = 1)) +
    xlab(NULL) 

barplot1 <-
  barplot_basis +
  geom_bar(stat = "identity", fill='royalblue')

barplot2 <- 
  barplot_basis +
  geom_bar(aes(fill = GESLACHT), stat = "identity") +
  scale_fill_manual(values = c("royalblue", "orange"))

barplot3 <- 
  barplot_basis +
  geom_bar(aes(fill = GESLACHT), stat = "identity", position = 'dodge') +
  scale_fill_manual(values = c("royalblue", "orange"))

barplot1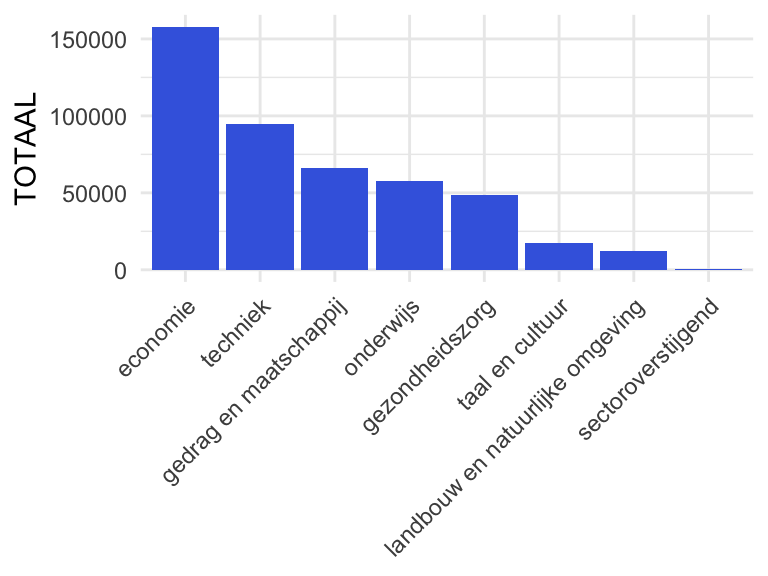

Figuur 1: Barplot, aantal ingeschreven studenten per studierichting in academisch jaar 2018-2019 bij hbo-instellingen in Nederland. Voorbeeld van univariate analyse van een categoriale variabele

barplot2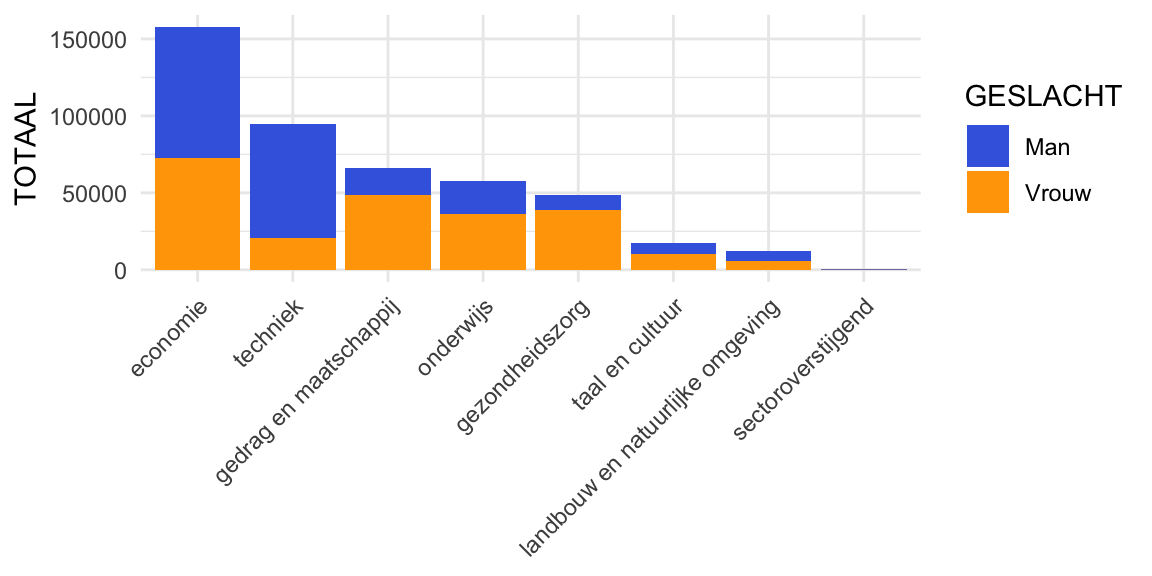

Figuur 2: Barplot stacked, aantal ingeschreven studenten per studierichting in academisch jaar 2018-2019 bij hbo-instellingen in Nederland uitgesplitst naar geslacht. Voorbeeld van bivariate analyse van verband tussen twee categoriale variabelen

barplot3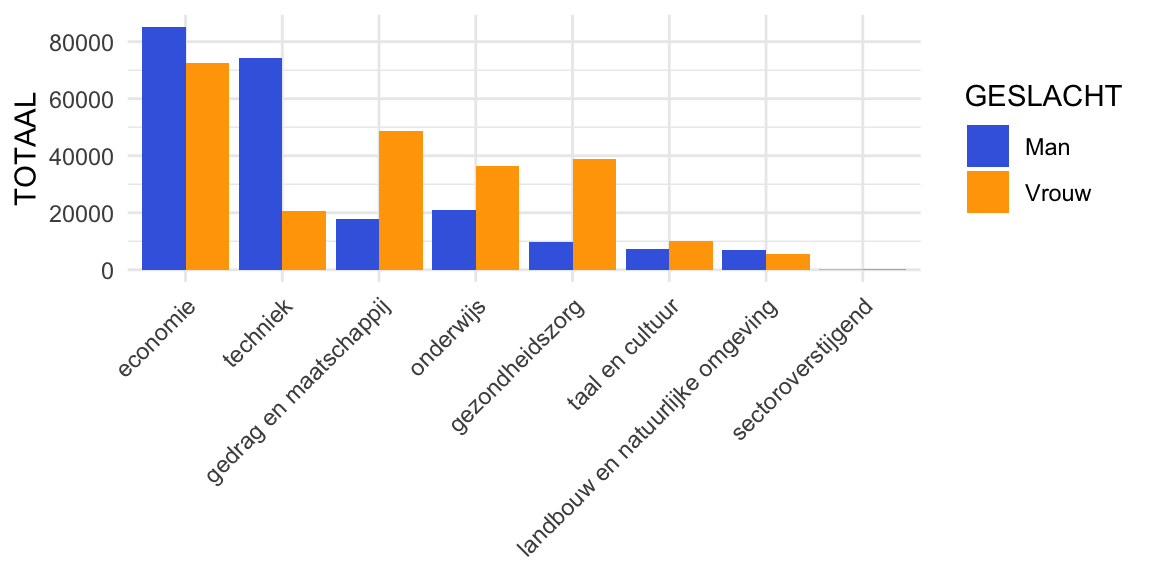

Figuur 3: Barplot dodged, aantal ingeschreven studenten per studierichting in academisch jaar 2018-2019 bij hbo-instellingen in Nederland uitgesplitst naar geslacht. Voorbeeld van bivariate analyse van verband tussen twee categoriale variabelen

2.2.2 Lijndiagram

Een tijdreeks is een reeks metingen in de tijd, gewoonlijk met gelijke tussenliggende tijdsintervallen.
Voorbeelden:

aangekomen passagiers op Schiphol per maand
uurlijkse metingen NO₂-niveau op een meetlocatie
geregistreerd aantal ongelukken per dag in regio Haaglanden

Om patronen in de data zoals seizoensinvloeden en trend in de tijd te ontdekken kan een lijndiagram worden gebruikt.

library(cbsodataR)
df <- cbs_get_data(id="37478hvv") %>% 
  cbs_add_label_columns()

schiphol_pass_vert_kwartaal <-
  df %>% 
  filter(str_sub(Perioden, 5, 6) == "KW",
         Luchthavens_label == "Amsterdam Airport Schiphol") %>% 
  select(
    PERIOD = Perioden,
    PASSENGERS_DEPARTED= TotaalVertrokkenPassagiers_18,
    PASSAGIERS_ARRIVED = TotaalAangekomenPassagiers_15) %>% 
  mutate(PERIOD = str_replace(PERIOD, "KW", " Q"),
         YEAR = as.numeric(str_sub(PERIOD, 1, 4)))


schiphol_pass_vert_kwartaal %>% 
  ggplot(aes(x = PERIOD, y = PASSENGERS_DEPARTED)) +
  geom_line(aes(group = 1), size = .2, col = "blue") +
  geom_point(col = "blue", size = 0.5) +
  theme_light() +
  theme(axis.text.x = element_text(angle = 90)) +
  scale_x_discrete(breaks = 
                     schiphol_pass_vert_kwartaal$PERIOD[seq(1,nrow(schiphol_pass_vert_kwartaal), by = 4)],
                   labels = 1999:max(schiphol_pass_vert_kwartaal$YEAR)) +
  scale_y_continuous(labels = comma) +
  xlab(NULL)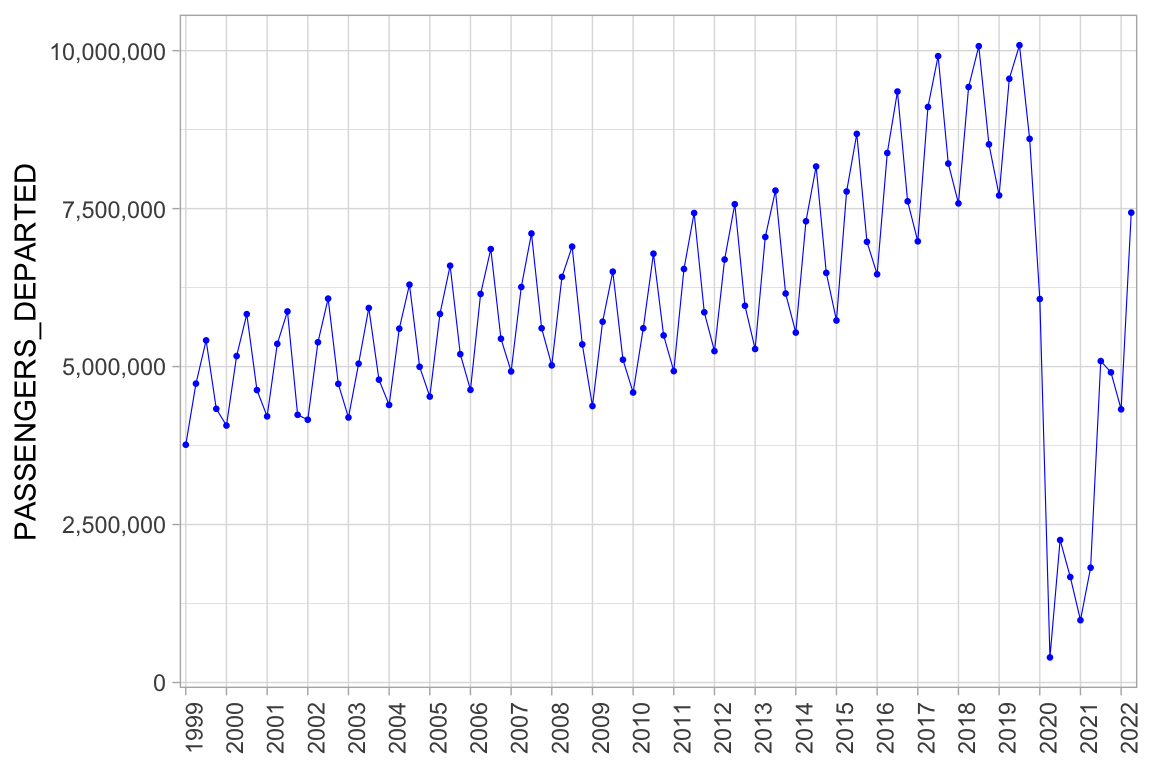

Figuur 4: Lijn diagram passagiers vertrokken van Schiphol per kwartaal. Naast de trendbreuk door covid crisis in 2020 heeft de financiele crisis die begon in 2007/2008 tot een tijdelijke trendbreuk geleid

2.2.2.1 Histogrammen

rdw <- read_csv("input/rdw_data.csv")

hist_basis <- rdw %>% 
  ggplot(aes(x=catalogusprijs)) +
  theme_minimal()

hist1 <- hist_basis +
  geom_histogram(fill = 'royalblue', col='grey', bins=30) +
  xlab("euro") +
  ylab("aantal")

hist2 <- hist_basis +
  geom_histogram(fill = 'royalblue', col='grey', bins = 50) +
  xlab("euro") +
  ylab("aantal")

hist3 <- hist_basis +
  geom_histogram(fill = 'royalblue', col='grey', bins = 50) +
  xlab("euro") +
  ylab("aantal") +
  facet_grid(merk~., scales = 'free_y') +
  theme(strip.text.y = element_text(angle=0))

options(scipen = 999)
hist1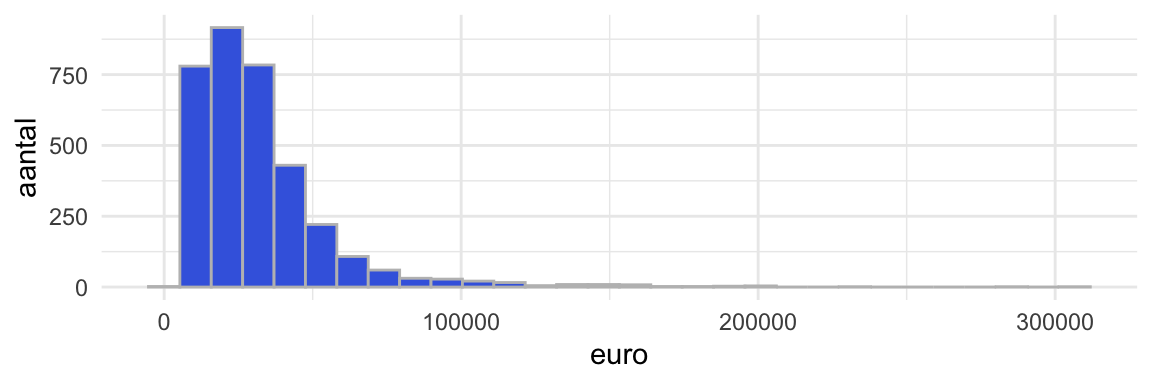

Figuur 5: Histogram van catalogusprijzen van steekproef van 5000 geregistreeerde personenauto’s in Nederland. Het betreft een steekproef van vijf merken - AUDI, KIA, MERCEDES-BENZ, OPEL en PEUGEOT - en van elk merk 1000 observaties. Voorbeeld van univariate analyse van een numerieke variabele. Data source: https://opendata.rdw.nl.

options(scipen = 999)
hist2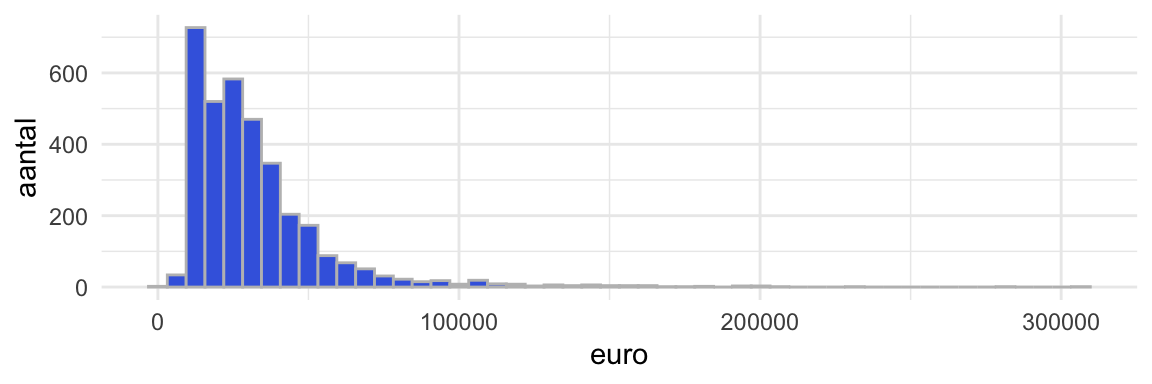

Figuur 6: Histogram van catalogusprijzen van steekproef van 5000 geregistreeerde personenauto’s in Nederland. Voorbeeld van univariate analyse van een numerieke variabele. Het betreft dezelfde data als in Figuur 5.

options(scipen = 999)
hist3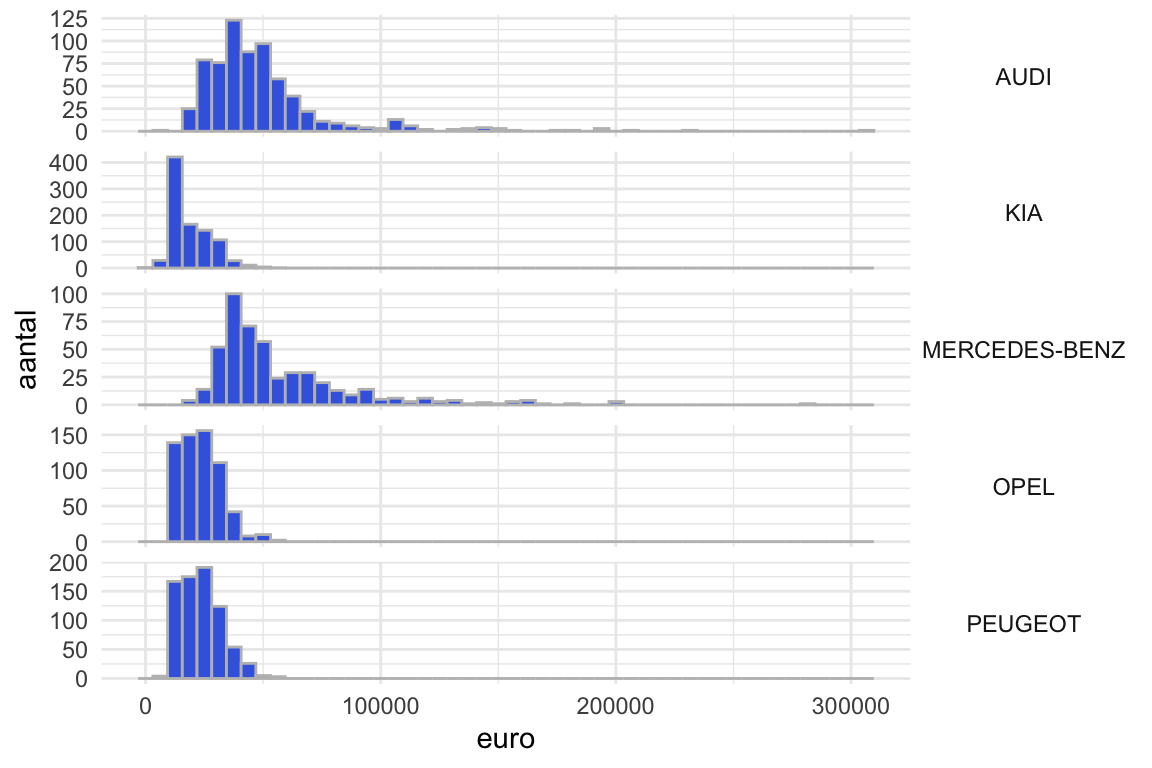

Figuur 7: Side-by-side histogrammen van catalogusprijzen van steekproef van 5000 geregistreeerde personenauto’s in Nederland naar MERK Voorbeeld van bivariate analyse van een numerieke en een categoriale variabele. Het betreft dezelfde data als in Figuur 5.

2.2.3 Boxplots

Boxplots (box and whisker plots) zijn ook geschikt om numerieke variabelen te visualiseren, in het bijzonder om de verdeling van een numerieke variabele in verschillende categorieen te vergelijken.
Een boxpl;ot is gebaseerd op de zogenaamde vijf-getallen samenvatting van de data:

Minimum
Eerste kwartiel
Mediaan (Tweede kwartiel)
Derde Kwartiel
Maximum
Ze zijn ook nuttig om de aandacht te vestigen op uitschieters (outliers) in de verdeling.

Klik hier voor een uitleg van boxplots.

boxplot_basis <- rdw %>% 
  ggplot(aes(x="", y=catalogusprijs)) +
  theme_minimal() +
  coord_flip()

boxplot1 <- boxplot_basis +
  geom_boxplot(fill = 'royalblue') +
  xlab("") +
  ylab("euro")

boxplot2 <- boxplot_basis +
  geom_boxplot(aes(x=merk), fill = 'royalblue') +
  xlab("") +
  ylab("euro")

boxplot1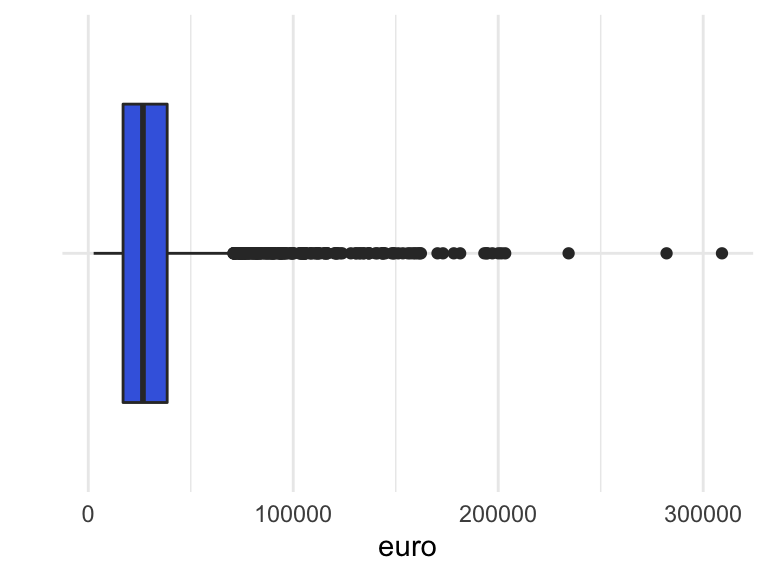

Figuur 8: Boxplot catalogusprijzen steekproef 5000 in Nederland geregistreerde personenauto’s. Het betreft dezelfde data als in Figuur 5

boxplot2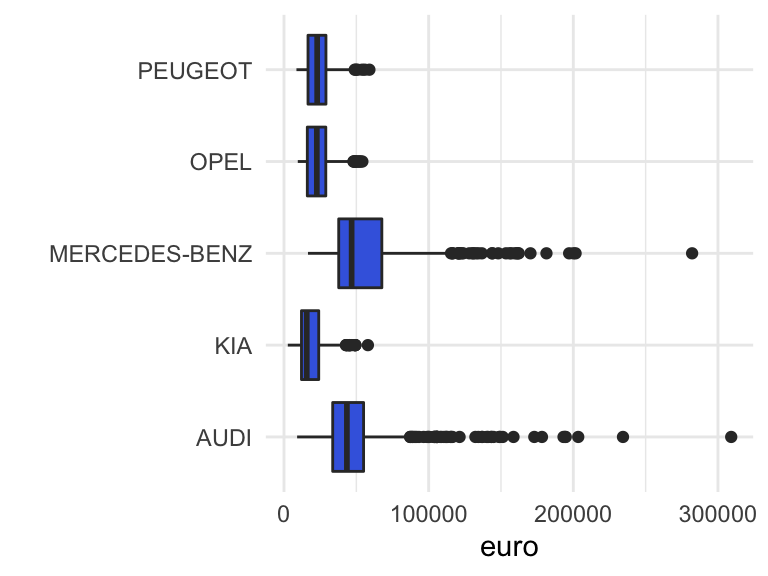

Figuur 9: Boxplot catalogusprijzen steekproef 5000 in Nederland geregistreerde personenauto’s. Het betreft dezelfde data die gebruikt zijn in Figuur 8. Voorbeeld van een bivariate analyse van een numerieke en een categoriale variabele.

2.2.4 Scatterplots

rdw %>% 
  ggplot(aes(x=catalogusprijs, y=bruto_bpm)) +
  theme_minimal() +
  geom_point(col="royalblue") +
  xlab('catalogusprijs (euro)') +
  ylab('bruto BPM (euro)')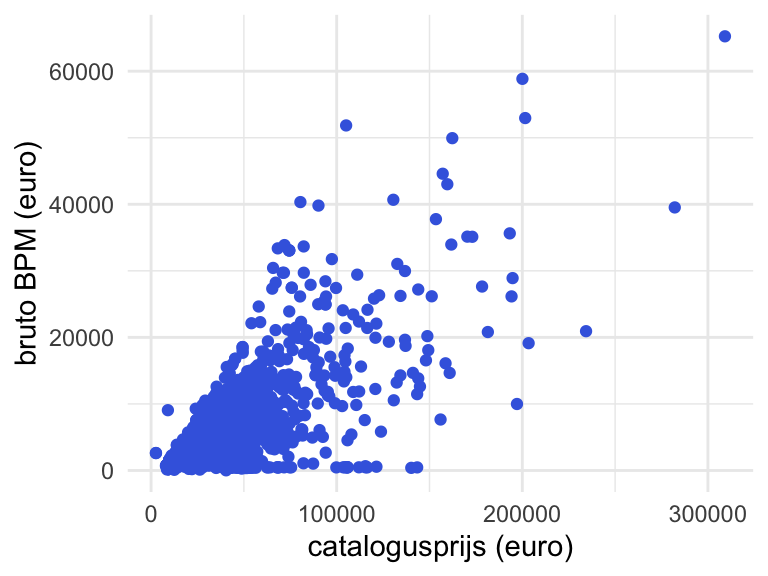

Figuur 10: Scatterplot bruto BPM tegen catalogusprijs voor steekproef van 5000 in Nederland geregistreerde personenauto’s. Steekproef is getrokken van open data van RDW, https://opendata.rdw.nl.

2.2.5 Eisen aan grafieken in rapporten:

informatief;
zelfstandig leesbaar: titel¹, bijschriften bij assen, vermelden eenheden);
vermelding databron.

Voorbeelden hoe het niet moet en hoe wel, zie bijvoorbeeld http://peilingpraktijken.nl/weblog/category/grafieken.

2.3 Grafieken in Excel

Opdracht 2.2.1
Open in Excel het bestand RDW_data.csv.
Dit bestand bevat gegevens van 5000 bij het RDW geregistreerd staande gekentekende voertuigen (bron: https://opendata.rdw.nl).
a. Genereer in Excel een histogram van de catalogusprijzen.
b. Genereer een boxplot van de catalogusprijzen.
d. Filter de gegevens van de PEUGEOTS naar een apart tabblad (gebruik ‘Advanced filter’).
e. Genereer een histogram van de catalogusprijzen van de Peugeots.
f. Genereer een tabel met de frequenties per merk. Gebruik hiervoor een pivot-table.
g. Gebruik de tabel bij onderdeel f. om een staafdiagram te genereren met de frequenties per merk.
h. Maak een staafdiagram met de gemiddelde catalogusprijs per merk.
i. Maak een side-by-side boxplot van de catalogusprijzen naar merk met alleen de merken: Audi, Volkswagen en Opel.

2.4 Samenvattende statistieken

Naast grafieken worden samenvattende statistieken gebruikt om inzicht in data te krijgen. De belangrijkste statistieken betreffen statistieken die informatie geven over het centrum van de verdeling van de data en over de spreiding in de data.
Centrummaten:

(rekenkundig) gemiddelde
mediaan
modus; de modus van een reeks numerieke waarden is veelal geen goede maat voor het centrum van de verdeling.

Spreidingsmaten:

range
interkwartielafstand
variantie en standaarddeviatie.

Vaak wordt de vijf-getallen-samenvatting, of een variatie daarop, gerapporteerd om een dataverzameling samen te vatten:

minimum
1e kwartiel
2e kwartiel (mediaan)
3e kwartiel
maximum

2.4.1 Samengestelde formules in Excel

Om samenvattende statistieken per categorie te berekenen, kent Excel een aantal samengestelde functies, zoals COUINTIF() en AVERAGEIF().
Er is geen samengestelde functie om de mediaan per categorie te berekenen. Deze kan wel door de gebruiker gemaakt worden: MEDIAN(IF(condition, variable)). Voor een voorbeeld, zie het bestand 20190312forsale.xlsx met vraagprijzen van koopwoningen op 3 december 2019 (bron: jaap.nl).
Data staan op het tabblad ‘data’. Het tabblad ‘sum_stats’ bevat een gedeeltelijk ingevulde tabel met samenvattende statistieken per gemeente.

Opdracht 2.2.2 Open in Excel het bestand RDW01.
a. Gebruik formules in Excel om een 5-getallen samenvatting van de catalogusprijzen te genereren.
b. Gebruik formules in Excel om gemiddelde en standaarddeviatie van de catalogusprijzen te berekenen.
c. Gebruik Pivot Table (draaitabel) in het Insert (Invoegen) lint om een samenvatting van de catalogusprijzen per merk te genereren.

3 Toetsende statistiek

Bij data-analyse wordt regelmatig een significantietoets gebruikt.
Voor een eenvoudige uitleg over principes van een significantietoets zie: https://www.youtube.com/watch?annotation_id=annotation_575366&feature=iv&src_vid=UApFKiK4Hi8&v=yTczWL7qJ-Y.

Steekproeven worden o.a. gebruikt om beweringen over een populatie te toetsen. Voorbeelden van dergelijke beweringen:

meer dan 5% van de bezoekers van deze webpagina klikt door op deze banner;
bij een bezoek aan deze supermarkt besteden klanten met een klantenkaart gemiddeld meer dan klanten zonder klantenkaart;
een mailbericht waarin meer dan 10 woorden uit een bepaalde verzameling woorden voorkomen, behoort in meer dan 80% van de gevallen tot spam;
er bestaat een significante samenhang tussen aantal jaren werkervaring en de hoogte van het salaris bij dit bedrijf.

Het begrip ‘statistisch significant’ speelt hierbij een belangrijke rol. Dit begrip wordt hieronder toegelicht aan de hand van analogie met een gerechtelijke procedure.

Toetsen in de rechtspraak
Onderstaande is bedoeld ter illustratie van het onderwerp: statistische toetsen. Bij toetsen van hypothesen (hypothese = veronderstelling) gaat het erom ondersteuning/bewijs te vinden voor een veronderstelling die iemand doet. In de rechtspraak betreft dit de hypothese: de verdachte is schuldig. Dit is de hypothese die de openbare aanklager moet bewijzen. Tot het moment dat deze hypothese juridisch (wettig en overtuigend, “without reasonable doubt”) is bewezen, geldt het alternatief als waarheid: de verdachte is onschuldig. Dit laatste is het uitgangspunt, de bewijslast ligt bij de aanklager (de verdachte hoeft niet te bewijzen dat hij onschuldig is). Bij het toetsen van hypothesen in de statistiek wordt op dezelfde manier te werk gegaan: er is een hypothese (een claim) waarvoor statistische ondersteuning wordt gezocht (de H_A- of H₁- hypothese); uitgangspunt in de procedure is dat de tegenovergestelde hypothese (H₀) juist is. De data analyse richt zich op de vraag of de data de H₀-hypothese tegenspreken ten gunste van de H_A-hypothese.

In statistische termen zou een rechtszaak als volgt genoteerd worden:
H₀: de verdachte is onschuldig
H_A: de verdachte is schuldig
Na alle argumenten gehoord te hebben komt de rechter tot één van de volgende twee uitspraken:

Veroordeling (omdat wettig en overtuigend bewezen is dat de verdachte schuldig is)
Vrijspraak (omdat aangetoond is dat de verdachte onschuldig is, of omdat er gebrek is aan bewijs)
Er kunnen zich nu vier situaties voordoen, zie onderstaand schema.

		WERKELIJK
		onschuldig	schuldig
BESLUIT	vrijspraak	juiste beslissing	onjuiste beslissing, fout van de tweede soort
BESLUIT	veroordeling	onjuiste besliossing, fout van de eerste soort	juiste beslissing

In statistische termen ziet het schema er zo uit:

		WERKELIJK
		H₀ is juist	H_A is juist
BESLUIT	H₀ wordt niet verworpen	juiste beslissing	onjuiste beslissing, fout van de tweede soort; \(\beta\)-risico
BESLUIT	H₀ wordt verworpen	onjuiste besliossing, fout van de eerste soort; \(\alpha\)-risico	juiste beslissing

Let op: niet verwerpen van H₀, betekent niet dat er statistische ondersteuning voor H₀ is gevonden.
De principes bij toetsingsprocedures in de statistiek zijn hiermee gegeven: er wordt uitgegaan van de juistheid van de H₀-hypothese tenzij er statistisch ‘bewijs’ is op grond waarvan de H₀-hypothese wordt verworpen.
Statistisch bewijs is gebaseerd op kansrekening.
Cruciaal in de bewijsvoering is de kans dat, aangenomen dat H₀ juist is, een steekproefresultaat wordt gevonden dat even ver of nog verder van de verwachte waarde ligt dan de steekproefwaarde. Deze kans wordt de p-waarde (p-value) van de steekproef genoemd. Als deze kleiner is dan een van tevoren afgesproken waarde \(\alpha\) (alpha; meestal 0.05), dan wordt H₀ verworpen.

Voorbeeld
De Independent Investigations Group in de USA onderzoekt onder andere claims van mensen die beweren paranormale gaven te hebben. In deze podcast (aanbevolen!) wordt uitgelegd op welke wijze dit onderzoek wordt vorm gegeven (onderzoeksdesign) en hoe hypothese toetsing gebruikt wordt.
Een vereenvoudigd onderzoeksdesign: Om de claim van paranormale begaafdheid te toetsen moet de proefpersoon van 10 aselect getrokken kaarten uit een kaartspel (getrokken met teruglegging) voorspellen of deze rood of zwart is. De proefpersoon wordt als paranormaal begaafd beschouwd als de kans dat hij de kleur van een kaart goed voorspelt meer dan 50% is.
De claim wordt geaccepteerd als de proefpersoon van alle 10 kaarten de juiste kleur voorspelt. Uitgangspunt van het design is dat de claim niet juist is.

		WERKELIJK
		Proefpersoon niet paranormaal begaafd	Proefpersoon paranormaal begaafd
BESLUIT	De proefpersoon voorspelt minder dan 10 kaarten correct en wordt niet als paranormaal begaafd beschouwd	juiste beslissing	onjuiste beslissing, fout van de tweede soort; \(\beta\)-risico; grootte hangt af van mate waarin proefpersoon paranormaal begaafd is
BESLUIT	De proefpersoon voorspelt 10 kaarten correct en wordt als paranormaal begaafd beschouwd	onjuiste besliossing, fout van de eerste soort; \(\alpha\)-risico = \(\frac{1}{1024}\)	juiste beslissing

Er kan ook voor gekozen worden de claim te accepteren als de proefpersoon minstens 9 kaarten goed voorspelt. Met enige kennis van kansrekening kan berekend worden dat in dat geval het \(\alpha\)-risico 0.0107 bedraagt.

Voorbeeld: één steekproef toets op het gemiddelde
\(\mu\): gemiddelde surftijd op zekere webpagina
H₀: \(\mu\) = 45 seconde (of minder)
H_A: \(\mu\) > 45
\(\alpha\) = 0.05
Steekproef: n = 120, steekproef gemiddelde x̅ = 55 sec, steekproefstandaarddeviatie s = 40 sec. Als H₀ juist is, wordt verwacht dat een steekproef een gemiddelde zal hebben van ongeveer 45 seconde. Minder is ook niet in strijd met de H0 hypothese. Als H₀ juist is, is ook een steekproefgemiddelde van iets boven de 45 seconde goed mogelijk. De vraag waar het om gaat is: stel dat H₀ juist is hoe groot is dan de kans op een steekproefresultaat van 55 seconde of meer (nog verder van de verwachte waarde af). Deze waarde wordt de p-waarde van de toets genoemd, elk statistisch pakket rapporteert bij een dergelijke toets deze P-waarde. De gebruiker hoeft deze alleen nog te vergelijken met de gekozen \(\alpha\) waarde (het significantieniveau) om te beslissen of H₀ wel of niet verworpen wordt. Hieronder de output zoals die gegenereerd is met R.

tsum.test(mean.x = 55, s.x = 40, n.x = 120,
          alternative = "greater", mu = 45)


    One-sample t-Test

data:  Summarized x
t = 2.7386, df = 119, p-value = 0.003559
alternative hypothesis: true mean is greater than 45
95 percent confidence interval:
 48.94672       NA
sample estimates:
mean of x 
       55

In de output is te zien dat het steekproefgemiddelde eerst genormeerd is naar een t-waarde (2.7386). De p-waarde van deze toets is 0.004 (het is gebruikelijk p-values af te ronden op 3 decimalen²). Als H₀ juist is, is de kans op een steekproefresultaat zoals gevonden is dermate klein, dat aangenomen wordt dat H₀ niet juist is. H₀ wordt verworpen, er is ondersteuning gevonden voor de hypothese dat de gemiddelde surftijd op de site meer is dan 45 seconden.

3.1 Diverse significantietoetsen

Er bestaat een groot aantal statistische toetsen voor allerlei onderzoeken. Een kleine greep:

t-toetsen op een gemiddelde;
z-toetsen op een proportie;
t-toetsen op verschil van twee gemiddelden (kan op basis van de steekproef geconcludeerd worden dat twee populaties een verschilend gemiddelde hebben);
z-toets op verschil van twee proporties;
chi-kwadraat aanpassingstoetsen (geeft de steekproef aanleiding te veronderstellen dat gegevens in een populatie anders zijn verdeeld dan verondersteld is);
chi-kwadraat toetsen op afhankelijkheid;
toetsen op de mediaan;
toetsen op significant zijn van samenhang tussen twee variabelen.

Bij al deze toetsen gelden bovenstaande principes: H₀ wordt alleen verworpen als er statistische ondersteuning is; in de praktijk betekent dit een p-waarde kleiner dan een vooraf vastgestelde waarde \(\alpha\) (meestal 0.05).

4 Data-analyse

4.1 Gestructureerde data

Min of meer overzichtelijke gegevensverzamelingen geordend in een data-matrix. Denk aan tabellen in een database.

4.2 Ongestructureerde data

Heel veel data is ongestructureerd, denk aan tekstbestanden, videobestanden, emailverkeer. Onderdeel big data-analyse: ongestructureerde data omzetten in informatie.

Voorbeelden

sentimentanalyse (vgl. Coosto, college Schaaphok);
analyse emailverkeer (NSA, onderzoek naar planning aanslagen);
voorspellen griepepidemie o.b.v. zoekgedrag (Google Flu Trends);
tekstanalyse (herkennen auteur).

4.3 Supervised learning

Doel supervised learning: modellen ontwikkelen die verband beschrijven tussen afhankelijke variabele(n) en onafhankelijke variabelen.

Doelstelling:

verbanden begrijpen; begrip van model is belangrijk; of:
voorspellingen doen; begrip van model is van secundair belang.

Voorbeelden (ongestructureerde data, supervised)

griepepidemie voorspellen o.b.v. zoekgedrag;
op basis van tekst in email classificeren als wel/niet junk.

Voorbeelden (gestructureerde data, supervised)

op basis van kenmerken klant (leeftijd, geslacht, inkomen, …) of klant contract wel/niet zal verlengen;
medisch onderzoek: wat zijn de genetische eigenschappen van een patiënt waarbij een bepaalde behandeling kans op succes heeft.

4.4 Unsupervised learning

Doel unsupervised learning: verbanden en structuren in data opsporen.

Voorbeelden (gestructureerde data, unsupervised)

analyseren welke producten in een supermarkt gezamenlijk gekocht worden;
dataset: iris, metingen aan 150 bloemen, 3 verschillende soorten; verbanden opsporen.

ggplot(data = iris, aes(x = Petal.Length, y = Petal.Width)) +
  geom_point(col = 'blue', size = .8) +
  theme_minimal()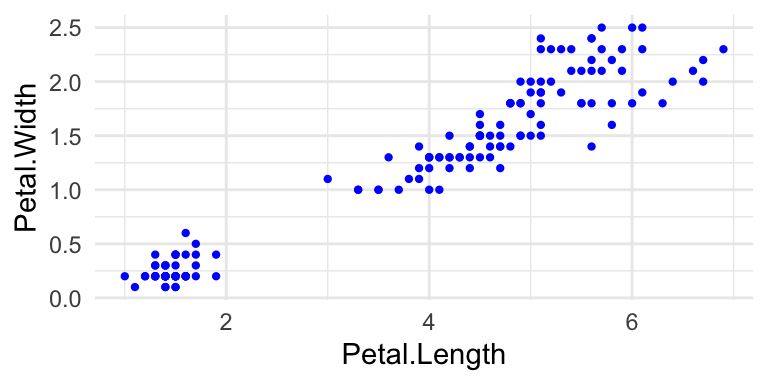

Figuur 11: Scatterplot gebaseerd op data uit Iris dataset. Er zijn duidelijk tenminste twee groepen waarnemingen te onderscheiden.

Voorbeelden (ongestructureerde data, unsupervised)

tekstanalyse;
clusteren nieuwsartikelen o.b.v. onderwerp.

5 Supervised learning met gestructureerde data

Doel: modellen vinden die verband beschrijven tussen een te verklaren (afhankelijke) Y-variabele en één of meer verklarende (onafhankelijke) X-variabelen.

De modellen worden ontleend aan de wiskunde en gezocht wordt naar een model dat zo goed mogelijk past bij de beschikbare data. Vergelijk prijs-afzet modellen in de bedrijfseconomie. Hiervoor wordt vaak het wiskundige model Y = \(\beta\)₀ + \(\beta\)₁X (lineair verband tussen X en Y) gebruikt om het verband tussen de prijs X en de verwachte afzet Y bij die prijs te beschrijven. Op basis van beschikbare data worden de waarden van \(\beta\)₀ en \(\beta\)₁ zo goed mogelijk geschat.

5.1 Classificatie modellen

Indien de Y-variabele een kwalitatieve variabele is, is sprake van een classificatiemodel. Voorbeelden classificatiemethoden:

logistische regressie;
lineaire discriminantanalyse;
decision trees.

5.2 Regressiemodellen

Indien de Y-variabele een numerieke variabele is, wordt gesproken van een regressiemodel.

Voorbeelden regressiemodellen:

enkelvoudig lineair regressiemodel: Y = \(\beta\)₀ + \(\beta\)₁X + \(\epsilon\);
meervoudig lineair regressiemodel: Y = \(\beta\)₀ + \(\beta\)₁X₁ + \(\beta\)₂X₂ + … + \(\epsilon\)
tweedegraads regressiemodel met één X-variabele: Y = \(\beta\)₀ + \(\beta\)₁X + \(\beta\)₂\(X^2\) + \(\epsilon\)
logaritmisch model: log(Y) = \(\beta\)₀ + \(\beta\)₁log(X) + \(\epsilon\);
lineair model met twee X-variabelen en interactieterm: Y = \(\beta\)₀ + \(\beta\)₁X₁ + \(\beta\)₂X₂ + \(\beta\)₁₂X₁X₂ + \(\epsilon\)

Uit deze voorbeelden zal duidelijk zijn dat het aantal regressiemodellen eindeloos is. Onderzoeken welk model in een concrete situatie het best bruikbaar is, behoort tot het vakgebied van wat ‘machine learning’ wordt genoemd.

6 Enkelvoudige en meervoudige lineaire regressiemodellen

6.1 Samenhang tussen kwantitatieve variabelen

Positieve en negatieve samenhang
Causale samenhang
Statistische samenhang
Statistische samenhang kan gemeten worden om vermoeden van causale samenhang te ondersteunen (of ontkrachten)

Voorbeelden (veronderstelde) causale samenhang:

Omzet – Winst;
Prijs – Afzet;
Uitgaven reclame – Afzet;
Temperatuur – Aantal bezoekers Scheveningsche strand;
Docent – tentamenresultaten.

Voorbeelden statistische (niet causale?) samenhang:

aantal ingezette brandweerlieden – totale schade bij de brand;
aantal buitenlanders in Ned. – aantal Nederlanders in buitenland;
afzet cola – aantal gemeten griepgevallen;
gezond ontbijten – levensverwachting;
aantal gelezen boeken – intelligentie (IQ).

Maatstaf lineaire samenhang: (Pearson product-moment) correlatiecoëfficiënt r.

r is een maat voor lineaire samenhang, geen maat voor causaliteit
-1 <= r <= +1
r=-1: perfecte negatieve lineaire samenhang
r=+1; perfecte poitieve lineaire samenhang
| r |> 0.8; sterke lineaire samenhang
0.4 < | r |< 0.8; redeijke lineaire samenhang
0.1 < | r | < 0.4; zwakke linaire samenhang
naast de sterkte van de lineaire samenhang is ook van belang of de samenhang significant is, d.w.z. of de correlatiecoëfficiënt significant van 0 verschilt; hiervoor bestaat een significantietoets; of gemeten lineaire samenhang significant is, hangt naast de waarde van de correlatiecoëfficiënt ook af van de grootte van de steekproef.

Opgave 6.1.1
Zie het bestand huisprijzen.xlsx.

Welke variabele kan gekozen worden als verklarende variabele voor de te verklaren variabele ‘PRICE’?

Welke samenhang tussen de twee variabelen wordt op voorhand verwacht?

Genereer een spreidingsdiagram in Excel.

Bevestigt het spreidingsdiagram het vermoeden met betrekking tot de verwachte samenhang?

Bereken de sterkte van de samenhang, bereken hiervoor de (Pearson product-moment) correlatiecoëfficiënt r.

Gebruik Excel voor het bepalen van de vergelijking van de best-passend regressielijn op basis van de kleinste kwadratenmethode (zie hierna).

Beoordeel het model op bruikbaarheid (zie hierna).

6.2 Enkelvoudige lineaire regressie

Zie James et al. (2013) sectie 3.1.
Het enkelvoudige lineaire regressiemodel gaat ervan uit dat er een verband is tussen de te verklaren variabele Y en de verklarende variabele X dat beschreven wordt door de formule:
Y = \(\beta\)₀ + \(\beta\)₁X + \(\epsilon\)

Hierin is \(\beta\)₁ de regressiecoëfficiënt, de toename van Y bij toename van X met één eenheid; \(\epsilon\) staat voor de invloed van andere factoren op de waarde van Y. Aangenomen wordt dat deze andere factoren onafhankelijk zijn van X.
De achterliggende gedachte is dat de gemiddelde Y-waarde behorende bij een gegeven X-waarde gelijk is aan \(\beta\)₀ + \(\beta\)₁X. Daarnaast veronderstelt het lineaire regressiemodel dat de mogelijke Y waarden bij een gegeven X-waarde normaal verdeeld zijn om \(\beta\)₀ + \(\beta\)₁X.
Het model is de populatie regressielijn, de coëfficiënten (parameters) van dit model zijn doorgaans onbekend en worden geschat op basis van een steekproef. Hierbij wordt gebruik gemaakt van het “kleinste kwadraten criterium”. Dit is de lijn waarvoor de som van de gekwadrateerde afstanden, verticaal gemeten, van de punten in de steekproef tot de lijn minimaal is.

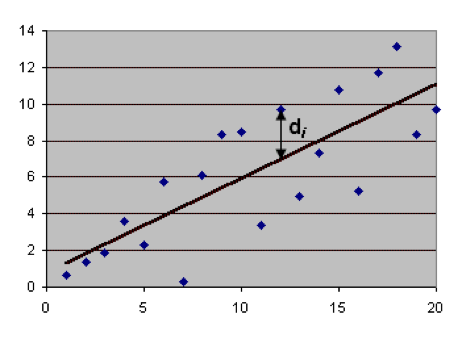
Figuur 8. De regressielijn is de lijn waarvoor de som van de kwadraten van de d_i’s minimaal is.

Elk statistisch pakket heeft de mogelijkheid om bij een gegeven steekproef van koppels (X, Y) de vergelijking van de best passende lijn te berekenen. Deze lijn met vergelijking Y = b₀ + b₁X geeft een schatting voor de populatie regressielijn en kan worden gebruikt om bij gegeven X-waarde de (gemiddelde) Y-waarde te schatten. Bij dergelijke schattingen moet rekening gehouden worden met een foutmarge, alleen al omdat er andere factoren zijn die van invloed zijn op de waarde van Y.

6.2.1 Beoordelen van een regressiemodel

Er bestaan verschillende criteria om een regressiemodel te beoordelen. Hierna wordt dit besproken aan de hand van een met Excel gemaakt regressiemodel.

Voorbeeld
Data, zie huisprijzen.xlsx
PRICE: verkoopprijs woning in USD x 100
SQFT: oppervlakte woning in square feet

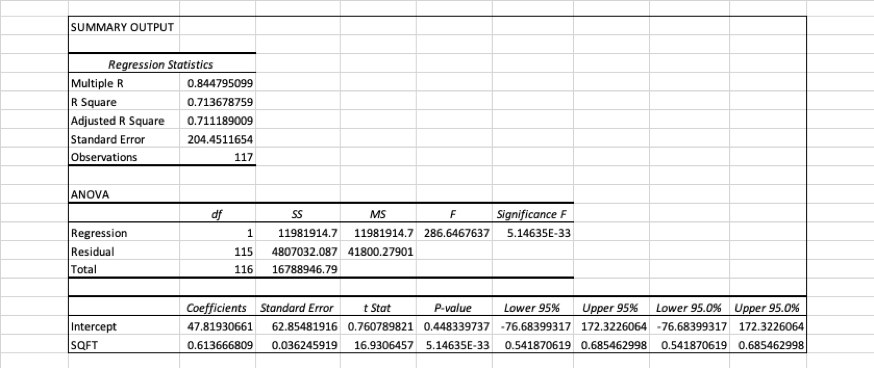
Figuur 12: Regressiemodel met Excel.³

Het model is te vinden in het laatste deel van de output:
PRICE = 47.819 + 0.614xSQFT

De geschatte regressiecoëfficiënt, \(\hat{\beta}\)₁ = 0.614; met 95% zekerheid kan worden gezegd dat de werkelijke waarde van \(\beta\)₁ ligt tussen 0.542 en 0.685.
De waarde onder p-value geeft de p-waarde van de statistische toets:
H₀: \(\beta\)₁ = 0 (d.w.z. er is geen lineaire samenhang tussen X en Y)
H_A: \(\beta\)₁ <> 0
De kleine p-waarde (p < .001) geeft aan dat H₀ verworpen zal worden, m.a.w. er is een significante samenhang tussen X en Y (het model heeft zin).
R squared, \(R^{2}\), is te berekenen met de formule:
\(R^{2} = \frac{\sum{(\hat{Y}-\bar{Y}})^{2}}{\sum{(Y-\bar{Y}})^{2}}\)
De noemer in deze breuk is een maatstaf voor de totale spreiding van de Y-waarden om \(\bar{Y}\), de teller is een maatstaf voor de spreiding in de model Y-waarden (de \(\hat{Y}\) waarden) om \(\bar{Y}\). Deze laatste spreiding is de door het model verklaarde spreiding in de Y-waarden (de spreiding in de Y-waarden veroorzaakt door de spreiding in de X-waarden). \(R^{2}\) geeft aan in welke mate de spreiding in de Y-waarden door het model wordt verklaard; \(R^{2}\) wordt ook wel de verklaringsgraad genoemd. Hoe dichter deze waarde bij 1 ligt, hoe beter het model.

De standard error, formule s_e = \(\sqrt{\frac{\sum(Y-\hat{Y})^{2}}{n-2}}\) is een maatstaf voor de spreiding van de punten om de regressielijn. Deze wordt gebruikt om de marge aan te geven waarmee rekening gehouden moet worden als het model gebruikt wordt om bij een gegeven X-waarde de Y waarde te schatten. Als vuistregel geldt dat een marge van 2xs_e moet worden aangehouden. Om een oordeel over de grootte van se te geven wordt deze gedeeld door \(\bar{Y}\) (de gemiddelde Y-waarde van de steekproefeenheden).

6.3 Meervoudige lineaire regressie

Zie James et al. (2013) sectie 3.2. Bovenstaande is eenvoudig uit te breiden tot een regressiemodel met meer verklarende variabelen: X₁, X₂, …, X_p:
Y = \(\beta\)₀ + \(\beta\)₁X₁ + \(\beta\)₂X₂ + … + \(\beta\)_pX_p + \(\epsilon\).
In de output van een (meervoudige) regressieanalyse staat ook de p-value van een F-toets vermeld. Dit is de p-value van de toets:
H₀: \(\beta\)₁ = \(\beta\)₂ = … = \(\beta\)_p =0
H_A: tenminste één van de regressiecoëfficiënten <> 0
Het belang van deze toets is na te gaan of het regressiemodel überhaupt zinvol is. Als H₀ niet wordt verworpen, is duidelijk dat het model niet zinvol is.

Enkele aandachtspunten:

pas op voor multicollineariteit, dat wil zeggen een sterke lineaire samenhang tussen twee of meer van de gebruikte verklarende variabelen; een goed gebruik is een meervoudige regressieanalyse te beginnen met het opstellen van een correlatiematrix, zie opgave 6.2.1b;
het is mogelijk een 0/1-dummy variabele in het model op te nemen, zie opgave 6.2.2 en James et al. (2013) sectie 3.3;
indien het gewenst is een kwalitatieve variabele op te nemen met meer dan twee waarden, dan moet deze gesplitst worden in meerdere 0/1-variabelen.

Opgave 6.2.1 (Advertising data)
In het bestand Advertising.csv staan de verkopen van een bepaald product in 200 marktsituaties gegeven de reclamebudgetten in drie verschillende media in deze situaties, bedragen in USDx1000.
Doel is een model te ontwikkelen dat gebruikt kan worden om de verkoopopbrengst te voorspellen gegeven de budgetten voor de drie media.

Plot drie scatterdiagrammen waarin de opbrengst wordt geplot tegen elk van de drie variabelen afzonderlijk.

Stel een correlatiematrix op met de vier variabelen.

Stel een model op waarin Sales wordt verklaard door één van de drie verklarende variabelen.

Stel een model op waarin Sales wordt verklaard door twee van de drie verklarende variabelen.

Stel een model op waarin Sales wordt verklaard door alle drie de verklarende variabelen.

Welk model heeft de voorkeur?

Opgave 6.2.2 (huisprijzen)
Gebruik de gegevens in het bestand huisprijzen.xlsx om een regressiemodel te ontwerpen waarmee de huisprijs kan worden geschat.
Probeer gebruik te maken van meerdere X-variabelen om een zo goed mogelijk regressiemodel te verkrijgen.

In wetenschappelijke rapporten is het goed gebruik de titel onder de grafiek te vermelden. Zie de grafieken in deze handout.↩︎
Indien de p-waarde kleiner is dan 0.001 dan wordt gerapporteerd p-waarde < .001.↩︎
menukeuze in Excel: Data/Data Analysis/Regression↩︎

BDA Data Analytics