2 La naturaleza del registro fósil
2.1 Distribución geográfica y ambiental de las rocas fosilíferas
La distribución geográfica y ambiental de las rocas fosilíferas es esencial para comprender el registro fósil a lo largo del tiempo geológico. Esta distribución varía significativamente debido a varios factores clave. Un patrón importante es que la exposición de rocas con fósiles aumenta de forma exponencial hacia edades geológicas más recientes (Fig. 2.1). Esto se debe a procesos geológicos como la erosión y la tectónica de placas, lo que hace que sea más probable encontrar afloramientos de rocas con fósiles de épocas más recientes en comparación con las más antiguas. Por otro lado, los registros fósiles marinos son más abundantes que los terrestres, principalmente debido a tasas de sedimentación más altas en ambientes marinos en comparación con ambientes terrestres, donde la erosión es común. Además, los registros de ambientes marinos someros superan en número a los de ambientes marinos profundos, ya que los sedimentos someros tienen tasas de acumulación más altas y, por lo tanto, tienen más probabilidades de conservar fósiles a lo largo del tiempo geológico. Sin embargo, en algunas áreas, como zonas con alta erosión, como regiones montañosas de elevada altitud, los registros fósiles son raros o están ausentes debido a la destrucción y erosión de las rocas sedimentarias que contienen fósiles.
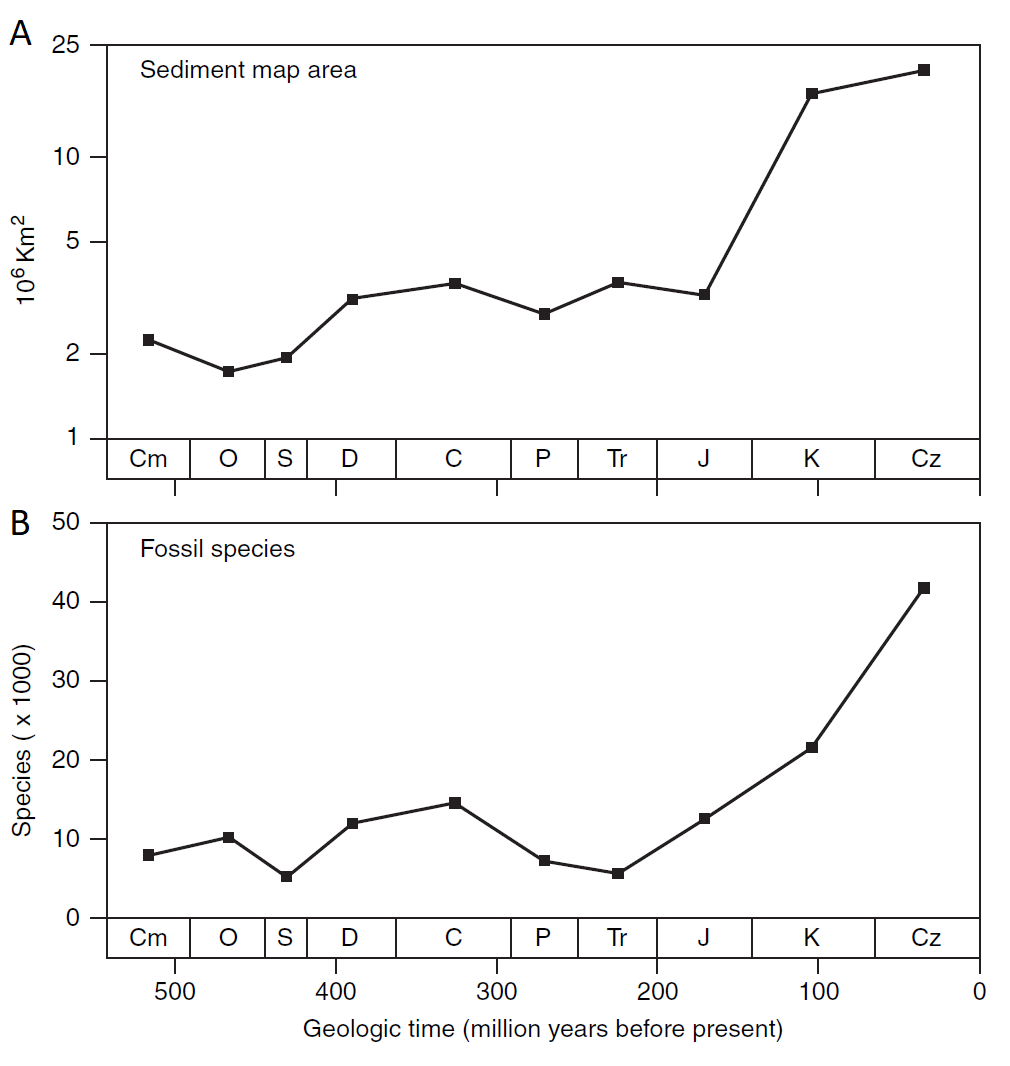
Figura 2.1: Rocas sedimentarias y diversidad fósil a lo largo del tiempo geológico. (A) Área de afloramiento de rocas sedimentarias según mapas geológicos para diferentes periodos del Fanerozoico. Los datos se presentan en una escala logarítmica para resaltar la variación proporcional entre los números. Una diferencia de unidad en esta escala representa una relación constante; por ejemplo, la diferencia entre 1 y 2 es la misma que entre 5 y 10. (B) Estimación del número de especies de invertebrados descubiertas y nombradas entre 1900 y 1975. Los datos del Pleistoceno y Holoceno se omiten en ambas figuras. Se observa que los periodos con mayor cantidad de roca sedimentaria tienden a correlacionarse con un mayor número de especies fósiles. Imagen tomada de Foote & Miller (2007).
2.2 Potencial de preservación del registro fósil
El potencial de preservación del registro fósil es notablemente bajo y está sujeto a varios sesgos tafonómicos, lo que resulta en una preservación desigual de tejidos mineralizados, partes corporales y grupos taxonómicos. Por ejemplo, es evidente que los grupos que carecen de partes mineralizadas, como los poliquetos, tienen una probabilidad de preservación mucho más baja, con una probabilidad de preservación por género e intervalo de tiempo de solo 0.05. En contraste, los grupos que están compuestos por múltiples partes mineralizadas, como los trilobites, tienen una probabilidad de preservación más alta, que varía entre 0.7 y 0.9 por género e intervalo de tiempo (Tablas 2.1 y 2.2). Esto destaca cómo la composición y las características de los organismos desempeñan un papel crucial en su potencial de preservación en el registro fósil.
| Grupo | Probabilidad |
|---|---|
| Esponjas | 0.4–0.45 |
| Corales | 0.4–0.5 |
| Poliquetos | 0.05 |
| Crustáceos malacostracos | 0.2–0.35 |
| Ostrácodos | 0.5 |
| Trilobites | 0.7–0.9 |
| Briozoos | 0.7–0.75 |
| Braquiópodos | 0.9 |
| Crinoideos | 0.4 |
| Asterozoos | 0.25 |
| Equinoideos | 0.55–0.65 |
| Bivalvos | 0.45–0.5 |
| Gastrópodos | 0.4–0.55 |
| Cephalópodos | 0.8–0.9 |
| Graptólitos | 0.65–0.9 |
| Conodontos | 0.7–0.9 |
| Peces cartilaginosos | 0.1–0.15 |
| Peces óseos | 0.15–0.3 |
| Grupo | Nivel taxonómico | Porcentaje |
|---|---|---|
| Esponjas | Familia | 48 |
| Corales | Familia | 32 |
| Poliquetos | Familia | 35 |
| Crustáceos malacostracos | Familia | 19 |
| Ostrácodos | Familia | 82 |
| Ostrácodos | Género | 42 |
| Briozoos | Familia | 74 |
| Braquiópodos | Familia | 100 |
| Braquiópodos | Género | 77 |
| Crinoideos | Familia | 50 |
| Asterozoos | Familia | 57 |
| Asterozoos | Género | 5 |
| Equinoideos | Familia | 89 |
| Equinoideos | Género | 41 |
| Bivalvos | Familia | 95 |
| Bivalvos | Género | 76 |
| Gastrópodos | Familia | 59 |
| Cephalópodos | Familia | 20 |
| Peces cartilaginosos | Familia | 95 |
| Peces óseos | Familia | 62 |
| Arácnidos | Género | 2 |
El registro fósil, aunque valioso, proporciona una muestra muy limitada de la vida en el pasado. La falta de completitud en este registro ha sido un tema ampliamente discutido en la paleontología. Sin embargo, es importante destacar dos aspectos cruciales:
Diseño de Experimentos Paleontológicos: A pesar de la imperfección del registro fósil, los paleontólogos pueden diseñar experimentos y análisis que tengan en cuenta esta limitación. Esto implica utilizar métodos estadísticos y enfoques que consideren la falta de datos y permitan realizar inferencias basadas en la información disponible.
Sesgo del Registro Fósil: Aunque el registro fósil está lejos de ser completo, el sesgo que presenta puede ser beneficioso desde una perspectiva científica. Cuando los datos recopilados muestran un patrón inesperado o contrario a lo que se podría esperar dada la falta de información, esto puede proporcionar información valiosa sobre la paleobiología.
En resumen, aunque el registro fósil es limitado y puede no proporcionar una imagen completa de la vida en el pasado, los paleontólogos pueden superar esta limitación mediante enfoques estadísticos y considerando el sesgo del registro. Esto permite obtener información fiable y valiosa sobre la evolución y la biología de especies extintas (Fig. 2.2).
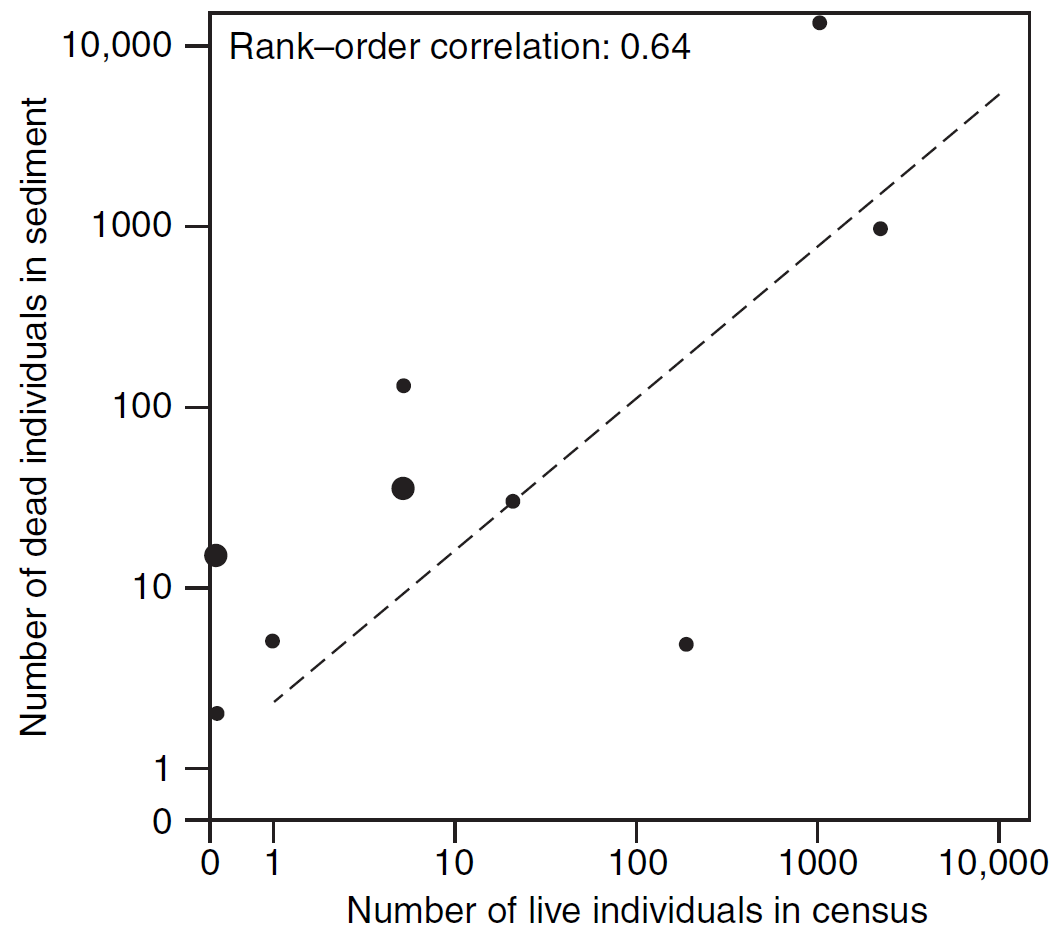
Figura 2.2: Comparación de abundancias de especies en comunidades vivas y sus restos subfósiles en un arroyo de marea en California. El gráfico muestra que las especies más abundantes en la muestra viva también tienden a ser más abundantes en la muestra de conchas muertas, con abundancias muertas generalmente más altas que las vivas. Este análisis es clave para comprender la relación entre las comunidades vivas y los fósiles. Imagen tomada de Foote & Miller (2007).
2.3 Medidas de la (in)completez del registro fósil
La evaluación de la completitud del registro fósil implica el uso de varias medidas que nos ayudan a comprender cuán bien se representa la historia de la vida en los fósiles. Aquí se detallan tres de estas medidas clave:
- Probabilidad de Muestreo por Unidad de Intervalo de Tiempo (Fig. 2.3): Esta probabilidad se calcula como el número de intervalos temporales en los que esa especie aparece dividido entre todos los intervalos potenciales en los que podría haber aparecido, considerando desde su primera hasta su última aparición en el registro fósil. Por ejemplo, si una especie se registra en 1 de los 4 intervalos temporales potenciales entre su primera y última aparición, su probabilidad de muestreo se calcula como 1 dividido por 4, lo que equivale a 0.25. Es importante señalar que realizar este cálculo para una sola especie puede resultar en un amplio margen de error debido a la variabilidad en los datos. Por esta razón, es común calcular estas probabilidades para conjuntos de especies, lo que proporciona estimaciones más robustas y representativas de la probabilidad de muestreo en el registro fósil.

Figura 2.3: Ilustración esquemática del análisis de intervalos utilizado para estimar la probabilidad promedio de muestreo de un grupo de especies. Cada marca X representa un intervalo de tiempo en el que se muestrea la especie correspondiente; los espacios en blanco intermedios son intervalos en los que no hay registro de la especie. Se tabulan las ocurrencias de cada especie como el número de intervalos en los que se encuentra, excluyendo los de primera y última aparición. Esto se compara con el número de oportunidades de muestreo, es decir, el número de intervalos de tiempo durante los cuales la especie tuvo la posibilidad de ser muestreada o no. Esto se calcula como la suma de los intervalos de tiempo entre la primera y última aparición. Dado que una especie necesariamente debe ser muestreada en sus intervalos de primera y última ocurrencia, estos no se incluyen en las tabulaciones para no sobreestimar la probabilidad de muestreo. En este caso, hay 16 oportunidades de muestreo y 5 ocurrencias, ambos números excluyen las primeras y últimas apariciones. Por lo tanto, la probabilidad de muestreo estimada para estas especies es de 5/16, o 31 por ciento por intervalo de tiempo. Imagen tomada de Foote & Miller (2007).
- Proporción de Taxones Conocidos desde un Solo Intervalo Estratigráfico (Fig. 2.4): Para calcular esta medida, se parte del principio de que un muestreo incompleto tiende a acortar los rangos estratigráficos observados. Por lo tanto, la proporción de taxones conocidos a partir de un solo intervalo estratigráfico se considera inversamente proporcional a la calidad del muestreo. Esto significa que, si la calidad del muestreo es baja, se espera que una mayor proporción de taxones sea conocida solo a partir de un solo intervalo estratigráfico. La fórmula para estimar la probabilidad de muestreo por unidad de tiempo se basa en esta idea y tiene en cuenta las proporciones de especies con rangos estratigráficos de un solo intervalo, dos intervalos y tres intervalos.
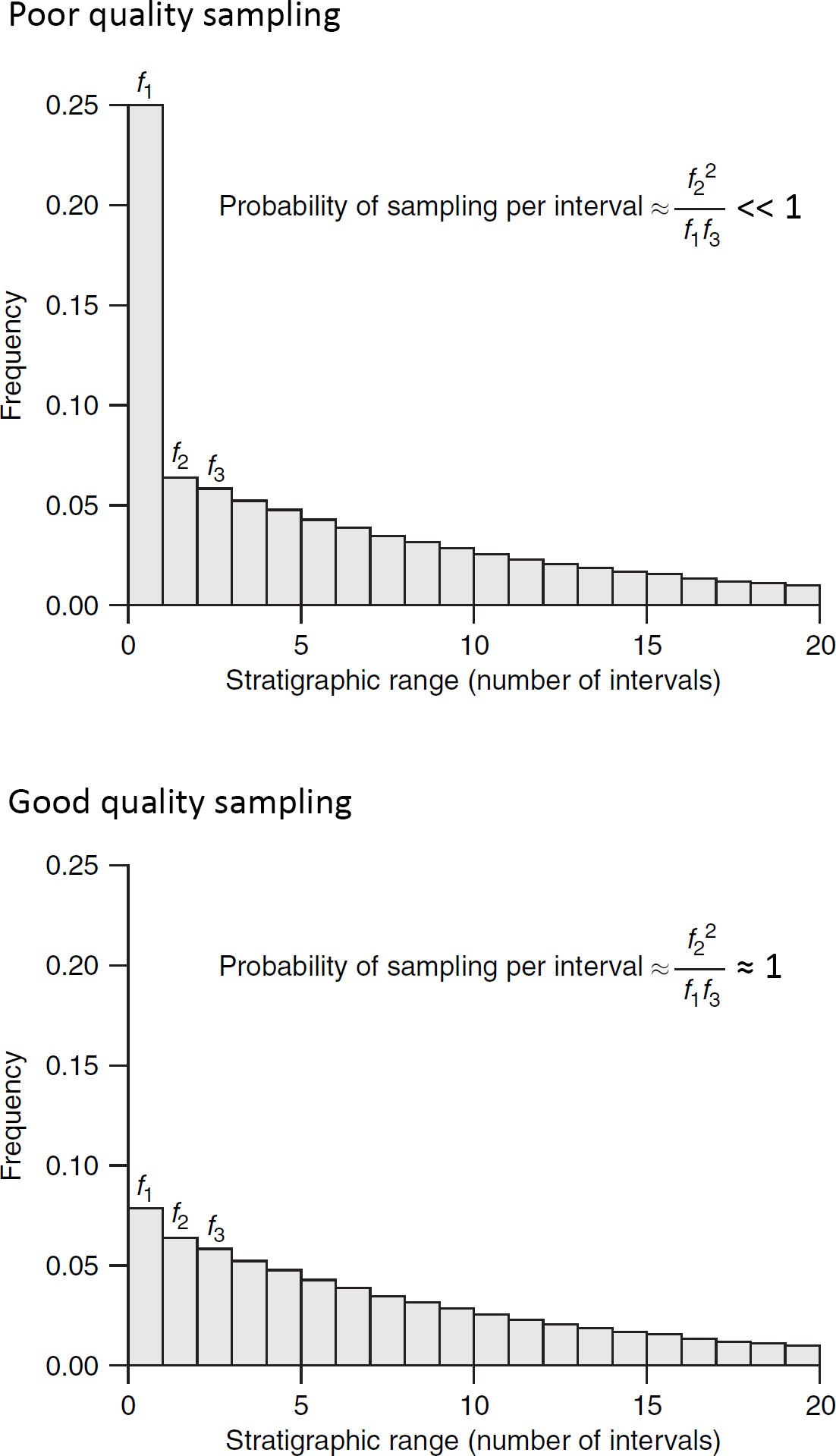
Figura 2.4: Distribución de frecuencia de rangos estratigráficos de taxones, asumiendo un muestreo incompleto pero uniforme. La probabilidad de muestreo por intervalo de tiempo puede estimarse a partir de las frecuencias de taxones con rangos de uno, dos y tres intervalos. Imagen tomada de Foote & Miller (2007).
- Estimación de la Completitud del Registro Fósil a lo Largo del Tiempo: Para evaluar cuán completo es el registro fósil en un período de tiempo extenso, como el Fanerozoico, los paleontólogos hacen estimaciones sobre el número total de especies que se cree que han existido durante ese período y lo comparan con la cantidad de especies conocidas en el registro fósil. Para realizar estas estimaciones, los expertos en paleontología utilizan suposiciones basadas en la longevidad promedio de las especies, que se estima en alrededor de 4 millones de años, y el supuesto de que la diversidad de especies se ha mantenido relativamente constante a lo largo del Fanerozoico. Bajo estas asunciones, se estima que, en promedio, alrededor del 25% de las especies existentes se extinguieron y fueron reemplazadas por nuevas especies cada millón de años. Aplicando esta estimación a lo largo de los 550 millones de años del Fanerozoico, podemos realizar algunos cálculos reveladores. Comenzamos con la diversidad actual, que consiste en aproximadamente 180,000 especies de grupos con un buen registro paleontológico, lo que significa que se han conservado bien como fósiles y han sido bien documentadas por paleontólogos. Luego, consideramos que, en el último medio billón de años, aproximadamente el 25% de la diversidad se reemplazó cada millón de años. Esto implica que durante ese tiempo se originaron alrededor de 25 millones de especies. Sin embargo, cuando comparamos esta estimación de 25 millones de especies con las 300,000 especies fósiles que se han descrito, se hace evidente que solo una pequeña fracción, alrededor del 1% o 2%, de las especies que existieron en el pasado se conocen a través de fósiles. Esta comparación resalta la notable limitación del registro fósil, ya que gran parte de la diversidad de especies que alguna vez poblaron la Tierra permanece en gran medida desconocida para nosotros.
2.4 Muestreo del registro fósil
El muestreo del registro fósil es una consideración fundamental en paleontología, y en lugar de preguntarnos si el registro fósil es completo, debemos preguntarnos si es adecuado para el propósito específico que tenemos en mente. Al hacerlo, dos aspectos importantes surgen en el diseño de nuestros estudios paleontológicos:
¿Es una muestra aleatoria? La respuesta es no. Incluso si intentamos realizar un muestreo de manera aleatoria, el registro fósil está sesgado en varios aspectos, como lo hemos discutido previamente. Por lo tanto, debemos ser precavidos al plantear preguntas o resolver problemas específicos utilizando el registro fósil, ya que el sesgo en los datos puede influir en los resultados y conclusiones.
¿Son nuestras medidas sensibles al tamaño muestral? Aquí entra en juego el concepto de “rarefacción”, que es un método utilizado para estimar el número de taxones que habríamos encontrado en una muestra más pequeña. En otras palabras, dado que nuestras muestras del registro fósil pueden variar en tamaño y extensión, la rarefacción nos permite estandarizar y comparar los datos entre diferentes muestras, incluso si son de diferentes tamaños.
La rarefacción es un método utilizado en ecología y paleontología para estandarizar las mediciones de biodiversidad o riqueza taxonómica cuando se trabaja con muestras de diferentes tamaños (Fig. 2.5). La idea principal detrás de la rarefacción es estimar cuántos taxones o especies habrían sido observados en una muestra de un tamaño específico si la muestra más grande se hubiera reducido al tamaño de la muestra más pequeña. En el ámbito de la paleontología, esta técnica se emplea frecuentemente al examinar el registro fósil, donde las dimensiones de las muestras pueden fluctuar debido a la cantidad variable de material fósil disponible. Cuando se aplica la rarefacción, los paleontólogos pueden ajustar los datos procedentes de distintas muestras, lo que simplifica la evaluación de la diversidad y riqueza taxonómica en diferentes conjuntos de fósiles.
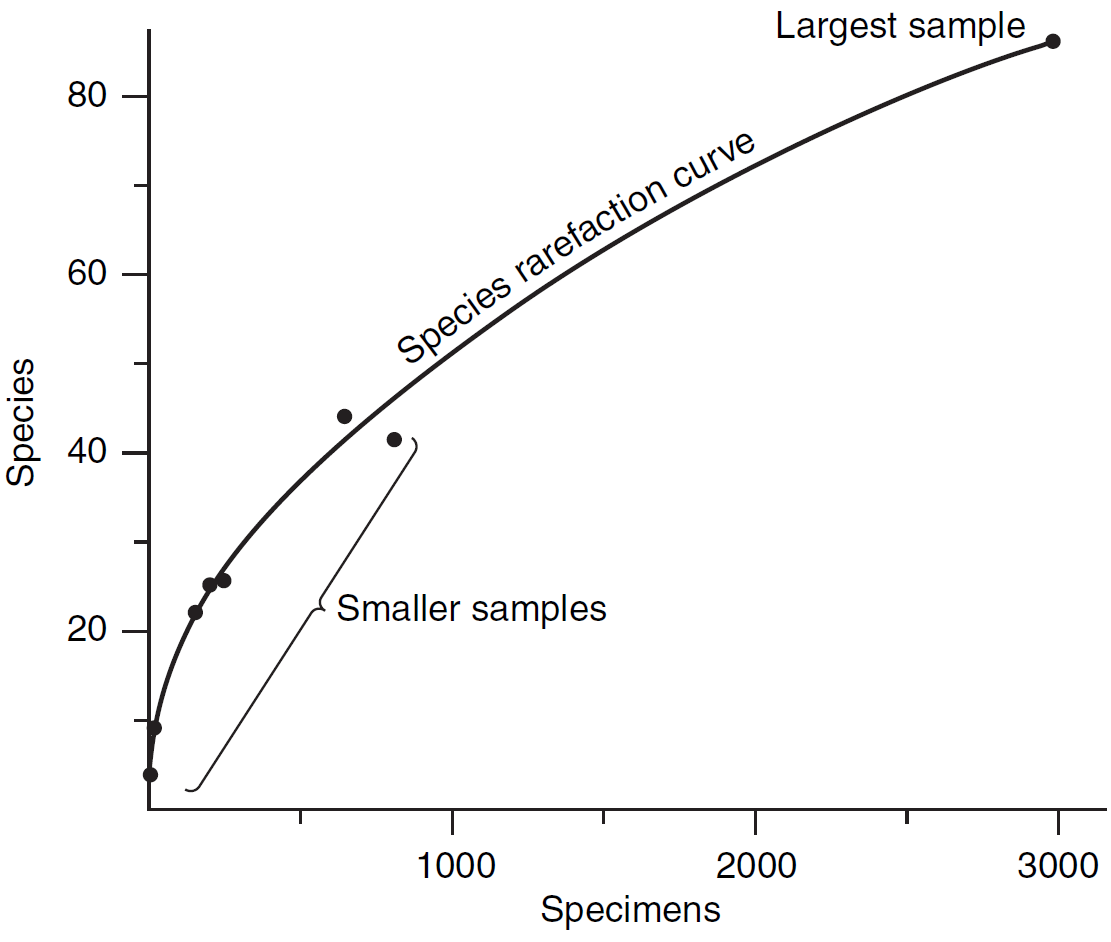
Figura 2.5: Ejemplo de curva de rarefacción. Imagen tomada de Foote & Miller (2007).
Los pasos a seguir para llevar a cabo la rarefacción son los siguientes:
Se elige un tamaño de muestra estándar o “tamaño de rarefacción” al que se reducirán todas las muestras para que sean comparables.
Se calcula el número de especies o taxones observados en la muestra original de tamaño completo.
A continuación, se reduce la muestra de tamaño completo al tamaño de rarefacción seleccionado, eliminando aleatoriamente un número específico de especímenes para que la muestra alcance el tamaño deseado, y se calcula el número de especies recogido.
Se repite este proceso varias veces para obtener una estimación promedio de la riqueza taxonómica ajustada al tamaño de la muestra.
Por lo tanto, la curva de rarefacción es una herramienta que muestra cuántas especies se han encontrado en muestras aleatorias de diferentes tamaños. La forma de esta curva es útil para evaluar dos aspectos clave en un yacimiento o formación fósil: (1) si se ha explorado adecuadamente la diversidad de un yacimiento fósil y (2) si es necesario recolectar más muestras para descubrir más especies. Si la curva alcanza una asintota, indica que se ha alcanzado un buen número de muestras y que se tiene una representación adecuada de la diversidad de especies en el yacimiento. Si la curva sigue en aumento y no se estabiliza, sugiere que todavía se pueden encontrar más especies. En este caso, aumentar el esfuerzo de muestreo podría ser beneficioso para descubrir una mayor diversidad. Es importante destacar que este efecto tiende a ser menos pronunciado a niveles taxonómicos más altos debido al anidamiento de las categorías taxonómicas (Fig. 2.6). En cualquier caso, es fundamental tener en cuenta que la curva de rarefacción no puede utilizarse para realizar extrapolaciones más allá de los datos observados, ya que se basa en los resultados actuales de muestreo y no puede predecir la diversidad futura sin una recolección de datos adicional.
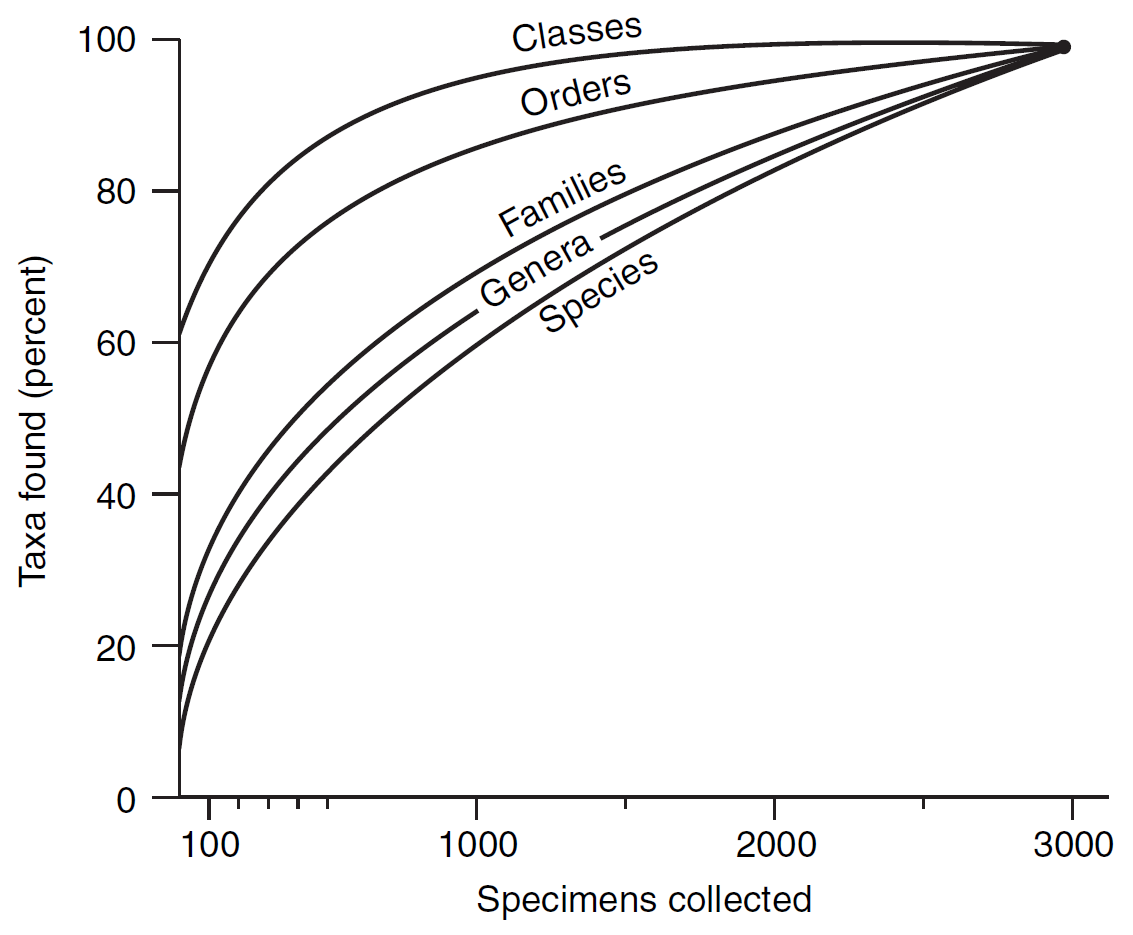
Figura 2.6: Curvas de rarefacción para fósiles de moluscos encontrados en una buena muestra de edad miocena en Dinamarca. El punto en la parte superior derecha representa la muestra real. Las curvas estiman cuántos taxones se habrían encontrado si la muestra hubiera sido más pequeña. Imagen tomada de Foote & Miller (2007).
La curva de rarefacción se calcula siguiendo estos pasos:
Selección de muestras decrecientes en el número de individuos: Se toman muestras del yacimiento o formación fósil en las que el número de individuos disminuye progresivamente. Por ejemplo, comienza con una muestra grande que contiene muchos individuos, como 3000, y luego toma muestras sucesivamente más pequeñas, como 2000, 1000, 500 individuos, y así sucesivamente.
Conteo de especies: Para cada una de estas muestras decrecientes en tamaño, se cuenta cuántas especies diferentes se han encontrado. Esto se hace para cada una de las muestras que se recolectan.
Gráfico de especies vs. número de muestras: Luego, se construye un gráfico que representa el número de especies (en el eje vertical) frente al número de muestras (en el eje horizontal). Cada muestra se representa como un punto en el gráfico. A medida que disminuye el tamaño de las muestras, la cantidad de especies encontradas debería aumentar.
Análisis de la curva: Al observar el gráfico resultante, se puede analizar la forma de la curva de rarefacción.
Ejercicio práctico:
Visualización de la Calidad del Muestreo en Europa a Través de Curvas de Rarefacción
En este ejercicio, nos proponemos visualizar la calidad del muestreo en Europa en dos momentos temporales distintos mediante la construcción de curvas de rarefacción. Se espera que, en el intervalo temporal más reciente, la calidad del muestreo sea mejor, lo que se reflejaría en una curva de rarefacción más asintótica. Esto indica una mayor captura de la diversidad paleobiológica, lo que sugiere un muestreo más exhaustivo y representativo.
Los datos utilizados en este análisis provienen de la Paleobiology Database, y realizaremos todos los análisis utilizando el lenguaje de programación R en el entorno de RStudio.
Antes de empezar, es aconsejable que miremos algunos tutoriales y cursos que nos serán útiles:
Tutorial de descarga e instalación de R y RStudio.
Curso introductiorio a R.
Curso introductiorio al uso de la Paleobiology Database.
Descargaremos estos archivos que contienen datos sobre ocurrencias a nivel de género en Europa, correspondientes a los períodos de 750 a 550 ma y 200 a 0 ma. Los datos provienen de la sección de descarga de datos de la Paleobiology Database.
Ejemplo de Submuestreo para Curva de Rarefacción
En este primer ejercicio obtendremos el número de especies que esperamos encontrar en una submuestra de nuestra muestra original. Esto nos dará un punto de datos que forma parte de la curva de rarefacción. Para construir esta curva, debemos repetir el proceso de submuestreo varias veces, tomando diferentes submuestras de tamaños crecientes (por ejemplo, 50, 100, 150, etc.) y anotando cuántas especies únicas encontramos en cada submuestra. Luego, representamos estos datos en un gráfico donde el eje X es el tamaño de la submuestra y el eje Y es el número de especies encontradas.
# Cargamos la muestra de ocurrencias de los géneros de Europa entre 750 y 550 m.a
genus <- read.csv("Data/genus_europe 750 550.csv") # Leer el archivo CSV y asignarlo a "genus"
# Transformamos "genus" en un vector
genus <- as.vector(genus[, 1]) # Extraer la primera columna y convertirla en un vector
# Extraemos el número total de especímenes en la muestra
num_specimens <- length(genus) # Contar el número total de elementos en el vector
print(num_specimens) # Imprimir el número total de especímenes## [1] 328# Extraemos el número total de especies en la muestra
num_species <- length(unique(genus)) # Contar el número de especies únicas
print(num_species) # Imprimir el número total de especies## [1] 106# ¿Cuántos especímenes esperaríamos en una submuestra de 250 especímenes?
# Número de especímenes en la submuestra
n_sub <- 250 # Establecer el tamaño de la submuestra
# Generamos la submuestra (muestreo aleatorio sin reemplazo)
subsample <- sample(genus, n_sub, replace = FALSE) # Realizar el muestreo aleatorio
# Extraemos las especies en la submuestra
unique_species <- unique(subsample) # Obtener las especies únicas en la submuestra
print(unique_species) # Imprimir las especies únicas de la submuestra## [1] "Cochlichnus" "Temnoxa" "Yorgia" "Vendomia" "Palaeopascichnus"
## [6] "Treptichnus" "Aspidella" "Nimbia" "Lossinia" "Cloudina"
## [11] "Symplassosphaeridium" "Dickinsonia" "Appendisphaera" "Platysolenites" "Kullingia"
## [16] "Chuaria" "Ediacaria" "Charnia" "Anfesta" "Tribrachidium"
## [21] "Kuckaraukia" "Palaeophragmodictya" "Inaria" "Tawuia" "Siphonophycus"
## [26] "Nemiana" "Leiosphaeridia" "Intrites" "Onega" "Pteridinium"
## [31] "Kimberella" "Tanarium" "Andiva" "Cyanorus" "Vaveliksia"
## [36] "Protolagena" "Parvancorina" "Protodipleurosoma" "Simia" "Yelovichnus"
## [41] "Asseserium" "Cambrotubulus" "Hiemalora" "Khatyspytia" "Kaisalia"
## [46] "Synsphaeridium" "Vendia" "Paliella" "Palaeoplatoda" "Beltanelliformis"
## [51] "Armillifera" "Boxonia" "Cavaspina" "Spirosolenites" "Beltanella"
## [56] "Ovatoscutum" "Stictosphaeridium" "Vendotaenia" "Renalcis" "Densisphaera"
## [61] "Beltanelloides" "Pseudovendia" "Stratifera" "Archangelia" "Coniunctiophycus"
## [66] "Bonata" "Pterospermopsimorpha" "Solza" "Palaeolyngbya" "Swartpuntia"
## [71] "Goniosphaeridium" "Brachina" "Irridinitus" "Paravendia" "Variomargosphaeridium"
## [76] "Calyptrina" "Rangea" "Staurinidia" "Tridia" "Cerebrosphaera"
## [81] "Oscillatoriopsis" "Multifronsphaeridium" "Mawsonites" "Sinotubulites" "Pomoria"
## [86] "Urasphaera" "Labruscasphaeridium" "Sabellidites" "Charniodiscus" "Korilophyton"
## [91] "Bomakellia" "Monomorphichnus" "Namacalathus" "Archaeaspinus" "Coneosphaera"
## [96] "Ceratosphaeridium" "Glaessnerina"# Contamos el número de especies únicas en la submuestra
num_unique_species <- length(unique_species) # Contar el número de especies únicas
print(num_unique_species) # Imprimir el número de especies únicas en la submuestra## [1] 97Evaluación de la Saturación en la Riqueza de Especies: Construcción de Curvas de Rarefacción
En este ejercicio, evaluaremos el grado de saturación en la riqueza de especies en dos intervalos temporales (750-550 millones de años y 200-0 millones de años) utilizando curvas de rarefacción normalizadas. Para cada intervalo temporal, extraeremos submuestras de tamaños crecientes (0%, 10%, 20%, … 100% del total de especímenes) y registraremos el número de especies únicas en cada una. Los resultados se normalizan dividiendo cada valor entre el máximo número de especies en la muestra completa, permitiéndonos comparar directamente la forma de ambas curvas. El gráfico resultante, con el tamaño relativo de la submuestra en el eje X y el número de especies normalizado en el eje Y, nos permite evaluar visualmente si alguna de las curvas se aproxima a una asíntota más rápidamente que la otra. Esto indicaría que en ese intervalo temporal se ha alcanzado una mayor representatividad en el registro fósil.# Cargamos los datos de ocurrencias de géneros
genus <- read.csv("Data/genus_europe 750 550.csv") # Cargar archivo CSV y asignarlo a la variable "genus"
# Convertimos la columna de géneros en un vector para su análisis
genus <- as.vector(genus[,1]) # Extraer solo la primera columna (géneros) y convertirla en un vector
# Definimos una secuencia de tamaños de muestra para realizar la curva de rarefacción
seq <- seq(0, length(genus), by = length(genus) / 100) # Secuencia que va de 0 al total de especímenes, en 100 pasos
# Inicializamos un vector vacío para almacenar el número de especies únicas en cada submuestra
subsamples <- c()
for (i in 1:length(seq)) {
# Realizamos una submuestra aleatoria sin reemplazo y contamos las especies únicas
subsamples[i] <- length(unique(sample(genus, seq[i], replace = FALSE)))
}
# Graficamos la curva de rarefacción para Europa entre 750 y 550 m.a.
plot(seq, subsamples, main = "Curva de Rarefacción para Europa (750-550 m.a.)",
xlab = "Número de especímenes", ylab = "Número de especies", pch = 19)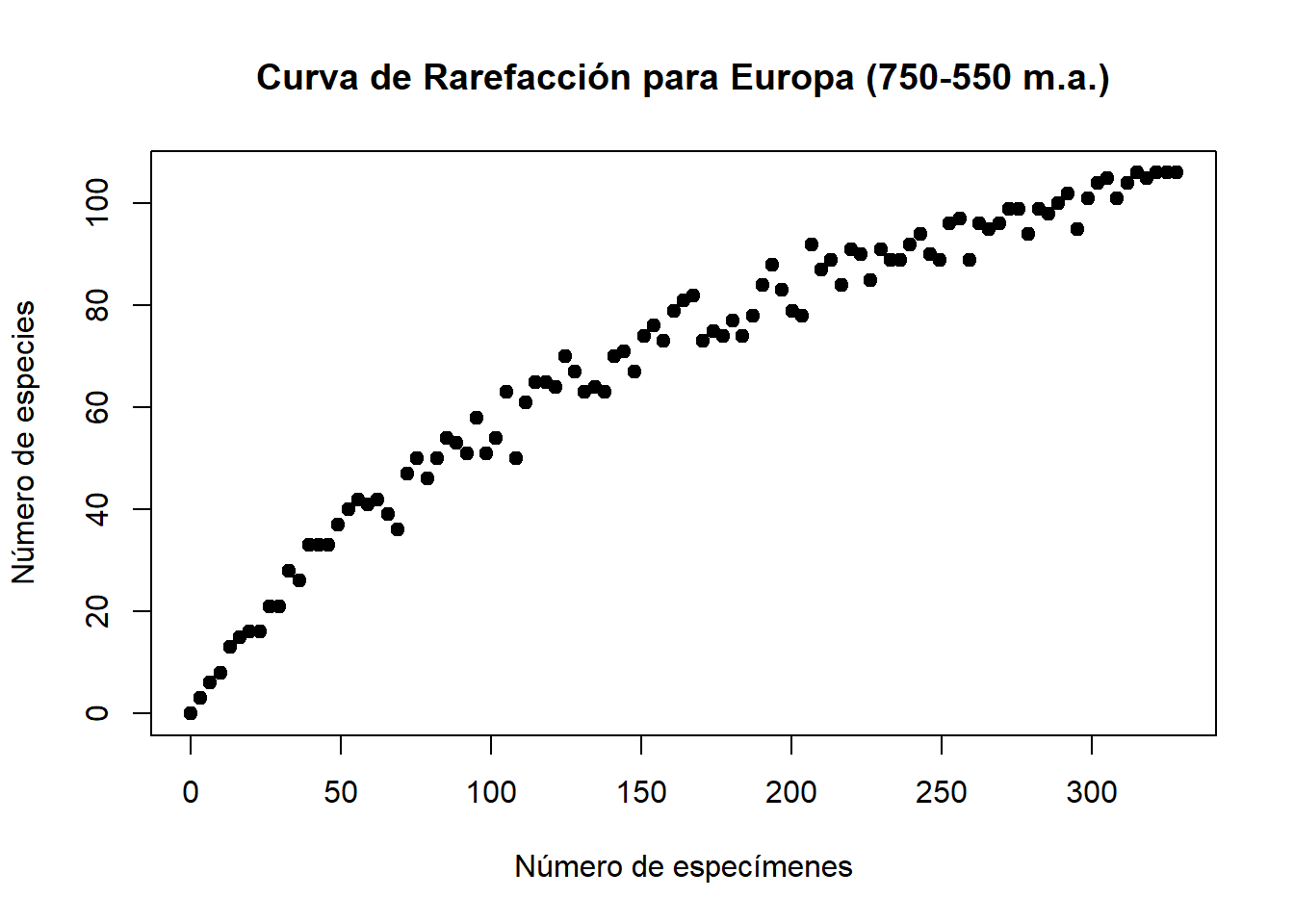
# Repetimos el mismo proceso para Europa entre 200 y 0 m.a.
genus <- read.csv("Data/genus_europe 200 0.csv") # Cargar el archivo de datos de géneros entre 200-0 m.a.
genus <- as.vector(genus[,1]) # Convertir en vector de géneros
seq <- seq(0, length(genus), by = length(genus) / 100) # Crear secuencia de 100 submuestras
subsamples <- c()
for (i in 1:length(seq)) {
# Submuestra aleatoria y cálculo de especies únicas
subsamples[i] <- length(unique(sample(genus, seq[i], replace = FALSE)))
}
# Graficamos la curva de rarefacción para Europa entre 200 y 0 m.a.
plot(seq, subsamples, main = "Curva de Rarefacción para Europa (200-0 m.a.)",
xlab = "Número de especímenes", ylab = "Número de especies", pch = 19)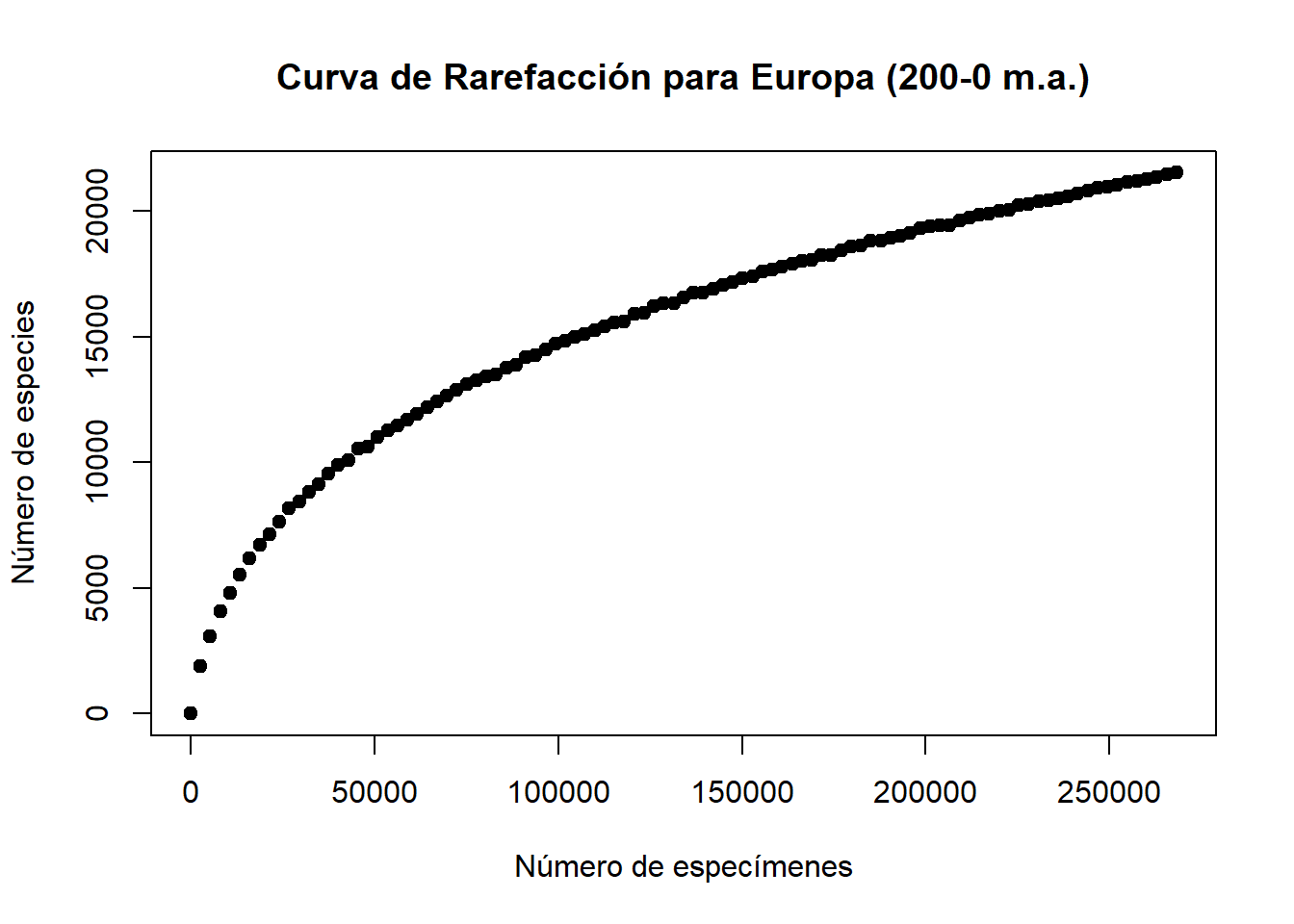
# Comparación de ambas curvas de rarefacción en una sola gráfica
# Datos para Europa entre 750 y 550 m.a.
genus1 <- read.csv("Data/genus_europe 750 550.csv")
genus1 <- as.vector(genus1[,1])
seq1 <- seq(0, length(genus1), by = length(genus1) / 100)
subsamples1 <- c()
for (i in 1:length(seq1)) {
subsamples1[i] <- length(unique(sample(genus1, seq1[i], replace = FALSE)))
}
# Datos para Europa entre 200 y 0 m.a.
genus2 <- read.csv("Data/genus_europe 200 0.csv")
genus2 <- as.vector(genus2[,1])
seq2 <- seq(0, length(genus2), by = length(genus2) / 100)
subsamples2 <- c()
for (i in 1:length(seq2)) {
subsamples2[i] <- length(unique(sample(genus2, seq2[i], replace = FALSE)))
}
# Creación del dataframe para graficar ambas curvas
df <- data.frame(
Numero_de_Especimenes = c(1:101,1:101),
Numero_de_Especies = c(subsamples1 / max(subsamples1), subsamples2 / max(subsamples2)),
Periodo = as.factor(c(rep("750-550 m.a.", length(seq1)), rep("200-0 m.a.", length(seq2))))
)
# Graficamos ambas curvas de rarefacción en la misma gráfica con plot()
# Separamos los datos por período
df_750_550 <- subset(df, Periodo == "750-550 m.a.")
df_200_0 <- subset(df, Periodo == "200-0 m.a.")
# Establecemos los límites del gráfico basados en el rango de datos
plot(range(df$Numero_de_Especimenes), range(df$Numero_de_Especies), type = "n", # Gráfico vacío para establecer los límites
xlab = "Número de especímenes (% sobre el total)",
ylab = "Número de especies (normalizado)",
main = "Comparación de Curvas de Rarefacción en Europa")
# Añadimos los puntos para cada período en diferentes colores
points(df_750_550$Numero_de_Especimenes, df_750_550$Numero_de_Especies, col = "black", pch = 19)
points(df_200_0$Numero_de_Especimenes, df_200_0$Numero_de_Especies, col = "grey", pch = 19)
# Opcionalmente, añadimos una leyenda para mayor claridad
legend("bottomright", legend = c("750-550 m.a.", "200-0 m.a."), col = c("black", "grey"), pch = 19)