1 Introduction to R and `tidyverse`

1.1 Access to RStudio Cloud

To perform data management, we will use RStudio Cloud. RStudio is “an Integrated Development Environment for R, a programming language for statistical computing and graphics.” For this book, we will use the cloud version of RStudio. Please visit RStudio Cloud to create an account for free.

In our first class, we will be setting up a project to use for our classroom sessions. A good practice when working with R is to use folders to group related files. We will create two folders in our classroom project:

A folder named data where we will store the various datasets that we will use throughout this book.
A folder named Rmd where we will store our R Markdown files (see Section 1.2).

1.2 Introduction to R Markdown

When we write code, we often want to be able to make changes so that we can build on the code we have already written. To facilitate this process, R allows us to create files that store our code. R Markdown files allow us to insert chunks of R code.

To create an R Markdown file, click on File $\rightarrow$ New File $\rightarrow$ R Markdown.... Click OK and then save this markdown file in your Rmd directory.

Do not write code in your console. Code written in the console cannot be edited and re-used.

In your R Markdown file, open a chunk by typing three left quotes, followed by the letter r inside curly brackets (```{r}); Close the chunk by typing three left quotes ```. Anything inside an R chunk is interpreted as R code.

You can create a new empty R chunk by typing Cmd + Option + I (Mac) or Ctrl + Alt + I (Windows)

1.2.1 Running chunks

To run an R chunk click on the green button at the end of the first line inside the chunk:

Or type:

Cmd + Shift + Enter (Mac)
Control + Shift + Enter (Windows)

To execute the code of a single line inside an R chunk you can type:

Cmd + Enter (Mac)
Control + Enter (Windows)

The results of the R chunk are also printed out in the console.

1.2.2 A basic example

Insert a new R chunk, and then type the following:

5+5
4+10
4-9

## [1] 10
## [1] 14
## [1] -5

Run the chunk to see the results.

1.3 Variables in R

In programming, variables are essentially nicknames that we use to store values or other language objects. For example, let us say that we want to store a person’s age in a variable. We can create a new variable and name it “age.” Then, we can store the appropriate age value to this variable.

In R, we store values to variables by using the symbol = (or <-, ->).

The name of a variable can be any sequence of characters given that it starts with a letter.

Variable names are case sensitive.

age=36 # A hashtag inside an R chunk creates a comment.
        # R knows to ignore comments (comments are explanations for humans)
age<-36 # age is a variable that stores the number 36

Other variable names that can store the number 36:

x <- 36 # x is a variable that also stores the number 36
age36 <- 36 #age36  is a variable that stores the number 36
z1 <- 36 # z1 is a variable that stores the number 36

Choose variable names that best represent the stored values.

1.4 Vectors

In R, lowercase c followed by a parenthesis is a special keyword that identifies a vector. A vector is a sequence of data elements. Below, the variable quiz_results is a vector that stores the scores of a hypothetical quiz.

quiz_results <-  c(9,8,4,10)
quiz_results

## [1]  9  8  4 10

Note that by just typing the name of a variable (in our example quiz_results) inside an R chunk and running it R prints out the value(s) of that variable.

Elements in a vector can be accessed by their position. For example, in our vector quiz_results:

9 $\rightarrow$ $1^{st}$ position
8 $\rightarrow$ $2^{nd}$ position
4 $\rightarrow$ $3^{rd}$ position
10 $\rightarrow$ $4^{th}$ position

Hence, we can access the element in the $2^{nd}$ position as follows:

quiz_results[2]

## [1] 8

And we can assign it to a new variable:

second_element <- quiz_results[2]
second_element

## [1] 8

1.5 Data types

In programming (and in R) each variable has a data type, which describes what kind of information the variable stores. For instance, in our previous example, variable age is a numeric variable, because it stores a numeric value.

R allows us to define variables that are not numeric. For example, we can create a variable that is a sequence of characters. Consider a variable that stores the word “data.” We can name this variable data_var and assign to it the characters data.

data_var <- 'data'
data_var

## [1] "data"

Any sequence of characters in single (') or double (") quotes is considered a string. For instance, the following line of code that uses double quotes has the same result:

data_var <- "data"
data_var

## [1] "data"

Variables that store strings are of data type character.

R allows for other types of variables, such as date variables and factors. We will introduce these types of variables later in the class.

If our variables are of data type numeric, we can add, subtract, divide, and multiply them as follows:

x <- 7
y <- 13
x + y
x - y
x / y
x * y

## [1] 20
## [1] -6
## [1] 0.5384615
## [1] 91

1.6 Functions in R

A function is a stored, pre-defined block of code that operates on some input value to return an output. R has multiple built-in functions that we can apply to our variables.
For instance, the function log() will estimate the logarithm of its input:

log(age)

## [1] 3.583519

In the above, age is the input of the function log, and the output of the function is the logarithm of variable age. Of course we can also apply the function log to a number:

log(36)

## [1] 3.583519

Similarly, the function sqrt() estimates the square root of a numeric variable (or a number):

sqrt(x)
sqrt(10)

## [1] 2.645751
## [1] 3.162278

The input of a function does not need to be a scalar (one-element) variable; functions can also operate on vectors (and other structures that we will learn in the future).

Since we have a vector of quiz results, it would be nice to know what was the average quiz performance. We can call the function mean() on the vector quiz_results:

meanQuiz <- mean(quiz_results)
meanQuiz

## [1] 7.75

Similarly, we can estimate the standard deviation of the quiz results with the function sd:

sdQuiz <- sd(quiz_results) 
sdQuiz

## [1] 2.629956

Since we have already estimated the mean and the standard deviation of the vector quiz_results, we can also standardize it by subtracting the mean and dividing with the standard deviation.

You can find more about standardization here: https://en.wikipedia.org/wiki/Standard_score

standardQuiz <- (quiz_results - meanQuiz)/sdQuiz 
quiz_results
standardQuiz

## [1]  9  8  4 10
## [1]  0.47529319  0.09505864 -1.42587956  0.85552774

By standardizing the quiz results we created a new vector standardQuiz which has a zero mean and standard deviation of 1.

mean(standardQuiz)
sd(standardQuiz)

## [1] 1.734723e-17
## [1] 1

We can plot and compare the histograms of the two vectors with the function hist:

hist(quiz_results,main = "") # the option main = "" removes the title from the figure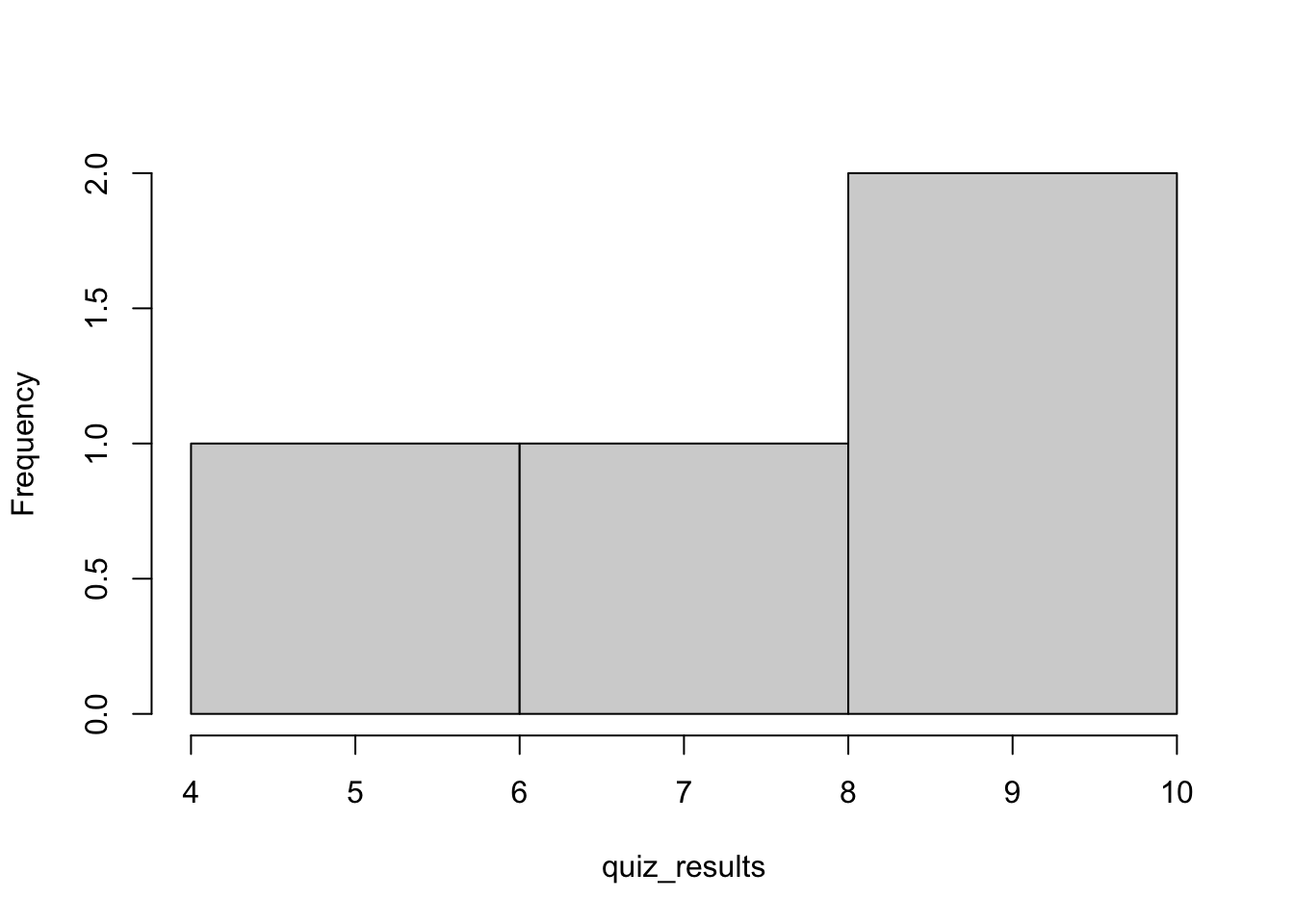

Figure 1.1: Histogram of the original vector

hist(standardQuiz, main = "")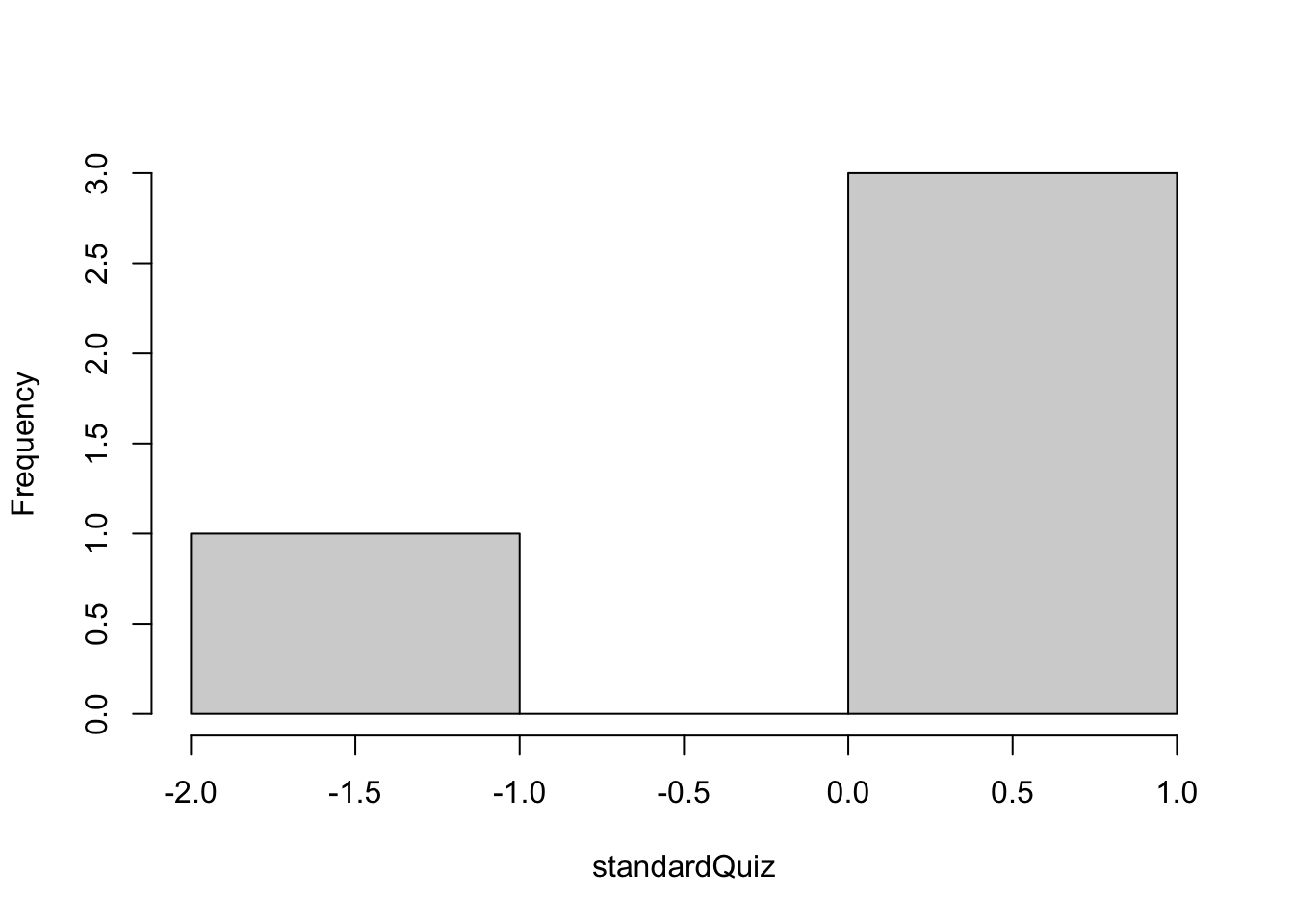

Figure 1.2: Histogram of the standardized vector

When calling the function hist() in the previous two examples we used two inputs: the first input was the vector name (quiz_results or standardQuiz); the second input was the empty string "", which told function hist() to not print a title for the figure. In general, a function can take as input multiple variables.

You can experiment with the above code by changing the empty quote to a string, for instance, main="what a great histogram".

Variables and values that are passed in a function are called arguments. (e.g., standardQuiz in hist(standardQuiz, main = "") is an argument.)

Variables used within a function that can take input values are called parameters. (e.g., main in hist(standardQuiz, main = "") is a parameter.)

1.7 Logic

Besides numeric and character variables we can also have logical variables. A logical variable can either be TRUE or FALSE. (TRUE and FALSE are special keywords in R).

We can also use the letters T and F to indicate TRUE and FALSE respectively.

x <- F #FALSE, assign the logical value FALSE to variable x
y <- T #TRUE, assign the logical value True to variable x
x

## [1] FALSE

## [1] TRUE

1.7.1 Logical operators

With logical variables we can use logical operators. A logical operator is a way to make a test in R. R supports the following logical operators:

Operator	Description
<	Less than
<=	Less than or equal to
>	Greater than
>=	Greater than or equal to
==	Exactly equal to
!	Not (negation)
&	Logical AND
\|	Logical OR

A logical AND compares two statements. If both statements are TRUE then the result of the comparison is also TRUE; Otherwise the result of the comparison is FALSE

Here is the truth table of logical AND:

X	Y	X AND Y
TRUE	TRUE	TRUE
TRUE	FALSE	FALSE
FALSE	TRUE	FALSE
FALSE	FALSE	FALSE

A logical OR compares two statements. If either or both of the statements are TRUE then the result of the comparison is TRUE; Otherwise, if both statements are FALSE the result of the comparison is FALSE.

X	Y	X OR Y
TRUE	TRUE	TRUE
TRUE	FALSE	TRUE
FALSE	TRUE	TRUE
FALSE	FALSE	FALSE

Here are some examples that used the logical variables x and y from above:

x & y 
x | y 
!x & y

## [1] FALSE
## [1] TRUE
## [1] TRUE

x <- 5
y <- 6
x == y
x != y
x < y
x > y

## [1] FALSE
## [1] TRUE
## [1] TRUE
## [1] FALSE

We can group conditions together through parentheses:

z <- 10
(x != y) & (x < z)  #Both parentheses are TRUE and hence the result is TRUE

## [1] TRUE

(x != y) | (x < z)

## [1] TRUE

Note the difference between a single = and a double ==: A single = assignes a value to a variable; a double == is a logical test between the left-hand side and the right-hand side.

1.7.2 The `ifelse()` function

A particularly interesting function in R is the ifelse() function, which allows us to apply a transformation only if a condition is TRUE. For instance, we can partially update the quiz scores (in our vector quiz_results) that are less than 9:

# return 1 for those scores that are less or equal to 8. Otherwise return 0:
ifelse(quiz_results <= 8,1,0)

## [1] 0 1 1 0

Of course, we can assign the result of an ifelse() transformation to the original variable (or to a new variable):

# update scores lower than 9 with -1:
quiz_results_transformed <- ifelse(quiz_results < 9,-1,quiz_results) # assign the transformed result to a new variable
quiz_results <- ifelse(quiz_results < 9,-1,quiz_results) # assign the tranformed results to the original variable
quiz_results

## [1]  9 -1 -1 10

Be careful when updating the value of the original variable. If you run your code repeatedly then you will end up updating the updated value! To avoid this, always start from the very first variable definitions when you re-run your code.

1.7.3 More examples of logic and logical operators

Below are some additional examples of logic and logical operators.

A <- 6
B <- 7
C <- 10
D <- T 
A==B # Is A equal to B? 
!(B > C) | (!D) # Not B greater than C OR not D. 
# A less or equal than C AND  ( not B greater than C OR not D)
(A <= C) & (!(B > C) | (!D))

## [1] FALSE
## [1] TRUE
## [1] TRUE

1.8 R Packages and summarizing a real dataset

Very often we will need to use R functions that are not already built in. In these cases, we will need to install and load R packages. These packages include code written by independent developments and teams, and it is free for everyone to use and change.

As an example, let’s install the package mlbench by calling the function install.packages as follows:

install.packages("mlbench")

We can also install packages manually from RStudio: Packages tab $\rightarrow$ install.

You only need to install packages once. You should not re-install mlbench from this point on unless there is an updated version of it.

To see the available datasets from the newly installed package mlbench we can call the function data and pass the argument ‘mlbench’ to the parameter package as follows:

data(package='mlbench')

To make the functions and datasets of the package mlbench available to us we need to call the function library():

library(mlbench)

To avoid errors, always remember to load the necessary packages you will use by running library(package_name)

Now we can use the datasets and functions of the mlbench package. Let us load the dataset BreastCancer with function data().

data("BreastCancer")
head(BreastCancer)

##        Id Cl.thickness Cell.size Cell.shape Marg.adhesion Epith.c.size Bare.nuclei Bl.cromatin Normal.nucleoli Mitoses
## 1 1000025            5         1          1             1            2           1           3               1       1
## 2 1002945            5         4          4             5            7          10           3               2       1
## 3 1015425            3         1          1             1            2           2           3               1       1
## 4 1016277            6         8          8             1            3           4           3               7       1
## 5 1017023            4         1          1             3            2           1           3               1       1
## 6 1017122            8        10         10             8            7          10           9               7       1
##       Class
## 1    benign
## 2    benign
## 3    benign
## 4    benign
## 5    benign
## 6 malignant

The function head allows us to explore the first six rows of a dataset. Similarly, the function tail allows us to explore the last six rows of a dataset.

Now, we can get the summary statistics of this dataset with the function summary().

summary(BreastCancer)

##       Id             Cl.thickness   Cell.size     Cell.shape  Marg.adhesion  Epith.c.size  Bare.nuclei   Bl.cromatin 
##  Length:699         1      :145   1      :384   1      :353   1      :407   2      :386   1      :402   2      :166  
##  Class :character   5      :130   10     : 67   2      : 59   2      : 58   3      : 72   10     :132   3      :165  
##  Mode  :character   3      :108   3      : 52   10     : 58   3      : 58   4      : 48   2      : 30   1      :152  
##                     4      : 80   2      : 45   3      : 56   10     : 55   1      : 47   5      : 30   7      : 73  
##                     10     : 69   4      : 40   4      : 44   4      : 33   6      : 41   3      : 28   4      : 40  
##                     2      : 50   5      : 30   5      : 34   8      : 25   5      : 39   (Other): 61   5      : 34  
##                     (Other):117   (Other): 81   (Other): 95   (Other): 63   (Other): 66   NA's   : 16   (Other): 69  
##  Normal.nucleoli    Mitoses          Class    
##  1      :443     1      :579   benign   :458  
##  10     : 61     2      : 35   malignant:241  
##  3      : 44     3      : 33                  
##  2      : 36     10     : 14                  
##  8      : 24     4      : 12                  
##  6      : 22     7      :  9                  
##  (Other): 69     (Other): 17

We will use the functions head, tail, and summary() repeatedly throughout this book to get a first look at each new dataset.

1.9 `tidyverse`

tidyverse is a collection of R packages designed for data science. All packages share an underlying design philosophy, grammar, and data structures. Install the tidyverse package as follows:

install.packages("tidyverse")

Recall, you only need to install packages once. You should not re-install tidyverse from this point on unless there is an updated version of it.

Find more about tidyverse here: https://www.tidyverse.org

Once installed, load the package into your environment:

library(tidyverse)

1.9.1 `tibble`

The basic data structure that works with tidyverse is called tibble. You can think of a tibble as a spreadsheet in excel, or as a table in a relational database system, or as a dataframe in R or python. If you are familiar with dataframes in R or Python, tibbles are data frames but they tweak some behaviors to make coding a little bit easier.

In this book (and in real life) I will use the terms tibble and dataframe interchangeably.

We can create a new tibble from vectors by calling the function tibble(). Each vector will become a new column in the new tibble:

t <- tibble(
x <- c(0,2,4,6),    # vector x will become column x in the new tibble.
y <- c('a','b','d', 'amazing'), #vector y will become  column y in the new tibble.
z <- x^2) #vector z, which is vector x squared, will become column z in the new tibble.
t

## # A tibble: 4 × 3
##   `x <- c(0, 2, 4, 6)` `y <- c("a", "b", "d", "amazing")` `z <- x^2`
##                  <dbl> <chr>                                   <dbl>
## 1                    0 a                                           0
## 2                    2 b                                           4
## 3                    4 d                                          16
## 4                    6 amazing                                    36

R comes with many pre-loaded datasets. To explore these datasets run data().

Next, we will use the dataset population:

head(population) # The function head() prints out only the first six rows of the tibble.

## # A tibble: 6 × 3
##   country      year population
##   <chr>       <int>      <int>
## 1 Afghanistan  1995   17586073
## 2 Afghanistan  1996   18415307
## 3 Afghanistan  1997   19021226
## 4 Afghanistan  1998   19496836
## 5 Afghanistan  1999   19987071
## 6 Afghanistan  2000   20595360

1.9.2 `dplyr` and `filter`

Now, we can apply some logic on the population dataset. Assume that we are interested in selecting only population data from Brazil. How can we do this?

We can use the function filter() from package dplyr. dplyr is a grammar of data manipulation that provides a set of functions to solve some of the most common data manipulation challenges.

Find more about dplyr here: https://dplyr.tidyverse.org

The function filter() allows us to subset a tibble by retaining all rows that satisfy certain conditions. For instance, we can keep only rows for which the country column is equal to Brazil and the year column is greater or equal than 2000:

filter(population,country=='Brazil' & year >= 2000) # Recall the logical and operator &

## # A tibble: 14 × 3
##    country  year population
##    <chr>   <int>      <int>
##  1 Brazil   2000  174504898
##  2 Brazil   2001  176968205
##  3 Brazil   2002  179393768
##  4 Brazil   2003  181752951
##  5 Brazil   2004  184010283
##  6 Brazil   2005  186142403
##  7 Brazil   2006  188134315
##  8 Brazil   2007  189996976
##  9 Brazil   2008  191765567
## 10 Brazil   2009  193490922
## 11 Brazil   2010  195210154
## 12 Brazil   2011  196935134
## 13 Brazil   2012  198656019
## 14 Brazil   2013  200361925

Alternatively, we can show the population of every other country except Brazil, for the same years:

tf <- filter(population,country!='Brazil' & year >= 2000) # we also are saving the result into a new tibble, tf.
head(tf)

## # A tibble: 6 × 3
##   country      year population
##   <chr>       <int>      <int>
## 1 Afghanistan  2000   20595360
## 2 Afghanistan  2001   21347782
## 3 Afghanistan  2002   22202806
## 4 Afghanistan  2003   23116142
## 5 Afghanistan  2004   24018682
## 6 Afghanistan  2005   24860855

1.9.3 Distributions: `ggformula`

Often, when analyzing data, we need to create basic visualizations. For example, what is the distribution of the population column in our filtered tibble tf?

For such quick visualizations we can use the package ggformula. First, let’s install it:

install.packages("ggformula")

This package operates on the following structure:

$goal(y \sim x, data = mydata, ...)$ ,

where goal() is a function that creates the desired visualization, $y$ is the variable of the $y-axis$, $x$ is the variable of the $x-axis$, $mydata$ is the tibble that stores the focal data with columns y and x, and the $...$ identify additional arguments to be passed that customize the plot.

In our example, we want to display the population data through a distribution plot materialized by the gf_density() function:

library(ggformula)
gf_density(~ population, data = tf)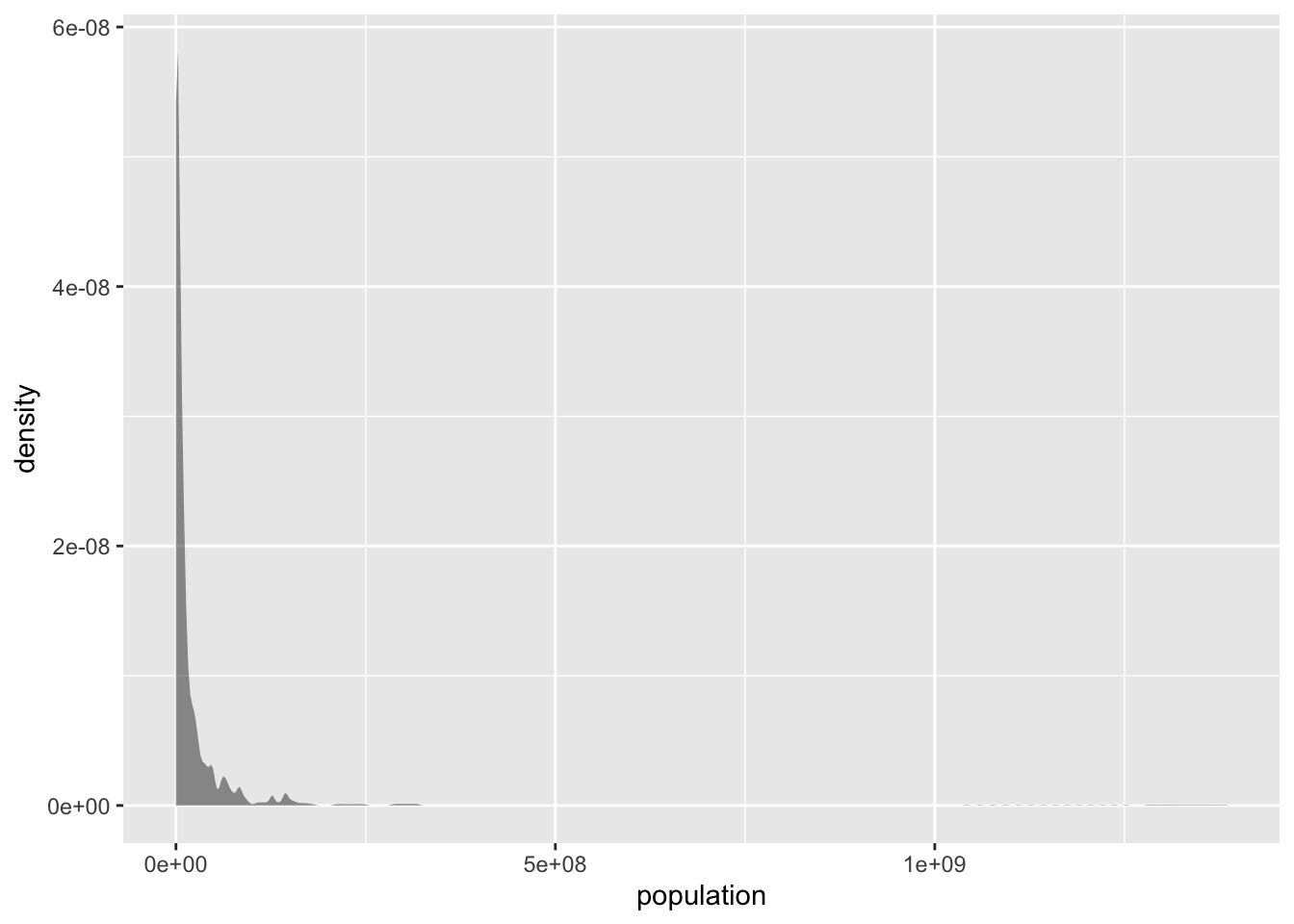

Figure 1.3: Population distribution

In a distribution plot, the y-axis shows the density and as a result it is calculated directly from the `gf_density() function. As a result, we do not need to define $y$ inside gf_density().

Find more about the available functions of ggformula here: https://cran.r-project.org/web/packages/ggformula/ggformula.pdf

The population distribution is highly skewed: most countries have low population numbers, but very few countries have very high population numbers (100s of millions or even more than a billion). This concentrates the plot in te left side and creates a very long tail. These types of distributions are broadly described as power-law distributions. Their means are not informative, as they are being stretched by the very high scores of very few points. Their standard deviation is large, often higher than their means. For instance, in our example we see that the mean population is $>30M$, even though the vast majority of the countries have lower population numbers (the $75^{th}$ percentile population number is $19M$):

summary(tf)

##    country               year        population       
##  Length:2986        Min.   :2000   Min.   :1.129e+03  
##  Class :character   1st Qu.:2003   1st Qu.:6.202e+05  
##  Mode  :character   Median :2007   Median :5.398e+06  
##                     Mean   :2007   Mean   :3.012e+07  
##                     3rd Qu.:2010   3rd Qu.:1.909e+07  
##                     Max.   :2013   Max.   :1.386e+09

The standard deviation, which we can estimate from function sd() is $124M$, greater than the mean of $30M$:

sd(tf$population)

## [1] 123915350

In fact, we can test it as follows:

sd(tf$population) > mean(tf$population)

## [1] TRUE

In the above exmamples I used the dollar sign $ to isolate the population column from the tibble tf. This is one way of accessing a single column from a tibble. As a single column, population is perceived as a vector from functions sd() and mean().

In such cases, log-transforming the variable often results in more “normal-like” distributions:

gf_density(~ log(population), data = tf)

Figure 1.4: Log-transformed population distribution

For comments, suggestions, errors, and typos, please email us at: kokkodis@bc.edu, wynerge@bc.edu

1 Introduction to R and tidyverse