Chapter 2 Basic Quantities and Models

Let \(X\) be a nonnegative characterize variable from a homogeneous populaton. There are five functions characterize the distribution of \(X\), say:

• survival function \(S(x)\)
• hazard rate/risk function \(h(x)\)
• probability density function \(f(x)\)
• mean residual life at time \(x\) \(mrl(x)\)
• cumulative hazard function \(H(x)\)

Survival function

The probability of an individual surviving beyond time \(x\) is defined as \[ \begin{equation} S(x) = Pr(X > x) = 1- F(x) = \int_x^\infty f(t)dt \tag{2.1} \end{equation} \]

where \(S(x)\) is referred to as the survival function or reliability function.

Therefore based on (2.1),

\[ f(x) = -\frac{dS(x)}{dx} \] For discrete case \[ S(x) = Pr(X > x) = \sum_{x_j > x} p(x_j) \] where \(p(x_j) = Pr(X = x_j)\) is the pmf.

Example for Weibull distribution

\[ S(x) = \exp(-\lambda x^\alpha) \] When \(\alpha = 1\), it becomes exponential distribution.

f1 <- function(x) exp(-0.26328 * x^0.5)
f2 <- function(x) exp(-0.1 * x)
f3 <- function(x) exp(-0.00208 * x^3)
curve(f1, from = 0, to = 20, ylim = c(0, 1), ylab = "Survival Prob")
curve(f2, from = 0, to = 20, add = T, col = "red")
curve(f3, from = 0, to = 20, add = T, col = "blue")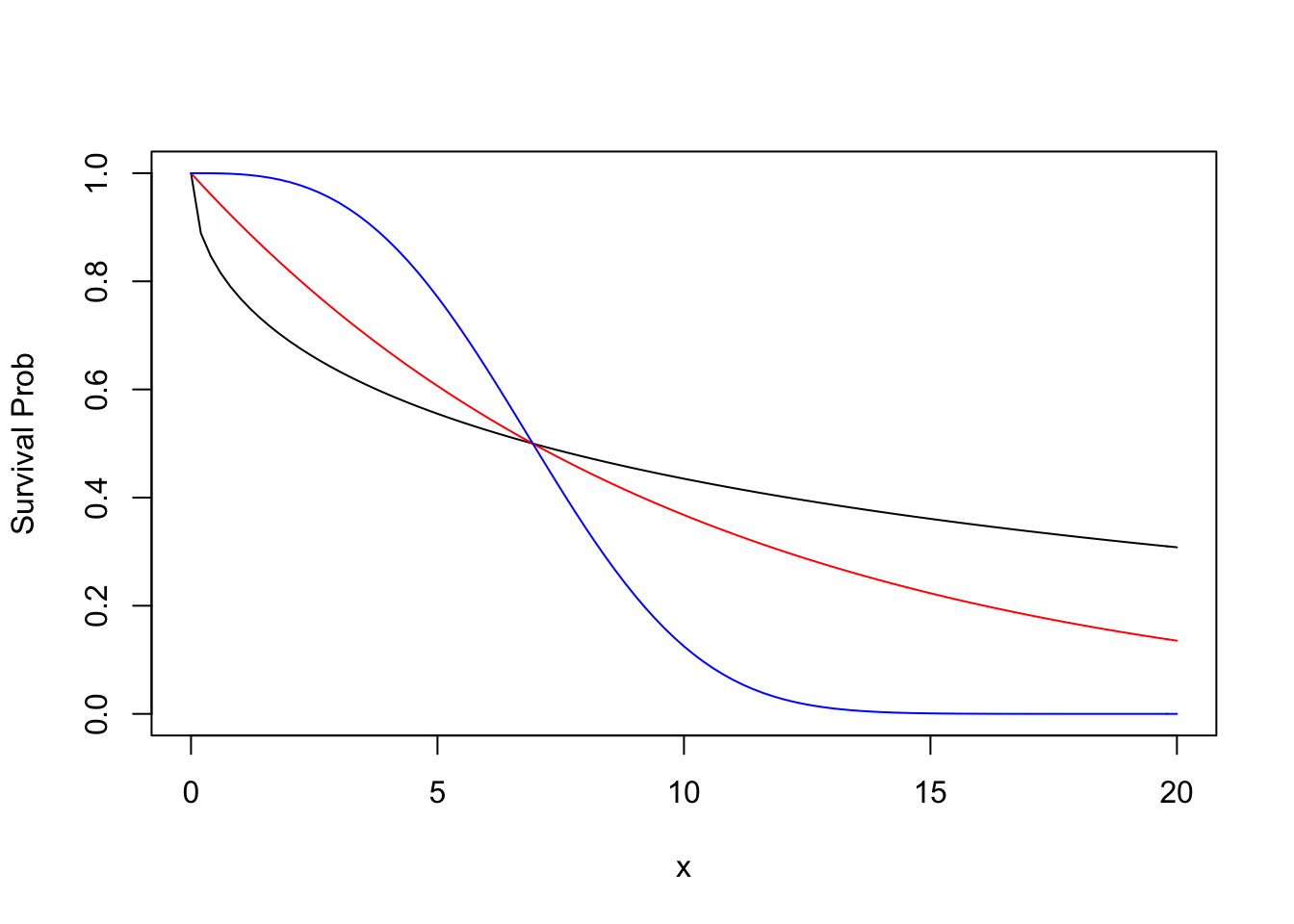

Hazard Function

Hazard function is also known as the conditional failure rate in reliability, the force of mortality in demography, the intensity function in stochastic processes, the age-specific failure rate in epidemiology, the inverse of the Mill’s ratio in economics, or simply as the hazard rate.

\[ h(x)=\lim _{\Delta x \rightarrow 0} \frac{P[x \leq X<x+\Delta x \mid X \geq x]}{\Delta x} \tag{2.2} \] From (2.2), \(h(x)dx\) can be viewed as the “approximate” probability of an individual of age \(x\) experiencing the event in the next instant.

If \(X\) is continuous, then \[ h(x) = f(x)/S(x) = -\frac{d\ln S(x)}{dx} \tag{2.3} \] In other word, \[ S(x) = \exp[-H(x)] = \exp[-\int_0^x h(u)du] \tag{2.4} \] When \(X\) is discrete, \[ h\left(x_j\right)=\operatorname{Pr}\left(X=x_j \mid X \geq x_j\right)=\frac{p\left(x_j\right)}{S\left(x_{j-1}\right)} = 1 - \frac{S\left(x_{j}\right)}{S\left(x_{j-1}\right)}, \quad j=1,2, \ldots \] The survival function can be written as the product of conditional survival probabilities: \[ S(x) = \prod_{x_j \leq x}S(x_j)/S(x_{j-1}) = \prod_{x_j \leq x}[1-h(x_j)] \]

Example for Weibull distribution

For Weibull distribution, the hazard function is \[ h(x) = \alpha\lambda x^{\alpha - 1} \]

curve(0.26328 * 0.5 * x^-0.5, from = 0, to = 10, ylim = c(0, 1), ylab = "Hazard Rate")
curve(0.1*x^0, from = 0, to = 20, add = T, col = "red")
curve(0.00208 * 3 * x^2, from = 0, to = 20, add = T, col = "blue")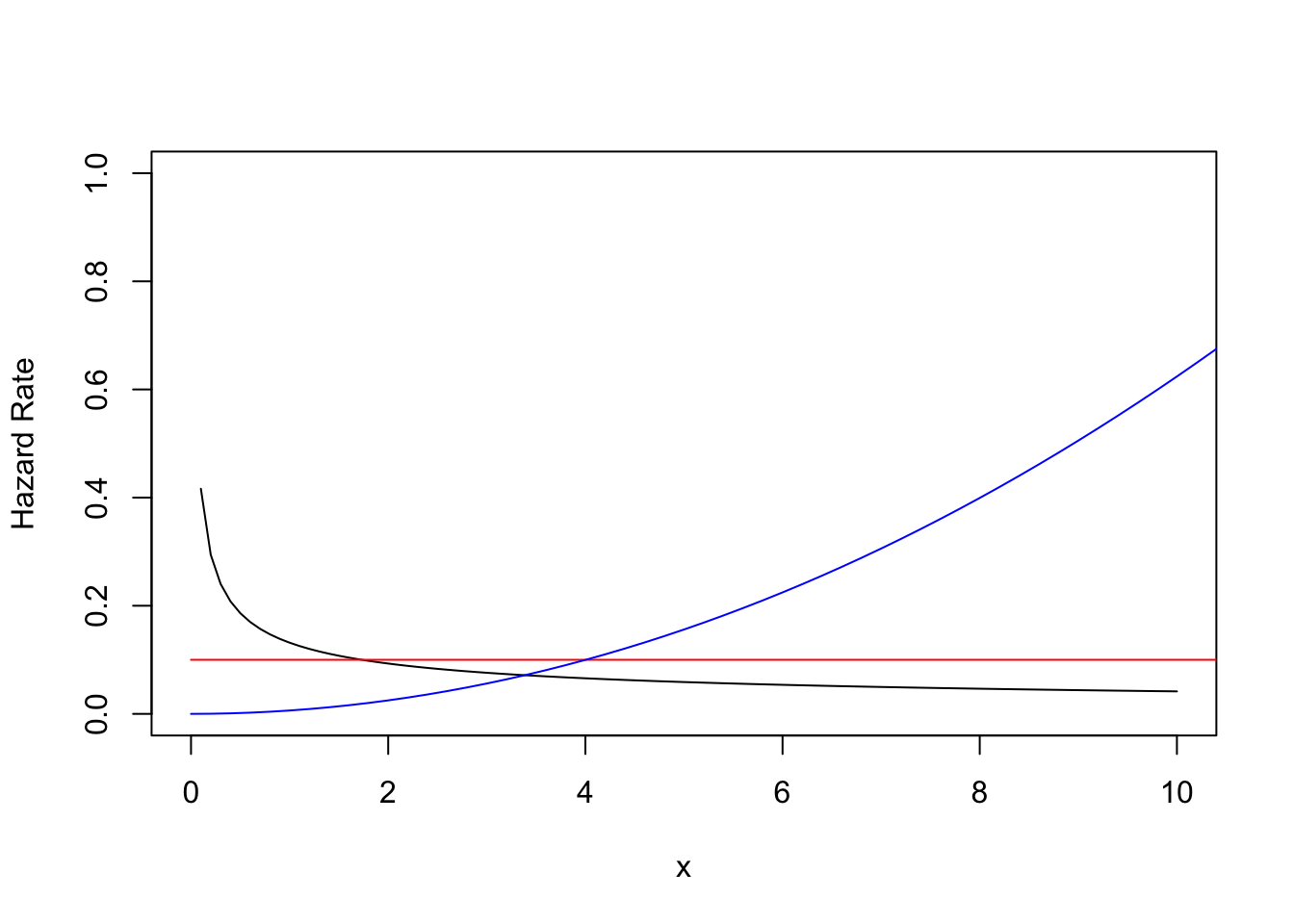

Cumulative hazard function

\[ H(x) = \int_0^x h(u)du = -\ln S(x) \tag{2.5} \] For discrete \(X\), \[ H(x) = \sum_{x_j \leq x} h(x_j) \] When \(X\) is discrete, \(S(x) = \exp[-H(x)]\) is no longer holds for true.

Mean residual life function and median life

The parameter measures the expected remaining lifetime \(mrl(x)\) is defined as

\[ mrl(x) = E(X - x\mid X > x) = \frac{\int_x^\infty (t - x)f(t)dt}{S(x)} = \frac{\int_x^\infty S(t)dt}{S(x)} \tag{2.6} \]

Note:

\[ \mu = E(X) = \int_0^\infty tf(t) dt = \int_0^\infty S(t) dt \] \[ Var(X) = 2 \int_0^\infty tS(t) dt - [ \int_0^\infty S(t)dt]^2 \]

Examples:

• The mean and median lifetimes for an exponential life distribution are \(1/\lambda\) and \((\ln 2)/\lambda\).
• The \(100p\)th percentile for the Weibull distribution is found by solving \(1 - p = \exp\{-\lambda x_p^\alpha\}\) so \(x_p = \{-\ln [1-p]/\lambda \}^{1/\alpha}\)

Common parametric models

Distribution	\(f(x)\)	\(S(x)\)	\(h(x)\)	\(E(X)\)
Exponential	\(\lambda\exp(-\lambda x)\)	\(\exp[-\lambda x]\)	\(\lambda\)	\(1/\lambda\)
Weibull	\(\alpha\lambda x^{\alpha - 1}\exp(-\lambda x^\alpha)\)	\(\exp[-\lambda x^\alpha]\)	\(\alpha\lambda x^{-\alpha - 1}\)	\(\frac{\Gamma(1 + 1/\alpha)}{\lambda^{1/\alpha}}\)
Gamma	\(\frac{\lambda^\beta x^{\beta - 1} \exp(-\lambda x)}{\Gamma(\beta)}\)	\(1 - I(\lambda x, \beta)^*\)	\(\frac{f(x)}{S(x)}\)	\(\beta/\lambda\)
Log normal	\(\frac{\exp \left[-\frac{1}{2}\left(\frac{\ln x-\mu}{\sigma}\right)^2\right]}{x(2 \pi)^{1 / 2} \sigma}\)	\(1 - \Phi(\frac{\ln x - \mu}{\sigma})\)	\(\frac{f(x)}{S(x)}\)	\(\exp(\mu + 0.5\sigma^2)\)
Log logistic	\(\frac{\alpha x^{\alpha - 1} \lambda}{[1 + \lambda x^\alpha]^2}\)	\(\frac{1}{1 + \lambda x^\alpha}\)	\(\frac{\alpha x^{\alpha - 1}\lambda}{1 + \lambda x^\alpha}\)	\(\frac{\pi \operatorname{Csc}(\pi / \alpha)}{\alpha \lambda^{1 / \alpha}} \text { if } \alpha>1\)
Gompertz	\(\theta e^{\alpha x} \exp [\frac{\theta}{\alpha}(1-e^{\alpha x})]\)	\(\exp[\frac{\theta}{\alpha}(1-e^{\alpha x})]\)	\(\theta e^{\alpha x}\)	\(\int_0^\infty S(x) dx\)
Pareto	\(\frac{\theta \lambda^\theta}{x^{\theta + 1}}\)	\(\frac{\lambda^\theta}{x^\theta}\)	\(\frac{\theta}{x}\)	\(\frac{\theta\lambda}{\theta - 1}\) if \(\theta > 1\)

where \(I(t, \beta) = \int_0^t u^{\beta - 1} \exp(-u) du/\Gamma(\beta)\)