1 Organização básica
Apagamos os gráficos, se houver algum, limpamos a memória e o console.
dev.off()
rm(list=ls(all=TRUE))
cat("\014")
#getwd()
#dir <- getwd()
#shell.exec(getwd())
#apaga os graficos, se houver algum, limpa a memória e o console1.1 Pacotes do módulo
Instalando os pacotes necessários para esse módulo. Nos computadores do Laboratório de Ecologia não instale esses pacotes, eles já estão instalados.
1.2 Organizando as matrizes de dados
library(readxl)
dados_quest <- read_excel("D:/Elvio/OneDrive/Paralelos/Scarlet_lic/dados.quest-atualizado.xlsx",
sheet = "matriz")
Questões <- dados_quest$Questões
dados_quest <- cbind(Questões, dados_quest)
#adicionando prefixos
dados_quest$Questões[1:17] <- paste("pre", dados_quest$Questões[1:17], sep = "-")
dados_quest$Questões[18:34] <- paste("pos", dados_quest$Questões[18:34], sep = "-")
dados_quest$Grupo2[1:17] <- paste("pre", dados_quest$Grupo2[1:17], sep = "-")
dados_quest$Grupo2[18:34] <- paste("pos", dados_quest$Grupo2[18:34], sep = "-")
#primeira coluna para nomes das linhas
dados_quest <- as.data.frame(dados_quest)
class(dados_quest)## [1] "data.frame"## Questões Grupo1 Grupo2 A1 A2 A3
## pre-1 1 pre pre-a 1 0 1
## pre-2a 2a pre pre-a 1 1 1
## pre-2bi 2bi pre pre-a 1 0 1
## pre-2bii 2bii pre pre-a 0 1 1
## pre-2biii 2biii pre pre-a 0 0 1
## pre-2biv 2biv pre pre-a 1 1 1## Questões Grupo1 Grupo2 A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13
## pre-1 1 pre pre-a 1 0 1 1 1 1 1 1 0 1 1 1 1
## pre-2a 2a pre pre-a 1 1 1 1 1 1 1 1 1 1 1 1 1
## pre-2bi 2bi pre pre-a 1 0 1 1 1 1 1 1 0 1 1 1 1
## pre-2bii 2bii pre pre-a 0 1 1 0 1 1 1 1 1 0 1 1 0
## pre-2biii 2biii pre pre-a 0 0 1 0 0 0 0 0 0 1 0 1 1
## pre-2biv 2biv pre pre-a 1 1 1 1 1 1 1 1 0 0 1 1 0
## pre-2c 2c pre pre-a 0 0 0 0 0 0 0 0 1 0 1 0 0
## pre-3 3 pre pre-b 0 0 1 0 1 1 1 0 1 0 0 1 0
## pre-4 4 pre pre-b 0 1 1 0 1 1 1 1 0 1 0 0 1
## pre-5 5 pre pre-b 1 0 0 0 0 0 0 0 0 0 1 1 0
## pre-6 6 pre pre-b 1 1 1 0 1 1 1 1 1 0 0 1 0
## pre-7i 7i pre pre-b 1 1 1 1 1 0 1 1 1 1 1 1 1
## pre-7ii 7ii pre pre-a 0 1 1 1 0 0 0 1 1 0 1 0 0
## pre-7iii 7iii pre pre-a 1 1 0 1 1 0 1 1 0 1 0 1 1
## pre-7iv 7iv pre pre-a 0 1 0 1 0 0 0 1 0 1 0 1 0
## pre-7v 7v pre pre-c 1 1 1 1 1 1 1 1 1 1 1 1 1
## pre-7vi 7vi pre pre-c 0 1 1 0 1 1 1 1 0 1 1 1 1
## pos-1 1 pos pos-a 1 1 1 1 1 1 1 1 1 1 0 1 1
## pos-2a 2a pos pos-a 1 1 1 1 1 1 1 1 1 1 0 1 1
## pos-2bi 2bi pos pos-a 1 1 0 1 1 1 1 1 1 1 1 1 1
## A14 A15 A16 A17 A18 A19 A20 A21 A22 A23 A24 A25 A26 A27 A28 A29
## pre-1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## pre-2a 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 0
## pre-2bi 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
## pre-2bii 0 0 1 0 1 0 0 0 0 1 1 1 0 1 1 1
## pre-2biii 1 1 1 1 0 1 1 1 1 0 0 1 1 1 0 0
## pre-2biv 1 0 1 0 1 1 1 0 1 1 1 1 1 1 1 1
## pre-2c 0 0 0 0 1 1 0 0 0 0 1 0 1 1 0 0
## pre-3 0 0 0 0 1 0 0 0 0 1 1 1 1 1 0 0
## pre-4 1 1 0 1 0 0 0 1 0 1 0 0 0 1 1 0
## pre-5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## pre-6 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1
## pre-7i 1 1 1 1 1 1 0 0 1 1 0 1 1 1 0 0
## pre-7ii 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0
## pre-7iii 1 1 1 1 0 1 0 1 0 1 1 1 1 1 1 1
## pre-7iv 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 1
## pre-7v 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
## pre-7vi 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1
## pos-1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## pos-2a 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1
## pos-2bi 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1
## A30 A31 A32 A33 A34 A35 A36 A37 A38 A39 A40 A41 A42 A43 A44 A45
## pre-1 0 1 1 1 1 1 1 0 1 1 1 0 1 1 1 1
## pre-2a 1 1 1 0 1 1 1 1 1 1 0 0 0 0 1 0
## pre-2bi 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 0
## pre-2bii 0 1 1 0 1 0 1 1 1 1 0 0 0 0 0 1
## pre-2biii 1 0 1 0 1 1 1 0 1 1 1 0 1 0 0 1
## pre-2biv 0 1 1 1 1 1 1 1 1 1 0 1 1 0 0 1
## pre-2c 1 1 0 0 0 1 1 0 0 0 0 0 0 0 1 1
## pre-3 1 1 1 0 0 1 0 1 0 0 0 0 0 1 0 0
## pre-4 1 1 0 1 0 1 0 1 1 1 1 0 0 1 0 1
## pre-5 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0
## pre-6 0 0 1 1 0 0 0 1 0 0 1 0 0 0 1 0
## pre-7i 0 1 1 1 0 1 0 0 1 0 1 1 0 1 1 1
## pre-7ii 0 0 1 0 0 1 0 0 1 1 0 0 0 0 0 0
## pre-7iii 1 0 0 1 1 1 0 0 1 1 1 1 1 1 1 1
## pre-7iv 1 0 1 0 0 0 0 1 1 1 0 0 0 1 1 1
## pre-7v 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1
## pre-7vi 1 1 1 1 1 1 1 0 0 1 1 1 1 0 0 1
## pos-1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## pos-2a 1 0 1 0 1 1 1 0 1 1 1 1 0 0 1 1
## pos-2bi 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1
## A46 A47
## pre-1 1 0
## pre-2a 1 1
## pre-2bi 1 1
## pre-2bii 0 0
## pre-2biii 0 0
## pre-2biv 0 0
## pre-2c 1 1
## pre-3 0 0
## pre-4 0 0
## pre-5 0 0
## pre-6 1 1
## pre-7i 1 1
## pre-7ii 0 0
## pre-7iii 1 1
## pre-7iv 1 1
## pre-7v 1 1
## pre-7vi 0 0
## pos-1 1 1
## pos-2a 1 1
## pos-2bi 1 1
## [ reached 'max' / getOption("max.print") -- omitted 14 rows ]## [1] "Questões" "Grupo1" "Grupo2" "A1" "A2" "A3"
## [7] "A4" "A5" "A6" "A7" "A8" "A9"
## [13] "A10" "A11" "A12" "A13" "A14" "A15"
## [19] "A16" "A17" "A18" "A19" "A20" "A21"
## [25] "A22" "A23" "A24" "A25" "A26" "A27"
## [31] "A28" "A29" "A30" "A31" "A32" "A33"
## [37] "A34" "A35" "A36" "A37" "A38" "A39"
## [43] "A40" "A41" "A42" "A43" "A44" "A45"
## [49] "A46" "A47"m_bruta <- dados_quest[, -which(names(dados_quest) %in% c("Questões", "Grupo1", "Grupo2"))]
#ou
m_part <- dados_quest[,-1:-2]
#ou
dados_quest_part <- dados_quest[,-1:-3]
# Criando uma matriz de somas ##ALTERADO PARA MÉDIAS##
library(dplyr)
#m_avg_part <- aggregate(m_bruta_g[, 2:3], list(m_bruta_g$Grupos), mean)
#m_sum <- m_bruta_g %>%
# group_by(Grupos) %>%
# summarise(across(.cols = everything(), ~ sum(.x, na.rm = TRUE)))# %>%
# arrange(match(Grupos, agrup))mantem a mesma ordem de agrup
m_sum <- m_part %>% #MÉDIAS!
group_by(Grupo2) %>%
summarise(across(.cols = everything(), ~ mean(.x, na.rm = TRUE))) %>%
arrange(match(Grupo2, unique(m_part$Grupo2)))
#m_avg <- m_part %>%
# group_by(Grupo2) %>%
# summarise(across(.cols = everything(), list(mean = mean, sd = sd)))
#?across
#Primeira coluna para nomes das linhas
m_sum <- as.data.frame(m_sum)
class(m_sum)## [1] "data.frame"rownames(m_sum) <- m_sum[,1]
m_sum[,1] <- NULL
#Salvando a matriz
write.table(m_sum,
"m_sumcsv.csv",
append = F,
quote = TRUE,
sep = ";", dec = ",",
row.names = T)
m_sum_csv <- read.csv("m_sumcsv.csv",
sep = ";", dec = ",",
header = T,
row.names = 1,
na.strings = NA)
#removendo colunas zeradas
sum <- colSums(m_sum)
sum## A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14 A15 A16 A17 A18 A19
## 4.4 4.5 3.8 3.3 4.8 4.6 4.9 5.0 3.5 4.6 3.8 5.0 3.9 4.6 4.7 4.7 4.0 4.6 4.0
## A20 A21 A22 A23 A24 A25 A26 A27 A28 A29 A30 A31 A32 A33 A34 A35 A36 A37 A38
## 3.1 4.6 4.4 4.1 4.5 4.2 3.7 5.3 4.0 2.5 5.1 4.2 3.9 4.6 3.4 5.1 4.1 3.7 3.5
## A39 A40 A41 A42 A43 A44 A45 A46 A47
## 4.9 4.4 2.5 3.6 3.5 2.9 4.5 2.9 4.0## character(0)m_part <- m_sum[(colSums(m_sum) != 0)] #em != a exclamação inverte o sentido
zero_sum_cols2 <- names(which(colSums(m_part) == 0))
zero_sum_cols2 #nomes das colunas zeradas## character(0)## A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14 A15 A16 A17 A18 A19
## 4.4 4.5 3.8 3.3 4.8 4.6 4.9 5.0 3.5 4.6 3.8 5.0 3.9 4.6 4.7 4.7 4.0 4.6 4.0
## A20 A21 A22 A23 A24 A25 A26 A27 A28 A29 A30 A31 A32 A33 A34 A35 A36 A37 A38
## 3.1 4.6 4.4 4.1 4.5 4.2 3.7 5.3 4.0 2.5 5.1 4.2 3.9 4.6 3.4 5.1 4.1 3.7 3.5
## A39 A40 A41 A42 A43 A44 A45 A46 A47
## 4.9 4.4 2.5 3.6 3.5 2.9 4.5 2.9 4.0#removendo linhas zeradas
zero_sum_rows <- names(which(rowSums(m_part) == 0))
zero_sum_rows #nomes das linhas zeradas## character(0)m_part <- m_part[rowSums(m_part[]) > 0,] #atentar para a virgula
zero_sum_rows2 <- names(which(rowSums(m_part) == 0))
zero_sum_rows2 #nomes das linhas zeradas## character(0)## pre-a pre-b pre-c pos-a pos-b pos-c
## 28.8 23.0 40.0 31.3 30.8 40.0## A1 A2 A3 A4 A5 A6
## pre-a 0.5 0.6 0.7 0.7 0.6 0.5
## pre-b 0.6 0.6 0.8 0.2 0.8 0.6
## pre-c 0.5 1.0 1.0 0.5 1.0 1.0
## pos-a 0.8 0.7 0.6 0.6 0.6 0.7
## pos-b 1.0 0.6 0.2 0.8 0.8 0.8
## pos-c 1.0 1.0 0.5 0.5 1.0 1.01.4 Classificação
Para conhecermos os dados, vamos criar uma classificação baseada na distância Bray-Curtis e UPGMA como método de fusão, a partir das matrizes de dados de interesse ppbio** com suas devidas relativizações e transformações (Veja Figura 1.1).
1.4.1 Dendrograma e Heatmap
Daqui pra frente não foi feita nenhuma relativização ou transformação.
#Dendrograma
library(vegan)
#m_trns <- 2/pi*asin(sqrt(decostand(m_trab,
# method="total", MARGIN = 2)))
#m_trns <- decostand(m_trab, method="total", MARGIN = 2)
#m_trns <- sqrt(m_trab)
m_trns <- m_trab
vegdist <- vegdist(m_trns, method = "bray",
diag = TRUE,
upper = FALSE)
cluster_uas <- hclust(vegdist, method = "average")
plot (cluster_uas, main = "Cluster Dendrogram - Bray-Curtis da Matriz Comunitária",
hang = 0.1) #testar com -.01
#rect.hclust(cluster_uas, k = 3, h = NULL)
#h = 0.8 fornece os grupos formados na altura h
as.matrix(vegdist)[1:6, 1:6]
library(dendextend)
groupCodes <- c(rep("a", 1), rep("b", 1), rep("c", 1), rep("a", 1), rep("b", 1), rep("c", 1))
rownames(m_trns) <- make.unique(groupCodes)## aqui o problema, criar um novo vetor so pra isso
colorCodes <- c(a="red", b="green", c="blue")
dend <- as.dendrogram(cluster_uas)
labels_colors(dend) <- colorCodes[groupCodes][order.dendrogram(dend)]
col_labels <- colorCodes[groupCodes]
plot(dend)
#rownames(m_trns) <- original_row_names #não lembro o porque desse linha
#Heatmap
library("gplots")
heatdist <- as.matrix(vegdist)
col <- rev(heat.colors(999)) #rev() reverte as cores do heatmap
heatmap.2(x=(as.matrix(vegdist)), #objetos x objetos
Rowv = as.dendrogram(cluster_uas),
Colv = as.dendrogram(cluster_uas),
key = T, tracecol = NA, revC = T,
col = heat.colors, #dissimilaridade = 1 - similaridade
colRow = col_labels, # to add colored labels
colCol = col_labels, # to add colored labels
density.info = "none",
xlab = "UA´s", ylab = "UA´s",
mar = c(6, 6) + 0.2)
cluster_spp <- hclust((vegdist(t(m_trns), method = "bray",
diag = TRUE,
upper = FALSE)), method = "average")
plot (cluster_spp, main = "Dendrograma dos atributos")
heatmap.2(t(as.matrix(m_trns)), #objetos x atributos
Colv = as.dendrogram(cluster_uas),
Rowv = as.dendrogram(cluster_spp),
key = T, tracecol = NA, revC = T,
col = col,
colCol = col_labels, # to add colored labels
density.info = "none",
xlab = "Unidades amostrais", ylab = "Espécies",
mar = c(6, 6) + 0.1) # adjust margin size
h <- heatmap.2(t(as.matrix(m_trns)), #objetos x atributos
Colv = as.dendrogram(cluster_uas),
Rowv = as.dendrogram(cluster_spp),
key = T, tracecol = NA, revC = T,
col = col,
colCol = col_labels, # to add colored labels
density.info = "none",
xlab = "Unidades amostrais", ylab = "Espécies",
mar = c(6, 6) + 0.1) # adjust margin size## pre-a pre-b pre-c pos-a pos-b pos-c
## pre-a 0.0000000 0.2046332 0.1976744 0.1214642 0.1711409 0.2180233
## pre-b 0.2046332 0.0000000 0.2952381 0.2412523 0.1970260 0.2888889
## pre-c 0.1976744 0.2952381 0.0000000 0.1809257 0.1864407 0.0750000
## pos-a 0.1214642 0.2412523 0.1809257 0.0000000 0.1400966 0.1865358
## pos-b 0.1711409 0.1970260 0.1864407 0.1400966 0.0000000 0.1581921
## pos-c 0.2180233 0.2888889 0.0750000 0.1865358 0.1581921 0.0000000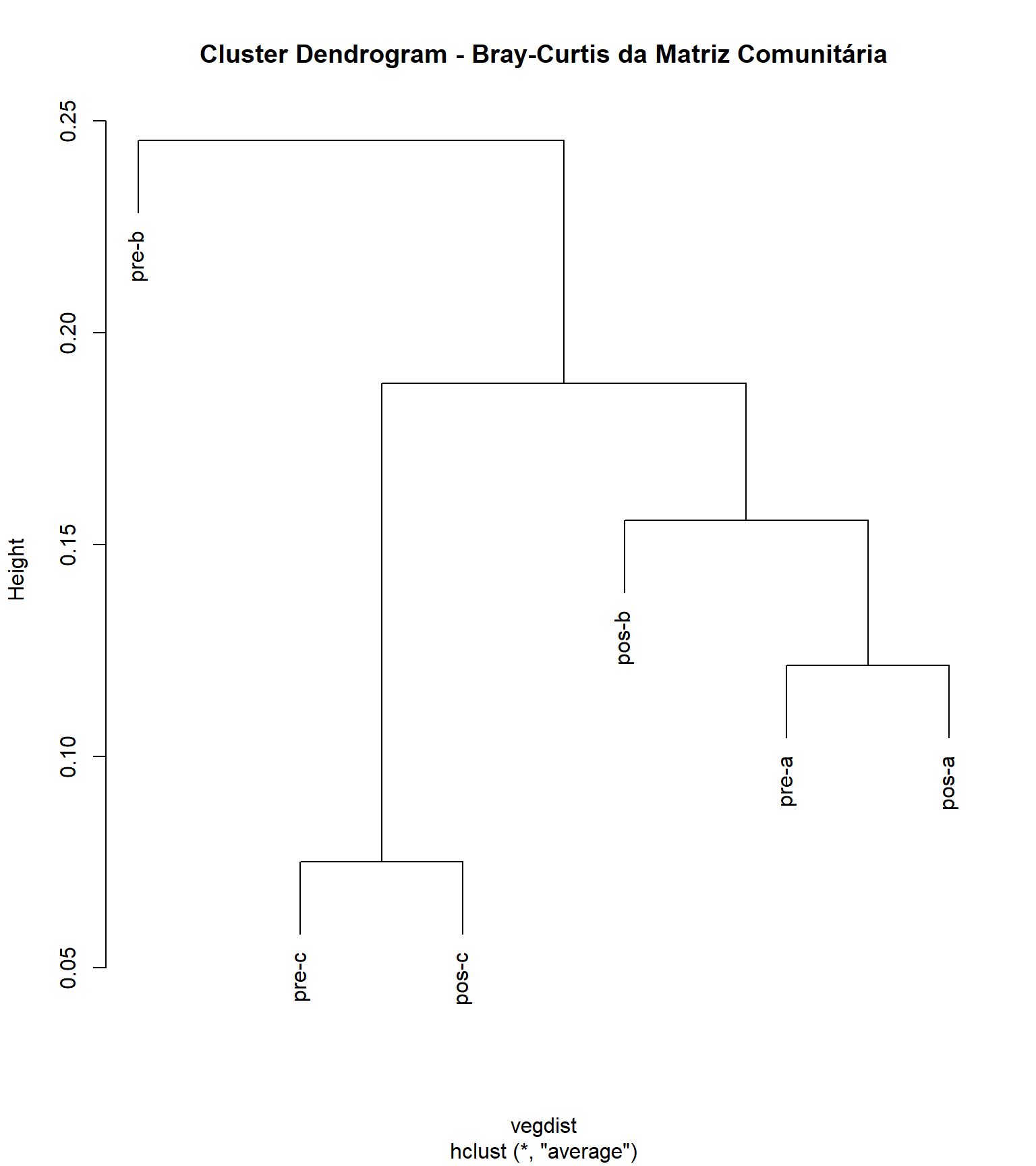
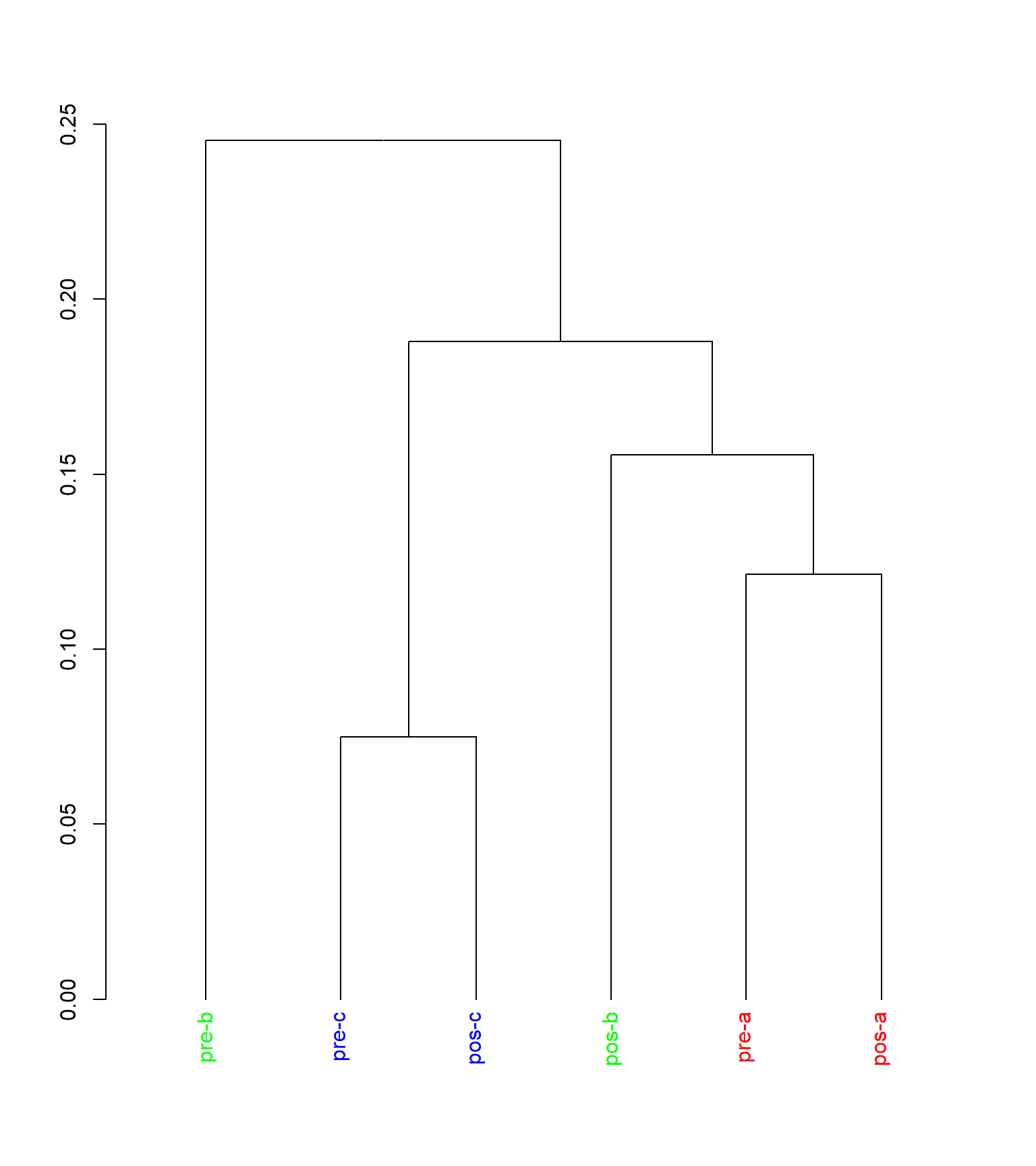
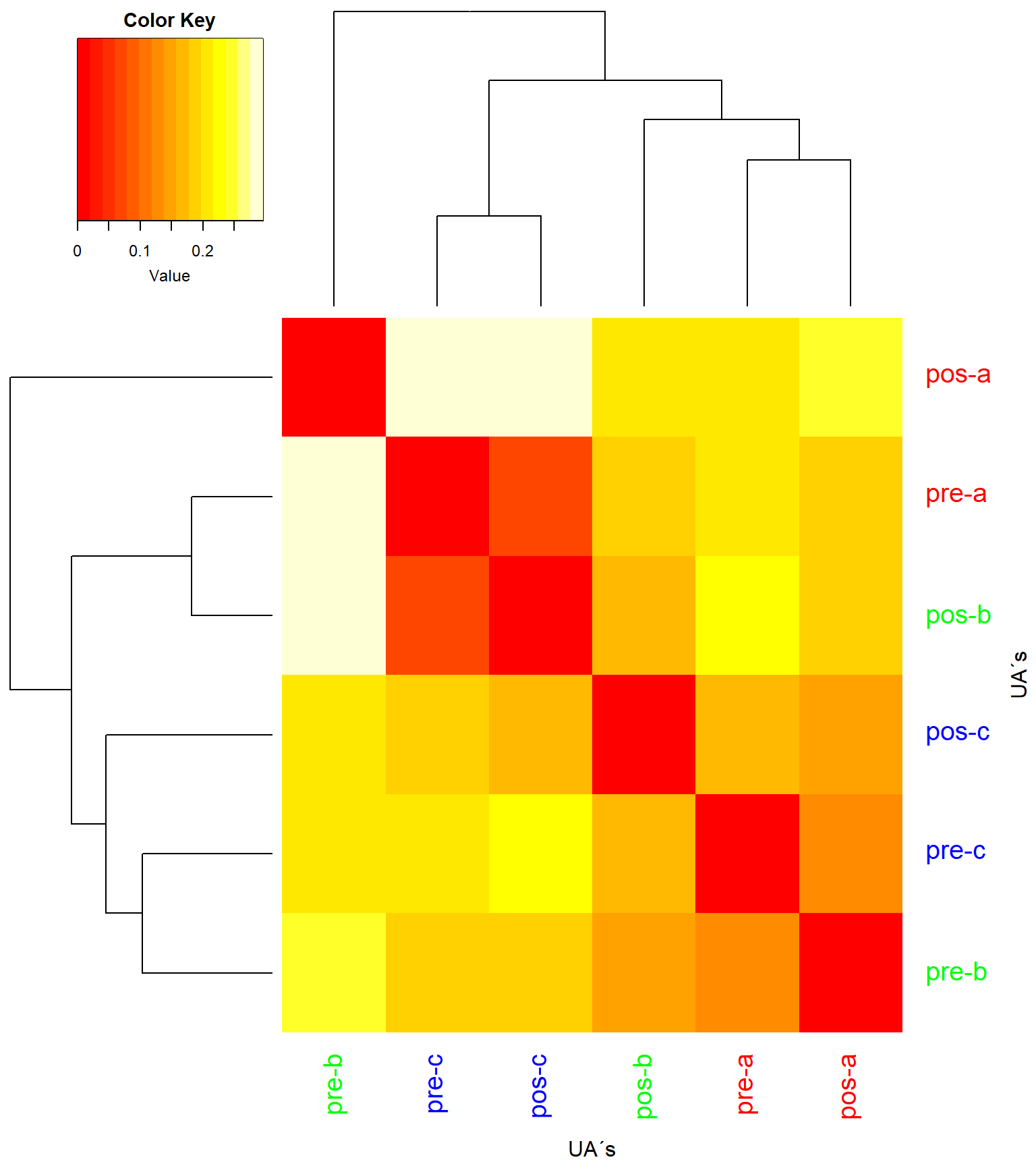
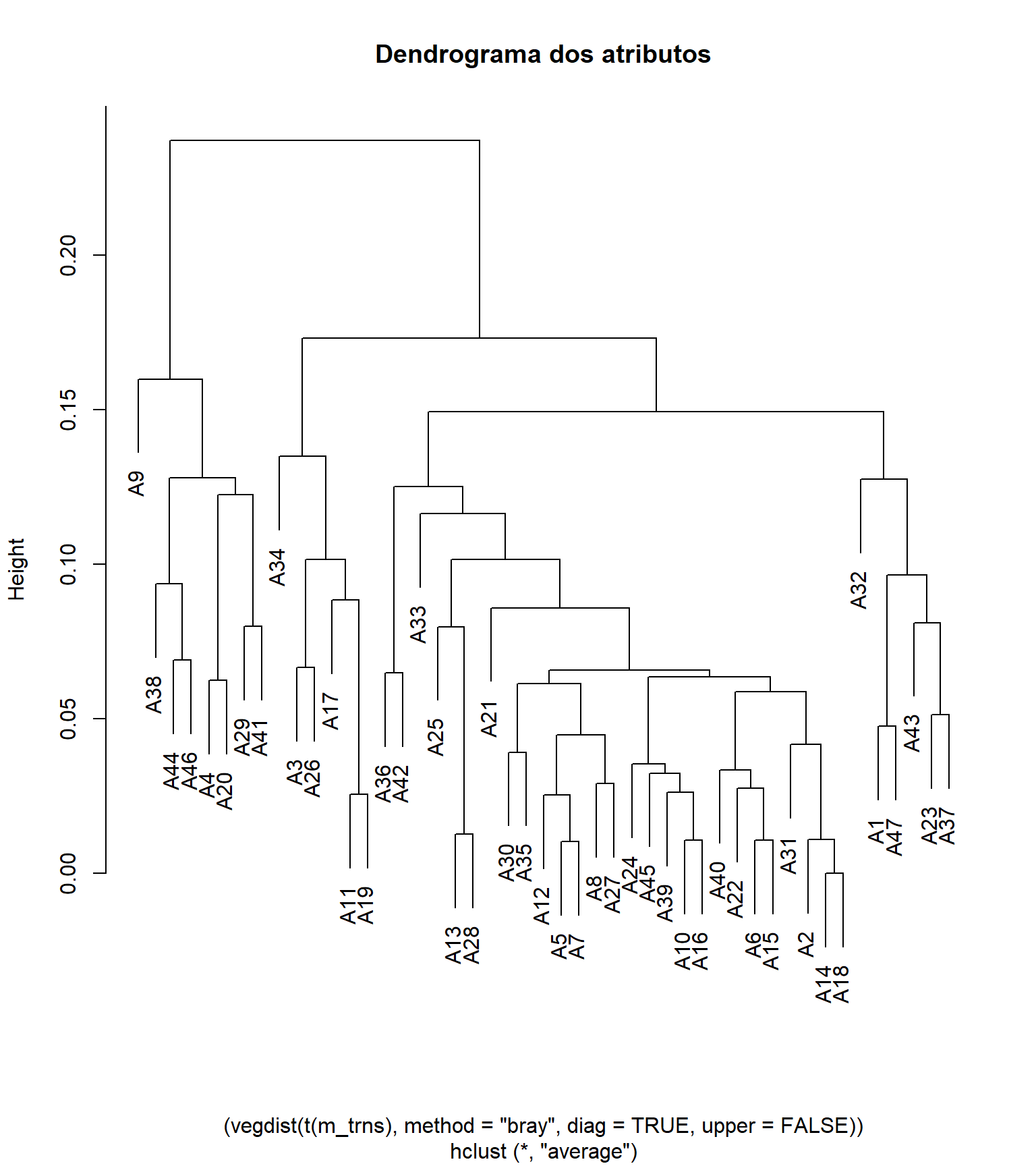
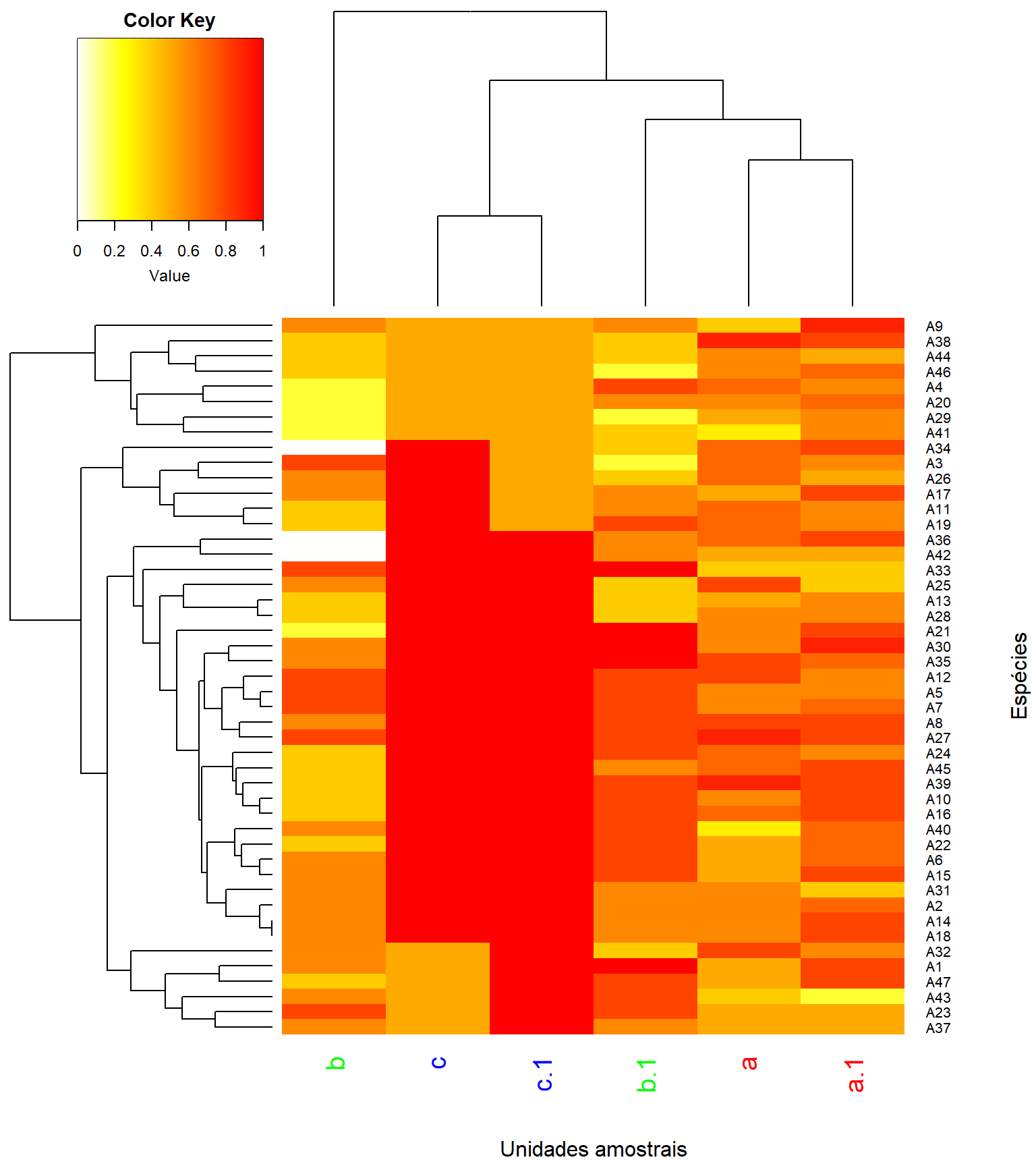
Figure 1.1: Análise de classificação da matriz binária (0/1), baseada na dissimilaridade de Bray-Curtis e método de fusão UPGMA.
Os valores individuais usados para criar a escala de cores do heatmap pode ser vistos a seguir.
## A37 A23 A43 A47 A1 A32 A18 A14 A2 A31 A15 A6 A22 A40 A16 A10 A39 A45
## b 0.6 0.8 0.6 0.4 0.6 0.6 0.6 0.6 0.6 0.6 0.6 0.6 0.4 0.6 0.4 0.4 0.4 0.4
## c 0.5 0.5 0.5 0.5 0.5 0.5 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
## c.1 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
## b.1 0.6 0.8 0.8 0.8 1.0 0.4 0.6 0.6 0.6 0.6 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.6
## a 0.5 0.5 0.4 0.5 0.5 0.8 0.6 0.6 0.6 0.6 0.5 0.5 0.5 0.3 0.7 0.6 0.9 0.7
## a.1 0.5 0.5 0.2 0.8 0.8 0.6 0.8 0.8 0.7 0.4 0.8 0.7 0.7 0.7 0.8 0.8 0.8 0.8
## A24 A27 A8 A7 A5 A12 A35 A30 A21 A28 A13 A25 A33 A42 A36 A19 A11 A17
## b 0.4 0.8 0.6 0.8 0.8 0.8 0.6 0.6 0.2 0.4 0.4 0.6 0.8 0.0 0.0 0.4 0.4 0.6
## c 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
## c.1 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.5 0.5 0.5
## b.1 0.8 0.8 0.8 0.8 0.8 0.8 1.0 1.0 1.0 0.4 0.4 0.4 1.0 0.6 0.6 0.8 0.6 0.6
## a 0.7 0.9 0.8 0.6 0.6 0.8 0.8 0.6 0.6 0.6 0.5 0.8 0.4 0.5 0.7 0.7 0.7 0.5
## a.1 0.6 0.8 0.8 0.7 0.6 0.6 0.7 0.9 0.8 0.6 0.6 0.4 0.4 0.5 0.8 0.6 0.6 0.8
## A26 A3 A34 A41 A29 A20 A4 A46 A44 A38 A9
## b 0.6 0.8 0.0 0.2 0.2 0.2 0.2 0.4 0.4 0.4 0.6
## c 1.0 1.0 1.0 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
## c.1 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
## b.1 0.4 0.2 0.4 0.4 0.2 0.6 0.8 0.2 0.4 0.4 0.6
## a 0.7 0.7 0.7 0.3 0.5 0.6 0.7 0.6 0.6 0.9 0.4
## a.1 0.5 0.6 0.8 0.6 0.6 0.7 0.6 0.7 0.5 0.8 0.91.4.2 Histórico das fusões
Criamos agora o histórico das fusões dos objetos. Na tabela gerada, as duas primeiras colunas (No. e UA) representam o número (No.) atribuido a cada unidade amostral (UA). As duas colunas subsequentes (Cluster1 e Cluster2) representam o par de objetos (indicado pelo sinal de “-”) ou grupo de objetos (indicado pela ausência do sinall de “-”) que foram agrupadas. A coluna Height, indica o valor de similaridade na qual um dado par de objetos (ou grupo de objetos) foi agrupado. O valor aproximado de Height também pode ser visualizado no eixo do dendrograma. Por último, na coluna Histórico, é mostrada a sequência das fusões da primeira até a m-1 última fusão entre os dois últimos grupos. Nesse caso, 5.
library(tidyverse)
library(gt)
merge <- as.data.frame(cluster_uas$merge)
merge[nrow(merge)+1,] = c("0","0")
height <- as.data.frame(round(cluster_uas$height, 2))
height[nrow(height)+1,] = c("1.0")
fusoes <- data.frame(Cluster_uas = merge, Height = height)
colnames(fusoes) <- c("Cluster1", "Cluster2", "Height")
UA <- rownames_to_column(as.data.frame(m_trns[, 0]))
colnames(UA) <- c("UAs")
No.UA <- 1:nrow(fusoes)
fusoes <- cbind(No.UA, UA, fusoes)
fusoes$Histórico <- 1:nrow(fusoes)
#fusoes
gt(fusoes)| No.UA | UAs | Cluster1 | Cluster2 | Height | Histórico |
|---|---|---|---|---|---|
| 1 | a | -3 | -6 | 0.07 | 1 |
| 2 | b | -1 | -4 | 0.12 | 2 |
| 3 | c | -5 | 2 | 0.16 | 3 |
| 4 | a.1 | 1 | 3 | 0.19 | 4 |
| 5 | b.1 | -2 | 4 | 0.25 | 5 |
| 6 | c.1 | 0 | 0 | 1.0 | 6 |
1.5 Ordenação
Para executar a NMDS, usa-se a função metaMDS do pacote vegan. metaMDS requer uma matriz de comunidade-por-espécies (CBE, “community-by-species”). De momento, cria-se essa matrizcom dados amostradoes aleatóriamente de um cojunto arbitrário de valores.
A função metaMDS vai calcular as distâncias, executar o algorítimo iterativo, determna o stress ou fitting entre os conjuntos de dados e etc. Precisa-se apenas definir a matriz de comunidade-por-espécies. Nesse caso:
## Run 0 stress 0
## Run 1 stress 0.07282821
## Run 2 stress 8.128333e-05
## ... Procrustes: rmse 0.04966081 max resid 0.0622544
## Run 3 stress 0
## ... Procrustes: rmse 0.1185044 max resid 0.1659816
## Run 4 stress 8.574597e-05
## ... Procrustes: rmse 0.1226497 max resid 0.2090308
## Run 5 stress 0.046818
## Run 6 stress 0.046818
## Run 7 stress 0
## ... Procrustes: rmse 0.0764651 max resid 0.1191276
## Run 8 stress 5.597597e-05
## ... Procrustes: rmse 0.07888537 max resid 0.10444
## Run 9 stress 0
## ... Procrustes: rmse 0.06014558 max resid 0.07776063
## Run 10 stress 9.699036e-05
## ... Procrustes: rmse 0.1125989 max resid 0.1617941
## Run 11 stress 0.2761338
## Run 12 stress 0.046818
## Run 13 stress 6.686963e-05
## ... Procrustes: rmse 0.09759577 max resid 0.1461209
## Run 14 stress 6.698734e-05
## ... Procrustes: rmse 0.0491271 max resid 0.06455857
## Run 15 stress 9.240158e-05
## ... Procrustes: rmse 0.1230026 max resid 0.2097206
## Run 16 stress 9.300693e-05
## ... Procrustes: rmse 0.1037329 max resid 0.1569334
## Run 17 stress 0
## ... Procrustes: rmse 0.07348939 max resid 0.1128799
## Run 18 stress 6.743162e-05
## ... Procrustes: rmse 0.05036694 max resid 0.07699749
## Run 19 stress 0.046818
## Run 20 stress 0
## ... Procrustes: rmse 0.05524344 max resid 0.09188521
## *** Best solution was not repeated -- monoMDS stopping criteria:
## 14: stress < smin
## 2: stress ratio > sratmax
## 4: scale factor of the gradient < sfgrmin## Warning in metaMDS(m_trns, k = 2): stress is (nearly) zero: you may have
## insufficient dataDeve-se observar cada iteração do NMDS até que uma solução seja alcançada (ou seja, o stress foi minimizado após algum número de reconfigurações dos pontos em 2 dimensões). Pode-se aumentar o número padrão de iterações usando o argumento trymax =.
## Run 0 stress 0
## Run 1 stress 0
## ... Procrustes: rmse 0.06468455 max resid 0.09032603
## Run 2 stress 8.559891e-05
## ... Procrustes: rmse 0.07953293 max resid 0.1197186
## Run 3 stress 9.511475e-05
## ... Procrustes: rmse 0.08108071 max resid 0.1215847
## Run 4 stress 9.10825e-05
## ... Procrustes: rmse 0.0749251 max resid 0.11211
## Run 5 stress 0
## ... Procrustes: rmse 0.02746635 max resid 0.05696472
## Run 6 stress 9.664143e-05
## ... Procrustes: rmse 0.1065221 max resid 0.1503125
## Run 7 stress 0.046818
## Run 8 stress 0.046818
## Run 9 stress 9.770383e-05
## ... Procrustes: rmse 0.1145595 max resid 0.180494
## Run 10 stress 0
## ... Procrustes: rmse 0.04093724 max resid 0.05360067
## Run 11 stress 0.046818
## Run 12 stress 9.463676e-05
## ... Procrustes: rmse 0.1417939 max resid 0.2205316
## Run 13 stress 8.677659e-05
## ... Procrustes: rmse 0.1091559 max resid 0.1563861
## Run 14 stress 8.655833e-05
## ... Procrustes: rmse 0.1417918 max resid 0.2205857
## Run 15 stress 8.044746e-05
## ... Procrustes: rmse 0.1331241 max resid 0.1739008
## Run 16 stress 0.1017926
## Run 17 stress 0
## ... Procrustes: rmse 0.04243629 max resid 0.05909437
## Run 18 stress 8.076102e-05
## ... Procrustes: rmse 0.1080641 max resid 0.1538904
## Run 19 stress 0
## ... Procrustes: rmse 0.05808718 max resid 0.06922275
## Run 20 stress 0
## ... Procrustes: rmse 0.04874974 max resid 0.07176066
## Run 21 stress 0
## ... Procrustes: rmse 0.03191155 max resid 0.0512849
## Run 22 stress 8.034455e-05
## ... Procrustes: rmse 0.1356691 max resid 0.2113826
## Run 23 stress 0
## ... Procrustes: rmse 0.06723686 max resid 0.09655544
## Run 24 stress 0.046818
## Run 25 stress 0
## ... Procrustes: rmse 0.04843107 max resid 0.06756897
## Run 26 stress 0
## ... Procrustes: rmse 0.1168155 max resid 0.1531661
## Run 27 stress 0.07282815
## Run 28 stress 5.592501e-05
## ... Procrustes: rmse 0.05384103 max resid 0.07630677
## Run 29 stress 0
## ... Procrustes: rmse 0.1415833 max resid 0.1801783
## Run 30 stress 0
## ... Procrustes: rmse 0.07485896 max resid 0.1102891
## Run 31 stress 8.982908e-05
## ... Procrustes: rmse 0.06689694 max resid 0.09549486
## Run 32 stress 0.1017925
## Run 33 stress 0
## ... Procrustes: rmse 0.05170539 max resid 0.07258838
## Run 34 stress 0
## ... Procrustes: rmse 0.04321008 max resid 0.0542623
## Run 35 stress 0
## ... Procrustes: rmse 0.0373869 max resid 0.06391215
## Run 36 stress 0.07282815
## Run 37 stress 9.006783e-05
## ... Procrustes: rmse 0.1404387 max resid 0.1841635
## Run 38 stress 4.774355e-07
## ... Procrustes: rmse 0.06602665 max resid 0.09698266
## Run 39 stress 0
## ... Procrustes: rmse 0.05199299 max resid 0.06679064
## Run 40 stress 0.046818
## Run 41 stress 0.07282813
## Run 42 stress 0.046818
## Run 43 stress 0.046818
## Run 44 stress 0.046818
## Run 45 stress 0
## ... Procrustes: rmse 0.1208764 max resid 0.1714577
## Run 46 stress 9.511325e-05
## ... Procrustes: rmse 0.1448102 max resid 0.1958072
## Run 47 stress 0.046818
## Run 48 stress 0
## ... Procrustes: rmse 0.04401808 max resid 0.06408316
## Run 49 stress 0.2761338
## Run 50 stress 0.07282813
## Run 51 stress 0
## ... Procrustes: rmse 0.05234416 max resid 0.06479425
## Run 52 stress 5.535495e-05
## ... Procrustes: rmse 0.1439921 max resid 0.1875952
## Run 53 stress 0.07282809
## Run 54 stress 0
## ... Procrustes: rmse 0.07374052 max resid 0.1017021
## Run 55 stress 0.046818
## Run 56 stress 0
## ... Procrustes: rmse 0.05983119 max resid 0.08806285
## Run 57 stress 0
## ... Procrustes: rmse 0.06569667 max resid 0.08739604
## Run 58 stress 0
## ... Procrustes: rmse 0.0454386 max resid 0.06487699
## Run 59 stress 8.522103e-05
## ... Procrustes: rmse 0.08333851 max resid 0.1066099
## Run 60 stress 0
## ... Procrustes: rmse 0.05127334 max resid 0.09032206
## Run 61 stress 0.046818
## Run 62 stress 0.0728281
## Run 63 stress 7.028783e-05
## ... Procrustes: rmse 0.07453132 max resid 0.1110597
## Run 64 stress 0
## ... Procrustes: rmse 0.05381885 max resid 0.0678841
## Run 65 stress 0
## ... Procrustes: rmse 0.06233724 max resid 0.08968574
## Run 66 stress 0
## ... Procrustes: rmse 0.05967198 max resid 0.09742989
## Run 67 stress 0
## ... Procrustes: rmse 0.04501244 max resid 0.05753556
## Run 68 stress 0
## ... Procrustes: rmse 0.03280019 max resid 0.05026186
## Run 69 stress 0.07282812
## Run 70 stress 0.2761337
## Run 71 stress 0.1017926
## Run 72 stress 1.261141e-05
## ... Procrustes: rmse 0.05748604 max resid 0.07239735
## Run 73 stress 0
## ... Procrustes: rmse 0.05261151 max resid 0.09282866
## Run 74 stress 0.046818
## Run 75 stress 0
## ... Procrustes: rmse 0.04365859 max resid 0.06293039
## Run 76 stress 8.449615e-05
## ... Procrustes: rmse 0.1105302 max resid 0.1579375
## Run 77 stress 0
## ... Procrustes: rmse 0.05645027 max resid 0.07147257
## Run 78 stress 0.046818
## Run 79 stress 6.680464e-05
## ... Procrustes: rmse 0.1091909 max resid 0.1502897
## Run 80 stress 0
## ... Procrustes: rmse 0.07032179 max resid 0.09782012
## Run 81 stress 9.259781e-05
## ... Procrustes: rmse 0.1343955 max resid 0.2074869
## Run 82 stress 0
## ... Procrustes: rmse 0.04048519 max resid 0.06322947
## Run 83 stress 0
## ... Procrustes: rmse 0.05813692 max resid 0.08367314
## Run 84 stress 9.670405e-05
## ... Procrustes: rmse 0.1055506 max resid 0.1444712
## Run 85 stress 0
## ... Procrustes: rmse 0.04019303 max resid 0.05166587
## Run 86 stress 0
## ... Procrustes: rmse 0.05057963 max resid 0.06797582
## Run 87 stress 0
## ... Procrustes: rmse 0.04358923 max resid 0.06525633
## Run 88 stress 0
## ... Procrustes: rmse 0.03091901 max resid 0.04110686
## Run 89 stress 0.046818
## Run 90 stress 0
## ... Procrustes: rmse 0.06058491 max resid 0.07345755
## Run 91 stress 8.907238e-05
## ... Procrustes: rmse 0.08040416 max resid 0.1192165
## Run 92 stress 0
## ... Procrustes: rmse 0.06744855 max resid 0.09959249
## Run 93 stress 0
## ... Procrustes: rmse 0.06141511 max resid 0.08746016
## Run 94 stress 0.07282823
## Run 95 stress 0
## ... Procrustes: rmse 0.03367245 max resid 0.04180265
## Run 96 stress 0
## ... Procrustes: rmse 0.03236209 max resid 0.0552837
## Run 97 stress 0
## ... Procrustes: rmse 0.1006823 max resid 0.1372013
## Run 98 stress 0
## ... Procrustes: rmse 0.05307067 max resid 0.06905205
## Run 99 stress 0.046818
## Run 100 stress 9.326968e-05
## ... Procrustes: rmse 0.141793 max resid 0.2205108
## *** Best solution was not repeated -- monoMDS stopping criteria:
## 72: stress < smin
## 14: stress ratio > sratmax
## 14: scale factor of the gradient < sfgrmin## Warning in metaMDS(m_trns, distance = "jaccard", k = 2, trymax = 100):
## stress is (nearly) zero: you may have insufficient data#method = "manhattan", "euclidean", "canberra", "clark", "bray", "kulczynski", "jaccard", "gower", #"altGower", "morisita", "horn", "mountford", "raup", "binomial", "chao", "cao", "mahalanobis", "chisq", #"chord", "hellinger", "aitchison", or "robust.aitchison".Pode-se agora examinar o objeto NMDS.
##
## Call:
## metaMDS(comm = m_trns, distance = "jaccard", k = 2, trymax = 100)
##
## global Multidimensional Scaling using monoMDS
##
## Data: m_trns
## Distance: jaccard
##
## Dimensions: 2
## Stress: 0
## Stress type 1, weak ties
## Best solution was not repeated after 100 tries
## The best solution was from try 0 (metric scaling or null solution)
## Scaling: centring, PC rotation, halfchange scaling
## Species: expanded scores based on 'm_trns'## $sites
## NMDS1 NMDS2
## a -0.10100683 0.25348310
## b -0.44820138 -0.15218169
## c 0.30161159 -0.06588190
## a.1 0.06154400 0.18164623
## b.1 -0.06015995 -0.06375019
## c.1 0.24621257 -0.15331556
##
## $species
## NMDS1 NMDS2
## A1 -0.197884732 -0.07584919
## A2 0.084353001 -0.07366836
## A3 -0.277095094 0.05987233
## A4 -0.069602347 0.25687916
## A5 -0.122552110 -0.16172697
## A6 0.072160142 -0.13288915
## A7 -0.116435332 -0.12995348
## A8 0.001712465 0.02147775
## A9 -0.357611938 0.09621400
## A10 0.222767221 -0.01308328
## A11 0.053127911 0.12924452
## A12 -0.163128870 -0.07803636
## A13 0.365561600 -0.09200369
## A14 0.086370762 -0.04173701
## A15 0.074394395 -0.10037717
## A16 0.193836618 0.02827037
## A17 -0.081014596 0.04138013
## A18 0.086370762 -0.04173701
## A19 0.010134275 0.10110014
## A20 0.020346880 0.28415918
## A21 0.359163679 0.01557046
## A22 0.254706664 -0.08926233
## A23 -0.378357936 -0.21563311
## A24 0.194577355 -0.03248089
## A25 0.061998151 -0.06600560
## A26 -0.119798554 0.05940666
## A27 -0.168661783 0.01545411
## A28 0.327998282 -0.04144014
## A29 0.192701342 0.28871180
## A30 0.018102861 -0.04430002
## A31 0.077723213 -0.17858566
## A32 -0.195684942 0.05809645
## A33 -0.121225843 -0.33220880
## A34 0.581239519 0.38057770
## A35 -0.033432086 -0.02330534
## A36 0.646323513 0.16016365
## A37 -0.162471867 -0.15644090
## A38 -0.253635059 0.41936146
## A39 0.139517936 0.10591396
## A40 0.127120653 -0.22668130
## A41 0.219119445 0.09957730
## A42 0.784491559 -0.04110800
## A43 -0.200556791 -0.36490455
## A44 -0.206821513 0.16208672
## A45 0.238306903 0.04879986
## A46 -0.138965318 0.28821204
## A47 0.019857202 -0.00711800É necessário examinar o Gráfico de Shepard (Figura 1.2), que mostra a dispersão em torno da regressão entre as distâncias entre pontos da configuração final (distâncias entre cada par de comunidades) versus as dissimilaridades originais.
stressplot(nmds)
gof <- goodness(nmds)
gof
plot(nmds, display = "sites", type = "n")
points(nmds, display = "sites", cex = 2*gof/mean(gof))## [1] 0 0 0 0 0 0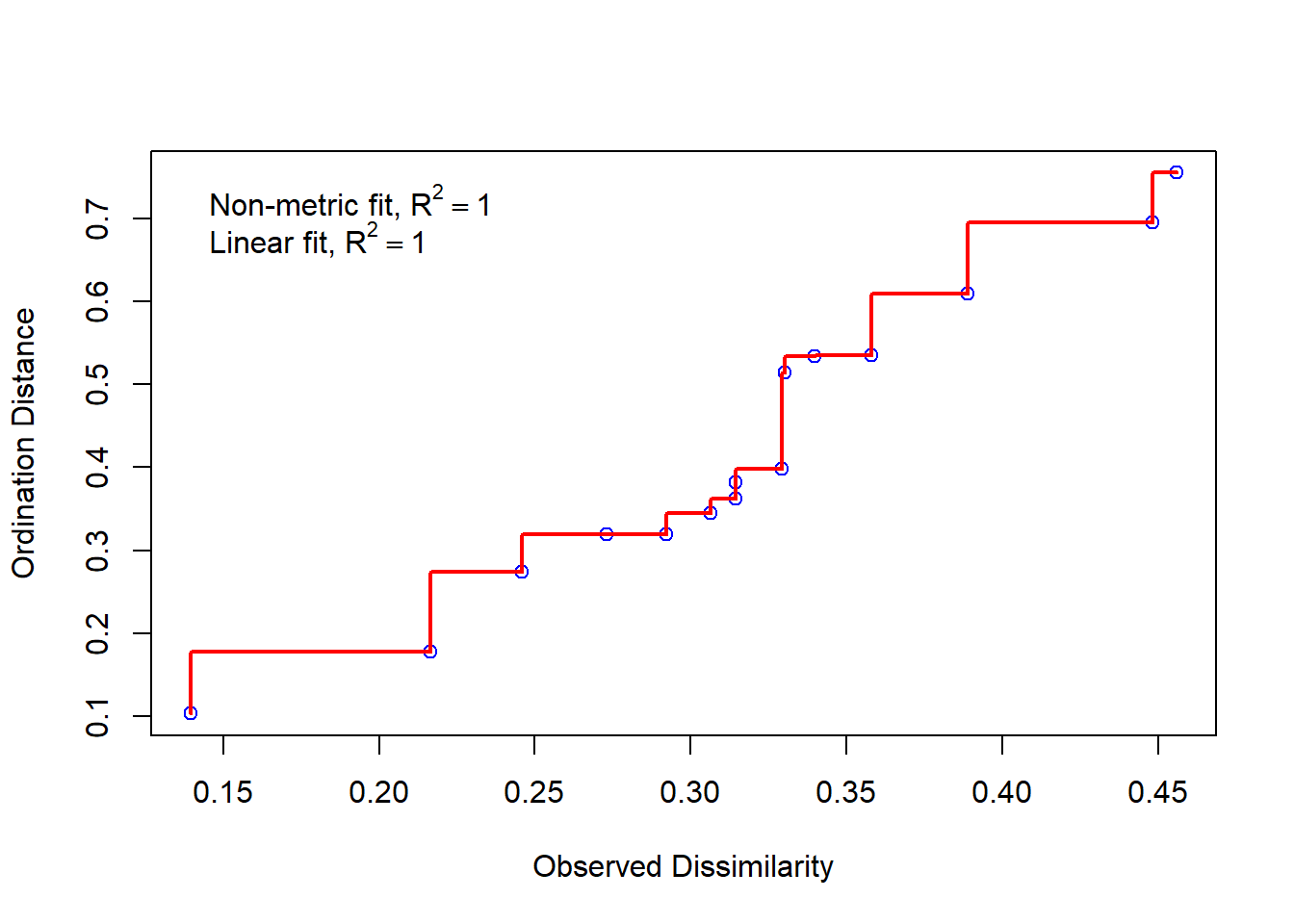
Figure 1.2: Stress da análise de ordenação da matriz binária (0/1), baseada na dissimilaridade de Bray-Curtis e método de fusão UPGMA.
Uma dispersão grande ao redor da linha sugere que as dissimilaridades originais não são bem preservadas no número reduzido de dimensões.
1.5.1 Gráficos de ordenação
Agora podemos plotar a NMDS
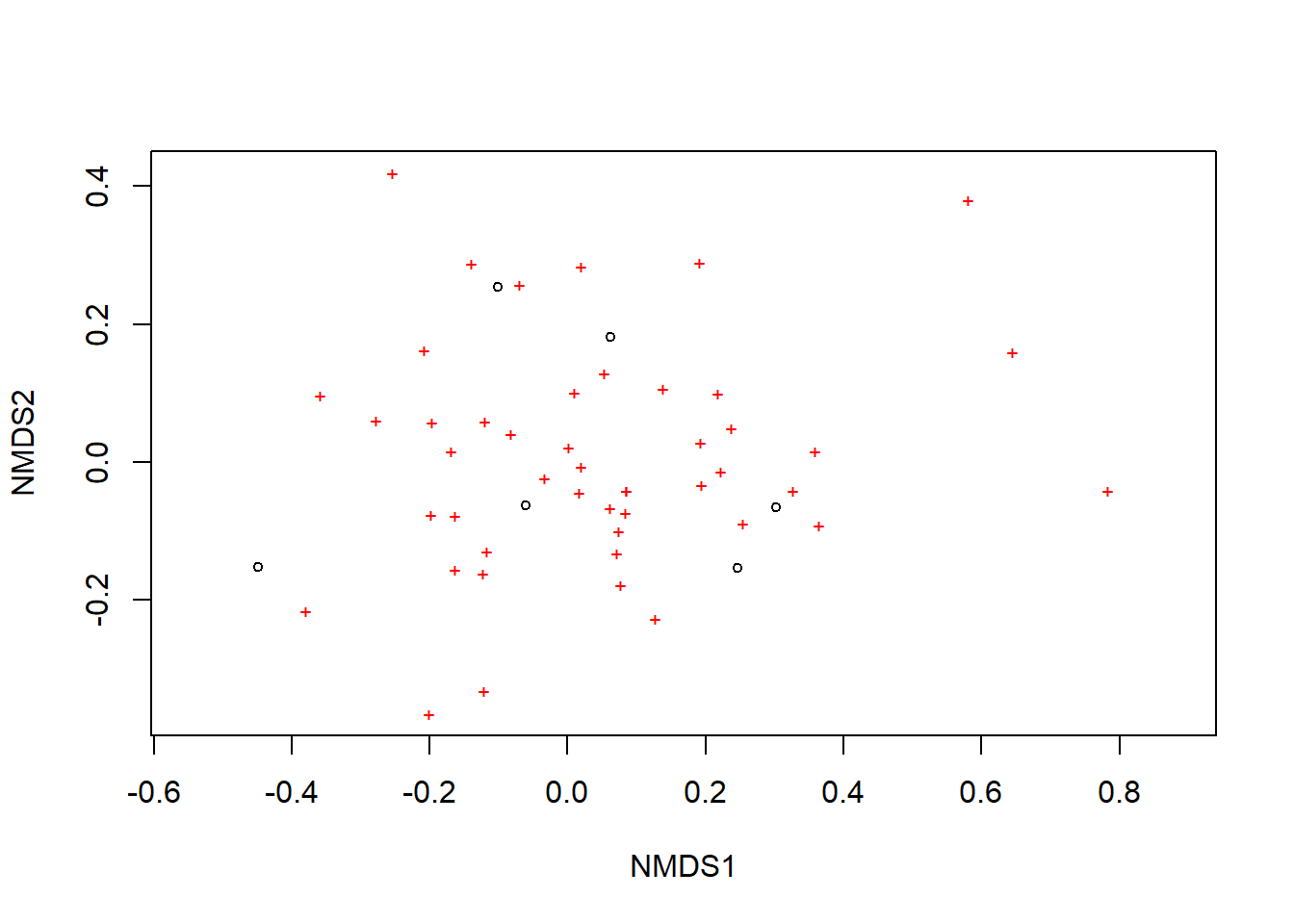
Figure 1.3: Gráfico de ordenação da matriz binária (0/1), baseada na dissimilaridade de Bray-Curtis e método de fusão UPGMA.
A ordenação mostra tanto as comunidades (“locais”, círculos abertos) quanto as espécies (cruzes vermelhas).
Aqui, pode-se usar as funções ordiplot e orditorp para adicionar texto ao gráfico no lugar dos pontos.
ordiplot(nmds, choices = c(1,2), type = "n")
orditorp(nmds, display = "species", col="red", air=0.01)
orditorp(nmds, display = "sites", cex=1.25, air=0.01)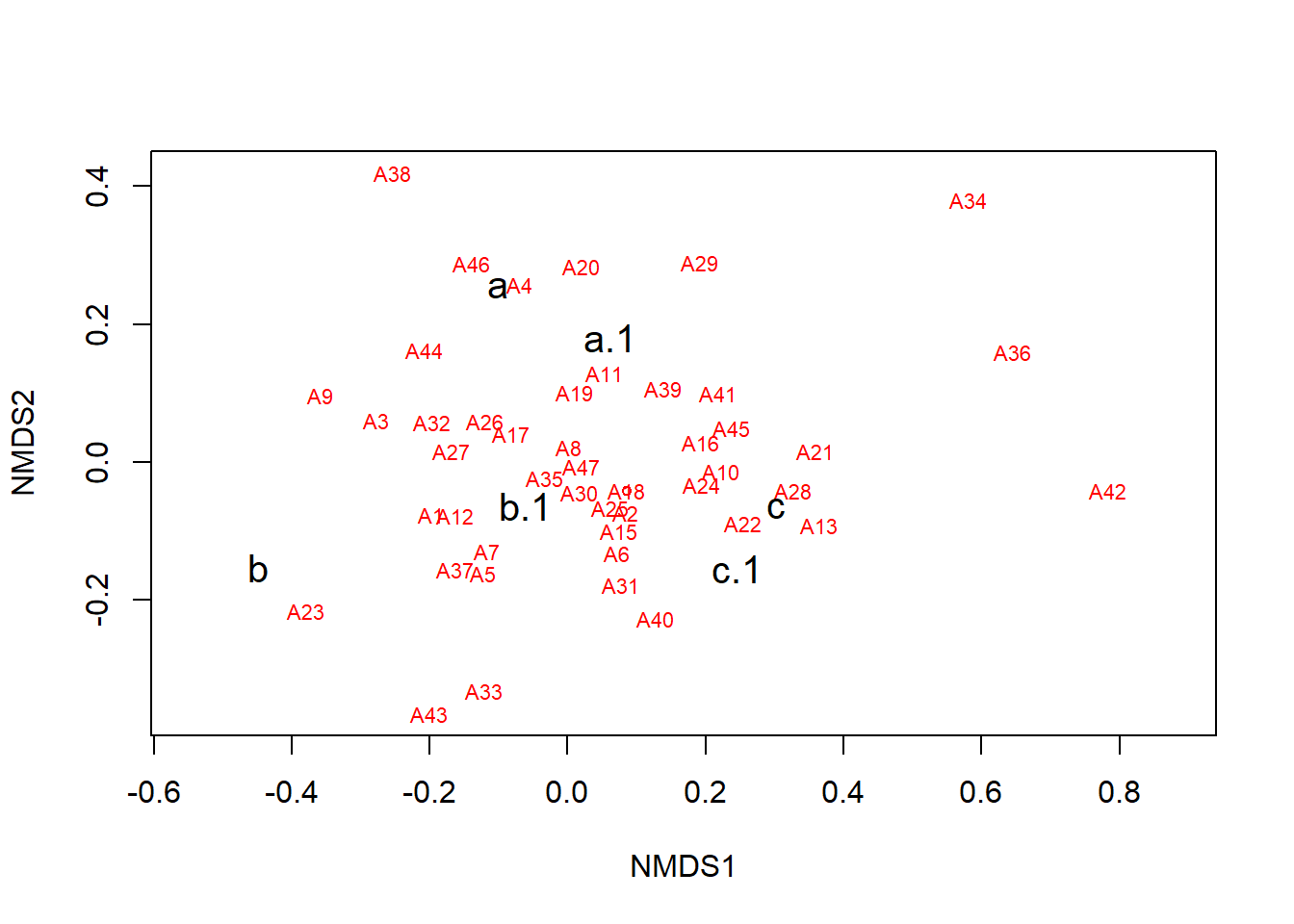
Existem algumas funções adicionais que podem ser de interesse. Pode-se desenhar polígonos convexos conectando os vértices dos pontos feitos por certos grupos de comunidades no gráfico.
Para isso, cria-se um vetor de valores de tratamento.
## [1] "antes" "antes" "antes" "depois" "depois" "depois"colors <- c(rep("green",3), rep("blue",3))
ordiplot(nmds, type = "n")
ordihull(nmds, groups = treat, draw = "polygon", col= "grey90", label = TRUE)
orditorp(nmds, display = "species", col = "red", air = 0.01)
orditorp(nmds, display = "sites", col = colors, air = 0.01, cex = 1.25)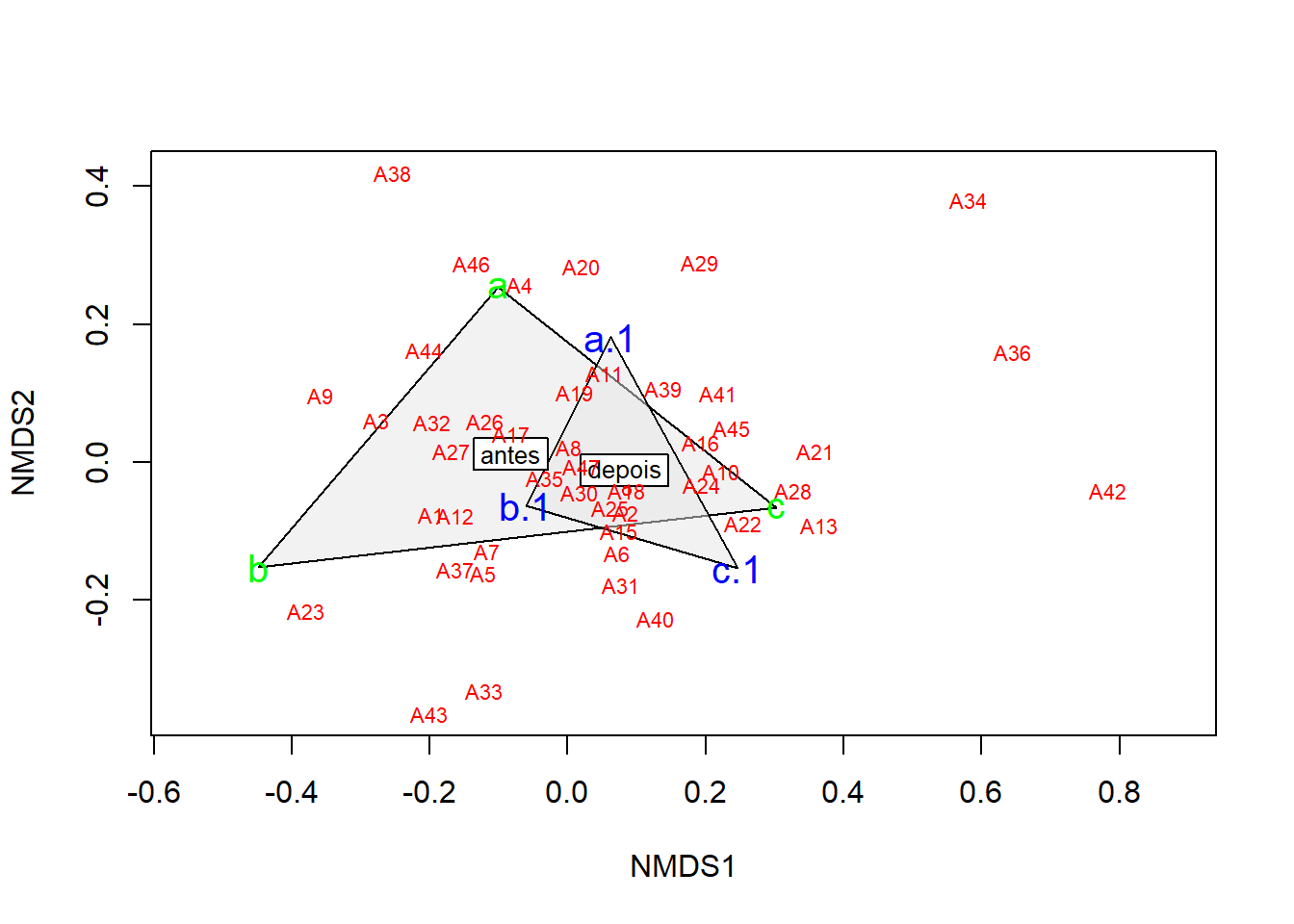
Essa é uma maneira intuitiva de entender como as linhas e colunas se agrupam com base nos tratamentos possveis. Nesse caso, um grupo em verde e e o outro em azul. Também é possível plotar elipses e “gráficos de aranha” usando as funções ordiellipse e orderspider, que enfatizam o centróide das comunidades em cada tratamento.
par(mfrow=c(2,2))
ordiplot(nmds, type = "n")
orditorp(nmds, display = "species", col = "red", air = 0.01)
orditorp(nmds, display = "sites", col = colors, air = 0.01, cex = 1.25)
ordihull(nmds, groups = treat, draw = "polygon", col = "grey90", label = TRUE)
ordiplot(nmds, type = "n")
orditorp(nmds, display = "species", col = "red", air = 0.01)
orditorp(nmds, display = "sites", col = colors, air = 0.01, cex = 1.25)
ordiellipse(nmds, groups = treat, display = "sites", draw = "polygon", col = "grey90", label = T)
ordibar(nmds, treat, display = "sites")
ordiplot(nmds, type = "n")
orditorp(nmds, display = "species", col = "red", air = 0.01)
orditorp(nmds, display = "sites", col = colors, air = 0.01, cex = 1.25)
ordispider(nmds, treat, display="sites")
ordiplot(nmds, type = "n")
orditorp(nmds, display = "species", col = "red", air = 0.01)
orditorp(nmds, display = "sites", col = colors, air = 0.01, cex = 1.25)
ordicluster(nmds, cluster_uas, prune = 0, display = "sites")
par(mfrow=c(1,1))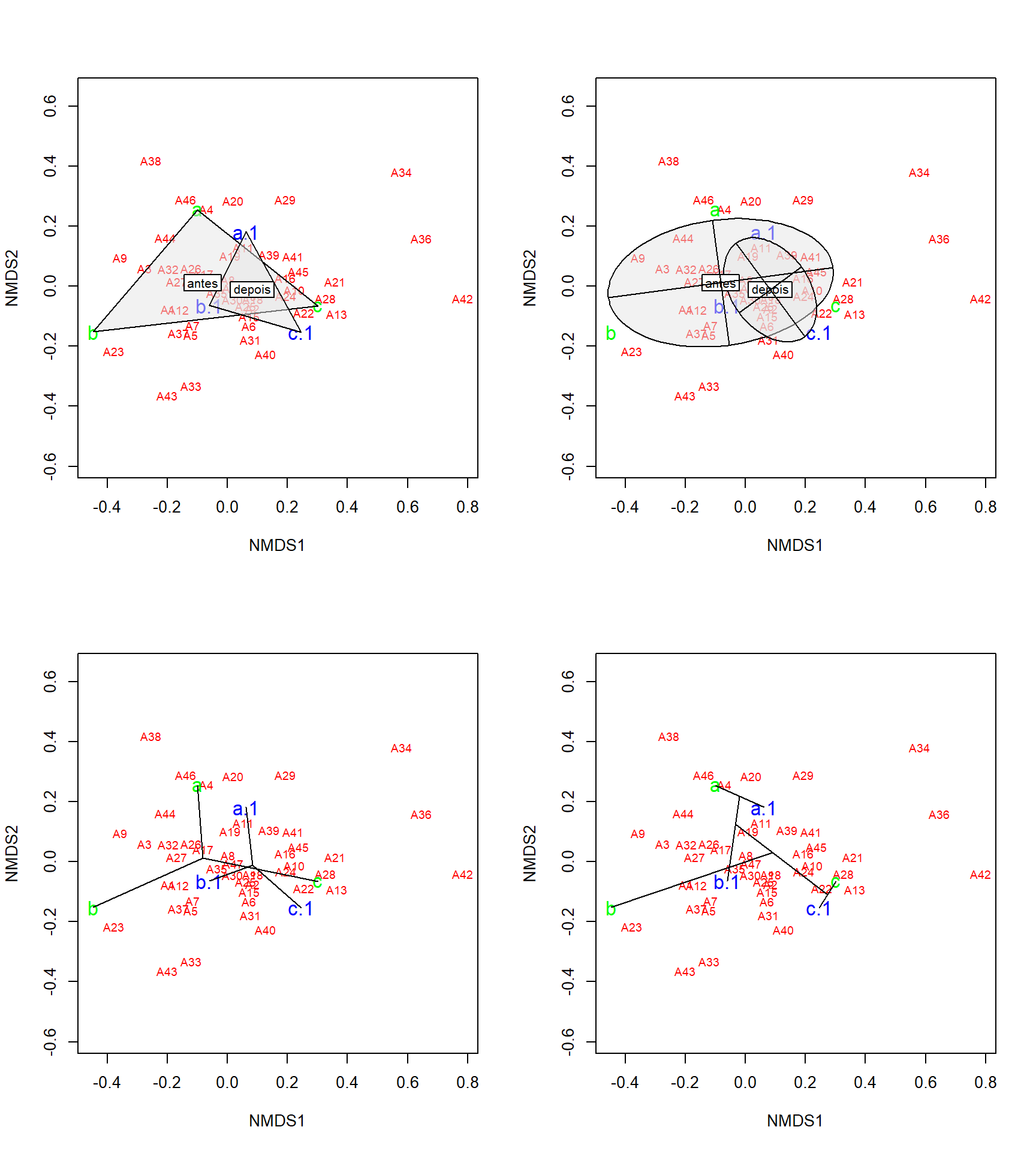
Outra alternativa é plotar uma “árvore de abrangência mínima” (da função hclust), que agrupa as comunidades com base em suas dissimilaridades originais e projeta o dendrograma no gráfico 2D.
ordiplot(nmds, type = "n")
orditorp(nmds, display = "species", col = "red", air = 0.01)
orditorp(nmds, display = "sites", col = colors, air = 0.01, cex = 1.25)
ordicluster(nmds, hclust(vegdist(m_trns, "bray")))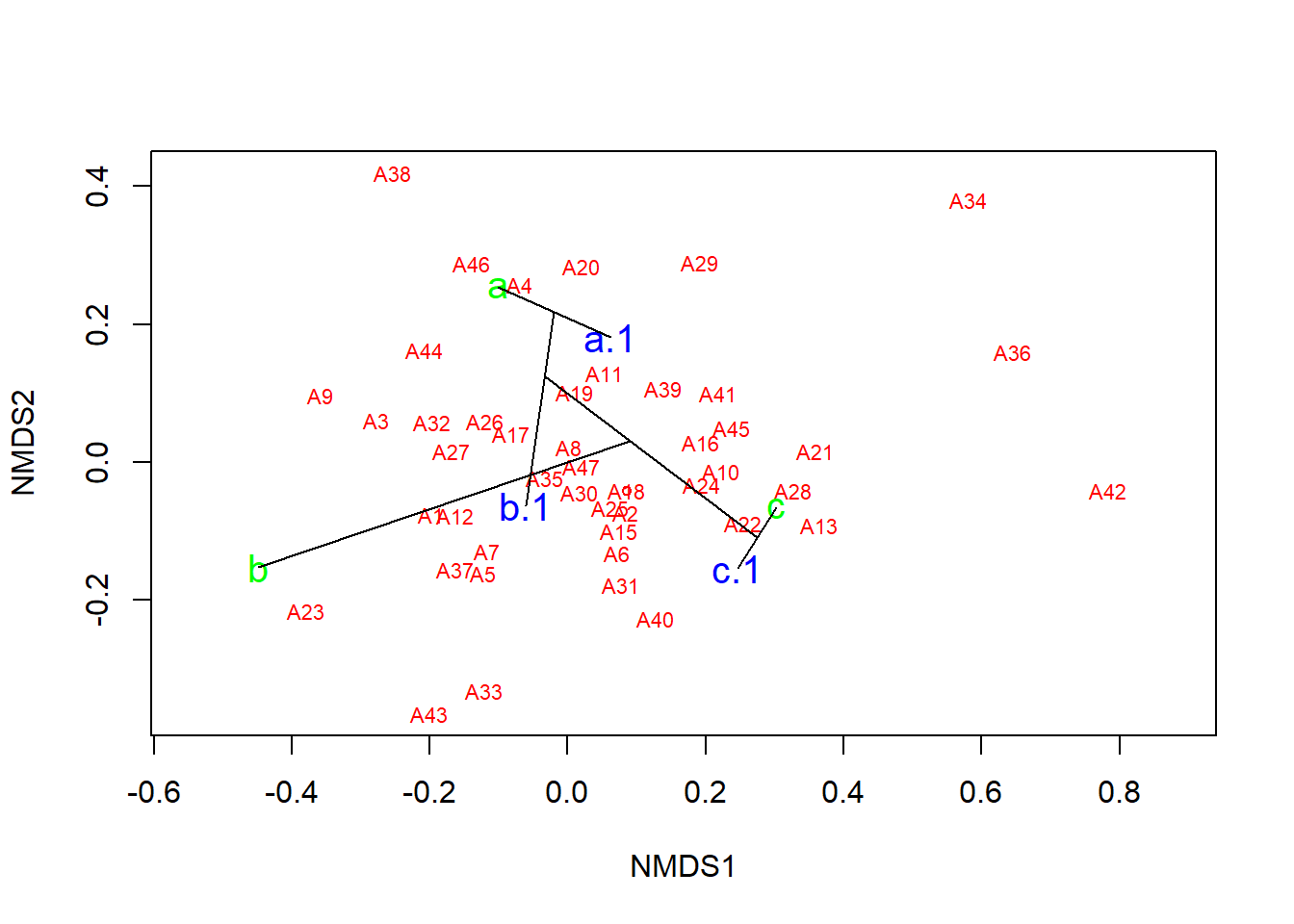
Observe que o agrupamento é baseado em distâncias de Bray-Curtis. Este é um método sugerido para verificar a precisão do gráfico 2D.
Pode-se ainda plotar os polígonos convexos, elipses, gráficos de aranha, etc., coloridos com base nos tratamentos. Mas primeiro, cria-se um vetor de valores de cor com a mesma extensão do vetor de valores de tratamento.
ordiplot(nmds, type = "n")
#Plot convex hulls with colors baesd on treatment
for(i in unique(treat)) {
ordihull(nmds$point[grep(i,treat),],draw="polygon",groups=treat[treat==i],col=colors[grep(i,treat)],label=F) }
orditorp(nmds, display = "species", col= "red", air = 0.01)
orditorp(nmds, display = "sites", col = colors, air = 0.01, cex = 1.25)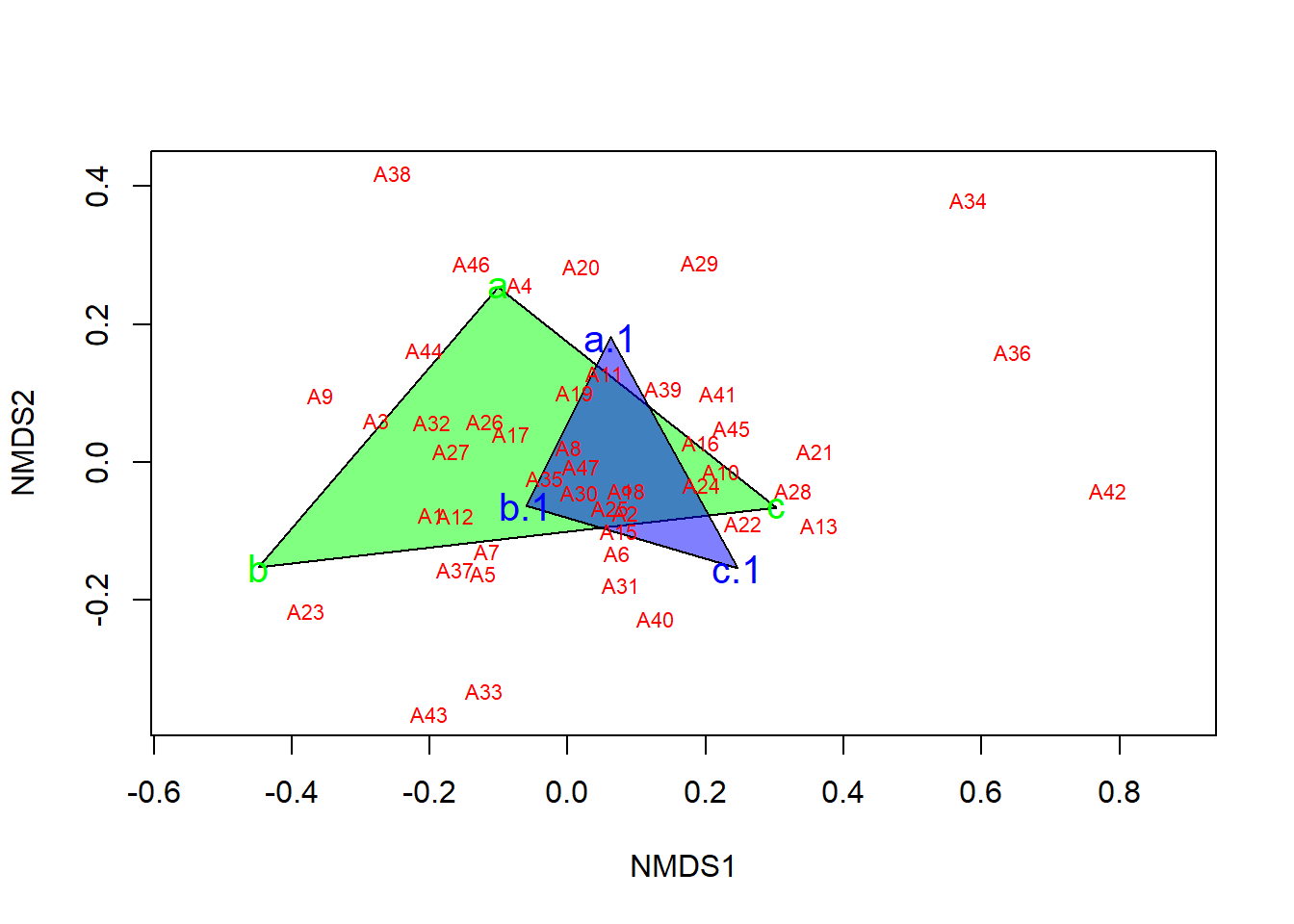
Esse agrupamento é baseado em distâncias de Bray-Curtis. Este é um método sugerido para verificar a precisão do gráfico 2D.
Pode-se plotar os polígonos convexos, elipses, gráficos de aranha, etc., coloridos com base nos tratamentos. Primeiro, cria-se um vetor de valores de cor com a mesma extensão do vetor de valores de tratamento.
Se o tratamento for uma variável contínua, deve-se considerar linhas de mapeamento de contorno sobrepostas no gráfico. Para este exemplo, considera-se que os tratamentos foram aplicados ao longo de um gradiente de elevação. Podemos definir elevações aleatórias para o mesmo exemplo.
#Variable to be plotted / modelled as a function of the ordination scores
surf <- seq(1, 19)
surf <- c(cluster_uas$height, 1)
knots <- nrow(m_trns)Agora usa-se a função ordisurf para plotar as linhas de contorno. A quantidade de linhas de contorno é definida pelo comando knots =. Se knots = 0 ou knots = 1 a função ordisurf ajustará uma tendencia linear a superfície, e se knots = 2 a função ajustará uma tendência quadrática, ao inves de linhas retas.
##
## Family: gaussian
## Link function: identity
##
## Formula:
## y ~ s(x1, x2, k = 6, bs = "tp", fx = FALSE)
##
## Estimated degrees of freedom:
## 0.408 total = 1.41
##
## REML score: 2.710623orditorp(nmds, display = "sites", col = "grey30", air = 0.1, cex = 1)
orditorp(nmds, display = "species", col = "grey30", air = 0.1, cex = 1)
1.6 MRPP
Primeiro criamos uma tabela de grupos a priori.
Valores médios:
library(tibble)
library (dplyr)
m_sum
m_sum_g <- rownames_to_column(m_sum, "Grupo1")
m_sum_g$Grupo2 <- substr(m_sum_g$Grupo1, 1,3)
m_sum_g$Grupo3 <- substr(m_sum_g$Grupo1, 5,5)
m_sum_g <- m_sum_g %>% relocate(Grupo2, Grupo3, .after=Grupo1)
m_sum_g <- m_sum_g[,1:3]# <- NULL
m_sum_gValores brutos p/a:
## Questões Grupo1 Grupo2
## pre-1 1 pre pre-a
## pre-2a 2a pre pre-a
## pre-2bi 2bi pre pre-a
## pre-2bii 2bii pre pre-a
## pre-2biii 2biii pre pre-a
## pre-2biv 2biv pre pre-a
## pre-2c 2c pre pre-a
## pre-3 3 pre pre-b
## pre-4 4 pre pre-b
## pre-5 5 pre pre-b
## pre-6 6 pre pre-b
## pre-7i 7i pre pre-b
## pre-7ii 7ii pre pre-a
## pre-7iii 7iii pre pre-a
## pre-7iv 7iv pre pre-a
## pre-7v 7v pre pre-c
## pre-7vi 7vi pre pre-c
## pos-1 1 pos pos-a
## pos-2a 2a pos pos-a
## pos-2bi 2bi pos pos-a
## pos-2bii 2bii pos pos-a
## pos-2biii 2biii pos pos-a
## pos-2biv 2biv pos pos-a
## pos-2c 2c pos pos-a
## pos-3 3 pos pos-b
## pos-4 4 pos pos-b
## pos-5 5 pos pos-b
## pos-6 6 pos pos-b
## pos-7i 7i pos pos-b
## pos-7ii 7ii pos pos-a
## pos-7iii 7iii pos pos-a
## pos-7iv 7iv pos pos-a
## pos-7v 7v pos pos-c
## pos-7vi 7vi pos pos-c1.6.1 Testes entre combinações possiveis (valores médios)
Em m_sum_grp
Grupo 1 = pré- vs. pós-
Grupo 2 = a vs. b vs. c
library(vegan)
mrpp1 <- with(m_sum_grp, mrpp(m_sum, Grupo1, distance = "bray"))
mrpp1
mrpp2 <- with(m_sum_grp, mrpp(m_sum, Grupo2, distance = "bray"))
mrpp2##
## Call:
## mrpp(dat = m_sum, grouping = Grupo1, distance = "bray")
##
## Dissimilarity index: bray
## Weights for groups: n
##
## Class means and counts:
##
## pos pre
## delta 0.3504 0.4452
## n 17 17
##
## Chance corrected within-group agreement A: 0.00147
## Based on observed delta 0.3978 and expected delta 0.3984
##
## Significance of delta: 0.374
## Permutation: free
## Number of permutations: 999
##
##
## Call:
## mrpp(dat = m_sum, grouping = Grupo2, distance = "bray")
##
## Dissimilarity index: bray
## Weights for groups: n
##
## Class means and counts:
##
## pos-a pos-b pos-c pre-a pre-b pre-c
## delta 0.375 0.3799 0.175 0.4315 0.5745 0.175
## n 10 5 2 10 5 2
##
## Chance corrected within-group agreement A: 0.0006062
## Based on observed delta 0.3981 and expected delta 0.3984
##
## Significance of delta: 0.456
## Permutation: free
## Number of permutations: 9991.6.2 Alguns gráficos
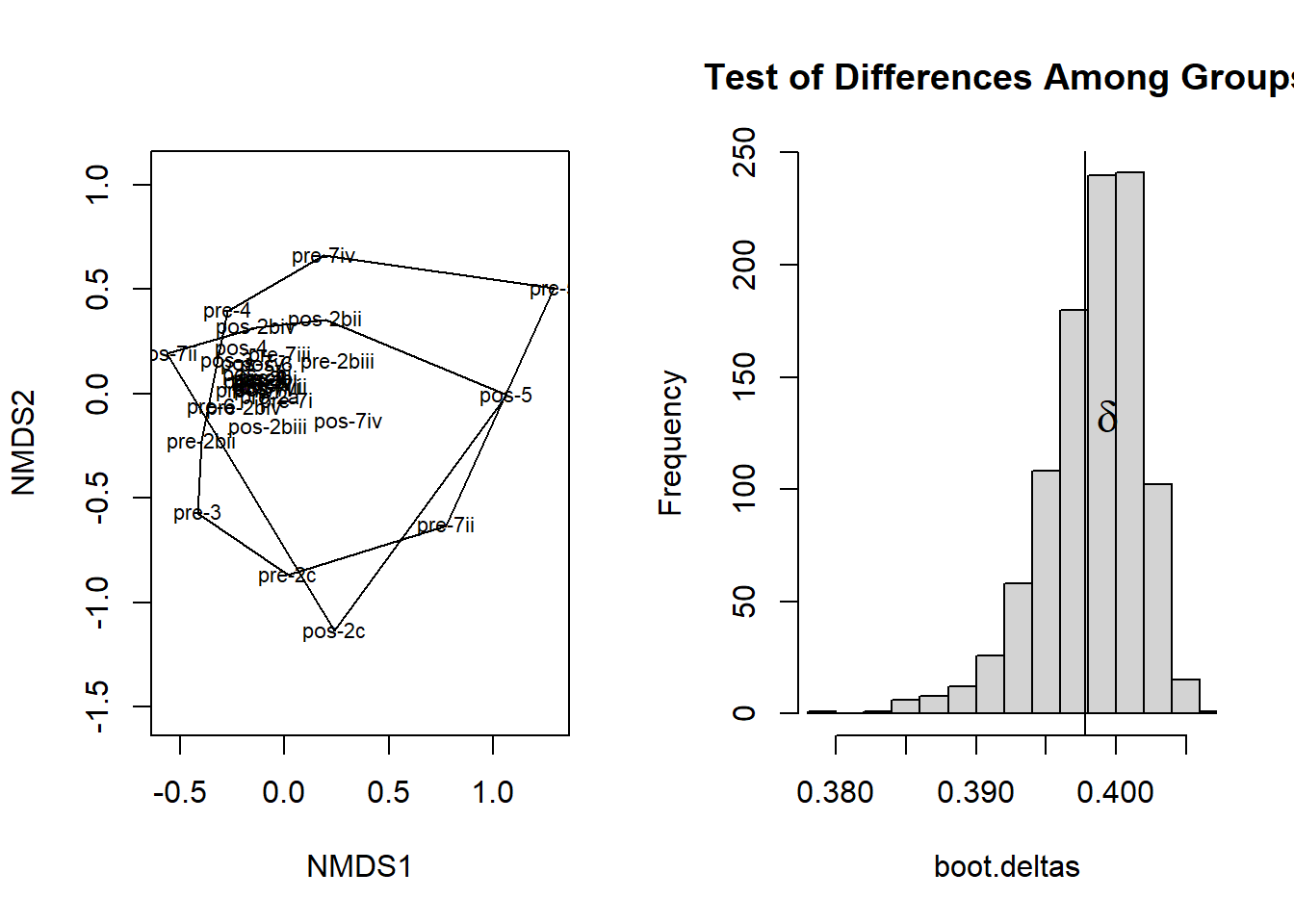
1.6.2.1 Agrupamento 1 (pré vs. pós)
# Save and change plotting parameters
def.par <- par(no.readonly = TRUE)
layout(matrix(1:2,nr=1))
set.seed(1234567890)
plot(ord <- metaMDS(m_sum), type="text", display="sites" )
with(m_sum_grp, ordihull(ord, Grupo1))
with(mrpp1, {
fig.dist <- hist(boot.deltas, xlim=range(c(delta,boot.deltas)),
main="Test of Differences Among Groups")
abline(v=delta);
text(delta, 2*mean(fig.dist$counts), adj = -0.5,
expression(bold(delta)), cex=1.5 ) }
)
par(def.par)
## meandist
md <- with(m_sum_grp, meandist(vegdist(m_sum), Grupo1))
md
summary(md)
par(mfrow=c(1,2))
plot(md)
plot(md, kind="histogram")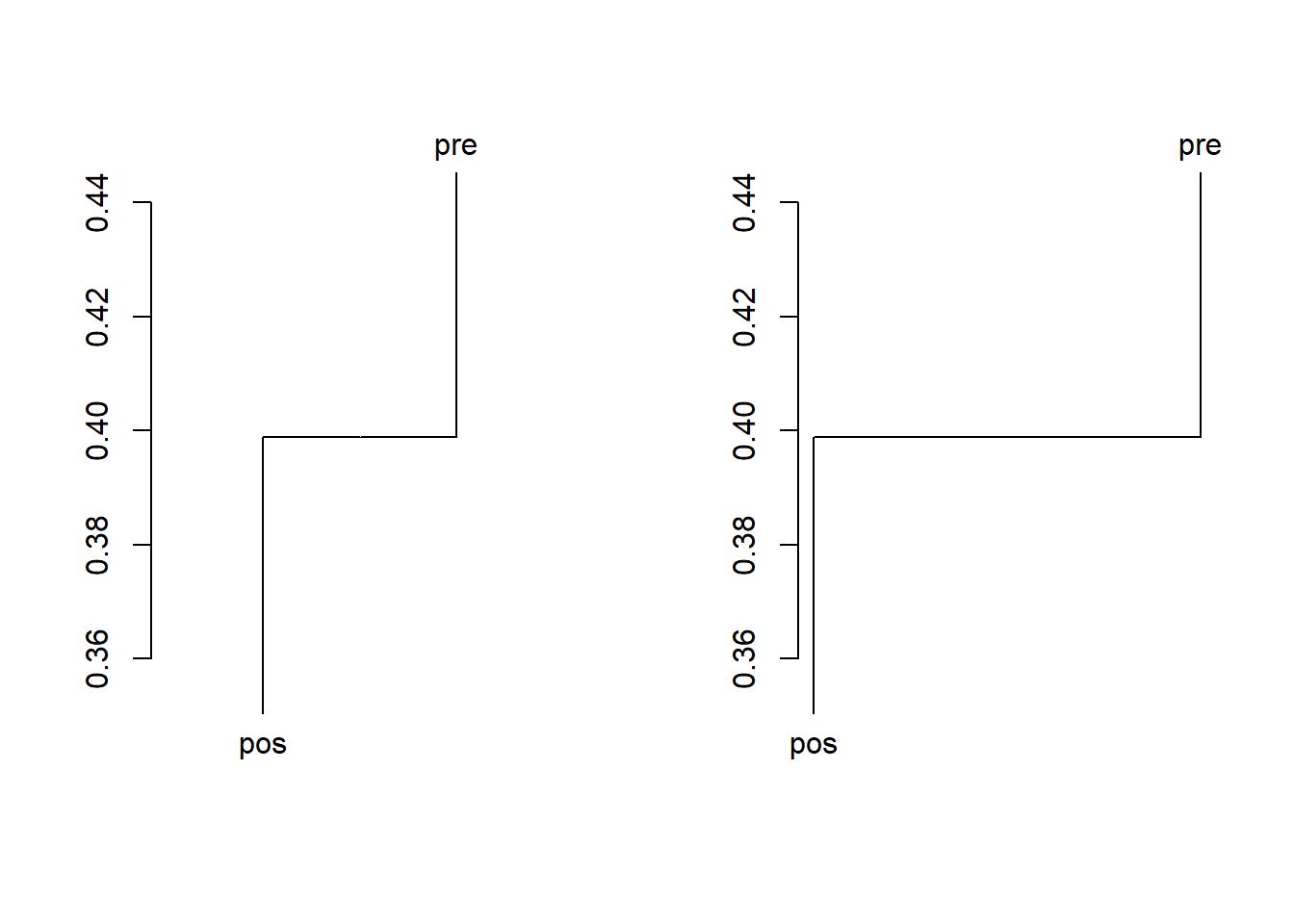
## Run 0 stress 0.1650654
## Run 1 stress 0.1817589
## Run 2 stress 0.1744961
## Run 3 stress 0.1788412
## Run 4 stress 0.1712839
## Run 5 stress 0.1731923
## Run 6 stress 0.1652816
## ... Procrustes: rmse 0.009049487 max resid 0.04888196
## Run 7 stress 0.1776972
## Run 8 stress 0.1784241
## Run 9 stress 0.1658834
## Run 10 stress 0.1827128
## Run 11 stress 0.2012255
## Run 12 stress 0.1652819
## ... Procrustes: rmse 0.009061044 max resid 0.04888896
## Run 13 stress 0.195388
## Run 14 stress 0.1864688
## Run 15 stress 0.1947367
## Run 16 stress 0.1801264
## Run 17 stress 0.2034202
## Run 18 stress 0.1723159
## Run 19 stress 0.1768435
## Run 20 stress 0.1836952
## *** Best solution was not repeated -- monoMDS stopping criteria:
## 1: no. of iterations >= maxit
## 19: stress ratio > sratmax
## pos pre
## pos 0.3503681 0.3989295
## pre 0.3989295 0.4452180
## attr(,"class")
## [1] "meandist" "matrix"
## attr(,"n")
## grouping
## pos pre
## 17 17
##
## Mean distances:
## Average
## within groups 0.3977931
## between groups 0.3989295
## overall 0.3983785
##
## Summary statistics:
## Statistic
## MRPP A weights n 0.001469563
## MRPP A weights n-1 0.001469563
## MRPP A weights n(n-1) 0.001469563
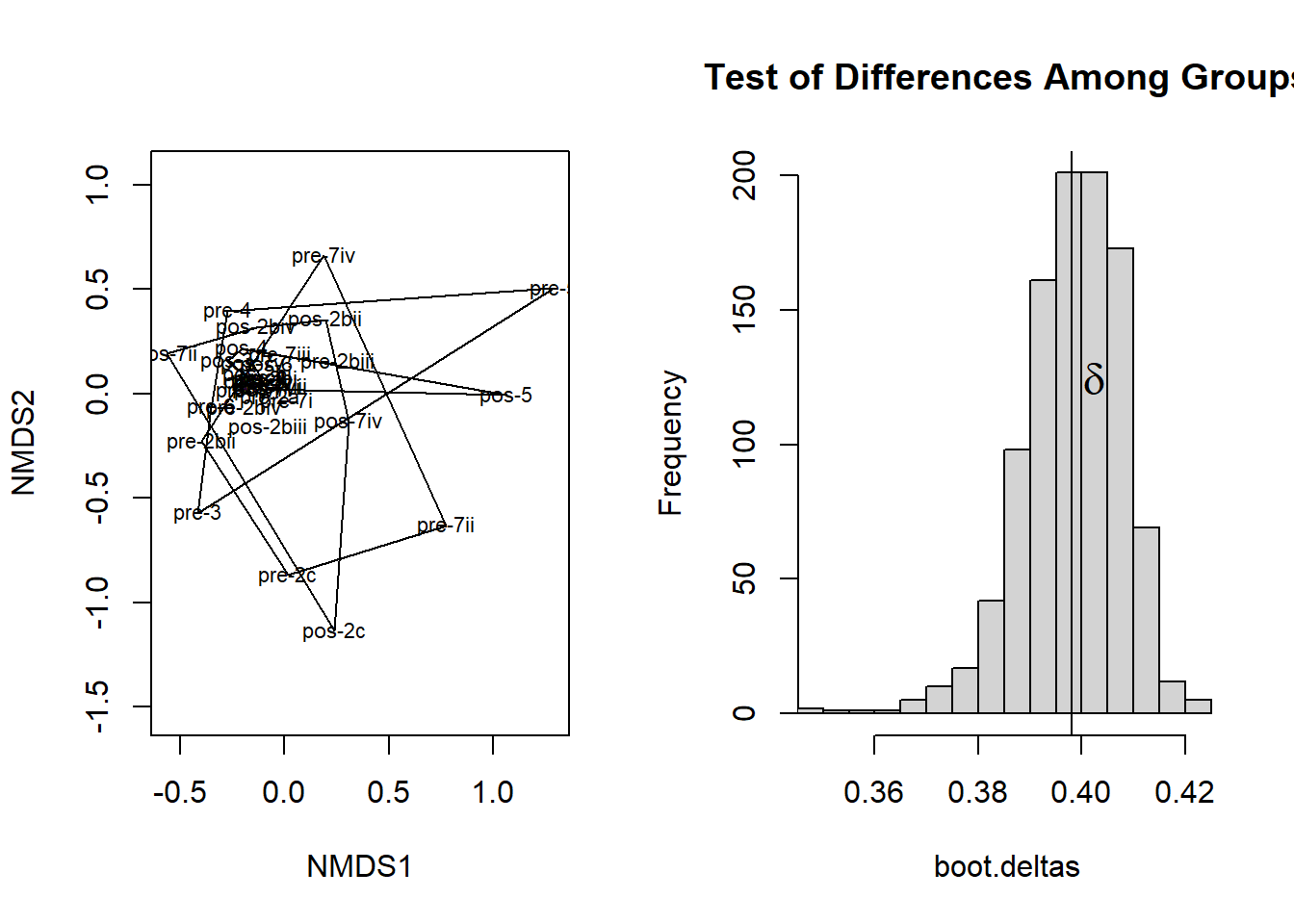
## Classification strength 0.0011364471.6.2.2 Agrupamento 3 (tipos de questões: a, b, c)
# Save and change plotting parameters
def.par <- par(no.readonly = TRUE)
layout(matrix(1:2,nr=1))
plot(ord <- metaMDS(m_sum), type="text", display="sites" )
with(m_sum_grp, ordihull(ord, Grupo2))
with(mrpp2, {
fig.dist <- hist(boot.deltas, xlim=range(c(delta,boot.deltas)),
main="Test of Differences Among Groups")
abline(v=delta);
text(delta, 2*mean(fig.dist$counts), adj = -0.5,
expression(bold(delta)), cex=1.5 ) }
)
par(def.par)
## meandist
md <- with(m_sum_grp, meandist(vegdist(m_sum), Grupo2))
md
summary(md)
par(mfrow=c(1,2))
plot(md)
plot(md, kind="histogram")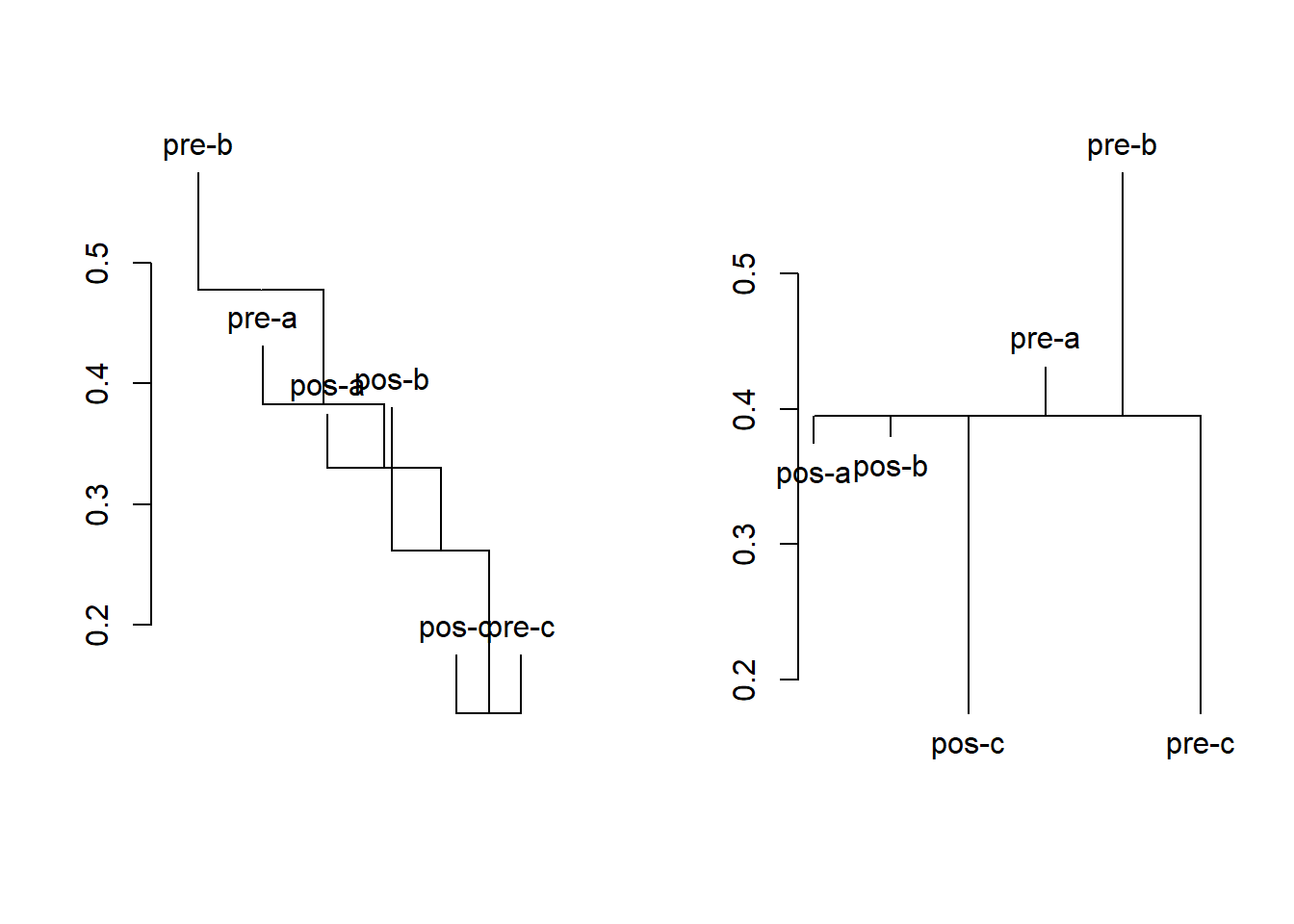
## Run 0 stress 0.1650654
## Run 1 stress 0.1697742
## Run 2 stress 0.1894365
## Run 3 stress 0.1804592
## Run 4 stress 0.1658963
## Run 5 stress 0.1838039
## Run 6 stress 0.1917953
## Run 7 stress 0.170931
## Run 8 stress 0.1850238
## Run 9 stress 0.1712842
## Run 10 stress 0.1658846
## Run 11 stress 0.1801839
## Run 12 stress 0.1899631
## Run 13 stress 0.1801077
## Run 14 stress 0.1720452
## Run 15 stress 0.1674728
## Run 16 stress 0.1652817
## ... Procrustes: rmse 0.009047799 max resid 0.04889333
## Run 17 stress 0.16979
## Run 18 stress 0.1788366
## Run 19 stress 0.1855577
## Run 20 stress 0.1769431
## *** Best solution was not repeated -- monoMDS stopping criteria:
## 3: no. of iterations >= maxit
## 17: stress ratio > sratmax
## pos-a pos-b pos-c pre-a pre-b pre-c
## pos-a 0.3750111 0.3746484 0.2776240 0.3946216 0.4930180 0.2707535
## pos-b 0.3746484 0.3799422 0.2515239 0.4167868 0.4620283 0.2711985
## pos-c 0.2776240 0.2515239 0.1750000 0.3141893 0.3870520 0.1265397
## pre-a 0.3946216 0.4167868 0.3141893 0.4314576 0.5023866 0.3040554
## pre-b 0.4930180 0.4620283 0.3870520 0.5023866 0.5744519 0.4014099
## pre-c 0.2707535 0.2711985 0.1265397 0.3040554 0.4014099 0.1750000
## attr(,"class")
## [1] "meandist" "matrix"
## attr(,"n")
## grouping
## pos-a pos-b pos-c pre-a pre-b pre-c
## 10 5 2 10 5 2
##
## Mean distances:
## Average
## within groups 0.4123664
## between groups 0.3948893
## overall 0.3983785
##
## Summary statistics:
## Statistic
## MRPP A weights n 0.0006061969
## MRPP A weights n-1 -0.0243125982
## MRPP A weights n(n-1) -0.0351120448
## Classification strength -0.0032476867