Chapter 3 Measure Theory

측도론이란, 간단히 말하면 집합의 크기를 측정하기 위한 학문입니다. 특히, 함수공간과 확률공간 같이 추상적인 공간을 다룰 때에 중요한 학문이죠.

우리는 흔히 고등학교 과정에서 확률과 통계를 접하고는 확률을 다룰 수 있다라고 착각합니다. 예를 들어, 확률이란 무엇인가? 라는 질문에 대해서 보통 다음과 같은 정의를 인용할 것입니다.

Example 1 - High School Probability

Probability of occurrence of events \(A\) in sample space \(\Omega\) is \[ \mathbf{P}(A) = \frac{n(A)}{n(\Omega)}\]

위의 정의를 이용하면 아주 간단명료하게 수학적 확률을 계산할 수 있습니다. 예를 들어, 주사위를 던졌을 때, 1이 나올 확률은 \(\left\{1,2,3,4,5,6 \right\}\)을 전체집합으로 설정하면 전체 6개 중에 1이 발생할 사건은 1개이기에 확률은 \(\frac{1}{6}\)이 됩니다. 하지만, 다음의 경우에는 난처해집니다.

Example 2 - Common High School Problem

정사각형 과녁 안에 원 모양 과녁이 네 변에 모두 내접하여 있을 때, 화살이 원 안에 명중할 확률을 구하여라.

간단한 확률 지식이 있는 사람이라면 이 문제를 \(\frac{\text{원의 넓이}}{\text{전체 정사각형의 넓이}}\)로 접근하여 \(\frac{\pi}{4}\)임을 알아낼 수 있을 것입니다. 그런데 이는 앞에서의 정의와 대치됩니다. 분명 우리가 배운 정의에 의하면 사건이 발생할 경우의 수를 전체 경우의 수로 나누어 구해야 하는데, 전체 경우의 수는 얼마일까요? 하다 못해 원의 경우의 수는 어떻게 접근해야 할까요? 우리는 지금까지 아무런 의심 없이 구해왔습니다만, 이제부터 의심을 가질 필요가 있습니다. 확률은 특정 경우에서는 경우의 수 문제로 치환될 수 있지만, 집합이 무한해지는 순간 우리가 정의한 확률에 부합하지 않게 됩니다. 따라서 우리는 확률을 보다 엄밀하게 정의해야할 필요가 있습니다. 그리고 그것을 위해서는 먼저 집합의 크기를 정의해야 합니다. 바로 이를 위해서 측도론이 필요한 것입니다.

이제 측도론의 필요성은 잘 알았지만, 측도론은 상당히 추상적인 학문이라 곧바로 집합의 크기를 정의내릴 수는 없습니다. 집합의 크기가 무엇이다 말하기 전에 측정 가능한 집합에 대해서 먼저 논의해봅시다. 일단, 측정도 모르고 측정 가능성도 모르겠지만 일단 어떤 집합 \(U, V\)가 크기를 잴 수 있는 집합(가측집합; Measurable Set)이라 전제해봅시다. 그렇다면 직관적으로 다음의 사실들을 받아 들일 수 있습니다.

• \(U\cup V\) is measurable
• \(U \cap V\) is measurable
• \(U^c,~ V^c\) is measurable

하지만 수학자들은 이런 모호한 직관으로서의 정의를 좋아하지 않습니다. 이런 규칙들을 모아 좀 더 엄밀한 표현으로 바꾸어 하나의 우아한 규칙으로 정의내리고 받아들입니다. 수학에서 이러한 규칙을 대수(Algebra)라고 부릅니다.

3.1 Sigma-algebra

Definition 1 - \(\sigma\)-algebra

Let \(S\) be a set, and let \(\mathcal{F}\) be a family of subsets of \(S\). \(\mathcal{F}\) is called a \(\sigma\)-algebra if 1. \(\emptyset \in \mathcal{F}\) 2. \(A \in \mathcal{F}\) implies \(A^c \in \mathcal{F}\) 3. \(A_1, A_2,\cdots \in \mathcal{F}\) implies \(\bigcup_{i=1}^\infty A_i \in \mathcal{F}\)

정의는 무척 복잡해보이지만, 사실 의미 자체는 간단합니다. 대수는 일종의 규칙을 담아 놓은 집합입니다. 예를 들어, 위상수학에서의 Topology는 모든 열린 집합들의 집합이고, 여기서 말하는 \(\sigma\)-algebra(시그마대수)는 모든 가측집합들의 집합입니다. 정의자체도 하나씩 살펴보면 충분히 납득이 가능합니다. 공집합은 당연하게도 크기가 0일 것이므로 측정가능한 집합이며, 어떤 집합 \(A\)가 측정가능하다면 (이를 수학에서는 \(A\in\mathcal{F}\)라 표현합니다.) 그의 여집합 또한 측정할 수 있을 것입니다. 마지막으로 측정 가능한 집합들의 합집합 또한 측정 가능할 것입니다. 이 외에도 전체집합이 측정가능하다는 사실을 1번과 2번 정의로부터 이끌어낼 수 있고, 2번과 3번 정의를 이용하면 합집합 뿐만 아니라 교집합 또한 측정 가능하다는 사실을 유추해낼 수 있습니다.

이제 대수를 정의하였으니 우리가 다룰 공간을 명시해봅시다.

Definition 2 - Measurable Space

Let \(S\) be a set, and let \(\mathcal{F}\) be a \(\sigma\)-algebra of subsets of \(S\). Then \((S, \mathcal{F})\) is called a measurable space. The elements of \(\mathcal{F}\) are called measurable sets.

이제 기본 틀은 정리했으니 적응하기 위하여 조금 더 생각을 해봅시다. 어떤 집합 \(S\)에 대하여 가장 작은 \(\sigma\)-algebra와 가장 큰 \(\sigma\)-algebra는 뭘까요? 일단, 정의에 의해 공집합은 무조건 측정가능하고 두 번째 정의에 의해 전체집합도 측정가능하므로 가장 작은 시그마대수는 \(\mathcal{F} = \left\{\emptyset, S \right\}\)가 됩니다. 또한 시그마 대수는 어떤 집합의 부분집합의 모임이기 때문에 모든 부분집합의 집합(멱집합; Power set)이 가장 큰 시그마 대수가 될 것입니다. 이는 \(\mathcal{F} = \mathcal{P}(S)\)로 표기합니다.

고등학교 시절에 부분집합을 배울 때, 어떤 집합을 포함하는 부분집합의 개수는? 이라는 문제를 본 적이 있을 겁니다. 되게 의미 없는 일 같지만 수학에서는 어떤 집합을 포함하고 있는 지의 여부가 상당히 중요합니다. 시그마 대수에서도 마찬가지인데 어떤 집합을 반드시 포함하고 있는 시그마 대수를 “그 집합에 의하여 발생한 시그마 대수이다” 라고 정의할 것입니다. 수학적 정의는 다음과 같습니다.

Definition 3 - Generated \(\sigma\)-algebra

Let \(S\) be a set and \(G\) be a family of subsets of \(S\). The smallest \(\sigma\)-algbera which contains \(G\) is called generated \(\sigma\)-algebra with respect to \(G\) denoted by \(\sigma(G)\).

이제 이 정의를 아주 유명한 규칙 공간에 적용해보겠습니다. 바로 위상공간(Topological Space)에 말이죠.

Definition 4 - Borel \(\sigma\)-algebra

The Borel \(\sigma\)-algebra \(\mathcal{B}\) of a topological space \((S, \mathcal{T})\) is the \(\sigma\)-algebra generated by \(\mathcal{T}\).

위 정의를 이해하기 위하여 굳이 위상수학까지 공부하지 않아도 됩니다. (물론, 하면 좋지만요.) 우리는 앞으로 관측 공간인 \(\mathbb{R}^d\)에서의 대수만 사용할 것이기 때문이죠. 간단히 말하자면 \(n\)차원 실수공간의 위상은 \(n\)차원 직육면체로 표현됩니다. 1차원에서는 직선, 2차원에서는 직사각형 이런 식이죠. 따라서 위의 정의에 따르면 이런 직사각형들이 모두 측정가능하다면, 그 공간을 일컬어 Borel \(\sigma\)-algebra 가 존재하는 공간이라 합니다.

지금까지는 공간, 집합에 대해서만 다뤘는데, 정작 가장 중요하게 다룰 것은 그 공간과 집합에 작용하는 함수입니다. 위상수학이나 해석학을 배웠다면 다음의 정의는 아주 쉽게 다가올 것입니다만, 하지 않았더라도 받아들이면 큰 문제는 없습니다.

Definition 5 - Measurable function

Let \((S, \mathcal{F})\), \((S', \mathcal{F}')\) be measurable spaces and \(f:\, S \rightarrow S'\). If \(\forall X \in \mathcal{F}'\), \(f^{-1}(X) \in \mathcal{F}\) then \(f\) is called measurable function.

이 정의를 어떻게 사용하는지 간단한 예시로 설명해보겠습니다.

Definition 6 - Indicator function

The indicator function of a subset \(A\) of a set \(X\) is a function \[I_A(x): \, X \rightarrow \left\{0, 1 \right\}\] defined as \[I_A(x) \equiv \begin{cases} 1 & \text{if } x \in A, \\ 0 & \text{if } x \neq A. \end{cases}\]

Example 3 - Indicator function is measurable

Let \(A\in\mathcal{F}\) then \(I_A\) is measurable function.

위 예시의 증명은 아주 간단하므로 생략하겠습니다. 한 번 해보고 넘어가면 이해가 잘 될테니 꼭 해보시길 바랍니다. 이제 측정가능성은 대부분 논의했으니 진정한 목표인 측도로 가봅시다.

3.2 Measure

Definition 7 - Measure

Let \((S,\mathcal{F})\) be measurable space and let \(\mu:\, \mathcal{F} \rightarrow [0,\infty)\) be a function. \(\mu\) is measure on \(\mathcal{F}\) if 1. \(\mu(\emptyset) = 0\) 2. \(\mu\) is \(\sigma\)-additive. That is, for disjoint family \(\left\{A_i \right\}_{i=1}^\infty \in \mathcal{F}\), \[\mu \left(\bigcup_{i=1}^\infty A_i\right) = \sum_{i=1}^\infty \mu(A_i)\]

정의는 아주 자명합니다. 비록 크기가 무엇인지 감이 잘 오진 않더라도 공집합의 크기는 반드시 0일 것이며 전혀 겹치지 않는 집합들의 합집합의 크기는 각 집합들의 크기의 합과 같을 것입니다. 또한 위 정의에서 유심히 보아야 할 부분은 \(\mu\) 즉, 측도가 측정가능한 집합을 음이 아닌 값의 실수로 보내는 함수라는 것입니다. 우리는 음의 부피를 정의하지 않고 또한 음의 확률을 정의하지 않습니다. 사실 너무나 당연하게 써 왔던 이러한 사실을 측도라는 비교적 간단한 정의를 이용하여 수학적으로 못 박아둔 것이죠. 이제 측도도 생겼으니 새로운 공간을 정의하여 봅시다.

Definition 8 - Measure space

The triple \((S, \mathcal{F}, \mu)\) is a measure space if \((S,\mathcal{F})\) is a measurable space and \(\mu\) is a measure on \(\mathcal{F}\).

순수 수학자들이 아닌 이상 응용수학이나 물리, 통계학에서는 측정 가능성도 꽤 중요하겠지만 더욱 중요한 것은 정확히 측정하는 것입니다. 따라서 이제부터는 새로 정의한 측도공간(Measure Space) 을 사용할 것입니다. 이러한 측도 공간에서도 \(n\)차원 실수 공간은 특히 더욱 중요해서 따로 이름을 붙입니다.

Definition 9 - Lebesgue measure

The Lebesgue measure \(\lambda\) on \(\mathbb{R}^d\) is a measure on the Borel \(\sigma\)-algebra of \(\mathbb{R}^d\) such that the \(\lambda\) measure of each rectangle equals to its volume.

정의는 조금 복잡할지라도 의미는 간단합니다. 직육면체의 부피를 측정하는 측도를 르벡 측도(Lebesgue measure)라고 부른다는 것이죠. Lebesgue의 이름은 수학 어디서나 등장하기 때문에 익숙해지는 것이 좋습니다. 이제 측도도 생겼으니 본격적으로 집합의 크기를 측정해봅시다. 물론, 처음부터 복잡한 함 수로 표현되는 공간의 크기를 구하기란 아주 어려운 일이므로, 우리는 아주 단순한 함수부터 시작해서 일반화하는 방향으로 접근할 것입니다.

Definition 10 - Simple function

A function, which image is finite, is called simple function.

Property 1 - Simple function with indicator function

If \(\varphi: \chi \rightarrow \mathbb{R}\) is simple function then we can write \[\varphi = \sum_{i=1}^n a_i I_{E_i}\] where \(\left\{a_i \right\}\) is image of \(\varphi\) and \(E_i = \varphi^{-1}(\left\{a_i \right\})\).

수학에서 사용되는 전형적인 단순한 함수는 바로 위에서 정의한 Simple function입니다. 사실 본래 정의는 매우 간단하지만, 보통 Simple function이라 하면 대개 Property 1을 생각합니다. 대체 이 함수가 뭐가 단순한건지 의아하겠지만, 이러한 함수에 대해서는 적분을 아주 쉽게 정의할 수 있습니다.

Definition 11 - Lebesgue integral for simple function

Let \((S,\mathcal{F}, \mu)\) be measure space and \(\displaystyle f = \sum_{i=1}^n a_i I_{E_i}\) be a simple function. Then the Lebesgue Integral of \(f\) with respect to \(\mu\) is defined by \[ \int_S f d\mu = \sum_{i=1}^n a_i \mu(E_i) \]

분명 정의는 했는데 대체 무슨 뜻인지 의아할 수 있으므로 쉽게 예시를 들어봅시다.

Example 4 - Example of Lebesgue integral for simple function

\(f\) is a simple function given as: \[f = \begin{cases} 1 & \text{if } 0 \leq x < 1 \\ 2 & \text{if } 1 \leq x < 3 \\ 3 & \text{if } 3 \leq x < 4 \\ 0 & \text{otherwise} \end{cases}\] then find integral of \(f \in \mathbb{R}\).

이 문제는 직사각형의 넓이만 구할 수 있으면 아주 쉽게 구할 수 있습니다. 일단 위 함수를 그리면 다음과 같습니다.

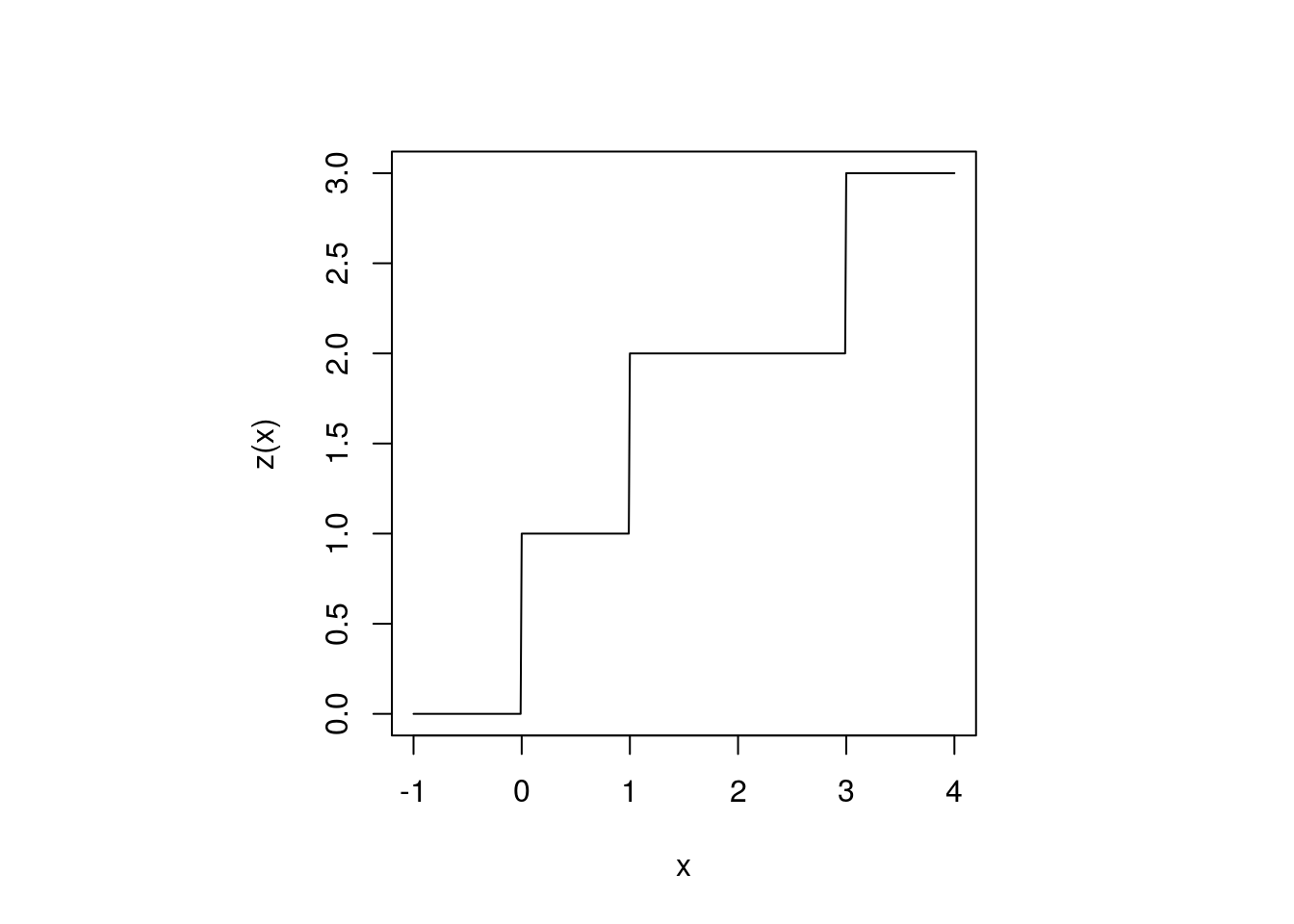
Figure 3.1: Simple function example

이 함수를 Indicator function을 이용하여 식으로 구해보면 다음과 같습니다.

\[f(x) = 1 \times I_{E_1} + 2 \times I_{E_2} + 3 \times I_{E_3}\]

이때, \(E_1, E_2, E_3\)는 각각 \([0, 1),\, [1, 3),\, [3, 4)\)입니다. 이제 앞에서 정의했던대로 이 함수의 르벡 적분(Lebesgue Integral)을 구해보면 쉽게 답을 얻을 수 있습니다.

\[ \int_{\mathbb{R}} f d\mu = \sum_{i=1}^3 a_i \mu(E_i) = 1\times 1 + 2\times 2 + 3\times 1 = 8\]

식을 자세히 보면 그저 직사각형의 넓이들을 더한 값과 같다는 것을 알 수 있습니다. 이렇게보면 굳이 쉬운 문제를 어렵게 푸는 것 같아 보이지만, 르벡 적분의 의의는 이런 단순한 함수 뿐만 아니라, 무한한 집합이나 추상적인 집합에 대해서도 적분 값을 구할 수 있다는 것입니다.

항상 이런 단순한 정의로 문제를 풀 수 있으면 좋겠지만 대다수의 경우에 함수들은 Simple function 으로 나타낼 수 없습니다. (간단히 연속함수의 예시만 봐도 알 수 있죠.) 따라서 우리는 기존 정의를 확장해야할 필요가 있습니다.

Definition 12 - Lebesgue integral for positive definite function

Let \((S, \mathcal{F}, \mu)\) be a measure space and \(f: S \rightarrow [0, \infty)\) is measurable, then the Lebesgue integral of \(f\) with respect to \(\mu\) is defined by \[\int_S f d\mu = \sup \left\{\int_S \varphi d\mu:~ \varphi \text{ is simple and measurable}, ~ 0\leq \varphi \leq f \right\}\]

위 정의를 보면 앞에서 왜 Simple function을 도입해야 했는지 납득이 될 것입니다. 마치 리만 적분(Riemann integral)에서 작은 직사각형들로 잘게 쪼개어 적분을 표현하듯이 르벡 적분에서는 함수를 최대한의 Simple function으로 쪼개어 적분합니다.

물론 위 정의에서는 양의 함수만 정의하기에 음의 함수까지도 정의를 확장해야 합니다.

Definition 13 - Lebesgue integral for arbitrary measurable function

Let \((S, \mathcal{F}, \mu)\) be a measure space and \(f:\, S\rightarrow \mathbb{R}\) is arbitrary measurable function. Then \[ \int_S f d\mu = \int_S f^{+}d\mu - \int_S f^{-}d\mu\] where \(f^{+} = \max \left\{f(x), 0 \right\},~ f^- = \max \left\{-f(x), 0 \right\}\).

다음은 르벡 적분의 주요 정리들입니다.

Theorem 1 - Beppo-Levy theorem

If \(f_n \rightarrow f~(\text{mod } \mu)\) in a monotone increasing way then \[\int \lim_{n\rightarrow \infty} f_n d\mu = \lim_{n \rightarrow \infty} \int f_n d\mu\]

Theorem 2 - Fatou’s lemma

Let \((S, \mathcal{F}, \mu)\) be a measure space and \(\forall n \in \mathbb{N},~f_n: S\rightarrow [0,\infty)\) be measurable function. Then \[ \int_S \underset{n\rightarrow\infty}{\text{liminf}} f_n d\mu \leq \underset{n\rightarrow \infty}{\text{liminf}} \int_S f_n d\mu \]

Theorem 3 - Lebesgue dominated convergence theorem

Let \((S, \mathcal{F}, \mu)\) be a measure space. Assume that \(f_n\rightarrow f~(\text{mod }\mu)\) and \(|f_n(s)| \leq g(s),~\forall s \in S, ~n\in\mathbb{N}\) where \(\displaystyle \int_S g d\mu < \infty\). Then \[\int_S f d\mu = \lim_{n\rightarrow \infty} \int_S f_n d\mu\]

위 정리들은 수학에서는 상당히 중요한 정리지만, 지금 당장 우리에게는 많이 필요한 것은 아니니 한 번 보고 넘어가면 충분합니다.

하지만 다음 정의들과 정리들은 꽤 중요하니 눈여겨 봐두시길 바랍니다.

Definition 14 - Induced measure

Let \((S, \mathcal{F}, \mu)\) be a measure space and \(f\) be a measurable function. Then \(f\) induces a measure \(\nu\) on the Borel \(\sigma\)-algebra \(\mathcal{B}\) \[\nu(B) = \mu(f^{-1}(B)),~\forall B \in \mathcal{B}\]

Theorem 4 - Change measure

Let \(\nu\) be measure on the Borel \(\sigma\)-algebra of \(\mathbb{R}\) and let \(f, g\) be measurable functions. Then \(\forall B \in \mathcal{B}\), \[\int_B g d\mu = \int_{f^{-1}(B)} g \circ f d\nu\]

Definition 15 - Product measure

Let \(\nu_1,\nu_2\) be measures on \((S_1,\mathcal{F}_1),~(S_2,\mathcal{F}_2)\). Let \((S, \mathcal{F})\) be measurable space such that \(S = S_1 \times S_2\) and \(\mathcal{F} = F_1 \times F_2\) whenever \(F_1 \in \mathcal{F}_1,~F_2 \in \mathcal{F}_2\). \(\nu\) is called the product measure of \(\nu_1, \nu_2\) on \(\mathcal{F}\) if \[\nu(F_1 \times F_2) = \nu(F_1) \times \nu(F_2)\]

Theorem 5 - Fubini’s theorem

Let \(h\) be a measurable function on the product space \((S,\mathcal{F})\) then \[\int_S h(u,v)d\mu = \int_{S_1}\left(\int_{S_2}h(u,v)d\nu_2\right)d\nu_1 = \int_{S_2}\left(\int_{S_1}h(u,v)d\nu_1\right)d\nu_2\]

위 정의와 정리들은 우리가 흔히 리만 적분에서 적분 변수를 변경할 때 사용했던 것과 비슷하므로 외우기는 쉬울 겁니다. 여기서는 굳이 증명이 필요치 않으니 생략하고 넘어가겠습니다.

그럼 이제 본격적으로 확률론의 세계로 들어가겠습니다.