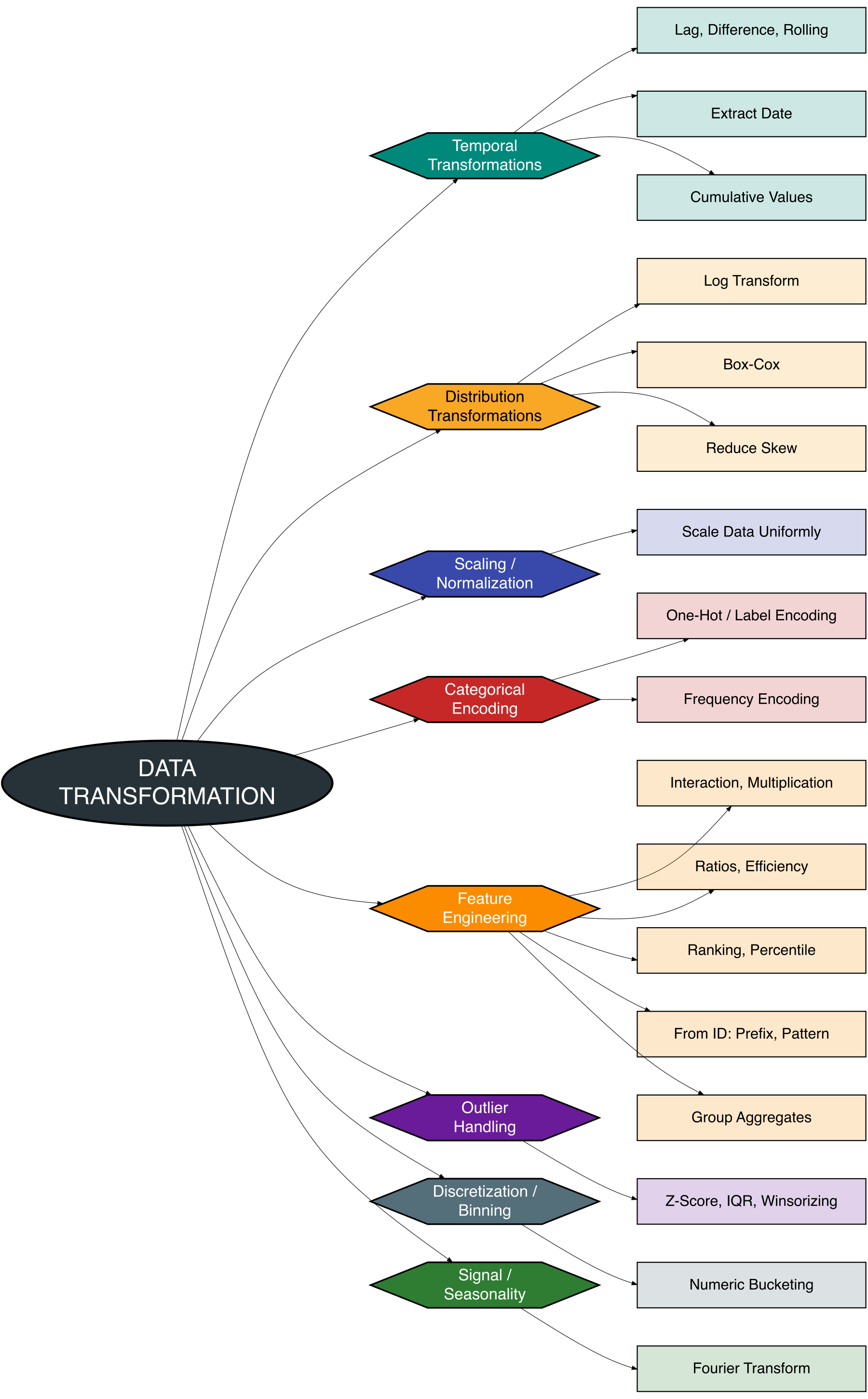
6 Data-Transformation
Data transformation is a crucial step in the data analysis process, aiming to convert raw data into more useful and meaningful information. This process involves various techniques to adjust data formats, improve data quality, and convert it into a form that is easier to analyze and interpret. Data transformation also plays an important role in enhancing the accuracy and effectiveness of analytical models, especially when dealing with large and complex datasets.
In the following mind map, we will explore various data transformation techniques that can be used to improve data quality and generate better insights. This mind map includes major categories such as:
Dummy Dataset
Below is a dummy business-related dataset created using R (demonstrated via Python). You can also generate it yourself in R using packages such as dplyr, lubridate, and stringi. This dataset simulates transaction data from a retail business with the following key elements:
| Column | Description |
|---|---|
Transaction_ID |
Unique ID for each transaction |
Transaction_Date |
Transaction date |
Customer_ID |
Unique customer ID |
Product_Category |
Product category (Electronics, Clothing, etc.) |
Product_ID |
Product ID |
Quantity |
Number of items purchased |
Unit_Price |
Price per product unit |
Discount |
Transaction discount (0–0.3) |
Region |
Region (North, South, East, West) |
Sales_Channel |
Sales channel (Online / Offline) |
Total_Price |
Total price after discount |
6.1 Temporal Transformations
Temporal transformations refer to techniques used to manipulate and extract meaningful patterns from time-based data. These transformations are essential when dealing with time series or datasets containing date and time information. The goal is to uncover trends, seasonal patterns, or lagged relationships that improve the predictive power of models.
Common temporal transformation techniques include:
- Lag, Difference, and Rolling: Capture temporal dependencies and smooth fluctuations.
- Extract Hour, Day, Weeek, Month, Year: Derive time-based features that often influence behavior or outcomes.
- Cumulative Sum / Count / Mean: Track running totals or averages over time for trend analysis.
These methods help structure time-based data in a way that enables deeper insights and improved decision-making.
6.1.1 Lag, Diff, Rolling
library(knitr)
# (Contoh untuk Quantity, berdasarkan tanggal transaksi)
Tempral <- data_bisnis %>%
arrange(Customer_ID, Transaction_Date) %>%
group_by(Customer_ID) %>%
mutate(
Lag_Quantity = lag(Quantity),
Diff_Quantity = Quantity - lag(Quantity),
RollingMean_3 = zoo::rollapply(Quantity, width = 3, FUN = mean, fill = NA, align = 'right')
) %>%
ungroup()
# Tampilkan 5 baris pertama
kable(head(Tempral,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Lag_Quantity | Diff_Quantity | RollingMean_3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1PaWvGiAokHB | 2023-02-09 | 02kNipUny9 | Groceries | P0253 | 3 | 13.11 | 0.07 | East | Offline | 10 | 36.58 | NA | NA | NA |
| IYlg0MAGwsUw | 2020-11-30 | 04npfK5VJa | Books | P0113 | 3 | 15.90 | 0.24 | North | Offline | 3 | 36.25 | NA | NA | NA |
| 0kgKWZOpEp6Z | 2020-03-18 | 0NwgTyo7P2 | Clothing | P0445 | 5 | 2.65 | 0.20 | North | Offline | 8 | 10.60 | NA | NA | NA |
| ddFsMFlQOa2J | 2023-05-19 | 0PlvCaxPuS | Electronics | P0298 | 3 | 9.12 | 0.20 | East | Online | 8 | 21.89 | NA | NA | NA |
| VOCzzxDOxQps | 2020-07-07 | 0S9qOEuCr9 | Clothing | P0353 | 3 | 1.31 | 0.12 | West | Online | 2 | 3.46 | NA | NA | NA |
6.1.2 Extract Date
Extract <- data_bisnis %>%
mutate(
Day_of_Week = weekdays(Transaction_Date),
Month = month(Transaction_Date, label = TRUE),
Year = year(Transaction_Date),
Is_Weekend = ifelse(Day_of_Week %in% c("Saturday", "Sunday"), 1, 0),
Region = as.factor(Region),
Product_Category = as.factor(Product_Category)
) %>%
bind_cols(
as.data.frame(model.matrix(~ Region - 1, data = .)),
as.data.frame(model.matrix(~ Product_Category - 1, data = .))
)
# Tampilkan 5 baris pertama
kable(head(Extract,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Day_of_Week | Month | Year | Is_Weekend | RegionEast | RegionNorth | RegionSouth | RegionWest | Product_CategoryBooks | Product_CategoryClothing | Product_CategoryElectronics | Product_CategoryGroceries | Product_CategoryHome |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | Wednesday | Jul | 2021 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | Monday | Nov | 2020 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | Wednesday | Mar | 2023 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | Monday | Jan | 2023 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | Monday | Jun | 2023 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
6.1.3 Cumulative Values
Cumulative <- data_bisnis %>%
group_by(Customer_ID) %>%
mutate(
Cumulative_Quantity = cumsum(Quantity),
Cumulative_Spend = cumsum(Total_Price),
Cumulative_AvgPrice = cummean(Unit_Price)
) %>%
ungroup()
# Tampilkan 5 baris pertama
kable(head(Cumulative,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Cumulative_Quantity | Cumulative_Spend | Cumulative_AvgPrice |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | 2 | 30.36 | 15.18 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | 5 | 43.44 | 10.22 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | 3 | 50.56 | 17.74 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | 6 | 132.44 | 28.30 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | 3 | 31.09 | 11.91 |
6.2 Distribution Tranformations
Distribution transformations are techniques used to modify the shape of a dataset’s distribution, making it more suitable for analysis or modeling. Many statistical models assume that data follows a normal distribution; therefore, transforming skewed or irregularly distributed data can lead to better model performance and more reliable insights.
Key distribution transformation techniques include:
- Log Transform: Compresses large values and reduces right-skewness.
- Box-Cox and Yeo-Johnson: Flexible transformations that stabilize variance and normalize data.
- Variance Stabilization / Skew Reduction: Improves symmetry and homoscedasticity in datasets.
These transformations are particularly useful when dealing with highly skewed data, outliers, or heteroscedastic variance, allowing for more robust and interpretable analyses.
6.2.1 Log Transform
min_positive <- min(data_bisnis$Total_Price[data_bisnis$Total_Price > 0])
Log <- data_bisnis %>%
mutate(
Safe_Total_Price = ifelse(Total_Price <= 0, min_positive, Total_Price),
Log_Total_Price = log1p(Safe_Total_Price)
)
# Tampilkan 5 baris pertama
kable(head(Log,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Safe_Total_Price | Log_Total_Price |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | 30.36 | 3.445533 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | 43.44 | 3.794140 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | 50.56 | 3.942746 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | 132.44 | 4.893652 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | 31.09 | 3.468545 |
6.2.2 Box-Cox
library(bestNormalize)
Box_Cox <- data_bisnis %>%
mutate(
YeoJ_Quantity = bestNormalize(Quantity)$x.t,
YeoJ_TotalPrice = bestNormalize(Total_Price)$x.t
)
# Tampilkan 5 baris pertama
kable(head(Box_Cox,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | YeoJ_Quantity | YeoJ_TotalPrice |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | -0.5858148 | -0.0570735 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | 0.9985763 | 0.4180569 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | 0.0025066 | 0.6480661 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | 1.5141019 | 2.6149565 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | 0.0025066 | -0.0282888 |
6.2.3 Stabilize Variance
6.3 Scaling & Normalization
Scaling and normalization are essential preprocessing steps in data transformation that ensure all numerical features contribute equally to model performance. These techniques adjust the range or distribution of data values, especially when features have different units or magnitudes.
Common techniques include:
- Min-Max Scaling: Rescales values to a fixed range (typically 0 to 1).
- Standardization (Z-score):Centers data around zero with unit variance.
- Robust Scaling: Uses median and IQR, making it more resistant to outliers.
Applying these transformations improves the convergence and accuracy of algorithms such as gradient descent and distance-based models (e.g., k-NN, SVM), which are sensitive to feature magnitude.
# Z-Score Standardization
data_std <- data_bisnis %>%
mutate(
Quantity_Std = scale(Quantity),
Unit_Price_Std = scale(Unit_Price)
)
# Tampilkan 5 baris pertama
kable(head(data_std,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Quantity_Std | Unit_Price_Std |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | -0.6497275 | 0.2623825 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | 1.0600817 | -0.6056456 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | -0.0797911 | 0.7103970 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | 1.6300181 | 2.5584570 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | -0.0797911 | -0.3098860 |
# Min-Max Normalization
data_norm <- data_bisnis %>%
mutate(
Quantity_Norm = (Quantity - min(Quantity)) / (max(Quantity) - min(Quantity)),
Total_Price_Norm = (Total_Price - min(Total_Price)) / (max(Total_Price) - min(Total_Price))
)
# Tampilkan 5 baris pertama
kable(head(data_norm,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Quantity_Norm | Total_Price_Norm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | 0.2222222 | 0.1848526 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | 0.5555556 | 0.2587259 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | 0.3333333 | 0.2989382 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | 0.6666667 | 0.7613803 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | 0.3333333 | 0.1889755 |
6.4 Categorical Encoding
Categorical encoding transforms non-numeric (categorical) variables into a numerical format that can be used by machine learning algorithms. Since most models cannot handle text or label data directly, encoding is crucial for integrating categorical features into predictive modeling.
Popular encoding techniques include:
- One-Hot Encoding: Creates binary columns for each category, useful for nominal data.
- Label Encoding: Assigns each category a unique integer, best for ordinal variables.
- Frequency Encoding: Replaces categories with their frequency or count in the dataset.
Choosing the right encoding method helps preserve the meaning of categorical data while maintaining model performance and interpretability.
6.4.1 One-hot Encoding
library(fastDummies)
one_hot <- dummy_cols(data_bisnis,
select_columns = c("Region",
"Sales_Channel",
"Product_Category"),
remove_first_dummy = TRUE,
remove_selected_columns = TRUE)
# Tampilkan 5 baris pertama
kable(head(one_hot,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_ID | Quantity | Unit_Price | Discount | Delivery_Time | Total_Price | Region_North | Region_South | Region_West | Sales_Channel_Online | Product_Category_Clothing | Product_Category_Electronics | Product_Category_Groceries | Product_Category_Home |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | P0370 | 2 | 15.18 | 0.00 | 5 | 30.36 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | P0185 | 5 | 10.22 | 0.15 | 2 | 43.44 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | P0443 | 3 | 17.74 | 0.05 | 8 | 50.56 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | P0035 | 6 | 28.30 | 0.22 | 8 | 132.44 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | P0375 | 3 | 11.91 | 0.13 | 7 | 31.09 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
6.4.2 Frequency Encoding
freq_enc <- function(col) {
tab <- table(col)
return(as.numeric(tab[col]) / length(col))
}
Frequency <- data_bisnis %>%
mutate(
Region_freq = freq_enc(Region),
Product_Category_freq = freq_enc(Product_Category)
)
# Tampilkan 5 baris pertama
kable(head(Frequency,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Region_freq | Product_Category_freq |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | 0.282 | 0.222 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | 0.240 | 0.176 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | 0.240 | 0.220 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | 0.282 | 0.220 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | 0.282 | 0.192 |
6.5 Feature Engineering
Feature engineering is the process of creating new input features from existing data to improve model performance. It involves extracting, transforming, or combining variables in ways that make patterns more accessible to machine learning algorithms.
Effective feature engineering often leads to significant boosts in model accuracy and interpretability, making it one of the most impactful steps in a data pipeline. Let’s consider the following feature engineering examples:
- Product of Features, Crossed Terms
- Price per Unit, Efficiency
- Ranking, Percentile
- From IDs: Prefix, Length, Pattern
- Avg, Sum, Count by Group
Feature_Eng <- data_bisnis %>%
# 1, 2, 3, 4, 5: Row-wise transformations
mutate(
Price_per_Unit = Total_Price / Quantity, # 2. Price per Unit
Efficiency = Quantity / Delivery_Time, # 2. Efficiency
Feature_Interaction = Quantity * Discount, # 1. Product of Features
Cross_Term = paste0(Product_Category, "_", Region),# 1. Crossed Term
ID_Prefix = substr(Product_ID, 1, 2), # 4. ID Prefix
ID_Length = nchar(Product_ID), # 5. ID Length
ID_HasPattern = grepl("^PR", Product_ID), # 5. Pattern Detection
Discount_Level = ntile(Discount, 4), # 3. Discount Percentile
Sales_Rank = rank(-Total_Price, ties.method = "min") # 3. Sales Ranking
) %>%
# 5: Group-wise aggregations
group_by(Region) %>%
mutate(
Avg_Quantity_Region = mean(Quantity, na.rm = TRUE),
Sum_Sales_Region = sum(Total_Price, na.rm = TRUE),
Count_Product_Region = n()
) %>%
ungroup()
# Tampilkan 5 baris pertama
kable(head(Feature_Eng,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Price_per_Unit | Efficiency | Feature_Interaction | Cross_Term | ID_Prefix | ID_Length | ID_HasPattern | Discount_Level | Sales_Rank | Avg_Quantity_Region | Sum_Sales_Region | Count_Product_Region |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | 15.18000 | 0.4000000 | 0.00 | Clothing_North | P0 | 5 | FALSE | 1 | 253 | 2.992908 | 4864.94 | 141 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | 8.68800 | 2.5000000 | 0.75 | Electronics_West | P0 | 5 | FALSE | 2 | 157 | 3.116667 | 4169.72 | 120 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | 16.85333 | 0.3750000 | 0.15 | Home_West | P0 | 5 | FALSE | 1 | 121 | 3.116667 | 4169.72 | 120 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | 22.07333 | 0.7500000 | 1.32 | Home_North | P0 | 5 | FALSE | 3 | 4 | 2.992908 | 4864.94 | 141 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | 10.36333 | 0.4285714 | 0.39 | Groceries_North | P0 | 5 | FALSE | 2 | 246 | 2.992908 | 4864.94 | 141 |
6.6 Outlier Handling
Outlier detection is an essential part of data preprocessing, especially when working with statistical modeling or machine learning. Outliers are data points that differ significantly from the rest of the dataset and can adversely affect model performance or assumptions. Identifying and handling outliers ensures more accurate predictions and insights. There are two common outlier detection methods:
- Z-score Method
- Interquartile Range (IQR) Method
Each method has its own strengths and is suited for different types of data. Let’s explore both.
6.6.1 Z-score Method
The Z-score method measures how many standard deviations a data point is from the mean. It is commonly used for identifying outliers in normally distributed data. If the Z-score of a data point exceeds a threshold (commonly 3 or -3), it can be considered an outlier.
Formula:
\[ Z = \frac{X - \mu}{\sigma} \]
Where:
- \(X\) is the data point.
- \(\mu\) is the mean of the data.
- \(\sigma\) is the standard deviation.
# Z-score method for detecting outliers
z_scores <- scale(data_bisnis$Quantity)
z_scores_outliers <- data_bisnis %>%
mutate(Outlier_Flag = ifelse(abs(z_scores) > 3, "Outlier", "Normal"))
# Tampilkan 5 baris pertama
kable(head(z_scores_outliers,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Outlier_Flag |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | Normal |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | Normal |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | Normal |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | Normal |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | Normal |
6.6.2 IQR method
The IQR method is a non-parametric approach to detecting outliers. It uses the quartiles (25th percentile, \(Q1\) and 75th percentile, \(Q3\)) to determine the spread of the middle 50% of the data. Any data point outside the range defined by:
Lower Bound:
\[ \text{Lower Bound} = Q1 - 1.5 \times \text{IQR} \]
Upper Bound:
\[ \text{Upper Bound} = Q3 + 1.5 \times \text{IQR} \]
is considered an outlier.
IQR Calculation:
\[ \text{IQR} = Q3 - Q1 \]
Where:
- \(Q1\): 25th percentile.
- \(Q3\): 75th percentile.
# IQR method for detecting and removing outliers
Q1 <- quantile(data_bisnis$Total_Price, 0.25) # Calculate the 25th percentile
Q3 <- quantile(data_bisnis$Total_Price, 0.75) # Calculate the 75th percentile
IQR_val <- Q3 - Q1 # Compute the IQR
# Remove outliers outside the IQR range
IQR_outliers <- data_bisnis %>%
filter(Total_Price > (Q1 - 1.5 * IQR_val) & Total_Price < (Q3 + 1.5 * IQR_val))
# Tampilkan 5 baris pertama
kable(head(IQR_outliers,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 |
| aI0KADT0mn7C | 2023-03-15 | YxqAmfTU9M | Clothing | P0447 | 1 | 5.43 | 0.07 | North | Offline | 9 | 5.05 |
Outliers Removed: This code removes any data points where the Total_Price is outside the range defined by \(Q1 - 1.5 \times \text{IQR}\) and \(Q3 + 1.5 \times \text{IQR}\).
6.7 Discretization
Discretization is the process of converting continuous numerical variables into discrete categories. This technique is useful for: - Simplifying models. - Identifying patterns. - Making data more interpretable for statistical analysis or visualization.
6.7.1 Fixed-Width Binning
Divides data into intervals with fixed width.
Quantity_Bin <- data_bisnis %>%
mutate(
Quantity_Bin = cut(Quantity, breaks = c(0, 2, 4, 6, Inf), labels = c("Low", "Medium", "High", "Very High"))
)
# Tampilkan 5 baris pertama
kable(head(Quantity_Bin,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Quantity_Bin |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | Low |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | High |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | Medium |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | High |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | Medium |
6.7.2 Quantile Binning
Divides data into bins with equal number of observations using quantiles (e.g., quartiles, deciles).
Quantile_Bin <- data_bisnis %>%
mutate(
Price_Bin_Quantile = ntile(Total_Price, 4) # Quartile binning
)
# Tampilkan 5 baris pertama
kable(head(Quantile_Bin,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Price_Bin_Quantile |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | 2 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | 3 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | 4 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | 4 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | 3 |
6.7.3 Custom Binning
Uses business rules or custom logic to define bins.
Custom_Bin <- data_bisnis %>%
mutate(
Discount_Level = case_when(
Discount == 0 ~ "No Discount",
Discount <= 0.1 ~ "Low",
Discount <= 0.2 ~ "Medium",
TRUE ~ "High"
)
)
# Tampilkan 5 baris pertama
kable(head(Custom_Bin,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Discount_Level |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | No Discount |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | Medium |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | Low |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | High |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | Medium |
6.8 Seasonality
Seasonality refers to periodic fluctuations in data that occur at regular time intervals, such as daily, monthly, or yearly patterns. In business and economic data, seasonal trends often reflect consumer behavior, holidays, weather patterns, and other recurring events.
6.8.1 Annual Seasonality
To capture yearly seasonality, we can use sine and cosine transformations of the day of the year. This approach embeds cyclical patterns into the data, helping models learn time-dependent behaviors.
library(lubridate)
library(dplyr)
Seasonality <- data_bisnis %>%
mutate(
Year = year(Transaction_Date),
DayOfYear = yday(Transaction_Date),
DaysInYear = if_else(leap_year(Transaction_Date), 366, 365),
sin_year = sin(2 * pi * DayOfYear / DaysInYear),
cos_year = cos(2 * pi * DayOfYear / DaysInYear)
)
# Tampilkan 5 baris pertama
kable(head(Seasonality,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Year | DayOfYear | DaysInYear | sin_year | cos_year |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | 2021 | 195 | 365 | -0.2135209 | -0.9769385 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | 2020 | 321 | 366 | -0.6979442 | 0.7161522 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | 2023 | 81 | 365 | 0.9844738 | 0.1755315 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | 2023 | 2 | 365 | 0.0344216 | 0.9994074 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | 2023 | 156 | 365 | 0.4405188 | -0.8977434 |
6.8.2 Linearity Over Time
Sometimes, patterns evolve in a linear fashion over time. Adding a simple time index or extracting the year from dates can help capture long-term trends:
Linearity <- Seasonality %>%
mutate(
Linearity = as.numeric(difftime(Transaction_Date, min(Transaction_Date), units = "days"))
)
# Tampilkan 5 baris pertama
kable(head(Linearity,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Year | DayOfYear | DaysInYear | sin_year | cos_year | Linearity |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | 2021 | 195 | 365 | -0.2135209 | -0.9769385 | 559 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | 2020 | 321 | 366 | -0.6979442 | 0.7161522 | 319 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | 2023 | 81 | 365 | 0.9844738 | 0.1755315 | 1175 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | 2023 | 2 | 365 | 0.0344216 | 0.9994074 | 1096 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | 2023 | 156 | 365 | 0.4405188 | -0.8977434 | 1250 |
6.8.3 Exponential Trends
Some trends grow or decay exponentially. For instance, rapid adoption or decay can be modeled with log or exponential transformations:
Exponential <- Linearity %>%
mutate(
Exp_Growth = exp(Linearity / 1000),
Log_Growth = log(Linearity + 1)
)
# Tampilkan 5 baris pertama
kable(head(Exponential,5))| Transaction_ID | Transaction_Date | Customer_ID | Product_Category | Product_ID | Quantity | Unit_Price | Discount | Region | Sales_Channel | Delivery_Time | Total_Price | Year | DayOfYear | DaysInYear | sin_year | cos_year | Linearity | Exp_Growth | Log_Growth |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7zmPHxF7XfN9 | 2021-07-14 | BAl3Y7yxev | Clothing | P0370 | 2 | 15.18 | 0.00 | North | Online | 5 | 30.36 | 2021 | 195 | 365 | -0.2135209 | -0.9769385 | 559 | 1.748923 | 6.327937 |
| y4bCY9pKTBWU | 2020-11-16 | TYY0h5C190 | Electronics | P0185 | 5 | 10.22 | 0.15 | West | Offline | 2 | 43.44 | 2020 | 321 | 366 | -0.6979442 | 0.7161522 | 319 | 1.375751 | 5.768321 |
| 8k0B7XX19Ykf | 2023-03-22 | nUX640AaXg | Home | P0443 | 3 | 17.74 | 0.05 | West | Online | 8 | 50.56 | 2023 | 81 | 365 | 0.9844738 | 0.1755315 | 1175 | 3.238143 | 7.069874 |
| l8ahQz5YNOKz | 2023-01-02 | sBZyUSJLEP | Home | P0035 | 6 | 28.30 | 0.22 | North | Offline | 8 | 132.44 | 2023 | 2 | 365 | 0.0344216 | 0.9994074 | 1096 | 2.992173 | 7.000335 |
| kmufgw8wx5qk | 2023-06-05 | GMfVH2ZWNX | Groceries | P0375 | 3 | 11.91 | 0.13 | North | Offline | 7 | 31.09 | 2023 | 156 | 365 | 0.4405188 | -0.8977434 | 1250 | 3.490343 | 7.131698 |
By combining cyclic seasonal patterns, linear trends, and exponential growth or decay, we can build rich feature sets that improve model performance in time-dependent data analysis.
- Sine/Cosine: capture cyclic behavior (e.g., yearly seasonality)
- Time Index: reflects linear trends
- Exponential/Log: model non-linear, accelerating, or decaying trends
6.9 Practicum
Your task is to demonstrate the various data transformation techniques that you have learned, including Temporal Transformations, Distribution Transformations, Scaling/Normalization, Categorical Encoding, Feature Engineering, Outlier Handling, Binning, Signal/Seasonality (Fourier), and other relevant transformations.
You will be divided into several groups, and each group will receive a dataset. Your objective is to apply the appropriate transformation techniques to the dataset, analyze the outcomes, and present your findings to the class.
6.9.1 Weather
Weather plays a critical role in shaping human activities, influencing agriculture, transportation, energy consumption, and even public health. Its variability across time and space makes it both fascinating and complex to study. As global awareness grows about climate change and extreme weather events, the need to understand and analyze weather data becomes increasingly important.
In this section, we introduce weather as a dataset-rich domain, where data science and statistical techniques are essential for extracting insights. Before we can build predictive models or generate visualizations, we must prepare and transform raw weather data into meaningful features.
To effectively analyze weather data, follow these key steps:
6.9.1.1 Import and Inspect the Data
- Load weather data from CSV, API, or database.
- Examine structure, date formats, and missing values.
6.9.1.2 Clean the Data
- Handle missing values (e.g., fill, remove, or impute).
- Standardize units (e.g., convert temperatures to Celsius or Fahrenheit).
- Parse datetime fields into usable components (e.g., year, month, day, hour).
6.9.1.3 Feature Engineering
- Derive new features such as:
- Daily, weekly, and monthly averages.
- Temperature change (lag or difference).
- Humidity Index or Heat Index.
- Wind direction in degrees or categories.
- Create cyclical features for seasonality using sine and cosine transformations:
\[ \text{sin\_year} = \sin\left(\frac{2\pi \cdot \text{DayOfYear}}{\text{DaysInYear}}\right) \]
\[ \text{cos\_year} = \cos\left(\frac{2\pi \cdot \text{DayOfYear}}{\text{DaysInYear}}\right) \]
6.9.1.4 Categorization and Binning
- Group continuous variables (e.g., rainfall intensity) into bins or labels.
- Define weather categories (e.g., “sunny”, “cloudy”, “stormy”) based on thresholds.
6.9.1.5 Detect and Handle Outliers
Use statistical methods to flag unusual values:
Z-score method: Mark values where \(|z| > 3\)
IQR method:
- Calculate:
\[ \text{IQR} = Q3 - Q1 \]
\[ \text{Lower Bound} = Q1 - 1.5 \times \text{IQR} \]
\[ \text{Upper Bound} = Q3 + 1.5 \times \text{IQR} \]
Decide whether to keep, transform, or remove outliers depending on context.
6.9.1.6 Temporal and Rolling Features
- Calculate rolling means or moving averages (e.g., 7-day temperature trends).
- Create lag variables to capture delayed effects (e.g., yesterday’s temperature).
6.9.1.7 Normalize or Scale Data
Apply standardization (Z-score) or Min-Max normalization to continuous variables for use in machine learning models.
6.9.2 General Health
General health encompasses the overall physical, mental, and social well-being of individuals and populations. With the increasing availability of health data—from electronic medical records and health surveys to wearable devices—data science plays a pivotal role in analyzing, predicting, and improving health outcomes.
Before we can apply machine learning models or conduct meaningful analyses, it’s essential to clean and transform raw health data into structured, analyzable features. Instructions for General Health Data Transformation
6.9.2.1 Import and Inspect the Dataset
- Load data from sources like public health records, surveys (e.g., BRFSS, NHANES), or hospital databases.
- Inspect structure, data types, and missing values.
6.9.2.2 Clean the Data
- Convert categorical variables (e.g., gender, smoking status) into factors.
- Handle missing or inconsistent entries (e.g., impute BMI or age if missing).
- Standardize units (e.g., weight in kg, height in cm).
6.9.2.3 Feature Engineering
- Create health risk indicators from raw inputs:
Body Mass Index (BMI):
\[ BMI = \frac{\text{Weight (kg)}}{\text{Height (m)}^2} \]
Age group classification: young, adult, elderly.
Chronic condition flag (e.g., has_diabetes = TRUE if glucose > threshold).
6.9.2.4 Categorization and Binning
- Convert numerical scores into health levels:
- Blood pressure into “normal”, “elevated”, “high”.
- Physical activity minutes into “low”, “moderate”, “high”.
- Create ordinal variables for satisfaction or self-rated health.
6.9.2.5 Detect and Handle Outliers
Use Z-score or IQR to detect abnormal values in clinical metrics (e.g., blood pressure, cholesterol):
IQR Calculation:
\[ IQR = Q3 - Q1 \]
\[ \text{Outlier Thresholds} = [Q1 - 1.5 \times IQR,\ Q3 + 1.5 \times IQR] \]
Consider domain knowledge before removing outliers (e.g., extremely high glucose may be valid for diabetic patients).
6.9.2.6 Temporal and Rolling Features
If longitudinal, compute:
- Changes in weight or BMI over time.
- Rolling averages of physical activity or vitals.
6.9.2.7 Encode Categorical Variables
Convert categories to numerical codes:
- One-hot encode lifestyle habits (smoking, drinking).
- Label encode ordered health levels.
6.9.2.8 Normalize or Scale Features
- Apply Z-score normalization to clinical measurements.
- Min-max scale features for use in neural networks.
6.9.3 Financial Market
Financial markets are dynamic systems where assets such as stocks, bonds, and derivatives are traded. Analyzing financial market data requires meticulous data preparation to extract meaningful insights. This involves cleaning, transforming, and engineering features from raw data to facilitate accurate analysis and modeling.
Before conducting financial modeling or applying machine learning to stock prices or indices, it’s critical to preprocess and transform raw financial data into meaningful, structured features. Below are the steps tailored for Financial Market Data Transformation.
6.9.3.1 Import and Inspect the Dataset
- Load data from CSV, APIs (e.g., Yahoo Finance), or financial terminals (e.g., Bloomberg, Refinitiv).
- Ensure date columns are in proper
Dateformat. - Check for missing values, incorrect symbols, or duplicate rows.
6.9.3.2 Clean the Data
- Remove non-trading days or fill missing prices using forward-fill.
- Ensure consistency of numeric types (
Open,High,Low,Close,Volume). - Filter for relevant date ranges or securities if needed.
6.9.3.3 Feature Engineering
Daily Return:
\[ \text{Return}_t = \frac{P_t - P_{t-1}}{P_{t-1}} \]
Log Return:
\[ \text{LogReturn}_t = \log\left(\frac{P_t}{P_{t-1}}\right) \]
Add lag features for past prices and returns.
6.9.3.4 Temporal and Rolling Features
Rolling mean (moving average) and volatility (rolling standard deviation):
\[ \text{RollingMean}_t = \frac{1}{n} \sum_{i=0}^{n-1} P_{t-i} \]
\[ \text{Volatility}_t = \sqrt{\frac{1}{n} \sum_{i=0}^{n-1} (R_{t-i} - \bar{R})^2} \]
Common rolling windows: 5, 20, 50, or 200 days.
6.9.3.5 Technical Indicators
- RSI (Relative Strength Index) – momentum indicator.
- MACD (Moving Average Convergence Divergence) – trend-following indicator.
- Bollinger Bands – measure price deviation from a moving average.
6.9.3.6 Categorization and Binning
- Classify returns into categories (e.g., “gain”, “loss”, “neutral”).
- Bin volatility into “low”, “medium”, “high” risk.
- Create flags for price crossing key moving averages.
6.9.3.7 Detect and Handle Outliers
Use statistical or financial logic:
Z-Score Method:
\[ Z = \frac{x - \mu}{\sigma} \]
IQR Method:
\[ IQR = Q3 - Q1 \]
\[ \text{Bounds} = [Q1 - 1.5 \times IQR,\ Q3 + 1.5 \times IQR] \]
Consider keeping extreme values if they represent market crashes or bubbles.
6.9.3.8 Encode Categorical Variables
Convert sector, ticker, or market to one-hot or label encoded values.
6.9.3.9 Normalize or Scale Features
- Z-score normalization for returns, volume, volatility.
- Min-max scaling for deep learning or neural models.
