2 Real Numbers
Understanding Real Numbers (\(\mathbb{R}\)) is the first step in exploring the world of real analysis. These numbers serve as the essential building blocks for calculus, algebra, numerical modeling, and various applied sciences. They provide a framework for representing quantities, measuring change, and describing continuous processes in both mathematics and real-world applications [1]–[3].
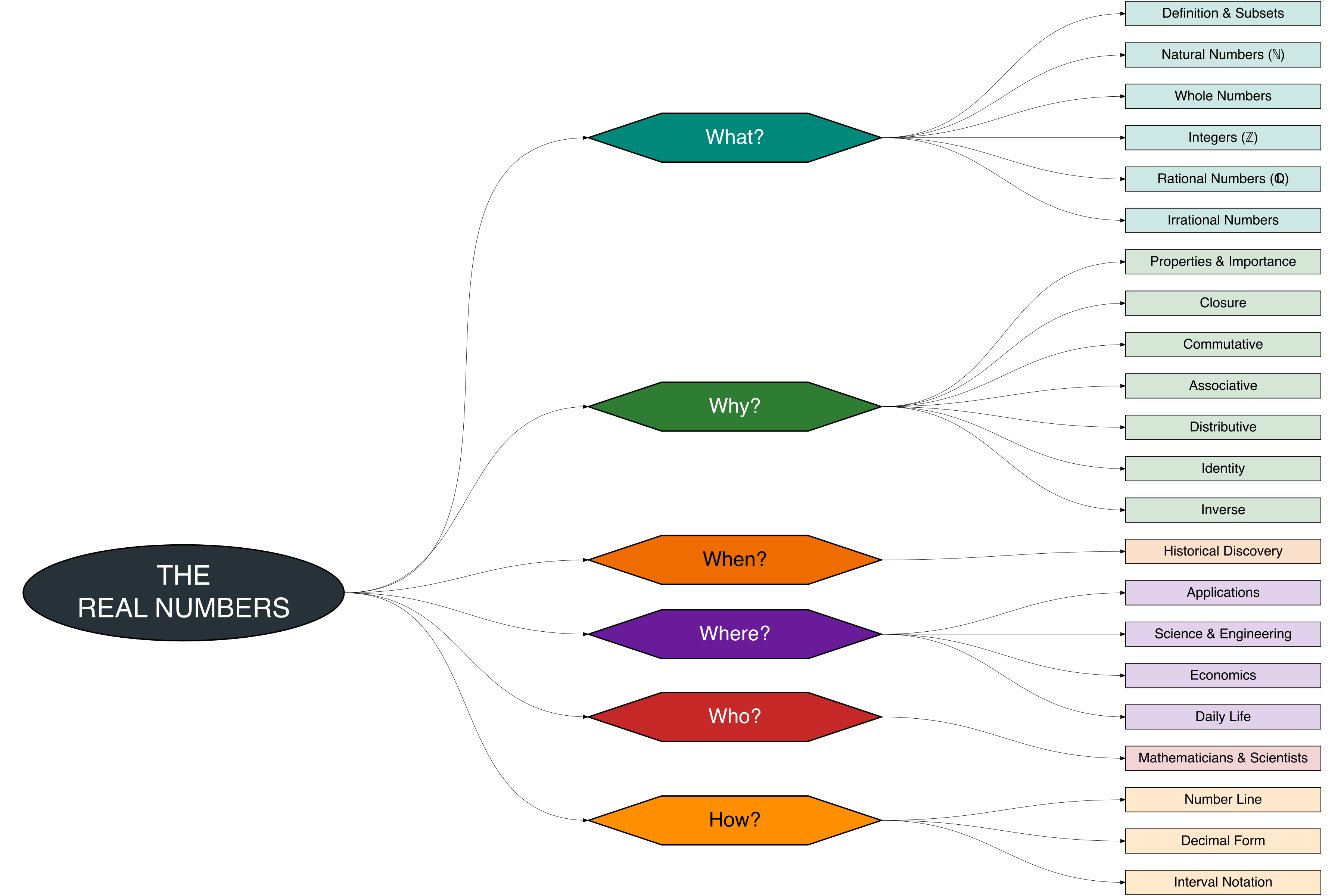
To help navigate the key aspects of real numbers, the Figure 2.1 offers a 5W+1H mind map. This visualization guides learners through the What—definitions and subsets; the Why—their importance and significance; the When—historical discoveries and formalization; the Where—applications in science, engineering, economics, and daily life; the Who—mathematicians and everyday users; and the How—representation on the number line, decimal forms, and intervals. By following this map, one can see not just the numbers themselves, but their role and relevance across disciplines.

The following Table 2.1 presents a structured summary of the 5W+1H questions related to Real Numbers, based on the Figure 2.1 mind map. It organizes the material into categories—What, Why, When, Where, Who, How—to guide learners in understanding the definitions, subsets, properties, number line representation, and applications of real numbers in science, engineering, economics, and daily life.
| Question | Notes |
|---|---|
| WHAT? | |
| What are real numbers (\(\mathbb{R}\))? | Definition of real numbers |
| What are the subsets of real numbers? | Natural, Whole, Integers, Rational, Irrational |
| What is the difference between rational and irrational numbers? | Rational can be expressed as p/q, irrational cannot |
| What are the key properties of real numbers? | Closure, Commutative, Associative, Distributive, Identity, Inverse |
| WHY? | |
| Why are real numbers important in mathematics? | Used in mathematics, science, engineering, daily life |
| Why do we need to know properties like closure and distributive law? | Ensures operations are valid within real numbers |
| Why are irrational numbers significant in science and engineering? | Irrational numbers appear in physics, geometry, engineering constants |
| WHEN? | |
| When were irrational numbers discovered? | Ancient Greek mathematicians discovered √2 |
| When did mathematicians formalize the set of real numbers? | Formalized in 19th century by Dedekind and Cantor |
| When do we use real numbers in real-life applications? | Used in measurement, finance, statistics, and computations |
| WHERE? | |
| Where are real numbers applied in science and engineering? | Physics formulas, engineering measurements, chemistry calculations |
| Where can real numbers be observed in daily life? | Counting, money, time, distances |
| Where in mathematics do we need to distinguish rational and irrational numbers? | Algebra, number theory, functions |
| WHO? | |
| Who were the key mathematicians in the development of real numbers? | Euclid, Cantor, Dedekind |
| Who uses real numbers most frequently in practical applications? | Scientists, engineers, mathematicians |
| Who introduced the concept of number line and interval representation? | Mathematicians formalized number line representation |
| HOW? | |
| How are real numbers represented on the number line? | Graphically as points on the number line |
| How do we write rational numbers in decimal form? | Terminating, repeating, or non-repeating decimals |
| How do we express intervals using real numbers? | Using [a,b] or (a,b) interval notation |
| How do real numbers help in calculations and problem-solving? | Supports problem solving and calculations in real-world scenarios |
2.1 Definition
The real numbers (\(\mathbb{R}\)) are the set of numbers that include both rational numbers (fractions of integers) and irrational numbers (numbers that cannot be expressed as fractions). They can be represented on the number line, which extends infinitely in both positive and negative directions [1], [2].
Formally: \[ \mathbb{R} = \{ x \mid x \text{ corresponds to a point on the number line} \}. \]
2.2 Subsets of Real Numbers
Real numbers (\(\mathbb{R}\)) consist of several subsets, each with distinct properties and applications. Understanding these subsets is fundamental in mathematics, physics, and engineering.
2.2.1 Natural Numbers (\(\mathbb{N}\))
Natural numbers are the set of positive counting numbers used for enumerating objects. Formally, the set of natural numbers is written as
\[ \mathbb{N} = \{1, 2, 3, 4, \dots\}. \]
Natural numbers have several important properties. They are always positive, and they are closed under addition and multiplication. However, they are not closed under subtraction or division; for example, \(2-3 \notin \mathbb{N}\). Some examples of natural numbers include \(1, 2, 3, 10, 100,\) and so on. These numbers are widely used in everyday life and in mathematics for counting discrete objects, numbering sequences, and performing basic arithmetic operations.
2.2.2 Whole Numbers
Whole numbers extend natural numbers by including zero. Formally, the set of whole numbers is written as
\[ \text{Whole Numbers} = \{0, 1, 2, 3, \dots\}. \]
Whole numbers have several important properties. They are non-negative and are closed under addition and multiplication. However, they are not closed under subtraction; for example, \(0-1 \notin \text{Whole Numbers}\). Some examples of whole numbers include \(0, 1, 2, 50, 1000,\) and so on. Whole numbers are widely used in numbering positions, indexing in programming, and counting objects when zero is included.
2.2.3 Integers (\(\mathbb{Z}\))
Integers include all whole numbers and their negative counterparts. Formally, the set of integers is written as
\[ \mathbb{Z} = \{\dots, -3, -2, -1, 0, 1, 2, 3, \dots\}. \]
Integers have several important properties. They are closed under addition, subtraction, and multiplication, but they are not closed under division; for example, \(1/2 \notin \mathbb{Z}\). Some examples of integers include \(-10, -1, 0, 3, 15,\) and so on. Integers are widely used for representing gains and losses, elevations, temperatures, and positions relative to a reference point.
2.2.4 Rational Numbers (\(\mathbb{Q}\))
Rational numbers are numbers that can be expressed as a fraction \(\frac{p}{q}\) where \(p, q \in \mathbb{Z}\) and \(q \neq 0\). Formally, the set of rational numbers is written as
\[ \mathbb{Q} = \left\{\frac{p}{q} \mid p, q \in \mathbb{Z}, q \neq 0 \right\}. \]
Rational numbers have several important properties. They can be positive, negative, or zero, and they are closed under addition, subtraction, multiplication, and division (except division by zero). They can also be represented as terminating or repeating decimals. Some examples of rational numbers include \(\frac{1}{2}, -\frac{7}{3}, 0.75,\) and \(0.333\ldots\). Rational numbers are widely used in fractions for measurements, probabilities, ratios, and proportional relationships.
2.2.5 Irrational Numbers
Irrational numbers cannot be expressed as a fraction \(\frac{p}{q}\) with integers \(p\) and \(q\), and their decimal expansions are non-terminating and non-repeating. They can be positive or negative and are generally closed under addition, subtraction, multiplication, and sometimes division, but they cannot be represented exactly as a fraction. Examples of irrational numbers include \(\pi, e, \sqrt{2}, \sqrt{3},\) and \(\ln 2\). These numbers are widely used in geometry, such as \(\pi\) for circles, in calculus, in physical constants, and in modeling exponential growth or decay.
2.3 Properties of Real Numbers
The set of real numbers (\(\mathbb{R}\)) follows several fundamental rules that govern arithmetic operations, essential in algebra, calculus, and applied mathematics.
2.3.1 Closure
\(\mathbb{R}\) is closed under addition and multiplication, meaning the sum or product of any two members is still a real number. Division by zero is the only exception.
2.3.2 Commutative
Addition and multiplication are commutative, so the order of numbers does not affect the result: \[ a + b = b + a \quad \text{and} \quad a \cdot b = b \cdot a. \]
2.3.3 Associative
Grouping of numbers does not change the outcome, reflecting the associative rule for both operations: \[ (a + b) + c = a + (b + c) \quad \text{and} \quad (a \cdot b) \cdot c = a \cdot (b \cdot c). \]
2.3.4 Distributive
Multiplication distributes over addition, meaning multiplying a number by a sum equals multiplying each term individually and then adding: \[ a \cdot (b + c) = a \cdot b + a \cdot c. \]
2.3.5 Identity
There exist identities for addition and multiplication. Adding \(0\) or multiplying by \(1\) leaves any number unchanged: \[ a + 0 = a \quad \text{and} \quad a \cdot 1 = a. \]
2.3.6 Inverse
Every number has additive and multiplicative inverses (except zero for multiplication). The additive inverse \(-a\) satisfies \(a + (-a) = 0\), and the reciprocal \(\frac{1}{a}\) satisfies \(a \cdot \frac{1}{a} = 1\).
2.4 Representation on Number Line
Figure Figure 2.2 illustrates a number line, a visual tool representing real numbers in order, which helps to clearly understand their relative positions and relationships.
The number line is a fundamental visual tool in mathematics that allows us to represent real numbers in order. It provides a clear way to understand the relative positions of numbers, including zero as the central reference point, positive numbers to the right, and negative numbers to the left. Rational numbers can be located precisely on the line, while irrational numbers occupy approximate positions between integers, filling in the gaps and illustrating the density of real numbers. The key concepts summarized in Table Table 2.2 highlight the main categories and their properties, helping to organize the understanding of real numbers on the number line.
| Concept | Description | Notes |
|---|---|---|
| Zero as Center | Central reference point separating positive and negative numbers. | Acts as reference for measuring distance and direction (Figure Figure 2.2) |
| Positive Numbers | Numbers greater than zero placed to the right of the origin; includes natural, whole, and positive fractions or decimals. | Magnitude increases to the right of zero |
| Negative Numbers | Numbers less than zero placed to the left of the origin; represents deficits, losses, or positions below reference. | Includes negative fractions and decimals |
| Rational Numbers | Numbers expressible as fractions or terminating/repeating decimals; located exactly on the number line. | Each fraction corresponds to a precise point between integers |
| Irrational Numbers | Numbers not exactly expressible as fractions; approximate positions between integers filling in the gaps. | Examples: π, √2, e; shows density of real numbers |
2.5 Applications of Real Numbers
Real numbers play a crucial role in many fields because they can represent continuous quantities, perform precise measurements, and quantify relationships. Table Table 2.3 summarizes their main applications in science and engineering, economics, and everyday life.
| Domain | Description | Examples |
|---|---|---|
| Science & Engineering | Used to model measurements, physical quantities, and constants such as distance, mass, temperature, and speed; essential for calculations, simulations, and analyses in physics, chemistry, and engineering design. | Distance = 12.5 m, Temperature = 36.6°C, Speed = 60 km/h |
| Economics | Represents prices, costs, profits, interest rates, and statistical data; allows precise modeling of financial transactions, economic trends, and optimization problems. | Price = $25.50, Profit = $1200, Interest rate = 3.5% |
| Daily Life | Appears in counting money, measuring lengths or weights, telling time, and evaluating percentages; supports planning, cooking, shopping, and daily quantitative decision-making. | Buying 3 apples, Cooking 250 g flour, Meeting at 14:30 |
